Application of equivalent analysis to analyzing anti-collision performance of aged ships
-
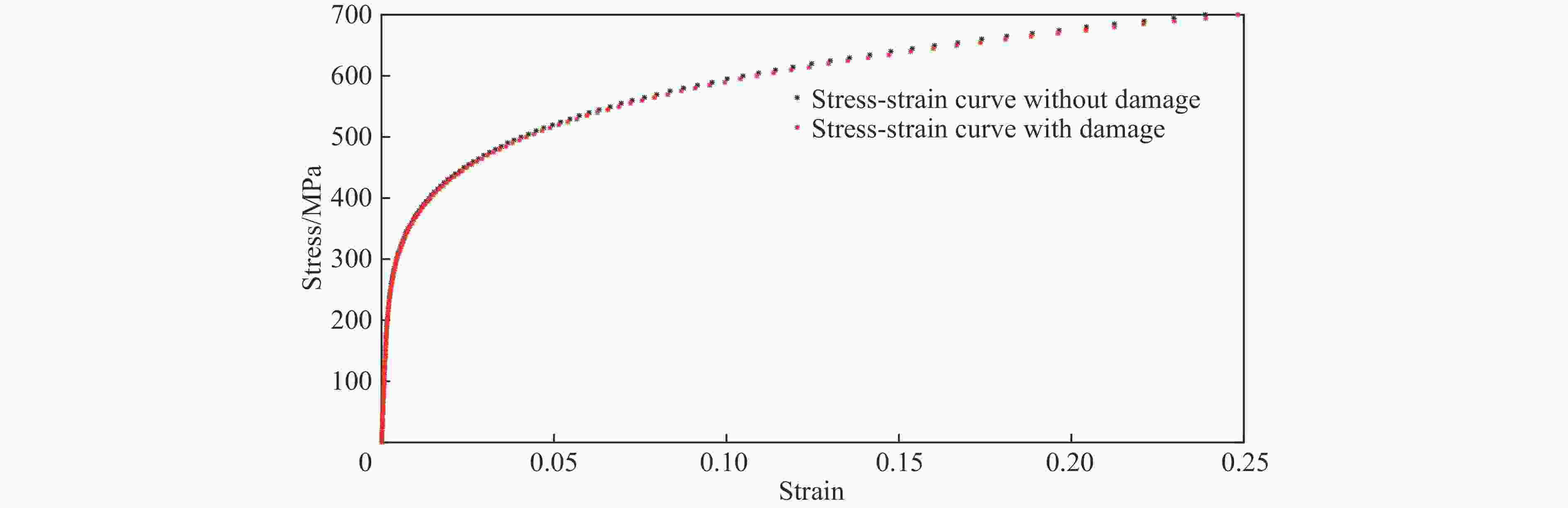
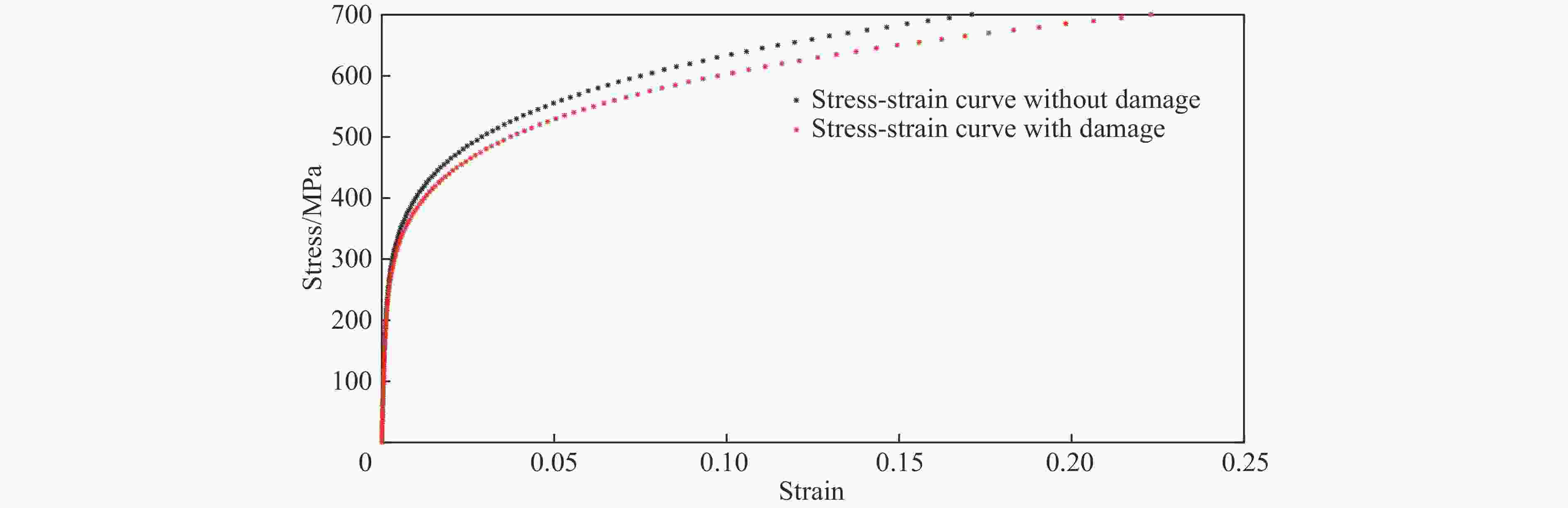
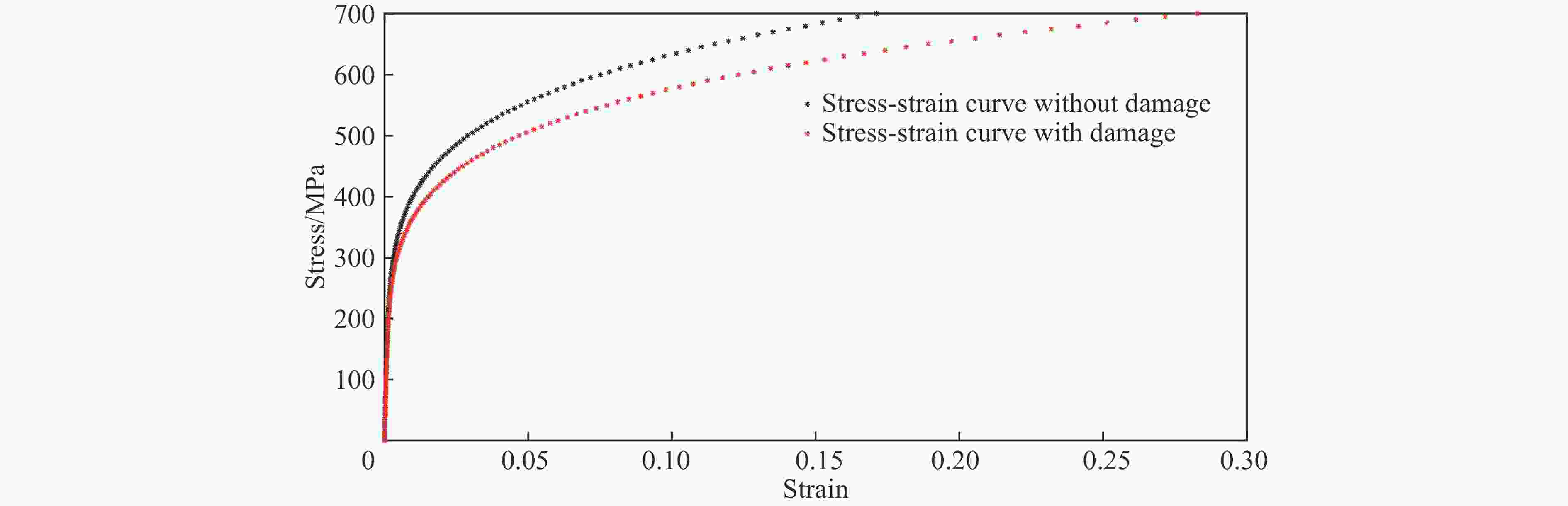
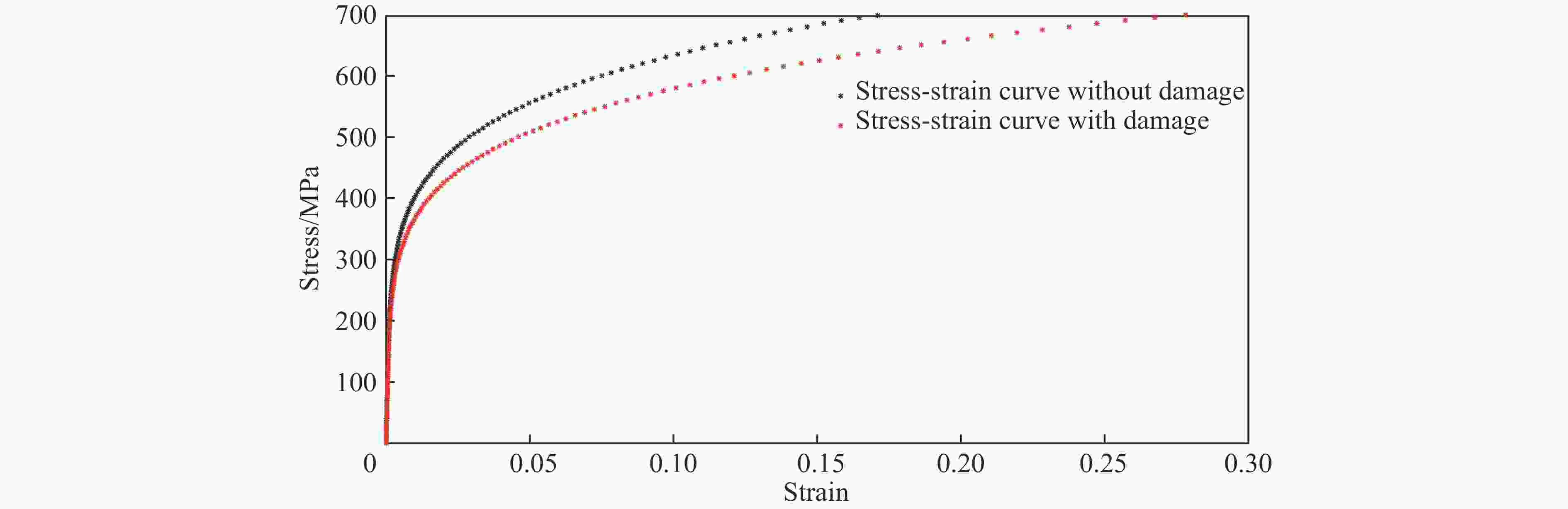
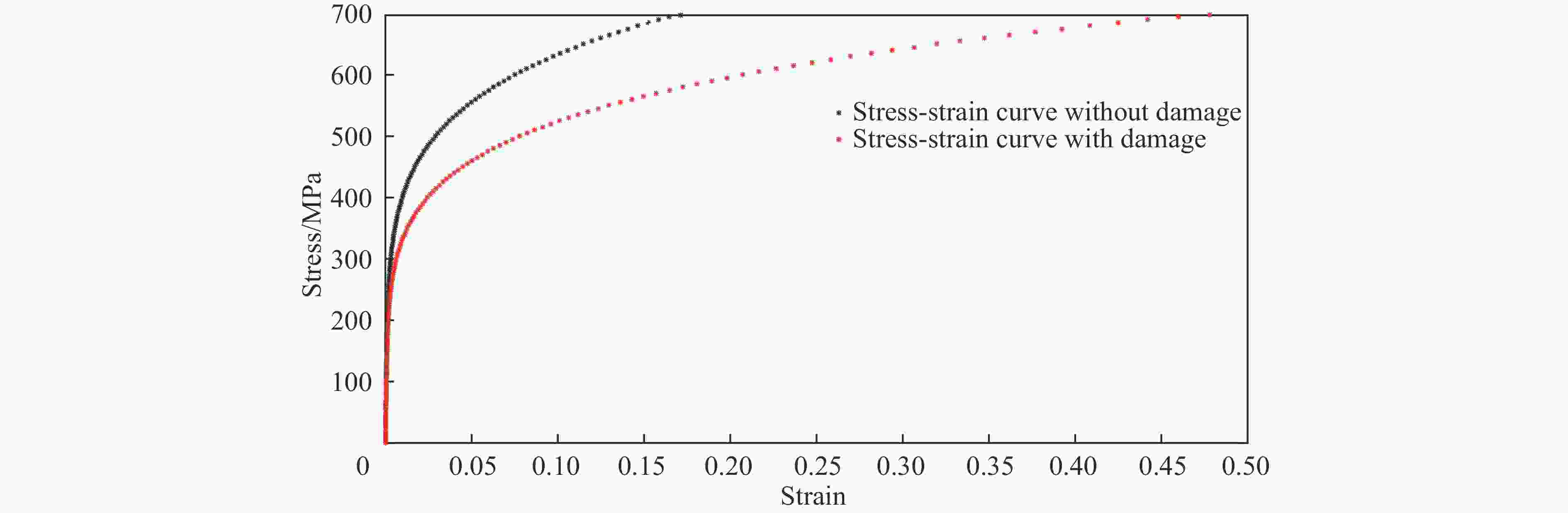
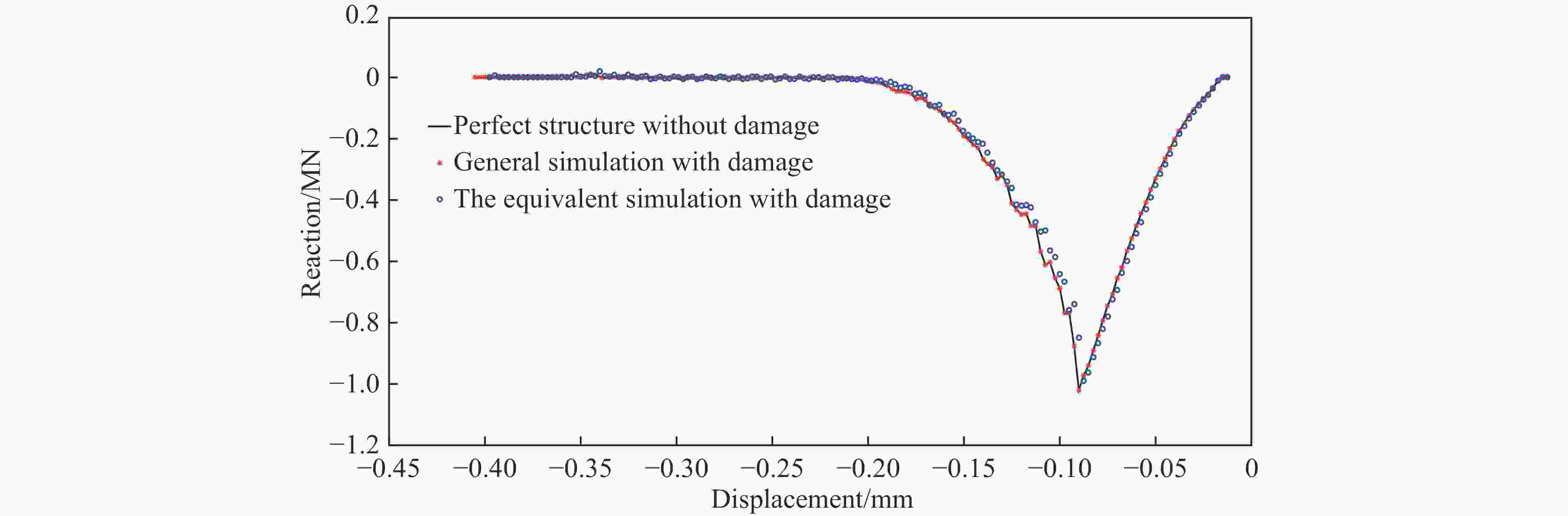
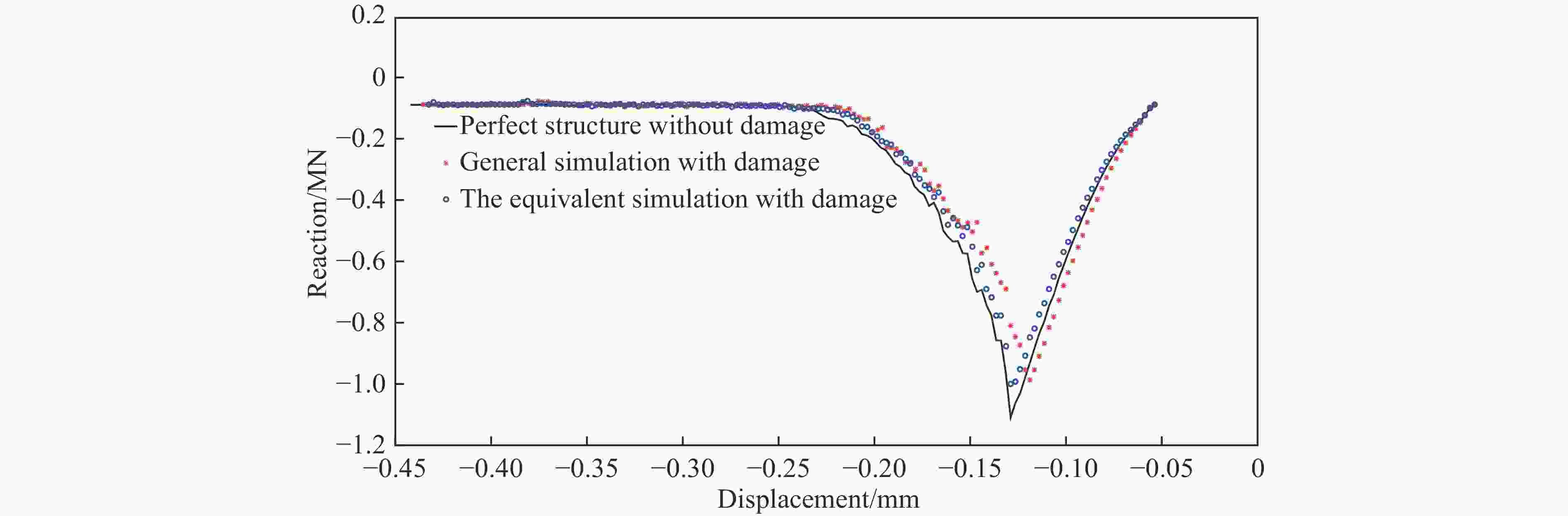
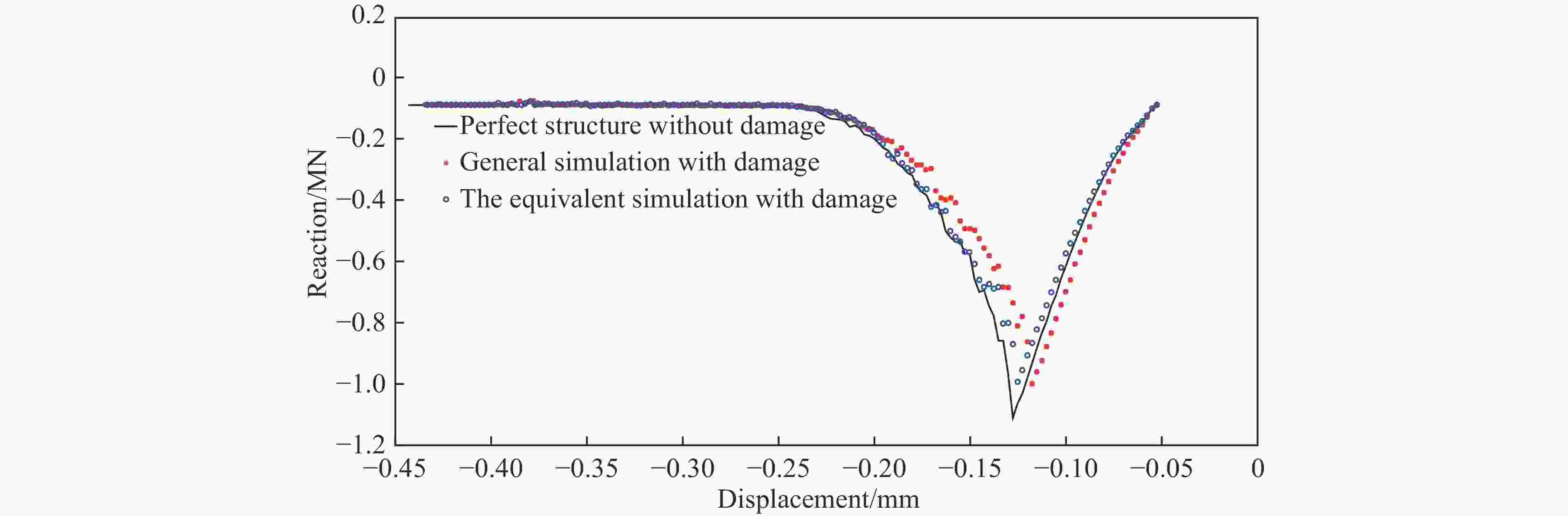
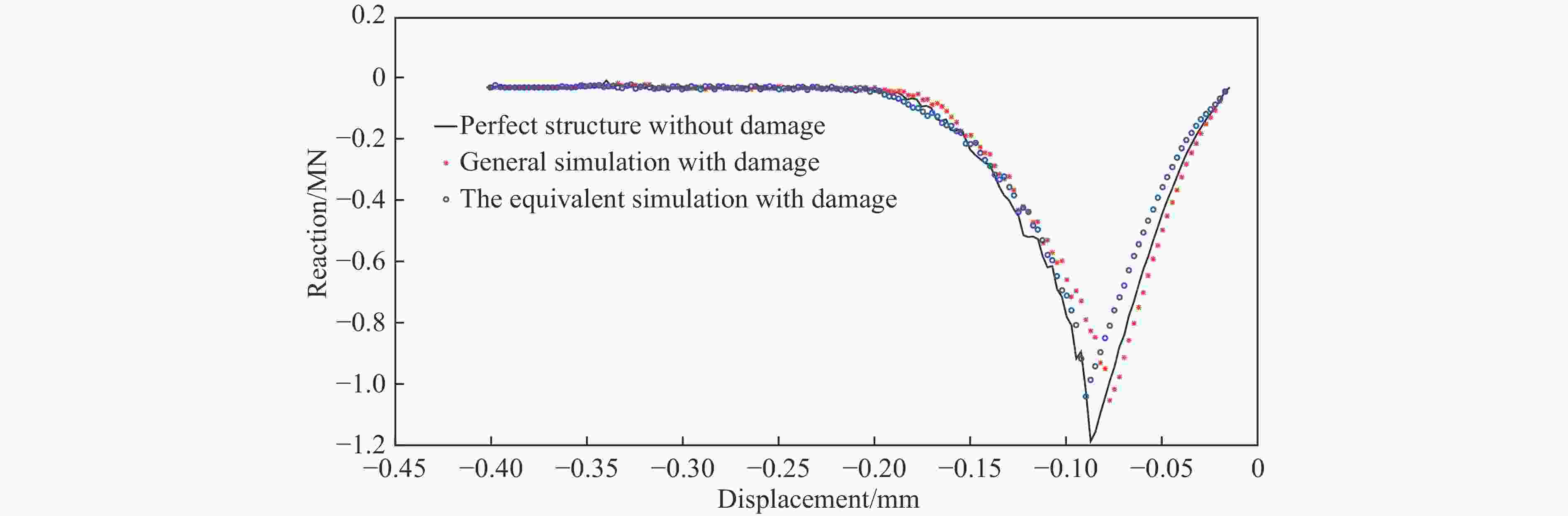
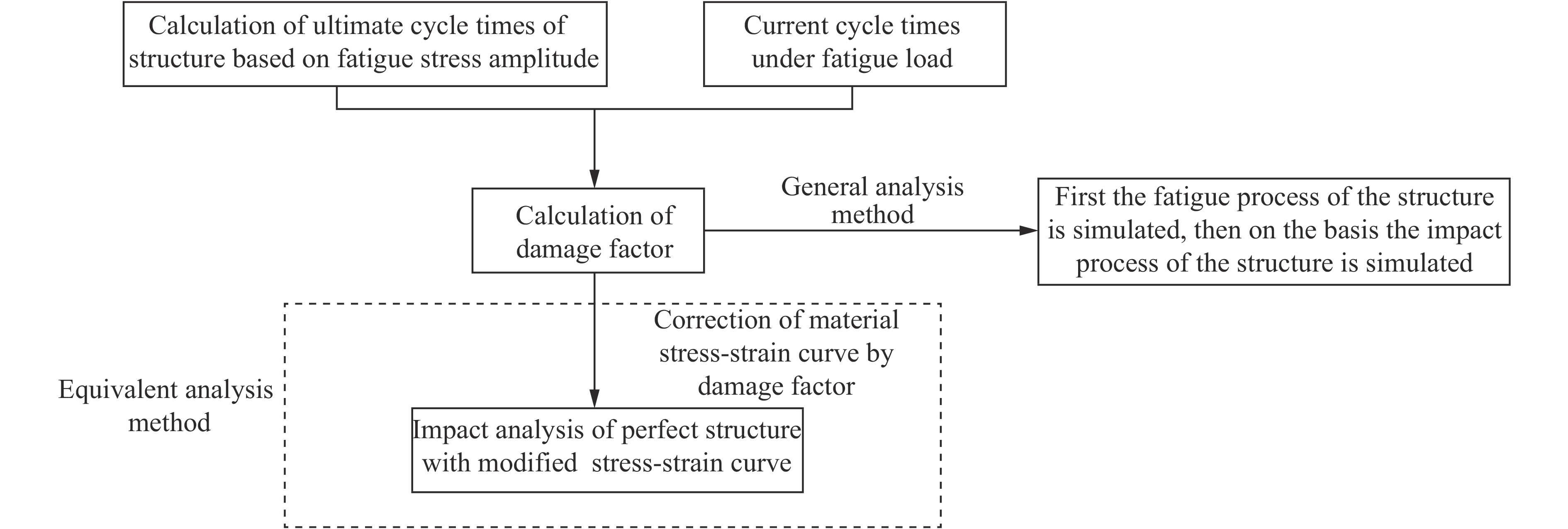
摘要: 为了简化评估结构疲劳损伤后的抗碰撞性能，仿照结构蠕变分析中的等时应力-应变曲线的思想，提出了一种基于应变等效的等效分析法，并与通常的一般分析方法进行了比较。对比分析结果表明：等效分析法与通常的一般分析方法模拟的结构最大抗破坏作用力几乎相同，并且两者模拟的结构破坏能相对误差较小。这验证了等效分析法的有效性，说明等效分析法可用于船舶全寿命期内抗碰撞性能的快速评估。Abstract: In order to simplify the evaluation of the anti-collision performance after structural fatigue damage, an equivalent stress-strain curve method based on strain equivalence was proposed in the same way as the isochronous stress-strain curve in structural creep analysis. And compared with the general analysis, the results of comparative analysis show that the maximum damage reaction force from the equivalence analysis method is almost the same as that from the general analysis method, and the relative error of the structural failure energy simulated by the two methods is relatively small. It validates the effectiveness of the equivalence analysis method. And the equivalence analysis method is more friendly to model and evaluate rapidly the anti-collision performance over the entire life of a ship.
-
Key words:
- fatigue /
- damage /
- collision /
- strain equivalence /
- equivalent stress-strain
-
图 1 疲劳损伤老龄化船舶抗碰撞冲击分流程图
Figure 1. Flowchart of anti-collision analysis for aged ship with fatigue damage
图 3 在工况1中的材料等效应力应变曲线
Figure 3. Equivalent stress-strain curves of material in the load case 1
图 4 在工况2中的材料等效应力应变曲线
Figure 4. Equivalent stress-strain curves of material in the load case 2
图 5 在工况3中的材料等效应力应变曲线
Figure 5. Equivalent stress-strain curves of material in the load case 3
图 6 在工况4中的材料等效应力应变曲线
Figure 6. Equivalent stress-strain curves of material in the load case 4
图 7 在工况5中的材料等效应力应变曲线
Figure 7. Equivalent stress-strain curves of material in the load case 5
图 8 工况1下一般分析法与等效分析法结果对比
Figure 8. Comparison of the general simulation and the equivalent simulation in the load case 1
图 9 工况2下一般分析法与等效分析法结果对比
Figure 9. Comparison of the general simulation and the equivalent simulation in the load case 2
图 10 工况3下一般分析法与等效分析法结果对比
Figure 10. Comparison of the general simulation and the equivalent simulation in the load case 3
图 11 工况4下一般分析法与等效分析法结果对比
Figure 11. Comparison of the general simulation and the equivalent simulation in the load case 4
图 12 工况5下一般分析法与等效分析法结果对比
Figure 12. Comparison of the general simulation and the equivalent simulation in the load case 5
表 1 疲劳损伤分析及碰撞分析工况
Table 1. The load cases of fatigue damage analysis and collision analysis
工况 疲劳工程应力幅/MPa 循环次数 极限循环次数 碰撞冲击速度/(m·s–1) 1 397.5 100 1 680 0.5 2 496.9 50 146 3 80 4 596.2 10 18 5 15 
下载: 导出CSV
表 2 不同工况下一般分析法与等效分析法结果对比
Table 2. Comparison of the general simulation and the equivalent simulation in the different load cases
工况 破坏能/J 一般分析方法与等效分析法相对误差/% 不考虑损伤的结构 考虑损伤的一般分析方法 考虑损伤的等效分析法 1 63 648 62 605 61 338 2.02 2 57 490 60 049 4.45 3 56 177 56 260 0.14 4 56 830 57 900 1.88 5 56 984 54 234 4.82
下载: 导出CSV
-
[1] XUE K G, TORGEIR M. Long-term fatigue damage of ship structures under nonlinear wave loads [J]. Marine Technology, 2002, 39(2): 85–104. [2] 魏东. 舰船结构损伤剩余强度计算与安全评估 [D]. 上海: 上海交通大学, 1999: 67−85. [3] 郭爱宾, 邵文蛟. 船舶结构疲劳强度分析中的几个问题 [J]. 中国造船, 2000, 41(1): 52–59. DOI: 10.3969/j.issn.1000-4882.2000.01.008.GUO Aibin, SHAO Wenjiao. New technologies for fatigue strength analysis of ship structures [J]. Shipbuilding of China, 2000, 41(1): 52–59. DOI: 10.3969/j.issn.1000-4882.2000.01.008. [4] KAZUO T, TAKESHI H, KUNIAKI M. A prediction model for extremely low cycle fatigue strength of structural steel [J]. International Journal of Fatigue, 2007, 29: 887–896. DOI: 10.1016/j.ijfatigue.2006.08.001. [5] 王东海, 庄惠忠, 任惠龙, 等. 船体结构在非线性波浪载荷作用下疲劳累积损伤计算 [J]. 中国造船, 1999, 40(1): 59–67.WANG Donghai, ZHUANG Huizhong, REN Huilong, et al. Fatigue damage calculation of ship structures acted by nonlinear wave bending moments [J]. Shipbuilding of China, 1999, 40(1): 59–67. [6] 韩芸, 催维成, 黄小平, 等. 大型船舶结构的疲劳强度校核方法 [J]. 中国造船, 2007, 48(2): 60–67. DOI: 10.3969/j.issn.1000-4882.2007.02.008.HAN Yun, CUI Weicheng, HUANG Xiaoping, et al. Fatigue strength assessment of large-scale ship structures [J]. Shipbuilding of China, 2007, 48(2): 60–67. DOI: 10.3969/j.issn.1000-4882.2007.02.008. [7] 余小川, 唐永生, 李润培, 等. 8530TEU集装箱船船舯上甲板角隅疲劳寿命预估 [J]. 中国造船, 2006, 47(4): 101–105. DOI: 10.3969/j.issn.1000-4882.2006.04.016.YU Xiaochuan, TANG Yongsheng, LI Runpei, et al. Fatigue life predication of upper deck hatch corners in midship area of a 8530TEU container ship [J]. Shipbuilding of China, 2006, 47(4): 101–105. DOI: 10.3969/j.issn.1000-4882.2006.04.016. [8] XUE L. A unified expression for low cycle fatigue and extremely low cycle fatigue and its implication for monotonic loading [J]. International Journal of Fatigue, 2008, 30(10/11): 1691–1698. DOI: 10.1016/j.ijfatigue.2008.03.004. [9] 田雨, 纪卓尚. 低周疲劳损伤对老化船舶结构剩余极限强度的影响 [J]. 中国造船, 2010, 51(1): 115–120. DOI: 10.3969/j.issn.1000-4882.2010.01.014.TIAN Yu, JI Zhuoshang. Effect of low-cycle-fatigue damage on ultimate strength of aged ships [J]. Shipbuilding of China, 2010, 51(1): 115–120. DOI: 10.3969/j.issn.1000-4882.2010.01.014. [10] 李兆霞. 损伤力学及其应用 [M]. 北京: 科学出版社, 2002: 45−68. [11] LEMAITRE J. A continuous damage mechanics model for ductile fracture [J]. Journal of Engineering Material and Technology, 1985, 107(1): 83–89. DOI: 10.1115/1.3225775. [12] SEWERYN A, BUCYNSKI A, SZUSTA J. Damage accumulation model for low-cycle fatigue [J]. International Journal of Fatigue, 2008, 30(4): 756–765. DOI: 10.1016/j.ijfatigue.2007.03.019. [13] 李营, 吴卫国, 张磊, 等. 基于多轴应力损伤的薄板花瓣型破口形成机理研究 [J]. 爆炸与冲击, 2017, 37(3): 554–559. DOI: 10.11883/1001-1455(2017)03-0554-06.LI Ying, WU Weiguo, ZHANG Lei, et al. Mechanism research of thin plate petaling under local loading based on multiaxial stress damage [J]. Explosion and Shock Waves, 2017, 37(3): 554–559. DOI: 10.11883/1001-1455(2017)03-0554-06. [14] MA C W, XUAN F Z, WANG Z D, et al. Isochronous stress-strain curves of low alloy steel crosss-weld-specimen at high temperature [J]. Acta Metallurgica Sinica, 2004, 17(4): 612–617. [15] The American Society of Mechanical Engineers. Rules for construction of nuclear power plant components [M]. New York: The American Society of Mechanical Engineers, 2007: 251−267. [16] 王自力, 顾永宁. 船舶碰撞动力学过程的数值仿真研究 [J]. 爆炸与冲击, 2001, 21(1): 29–34. DOI: 10.11883/1001-1455(2001)01-0029-06.WANG Zili, GU Yongning. Numerical simulations of ship collisions [J]. Explosion and Shock Waves, 2001, 21(1): 29–34. DOI: 10.11883/1001-1455(2001)01-0029-06. [17] 田雨. 船体结构低周疲劳损伤极限强度研究 [D]. 大连: 大连理工大学, 2010: 32−45. [18] 陈鹏宇, 侯海量, 吴林杰. 水下舷侧多层防护隔舱接触爆炸毁伤载荷特性分析 [J]. 爆炸与冲击, 2017, 37(2): 283–290. DOI: 10.11883/1001-1455(2017)02-0283-08.CHEN Pengyu, HOU Hailiang, WU Linjie. Analysis of the damage load of the underwater contact explosion on multi-layered defend cabins [J]. Explosion and Shock Waves, 2017, 37(2): 283–290. DOI: 10.11883/1001-1455(2017)02-0283-08. [19] Det Norske Veritas. Fatigue assessment of ship structure [S]. Norway: Det Norske Veritas, 2003. -
计量
- 文章访问数: 6266
- HTML全文浏览量: 1879
- PDF下载量: 30
- 被引次数: 0