轮廓爆破孔壁压力峰值计算方法

陈明; 刘涛; 叶志伟; 卢文波; 严鹏

doi:10.11883/bzycj-2018-0171

轮廓爆破孔壁压力峰值计算方法

doi: 10.11883/bzycj-2018-0171

陈明^{1, 2,},
刘涛¹,
叶志伟²,
卢文波^{1, 2},
严鹏^{1, 2}

1.
武汉大学水资源与水电工程科学国家重点实验室，湖北武汉 430072
2.
武汉大学水工岩石力学教育部重点实验室，湖北武汉 430072

基金项目: 国家自然科学基金（51479147，51779193）

详细信息

作者简介:
陈　明（1977－　），男，博士，教授，whuchm@whu.edu.cn

中图分类号: O383
计量
- 文章访问数: 7556
- HTML全文浏览量: 2006
- PDF下载量: 71
- 被引次数: 0
出版历程
- 收稿日期: 2018-05-21
- 修回日期: 2018-07-29
- 网络出版日期: 2019-05-25
- 刊出日期: 2019-06-01

Calculation methods for peak pressure on borehole wall of contour blasting

CHEN Ming^{1, 2
,},
LIU Tao¹,
YE Zhiwei²,
LU Wenbo^{1, 2},
YAN Peng^{1, 2}

1.
State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, Hubei, China
2.
Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, Hubei, China

摘要

摘要: 爆破孔壁压力峰值是进行非流固耦合爆破动力响应分析的重要参数。针对轮廓爆破孔壁压力峰值的计算方法问题，理论分析了爆炸冲击波与弹性壁面的相互作用，推导了空气冲击波与弹性壁碰撞后压力增大倍数的理论解，并采用流固耦合动力有限元数值分析方法，研究了3种岩体介质、2种轮廓爆破常用炸药、5种常用不耦合系数、2种轴向装药系数工况下轮廓爆破的冲击波碰撞压力增大倍数和炮孔壁压力峰值。结果表明：轮廓爆破时，爆炸冲击波与孔壁碰撞后压力增大倍数并不是常值，与炸药特性、孔壁介质条件、不耦合装药系数等因素相关，孔壁压力峰值也与上述因素密切相关。基于模拟的孔壁压力峰值数据的统计分析，并结合理论推导成果及常用爆破孔壁压力峰值计算形式，提出了一种新的轮廓爆破孔壁压力峰值计算方法。
- 轮廓爆破 /
- 孔壁压力峰值 /
- 冲击波 /
- 压力增大倍数 /
- 不耦合系数
Abstract: The peak pressure on the borehole wall is an important parameter for non-fluid solid coupling dynamic analysis of blasting. Aiming at the method for calculating the borehole peak pressure of the contour blasting, the interaction between explosion shock wave and elastic wall is theoretically analyzed, and the theoretical solution of pressure increase multiple after the collision of air shock wave and elastic wall is derived. The fluid solid coupling dynamic finite element numerical analysis method is used to study the blast air shock wave increase factor and borehole peak pressure under three kinds of rock mass media, two kinds of commonly used explosives for contour blasting, five common decoupling coefficients and two kinds of axial charging coefficient conditions. The results show that: the explosion shock wave increase factor of contour blasting is not a constant, and it is related to explosives characteristics, borehole medium conditions, decouple coefficient and other factors, correspondingly, the borehole peak pressure is also related to the above factors. Based on the statistical analysis results of borehole peak pressure simulation, combined with the theoretical deduction results and the commonly used calculation formula for the peak pressure on borehole wall, a new method for calculating borehole peak pressure in the contour blasting is proposed.
- contour blasting /
- borehole peak pressure /
- shock wave /
- pressure increase multiple /
- decouple coefficient

HTML全文

图 1 冲击波反射和折射示意图

Figure 1. Schematic diagram for shock wave reflection and refraction

下载: 全尺寸图片幻灯片

图 2 不同入射压力下p₃/p₁与介质波阻抗的关系

Figure 2. Relationship between p₃/p₁ and wave impedance of transmission medium at different incident pressures

下载: 全尺寸图片幻灯片

图 3 计算模型示意图

Figure 3. Sketch of calculational model

下载: 全尺寸图片幻灯片

图 4 部分典型工况下冲击波与孔壁作用压力时程曲线

Figure 4. Pressure-time curves representing the interaction between shock wave and borehole wall under some typical working conditions

下载: 全尺寸图片幻灯片

图 5 乳化炸药作用下空气冲击波反射压力与入射压力比值

Figure 5. Ratio between reflected pressure and incident pressure of air blast wave induced by emulsion explosive

下载: 全尺寸图片幻灯片

图 6 乳化炸药作用下空气冲击波透射压力与入射压力比值

Figure 6. Ratio between transmission pressure and incident pressure of air blast wave induced by emulsion explosive

下载: 全尺寸图片幻灯片

图 7 压力增大倍数随不耦合系数的变化

Figure 7. Pressure increase multiple varying with decoupling coefficient

下载: 全尺寸图片幻灯片

表 1 岩石物理力学参数

Table 1. Physical and mechanical parameters of rock

岩石种类	密度/(kg·m⁻³)	泊松比	弹性模量/GPa	屈服应力/MPa	切线模量/GPa
粉砂岩	2 170	0.25	6.70	39.20	0.6
石灰岩	2 600	0.25	32.5	72.9	3.0
花岗岩	2 700	0.24	68.00	150.00	7.0
注：Cowper-Symonds 参数 C 取 2.5 s⁻¹，Cowper-Symonds 参数 P 取 4.0。

下载: 导出CSV

表 2 炸药相关参数

Table 2. Parameters of explosive

炸药种类	密度/(kg·m⁻³)	爆速/(m·s⁻¹)	A/GPa	B/GPa	R₁	R₂	ω	E₀/GPa
乳化炸药^[18]	1 300	4 000	214.40	0.182	4.20	0.90	0.15	4.192
多孔粒状铵油炸药^[19]	1 100	2 700	191.21	0.164	4.20	0.90	0.15	2.800

下载: 导出CSV

表 3 乳化炸药作用下空气冲击波反射压力与入射压力比值

Table 3. Ratio between reflected pressure and incident pressure of air blast wave induced by emulsion explosive

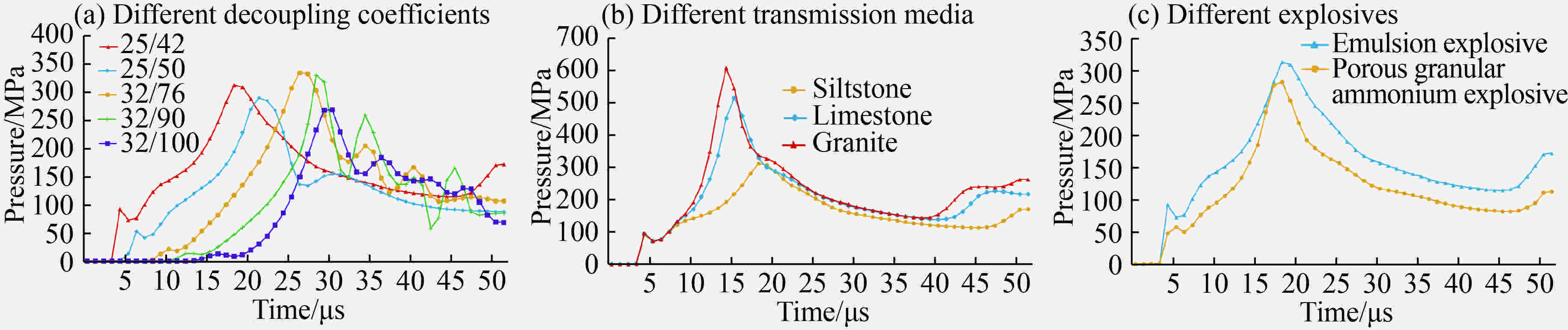
装药条件	不耦合系数	p₁/MPa	p₂/MPa			p₂/p₁
装药条件	不耦合系数	p₁/MPa	粉砂岩	石灰岩	花岗岩	粉砂岩	石灰岩	花岗岩
25/42	1.68	96.9	313	518	610	3.2	5.3	6.3
25/50	2.00	52.3	290	398	437	5.5	7.6	8.4
32/76	2.38	21.3	334	444	488	15.7	20.8	22.9
32/90	2.81	13.5	330	354	355	24.4	26.2	26.3
32/110	3.44	12.9	269	304	308	20.9	23.6	23.9

下载: 导出CSV

表 4 乳化炸药作用下空气冲击波透射压力与入射压力比值

Table 4. Ratio between transmission pressure and incident pressure of air blast wave induced by emulsion explosive

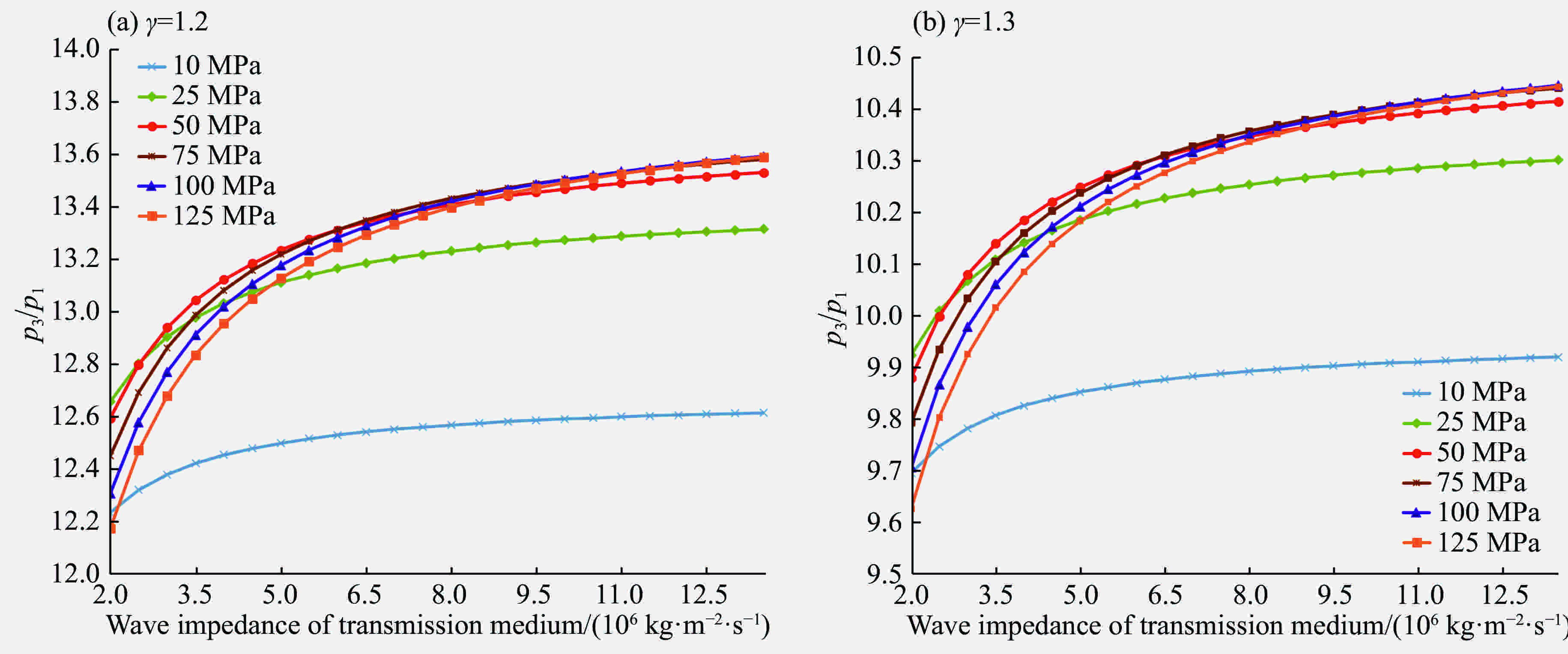
装药条件	不耦合系数	p₁/MPa	P₃/MPa			p₃/p₁
装药条件	不耦合系数	p₁/MPa	粉砂岩	石灰岩	花岗岩	粉砂岩	石灰岩	花岗岩
25/42	1.68	96.9	619	761	858	6.4	7.9	8.9
25/50	2.00	52.3	534	677	695	10.2	12.9	13.3
32/76	2.38	21.3	465	528	502	21.8	24.8	23.6
32/90	2.81	13.5	400	428	402	29.6	31.7	29.8
32/110	3.44	12.9	324	304	310	25.1	23.6	24.0

下载: 导出CSV

表 5 模拟与理论计算孔壁压力峰值对比

Table 5. Comparison of borehole peak pressure between simulation and theoretical calculation

炸药种类	装药条件	孔壁压力峰值/MPa
		数值模拟				理论计算
		粉砂岩	石灰岩	花岗岩	平均值	方法1（n=8）	方法2
乳化炸药	25/42	619	761	858	746	925	792
	25/50	534	677	695	635	802	602
	32/76	465	528	502	498	513	439
	32/90	400	428	402	410	331	319
	32/110	324	304	310	313	196	232
多孔粒状铵油炸药	25/42	521	625	671	606	835	649
	25/50	454	542	551	516	531	493
	32/76	379	413	389	394	339	358
	32/90	322	329	303	318	219	258
	32/110	248	229	233	237	130	187

下载: 导出CSV

表 6 不同装药条件下的孔壁压力峰值

Table 6. Borehole peak pressure under different charge conditions

炸药种类	装药条件	孔壁峰值压力的 0.6 倍/MPa			装药系数 0.6 时的平均压力/MPa			孔壁峰值压力的 0.3 倍/MPa			装药系数 0.3 时的平均压力/MPa
炸药种类	装药条件	花岗岩	石灰岩	粉砂岩	花岗岩	石灰岩	粉砂岩	花岗岩	石灰岩	粉砂岩	花岗岩	石灰岩	粉砂岩
乳化炸药	25/42	515	457	371	527	472	386	257	228	186	286	263	225
	25/50	417	406	320	410	411	334	208	203	160	222	223	219
	32/76	301	317	279	287	300	277	151	158	140	171	178	165
	32/90	241	257	240	234	244	232	121	128	120	136	142	136
	32/110	186	182	194	175	178	180	93	91	97	100	102	104
多孔粒状铵油炸药	25/42	403	375	313	388	382	318	201	188	156	214	211	180
	25/50	331	325	272	316	315	274	165	163	136	170	172	157
	32/76	233	248	227	216	231	218	117	124	114	126	133	127
	32/90	182	197	193	177	183	178	91	99	97	102	104	103
	32/110	140	137	149	130	131	135	70	69	75	75	75	76

下载: 导出CSV

表 7 不同条件下的压力增大倍数

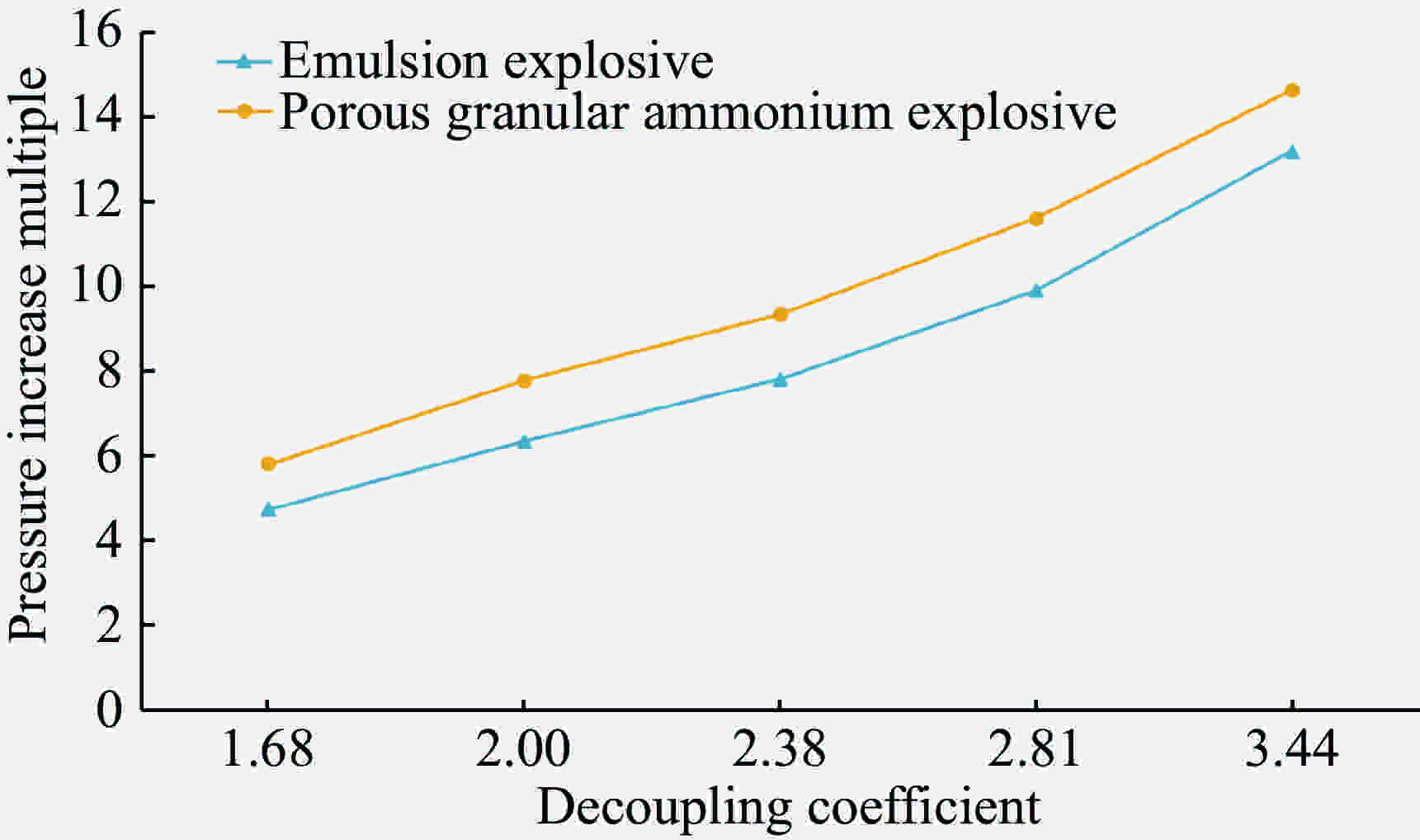
Table 7. Pressure increase multiples under different conditions

装药条件	不耦合系数	n'
装药条件	不耦合系数	乳化炸药	多孔粒状铵油炸药
25/42	1.68	4.7	5.8
25/50	2.00	6.3	7.8
32/76	2.38	7.8	9.3
32/90	2.81	9.9	11.6
32/110	3.44	13.2	14.6

下载: 导出CSV

参考文献(19)

[1]	朱瑞赓, 王雪峰. 不耦合装药爆破孔壁压力计算: 一 [J]. 爆破, 1990, 7(3): 1–4.
[2]	费鸿禄, 李守巨, 何庆志. 光面爆破装药不偶合系数的计算 [J]. 爆炸与冲击, 1992, 12(3): 270–274. DOI: 10.11883/1001-1455(1992)03-0270-05. FEI Honglu, LI Shouju, HE Qingzhi. Calculation of de-coupling coefficient of smooth blasting charge [J]. Explosion and Shock Waves, 1992, 12(3): 270–274. DOI: 10.11883/1001-1455(1992)03-0270-05.
[3]	王志亮, 李永池. 工程爆破中径向水不耦合系数效应数值仿真 [J]. 岩土力学, 2005, 26(12): 1926–1930. DOI: 10.3969/j.issn.1000-7598.2005.12.012. WANG Zhiliang, LI Yongchi. Numerical simulation on effects of radial water-decopling coefficient in engineering blast [J]. Rock and Soil Mechanics, 2005, 26(12): 1926–1930. DOI: 10.3969/j.issn.1000-7598.2005.12.012.
[4]	凌伟明. 岩石爆破炮孔孔壁压力的试验研究 [J]. 矿冶, 2004, 13(4): 13–16. DOI: 10.3969/j.issn.1005-7854.2004.04.004. LING Weiming. Experimental research on explosion pressure on the wall of a borehole in rock [J]. Mining and Metallurgy, 2004, 13(4): 13–16. DOI: 10.3969/j.issn.1005-7854.2004.04.004.
[5]	王伟, 李小春, 石露, 等. 深层岩体松动爆破中不耦合装药效应的探讨 [J]. 岩土力学, 2008, 29(10): 2837–2842. DOI: 10.3969/j.issn.1000-7598.2008.10.046. WANG Wei, LI Xiaochun, SHI Lu, et al. Discussion on decoupled charge loosening blasting in deep rock mass [J]. Rock and Soil Mechanics, 2008, 29(10): 2837–2842. DOI: 10.3969/j.issn.1000-7598.2008.10.046.
[6]	刘云川, 汪旭光, 刘连生, 等. 不耦合装药条件下炮孔初始压力计算的能量方法 [J]. 中国矿业, 2009, 18(6): 104–107. DOI: 10.3969/j.issn.1004-4051.2009.06.031. LIU Yunchuan, WANG Xuguang, LIU Liansheng, et al. An energy method for calculate borehole pressure under decoupled charging [J]. China Mining Magazine, 2009, 18(6): 104–107. DOI: 10.3969/j.issn.1004-4051.2009.06.031.
[7]	FELDGUN V R, KARINSKI Y S, YANKELEVSKY D Z. Experimental simulation of blast loading on structural elements using rarefaction waves-theoretical analysis [J]. International Journal of Impact Engineering, 2017, 102: 86–101. DOI: 10.1016/j.ijimpeng.2016.12.010.
[8]	SAHARAN M R, MITRI H S. Numerical procedure for dynamic simulation of discrete fractures due to blasting [J]. Rock Mechanics and Rock Engineering, 2008, 41(5): 641–670. DOI: 10.1007/s00603-007-0136-9.
[9]	OZGUR Yilmaz, TUGRUL Unlu. Three dimensional numerical rock damage analysis under blasting load [J]. Tunnelling and Underground Space Technology, 2013, 38: 266–278. DOI: 10.1016/j.tust.2013.07.007.
[10]	YI C, JOHANSSON D, GREBER J. Effects of in-situ stresses on the fracturing of rock by blasting [J]. Computers and Geotechnics, 2018, 104: 321–330. DOI: 10.1016/j.compgeo.2017.12.004.
[11]	HENRYCH J. The dynamics of explosion and its use [M]. New York: Elsevier Scientific Publishing Company, 1979.
[12]	钮强. 岩石爆破机理 [M]. 沈阳: 东北工学院出版社, 1990: 18−19.
[13]	王礼立. 应力波基础 [M]. 北京: 国防工业出版社, 2005: 45−47.
[14]	李维新. 一维不定常流与冲击波 [M]. 北京: 国防工业出版社, 2003: 204−210.
[15]	戴俊. 岩石动力学特性与爆破理论 [M]. 北京: 冶金工业出版社, 2013: 88−91.
[16]	Livermore Software Technology Corporation. LS-DYNA theoretical manual [M]. California: Livermore Software Technology Corporation, 2003: 1012−1013.
[17]	水利水电科学研究院. 岩石力学参数手册 [M]. 北京: 水利电力出版社, 1991: 429−434.
[18]	夏祥, 李海波, 李俊如, 等. 岭澳核电站二期工程基岩爆破安全阈值分析 [J]. 岩土力学, 2008, 29(11): 2945–2951. DOI: 10.3969/j.issn.1000-7598.2008.11.010. XIA Xiang, LI Haibo, LI Junru, et al. Research on vibration safety threshold for rock under blasting excavation [J]. Rock and Soil Mechanics, 2008, 29(11): 2945–2951. DOI: 10.3969/j.issn.1000-7598.2008.11.010.
[19]	刘军. 岩体在冲击载荷作用下的各向异性损伤模型及其应用 [J]. 岩石力学与工程学报, 2004, 23(4): 635–640. DOI: 10.3321/j.issn:1000-6915.2004.04.020. LIU Jun. Anisotropic damage model and its application to rock materials under impact load [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(4): 635–640. DOI: 10.3321/j.issn:1000-6915.2004.04.020.