平面激波加载下砂墙结构的冲击响应特性

王宏亮; 田宙; 浦锡锋; 姚成宝; 寿列枫

doi:10.11883/bzycj-2018-0179

平面激波加载下砂墙结构的冲击响应特性

doi: 10.11883/bzycj-2018-0179

王宏亮^1,,
田宙¹,
浦锡锋¹,
姚成宝^{1, 3},
寿列枫^{1, 2}

1.
西北核技术研究院，陕西西安 710024
2.
北京理工大学爆炸科学与技术国家重点实验室，北京 100081
3.
北京大学数学学院，北京 100871

详细信息

作者简介:
王宏亮（1983－　），女，博士研究生，助理研究员，wanghl_2105@163.com

中图分类号: O383
计量
- 文章访问数: 5466
- HTML全文浏览量: 1873
- PDF下载量: 59
- 被引次数: 3
出版历程
- 收稿日期: 2018-05-25
- 修回日期: 2018-07-23
- 网络出版日期: 2019-06-25
- 刊出日期: 2019-07-01

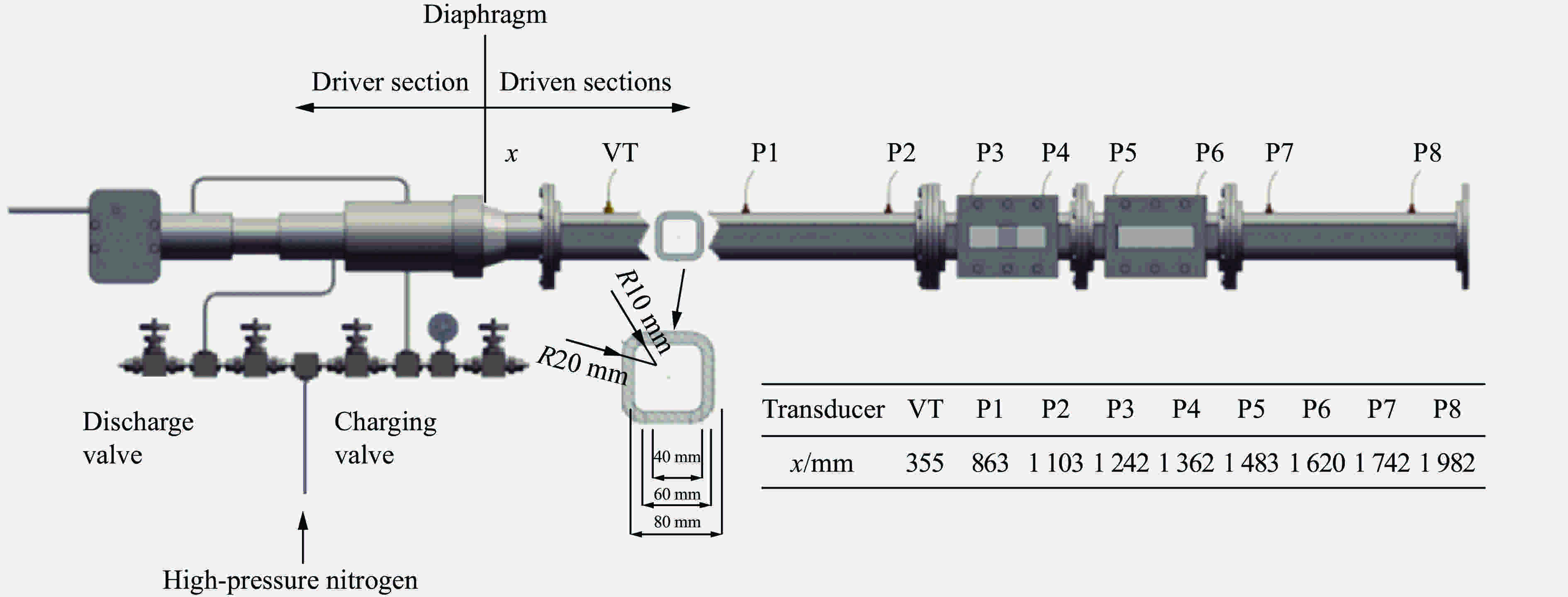
Dynamic responses of sand wall under planar shock loading

1.
Northwest Institute of Nuclear Technology, Xi’an 710024, Shaanxi, China
2.
State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China
3.
School of Mathematical Sciences, Peking University, Beijing 100871, China

摘要

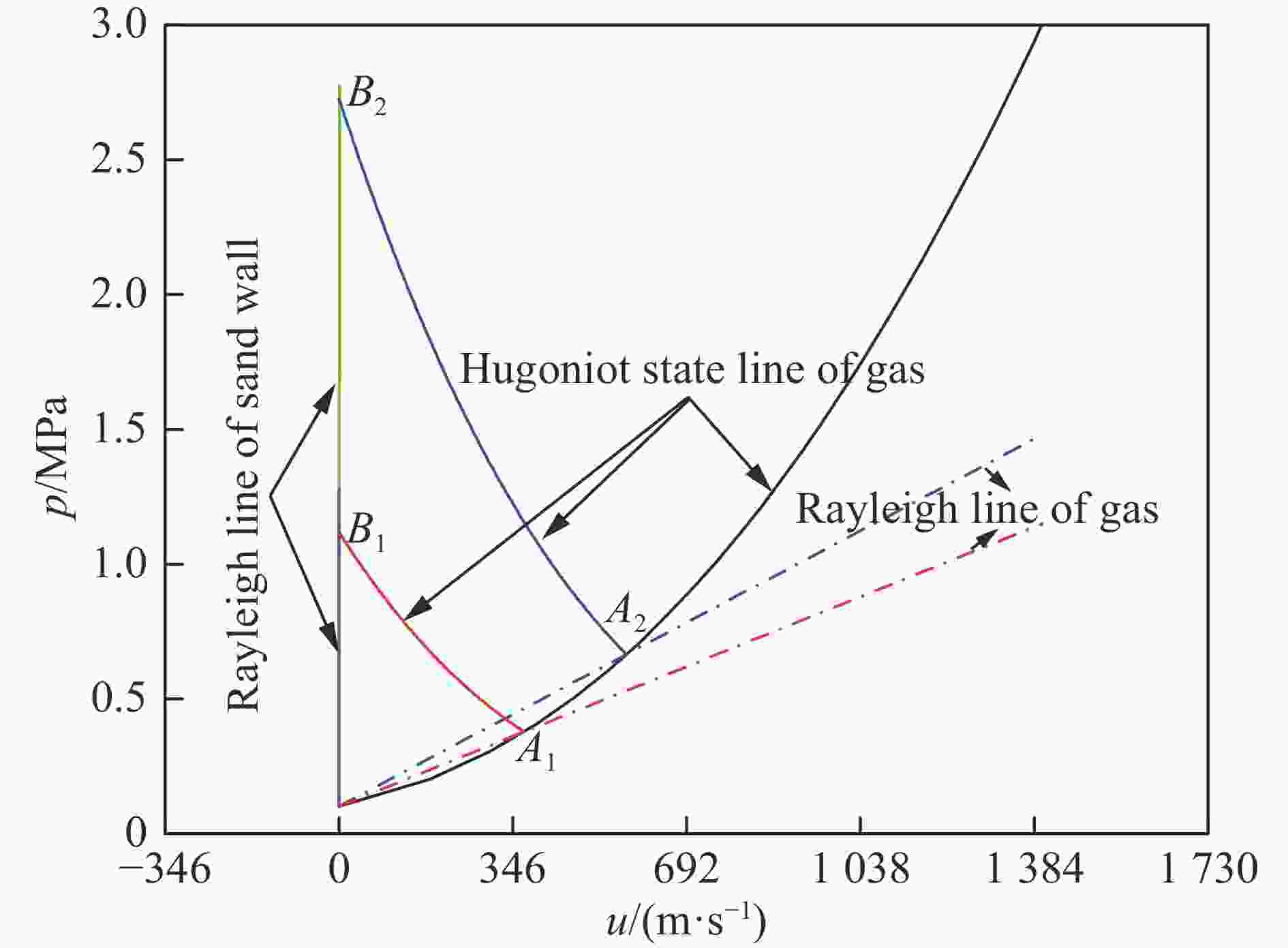
摘要: 砂墙结构在爆炸安全防护领域具有广泛应用，为了研究激波加载下砂墙结构的冲击响应特性，基于水平激波管实验装置，开展平面激波冲击砂墙结构系列实验，采用高速纹影摄像系统捕捉流场中激波波系的演化过程和砂墙结构的运动过程。入射激波马赫数为1.827～2.413，相应入射激波载荷强度为0.378～0.724 MPa。砂墙结构利用铁砂、矾土、石英砂3种实验用砂制备，所制备砂墙结构孔隙度分别为56.6%、69.3%、56.6%。高速纹影照片显示：平面激波冲击砂墙结构发生反射和透射，伴随入射激波和透射激波的传播，在百微秒内，砂墙未产生显著运动，表现出显著的类固体动力学响应特性。基于冲击理论，确定了铁砂墙、矾土砂墙、石英砂墙的线性冲击关系，冲击关系中线性常数λ值量级为100，根据凝聚介质实用状态方程推断：较低强度载荷冲击作用下，砂墙主要产生体积变形，而由冲击引起的热能效应则可以忽略。
- 平面激波 /
- 砂墙 /
- 冲击响应 /
- 高速纹影
Abstract: In order to study the dynamic response behavior of a sand wall in the process of the shock-sand wall interaction, experiments are carried out in a horizontal shock tube. A high-speed schlieren imaging system is used to capture the instantaneous structures of shock wave and moving process of the sand wall in the flow field. The incident shock Mach number ranges from 1.827 to 2.413, and the incident shock strength ranges from 0.378 MPa to 0.724 MPa. Three different kinds of sand walls are constructed using well-size-distributed iron sand, bauxite sand and quartz sand, the corresponding porosities of these sand walls are 56.6%, 69.3% and 56.6%, respectively. High-speed schlieren photographs show that regular reflection occurs when the incident shock wave impacts the sand wall. Moreover, the sand wall does not move significantly until the hundreds of microseconds after the onset of the interaction, indicating that the dynamic response behavior of the sand wall is similar to that of a rigid body. Basing on the shock wave theory, the Hugoniot relations for sand walls made from three different materials are established. The bulk elastic moduli of iron-, bauxite- and quartz-sand walls are 0.913, 0.478, and 0.225 GPa, respectively. The constant λ in the Hugoniot relations is on the order of 100. It is concluded that the relatively low shock impacting majorly leads to the volume deformation of the sand wall, and the heat effect of the sand wall caused by shock loading may be unimportant.
- planar shock wave /
- sand wall /
- dynamic response /
- high-speed schlieren

HTML全文

在不同厚度飞片相互撞击过程中，冲击波从材料自由表面反射，材料内部或近自由表面区域受到卸载稀疏波作用，如果延性金属材料内部的拉伸应力足够高，以孔洞形式的损伤将经历成核、增长和汇合演化过程，当微孔洞的数量和尺寸增长到一定阶段之后，它们的(强)相互作用就变得十分重要，这时，微孔洞之间的汇合以及细观尺度上的不稳定性将导致材料的最终破坏。实验结果分析表明：在强动态拉伸载荷作用下，孔洞汇合可能开始于孔洞成核后，并伴随损伤演化整个过程，此时，孔洞汇合对孔洞增长起到抑制作用^[1]；孔洞增长不仅以孤立孔洞形式增长，而且可能主要以孔洞汇合形式增长^[2]。因此，在连续损伤模型中耦合孔洞汇合的影响，有助于精细描述延性材料损伤演化过程、分析不同因素对损伤演化过程的影响^[3-5]。

由于微孔洞之间强相互作用在理论分析方面遇到的困难，至今还没有一个较好的模型对孔洞汇合进行合理的描述^[6]。一个合理的孔洞汇合模型不仅应给出开始汇合的准则，而且还应该对其间的应力松弛或材料软化予以适当的描述。当然要作以上分析是非常困难的，因而许多学者通过数值模拟两个孔洞之间的相互关系给出一些半经验性的孔洞汇合临界条件，即以孔洞之间的相互距离或临界损伤作为孔洞汇合的临界判据：T.Pardoen等^[7]认为孔洞汇合的临界损伤依赖于微孔洞初始体积分数、加载应力三轴度及微孔洞形状；M.F.Horstemeyer等^[8]采用微力学有限元计算方法研究准静态加载条件下两个孔洞之间的贯通行为，指出孔洞开始汇合的临界韧带距离依赖于边界条件和材料韧性，且约为2~8倍的孔洞直径；E.T.Seppala等^[9]采用分子动力学方法对动态条件下铜材料中孔洞的增长和聚集行为进行了数值模拟，结果显示临界韧带距离约为0.5倍孔洞直径时，孔洞周围塑性区相遇，孔洞增长速度突然增加，从而导致孔洞汇合。此外，在理论分析方面，P.F.Thomson^[10]简化了塑性极限载荷的滑移线场解, 提出了一种孔洞汇合的判断准则；D.L.Tonks等^[11]进一步用高应变率下的随机滤渗理论解释了断裂点, 提出了一种通过孔洞聚集形成小尺度孔洞簇增长的模型；T.Pardoen等^[12]讨论了基于微结构机理的孔洞汇合模型的进展，并指出因微孔洞汇合引起金属断裂过程最后阶段的模拟需要反映微结构演化重要信息的延性损伤模型。在过去的十多年里，孔洞汇合研究的重要进步是基于简单的孔隙度准则或临界应变准则发展为基于微观机理认识的进展。不过，目前的研究主要是分析相同大小孔洞间的汇合，还需要将其扩展到更一般的情况，即不同大小的孔洞之间的汇合问题；此外，对于孔洞汇合最初发生于相同的大孔洞之间、小孔洞之间亦或不同大小孔洞之间，目前还没有确切的说明。同时，现有的孔洞汇合模型严格来说是描述孔洞变形对损伤的影响，且一般采用指数函数来唯像描述孔洞汇合后损伤的快速增长^[13]，而根据损伤度的定义，孔洞汇合时刻并没有引起损伤的改变，但实际却促进了损伤的快速发展，目前对于其物理机理至今仍处于探讨之中。

本文中基于两个不同大小孔洞之间的几何关联，给出孔洞汇合的临界判定方法，并基于能量守恒原理，揭示孔洞汇合后引起损伤增长的物理机理，同时，耦合孔洞汇合的影响，采用数值方法讨论孔洞汇合对延性金属层裂损伤演化特性的影响。

1. 孔洞汇合的判定方法

现阶段对于孔洞汇合机理的分析已经成为层裂损伤研究的主要关注点^[14-16]，不过，现有的汇合判据还存在不足之处：距离判据没有考虑损伤的影响；损伤(或应力、应变)判据没有考虑孔洞大小的影响。此外，在强动态加载情况下，孔洞增长过程不易发生塑性局域化，孔洞几乎仍然保持球形形状，孔洞汇合时，损伤度较高，且孔洞之间产生相互接触，这可能是因为惯性对孔洞间的颈缩起了阻碍作用^[14]，这种情况在一些层裂实验^[17-18]以及裂纹扩展实验^[19]中均可以观测到(见图 1)。因汇合前孔洞基本保持球形形状，且相邻孔洞间距较小，则因孔洞间基体材料颈缩引起孔洞变化对损伤的影响较小，因此相对于基于颈缩过程分析得到的孔洞汇合判据，采用孔洞间距离判据更加简单、适宜。

图 1 孔洞汇合实验结果

Figure 1. Void coalescence by direct impingement in tantalum

下载: 全尺寸图片幻灯片

为此，我们考虑两个空心球壳之间的几何关联(见图 2)，并定义孔隙度：

$\alpha = {b^3}/({b^3} - {a^3})$

图 2 孔洞间的几何关系

Figure 2. Porous material model

下载: 全尺寸图片幻灯片

则孔洞间距离可以表示为：

$d = \left[ {{{\left( {\frac{\alpha }{{\alpha - 1}}} \right)}^{1/3}} - 1} \right]\left( {{a_1} + {a_2}} \right)$

(1)

本文中仍将采用孔洞间的距离作为孔洞开始汇合的判据，并根据实验结果确定临界孔洞距离d_cr(根据文献[2]的实验结果，本文中采用d_cr=4min(a₁, a₂))，即当两个孔洞间的距离d≤d_cr时，认为相应的两个孔洞之间发生汇合。与现有的距离计算方法不同，公式(1)不仅包含了孔洞大小，同时也包含了损伤度的影响。众所周知，在相同加载条件下小孔洞周边的应力集中更明显，同时，在大孔洞不变的情况下，小孔洞越小，其对应的损伤度越小，因此，孔洞汇合应该首先发生于最大孔洞与最小孔洞之间，这也从侧面说明了实验最后的观测结果以及相关的数值模拟结果中小孔洞很少的可能原因。

取a₁=ka₂、d=ma₁=mka₂，则公式(1)可以转化为损伤度D的表达式：

$D = \frac{{\alpha - 1}}{\alpha } = {\left[ {\frac{{1 + k}}{{1 + \left( {m + 1} \right)k}}} \right]^3}$

(2)

两个特例：

当m=k=1时，D=0.296，这与分析层裂问题时常采用的临界断裂损伤度相近；

当m=1时，有 $D = \frac{{\alpha - 1}}{\alpha } = \mathop {\lim }\limits_{k \to \infty } {\left[{\frac{{1 + k}}{{1 + 2k}}} \right]^3} = 0.125$ 。

这与L.M.Brown等^[20]和D.L.Tonks等^[11]分析的孔洞汇合初始临界损伤度完全一致，换句话说，文献[11, 20]中所采用的孔洞汇合临界损伤度只是我们所讨论的特例，图 3显示了孔洞汇合损伤度与汇合孔洞相对大小比值之间的对应关系，同时，计算结果也显示了孔洞汇合损伤度的取值范围在0.296~0.125之间。

图 3 孔洞相对大小与孔洞汇合临界损伤度关系

Figure 3. Critical damage for void coalescence vs. relative difference in size between two voids

下载: 全尺寸图片幻灯片

当k=10时，图 4显示了孔洞汇合损伤度与孔洞距离之间的对应关系。综合分析图 3~4和公式(2)可知，孔洞汇合是损伤、孔洞相对大小以及孔洞间距离综合影响的结果。对于材料性质、应力状态对孔洞汇合的影响：一方面，损伤与应力、应变耦合在一起^[21]，损伤对孔洞汇合的影响也间接地反映了材料性质和应力状态对孔洞汇合的影响；另一方面，针对强加载情况，直至汇合前孔洞仍基本保持球形形状，因此，材料的性质和应力状态的影响主要反映在汇合前的孔洞增长过程。

图 4 孔洞间距离与孔洞汇合临界损伤度关系

Figure 4. Critical damage for void coalescence vs. distance between two voids

下载: 全尺寸图片幻灯片

2. 孔洞汇合对损伤增长的影响

现有的孔洞汇合判据(模型)，包括距离判据或应力、应变判据(如Tonks模型和Thomason模型)，都是基于孔洞间材料颈缩过程得到的，描述的是汇合前孔洞的变化情况，而没有涉及孔洞汇合后对损伤的影响。对于在强动态拉伸载荷作用下，因汇合前孔洞基本保持球形形状，且孔洞间距很小，则孔洞间材料颈缩过程对损伤的影响减弱。目前已经有大量的文献研究孔洞间材料颈缩过程对损伤的影响，因此本文中忽略颈缩的影响，主要讨论孔洞汇合后对损伤度增长的影响。

孔洞汇合遵循能量守恒原则，即在孔洞汇合前后有：

${E_{\rm{i}}} + {E_{\rm{k}}} = {{\bar E}_{\rm{i}}} + {{\bar E}_{\rm{k}}}$

(3)

式中：E_i、E_k分别表示孔洞周围基体材料的内能和动能，E_i、E_k为孔洞汇合后对应的值。

对于内能的变化，在绝热条件下有：

$\dot e = - p\frac{{\partial v}}{{\partial t}}$

(4)

式中：e、p、v分别表示单位体积的内能、压力和材料的相对比容。因基体材料不可压假设，并且假设孔洞汇合并没有改变材料内部的孔隙度，因此有：

$\frac{{\partial v}}{{\partial t}} = 0$

即孔洞汇合时内能守恒。

此外，针对单一的空心球壳，设r₀为基体材料内部的Lagrange坐标，相应的r为Euler坐标，a₀、α₀为初始孔洞半径和初始孔隙度，则根据不可压缩假设有^[21]：

${r^3} = r_0^3 - a_0^3\frac{{{\alpha _0} - \alpha }}{{{\alpha _0} - 1}}$

(5)

$\dot r = \frac{{a_0^3}}{{3{r^2}({\alpha _0} - 1)}}\dot \alpha$

(6)

则其动能可以表示为：

${E_{\rm{k}}} = \frac{1}{2}\int_a^b {4{\rm{ \mathsf{ π} }}\rho {r^2}{{\dot r}^2}{\rm{d}}r = \frac{{2{\rm{ \mathsf{ π} }}\rho }}{9}\frac{{a_0^6}}{{{{\left( {{\alpha _0} - 1} \right)}^2}}}\left[ {1 - {{\left( {\frac{{\alpha - 1}}{\alpha }} \right)}^{^{1/3}}}} \right]{{\dot \alpha }^2}\frac{1}{a}}$

(7)

损伤材料内部含有大量不同大小的孔洞，不妨将其等效为不同大小的空心球壳，且每一个空心球壳的内外径之比相同，即α和α₀相同，这样不仅方便损伤的计算，而且可以间接地考虑孔洞之间的相互作用^[22-23]。因孔洞汇合前后α、α₀和基体材料的密度ρ不变，则根据动能守恒原则，由公式(7)有：

$\dot {\bar \alpha} = \dot \alpha \sqrt {\frac{{\sum ({n_i}/{a_i})}}{{\sum ({N_j}/{R_j})}}}$

(8)

式中： ${\dot \alpha }$ 、a_i以及n_i为孔洞汇合前的孔隙度增长率、孔洞半径以及对应的孔洞数， ${\dot {\bar \alpha} }$ 、R_j以及N_j为孔洞汇合后的值。式(8)显示了因孔洞汇合引起的孔洞数减少、孔洞尺寸增加，从而造成孔隙度增长速度的提高，这也明确了因孔洞汇合引起损伤增长的物理机理。

3. 孔洞汇合影响的数值分析

对于延性金属层裂损伤的研究，我们已经建立了反映初始损伤及孔洞大小、惯性和材料弹塑性效应的层裂损伤物理统计描述方法^[22]，同时，基于材料晶粒尺寸与潜在孔洞成核数之间的关系，构建了一个耦合晶粒尺寸影响的孔洞成核方程^[24]。在前期工作的基础上，我们将孔洞汇合的影响引入到已有的层裂损伤模型中，即在计算损伤演化过程中，根据公式(1)，当孔洞间距离d≤d_cr时，采用公式(8)调整孔隙度的增长率，同时结合相关文献对实验结果的分析^[2]，探讨孔洞汇合对层裂损伤演化过程的影响。层裂实验靶材料分别选用30、60、100和200 μm等4种晶粒尺寸的高纯铜，靶厚均为4 mm；飞片材料为石英(Z-cut quartz)，厚度约2 mm，飞片速度约131 m/s。对4种靶材料的实验结果进行了数值模拟，同时，在30 μm晶粒尺寸高纯铜的计算模型中考虑了孔洞汇合的影响。计算中所采用的模型参数和材料参数均与我们前期的工作^{[22, 24]}所采用的参数相同。

图 5显示了汇合对孔洞尺寸d增长的影响：因汇合以及汇合导致孔隙度增长率的提高，相对于没有考虑汇合的计算结果，孔洞尺寸迅速增长。图 6的计算结果显示：虽然孔洞汇合时损伤度没有增加，但因为汇合引起孔隙度增长率的提高，从而导致了损伤的快速增长。

图 5 孔洞汇合对孔洞增长的影响

Figure 5. Influences of void coalescence on void size

下载: 全尺寸图片幻灯片

图 6 孔洞汇合对损伤发展的影响

Figure 6. Influences of void coalescence on spall damage

下载: 全尺寸图片幻灯片

图 7左图显示了晶粒尺寸、孔洞汇合对自由面速度v_f的影响：随着材料平均晶粒尺寸的增加，自由面速度曲线的回跳点降低，即层裂强度增加，这与P.B.Trivedi等^[25]对不同晶粒尺寸高纯铝层裂实验结果的分析在定性上一致；同时，对于平均晶粒尺寸为30 μm的材料，考虑孔洞汇合的影响，曲线回跳后的斜率显著增加，上升的幅度增高，图 7右图为对应的自由面速度曲线实验结果：平均晶粒尺寸d_g=30、200 μm的损伤材料中存在大量的孔洞汇合现象，相对于没有发生孔洞汇合的自由面速度曲线(60、100 μm)，自由面速度曲线回跳后的斜率和上升的幅度增加^[2]，关于孔洞汇合的计算结果和实验结果定性上符合也较好。

图 7 晶粒尺寸、孔洞汇合对自由面速度曲线的影响

Figure 7. Influences of void coalescence and grain size on free surface velocities

下载: 全尺寸图片幻灯片

表 1列出了不同平均晶粒尺寸d_g损伤材料内部层裂面处孔洞数N和平均孔洞直径d_v的实验统计结果和数值计算结果(注：实验给出的是可观测到的孔洞数，而计算给出的是单位体积(cm³)内的孔洞数)。实验观测结果显示：随着晶粒尺寸的增加，损伤材料内部的孔洞数减少、平均孔洞尺寸增加。计算结果与实验定性符合。同时，对实验观测结果和计算结果的分析表明(30 μm样品)：孔洞汇合引起孔洞数减少、平均孔洞尺寸增加。

表 1 损伤材料内部孔洞数及孔洞大小的统计结果

Table 1. Damage statistics

d_g /μm	N		d_v
d_g /μm	实验	计算	实验	计算
30	236	11.460	38.1	12.17
30	236	0.044(考虑汇合)		37.12(考虑汇合)
60	363	3.236	22.7	22.36
100	267	1.421	33.0	34.51
200	111	0.566	55.1	42.60

下载: 导出CSV

| 显示表格

图 8显示了选取不同孔洞汇合临界损伤度D对自由面速度曲线的影响：孔洞汇合发生越早，材料内部损伤发展越快，即自由面曲线回跳后曲线上升的斜率和幅度越大。

图 8 孔洞汇合临界损伤度对自由面速度曲线的影响

Figure 8. Influences of critical damage for void coalescence on free surface velocities

下载: 全尺寸图片幻灯片

4. 结语

耦合孔洞汇合的影响是精细化描述延性金属材料层裂损伤演化过程的关键。针对强动态拉伸载荷作用下延性金属层裂损伤问题，尝试建立了一个反映材料损伤和材料内部孔洞之间几何信息的孔洞汇合判定方法，从而弥补了现有判据只考虑单一影响因素的不足。同时，基于孔洞汇合前后能量守恒原理，给出了孔洞汇合对损伤增长影响的关系式，明确了孔洞汇合引起损伤增长的物理机理。

将材料平均晶粒尺寸影响和孔洞汇合影响引入到层裂损伤模型中，结合相关文献的实验分析结果，数值计算分析结果显示：晶粒尺寸越小，损伤材料内部成核孔洞越多、平均孔洞尺寸越小，自由面速度回跳点增高(即层裂强度降低)、回跳后速度曲线上升的斜率降低；孔洞汇合引起回跳后速度曲线上升的斜率增加、损伤材料内部的孔洞数减少、平均孔洞尺寸增加。计算结果与实验结果定性上符合较好，从而在一定程度上推进了延性金属层裂损伤的微细观物理建模研究。

图 1 水平激波管实验测试系统照片^[9]

Figure 1. A photo of horizontal shock tube test system^[9]

下载: 全尺寸图片幻灯片

图 2 水平激波管示意图^[9]

Figure 2. Schematic diagram of horizontal shock tube^[9]

下载: 全尺寸图片幻灯片

图 3 制备完成的砂墙结构及其装配完成照片^[9]

Figure 3. Photos for the prepared sand structure and its assembly^[9]

下载: 全尺寸图片幻灯片

图 4 工况1的流场瞬时高速纹影照片

Figure 4. High-speed schlieren photos of flow field at different times in the case 1

下载: 全尺寸图片幻灯片

图 5 工况2的流场瞬时高速纹影照片

Figure 5. High-speed schlieren photos of flow field at different times in the case 2

下载: 全尺寸图片幻灯片

图 6 工况3的流场瞬时高速纹影照片

Figure 6. High-speed schlieren photos of flow field at different times in the case 3

下载: 全尺寸图片幻灯片

图 7 工况4的流场瞬时高速纹影照片

Figure 7. High-speed schlieren photos of flow field at different times in the case 4

下载: 全尺寸图片幻灯片

图 8 工况5的流场瞬时高速纹影照片

Figure 8. High-speed schlieren photos of flow field at different times in the case 5

下载: 全尺寸图片幻灯片

图 9 工况6的流场瞬时高速纹影照片

Figure 9. High-speed schlieren photos of flow field at different times in the case 6

下载: 全尺寸图片幻灯片

图 10 砂墙冲击状态关系图

Figure 10. Diagram illustrating the determination of Hugoniot particle velocity and stress state of sand wall

下载: 全尺寸图片幻灯片

图 11 不同材料砂墙冲击状态关系对比

Figure 11. Comparison of D-u relations of different sand walls made with quartz, iron and bauxte particles

下载: 全尺寸图片幻灯片

表 1 砂墙结构参数

Table 1. Characteristic parameters of sand walls in seven experimental cases

工况	充气压力/MPa	厚度/mm	颗粒直径/μm	孔隙度/%	初始表观密度/(kg·m⁻³)	材料
1	2	20	250	56.6	3 060	铁砂
2	4	20	250	56.6	3 060	铁砂
3	2	20	10	69.3	1 196	矾土
4	4	20	10	69.3	1 196	矾土
5	5	30	250	56.6	1 146	石英砂
6	5	30	250	56.6	1 146	石英砂
7	4	20	250	56.6	1 146	石英砂

下载: 导出CSV

表 2 所有工况中冲击波的传播速度

Table 2. Propagation velocities of shock waves in all cases

工况	入射激波马赫数	入射激波速度/(m·s⁻¹)	透射激波速度/(m·s⁻¹)	反射激波速度/(m·s⁻¹)
1	1.827	632	767	331
2	2.402	831	993	391
3	2.000	692	767	331
4	2.413	835	858	361
5	2.402	831	948	361
6	2.503	866	993	391
7	2.402	831	933

下载: 导出CSV

表 3 砂墙冲击关系确定所涉及的过程状态数据

Table 3. Process state data for determining impact relation of sand wall

工况	入射激波波后流体速度/(m·s⁻¹)	入射激波波阵面压力/MPa	入射激波波后流体密度/(kg·m⁻³)	反射激波运动速度/(m·s⁻¹)	冲击界面运动速度/(m·s⁻¹)	砂墙冲击关系
1	369	0.378	2.846	331	0.43	D=513.7u+546.1
2	572	0.665	3.809	383	0.87	D=513.7u+546.1
3	433	0.456	3.160	344	1.54	D=87.6u+632.1
4	576	0.652	3.826	369	2.58	D=87.6u+632.1
5	572	0.665	3.809	372	2.41	D=209.7u+443.5
6	606	0.724	3.954	382	2.62	D=209.7u+443.5

下载: 导出CSV

表 4 干砂冲击状态关系文献发表实验结果

Table 4. Hugoniot relations of dry sand reported in other literatures

序号	应力/GPa	初始粒径/μm	初始密度/(kg·m⁻³)	体积声速/(m·s⁻¹)	斜率 λ	参考文献
序号	应力/GPa	砂样条件		冲击绝热线		参考文献
1	1～6	70～140	1 490	504	1.6	Dianov, et al^[14]
2	0.5～3.0	< 850	1 380～1 450	560	1.69	Perry, et al^[17]
3	0.53～5.76	230	1 430 ± 50	530	1.64	Chapman, et al^[15]
4	0.3～1.8	～200	1 570	243	2.348	Brown, et al^[16]

下载: 导出CSV

参考文献(18)

[1]	SMITH P D. Blast walls for structural protection against high explosive treats: a review [J]. International Journal of Protective Structure, 2010, 1(1): 67–84. DOI: 10.1260/2041-4196.1.1.67.
[2]	王等旺, 张德志, 李焰, 等. 沙墙吸能作用对爆炸冲击波影响的实验研究 [J]. 实验力学, 2011, 26(1): 37–42. DOI: 1001-4888(2011)01-0037-06. WANG Dengwang, ZHAND Dezhi, LI Yan, et al. Experimental study of sand wall energy absorption effect on blastwave [J]. Journal of Experimental Mechanics, 2011, 26(1): 37–42. DOI: 1001-4888(2011)01-0037-06.
[3]	ZHANG F, FROST DL, THIBAULT PA, et al. Explosive dispersal of solid particles [J]. Shock Waves, 2001, 10(6): 431–443. DOI: 10.1007/PL00004050.
[4]	WAGNER J L, BERESH S J, KEARNEY S P, et al. Interaction of a planar shock with a dense field of particles [C] // KONTIS K. 28th International Symposium on Shock Waves. Springer, Berlin, Heidelberg, 2012: 115−120. DOI: 10.1063/1.3686604.
[5]	WAGNER JL, BERESH SJ, KEARNEY SP, et al. A multiphase shock tube for shock wave interactions with dense particle fields [J]. Experiments in Fluids, 2012, 52(6): 1507–1517. DOI: 10.1007/s00348-012-1272-x.
[6]	EDWARD P D, WAGNER J L, DECHANT L J, et al. Measures of the initial transient of a dense particle curtain following shock wave impingement [C] // 55th AIAA Aerospace Sciences Meeting. Grapevine, Texas: American Institute of Aeronautics and Astronautics, 2017: 1466.
[7]	LING Y, WAGNER J L, BERESH S J, et al. Interaction of a planar shock wave with a dense particle curtain: modeling and experiments [J]. Physics of Fluids, 2012, 24(11): 113301. DOI: 10.1063/1.4768815.
[8]	ROGUE X, RODRIGUEZ G, HAAS J F, et al. Experimental and numerical investigation of the shock-induced fluidization of a particles bed [J]. Shock Waves, 1998, 8(1): 29–45. doi: 10.1007/s001930050096
[9]	LV Hua, WANG Zhongqi, LI Jianping. Experimental study of planar shock wave interactions with dense packed sand wall [J]. International Journal of Multiphase Flow, 2017, 89: 255–265. DOI: 10.1016/j.ijmultiphaseflow.2016.07.019.
[10]	THEOFANOUS T G, MITKIN V, CHANG C H. The dynamics of dense particle clouds subjected to shock waves: Part 1: experiments and scaling laws [J]. Journal of Fluid Mechanics, 2016, 792: 658–681. DOI: 10.1017/jfm.2016.97.
[11]	ZHANG Lite, SHI Honghui, WANG Chao, et al. Aerodynamic characteristics of solid particles’ acceleration by shock waves [J]. Shock Waves, 2011, 21: 243–252. DOI: 10.1007/s00193-011-0317-z.
[12]	KELLENBERGER M, JOHANSEN C, CICCARELLI G, et al. Dense particle cloud dispersion by a shock wave [J]. Shock Waves, 2013, 23(5): 415–430. DOI: 10.1007/s00193-013-0432-0.
[13]	OMIDVAR M, ISKANDER M, BLESS S. Stress-strain behavior of sand at high strain rates [J]. International Journal of Impact Engineering, 2012, 49: 192–213. DOI: 10.1016/j.ijimpeng.2012.03.004.
[14]	DIANOV M, ZLATIN N, MOCHALOV S, et al. Shock compressibility of dry and water-saturated sand [J]. Soviet Technical Physics Letters, 1976, 2: 207–208.
[15]	CHAPMAN D J, TSEMBELIS K, PROUD W G. The behaviour of water saturated sand under shock-loading [C] // Proceedings of the 2006 SEM Annual Conference and Exposition on Experimental and applied Mechanics. 2006, 2: 834−840.
[16]	BROWN J L, VOGLER T J, GRADY D E, et al. Dynamic compaction of sand [C] // AIP Conference Proceedings, 2007, 955(1): 1363−1366. DOI: 10.1063/1.2832977.
[17]	PERRY J I, BRAITHWAITE C H, TAYLOR N E, et al. Behaviour of moist and saturated sand during shock and release [J]. Applied Physics Letters, 2015, 107(17): 174102. doi: 10.1063/1.4934689
[18]	李维新. 一维不定常流与冲击波 [M]. 2版. 北京: 国防工业出版社, 2004: 204−294.