气泡及其破碎兴波对浮动冲击平台影响探究

王志凯; 周鹏; 孙波; 姚熊亮; 杨娜娜

doi:10.11883/bzycj-2018-0212

气泡及其破碎兴波对浮动冲击平台影响探究

doi: 10.11883/bzycj-2018-0212

王志凯^1,,
周鹏²,
孙波¹,
姚熊亮^1, ,,
杨娜娜¹

1.
哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001
2.
哈尔滨工程大学机电工程学院，黑龙江哈尔滨 150001

基金项目: 国家自然科学基金（11602069，51779056）；黑龙江省自然科学基金（E2017026）；中国博士后科学基金（2017M611359）支持

详细信息

作者简介:
王志凯（1989－　），男，博士，讲师，wangzhikai@hrbeu.edu.cn

通讯作者:
姚熊亮（1963－　），男，博士，教授，yaoxiongliang@hrbeu.edu.cn

中图分类号: O383.1
计量
- 文章访问数: 6116
- HTML全文浏览量: 1542
- PDF下载量: 61
- 被引次数: 0
出版历程
- 收稿日期: 2018-06-19
- 修回日期: 2019-03-11
- 网络出版日期: 2019-08-25
- 刊出日期: 2019-09-01

Influence of bubbles and breaking waves on floating shock platform

1.
School of Marine Engineering, Harbin Engineering University, Harbin 150001, Heilongjiang, China
2.
School of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, Heilongjiang, China

摘要

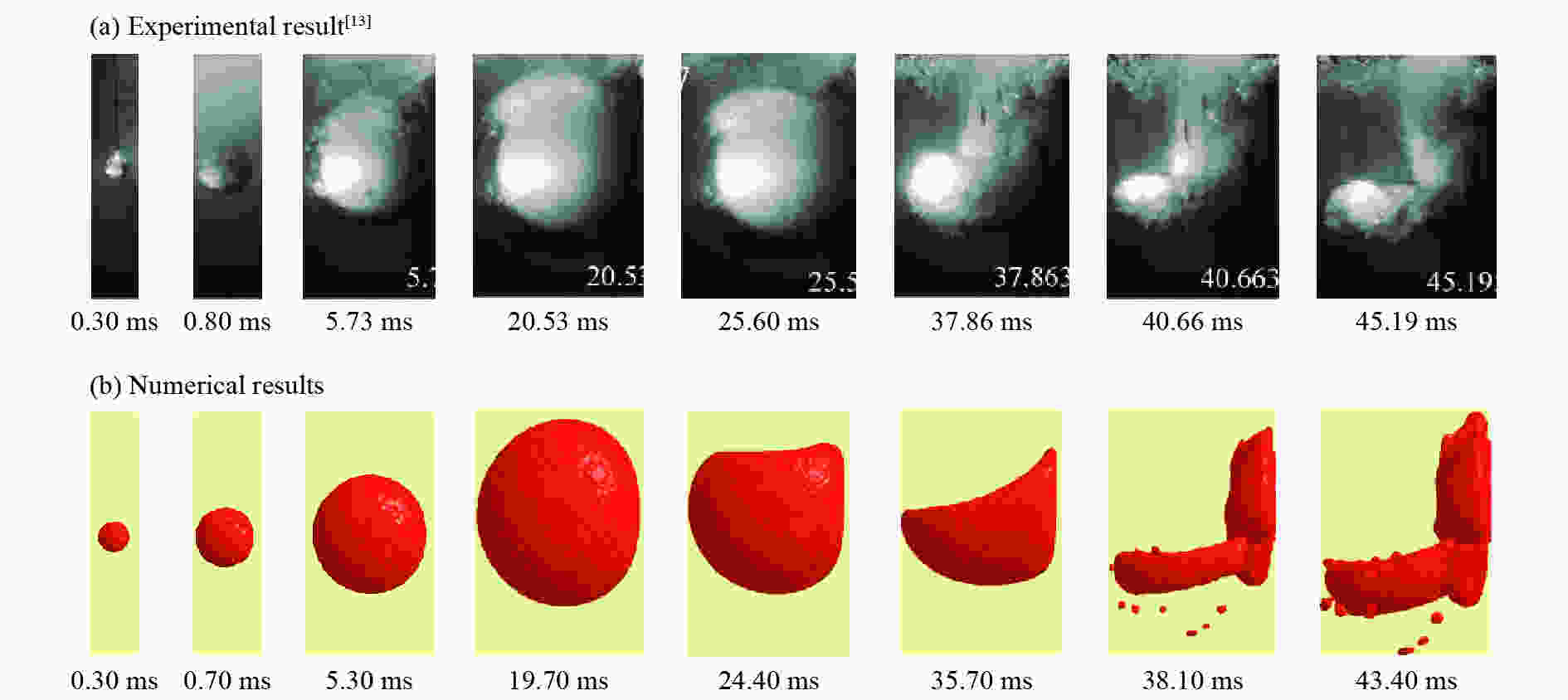
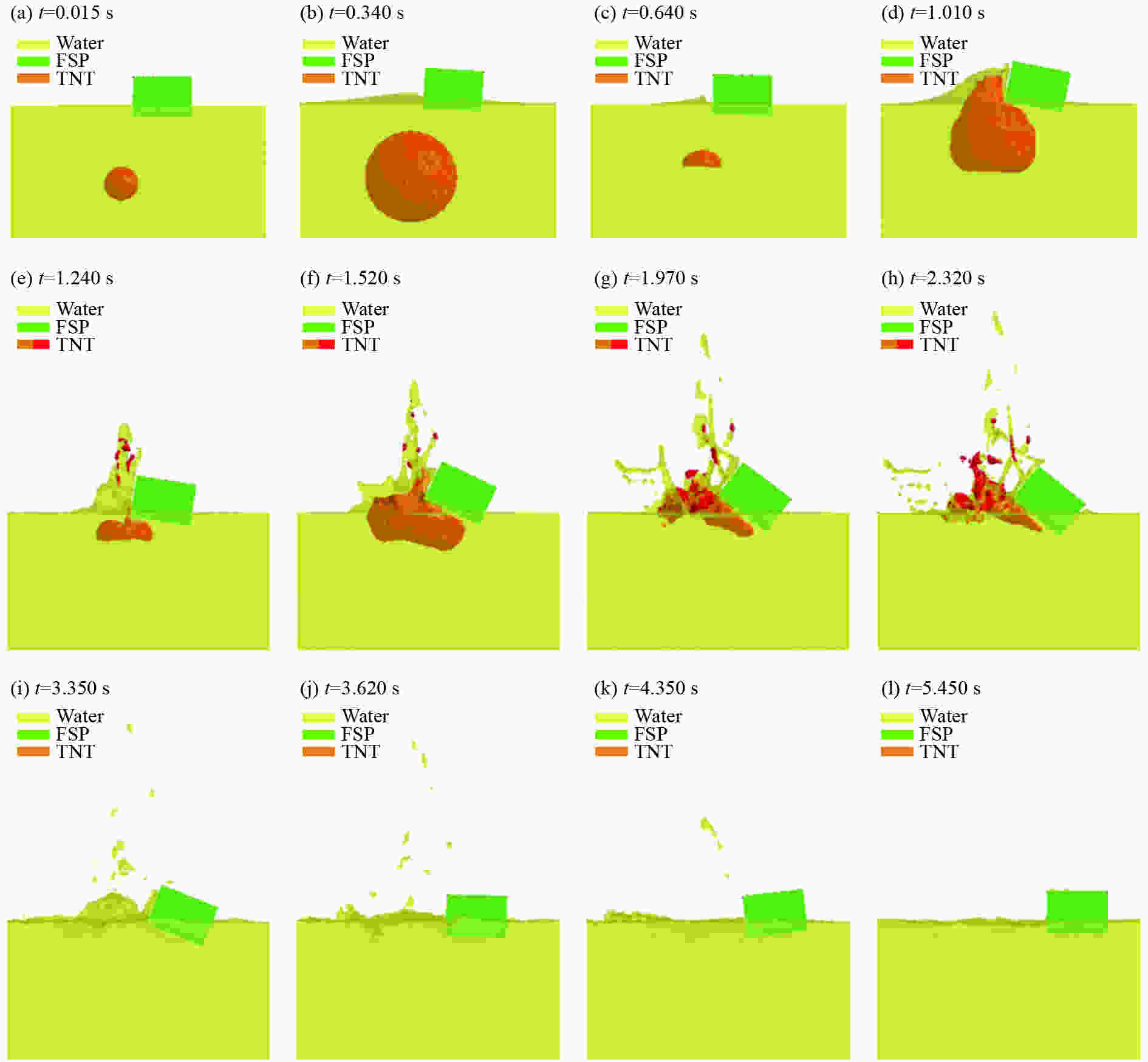
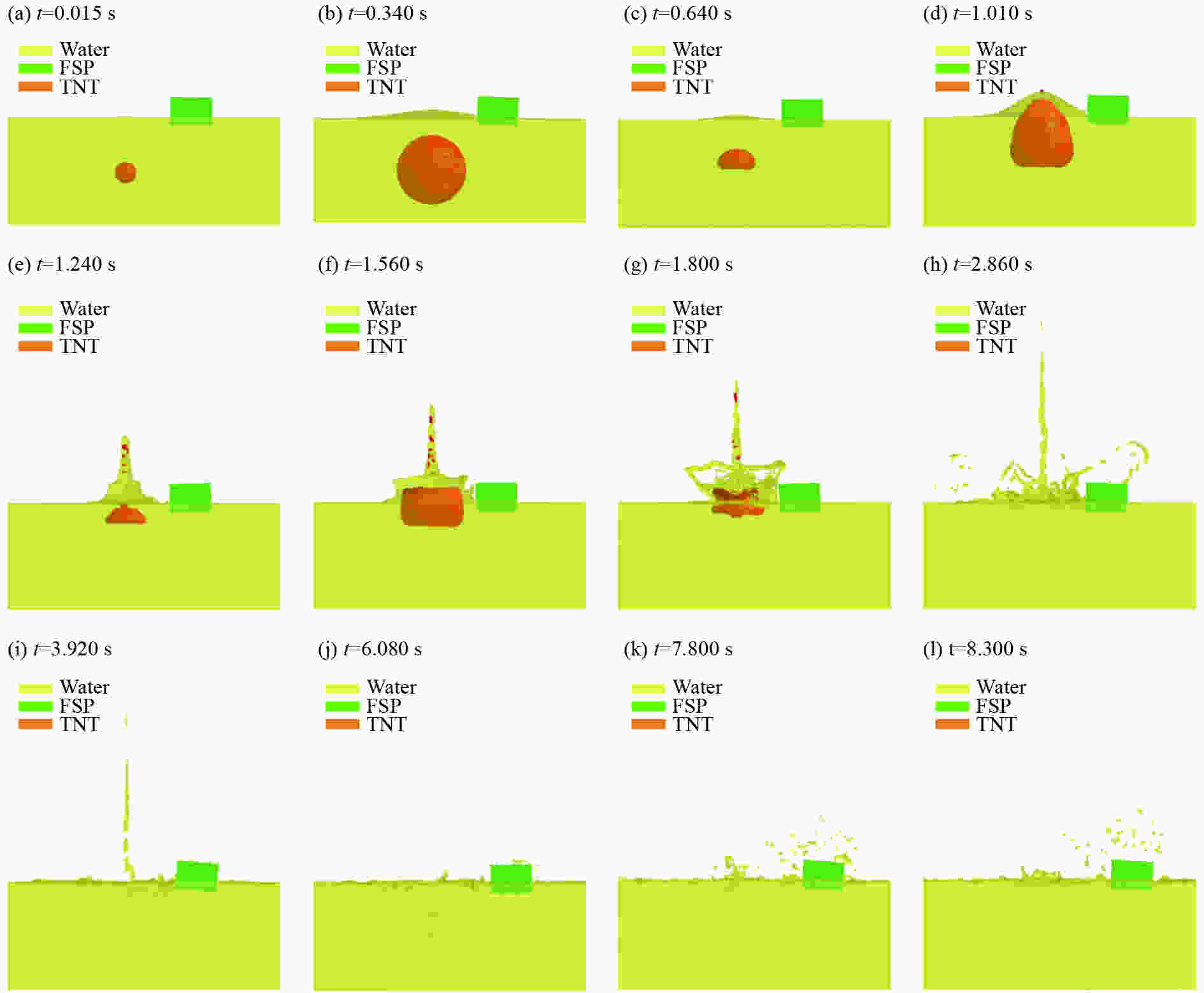
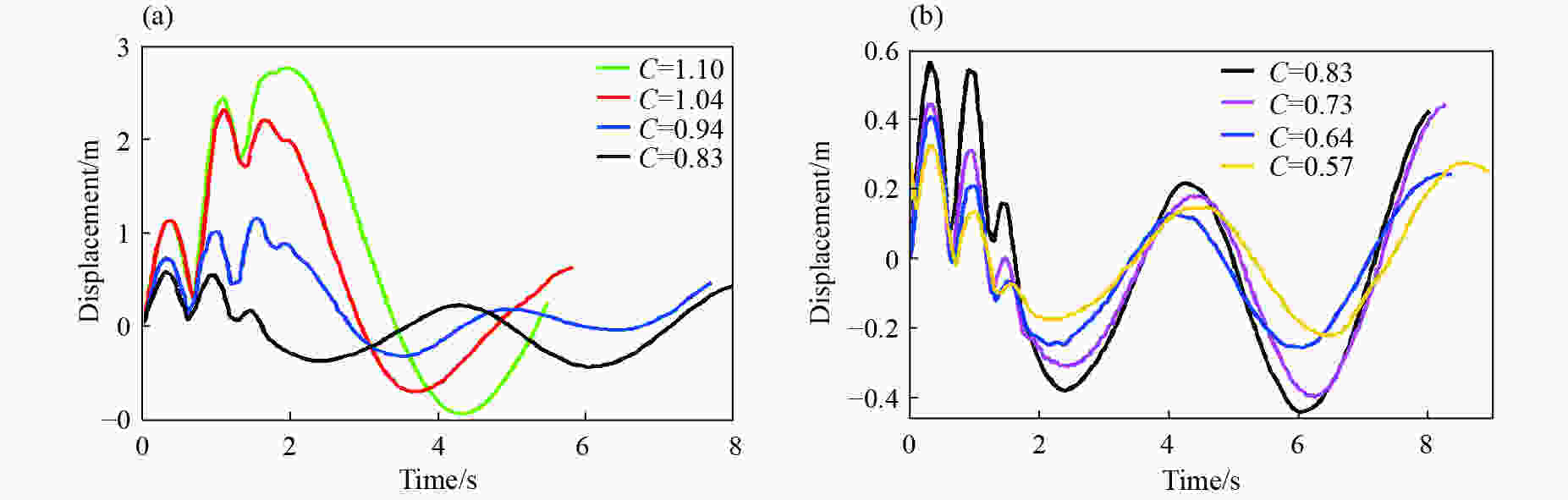
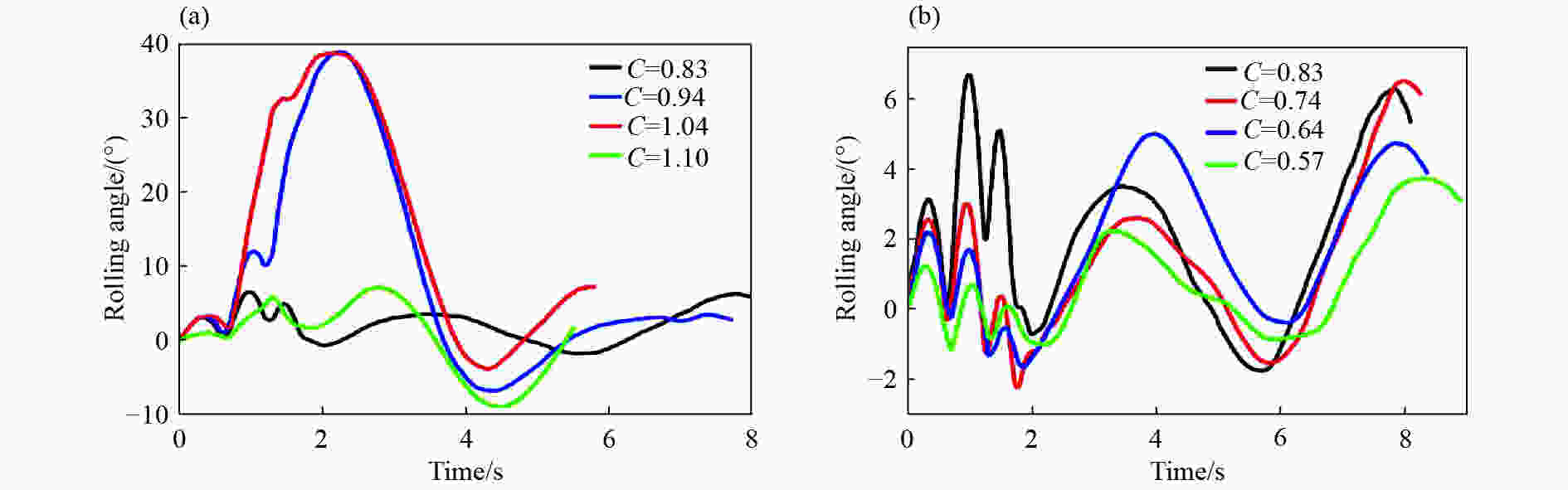
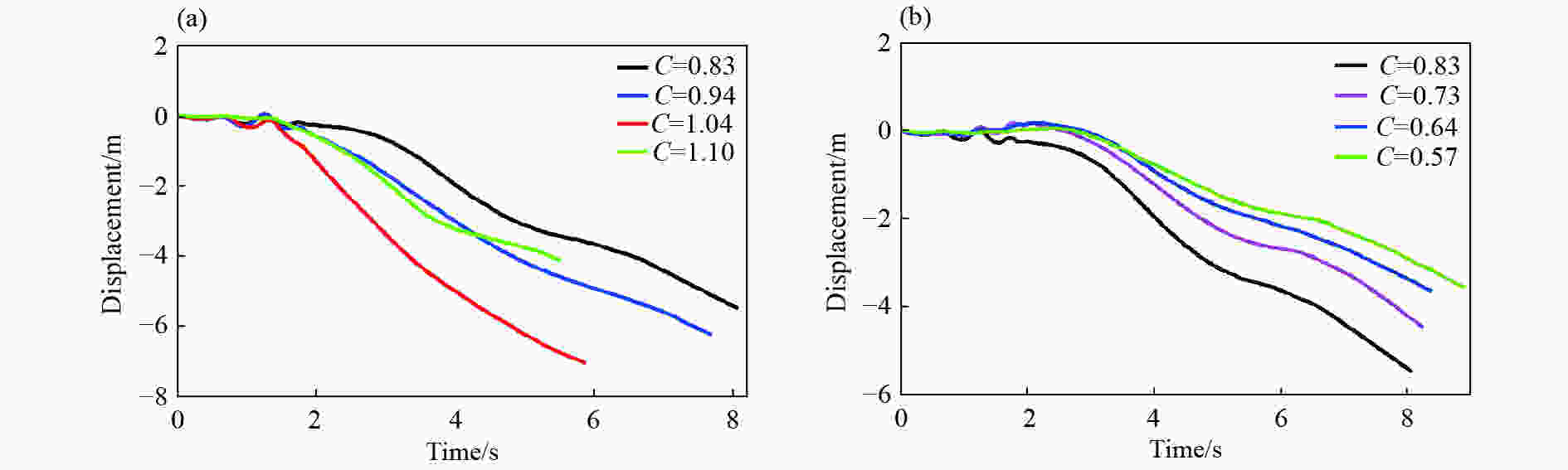
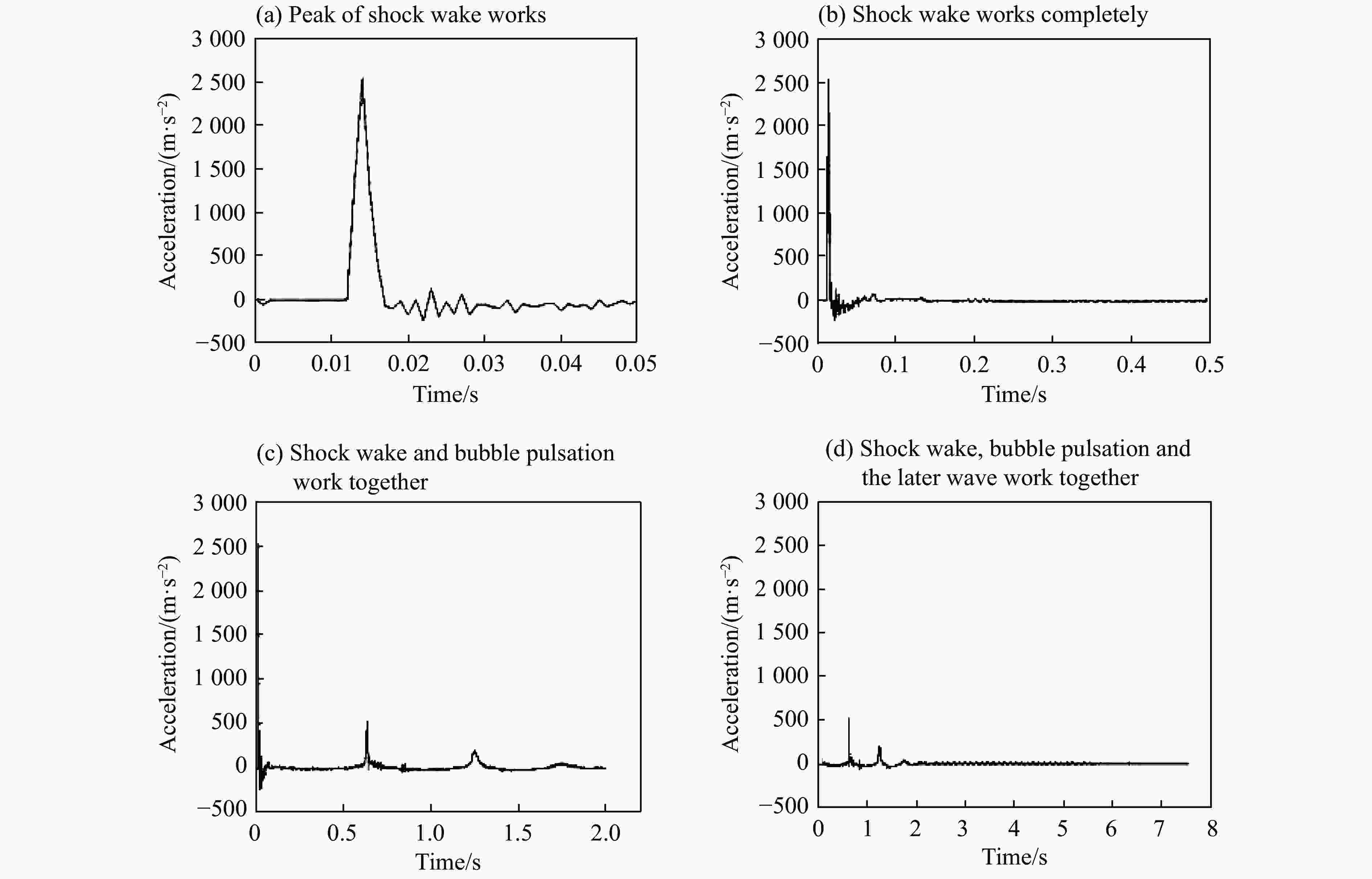
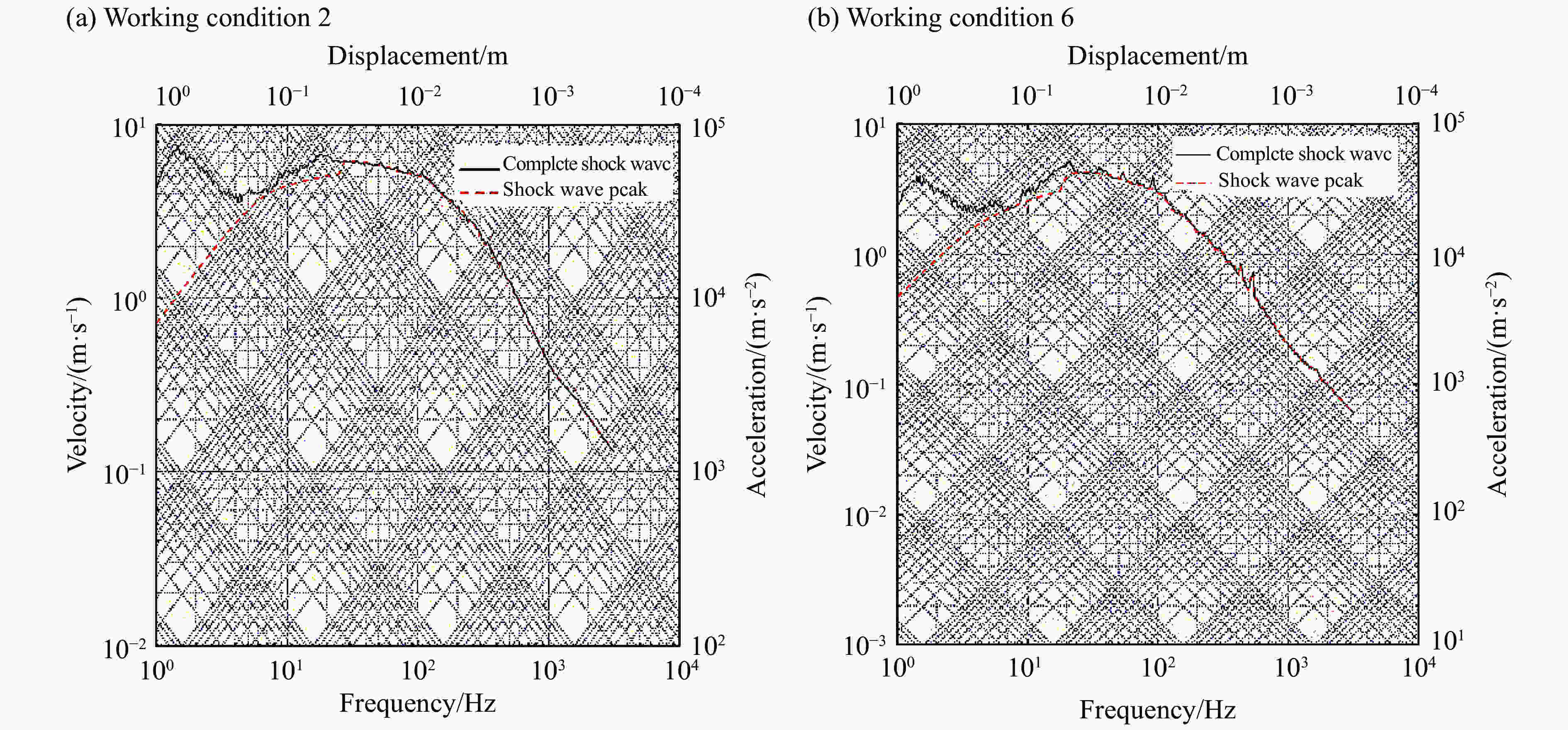
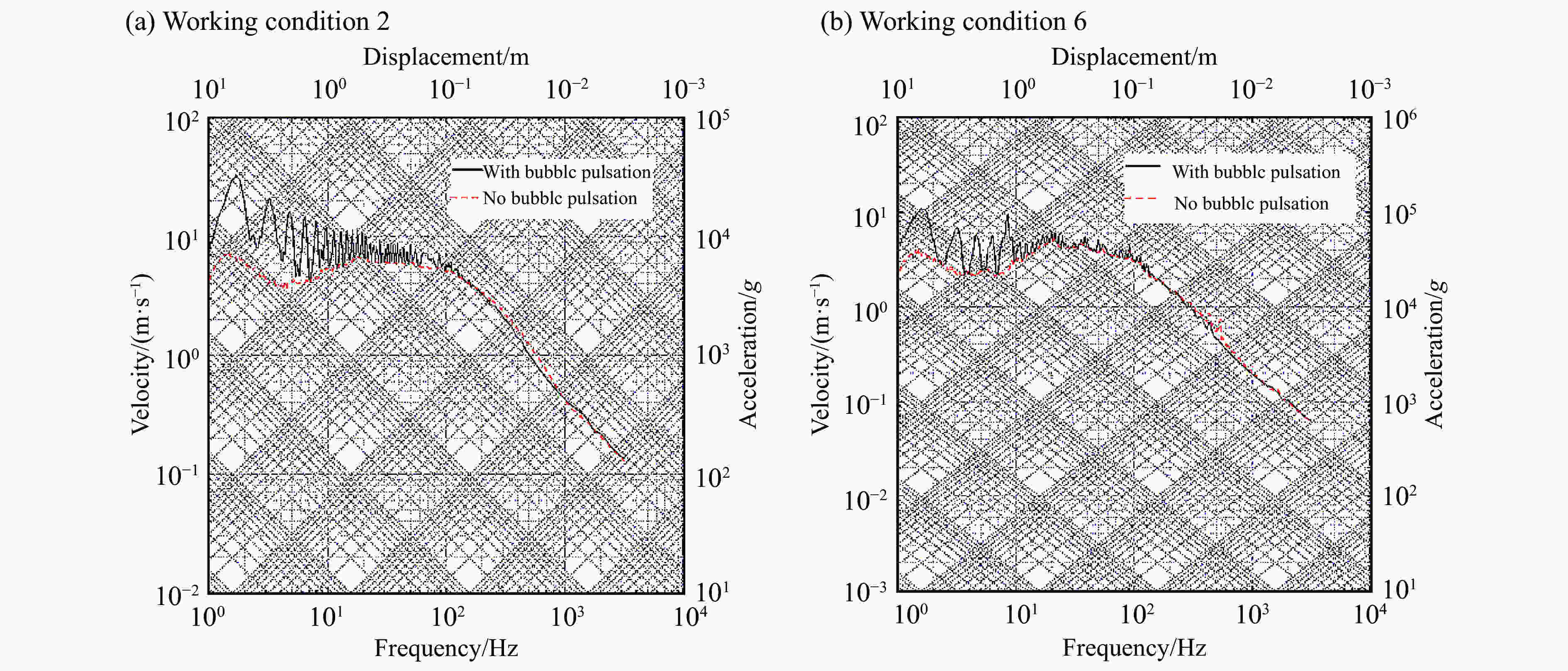
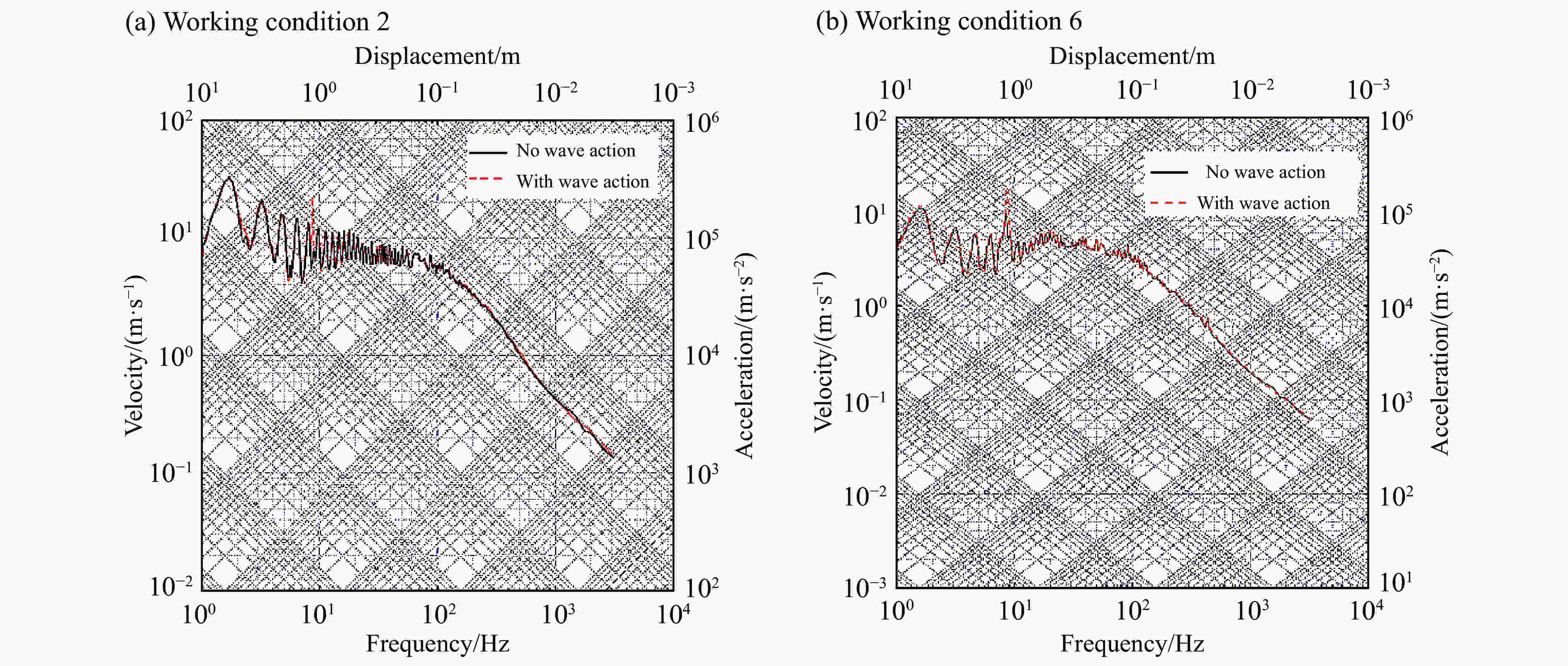
摘要: 基于LS-DYNA软件中的ALE算法，对近水面水下爆炸气泡脉动过程进行数值模拟并与实验结果进行对比，验证了近水面近壁面混合边界有限元模型和参数设置的正确性。设置不同爆炸工况，对气泡及其破碎兴波对浮动冲击平台影响进行探究，结果表明：在水下爆炸过程中，气泡、自由面、浮动冲击平台会发生强烈的耦合作用，在气泡脉动阶段，气泡会诱导出涌流和水冢效应，影响浮动冲击平台的安全性和使用性；冲击波是影响浮动冲击平台冲击环境的主要因素，由于气泡的低频性，气泡脉动及水冢对浮动冲击平台的直接冲击作用，会小幅度增加浮动冲击平台冲击环境的谱速度值、谱位移值，对谱加速度值几乎无影响；水冢抨击水面所形成的波浪和气泡破碎兴波，对浮动冲击平台造成的激励载荷呈周期性，其周期与波浪周期相同。波浪的激励载荷仅通过激励其对应频率的浮动冲击平台共振来改变平台的冲击环境。波浪载荷很小，对浮动冲击平台的冲击环境影响较小。
- 气泡脉动 /
- 浮动冲击平台 /
- 冲击环境 /
- 水下爆炸
Abstract: Based on the ALE algorithm in LS-DYNA software, the numerical simulation of the pulsation process of underwater explosion near water surface is carried out and compared with the experimental results. The correctness of the finite element model and parameter setting of the near-wall hybrid boundary near the water surface is verified. The different explosion conditions are set up, and the influence of air bubbles and their broken waves on the floating shock platform is explored. The results show that during the underwater explosion, the bubble, free surface and floating shock platform will have strong coupling effect, in the bubble pulsation stage. The bubble will induce the inrush current and the water ripple effect, affecting the safety and usability of the floating shock platform; the shock wave is the main factor affecting the shock environment of the floating shock platform. Due to the low frequency of the bubble, the bubble pulsation and the water ripple on the floating shock platform The direct shock effect will increase the spectral velocity value and spectral displacement value of the shock environment of the floating shock platform to a small extent, and has almost no effect on the spectral acceleration value; the waves and bubbles formed by the water slamming water surface are broken and waved, which is caused by the floating shock platform. The excitation load is periodic with the same period as the wave period. The excitation load of the wave changes the shock environment of the platform only by exciting the floating shock platform resonance of its corresponding frequency. The wave load is small and has little shock on the shock environment of the floating shock platform.
- bubble pulsation /
- floating shock platform /
- shock environment /
- underwater explosion

HTML全文

图 1 混合边界条件时工况示意图及有限元图

Figure 1. Illustration of working and finite element view in complex boundary conditions

下载: 全尺寸图片幻灯片

图 2 混合边界条件时爆炸气泡实验结果与计算结果对比

Figure 2. Experimental and numerical results of bubble in complex boundary conditions

下载: 全尺寸图片幻灯片

图 3 平台有限元模型

Figure 3. Finite element model of floating shock platform

下载: 全尺寸图片幻灯片

图 4 不同水平距离工况示意图

Figure 4. Illustration of working conditions at different horizontal dimensionless distances

下载: 全尺寸图片幻灯片

图 5 工况2水冢形态演变及平台运动响应

Figure 5. Water spike’s shape and evolution process and platform’s motion response in working condition 2

下载: 全尺寸图片幻灯片

图 6 工况6水冢形态演变及平台运动响应

Figure 6. Water spike’s shape and evolution process and platform’s motion response in working condition 6

下载: 全尺寸图片幻灯片

图 7 不同水平位移下平台升沉运动响应

Figure 7. Platform’s heave motion response in different horizontal displacements

下载: 全尺寸图片幻灯片

图 8 不同水平位移下平台横摇运动响应

Figure 8. Platform’s roll motion response in different horizontal displacements

下载: 全尺寸图片幻灯片

图 9 不同水平位移下平台横荡运动响应探究

Figure 9. Platform’s traverse motion response in different horizontal displacements

下载: 全尺寸图片幻灯片

图 10 工况2冲击加速度时历曲线

Figure 10. Shock acceleration time history curve of working condition 2

下载: 全尺寸图片幻灯片

图 11 冲击波作用时间对冲击响应谱影响对比图

Figure 11. Effect of shock wave’s action time on shock spectrum in comparison

下载: 全尺寸图片幻灯片

图 12 气泡脉动对冲击响应谱影响对比图

Figure 12. Effect of bubble pulsation on shock spectrum in comparison

下载: 全尺寸图片幻灯片

图 13 后期波浪对冲击响应谱影响对比图

Figure 13. Effect of later wave on shock spectrum in comparison

下载: 全尺寸图片幻灯片

图 14 波浪作用对平台加速度响应影响图

Figure 14. Later wave’s effect on shock acceleration response time

下载: 全尺寸图片幻灯片

图 15 波浪对比时冲击谱参数随冲击因子变化关系

Figure 15. Relationship between shock spectrum parameters and shock factor in wave contrast

下载: 全尺寸图片幻灯片

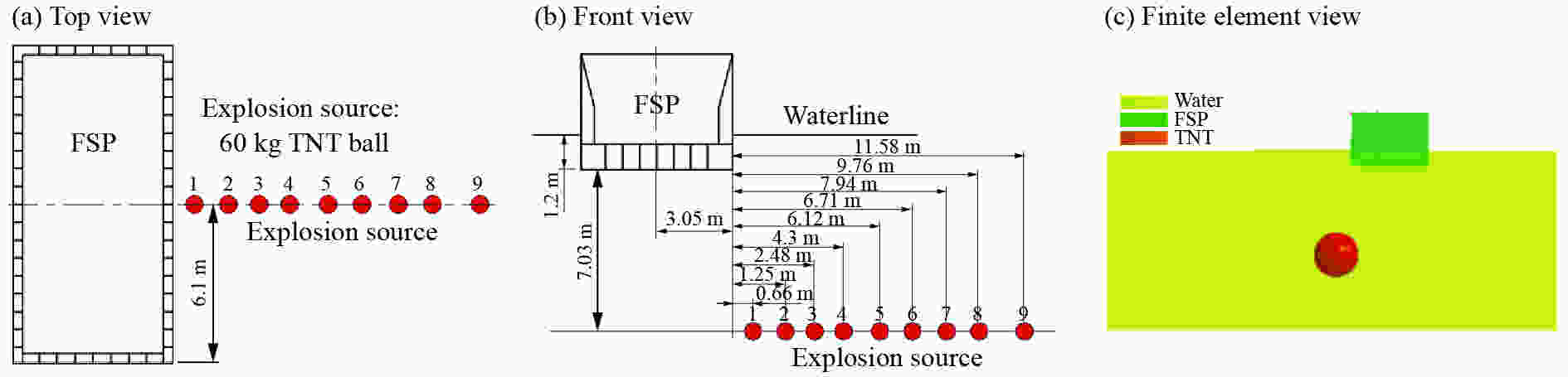
表 1 不同水平距离工况布置情况

Table 1. Layout of working conditions at different horizontal dimensionless distances

工况编号	炸药当量/kg	水平爆距/m	竖直爆距/m	爆距/m	冲击因子C
工况1	60	0.66	7.03	7.06	1.10
工况2	60	1.25	7.03	7.14	1.08
工况3	60	2.48	7.03	7.45	1.04
工况4	60	4.30	7.03	8.24	0.94
工况5	60	6.12	7.03	9.32	0.83
工况6	60	6.71	7.03	9.72	0.80
工况7	60	7.94	7.03	10.60	0.73
工况8	60	9.76	7.03	12.03	0.64
工况9	60	11.58	7.03	13.55	0.57

下载: 导出CSV

表 2 冲击环境参数与冲击因子关系式

Table 2. Relationship between shock response spectrum parameters and shock factor

冲击环境参数	近似拟合曲线方程
谱速度(Y₁)	Y₁=4.139 4C−0.829 8 (0.4＜C＜1.0), Y₁=18.631 2C−15.410 0 (1.0＜C＜1.1)
谱加速度(Y₂)	Y₂=221.35C−55.069 (0.4＜C＜1.0), Y₂=502.28C−341.02 (1.0＜C＜1.1)

下载: 导出CSV

参考文献(14)

[1]	周其新. 舰载设备冲击动力学数值实验技术体系研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
[2]	宫国田, 金辉, 张姝红, 等. 国外舰艇抗水下爆炸研究综述 [C] // 第九届全国冲击动力学学术会议. 河南焦作, 2009.
[3]	王军. 浮动冲击平台冲击动力特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
[4]	KEIL A H. The response of ships to underwater explosions [J]. Transactions-Society of Naval Architects and Marine Engineers, 2010, 69: 43.
[5]	KLASEBOER E, KHOO B C, HUNG K C. Dynamics of an oscillating bubble near a floating structure [J]. Journal of Fluids and Structures, 2005, 21(4): 395–412. DOI: 10.1016/j.jfluidstructs.2005.08.006.
[6]	ZHANG A M, ZENG L Y, CHENG X D, et al. The evaluation method of total damage to ship in underwater explosion [J]. Applied Ocean Research, 2011, 33(4): 240–251. DOI: 10.1016/j.apor.2011.06.002.
[7]	ZHANG N, ZONG Z. The effect of rigid-body motions on the whipping response of a ship hull subjected to an underwater bubble [J]. Journal of Fluids & Structures, 2011, 27(8): 1326–1336.
[8]	沈国光, 李德筠, 李润珊, 等. 大当量爆炸兴波的数值模拟 [J]. 海洋学报, 1996, 18(5): 128–133. SHEN Guoguang, LI Deyun, LI Runshan. Numerical simulation of large equivalent detonation wave [J]. Acta Oceanica Sinica, 1996, 18(5): 128–133.
[9]	李汪讳, 宗智, 孙雷. 水下爆炸兴波及其对结构物作用问题的数值模拟 [J]. 水动力学研究与进展: A辑, 2010, 25(6): 792–805. LI Wanghui, ZONG Zhi, SUN Lei. Numerical simulation of underwater explosion and wave propagation and its effect on structures [J]. Journal of Hydrodynamics: A, 2010, 25(6): 792–805.
[10]	WANG Q. The bursting of an underwater explosion bubble at a free surface [J]. Ocean Engineering, 2015, 109: 611–622. DOI: 10.1016/j.oceaneng.2015.09.017.
[11]	王军, 郭君, 姚熊亮. 冲击波作用下浮动冲击平台的刚体响应分析 [J]. 华中科技大学学报(自然科学版), 2015(2): 71–75. WANG Jun, GUO Jun, YAO Xiongliang. Rigid body response analysis of a floating shock platform under shock wave [J]. Journal of Huazhong University of Science and Technology, 2015(2): 71–75.
[12]	郑长允, 赵鹏远, 赵红光, 等. 设备缓冲平台在水下爆炸载荷作用下冲击响应分析 [J]. 科技导报, 2012, 30(18): 37–40. DOI: 10.3981/j.issn.1000-7857.2012.18.004. ZHENG Changyun, ZHAO Pengyuan, ZHAO Hongguang, et al. Shock response analysis of equipment buffer platform under underwater explosion loading [J]. Science & Technology Review, 2012, 30(18): 37–40. DOI: 10.3981/j.issn.1000-7857.2012.18.004.
[13]	CUI P, ZHANG A M, WANG S P. Small-charge underwater explosion bubble experiments under various boundary conditions [J]. Physics of Fluids, 2016, 28(11): 283.
[14]	王军, 姚熊亮, 杨棣. 浮动冲击平台冲击环境对设备响应的影响 [J]. 爆炸与冲击, 2015, 35(2): 236–242. DOI: 10.11883/1001-1455(2015)02-0236-07. WANG Jun, YAO Xiongliang, YANG Di. Shock of shock platform on the response of equipment to [J]. Explosion and Shock Waves, 2015, 35(2): 236–242. DOI: 10.11883/1001-1455(2015)02-0236-07.