Connecting modes of two cracks under impact loads
-
摘要: 脆性材料内部含有大量裂纹,当某一裂纹扩展时,其他裂纹会对扩展裂纹产生影响。为了研究冲击载荷下,脆性材料内两裂纹的相互影响、连通规律及裂纹尖端应力强度因子的变化规律,利用有机玻璃板制作了含非平行双裂纹的实验试件,利用落板冲击设备进行了中低速冲击实验,结合有限元分析软件ABAQUS计算出裂纹尖端应力强度因子,利用有限差分软件AUTODYN进行了动态数值模拟研究,并将其模拟结果与实验结果进行对比分析。实验及模拟结果表明:裂纹破坏形态与AUTODYN数值模拟破坏形态基本一致;试件的断裂形态随着两裂纹间距不同而不同;裂纹间的相互影响程度随着裂纹间间距增大而减小;裂纹尖端应力强度因子KI随着裂纹间距的增大而减小,而KII随着裂纹间距增大而增大。Abstract: A multitude of flaws always exists in brittle material and the influence will be exerted on by other flaws when one flaw is propagating. To investigate the propagation, coalition behavior and stress intensity factors of two cracks in brittle materials under impact loading, Polymethyl methacrylate (PMMA) was selected to manufacture the double cracked specimens. By using the medium-low speed impact system, impact experiments were conducted, and the crack tip SIFs were calculated by using finite element code ABAQUS. The finite difference code AUTODYN was used in the simulation crack propagation behavior, and the simulation results were compared with the test results. The results of experiment and simulation show that the simulation results generally agree with the experimental results in crack propagation paths; the crack propagation behavior varies with the change of the distance between the two cracks; the effect between the two cracks decreases with the increase of the distance between the two cracks; the stress intensity factors KI decrease with the increase of the distance between the two cracks while KII is the opposite.
-
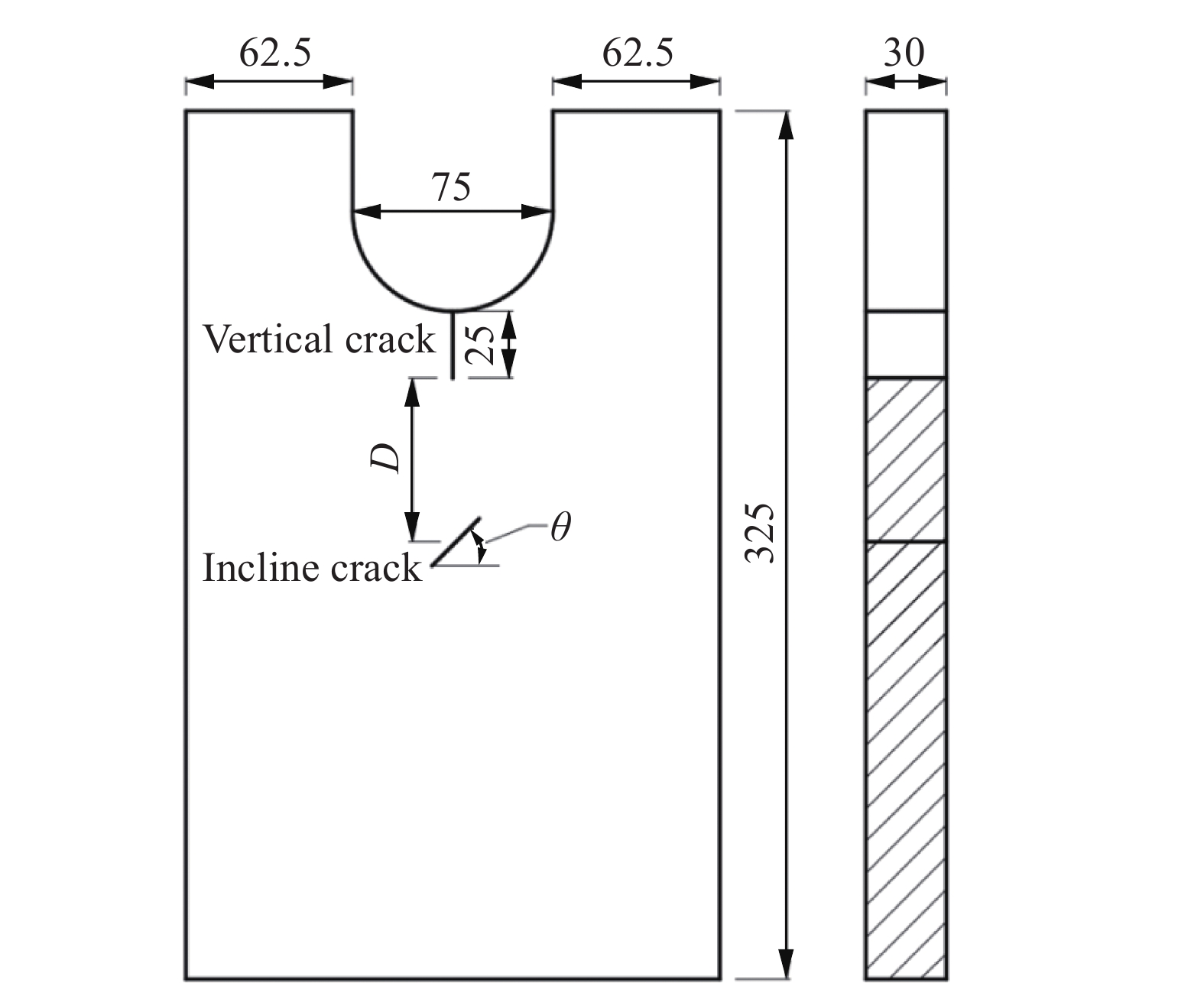
表 1 试件样本和实验时落板高度及冲击速度
Table 1. Height of drop weight plate and impact velocity for each specimen
试件编号 D/mm H/mm v/(m·s−1) D100−A45 100 1.840 6.005 D75−A45 75 1.865 6.046 D50−A45 50 1.827 5.984 D25−A45 25 1.834 6.000 D20−A45 20 1.854 6.028 D15−A45 15 1.847 6.017 D10−A45 10 1.828 5.986 表 2 落板冲击设备部件参数
Table 2. Parameters of impacting test system
部件名称 高度/mm 宽度/mm 厚度/mm 弹性模量/GPa 泊松比 落板 150 480 30 − − 入射板 3 000 300 30 72 0.33 透射板 2 000 300 30 72 0.33 表 3 各对照组起裂时刻及起裂韧度
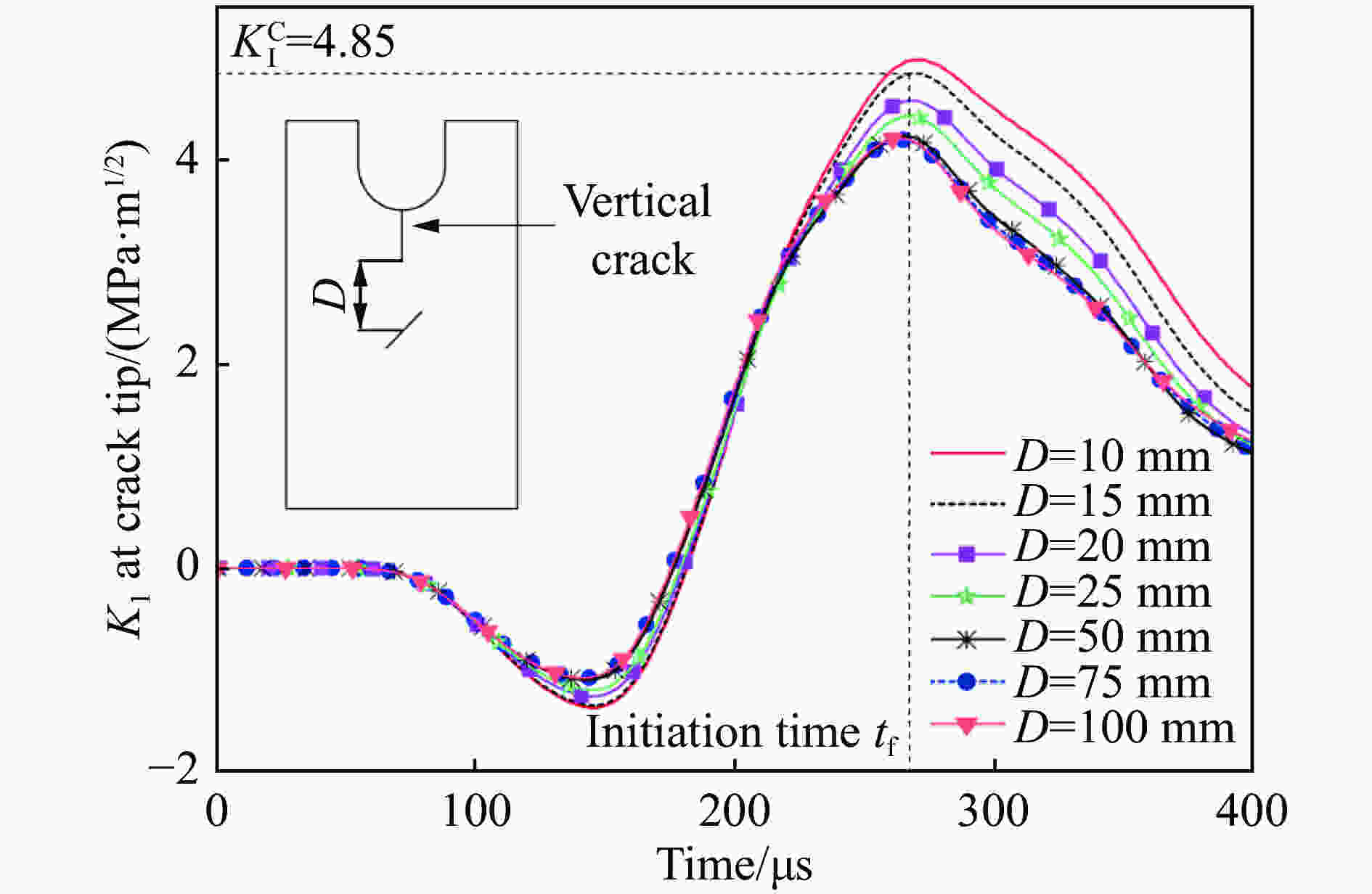
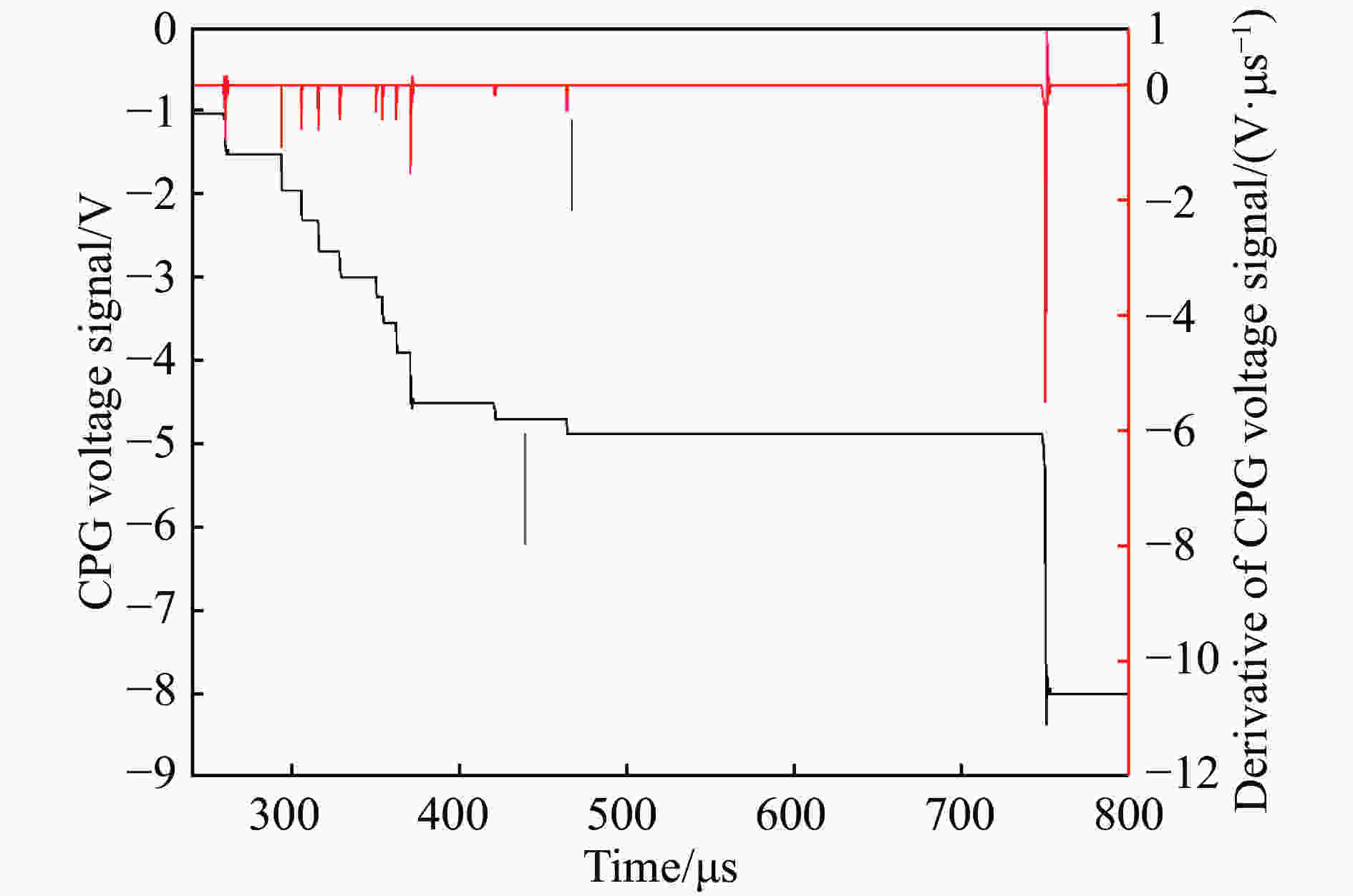
Table 3. Initiation time and initiation toughness for each specimen
试件编号 起裂时刻tf /μs 起裂韧度 D10−A45 272 4.99 D15−A45 267 4.85 D20−A45 275 4.53 D25−A45 259 4.36 D20−A45 264 4.24 D15−A45 260 4.19 D10−A45 263 4.22 -
[1] 劳恩. 脆性固体断裂力学 [M].2版.龚江洪, 译. 北京: 高等教育出版社; 2010: 2−5. [2] 李世愚, 和泰名, 尹祥础. 岩石断裂力学[M]. 北京: 科学出版社, 2015. 42−48. [3] 范天佑. 断裂理论基础[M]. 北京: 科学出版社; 2003. [4] 朱哲明, 汪元, 周章涛. 脆性材料在压缩载荷作用下的断裂破坏准则 [J]. 四川大学学报(工程科学版), 2008, 40(5): 13–21. DOI: 10.15961/j.jsuese.2008.05.003.ZHU Zheming, WANG Yuan, ZHOU Zhangtao, et al. A new fracture criterion for brittle materials under compression [J]. Journal of Sichuan University (Engineering Science Edition), 2008, 40(5): 13–21. DOI: 10.15961/j.jsuese.2008.05.003. [5] ZHU Zheming. An alternative form of propagation criterion for two collinear cracks under compression [J]. Mathematics and Mechanics of Solids, 2009, 14(8): 727–746. DOI: 10.1177/1081286508090043. [6] ZHU Zheming, XIE Heping, JI Shaocheng. The mixed boundary problems for a mixed mode crack in a finite plate [J]. Engineering Fracture Mechanics, 1997, 56(5): 647–655. DOI: 10.1016/S0013-7944(96)00123-3. [7] ZHU Zheming, WANG Laigui, MOHANTY B, et al. Stress intensity factor for a cracked specimen under compression [J]. Engineering Fracture Mechanics, 2006, 73(4): 482–489. DOI: 10.1016/j.engfracmech.2005.08.008. [8] ZHENG Tao, ZHU Zheming, WANG Bo, et al. Stress intensity factor for an infinite plane containing three collinear cracks under compression [J]. Journal of Applied Mathematics and Mechanics, 2015, 94(10): 853–861. DOI: 10.1002/zamm.201300001. [9] ITOU S. 3D dynamic stress intensity factors at three rectangular cracks in an infinite elastic medium subjected to a time-harmonic stress wave [J]. Archive of Applied Mechanics, 1999, 69(4): 286–298. DOI: 10.1007/s004190050220. [10] 钟波波, 张永彬, 李宏. 基于RFPA2D的岩石裂纹扩展模式的研究 [J]. 武汉理工大学学报, 2014, 36(2): 82–88. DOI: 10.3963/j.issn.1671-4431.2014.02.016.ZHONG Bobo, ZHANG Yongbin, LI Hong. Study of mechanisms of crack propagation of rock based on RFPA [J]. Journal of Wuhan University of Technology, 2014, 36(2): 82–88. DOI: 10.3963/j.issn.1671-4431.2014.02.016. [11] LOUIS N, LI Huaqiang. Numerical study on coalescence of two pre-existing coplanar flaws in rock [J]. International Journal of Solids and Structures, 2013, 50(22/23): 3685–3706. DOI: 10.1016/j.ijsolstr.2013.07.010. [12] YANG Shengqi, HUANG Yanhua. Erratum to: An experimental investigation on strength, deformation and crack evolution behavior of sandstone containing two oval flaws under uniaxial compression [J]. Engineering Geology, 2017, 217. DOI: 10.1016/j.enggeo.2016.12.004. [13] NASRI K, ABBADI M, ZENASNI M, et al. Double crack growth analysis in the presence of a bi-material interface using XFEM and FEM modelling [J]. Engineering Fracture Mechanics, 2014, 132: 189–199. DOI: 10.1016/j.engfracmech.2014.07.016. [14] HAERI H, SARFARAZI V, MARJI M F, et al. Experimental and numerical study of shear fracture in brittle materials with interference of initial double cracks [J]. Acta Mechanica Solida Sinica, 2016, 29(5): 555–566. DOI: 10.1016/S0894-9166(16)30273-7. [15] ZHANG Xiaoping, LIU Quansheng, WU Shunchuan, et al. Crack coalescence between two non-parallel flaws in rock-like material under uniaxial compression [J]. Engineering Geology, 2015, 199: 74–90. DOI: 10.1016/j.enggeo.2015.10.007. [16] CAO Ping, LIU Taoying, PU Chengzhi, et al. Crack propagation and coalescence of brittle rock-like specimens with pre-existing cracks in compression [J]. Engineering Geology, 2015, 187: 113–121. DOI: 10.1016/j.enggeo.2014.12.010. [17] 岳中文, 宋耀, 邱鹏, 等. 冲击载荷下双预置裂纹三点弯曲梁动态断裂实验 [J]. 振动与冲击, 2017, 36(4): 151–156. DOI: 10.13465/j.cnki.jvs.2017.04.024.YUE Zhongwen, SONG Yao, QIU Peng, et al. A dynamic fracture experiment of a three-point-bend beam containing double pre-existing cracks under impact load [J]. Journal of Vibration and Shock, 2017, 36(4): 151–156. DOI: 10.13465/j.cnki.jvs.2017.04.024. [18] 张华, 郭继鑫, 傅玉珍, 等. 冲击作用下混凝土裂纹扩展试验研究及数值模拟 [J]. 振动与冲击, 2016, 35(17): 107–112. DOI: 10.13465/j.cnki.jvs.2016.17.018.ZHANG Hua, GUO Jixin, FU Yuzhen, et al. Test and simulation for concrete crack propagation under impact load [J]. Journal of Vibration and Shock, 2016, 35(17): 107–112. DOI: 10.13465/j.cnki.jvs.2016.17.018. [19] 杨井瑞, 张财贵, 周妍, 等. 用SCDC试样测试岩石动态断裂韧度的新方法 [J]. 岩石力学与工程学报, 2015, 34(2): 279–292. DOI: 10.13722/j.cnki.jrme.2015.02.007.YANG Jingrui, ZHANG Caigui, ZHOU Yan, et al. A new method for determining dynamic fracture toughness of rock using SCDC specimens [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 279–292. DOI: 10.13722/j.cnki.jrme.2015.02.007. [20] 刘凯, 朱哲明, 何廉. 脆性材料裂纹动态扩展规律研究 [J]. 四川大学学报(工程科学版), 2015, 47(S2): 81–88. DOI: 10.15961/j.jsuese.2015.s2.013.LIU Kai, ZHU Zheming, HE Lian. The study of crack dynamic propagation law of brittle materials [J]. Journal of Sichuan University (Engineering Science Edition), 2015, 47(S2): 81–88. DOI: 10.15961/j.jsuese.2015.s2.013. [21] 汪小梦, 朱哲明, 施泽彬, 等. 基于VB-SCSC岩石试样的动态断裂韧度测试方法研究 [J]. 岩石力学与工程学报, 2018, 37(2): 302–311. DOI: 10.13722/j.cnki.jrme.2017.0351.WANG Xiaomeng, ZHU Zheming, SHI Zebin, et al. A method measuring dynamic fracture toughness of rock using VB-SCSC specimens [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(2): 302–311. DOI: 10.13722/j.cnki.jrme.2017.0351. [22] 刘德顺, 李夕兵. 冲击机械系统动力学 [M]. 北京: 科学出版社, 1999. [23] 郭伟国, 李玉龙, 索涛编. 应力波基础简明教程 [M]:西安: 西北工业大学出版社; 2007: 44−52. [24] ZHE Zheming, XIE Heping, MOHANTY B. Numerical investigation of blasting-induced damage in cylindrical rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(2): 111–121. DOI: 10.1016/j.ijrmms.2007.04.012. [25] ZHU Zheming, MOHANTY B, XIE Heping. Numerical investigation of blasting-induced crack initiation and propagation in rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(3): 412–424. DOI: 10.1016/j.ijrmms.2006.09.002. [26] 朱哲明, 刘凯, 康骥鸣, 等. 缓慢卸载P波诱发岩体不连续断裂破坏的可能性研究 [J]. 岩石力学与工程学报, 2014, 33(2): 3948–3955. DOI: 10.13722/j.cnki.jrme.2014.s2.070.ZHU Zheming, LIU Kai, KANG Jiming, et al. Study of slowly unloading P-waves causing discrete fracture mechanism [J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 3948–3955. DOI: 10.13722/j.cnki.jrme.2014.s2.070. [27] 周磊, 朱哲明, 董玉清, 等. 中低速冲击载荷下巷道内裂纹的动态响应 [J]. 岩石力学与工程学报, 2017, 36(6): 1363–1372. DOI: 10.13722/j.cnki.jrme.2016.1403.ZHOU Lei, ZHU Zheming, DONG Yuqing, et al. Dynamic response of cracks in tunnels under impact loading of medium-low speed [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(6): 1363–1372. DOI: 10.13722/j.cnki.jrme.2016.1403. [28] 刘瑞峰, 朱哲明, 李盟, 等. 爆炸载荷下I型裂纹的起裂及扩展规律研究 [J]. 岩石力学与工程学报, 2018, 37(2): 392–402. DOI: 10.13722/j.cnki.jrme.2017.1126.LIU Ruifeng, ZHU Zheming, LI Meng, et al. Initiation and propagation of mode I crack under blasting [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(2): 392–402. DOI: 10.13722/j.cnki.jrme.2017.1126. [29] 王蒙, 朱哲明, 王雄. 冲击荷载作用下的Ⅰ/Ⅱ复合型裂纹扩展规律研究 [J]. 岩石力学与工程学报, 2016, 35(7): 1323–1332. DOI: 10.13722/j.cnki.jrme.2015.1260.WANG Meng, ZHU Zheming, WANG Xiong. The growth of mixed-mode Ⅰ/Ⅱ crack under impacting loads [J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(7): 1323–1332. DOI: 10.13722/j.cnki.jrme.2015.1260. [30] 周磊, 朱哲明, 应鹏,等. 巷道内I型及I/II复合型裂纹在冲击载荷作用下的断裂行为分析 [J]. 振动与冲击, 2018, 37(13): 33. DOI: 10.13465/j.cnki.jvs.2018.13.033.ZHOU Lei, ZHU Zhe-ming, YING Peng, et al. Analysis of fracture behavior of mode I and mixed mode I/II cracks in tunnel under impact loads [J]. Journal of Vibration and Shock, 2018, 37(13): 33. DOI: 10.13465/j.cnki.jvs.2018.13.033. [31] CHEN Y M. Numerical computation of dynamic stress intensity factors by a Lagrangian finite-difference method (the HEMP code) [J]. Engineering Fracture Mechanics, 1975, 7(4): 653–660. DOI: 10.1016/0013-7944(75)90021-1. [32] 陈景杰, 黄一, 吴智敏. 平行双裂纹应力强度因子的计算方法 [J]. 上海交通大学学报, 2012, 46(8): 1263–1268. DOI: 10.16183/j.cnki.jsjtu.2012.08.015.CHEN Jinjie, HUNAG Yi, WU Zhimin. A new method to calculate stress intensity factor for parallel double cracks [J]. Journal of Shanghai Jiao Tong University, 2012, 46(8): 1263–1268. DOI: 10.16183/j.cnki.jsjtu.2012.08.015. [33] FREUND L B. Dynamic fracture mechanics [J]. Cambridge Monographs on Mechanics and Applied Mathematics, 1992, 72(8): 383–384. DOI: 10.1002/zamm.19920720818. -







 下载:
下载: