基于自适应和投影Wiener混沌的圆筒实验不确定度量化

梁霄; 王瑞利

doi:10.11883/bzycj-2018-0253

基于自适应和投影Wiener混沌的圆筒实验不确定度量化

doi: 10.11883/bzycj-2018-0253

梁霄^{1, 2,},
王瑞利^2, ,

1.
山东科技大学数学学院，山东青岛 266590
2.
北京应用物理与计算数学研究所，北京 100089

基金项目: 科学挑战专题(TZ2018001)；国家自然科学基金(91630312); 国防科工局国防基础科研计划(C1520110002)；山东省自然科学基金(ZR2017BA014)；山东科技大学公派访学基金(0103004)

详细信息

作者简介:
梁　霄（1984－　），男，博士，讲师，mathlx@163.com

通讯作者:
王瑞利（1964－　），男，研究员，wang_ruili@iapcm.ac.cn

中图分类号: O385
计量
- 文章访问数: 4744
- HTML全文浏览量: 1642
- PDF下载量: 35
- 被引次数: 0
出版历程
- 收稿日期: 2018-07-10
- 修回日期: 2018-10-01
- 网络出版日期: 2019-04-25
- 刊出日期: 2019-04-01

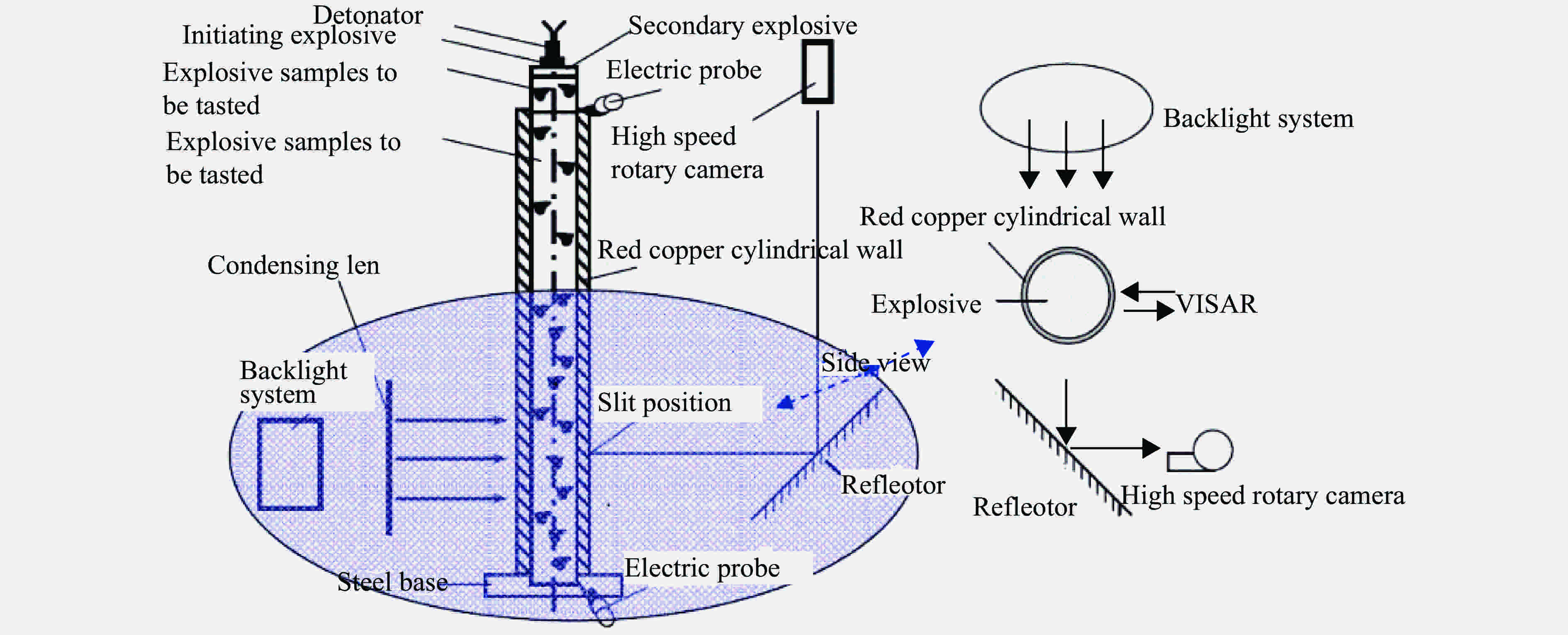
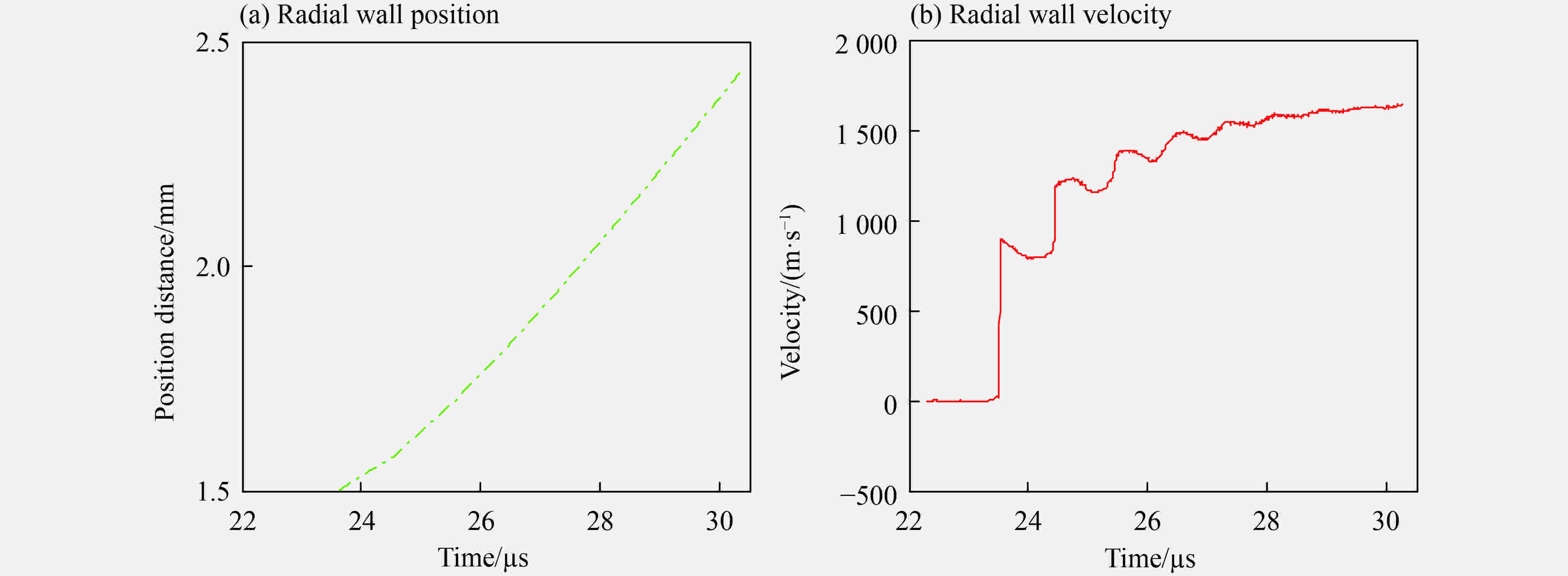
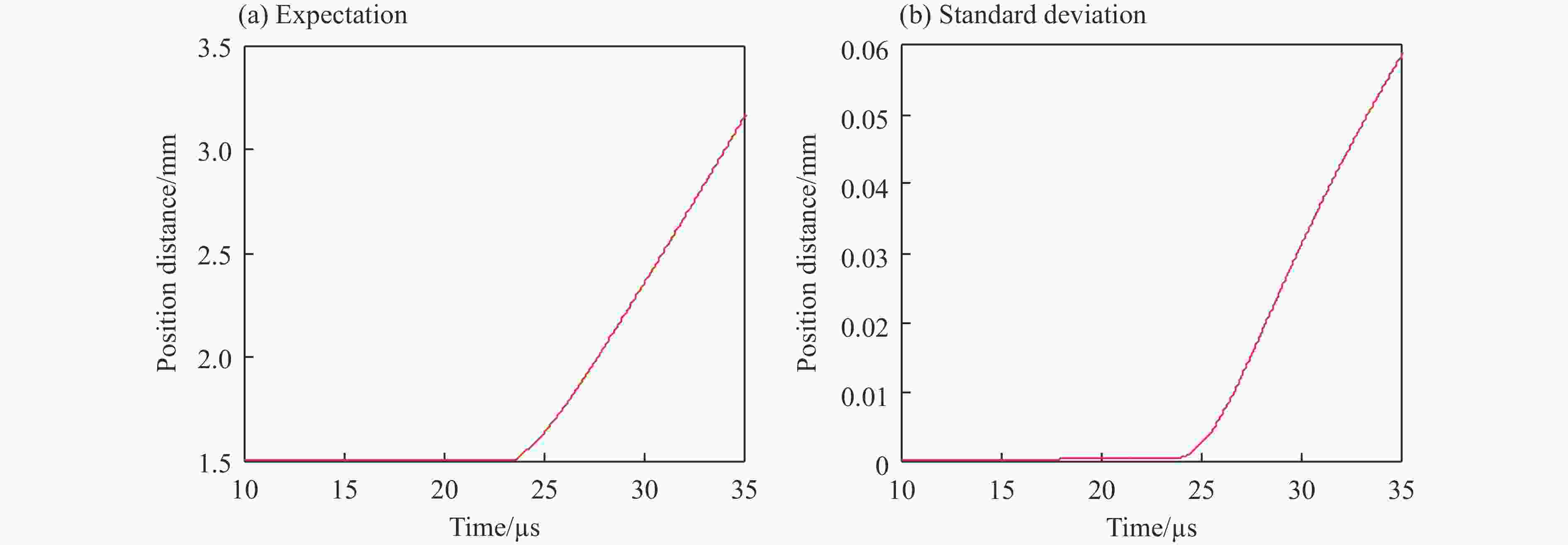
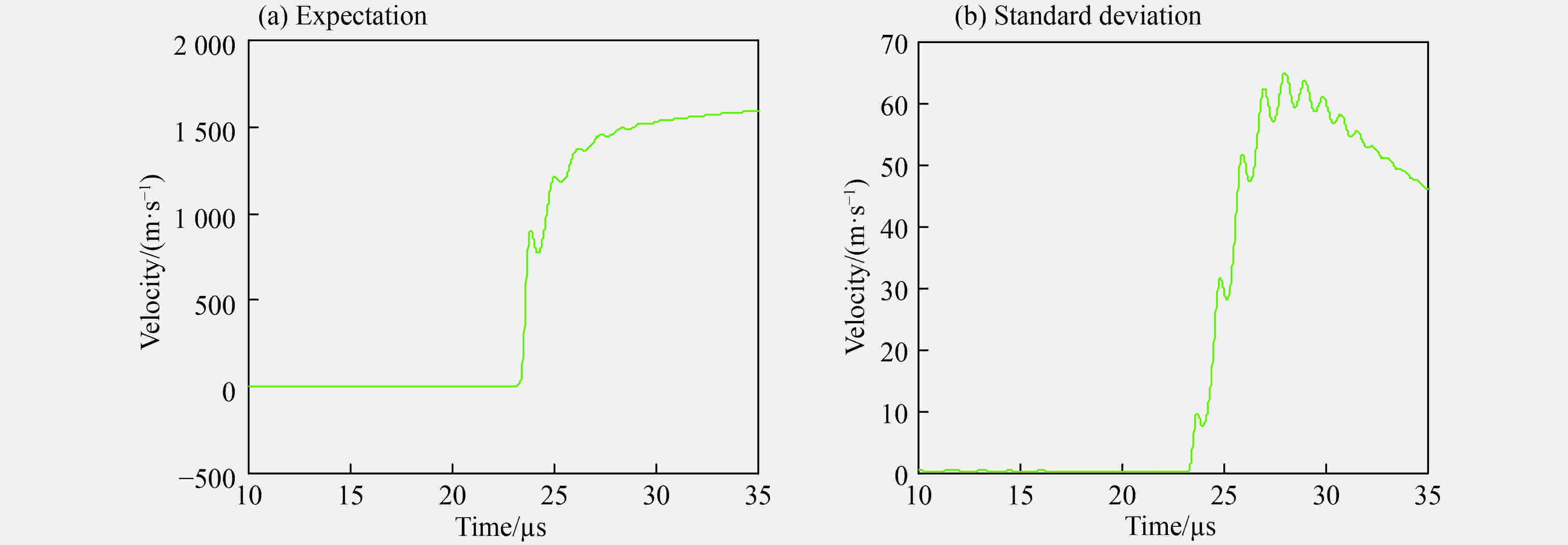
Uncertainty quantification of cylindrical test through Wiener chaos with basis adaptation and projection

LIANG Xiao^{1, 2
,},
WANG Ruili^{2
, ,}

1.
Department of Mathematics, Shandong University of Science and Technology, Qingdao 266590, Shandong, China
2.
Institute of Applied Physics and Computational Mathematics, Beijing 100089, China

摘要

摘要:
由于炸药爆轰现象的复杂性和人们对它的认知缺陷，其表征爆轰流体力学过程的物理数学模型具有较强的不确定性，要降低基于爆轰建模与模拟的数值结果做出决策的风险，量化和评估不确定输入对爆轰系统输出结果的影响尤为重要。本文中针对具有高维随机变量的爆轰问题的不确定度量化，使用自适应基函数的Wiener混沌方法、耦合旋转变换和投影方法，减少截断空间的长度。针对输入变量相关性，使用Rosenblatt变换使其相互独立。针对不符合标准正态分布的变量使用等概率原则，将它化为标准正态分布。最后，使用自主研发的具有完全知识产权的爆轰数值模拟软件LAD2D, 研究了具有高维不确定参数的圆筒实验的不确定度量化，给出期望、标准差、置信区间等统计信息，所得问题与实验数据比对，从而确认了模型的有效性。
- 圆筒模型 /
- 不确定度量化 /
- 自适应基函数 /
- JWL状态方程 /
- Rosenblatt变换
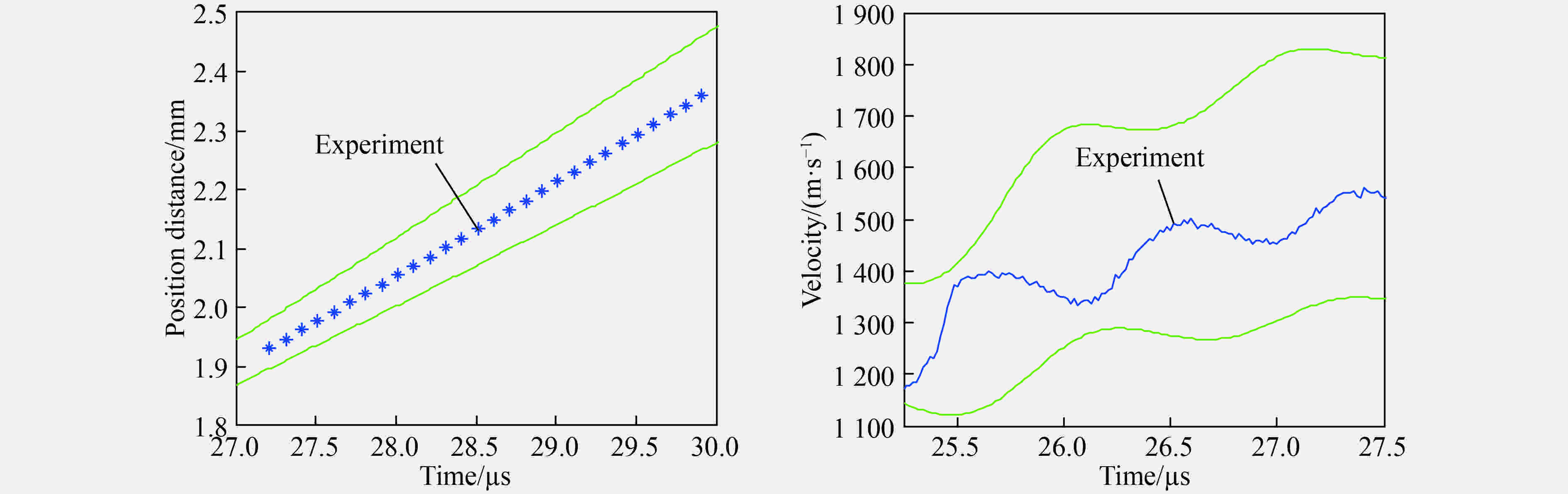
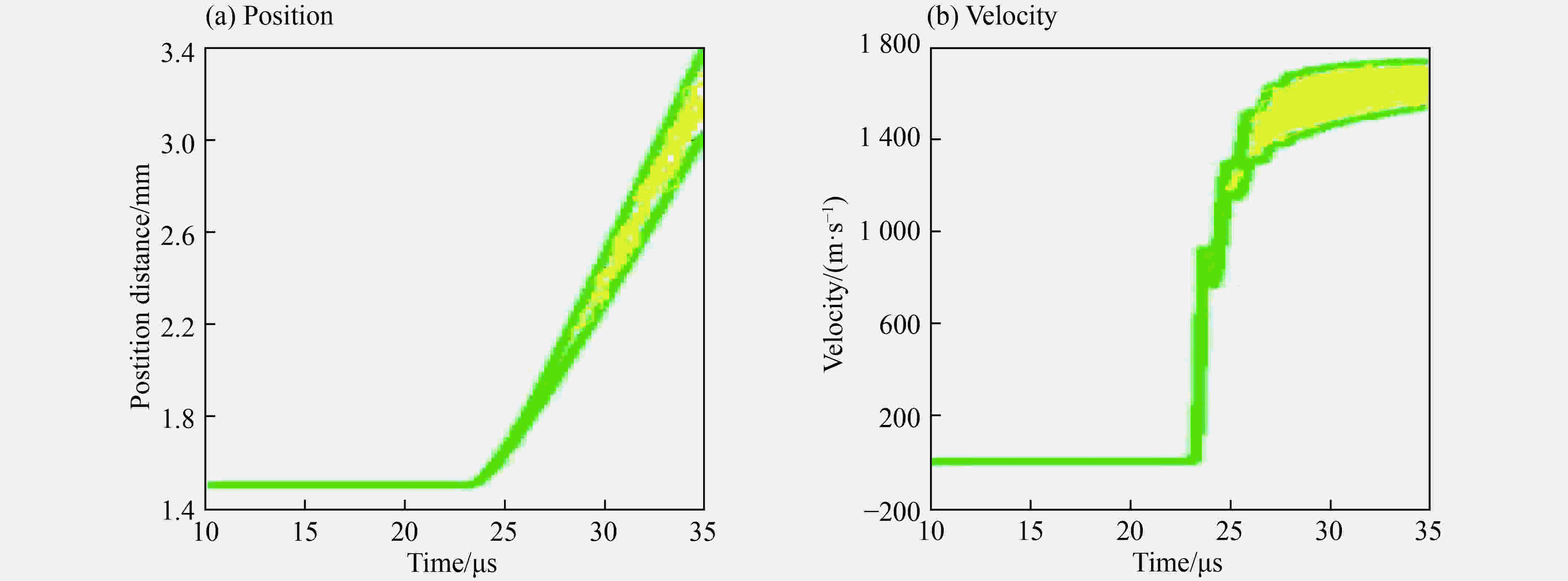
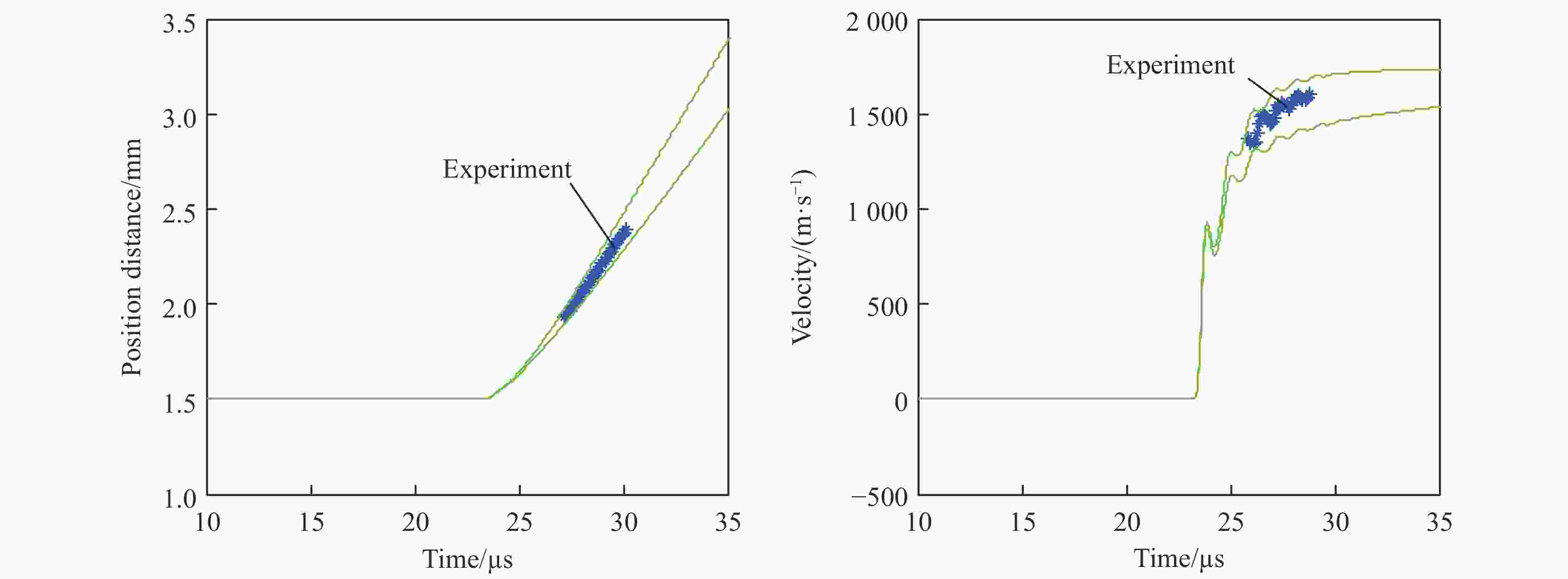
Abstract:
The mathematical-physical model used to describe the detonation dynamics has many uncertain factors due to the complexity and lack of knowledge for detonation phenomenon. Quantifying and assessing the impact of input uncertainties on output of detonation systems has a direct influence on reducing the risk based on the numerical model and simulation results for detonation. The Wiener chaos based on adapted basis is used to deal with the uncertainty quantification of high-dimensional random variables for detonation simulation. The rotation transformation and projection method is used to reduce the length of truncation number. Rosenblatt transformation is used to transform the set of dependent random variables into independent random variables. The equality of probability principle is used to change the non-Gaussian random variables into standard random variables. Uncertainty quantifications of the cylinder test with high dimensional input uncertainties are studied. The statistical informations such as mean, standard deviations, and confidence intervals are presented. The simulation results coincide with the experimental data, and the accuracy of the model is validated.
- cylinder test /
- uncertainty quantification /
- adapted basis /
- JWL EOS /
- Rosenblatt transform

HTML全文

图 1 不确定度的概率密度函数

Figure 1. Probability density function of uncertainty

下载: 全尺寸图片幻灯片

图 2 圆筒实验装置示意图

Figure 2. Schematic diagram of cylinder test

下载: 全尺寸图片幻灯片

图 3 JOB-9003圆筒实验结果

Figure 3. Experimental results of JOB-9003 in cylinder test

下载: 全尺寸图片幻灯片

图 4 管壁位置的期望与标准差

Figure 4. Expectation and standard deviation of cylindrical wall position

下载: 全尺寸图片幻灯片

图 5 管壁速度的期望与标准差

Figure 5. Expectation and standard deviation of cylindrical wall velocity

下载: 全尺寸图片幻灯片

图 8 实验数据和计算结果的置信区间的局部放大图

Figure 8. Local enlargement confidence intervals of experimental and simulation results

下载: 全尺寸图片幻灯片

图 6 管壁位置和速度的置信区间

Figure 6. Confidence intervals of position of cylindrical wall position and velocity

下载: 全尺寸图片幻灯片

图 7 实验数据和计算结果的置信区间

Figure 7. Confidence intervals of experimental and simulation results

下载: 全尺寸图片幻灯片

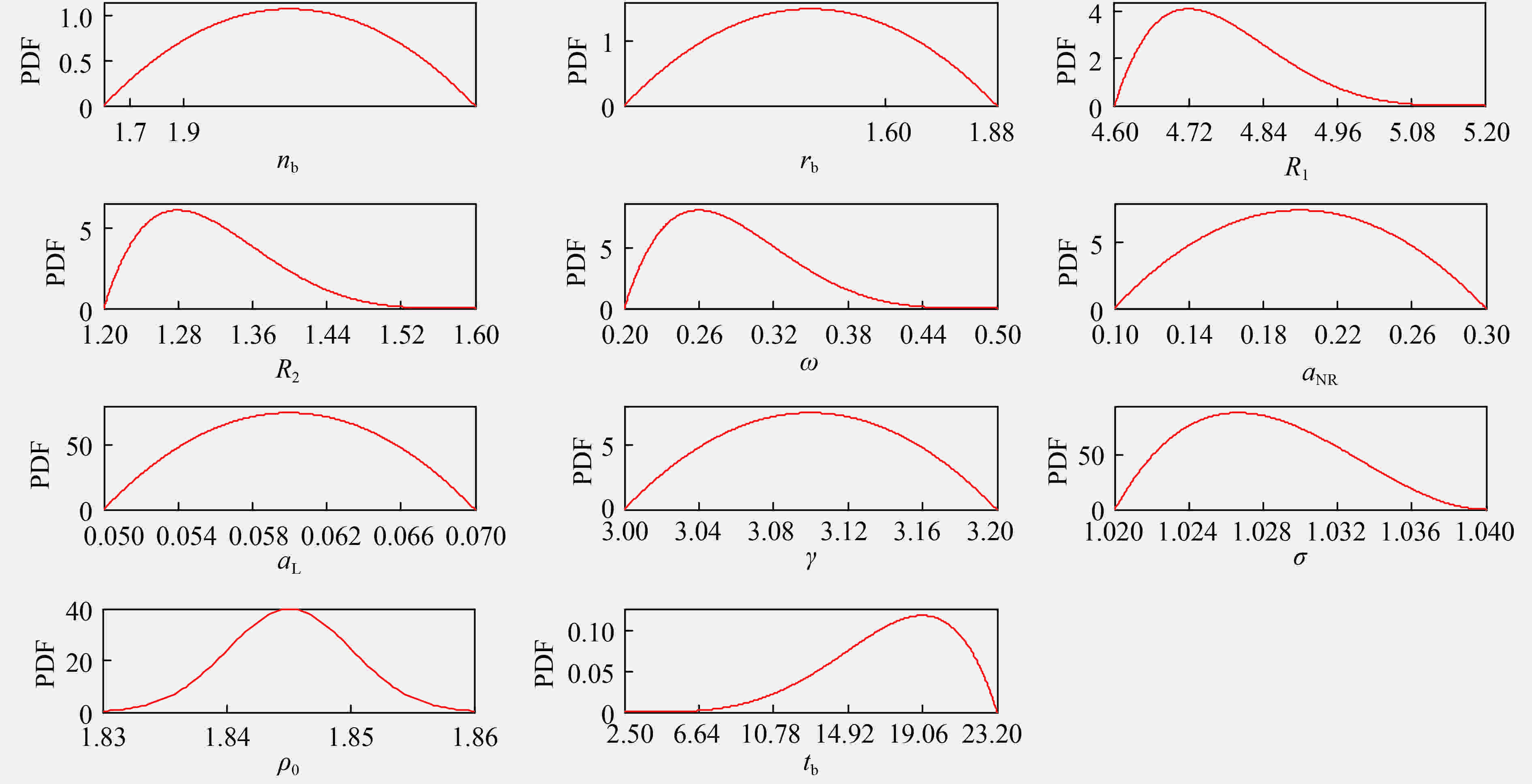
表 1 爆轰流体力学中的不确定度来源

Table 1. Sources of uncertainty in detonation hydrodynamics

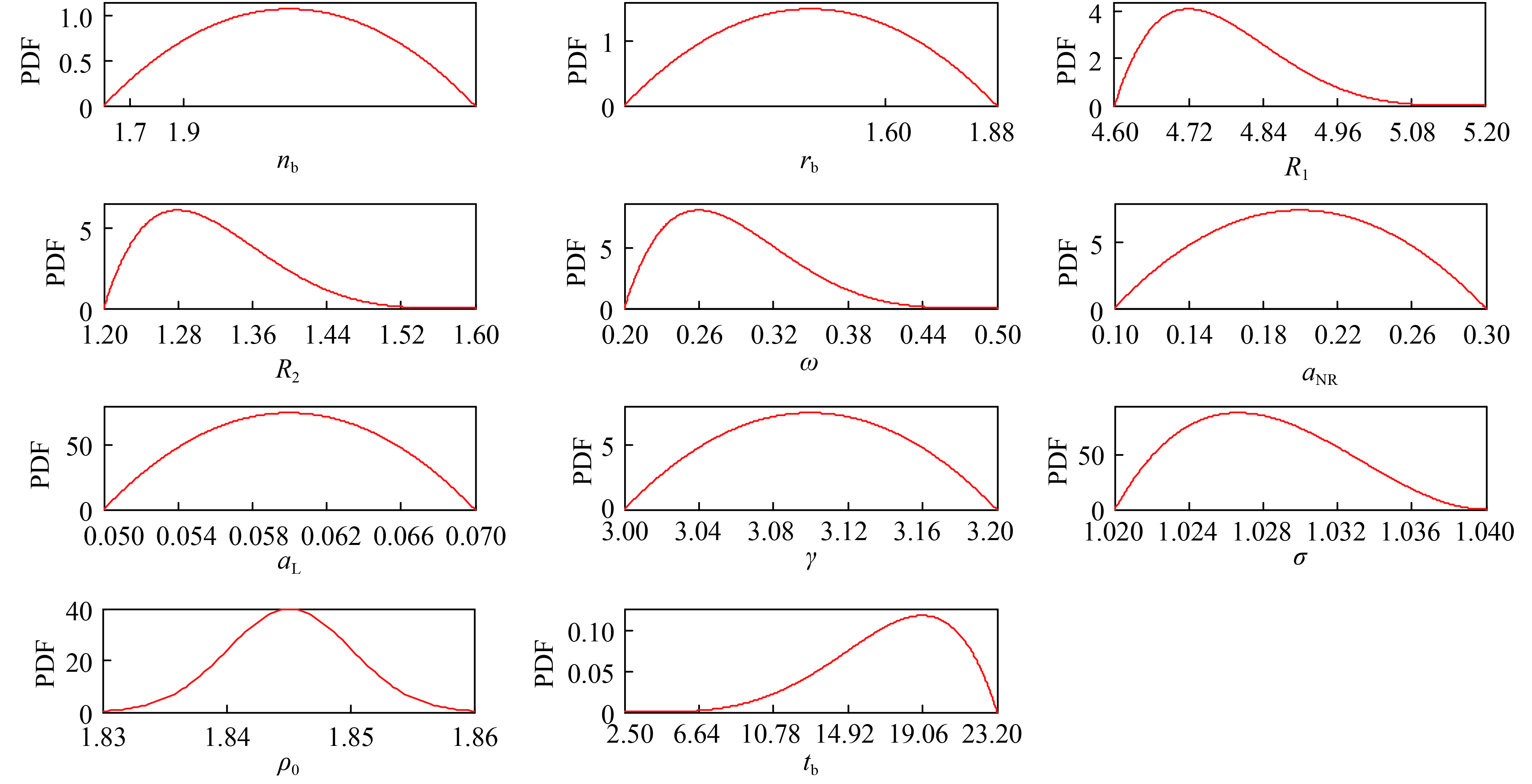
符号	不确定度	描述	概率分布
${\xi _1}$	${n_{\rm{b}}}$	可调参数	${n_{\rm{b}}}\simfont\text{～} {B}[{\alpha _{{{n}_{\rm{b}}}}},{\beta _{{{n}_{\rm{b}}}}},{a_{{{n}_{\rm{b}}}}},{b_{{{n}_{\rm{b}}}}}]$
${\xi _2}$	${r_{\rm{b}}}$	可调参数	${r_{\rm{b}}}\simfont\text{～} {B}[{\alpha _{{{r}_{\rm{b}}}}},{\beta _{{{r}_{\rm{b}}}}},{a_{{{r}_{\rm{b}}}}},{b_{{{r}_{\rm{b}}}}}]$
${\xi _3}$	${R_1}$	JWL EOS系数	${R_1}\simfont\text{～} {B}[{\alpha _{{\rm{R}_1}}},{\beta _{{\rm{R}_1}}},{a_{{\rm{R}_1}}},{b_{{\rm{R}_1}}}]$
${\xi _4}$	${R_2}$	JWL EOS系数	${R_2}\simfont\text{～} {B}[{\alpha _{{\rm{R}_2}}},{\beta _{{\rm{R}_2}}},{a_{{\rm{R}_2}}},{b_{{\rm{R}_2}}}]$
${\xi _5}$	$\omega $	JWL EOS系数	$\omega \simfont\text{～} {B}[{\alpha _{{\omega}} },{\beta _{{\omega}} },{a_{{\omega}} },{b_{{\omega}} }]$
${\xi _6}$	${a_{\rm{NR}}}$	N-R人为黏性系数	${a_{\rm{NR}}}\simfont\text{～} {B}[{\alpha _{{{a}_{\rm{NR}}}}},{\beta _{{{a}_{\rm{NR}}}}},{a_{{{a}_{\rm{NR}}}}},{b_{{{a}_{\rm{NR}}}}}]$
${\xi _7}$	${a_{\rm{L}}}$	Landshoff人为黏性系数	${a_{\rm{L}}}\simfont\text{～} {B}[{\alpha _{{{a}_{\rm{L}}}}},{\beta _{{{a}_{\rm{L}}}}},{a_{{{a}_{\rm{L}}}}},{b_{{{a}_{\rm{L}}}}}]$
${\xi _8}$	γ	Gruneissen系数	$\gamma \simfont\text{～} {B}[{\alpha _{{\gamma}} },{\beta _{{\gamma}} },{a_{{\gamma}} },{b_{{\gamma}} }]$
${\xi _9}$	σ	体积起爆阈值	$\sigma \simfont\text{～}{B}[{\alpha _\sigma },{\beta _\sigma },{a_\sigma },{b_\sigma }]$
${\xi _{10}}$	$\rho $	TNT初始密度	${N}\left({{\mu }_{{\rho}}},\ \sigma _{{\rho}} ^{2} \right)$
${\xi _{11}}$	${t_{\rm{b}}}$	起爆时间	${{t}_{\rm{b}}}\simfont\text{～}{B}[{{\alpha }_{{{{t}}_{\rm{b}}}}},{{\beta }_{{{{t}}_{\rm{b}}}}},{{a}_{{{{t}}_{\rm{b}}}}},{{b}_{{{{t}}_{\rm{b}}}}}]$

下载: 导出CSV

参考文献(16)

[1]	章冠人, 陈大年. 凝聚炸药起爆动力学[M]. 北京: 国防工业出版社, 1991.
[2]	孙锦山. 凝聚炸药非理想爆轰的数值模拟 [J]. 力学进展, 1995, 25(1): 127–133. DOI: 10.6052/1000-0992-1995-1-J1995-043 SUN Jinshan. Numerical modeling of non-ideal detonation in condensed explosives [J]. Advances in Mechanics, 1995, 25(1): 127–133. DOI: 10.6052/1000-0992-1995-1-J1995-043
[3]	王瑞利, 江松. 多物理耦合非线性偏微分方程与数值解不 [J]. 中国科学: 数学, 2015, 45(6): 723–738. DOI: 10.1360/N012014-00115 WANG Ruili, JIANG Song. Mathematical methods for uncertainty quantification in nonlinear multi-physics systems and their numerical simulations [J]. Scientia Sinica: Mathematica, 2015, 45(6): 723–738. DOI: 10.1360/N012014-00115
[4]	王成, SHU Chiwang. 爆炸力学高精度数值模拟研究进展 [J]. 科学通报, 2015, 60(10): 882–898. DOI: 10.1360/N972014-00936 WANG Cheng, SHU Chiwang. Progresses in high-resolution numerical simulation of explosion mechanics [J]. Chinese Science Bulletin, 2015, 60(10): 882–898. DOI: 10.1360/N972014-00936
[5]	梁霄, 王瑞利. 爆轰流体力学模型敏感度分析与模型确认 [J]. 物理学报, 2017, 66(11): 116401. DOI: 10.7498/aps.66.116401 LIANG Xiao, WANG Ruili. Sensitivity analysis and validation of detonation computational fluid dynamics model [J]. Acta Physica Sinica, 2017, 66(11): 116401. DOI: 10.7498/aps.66.116401
[6]	梁霄, 王瑞利. 混合不确定度量化方法及其在计算流体动力学迎风格式中的应用 [J]. 爆炸与冲击, 2016, 36(4): 505–519. DOI: 10.11883/1001-1455(2016)04-0509-07 LIANG Xiao, WANG Ruili. Mixed uncertainty quantification and its application in upwind scheme for computational fluid mechanics [J]. Explosion and Shock Waves, 2016, 36(4): 505–519. DOI: 10.11883/1001-1455(2016)04-0509-07
[7]	汤涛, 周涛. 不确定性量化的高精度数值方法和理论 [J]. 中国科学: 数学, 2015, 45(7): 891–928. DOI: 10.1360/N012014-00218 TANG Tao, ZHOU Tao. Recent developments in high order numerical methods for uncertainty quantification [J]. Scientia Sinica Mathematica, 2015, 45(7): 891–928. DOI: 10.1360/N012014-00218
[8]	GHANEM R, SPANOS R. Stochastic finite elements: A spectral approach[M]. New York: Springer, 1991.
[9]	梁霄, 王瑞利. 爆炸波中的混合不确定度量化方法 [J]. 计算物理, 2017, 34(5): 574–582. DOI: 1001-246X(2017)05-0574-09 LIANG Xiao, WANG Ruili. Mixed uncertainty quantification of blast wave problem [J]. Chinese Journal of Computational Physics, 2017, 34(5): 574–582. DOI: 1001-246X(2017)05-0574-09
[10]	HUAN X, GERACI G, SAFTA C, et al. Multifidelity statistical analysis of large eddy simulation in Scramjet computations[C]//AIAA non-deterministic Approaches Conference. 2018: 1−11. DOI: 10.2514/6.2017-1089.
[11]	HUAN X, SAFTA C, SARGSYAN K, et al. Compressive sensing with cross-validation and stop-sampling for sparse polynomial chaos expansions [J]. SIAM/ASA Journal on Uncertainty Quantification, 2018, 6(2): 907–936. DOI: 10.1137/17M1141096.
[12]	王瑞利, 林忠, 魏兰, 等. 利用前沿推进法计算复杂炸药结构的起爆时间 [J]. 高压物理学报, 2015, 29(4): 286–292. DOI: 10.11858/gywlxb.2015.04.008 WANG Ruili, LIN Zhong, WEI Lan, et al. Calculating the initiation time of the explosive with complex structure using the advancing front technique [J]. Chinese Journal of High Pressure Physics, 2015, 29(4): 286–292. DOI: 10.11858/gywlxb.2015.04.008
[13]	TIPIREDDY R, GHANEM R. Basis adaptation in homogeneous chaos spaces [J]. Journal of Computational Physics, 2014, 259(3): 304–317. DOI: 10.1016/j.jcp.2013.12.009.
[14]	TSILIFIS P, GHANEM R. Reduced Wiener chaos representation of random fields via basis adaptation and projection [J]. Journal of Computational Physics, 2017, 341: 102–120. DOI: 10.1016/j.jcp.2017.04.009.
[15]	CAMERON R, MARTIN W. The orthogonal development of nonlinear functional in series of Fourier-Hermite functional [J]. Annals Mathematics, 1947, 48(2): 385–392. DOI: 10.2307/1969178.
[16]	ROSENBLATT M. Remarks on a multivariate transformation [J]. Annals of Mathematical Statistics, 1952, 23: 470–472. DOI: 10.1007/978-l-4419-8339-8_8.