PBX-1炸药的力学性能和本构关系

孙文旭; 罗智恒; 唐明峰; 李明; 刘彤; 章定国

doi:10.11883/bzycj-2018-0398

PBX-1炸药的力学性能和本构关系

doi: 10.11883/bzycj-2018-0398

孙文旭^{1, 2, 3,},
罗智恒^{2, 3},
唐明峰²,
李明²,
刘彤^{3, 4, ,},
章定国¹

1.
南京理工大学理学院，江苏南京 210094
2.
中国工程物理研究院化工材料研究所，四川绵阳 621999
3.
中国工程物理研究院研究生院，四川绵阳 621999
4.
中国工程物理研究院成都科学技术发展中心，四川成都 610200

详细信息

作者简介:
孙文旭（1986－　），男，博士研究生，助理研究员，664729892@qq.com

通讯作者:
刘　彤（1964－　），男，研究员，Tliu@swust.edu.cn

中图分类号: O381
计量
- 文章访问数: 6001
- HTML全文浏览量: 2795
- PDF下载量: 133
- 被引次数: 0
出版历程
- 收稿日期: 2018-10-17
- 修回日期: 2018-12-03
- 刊出日期: 2019-07-01

Compressive mechanical properties and constitutive relations of PBX-1

SUN Wenxu^{1, 2, 3
,},
LUO Zhiheng^{2, 3},
TANG Mingfeng²,
LI Ming²,
LIU Tong^{3, 4
, ,},
ZHANG Dingguo¹

1.
School of Sciences, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China
2.
Institute of Chemical Materials, China Academy of Engineering Physics, Mianyang 621900, Sichuan, China
3.
Graduate School of China Academy of Engineering Physics, Mianyang 621999, Sichuan, China
4.
Chengdu Science Development Center of China Academy of Engineering Physics, Chengdu 610200, Sichuan, China

摘要

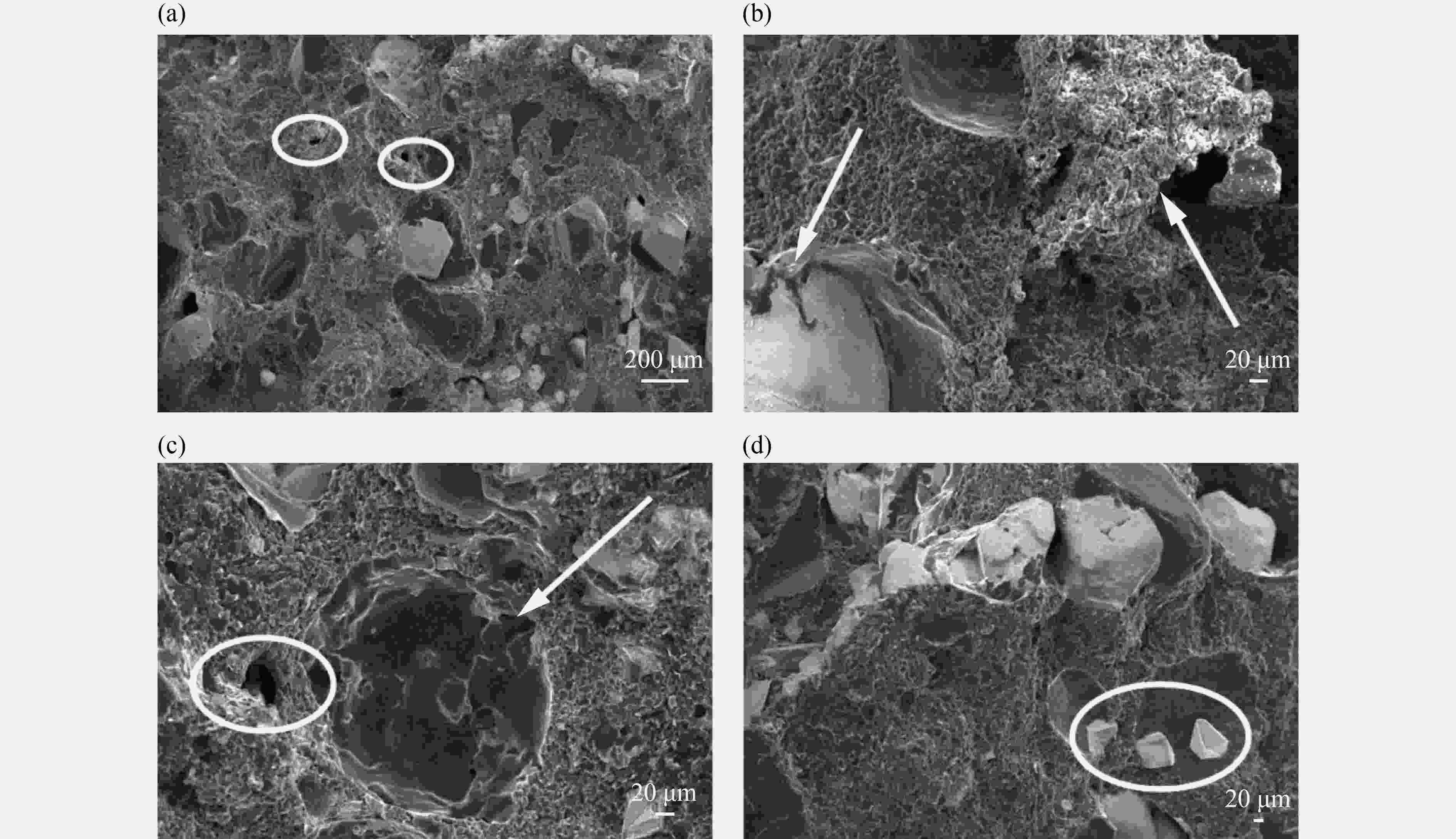
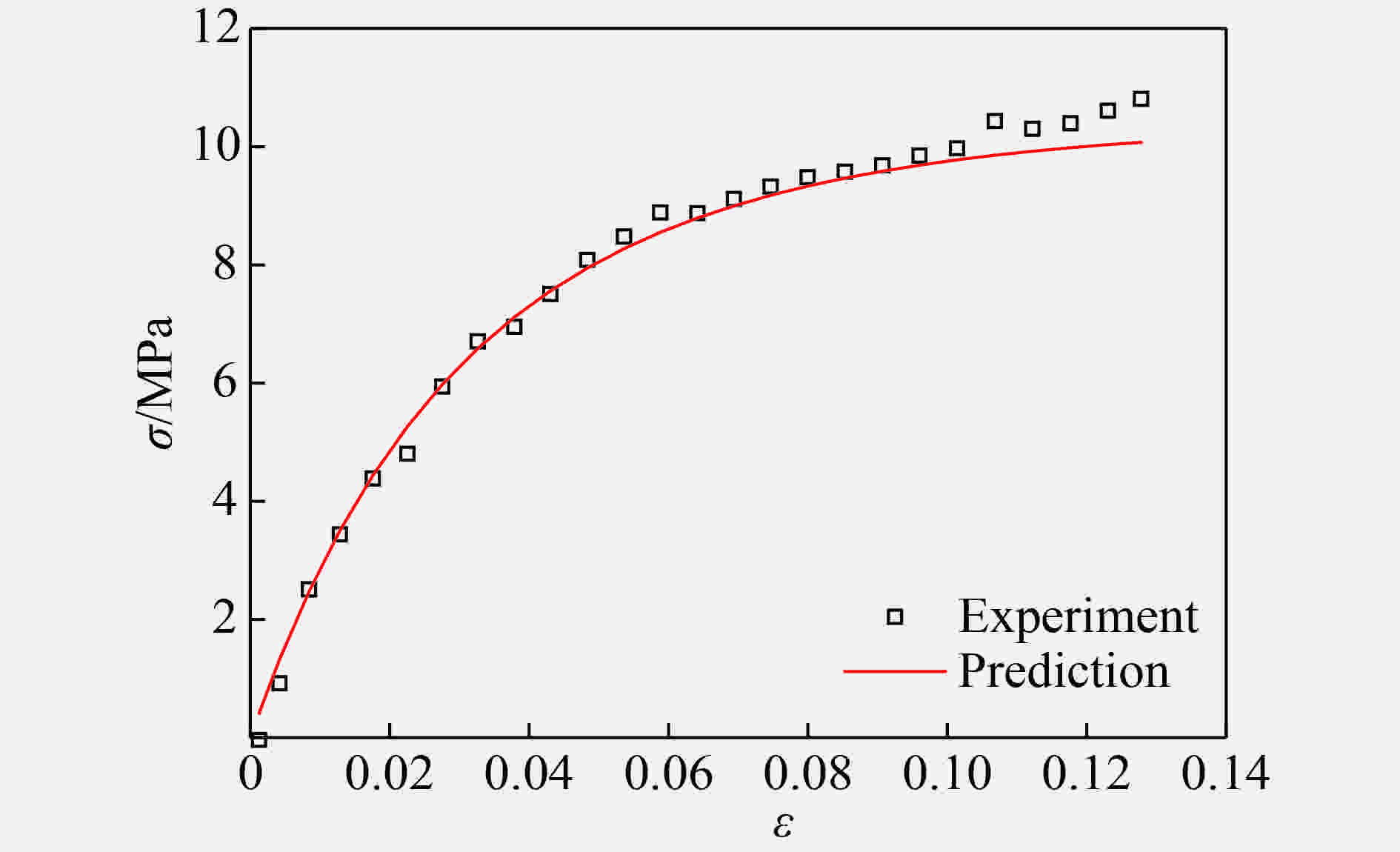
摘要: PBX的力学行为对其安全性有重要影响。为研究PBX-1的力学性能，以PBX-1为研究对象，进行准静态力学实验和SHPB（分离式霍普金森压杆）实验研究。结果表明，准静态压缩实验中，试样的裂纹出现在与加载方向大约成45°的最大剪应力方向。SHPB实验中，在应变率100～1 500 s⁻¹范围内，随着应变率的提高，PBX-1炸药的动态屈服强度、动态压缩强度和破坏应变不断提高。动态屈服强度逐渐从静态的2.77 MPa增加至16.1 MPa；压缩强度从7.46 MPa增加至16.1 MPa，破坏应变从6.23%增加到26.4%。同时，基于Z-W-T模型，建立了一种含损伤的动态黏弹性本构模型，在330～1 500 s⁻¹应变率范围内具有较高的精度，可以较好地描述PBX-1炸药在达到破坏前的动态力学行为。
- PBX-1炸药 /
- 动态力学行为 /
- 损伤 /
- Z-W-T模型
Abstract: The mechanical behavior of PBX has an important impact on its safety. In order to study the mechanical properties of PBX-1, the quasi-static mechanical experiments and SHPB (split-Hopkinson pressure bar) experiments were conducted. The results showed that the crack direction was the direction of maximum shear stress, which was about 45° to the loading direction in the quasi static compression tests. In the SHPB tests, the dynamic yield strength, dynamic compression strength and failure strain of PBX-1 explosive were continuously improved with the improvement of strain rate in the range of 100−1 500 s⁻¹.The dynamic yield strength gradually increased from the static 2.77 MPa to 16.1 MPa. The compression strength increased from 7.46 MPa to 16.1 MPa, and the failure strain increased from 6.23% to 26.4%. At the same time, based on the Z-W-T model, a dynamic viscoelastic constitutive model with damage was established. It has a high accuracy in the range of 330−1 500 s⁻¹ strain rate, and could be used to describe the dynamic mechanical behavior of PBX-1 before failure.
- PBX-1 explosive /
- dynamic behavior /
- damage /
- Z-W-T constitutive model

HTML全文

图 1 PBX-1炸药的宏观裂纹形貌

Figure 1. Macro crack feature of PBX-1

下载: 全尺寸图片幻灯片

图 2 PBX-1炸药的典型细观形貌

Figure 2. Typical meso-scale features of PBX-1

下载: 全尺寸图片幻灯片

图 3 不同速度加载后的试样破坏状态

Figure 3. Damage status under various velocity loading

下载: 全尺寸图片幻灯片

图 4 PBX-1炸药不同应变率下的应力(σ)-应变(ε)曲线

Figure 4. Stress-strain relationship of PBX-1 under various strain (σ)-rates (ε)

下载: 全尺寸图片幻灯片

图 5 PBX-1炸药强度和失效应变随应变率变化

Figure 5. Relations between strength/failure strain and strain rate

下载: 全尺寸图片幻灯片

图 6 Z-W-T非线性黏弹本构模型

Figure 6. Z-W-T non-linear viscoelastic constitutive model

下载: 全尺寸图片幻灯片

图 7 实验测试曲线与拟合曲线

Figure 7. Comparison between experimental and fitting curves

下载: 全尺寸图片幻灯片

图 8 模型计算曲线与实验测试曲线对比（$\dot \varepsilon $=660 s⁻¹）

Figure 8. Comparison between experimental and calculated curves ($\dot \varepsilon $=660 s⁻¹)

下载: 全尺寸图片幻灯片

表 1 本构模型材料参数

Table 1. Parameter values of constitutive models

D₀	D₁	c	a	σ_m/MPa	m	E₂/MPa	θ₂/μs
8.591	−0.484	1.167	5.480	5.480	43.687	101.156	75.482

下载: 导出CSV

参考文献(13)

[1]	舒远杰, 霍冀川. 炸药学概论 [M]. 北京: 化学工业出版社, 2011: 187−197. SHU Yuanjie, HUO Jichuan. Introduction to explosives [M]. Beijing: Chemical Industry Press, 2011: 187−197.
[2]	王礼立, 施绍裘, 陈江瑛, 等. ZWT非线性热粘弹性本构关系的研究与应用 [J]. 宁波大学学报(理工版), 2000, 139(S): 141–149. DOI: 1001-5132(2000)Sup-0141-09. WANG Lili, SHI Shaoqiu, CHEN Jiangying, et al. Study and application of nonlinear thermo-viscoelastic constitutive relations based on ZWT model [J]. Journal of Ningbo University (Natural Science and Engineering Edition), 2000, 139(S): 141–149. DOI: 1001-5132(2000)Sup-0141-09.
[3]	罗景润. PBX的损伤、断裂及本构关系研究 [D]. 绵阳: 中国工程物理研究院, 2001: 1−19. LUO Jingrun. Study on damage, fracture and constitutive relationship of PBX [D]. Mianyang: China Academy of Engineering Physics, 2001: 1−19.
[4]	陈广南, 张为华, 刘子如, 等. 固体推进剂裂纹摩擦热点形成细观模型分析 [J]. 国防科技大学学报, 2006, 28(1): 5–8. DOI: 10.3969/j.issn.1001-2486.2006.01.002. CHEN Guangnan, ZHANG Weihua, LIU Ziru, et al. Meso-scale hot-spot model of crack friction in solid propellant [J]. Journal of National University of Defense Technology, 2006, 28(1): 5–8. DOI: 10.3969/j.issn.1001-2486.2006.01.002.
[5]	SONG B, CHEN W, MING C. Novel model for uniaxial strain-rate-dependent stress-strain behavior of ethylene-propylene-diene monomer rubber in compression or tension [J]. Journal of Applied Polymer Science, 2002, 92(3): 1553–1558. DOI: 10.1002/app.20095.
[6]	王宝珍, 胡时胜, 周相荣. 不同温度下橡胶的动态力学性能及本构模型研究 [J]. 实验力学, 2007, 22(1): 1–6. DOI: 10.3969/j.issn.1001-4888.2007.01.001. WANG Baozhen, HU Shisheng, ZHOU Xiangrong. Research of dynamic mechanical behavior and constitutive model of rubber under different temperatures [J]. Journal of Experimental Mechanics, 2007, 22(1): 1–6. DOI: 10.3969/j.issn.1001-4888.2007.01.001.
[7]	卢强, 王占江, 王礼立, 等. 基于ZWT方程的线黏弹性球面波分析 [J]. 爆炸与冲击, 2013, 33(5): 463–470. DOI: 10.11883/1001-1455(2013)05-0463-08. LU Qiang, WANG Zhanjiang, WANG Lili, et al. Analysis of linear visco-elastic spherical waves based on ZWT constitutive equation [J]. Explosion and Shock Waves, 2013, 33(5): 463–470. DOI: 10.11883/1001-1455(2013)05-0463-08.
[8]	张延耿, 楼建锋, 周婷婷, 等. PBX炸药含各向异性损伤的黏弹性统计微裂纹本构模型初步研究 [J]. 高压物理学报, 2016, 30(4): 301–310. DOI: 10.11858/gywlxb.2016.04.006. ZHANG Yangeng, LOU Jianfeng, ZHOU Tingting, et al. Initial study on constitutive model of PBXs via viscoelastic statistical crack mechanics including anisotropic damage [J]. Chinese Journal of High Pressure Physics, 2016, 30(4): 301–310. DOI: 10.11858/gywlxb.2016.04.006.
[9]	敬仕明. PBX有效力学性能及本构关系研究 [D]. 绵阳: 中国工程物理研究院, 2009: 30−65. JIN Shiming. Study on the effective mechanical properties and constitutive relations of PBX [D]. Mianyang: China Academy of Engineering Physics, 2009: 30−65.
[10]	成丽蓉, 施惠基. PBX炸药含裂纹扩展损伤的粘塑性本构关系 [J]. 含能材料, 2015, 23(10): 999–1003. DOI: 10.11943/j.issn.1006-9941.2015.10.015. CHENG Lirong, SHI Huiji. Elastic-viscoplastic constitutive coupled micro-cracks propagation damage of PBX [J]. Chinese Journal of Energetic Materials, 2015, 23(10): 999–1003. DOI: 10.11943/j.issn.1006-9941.2015.10.015.
[11]	孙朝翔, 鞠玉涛, 郑亚, 等. 双基推进剂的高应变率力学特性及其含损伤ZWT本构 [J]. 爆炸与冲击, 2013, 33(5): 507–512. DOI: 10.11883/1001-1455(2013)05-0507-06. SUN Chaoxiang, JU Yutao, ZHENG Ya, et al. Mechanical properties of double-base propellant at high strain rates and its damage-modified ZWT constitutive mode [J]. Explosion and Shock Waves, 2013, 33(5): 507–512. DOI: 10.11883/1001-1455(2013)05-0507-06.
[12]	王礼立, 董新龙, 孙紫建. 高应变率下计及损伤演化的材料动态本构行为 [J]. 爆炸与冲击, 2006, 26(3): 193–198. DOI: 10.11883/1001-1455(2006)03-0193-06. WANG Lili, DONG Xinlong, SUN Zijian. Dynamic constitutive behavior of materials at high strain rate taking account of damage evolution [J]. Explosion and Shock Waves, 2006, 26(3): 193–198. DOI: 10.11883/1001-1455(2006)03-0193-06.
[13]	高军, 黄再兴. 多种群遗传算法在PBX本构模型参数识别中的应用 [J]. 爆炸与冲击, 2016, 36(6): 861–868. DOI: 10.11883/1001-1455(2016)06-0861-08. GAO Jun, HUANG Zaixing. Application of multiple-population genetic algorithm in parameter identification for PBX constitutive model [J]. Explosion and Shock Waves, 2016, 36(6): 861–868. DOI: 10.11883/1001-1455(2016)06-0861-08.