3D mesoscale modeling method and dynamic mechanical properties investigation of concrete
-
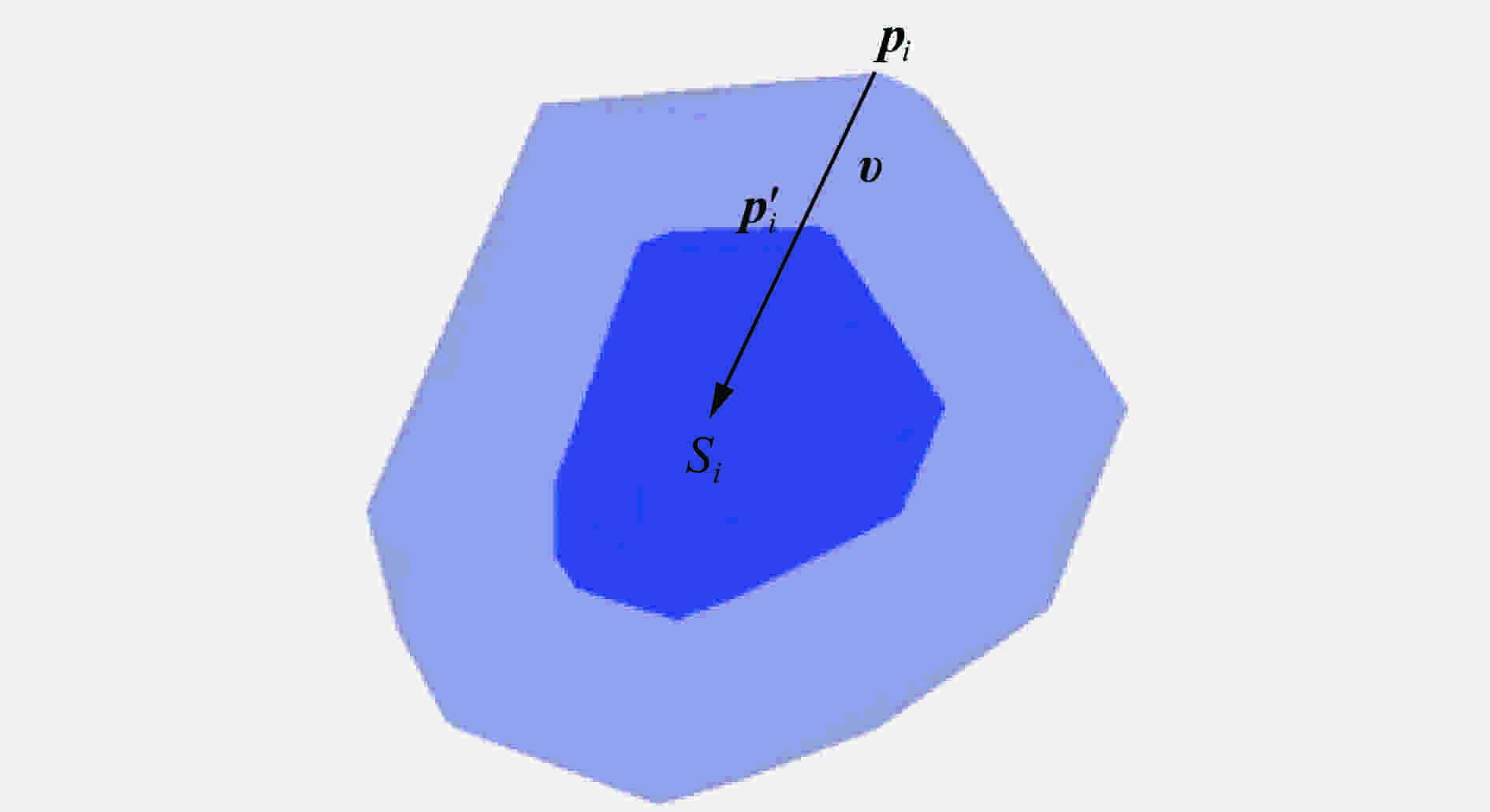
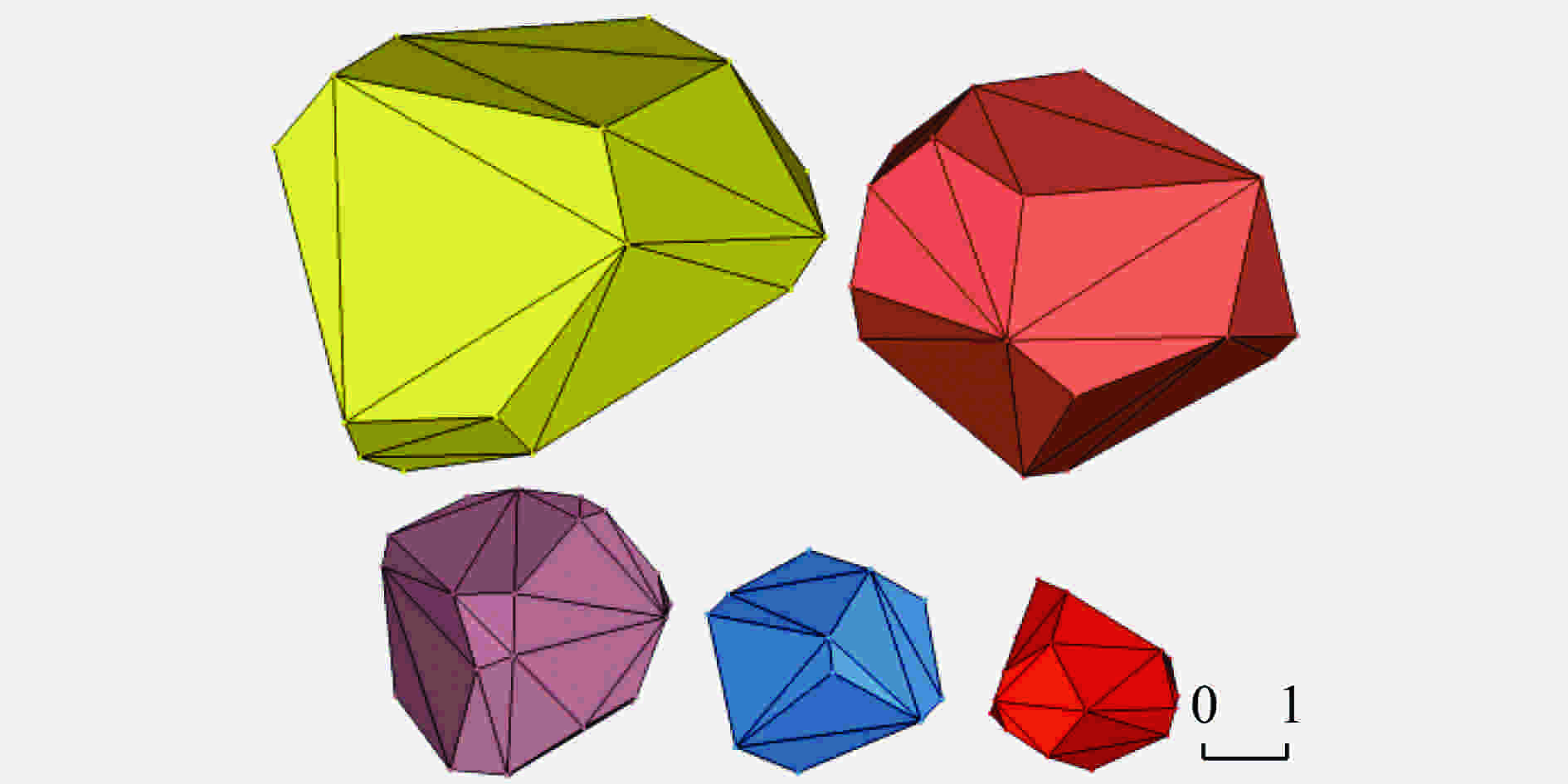
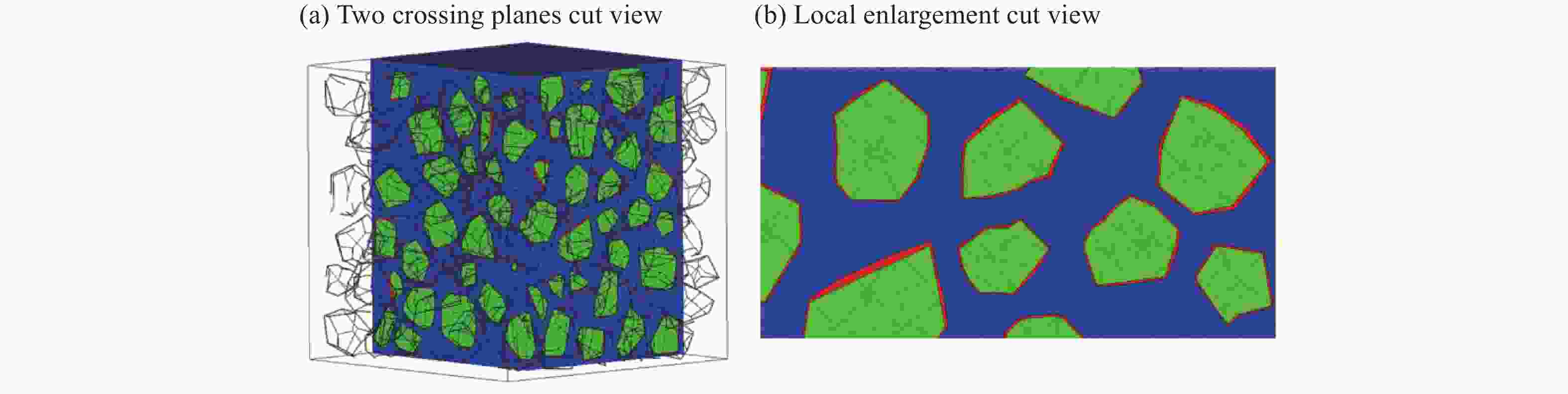
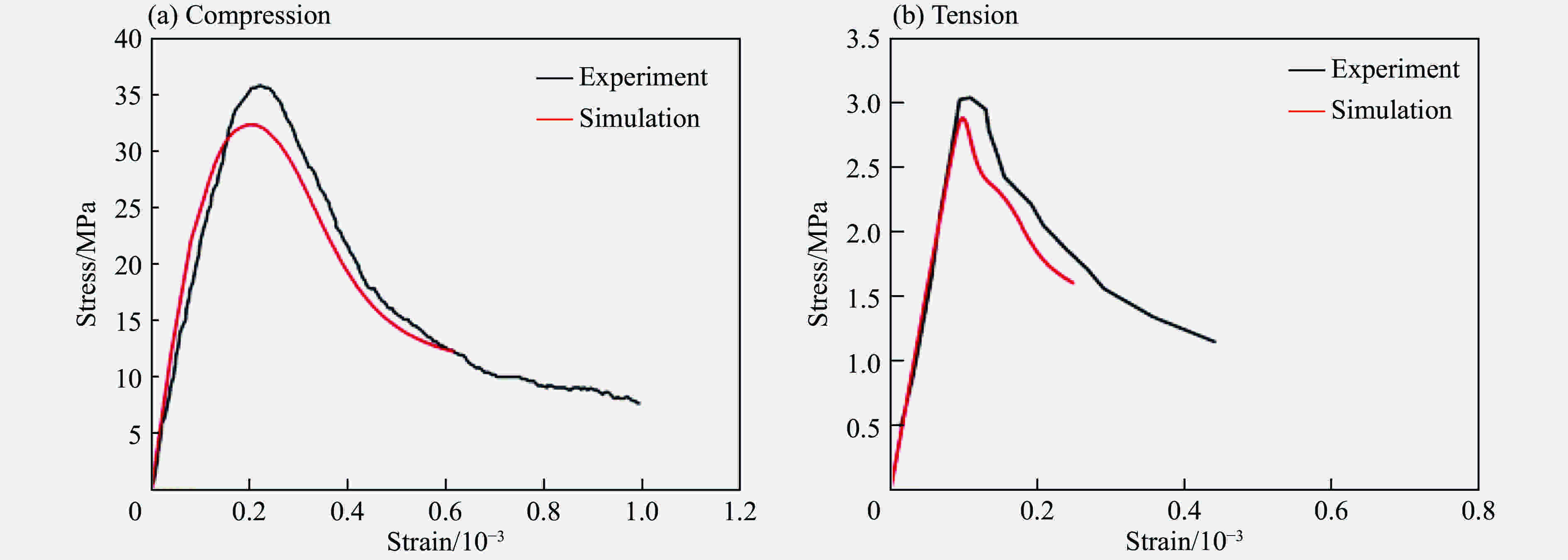
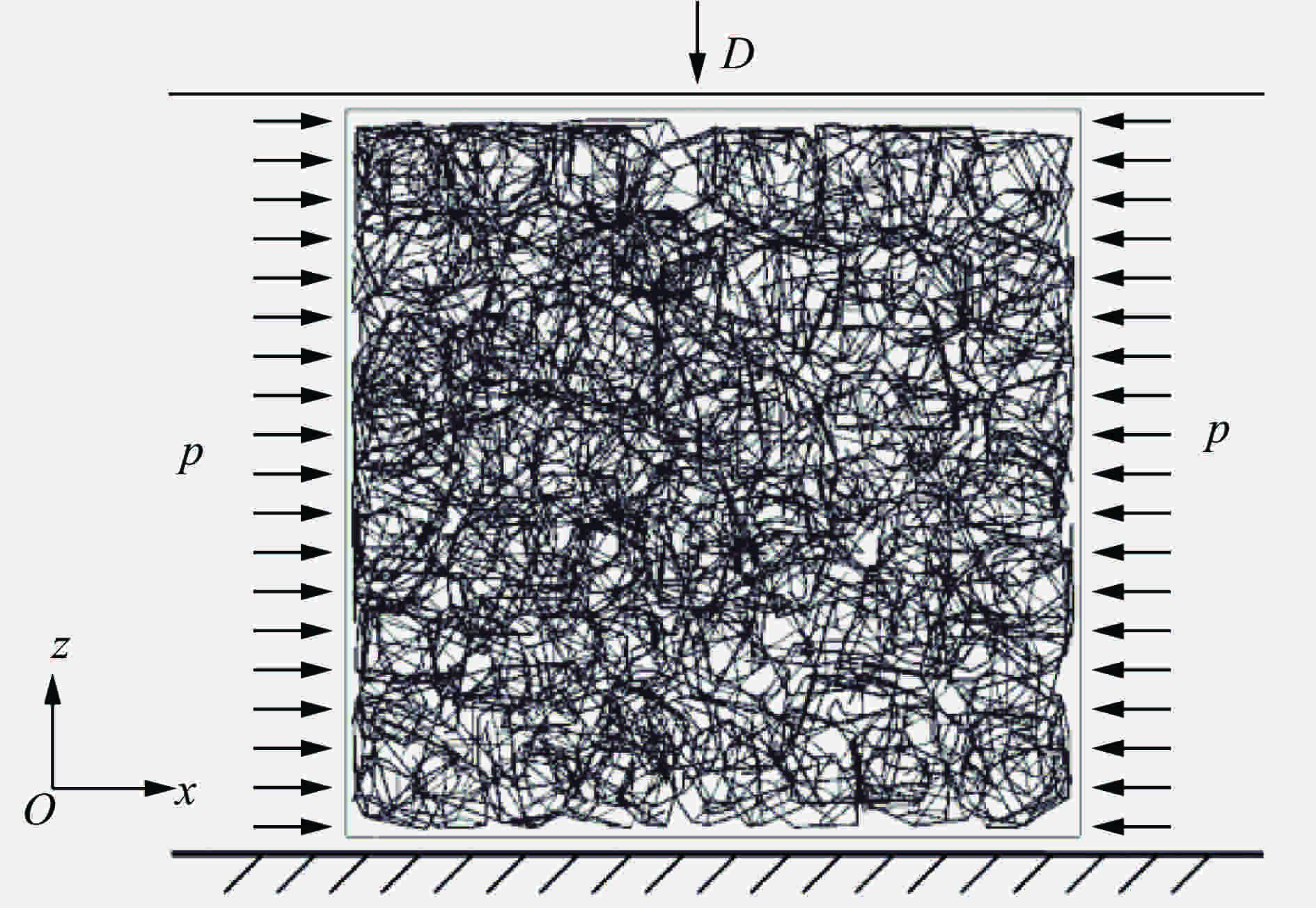
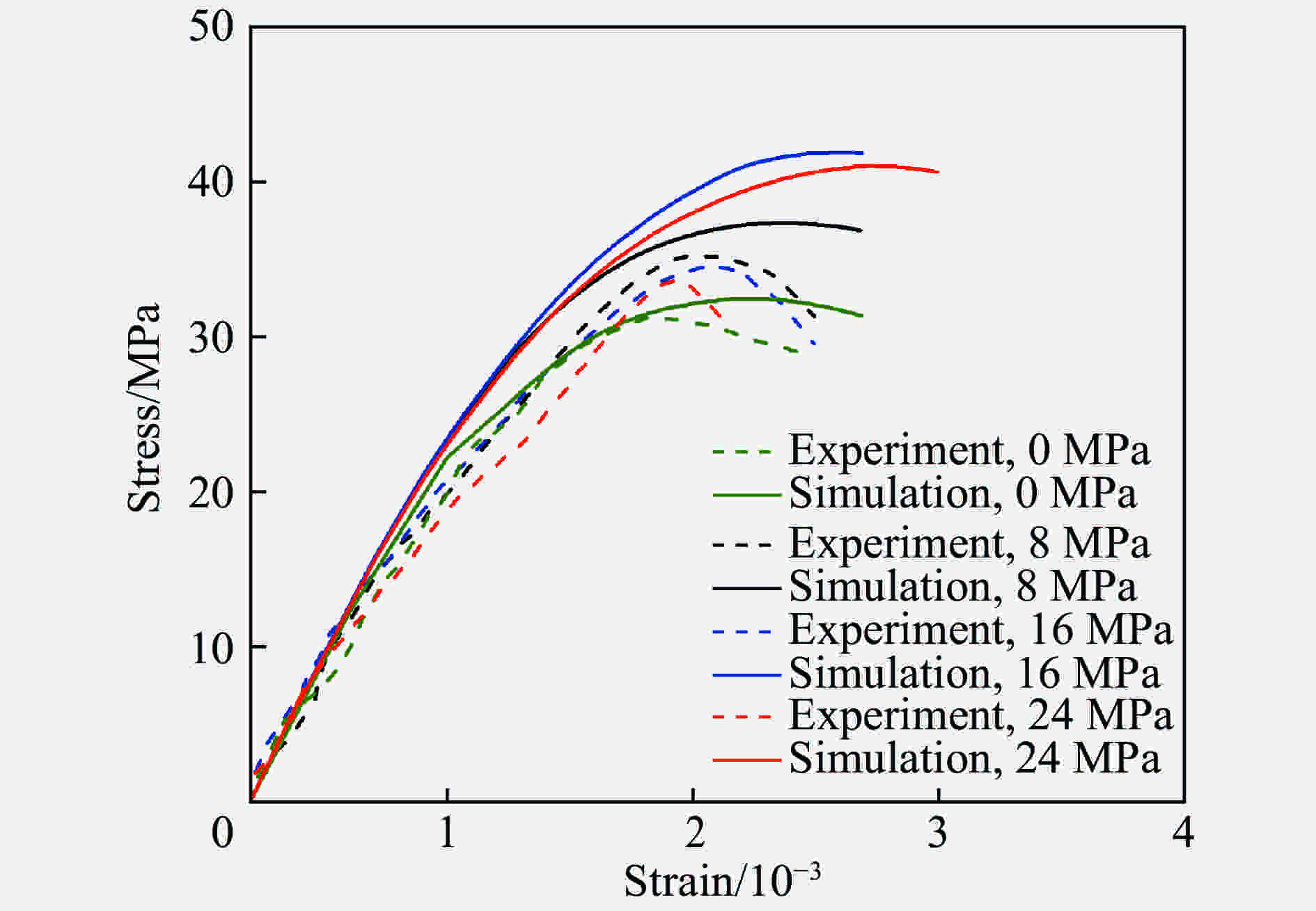
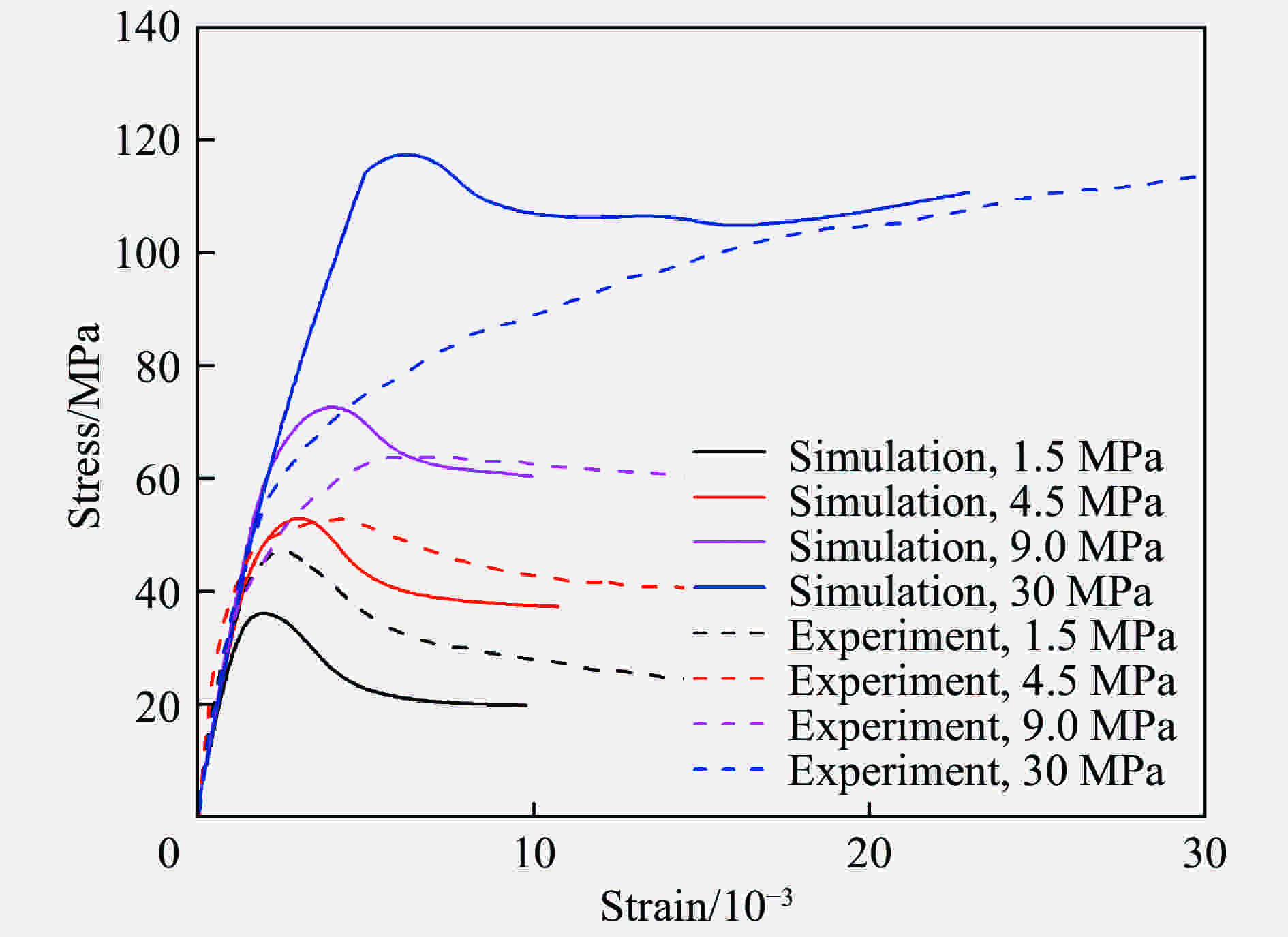
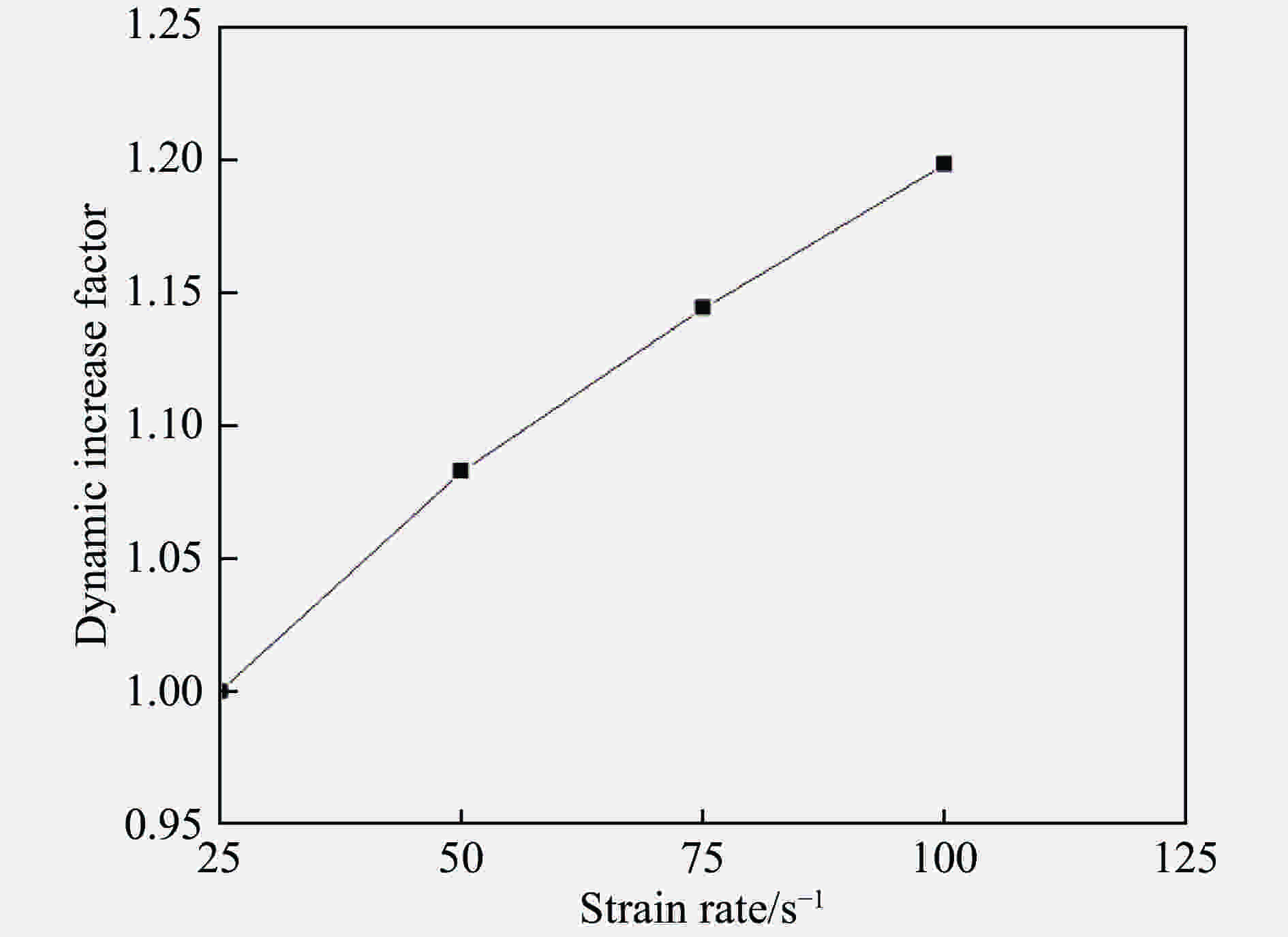
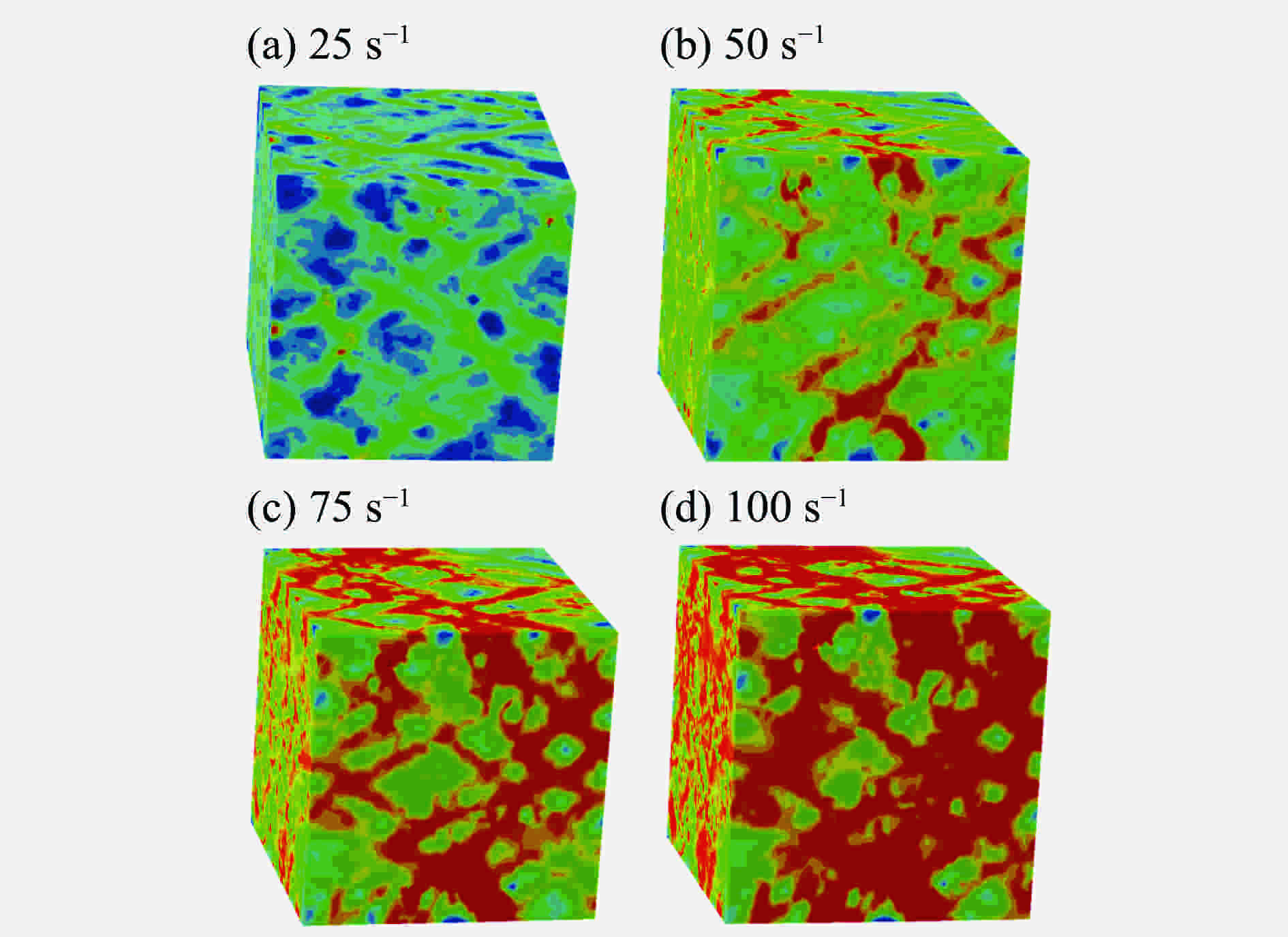
摘要: 根据混凝土材料的细观组成和结构特点，基于三维Voronoi图形提出了一种简单高效的混凝土细观模型生成方法，利用塑性损伤模型对该细观模型进行了单、多轴应力状态下的准静态分析以及SHPB动态有限元分析。结果表明，数值模拟得到的应力应变曲线和破坏模式与实验结果基本吻合，本文中提出的混凝土三维细观模型可较好地模拟混凝土的静、动态力学特性，为进一步从细观力学角度研究混凝土损伤演化规律和破坏机理提供了模型基础。Abstract: According to the mechanical properties and components of concrete from the mesoscale viewpoint, a simple and high-efficiency method based on 3D-Voronoi is proposed to construct realistic meso-structure model of concrete. In this paper, 3D mesoscale numerical simulation is conducted using damaged plasticity modeling under quasi-static and dynamic load. The simulation results resemble the corresponding experimental results both in strain-stress curves and failure modes. The current method can simulate static and dynamic mechanical properties well. In addition, the proved 3D model can provide an effective approach in elucidating fundamental mechanical behavior of concrete-like materials.
-
叠氮化铜异常敏感且威力大，曾经是一种严格禁用的起爆药[1]。但随着MEMS引信向灵巧化、智能化、微型化以及高可靠性、低成本等方向发展[2]，将叠氮化铜应用于MEMS引信系统中成为可能。J.Toon[3]制备了具有纳米多孔铜，将其作为军用雷管炸药的前驱体材料。L.Gerald[4]研究了一种薄膜炸药雷管，在基板上沉积铜金属层，然后利用金属层在装置中“原位”反应合成线性尺寸小于1 mm的起爆药，进而引爆下一级装药。J.Daniel[5]提出可将直径为2 mm、厚度为0.5 mm的多孔铜与叠氮酸“原位”反应生成一种起爆药。通过测试得出，该起爆药50%发火的临界能量为3.8 mJ(1 mF，87 V)，具有体积小、成本低、能耗低等优点，可用于子母弹和40 mm手榴弹等常规性弹药中。
为了进一步降低叠氮化铜的装药量，提高其使用的安全性，利用飞片聚能原理，叠氮化铜微装药爆轰驱动飞片冲击起爆钝感装药成为一项新的满足MEMS引信爆炸起爆序列需求的起爆技术。其原理是将具有孔隙结构的纳米多孔铜作为一种炸药前驱体材料组装于MEMS引信机构中，通过化学方法将纳米多孔铜“原位”转化成叠氮化物炸药，叠氮化铜爆轰驱动飞片冲击起爆下一级钝感装药。该微装药冲击起爆技术避免了装药和压药潜在的危险性，与MEMS技术集成可实现引信元器件的大批量生产，生产制备过程和爆炸作用后都不产生有害物质，对人与环境友好。
驱动飞片的完整性、平整性和速度是爆轰驱动技术中最关键的技术指标，影响这些指标的因素有微装药的尺寸、密度、飞片的尺寸和材料性质、加速膛的尺寸等等。通过系统的实验考核微装药爆轰驱动飞片的众多影响因素很困难。为此，本文中根据实际设计的MEMS微装药器件和部分实验，运用ANSYS/LS-DYNA数值模拟探究叠氮化铜爆轰驱动飞片的作用过程，分析微装药爆轰驱动飞片作用原理，以期为器件的优化设计提供相关技术支持和理论依据。
1. 数值模型
叠氮化铜爆轰驱动飞片运动属于接触爆炸作用问题。对于接触爆炸，虽然可以使用Lagrange算法，在叠氮化铜炸药和飞片之间定义接触来考虑相互作用，但由于炸药单元很容易在爆炸过程中发生严重畸变，往往使得计算中断。另外一种算法就是使用流固耦合方法计算炸药对飞片的作用过程中，炸药使用欧拉算法，飞片使用拉格朗日算法，炸药单元不存在畸变问题[6]。本文中采用流固耦合方法计算纳米多孔叠氮化铜炸药对飞片的作用。
数值模型如图 1所示，由叠氮化铜炸药、空气、玻璃纤维聚碳酸酯约束壳体和金属钛飞片4个部分组成。炸药和空气采用欧拉算法，空气域包含整个模型区域，钛飞片和聚碳酸酯约束壳体采用拉格朗日算法，通过*CONSTRAINED_LAGRANGE_IN_SOLID关键字进行耦合。建立二维模型，模拟叠氮化铜驱动飞片过程，采用cm-g-μs单位制建模。
叠氮化铜采用高能炸药燃烧模型和JWL状态方程。JWL状态方程能够比较准确地描述爆轰产物的膨胀驱动过程，其基本形式为[7]:
p=A(1−ωR1V)e−R1V+B(1−ωR2V)e−R2V+ωEV (1) 式中:p为爆轰产物压力，V为爆轰产物相对比容，E为单位体积内能，状态方程各参数为[8]：A=410 GPa，B=4.5 GPa，R1=4.90，R2=1.3，ω=0.3，ρ=2.29 g/cm3，爆速D=4.7 km/s，C-J爆压pCJ=12.55 GPa。
空气采用NULL材料模型和LINEAR_POLYNOMIAL状态方程，线性多项式状态方程：
p′=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E (2) 式中: μ=1V−1,p′为爆轰压力；E为单位体积内能；V为相对体积。通常情况下，为方便计算，将空气看作理想气体，设置：C0=C1=C2=C3=C6=0，C4=C5=γ-1，γ为气体的质量热容比[9]。
金属钛飞片和玻璃纤维聚碳酸酯约束壳体采用适用于金属和塑料的各向同性塑料模型[10]，其中金属钛飞片厚度为28 μm，具体材料参数如表 1所示。
表 1 钛飞片和聚碳酸酯的材料模型参数Table 1. Parameters of titanium and polycarbonate材料 ρ/(g·cm-3) E0/GPa G/GPa K/GPa ν 钛 4.51 113.76 43.755 94.803 0.30 聚碳酸酯 1.19 2.34 0.849 3.256 0.38 2. 结果分析
2.1 飞片的平整性和完整性分析
图 2所示为不同时刻叠氮化铜爆轰驱动飞片的压力场图，数值模型中，选用加速膛长度为0.68 mm，叠氮化铜装药尺寸为∅1.0 mm×0.6 mm，约束壳体的厚度为0.6 mm。
2(a) t=0.02 μs时叠氮化铜驱动飞片的压力分布2(a). Pressure distribution of flyer driven by Cu(N3)2 at t=0.02 μs
2(b) t=0.06 μs时叠氮化铜驱动飞片的压力分布2(b). Pressure distribution of flyer driven by Cu(N3)2 at t=0.06 μs
2(c) t=0.11 μs时叠氮化铜驱动飞片的压力分布2(c). Pressure distribution of flyer driven by Cu(N3)2 t=0.11 μs
2(d) t=0.20 μs时叠氮化铜驱动飞片的压力分布2(d). Pressure distribution of flyer driven by Cu(N3)2 t=0.20 μs
2(e) t=0.32 μs时叠氮化铜驱动飞片的压力分布2(e). Pressure distribution of flyer driven by Cu(N3)2 t=0.32 μs
2(f) t=0.38 μs时叠氮化铜驱动飞片的压力分布2(f). Pressure distribution of flyer driven by Cu(N3)2 t=0.38 μs在炸药爆轰驱动作用下，飞片被加速膛剪切成圆弧面状，冲击起爆下一级装药。由于点起爆的方式使得爆轰波从初始阶段就不能形成平面波，加之装药直径很小，爆轰波阵面率先到达飞片的中心部位，导致这部分飞片最先受到爆轰波的作用，从而形成圆弧形的飞片[11]。数值模拟中的飞片形状与实际的飞片形状较为相符，能够较为形象地反应叠氮化铜驱动飞片的作用过程。
图 3所示为飞片受到爆轰作用后破损情况的示意图。在建立的多组不同尺寸装药爆轰驱动钛飞片的数值模拟中，运用LS-PREPOST后处理查看运算结果动画时，剪切的钛飞片在加速膛中飞行到约700 μm时均出现不同程度的破裂，随着爆轰作用时间的延长，钛飞片破损程度不断加剧直至成为碎片，与实验发现的加速膛超过700 μm后，叠氮化铜爆轰驱动的飞片不能全部起爆HNS-Ⅳ药柱现象相符合。实验设计叠氮化铜MEMS微起爆器的加速膛长度分别为560、680、700、870和1070 μm，叠氮化铜药片尺寸为∅0.8 mm×0.6 mm，加速膛尺寸超过700 μm后，微起爆器均不能起爆下一级钝感HNS-Ⅳ炸药柱。因此，可认为由于加速膛过长和飞片破碎，碎片化的金属钛冲击下一级的钝感HNS-Ⅳ药柱时，不能形成完整且尺寸较大的应力作用面，进而不能起爆HNS-Ⅳ炸药柱。
2.2 装药直径对飞片速度的影响
图 4所示为不同装药直径下叠氮化铜驱动飞片的速度时程图，选用的装药直径分别为0.5、0.6、0.8和1.0 mm，叠氮化铜装药的厚度均为0.6 mm，采用相同的材料模型、状态方程、网格划分方式。从图 4中可以看出，不同装药直径对飞片速度的前期成长影响不大，但对飞片运行的最大速度却有较为明显的影响；装药的直径大于0.8 mm时，增加装药直径并不能使飞片最大速度明显增加。
图 4 不同直径装药驱动飞片的速度时程曲线Figure 4. Velocity histories of flyer driven by charge with different diameters根据哈里顿原理可知，在有限直径药柱内，爆轰波传播与化学反应的能量释放速度和侧向膨胀引起的能量耗散速度之比有关；能量损失随装药直径减小而增大，从而造成波阵面上参数的下降以及化学反应时间的增加[12]。通过纳米多孔铜“原位”合成的叠氮化铜的颗粒度较小，爆轰反应进行的相对较快，化学反应区内完成反应所经历的时间较短，爆轰波易传播，稳定爆轰的临界直径小。当微装药的厚度一定且直径较小时，微装药爆轰作用的能量有限，从而爆轰驱动飞片的速度不能达到最佳。当微装药的直径较大时，则不利于微装药器件的集成化设计。所以，微装药的直径存在一个最佳值。
2.3 装药厚度对飞片速度的影响
根据微型起爆装置的实际情况，考察药厚0.3~0.6 mm情况。采用相同的材料模型、状态方程、网格划分方式，装药厚度分别为0.3、0.4、0.5和0.6 mm，直径均为0.8 mm，钛飞片的厚度为28 μm。图 5所示为不同装药厚度下叠氮化铜驱动飞片的速度时程图。从图 5中可以看出，飞片速度与装药厚度关系密切。当装药厚度为0.3 mm时，飞片获得的最大速度约为2247.3 m/s，平均速度为2008.6 m/s；随着装药厚度的增加，飞片的极值速度和平均速度逐渐增大。微装药的厚度也存在一个较为合适的区间值，这是因为叠氮化铜药片太薄时不能稳定爆轰驱动飞片，飞片的驱动速度小，达不到钝感装药的起爆速度阈值，无法冲击起爆下一级钝感装药；叠氮化铜药片太厚时，则存在炸药爆轰作用能量过剩问题，对飞片驱动速度的成长意义不大。
图 5 不同厚度装药爆轰驱动飞片的速度时程曲线Figure 5. Velocity histories of flyer driven by charge with different thicknesses3. 结论
(1) 在数值模拟中飞片的剪切形状与飞片的实际形状较为相符，模型能够揭示叠氮化铜驱动飞片的作用过程。驱动飞片的完整性、平整性和速度与加速膛的长度关系密切，加速膛的长度应限制在700 μm以下，且长度不能过短。
(2) 不同装药直径对飞片速度的前期成长影响不大，但对飞片达到的最大速度却有较为明显的影响；微装药直径设计为0.8 mm较为合适。
(3) 飞片获得的驱动速度与微装药厚度关系密切，采用越小的装药厚度，飞片获得的极值速度和平均速度越小；随着装药厚度的增加，飞片获得的极值速度和平均速度逐渐增大并趋于稳定。
-
图 6 含有不同骨料体积分数的立方体试样
Figure 6. Cubic specimens with different volume fractions of aggregate
图 8 砂浆单轴准静态压缩应力应变曲线
Figure 8. Strain-stress curves of mortar phase under uniaxial load
图 10 单轴压缩与拉伸应力应变曲线
Figure 10. Comparison of strain-stress curves between experiment and simulation
图 14 双轴压缩应力应变曲线
Figure 14. Comparison of strain-stress curves between experiment and simulation
图 16 三轴压应力作用下应力应变曲线
Figure 16. Comparison of stress-strain curves between experiment and simulation
图 17 不同应变率下的动态增强因子
Figure 17. Dynamic increasing factor for concrete at different strain rates
表 1 细观组分材料参数
Table 1. Material parameters of three-phase materials
材料 弹性模量/
GPa泊松比 抗压强度/
MPa抗拉强度/
MPa砂浆 25 0.20 35 3.5 ITZ 18 0.20 20 3.0 粗骨料 43 0.23 − − 
下载: 导出CSV
-
[1] 张楚汉, 唐欣薇, 周元德, 等. 混凝土细观力学研究进展综述 [J]. 水力发电学报, 2015, 34(12): 1–18. doi: 10.11660/slfdxb.20151201ZHANG Chuhan, TANG Xinwei, ZHOU Yuande, et al. State-of-the-art literature review on concrete meso-scale mechanics [J]. Journal of Hydroelectric Engineering, 2015, 34(12): 1–18. doi: 10.11660/slfdxb.20151201 [2] 杜修力, 金浏. 细观分析方法在混凝土物理/力学性质研究方面的应用 [J]. 水利学报, 2016, 47(3): 355–371.DU Xiuli, JIN Liu. Applications of meso-scale analysis methods on the study of the physical/mechanical properties of concrete [J]. Journal of Hydraulic Engineering, 2016, 47(3): 355–371. [3] WITTMANN F H, ROELFSTRA P E, SADOUKI H. Simulation and analysis of composite structures [J]. Materials Science and Engineering, 1985, 68(2): 239–248. [4] ZHOU X Q, HAO H. Mesoscale modelling of concrete tensile failure mechanism at high strain rates [J]. Computers and Structures, 2008, 86(21−22): 2013–2026. [5] ZHOU X Q, HAO H. Modelling of compressive behaviour of concrete-like materials at high strain rate [J]. International Journal of Solids and Structures, 2008, 45(17): 4648–4661. [6] WANG X F, YANG Z J, YATES J R, et al. Monte Carlo simulations of mesoscale fracture modelling of concrete with random aggregates and pores [J]. Construction and Building Materials, 2015, 75: 35–45. [7] 吴成, 沈晓军, 王晓鸣, 等. 细观混凝土靶抗侵彻数值模拟及侵彻深度模型 [J]. 爆炸与冲击, 2018, 38(6): 1364–1371. DOI: 10.11833/bzycj-2017-0123.WU Cheng, SHEN Xiaojun, WANG Xiaoming, et al. Numerical simulation on anti-penetration and penetration depth model of mesoscale concrete target [J]. Explosion and Shock Waves, 2018, 38(6): 1364–1371. DOI: 10.11833/bzycj-2017-0123. [8] WANG X, ZHANG M, JIVKOV A P. Computational technology for analysis of 3D meso-structure effects on damage and failure of concrete [J]. International Journal of Solids and Structures, 2016, 80: 310–333. [9] ZHANG Z, SONG X, LIU Y, et al. Three-dimensional mesoscale modelling of concrete composites by using random walking algorithm [J]. Composites Science and Technology, 2017, 149: 235–245. [10] 邓勇军, 陈小伟, 姚勇, 等. 基于细观混凝土模型的刚性弹体正侵彻弹道偏转分析 [J]. 爆炸与冲击, 2017, 37(3): 377–386. DOI: 10.11833/1001-1455(2017)03-0377-10.DENG Yongjun, CHEN Xiaowei, YAO Yong, et al. On ballistic trajectory of rigid projectile normal penetration based on a meso-scopic concrete [J]. Explosion and Shock Waves, 2017, 37(3): 377–386. DOI: 10.11833/1001-1455(2017)03-0377-10. [11] ZHANG J, WANG Z, YANG H, et al. 3D meso-scale modeling of reinforcement concrete with high volume fraction of randomly distributed aggregates [J]. Construction and Building Materials, 2018, 164: 350–361. doi: 10.1016/j.conbuildmat.2017.12.229 [12] SHENG P, ZHANG J, JI Z. An advanced 3D modeling method for concrete-like particle-reinforced composites with high volume fraction of randomly distributed particles [J]. Composites Science and Technology, 2016, 134: 26–35. [13] HUANG Y, YANG Z, REN W, et al. 3D meso-scale fracture modelling and validation of concrete based on in-situ X-ray computed tomography images using damage plasticity model [J]. International Journal of Solids and Structures, 2015, 67-68: 340–352. [14] DU X, JIN L, MA G. Numerical simulation of dynamic tensile-failure of concrete at meso-scale [J]. International Journal of Impact Engineering, 2014, 66(4): 5–17. [15] 张锦华, 方秦, 龚自明, 等. 基于三维细观模型的全级配混凝土静态力学性能的数值模拟 [J]. 计算力学学报, 2012, 29(6): 927–933.ZHANG Jinhua, FANG Qin, GONG Ziming, et al. Numerical simulation of static mechanical properties based on 3D mesoscale model of fully-graded concete [J]. Chinese Journal of Computational Mechanics, 2012, 29(6): 927–933. [16] 方秦, 还毅, 张亚栋. ABAQUS混凝土损伤塑性模型的静力性能分析 [J]. 解放军理工大学学报(自然科学版), 2007, 8(3): 254–260.FANG Qin, HUAI Yi, ZHANG Yadong, et al. Investigation into static properties of damaged plasticity model for concrete in ABAQUS [J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2007, 8(3): 254–260. [17] VAN VLIET M R A, VAN MIER J G M. Softening behaviour of concrete under uniaxial compression [C] // WITTMANN F H. Fracuture mechanics of concrete structures. Freiburg: Aedificatio Publishers, 1995: 383−396. [18] 尚世明. 普通混凝土多轴动态性能试验研究[D]. 大连: 大连理工大学, 2013. [19] SFER D, CAROL I, GETTU R, et al. Study of the behavior of concrete under triaxial compression [J]. Journal of Engineering Mechanics, 2002, 128(2): 156–163. [20] 宁建国, 商霖, 孙远翔. 混凝土材料动态性能的经验公式、强度理论与唯象本构模型 [J]. 力学进展, 2006, 36(3): 389–405. doi: 10.3321/j.issn:1000-0992.2006.03.006NING Jianguo, SHANG Lin, SUN Yuanxiang. The developments of dynamic constitutive behavior of concrete [J]. Advance in Mechanics, 2006, 36(3): 389–405. doi: 10.3321/j.issn:1000-0992.2006.03.006 [21] 宁建国, 商霖, 孙远翔. 混凝土材料冲击特性的研究 [J]. 力学学报, 2006, 38(2): 199–208. doi: 10.3321/j.issn:0459-1879.2006.02.008NING Jianguo, SHANG Lin, SUN Yuanxiang. Investigation on impact behavior of concrete [J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(2): 199–208. doi: 10.3321/j.issn:0459-1879.2006.02.008 [22] 方秦, 洪建, 张锦华, 等. 混凝土类材料SHPB实验若干问题探讨 [J]. 工程力学, 2014, 31(5): 1–14.FANG Qin, HONG Jian, ZHANG Jinhua, et al. Issues of SHPB test on concrete-like material [J]. Engineering Mechanics, 2014, 31(5): 1–14. 期刊类型引用(5)
1. 姬广富. 极端条件下含能材料的模拟研究思考. 高压物理学报. 2025(01): 19-45 . 
百度学术2. 王晗程，王亚伟，陈硕，何勇，焦俊杰，单锋，崔东华. 同时起爆串联战斗部数值仿真及实验研究. 兵器材料科学与工程. 2020(02): 20-24 . 百度学术3. 王俊晓，向红军，吕庆敖，张华祥. 电磁轨道炮超高速弹丸软回收技术需求及研究现状分析. 飞航导弹. 2018(11): 6-10 . 百度学术4. 崔智丽，徐浩铭，经来旺. 炸高对侵彻效应影响试验和数值模拟研究. 爆破. 2016(02): 39-44 . 百度学术5. 陈闯，王晓鸣，李文彬，李伟兵. 串联聚能装药延迟时间与装药间距匹配关系研究. 北京理工大学学报. 2014(12): 1217-1222 . 百度学术其他类型引用(3)
-
下载:
百度学术
计量
- 文章访问数: 5628
- HTML全文浏览量: 2271
- PDF下载量: 146
- 被引次数: 8