Dynamic responses of hollow steel pipes directly buried in high-saturated clay to blast waves
-
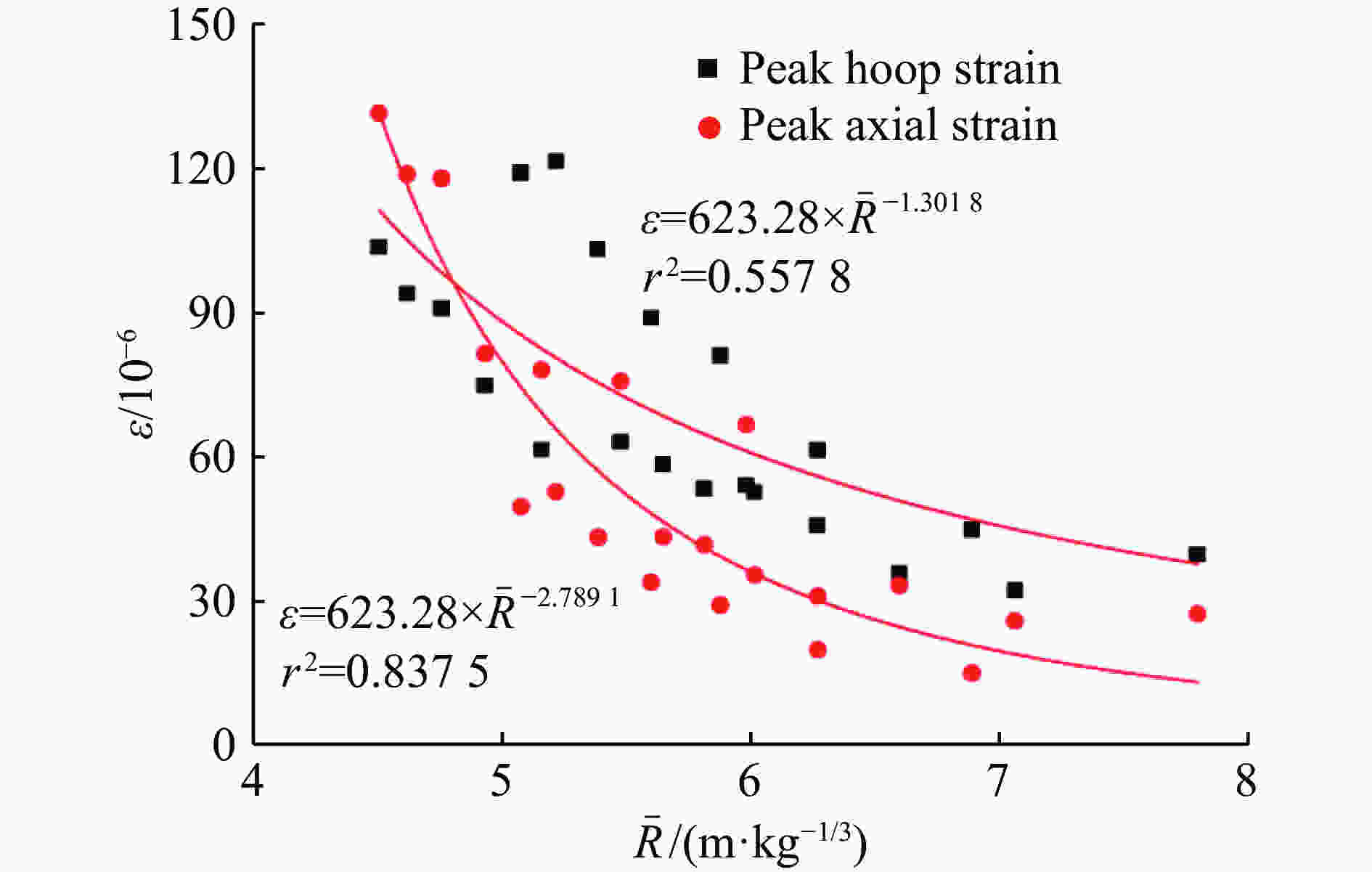
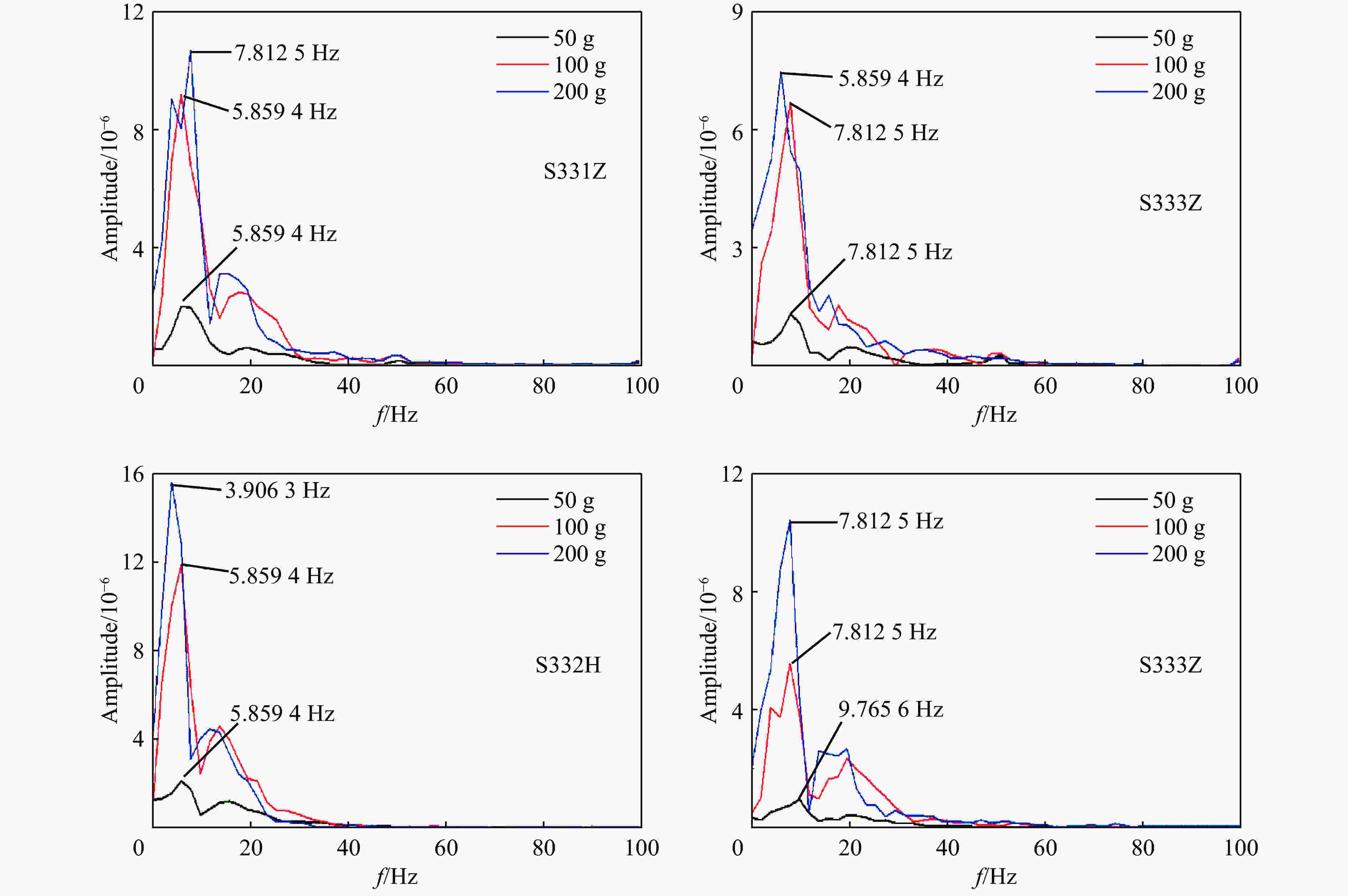
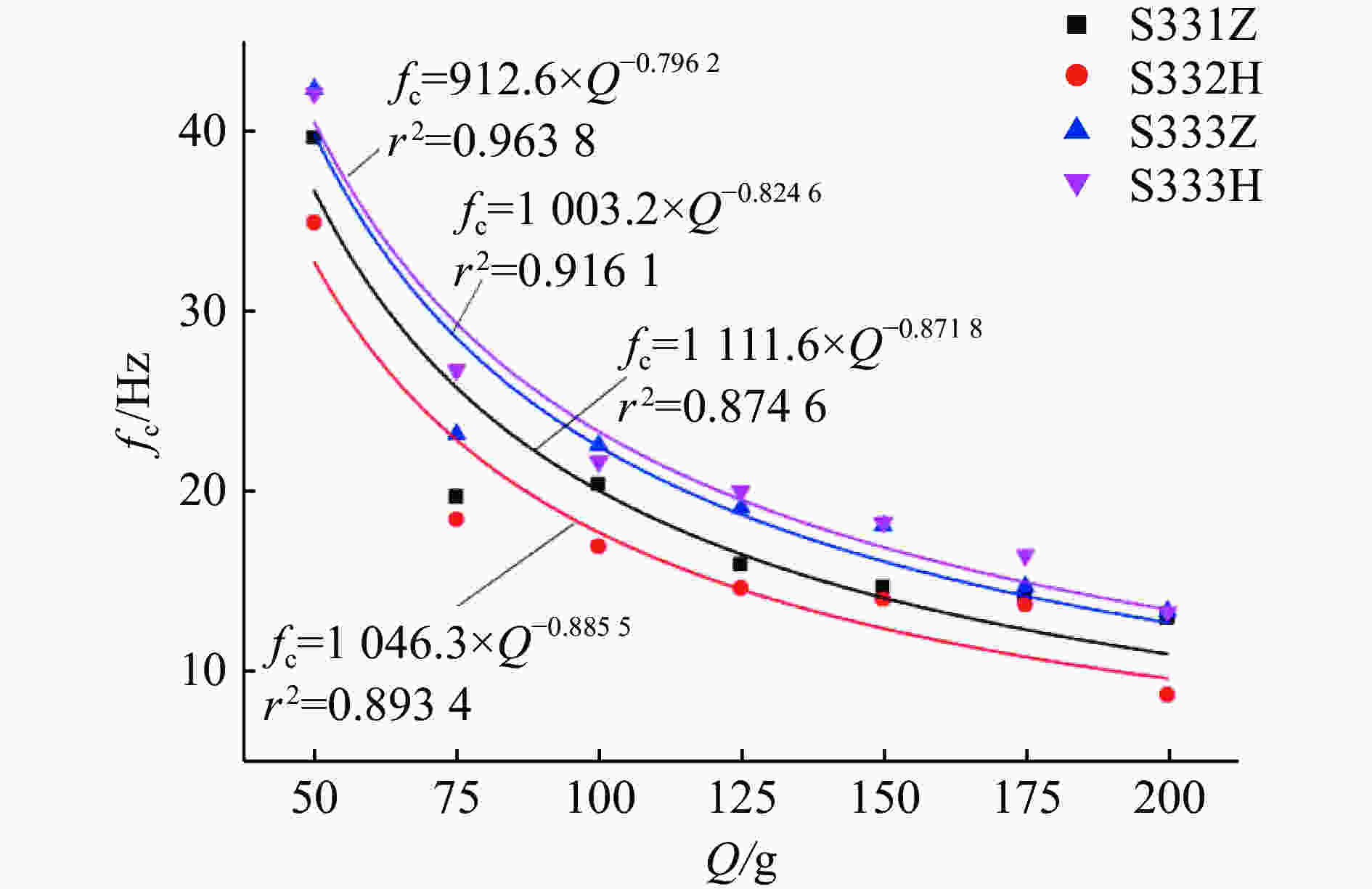
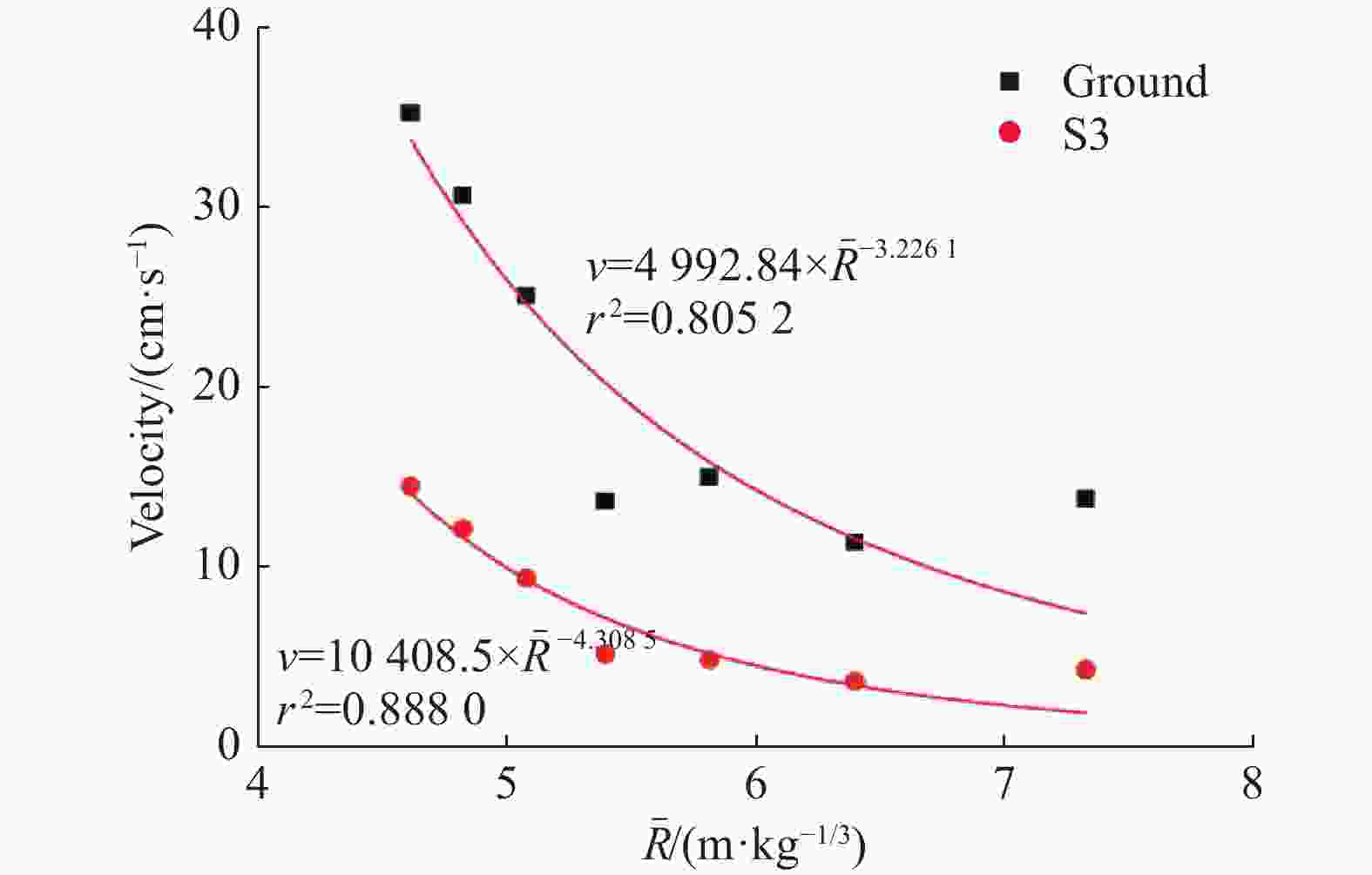
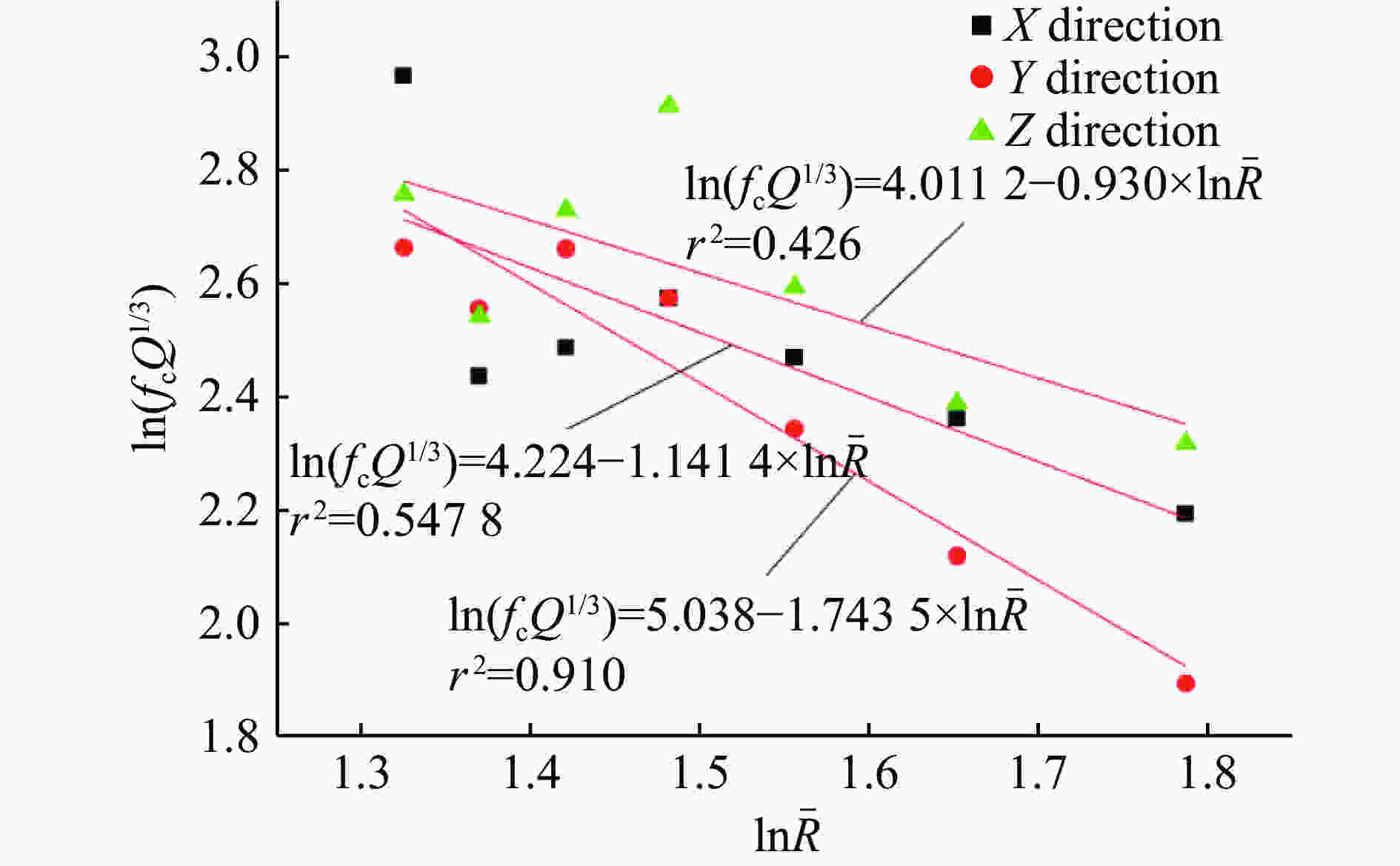
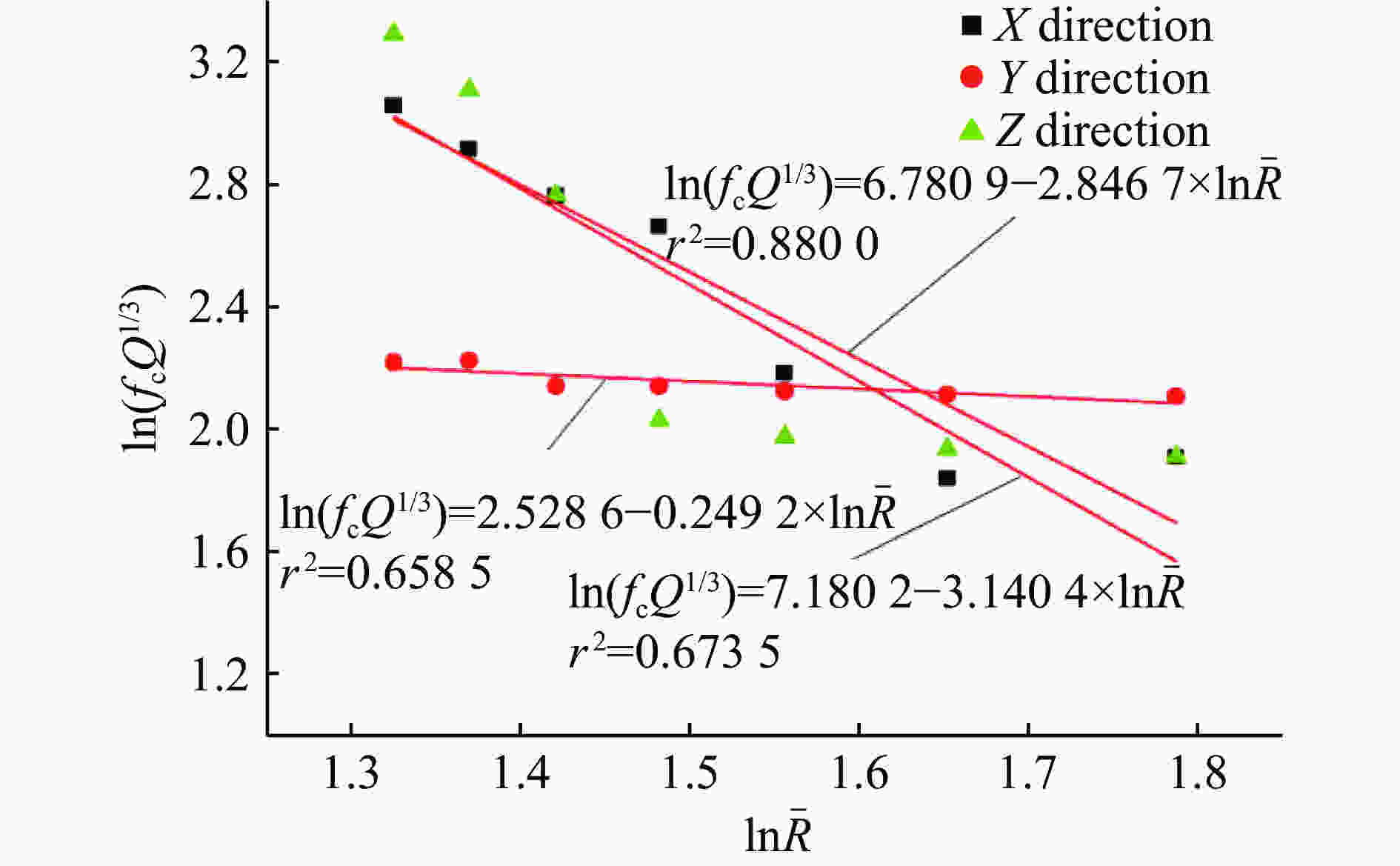
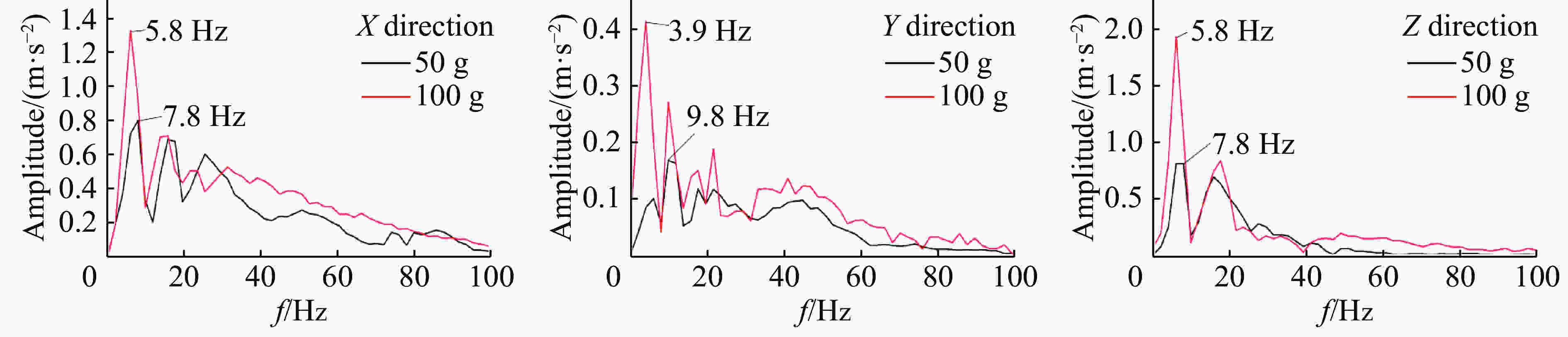
摘要: 设计和实施了系列爆炸波作用下钢管的动态响应实验，获得了管道应变、振动速度和加速度及地表振动速度的时间历程。分析实验数据可知：在爆炸波近中场，峰值应变大小同管土相对刚度因数负相关，并随比例距离呈幂函数形式衰减，且在爆炸波不同分区衰减指数不同；地表峰值粒子速度、各管的峰值振动速度和测点峰值应变之间具有良好的线性关系。对各测试量做FFT (Fast Fourier Transformation)频谱分析得：振动信号主要集中在低频段，质心频率在10～60 Hz范围内，频谱同天然地震波谱有明显差异，动应变谱质心频率随药量增加亦呈幂函数形式衰减；考虑了爆腔因素以后，管道和地表振速频谱的质心频率和比例距离取对数后具有线性衰减关系。实验所得数据可应用于相似条件下管道的抗震计算，一些结论可作为深入研究爆炸波作用下埋地管道冲击振动机理的依据。Abstract: A series of experiments were designed and implemented to explore dynamic responses of steel pipes to blast waves The time histories of dynamic strains, vibration velocities and accelerations of the steel pipes were obtained, and the vibration velocity-time curves were gained. It is known by analyzing the experimental data that in the near and middle fields of the blast wave, the peak dynamic strains are negatively correlated with the relative stiffness coefficient of the pipe and the soil, and they follow the attenuation law of the power function with scaled distance; that the attenuation indexes are different for the blast wave propagating in the different sections of the field. The peak particle vibration velocities of the ground and the pipes have good linear correlations with the peak strains of the measuring points at the pipes. On the basis of the spectrum analysis by the fast Fourier transform on each test quantity, it is found that the spectrum energy of each test quantity is mainly concentrated in the low-frequency band, the centroid frequency is in 10−60 Hz, but there are obvious differences compared to the spectra of natural seismic waves. The centroid frequency of the dynamic strain spectrum is decayed in the exponent form of a power function with the increase of the explosive charge. By taking logarithm, there is a linear attenuation relationship between the scaled distance and the centroid frequencies of velocity spectra that the blasting cavity factor is considered. The test data can be directly applied to the seismic calculation under similar conditions, and some conclusions can be used as the theoretical basis for further study of the impact damage mechanism of buried pipelines.
-
Key words:
- blast wave /
- spectrum analysis /
- buried pipe /
- dynamic strain /
- vibration velocity /
- vibration acceleration
-
图 4 不同测点的动应变波形对比
Figure 4. Comparison of dynamic strain waveforms at different measured points
图 5 S333应变衰减曲线(R=2.7 m，H=1.5 m)
Figure 5. Strain decay curves of S333 (R=2.7 m, H=1.5 m)
图 6 S233应变衰减曲线(R=2.7 m，H=1.0 m)
Figure 6. Decay curves of S332 strain (R=2.7 m, H=1.0 m)
图 7 S331Z最大拉和压应变(H=1.5 m)
Figure 7. The maximum tension and compression strains of S331Z (H=1.5 m)
图 11 动应变质心变频率衰减曲线(R=2.7 m, H=1.5 m)
Figure 11. The decay curves of dynamic strain centroid frequencies (R=2.7 m, H=1.5 m)
图 12 S3管道振动的峰值粒子速度和地表振动的峰值粒子速度随比例爆距的衰减
Figure 12. Attenuation of peak particle velocity with scaled explosion distance for vibrations of S3 pipe and ground
图 13 S3管道振动的峰值粒子速度(PPVPV)和地表振动的峰值粒子速度(PPVGV)的关系
Figure 13. Relations between peak particle velocities of S3 pipe vibrations (PPVPV) and ones of ground vibrations (PPVGV)
图 16 S3管振速质心频率衰减
Figure 16. Centroid frequency attenuation of pipe S3 vibration velocity
图 17 地面振速质心频率衰减
Figure 17. Centroid frequency attenuation of ground vibration velocity
图 18 S3管道的应变和地表振动峰值粒子速度（PPVGV）的关系
Figure 18. Relationships between strain of pipe S3 and peak particle velocity of ground vibration (PPVGV)
表 1 管道几何参数
Table 1. Geometrical parameters of pipes
管道编号 D/mm δ/mm L/m S1 110 4.24 4.6 S2 160 4.70 4.6 S3 300 4.40 4.6 
下载: 导出CSV
表 2 实验方案
Table 2. Experimental schemes
H/m R/m Q/g 2.0 2.2 50 75 100 125 150 175 200 2.7 50 75 100 125 150 175 200 1.5 2.2 50 75 100 125 150 175 200 2.7 50 75 100 125 150 175 200 3.2 50 75 100 125 150 175 200 1.0 2.7 50 75 100 125 150 175 200
下载: 导出CSV
表 3 实验参数
Table 3. Experimental parameters
H/m R/m Q/g $\bar R$/(m·kg−1/3) 管道编号 1.0 2.7 75 6.402 S3 1.0 3.2 125 6.4 S3
下载: 导出CSV
表 4 校验结果
Table 4. Results of check
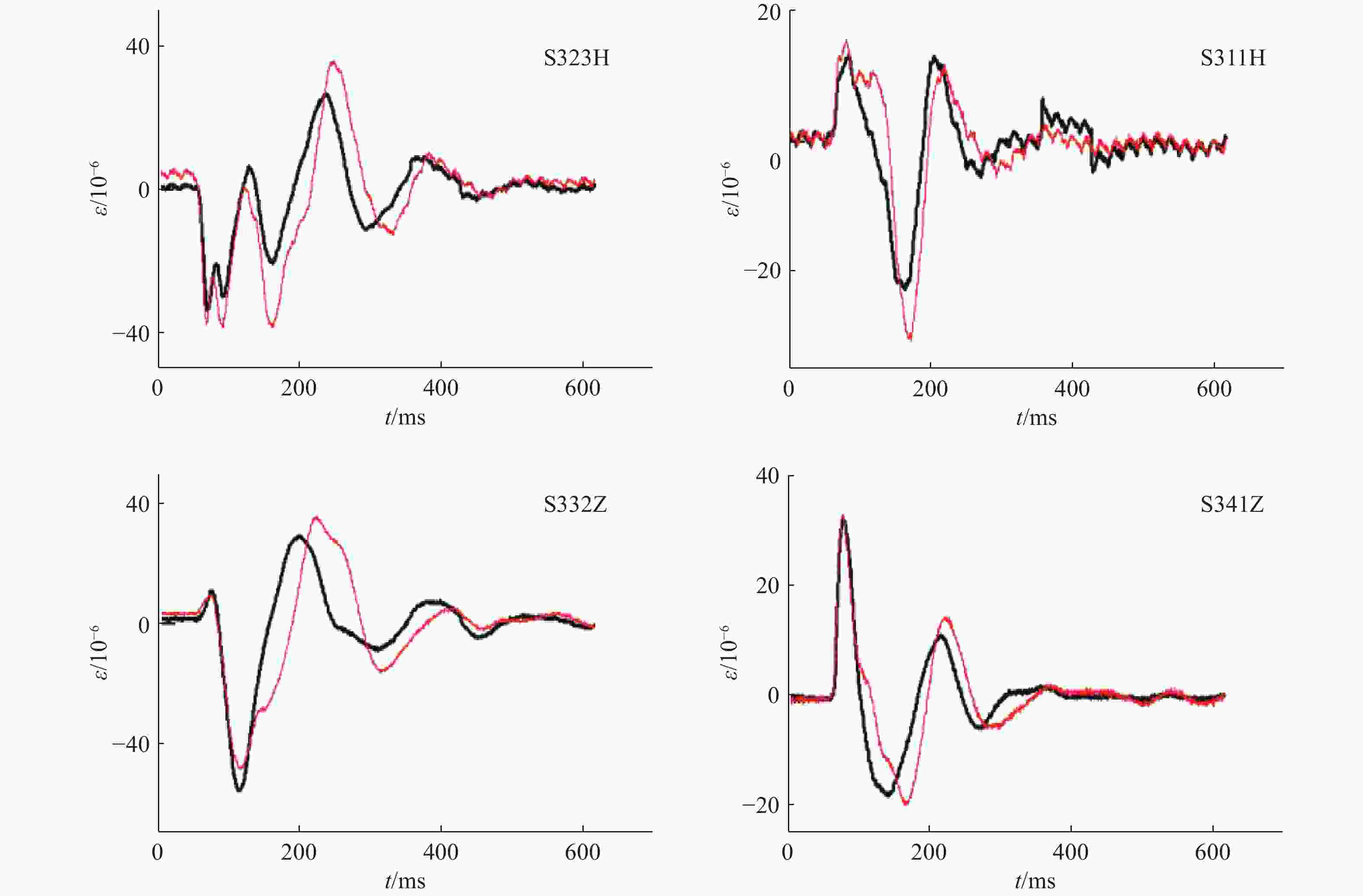
测点编号 相关系数 可信概率 测点编号 相关系数 可信概率 S323H 0.836 0.872 S332Z 0.855 0.893 S311H 0.786 0.834 S341Z 0.897 0.910
下载: 导出CSV
表 5 S3管不同测点的最大峰值应变(R=2.2 m)
Table 5. The maximum peak strains at different measured points of pipe S3 (R=2.2 m)
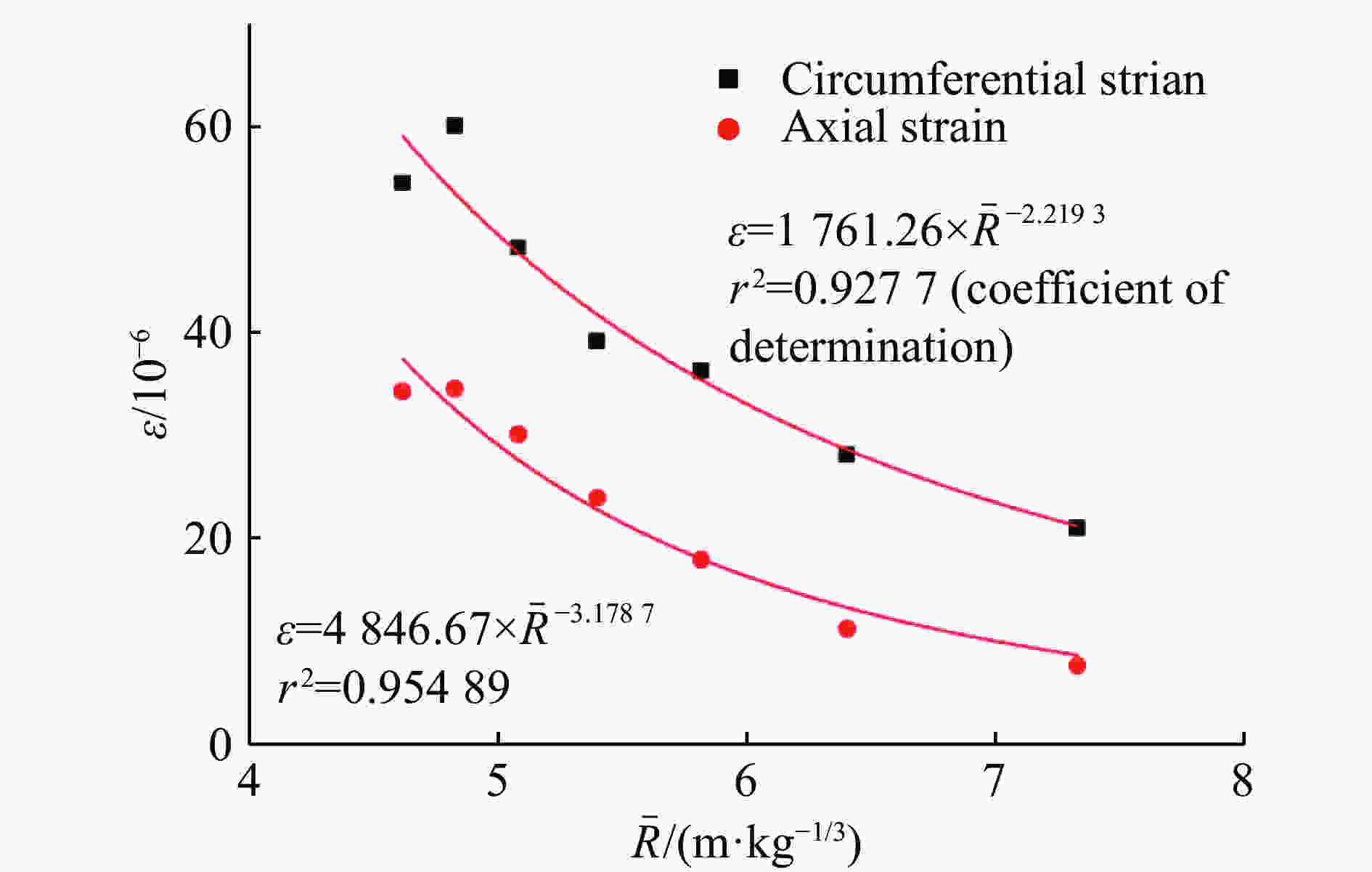
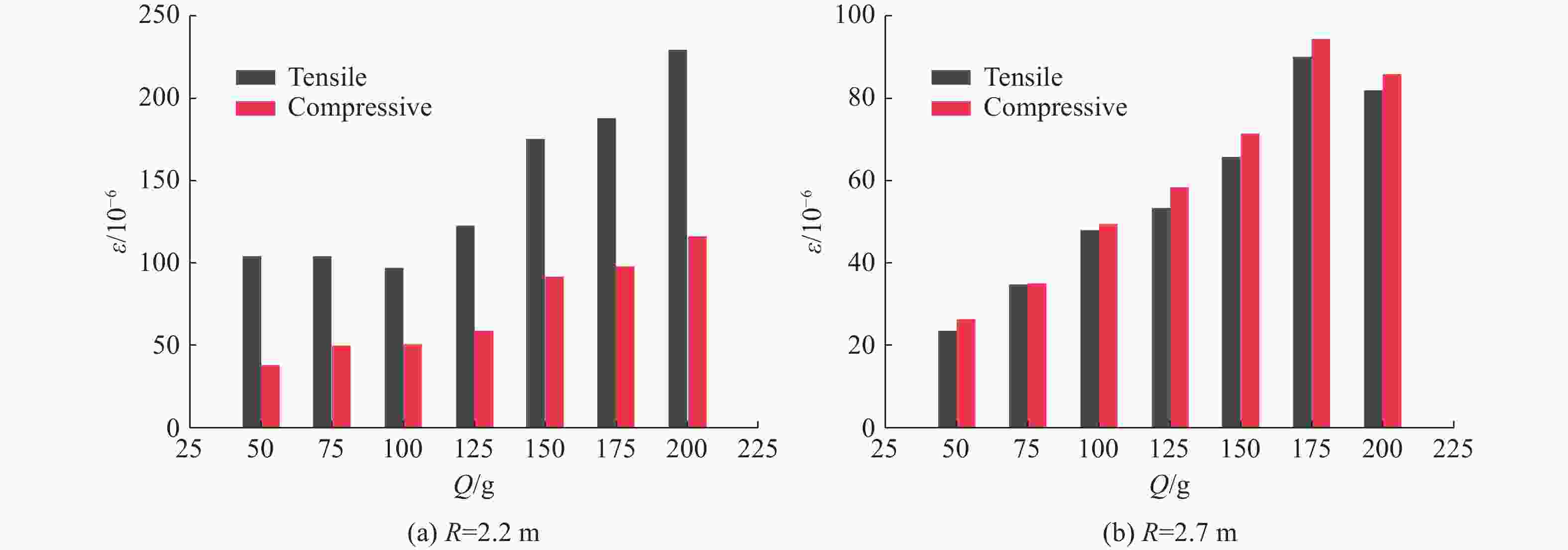
Q/g 最大峰值应变/10−6 S321H S341Z S323H S323Z S331Z S332H S332Z S333H S333Z S334Z 50 −31.1 35.1 −50.7 −31.7 104.3 53.8 −66.3 48.3 44.5 −58.5 75 −32.1 39.4 −51.8 −35.8 103.9 62.7 −75.4 43.8 50.4 −65.9 100 −30.7 52.9 −63.7 −35.9 97.3 61.1 −77.8 45.2 52.9 −61.6 125 −26.4 44.3 −45.2 −33.3 122.5 74.5 −81.2 60.3 54.3 −58.2 150 −42.7 60.7 −98.1 56.5 174.9 90.6 −117.7 69.6 76.4 −78.1 175 −78.5 72.2 −71.7 −64.3 187.8 93.6 −118.6 79.9 79.2 −79.3 200 −53.9 86.3 −89.2 −84.1 228.9 103.4 −131.3 100.5 90.4 −87.4 注：压应变按绝对值最大给出，下同。
下载: 导出CSV
表 6 S3管不同测点的最大峰值应变(R=2.7 m)
Table 6. The maximum peak strains at different measured points of pipe S3 (R=2.7 m)
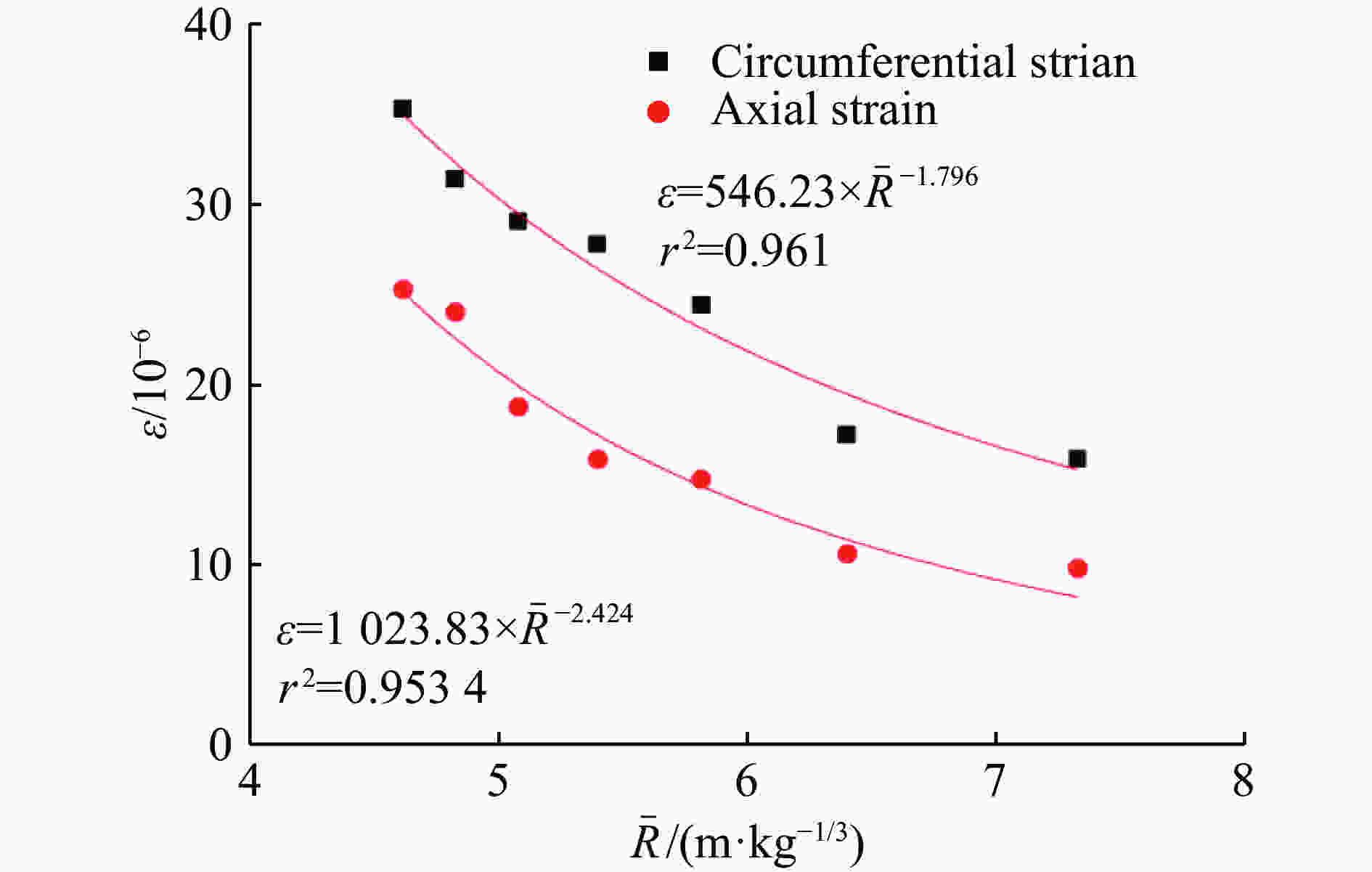
Q/g 最大峰值应变/10−6 S321H S341Z S323H S323Z S331Z S332H S332Z S333H S333Z S334Z 50 −16.5 7.2 −33.7 −14.4 −26.1 44.5 14.6 21.0 7.6 −29.8 75 −22.4 10.4 −52.0 −20.2 −34.9 61.1 19.4 28.1 11.2 −28.2 100 −28.2 14.9 −67.2 −28.3 −49.4 80.7 28.8 36.2 17.9 −31.3 125 −30.5 17.6 −69.6 −30.9 −58.3 88.7 33.6 39.1 23.9 −42.0 150 −36.5 21.0 −91.0 −37.1 −71.3 102.9 42.9 48.2 30.1 −48.4 175 −38.2 33.2 −103.2 −48.5 −94.1 121.3 52.3 60.1 34.5 −57.0 200 −42.1 28.9 −103.7 −44.6 −85.7 118.9 49.3 54.5 34.3 −48.5
下载: 导出CSV
表 7 S3管不同测点的最大峰值应变(R=3.2 m)
Table 7. The maximum peak strains at different measured points of pipe S3 (R=3.2 m)
Q/g 最大峰值应变/10−6 S321H S341Z S323H S323Z S331Z S332H S332Z S333H S333Z S334Z 50 −30.2 18.6 −36.9 −22.1 −49.1 39.3 −26.9 27.6 −15.5 34.4 75 −16.2 17.4 −32.0 −22.3 −45.9 31.8 −25.5 26.2 −16.8 32.8 100 −18.6 22.7 −36.6 −26.8 −52.8 35.4 −32.9 26.5 −19.6 33.3 125 −19.1 22.5 −38.9 −32.7 −34.1 45.3 −30.7 31.1 −20.9 37.9 150 −19.3 24.7 −41.5 −37.5 −61.1 52.3 −35.1 33.0 −22.1 38.2 175 −23.0 28.0 −43.0 −36.6 −71.8 53.0 −41.3 34.8 −28.6 40.9 200 −25.9 29.5 −47.7 −38.7 −90.8 58.1 −43.0 38.7 −38.1 42.5
下载: 导出CSV
表 8 S3管道振动的峰值粒子速度和地表振动的峰值粒子速度(R=2.7 m, H=2.0 m)
Table 8. Peak particle velocities of S3 pipe and ground vibrations (R=2.7 m, H=2.0 m)
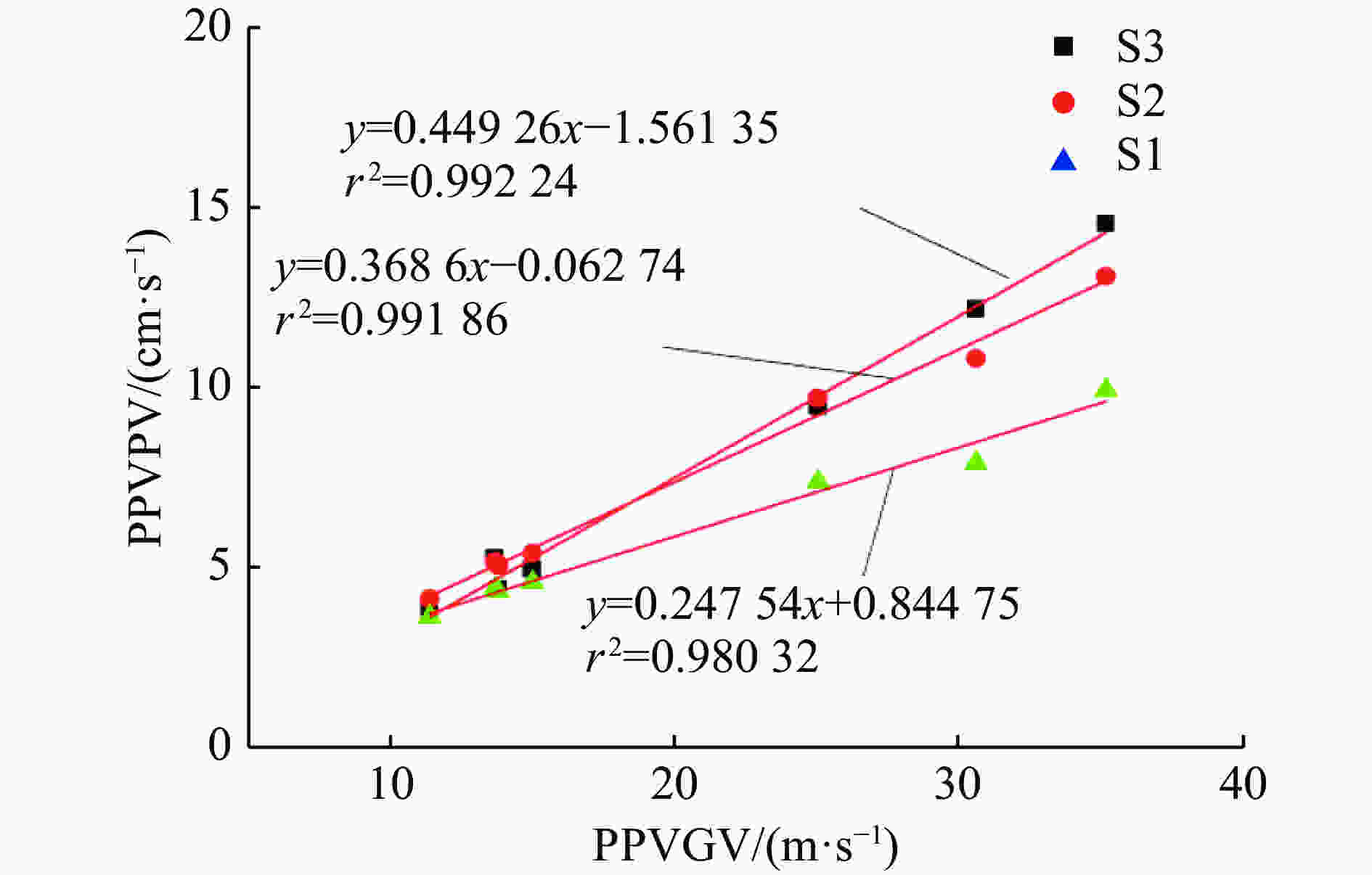
Q/g 峰值粒子速度/(cm∙s−1) 比值/% Q/g 峰值粒子速度/(cm∙s−1) 比值% S3管道振动 地表振动 S3管道振动 地表振动 50 4.3 13.8 31 150 9.4 25.1 37 75 3.7 11.4 32 175 12.1 30.6 39 100 4.9 15.0 33 200 14.5 35.2 41 125 5.2 13.7 38
下载: 导出CSV
表 9 管道S3和地面振动速度质心频率(R=2.7 m, H=2.0 m)
Table 9. Centroid frequencies of pipe S3 and ground vibration velocities (R=2.7 m, H=2.0 m)
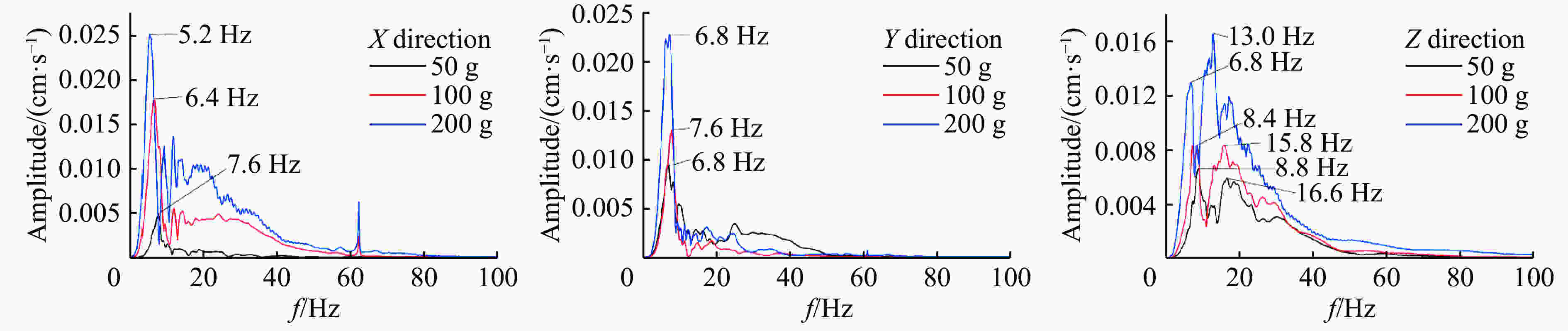
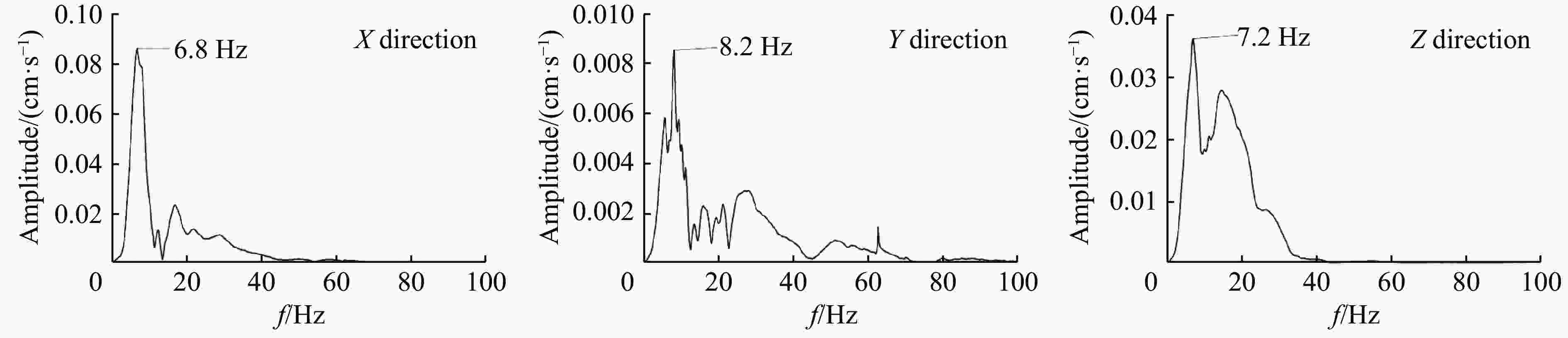
Q/g fc/Hz Q/g fc/Hz 管道 地表 管道 地表 X方向 Y方向 Z方向 X方向 Y方向 Z方向 X方向 Y方向 Z方向 X方向 Y方向 Z方向 50 24.3 18.0 27.5 18.3 22.3 18.3 150 22.6 26.9 28.8 29.7 16.0 29.8 75 25.1 19.7 25.8 14.9 19.6 16.4 175 20.4 23.0 22.7 32.9 16.5 39.9 100 25.4 22.4 28.8 19.1 18.0 15.5 200 33.2 24.5 26.9 36.3 15.7 45.8 125 26.2 26.2 36.8 28.6 17.0 15.2
下载: 导出CSV
表 10 S2管道振动的峰值加速度(H=1.5 m, R=2.7 m)
Table 10. Peak particle vibration acceleration of pipe S2 (H=1.5 m, R=2.7 m)
Q/g 加速度/(m·s−2) X方向 Y方向 Z方向 合成 Max Min Max Min Max Min 50 4.7 −11.1 3.7 0.3 6.7 −3.7 13.5 75 6.7 −12.9 4.0 0.0 8.1 −3.5 15.8 100 4.1 −10.4 2.2 −1.2 7.7 −2.5 13.2 125 4.7 −16.1 1.5 −2.9 8.4 −7.0 17.8 150 3.1 −15.5 0.9 −3.1 6.7 −6.5 17.1 175 1.7 −14.7 1.0 −3.3 6.8 −7.1 16.6 200 3.0 −18.2 0.3 −4.0 6.9 −7.4 20.1
下载: 导出CSV
表 11 加速度质心频率(H=1.5 m, R=2.7 m)
Table 11. Centroid frequencies of acceleration (H=1.5 m, R=2.7 m)
Q/g fc/Hz X方向 Y方向 Z方向 50 55.9 40.1 32.9 100 41.3 41.9 33.0 200 41.1 39.1 36.8
下载: 导出CSV
表 12 S3管加速度、速度和位移峰值(H=2.0 m, R=2.2 m)
Table 12. Peak acceleration, peak velocity and peak displacement of S3 (H=2.0 m, R=2.2 m)
Q/g dmax/mm vmax/(cm·s−1) amax/(m·s−2) $\left( {{v_{{\rm{max}}}} \cdot d_{\max }^{ - 1}} \right)/{\rm{Hz}}$ $\left( {{a_{{\rm{max}}}} \cdot v_{\max }^{ - 1}} \right)/{\rm{Hz}}$ 50 0.99 7.45 12.73 75.60 170.85 75 0.82 5.89 11.23 71.69 190.78 100 1.02 7.21 15.17 70.50 210.32 125 1.33 9.33 23.59 70.40 252.82 150 1.57 10.19 20.53 64.92 201.37 175 1.88 11.85 25.31 62.91 213.55 200 2.54 16.68 41.92 65.58 251.26
下载: 导出CSV
-
[1] 李强, 陈德利, 屈洋. 爆破对输气管道本体影响的监测 [J]. 油气储运, 2015, 34(2): 190–194. DOI: 10.6047/j.issn.1000-8241.2015.02.017.LI Q, CHEN D L, QU Y. Monitoring on effects of blasting on gas pipeline body distortion [J]. Oil & Gas Storage and Transportation, 2015, 34(2): 190–194. DOI: 10.6047/j.issn.1000-8241.2015.02.017. [2] 程围峰, 梁旭, 王振宇. 隧道爆破施工对邻近输油管道的影响评价 [J]. 石油工程建设, 2011, 37(4): 44–46; 9. DOI: 10.3969/j.issn.1001-2206.2011.04.013.CHENG W F, LIANG X, WANG Z Y. Assessment of blasting impact in tunnel excavation on nearby oil pipeline [J]. Petroleum Engineering Construction, 2011, 37(4): 44–46; 9. DOI: 10.3969/j.issn.1001-2206.2011.04.013. [3] 张紫剑, 赵昌龙, 张黎明, 等. 埋地管道爆破振动安全允许判据试验探究 [J]. 爆破, 2016, 33(2): 12–16. DOI: 10.3963/j.issn.1001-487X.2016.02.003.ZHANG Z J, ZHAO C L, ZHANG L M, et al. Experimental investigation of blasting vibration safety criterion on buried pipeline [J]. Blasting, 2016, 33(2): 12–16. DOI: 10.3963/j.issn.1001-487X.2016.02.003. [4] 戴联双, 张海珊, 孟国忠, 等. 在役油气管道周边爆破作业风险分析 [J]. 油气储运, 2012, 31(11): 801–803; 887. DOI: 10.6047/j.issn.1000-8241.2012.11.001.DAI L S, ZHANG H S, MENG G Z, et al. Risk analysis of blasting operations around in-service oil and gas pipelines [J]. Oil & Gas Storage and Transportation, 2012, 31(11): 801–803; 887. DOI: 10.6047/j.issn.1000-8241.2012.11.001. [5] 王振洪, 侯雄飞, 边明, 等. 爆破对天然气长输管道振动影响的安全判据 [J]. 油气储运, 2016, 35(8): 813–818. DOI: 10.60 47/j.issn.1000-8241.2016.08.003.WANG Z H, HOU X F, BIAN M, et al. Safety criterion for impacts of bursting on long-distance gas pipeline [J]. Oil & Gas Storage and Transportation, 2016, 35(8): 813–818. DOI: 10.60 47/j.issn.1000-8241.2016.08.003. [6] SISKIND D E, STAGG M S, WIEGAND J E, et al. Surface mine blasting near pressurized transmission pipelines [R]. Minneapolis, MN: US Department of the Interior Bureau of Mines, 1994: 2−3; 22−23. [7] DOWDING C H. Blast vibration monitoring and control [M]. New Jersey: Prentice-Hall, 1985: 167−171. [8] ESPARZA E D, WESTINE P S, WENZEL A B. Pipeline response to buried explosive detonations: Vol. 2 [R]. Arlington, USA: American Gas Association, 1981: 146−152. [9] KOURETZIS G P, BOUCKOVALAS G D, GANTES C J. Analytical calculation of blast-induced strains to buried pipelines [J]. International Journal of Impact Engineering, 2007, 34(10): 1683–1704. DOI: 10.1016/j.ijimpeng.2006.08.008. [10] ABEDI A S, HATAF N, GHAHRAMANI A. Analytical solution of the dynamic response of buried pipelines under blast wave [J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 88: 301–306. DOI: 10.1016/j.ijrmms.2016.07.014. [11] 钟冬望, 龚相超, 涂圣武, 等. 高饱和黏土中爆炸波作用下直埋聚乙烯管的动力响应 [J]. 爆炸与冲击, 2019, 39(3): 033102. DOI: 10.11883/bzycj-2017-0334.ZHONG D W, GONG X C, TU S W, et al. Dynamic responses of PE pipes directly buried in high saturated clay to blast wave [J]. Explosion and Shock Waves, 2019, 39(3): 033102. DOI: 10.11883/bzycj-2017-0334. [12] 冯双, 马郧, 徐光黎. 武汉地区基坑一般黏性土的力学特性与其物理指标间的相关性研究 [J]. 安全与环境工程, 2016, 23(5): 149–154. DOI: 10.13578/j.cnki.issn.1671-1556.2016.05.025.FENG S, MA Y, XU G L. Correlation between mechanical properties and physical indicators of general cohesive soil in foundation pits in Wuhan area [J]. Safety and Environmental Engineering, 2016, 23(5): 149–154. DOI: 10.13578/j.cnki.issn.1671-1556.2016.05.025. [13] 库特乌佐夫. 爆破工程师手册 [M]. 刘清泉, 译. 北京: 煤炭工业出版社, 1992: 137–138 [14] 卢文波, 张乐, 周俊汝, 等. 爆破振动频率衰减机制和衰减规律的理论分析 [J]. 爆破, 2013, 30(2): 1–6; 11. DOI: 10.3963/j.issn.1001-487X.2013.02.001.LU W B, ZHANG L, ZHOU J R, et al. Theoretical analysis on decay mechanism and law of blasting vibration frequency [J]. Blasting, 2013, 30(2): 1–6; 11. DOI: 10.3963/j.issn.1001-487X.2013.02.001. [15] 陈勇, 杨庆华. 埋地管道在地震波作用下的变形分析 [J]. 世界地震工程, 2015, 31(4): 275–279.CHEN Y, YANG Q H. Deformation analysis of buried pipelines under seismic waves [J]. World Earthquake Engineering, 2015, 31(4): 275–279. -
计量
- 文章访问数: 4997
- HTML全文浏览量: 1573
- PDF下载量: 80
- 被引次数: 0