Numerical computation of shock wave using wavelet methods
-
摘要: 基于自适应小波配点法和人工黏性技术，构造出一种简单稳定的冲击波数值计算方法。采用小波阈值滤波，生成适应流场分布的多尺度自适应网格，并利用密度场最细尺度的小波系数构造幂函数形式的冲击波定位函数，用以判断冲击波位置。联合人工黏性与冲击波定位函数，自动根据流场梯度严格控制人工黏性的大小和分布。对强/弱冲击波管问题进行计算，结果表明，该方法能够准确捕捉冲击波和有效抑制数值振荡，并且使用简单、分辨率高、计算量小。Abstract: A simple and stable wavelet method, which is based on adaptive wavelet collocation methods and artificial viscosity techniques, was proposed to compute shock waves. Dynamic multiscale grids generated by wavelet threshold filtering adaptive to the flow field were used. The shock waves can be checked out by the shock locator functions with power formula, which are constructed through using the magnitudes of the wavelet coefficients on the finest level in the density fields. Then, the artificial viscous terms including viscosity and shock locator functions strictly control the magnitudes and distributions of the artificial viscosity according to the gradients in the flow field. A strong and a weak shock tubes were computed, which shows that the method can accurately capture shock fronts and effectively restrain numerical oscillations. By the way, it is easy to manipulate, high of resolution and small of computational costs.
-
图 1 冲击波与对应的小波系数和定位函数
Figure 1. Shock and the corresponding wavelet coefficients and shock locator functions
图 6 自适应小波配点法相对迎风、ENO、WENO格式的计算时间
Figure 6. Relative computational time costs of AWCM to Up-wind, ENO and WENO schemes
图 7 J=12时三种格式密度分布对比
Figure 7. Spatial distributions of density through three schemes with J=12
表 1 弱冲击波管计算参数
Table 1. Computational parameters for weak shock tube
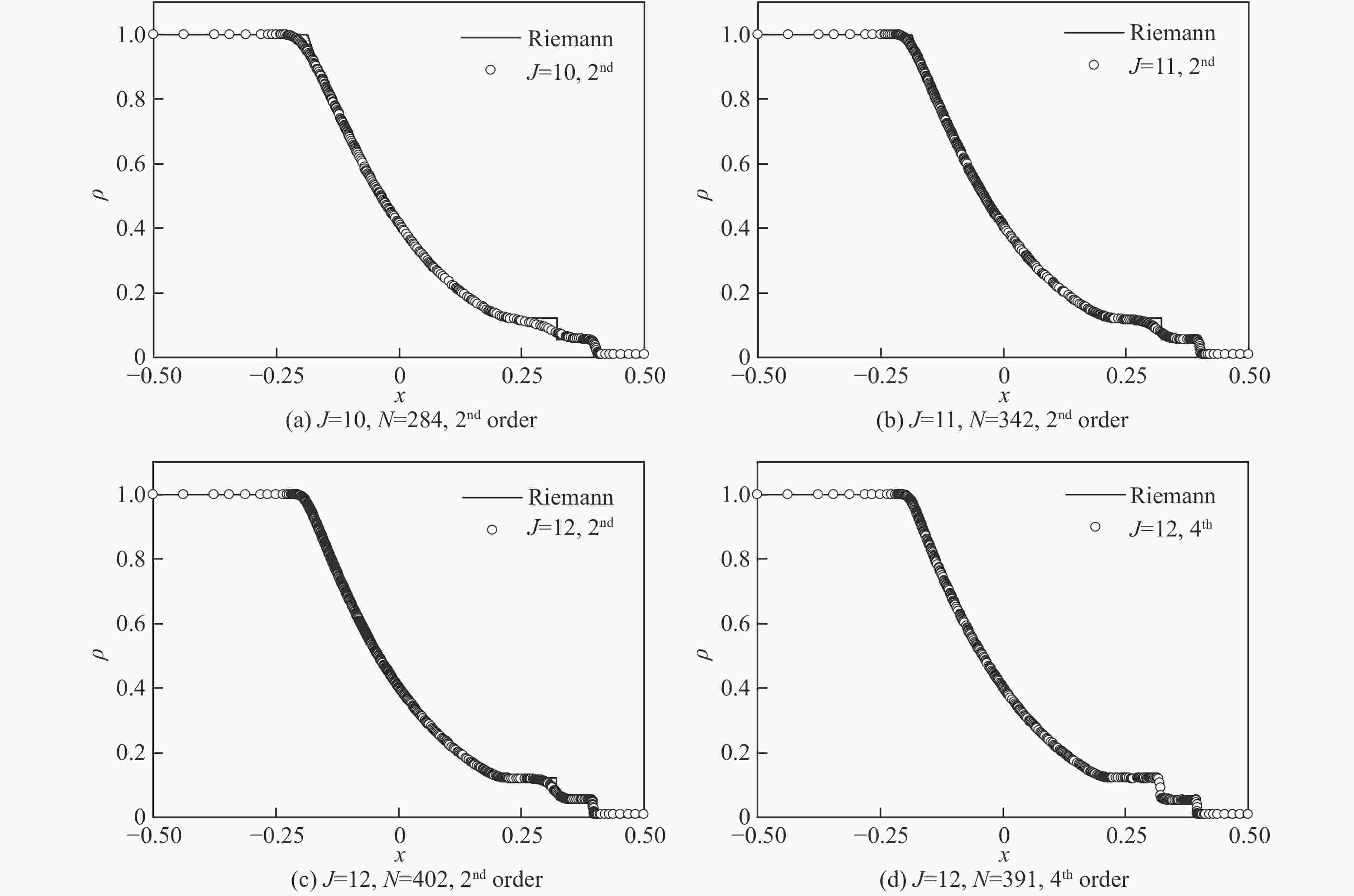
J N α ε/10−4 9 513 1.5 1.0 10 1 025 1.5 1.0 11 2 049 1.5 1.0 
下载: 导出CSV
表 2 强冲击波管计算参数
Table 2. Computational parameters for strong shock tube
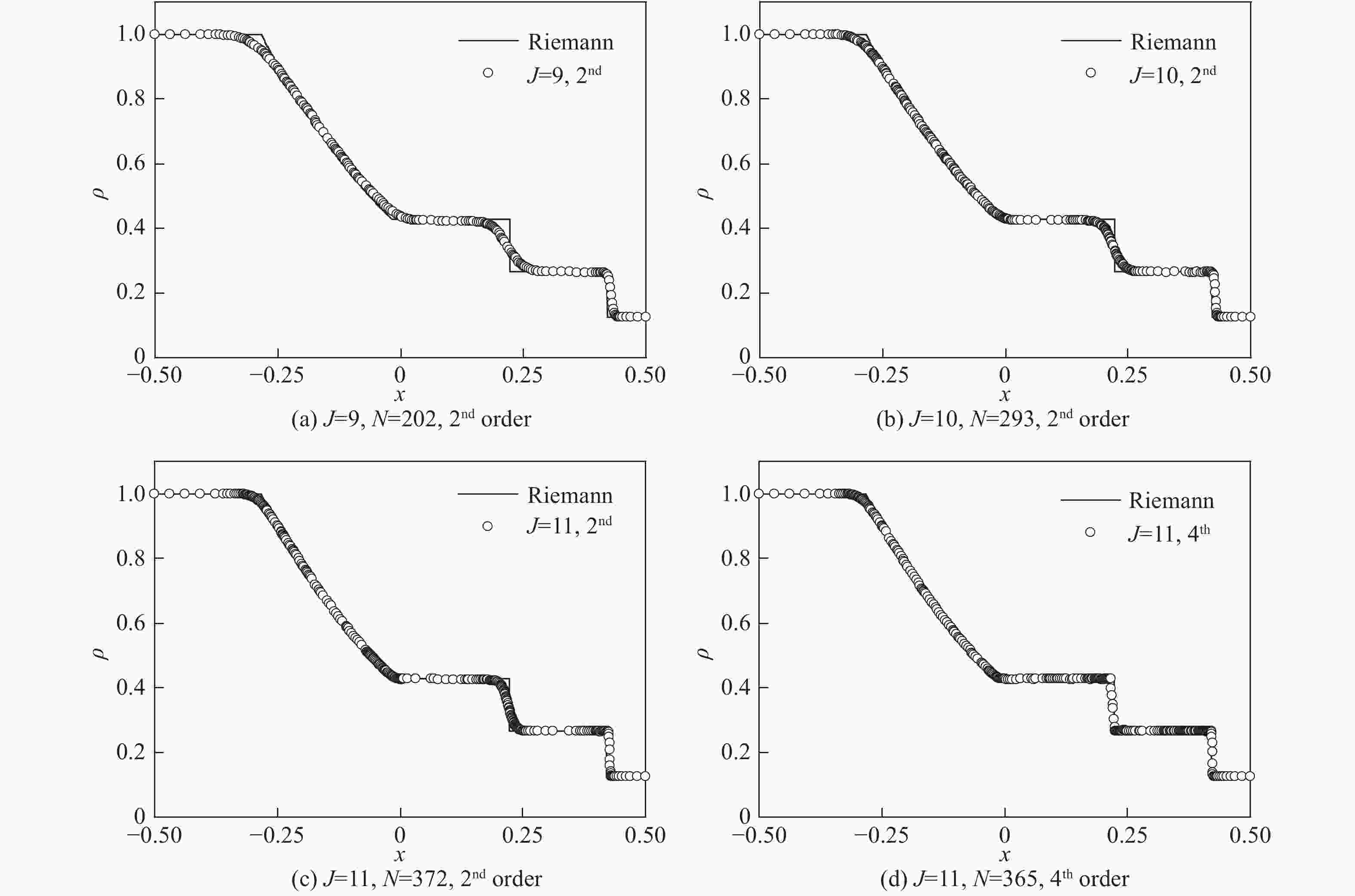
J N α ε/10−5 10 1 025 0.3 1.0 11 2 049 0.3 1.0 12 4 097 0.3 1.0
下载: 导出CSV
-
[1] REGELE J D, VASILYEV O V. An adaptive wavelet-collocation method for shock computations [J]. International Journal of Computational Fluid Dynamics, 2009, 23(7): 503–518. DOI: 10.1080/10618560903117105. [2] CAI W, WANG J Z. Adaptive multiresolution collocation methods for initial-boundary value problems of nonlinear PDEs [J]. SIAM Journal on Numerical Analysis, 1996, 33(3): 937–970. DOI: 10.1137/0733047. [3] 唐玲艳. 双曲型方程数值解的小波方法研究[D]. 长沙: 国防科学技术大学, 2007: 43−84. [4] 李慧敏. 小波分析在双曲型守恒律方程数值解中的应用研究[D]. 南京: 南京航空航天大学, 2002: 6−28.LI H M. Application of wavelet analysis to solving hyperbolic conservation laws [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2002: 6−28. [5] COHEN A, KABER S M, MÜLLER S, et al. Fully adaptive multiresolution finite volume schemes for conservation laws [J]. Mathematics of Computation, 2003, 72(241): 183–226. DOI: 10.1090/s0025-5718-01-01391-6. [6] 王一博, 唐建候, 杨慧珠. 自适应小波方法求解波传问题 [J]. 石油地球物理勘探, 2005, 40(6): 628–631. DOI: 10.3321/j.issn:1000-7210.2005.06.004.WANG Y B, TANG J H, YANG H Z. Using adaptive wavelet method to resolve issue of wave propagation [J]. Oil Geophysical Prospecting, 2005, 40(6): 628–631. DOI: 10.3321/j.issn:1000-7210.2005.06.004. [7] VASILYEV O V, BOWMAN C. Second-generation wavelet collocation method for the solution of partial differential equations [J]. Journal of Computational Physics, 2000, 165(2): 660–693. DOI: 10.1006/jcph.2000.6638. [8] VASILYEV O V. Solving multi-dimensional evolution problems with localized structures using second generation wavelets [J]. International Journal of Computational Fluid Dynamics, 2003, 17(2): 151–168. DOI: 10.1080/1061856021000011152. [9] HARTEN A. Adaptive multiresolution schemes for shock computations [J]. Journal of Computational Physics, 1994, 115(2): 319–338. DOI: 10.1006/jcph.1994.1199. [10] BÜRGER R, KOZAKEVICIUS A. Adaptive multiresolution WENO schemes for multi-species kinematic flow models [J]. Journal of Computational Physics, 2007, 224(2): 1190–1222. DOI: 10.1016/j.jcp.2006.11.010. [11] 王昱. 偏微分方程的小波求解法及其在燃烧计算中的初步应用[D]. 长沙: 国防科学技术大学, 2008: 81−128. [12] 孙阳, 吴勃英, 冯国泰. 利用多小波自适应格式求解流体力学方程 [J]. 力学学报, 2008, 40(6): 744–751. DOI: 10.3321/j.issn:0459-1879.2008.06.004.SUN Y, WU B Y, FENG G T. The AUSMPW scheme based on adaptive algorithm of interpolating multiwavelets applied to solve Euler equations [J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(6): 744–751. DOI: 10.3321/j.issn:0459-1879.2008.06.004. [13] 赵勇. 小波数值方法在船舶流体力学中的若干应用[D]. 大连: 大连理工大学, 2011: 29−56.ZHAO Y. Wavelet numerical method with some applications to marine hydrodynamics [D]. Dalian: Dalian University of Technology, 2011: 29−56. [14] 赵勇, 宗智, 王天霖. 一种抑制冲击波计算中数值震荡现象的双重小波数值方法 [J]. 应用数学和力学, 2014, 35(6): 620–629. DOI: 10.3879/j.issn.1000-0887.2014.06.004.ZHAO Y, ZONG Z, WANG T L. A dual wavelet shrinkage procedure for suppressing numerical oscillation in shock wave calculation [J]. Applied Mathematics and Mechanics, 2014, 35(6): 620–629. DOI: 10.3879/j.issn.1000-0887.2014.06.004. [15] REGELE J D, KASSOY D R, VASILYEV O V. Numerical modeling of acoustic timescale detonation initiation: AIAA 2008- 1037 [R]. USA: NASA, 2008. DOI: 10.1080/13647830.2011.647090. [16] REGELE J, RABINOVITCH J, COLONIUS T, et al. Numerical modeling and analysis of early shock wave interactions with a dense particle cloud: AIAA 2012-3161 [R]. USA: NASA, 2012. DOI: 10.2514/6.2012-3161. [17] REGELE J D. Purely gasdynamic multidimentioanal indirect detonation initiation using localized acoustic timescale power deposition: AIAA 2013-1172 [R]. USA: NASA, 2013. DOI: 10.2514/6.2013-1172. [18] KASSOY D, REGELE J, VASILYEV O. Detonation initiation on the microsecond time scale: one and two dimensional results obtained from adaptive wavelet-collocation numerical methods: AIAA 2007-986 [R]. USA: NASA, 2007. DOI: 10.1080/13647830.2014.971058. [19] SCHNEIDER K, VASILYEV O V. Wavelet methods in computational fluid dynamics [J]. Annual Review of Fluid Mechanics, 2010, 42(1): 473–503. DOI: 10.1146/annurev-fluid-121108-145637. [20] LANEY C B. Computational gasdynamics [M]. Cambridge: Cambridge University Press, 1998: 249−299. DOI: 10.1017/cbo9780511605604 -
图(7) / 表(2)
计量
- 文章访问数: 5862
- HTML全文浏览量: 1732
- PDF下载量: 88
- 被引次数: 0