An experimental study of dynamic bond-slip behaviors of plain steel barsin concrete at different strain rates
-
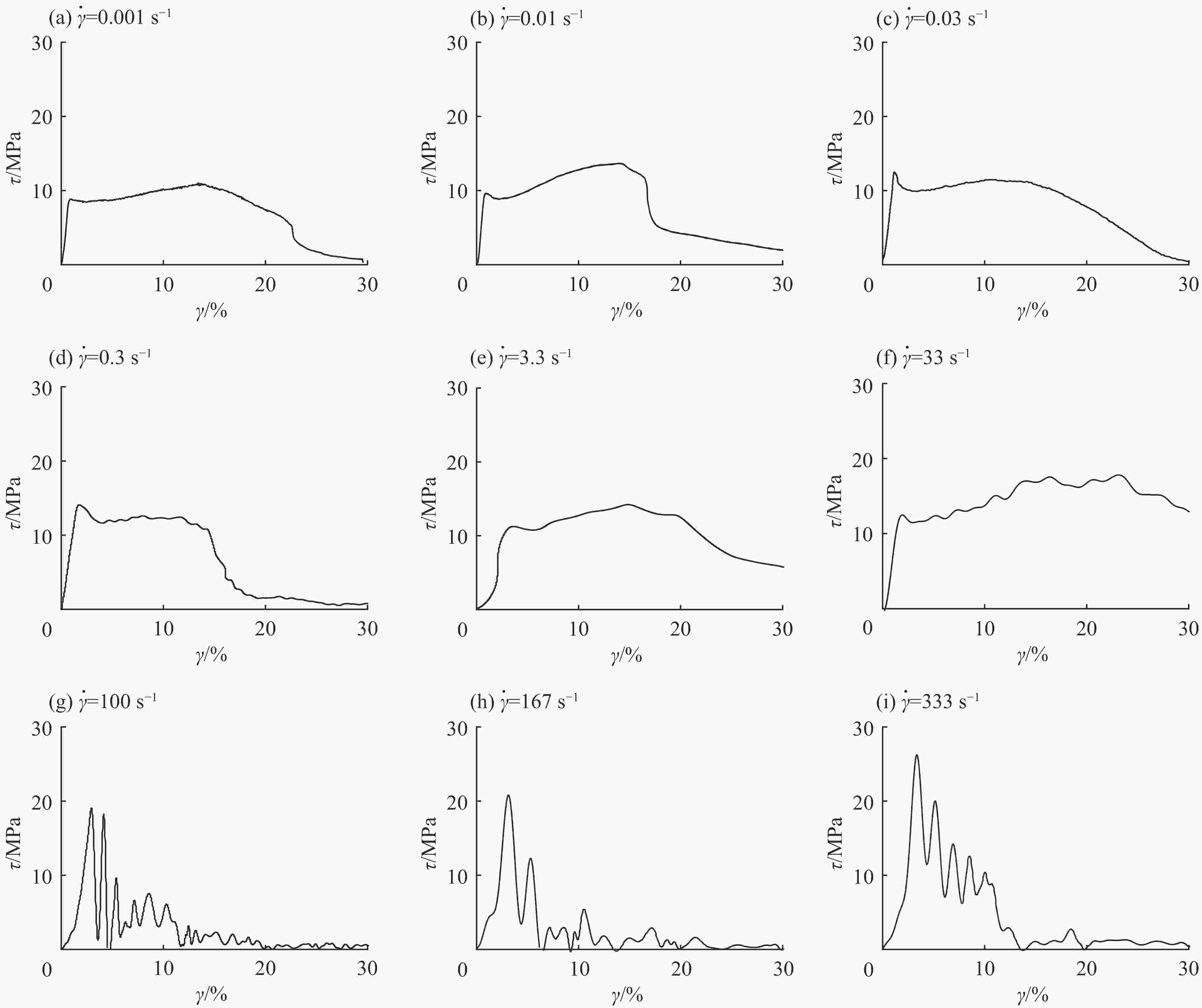
摘要: 为研究应变率对钢筋与混凝土界面粘结性能的影响,利用高速拉伸试验机进行了光圆钢筋的动态拔出实验。通过合理设计加载夹具和测试方法,得到不同应变率下光圆钢筋的“粘结-滑移”全程曲线。实验结果表明:随着应变率的增大,钢筋-混凝土界面的粘结强度显著提高,且界面失效形式由拔出失效为主转变为混凝土试件的破裂破坏为主;粘结强度的动态增强因子(f DIF)随应变率的增长斜率明显可以分为低应变率和高应变率两个区段。低应变率下,fDIF增长较为缓慢;而高应变率下,f DIF快速增长;转变应变率约为33 s−1。
-
关键词:
- 应变率 /
- 钢筋混凝土 /
- 动态粘结-滑移力学行为 /
- 粘结强度动态增强因子
Abstract: To investigate the effect of strain rate on the bond-slip behaviors of smooth steel bars in concrete, we conducted plain steel bar pullout tests from quasi-static to impact loading using a high-speed tensile test machine and obtained the whole bond-slip curves of the plane steel bar at different strain rate with reasonable designed stop devices and testing methods. The test results show that the bond strength increased obviously, and the failure mode transferred from pullout to splitting with the increase of the strain rate, that the dynamic increase factor(DIF) curve can be divided into two parts, those of the low and high strain rates, and that the DIF increased slowly with the increase of the strain rate at low strain rates, but increased sharply at high strain rates. -
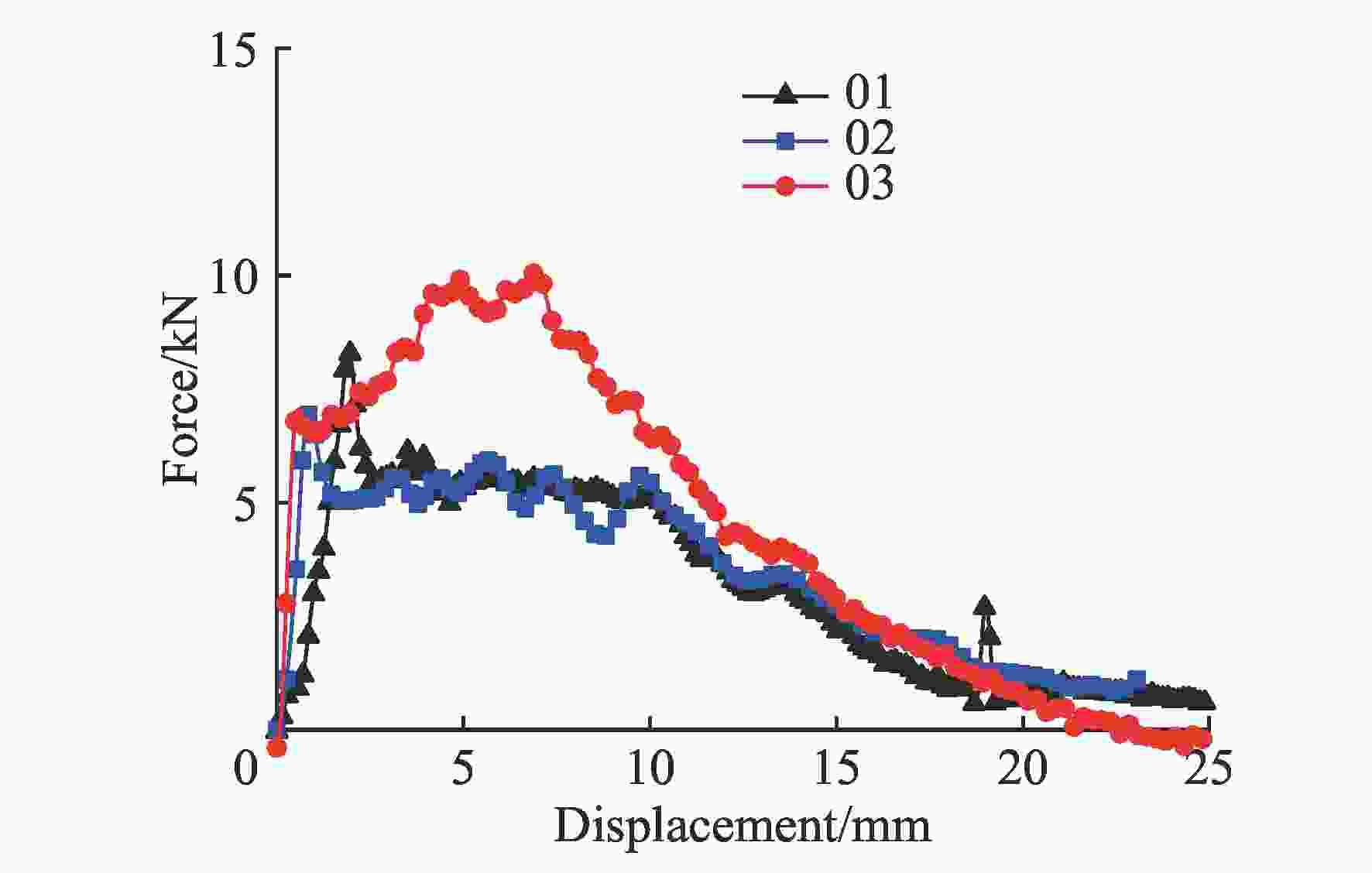
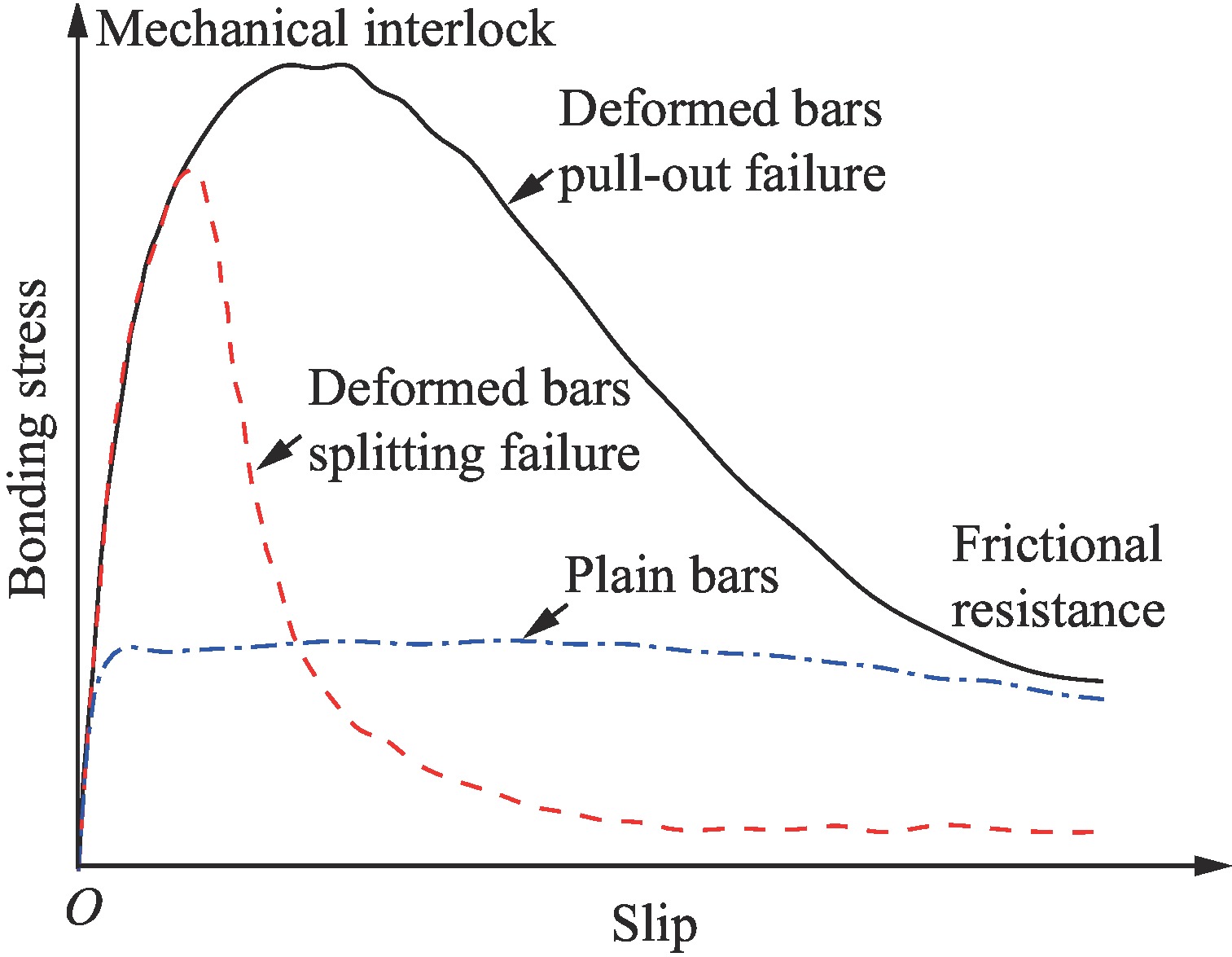
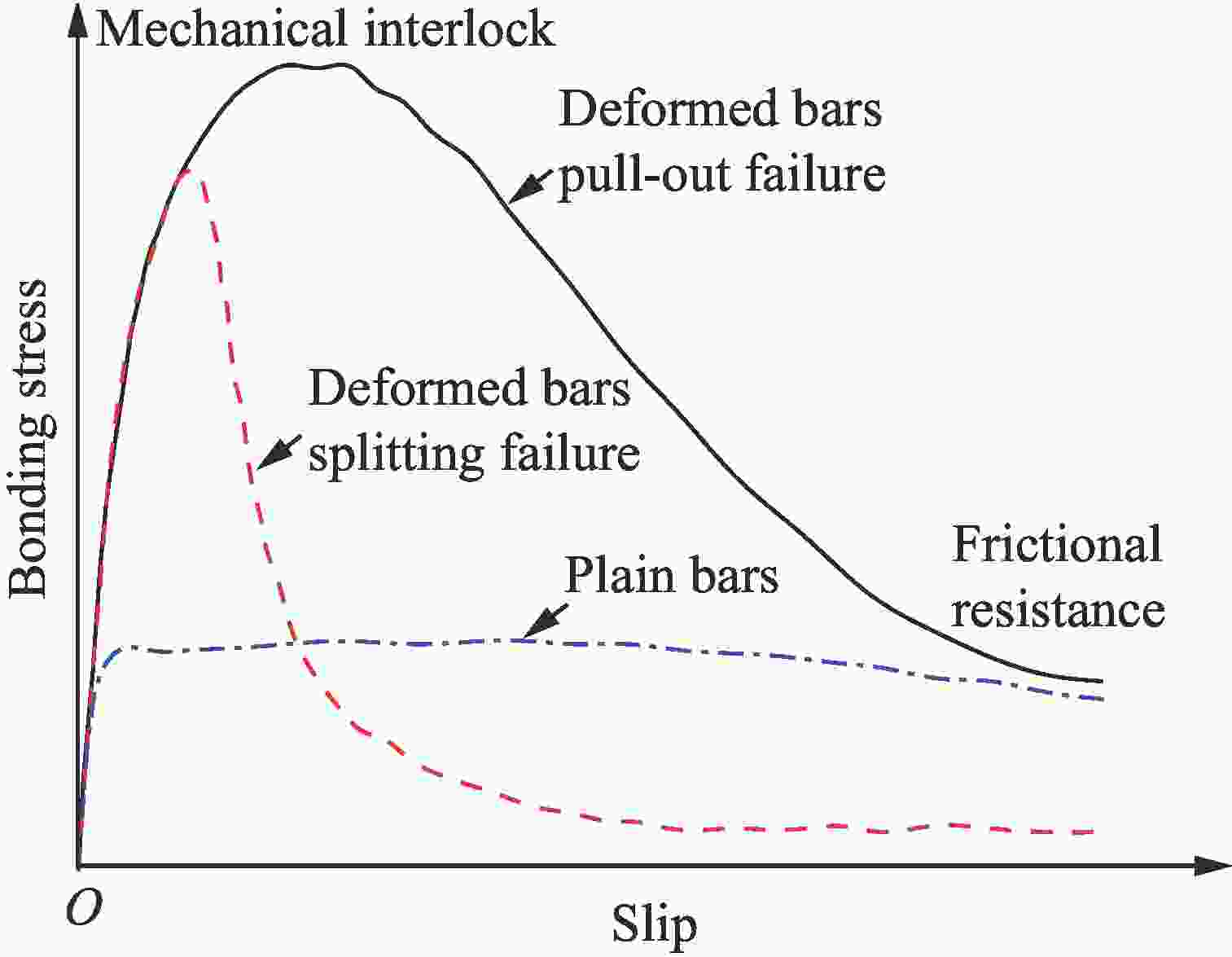
图 1 典型的准静态粘结-滑移曲线[11]
Figure 1. A typical quasi-static “bond-slip” curves
表 1 试验结果综合
Table 1. collection of the test results
加载速度/(mm·s−1) 名义应变率/s−1 编号 粘结强度/MPa 滑移应变εs /% 名义失效应变εf /% 破坏形态 0.03 0.001 01 8.85 0.88 10.95 拔出 02 8.44 1.27 12.3 拔出 03 10.9 0.95 11.2 拔出 0.30 0.010 01 9.59 0.88 14.2 拔出 02 11.4 0.97 11.6 劈裂 03 9.88 0.89 12.8 拔出 1.00 0.030 01 12.4 1.12 11.5 拔出 02 10.9 0.80 13.6 拔出 03 12.8 1.36 14.6 拔出 10.0 0.333 01 14.1 1.67 11.7 拔出 02 14.9 1.35 12.1 劈裂 03 11.2 2.03 15.4 拔出 100 3.333 01 11.2 3.41 14.7 拔出 02 11.8 1.89 12.9 拔出 03 10.4 1.33 16.8 拔出 1 000 33.33 01 14.8 1.85 23.2 拔出 02 12.4 0.93 31.6 拔出 03 12.2 2.18 30.9 拔出 3 000 100.0 01 19.0 2.91 − 劈裂 02 21.2 2.07 − 劈裂 03 19.9 1.91 劈裂 5 000 166.7 01 20.7 3.10 − 劈裂 02 21.3 2.35 − 劈裂 03 24.0 2.91 − 劈裂 10 000 333.3 01 26.3 3.33 − 劈裂 02 23.2 4.26 − 劈裂 03 26.8 2.79 − 劈裂 -
[1] MIRZA S M. Study of bond stress-slip relationships in reinforced concrete [J]. Aci Journal, 1979, 76(1): 19–46. DOI: 10.1016/0022-3115(79)90116-8. [2] DÍAZ T, JOSÉ R, HAACH V G. Equivalent stress-strain law for embedded reinforcements considering bond-slip effects [J]. Engineering Structures, 2018, 165: 247–253. DOI: 10.1016/j.engstruct.2018.03.045. [3] GAO X, LI N, REN X. Analytic solution for the bond stress-slip relationship between rebar and concrete [J]. Construction and Building Materials, 2019, 197: 385–97. DOI: 10.1016/j.conbuildmat.2018.11.206. [4] GAMBAROVA P G, ROSATI G P. Bond and splitting in reinforced concrete: test results on bar pull-out [J]. Materials & Structures, 1996, 29(5): 267–276. DOI: 10.1007/BF02486361. [5] MO Y L, CHAN J. Bond and slip of plain rebars in concrete [J]. Journal of Materials in Civil Engineering, 1996, 8(4): 208–211. DOI: 10.1061/(ASCE)0899-1561(1996)8:4(208). [6] FELDMAN L R, BARTLETT F M. Bond stresses along plain steel reinforcing bars in pullout specimens [J]. Aci Structural Journal, 2007, 104(6): 685–692. DOI: 10.1002/tal.417. [7] LUTZ L R A, GERGELY P. Mechanics of bond and slip of deformed bars in concrete [J]. ACI Journal, 1967, 64(11): 711–721. DOI: 10.14359/7600. [8] LUNDGREN K. Bond between ribbed bars and concrete. Part 1: modified model [J]. Magazine of Concrete Research, 2005, 57(7): 371–382. DOI: 10.1680/macr.2005.57.7.371. [9] BOMPA D V, ELGHAZOULI A Y. Bond-slip response of deformed bars in rubberised concrete [J]. Construction & Building Materials, 2017, 154: 884–898. DOI: 10.1016/j.conbuildmat.2017.08.016. [10] KIM S W, YUN H D, PARK W S, et al. Bond strength prediction for deformed steel rebar embedded in recycled coarse aggregate concrete [J]. Materials & Design, 2015, 83: 257–269. DOI: 10.1016/j.matdes.2015.06.008. [11] MICHAL M, KEUSER M, SOLOMOS G, et al. Experimental investigation of bond strength under high loading rates[C] // European Physical Journal Web of Conferences. European Physical Journal Web of Conferences, 2015. DOI: 10.1051/epjconf/20159401044. [12] ESFAHANI M R, RANGAN B V. Local bond strength of reinforcing bars in normal strength and high-strength concrete (HSC) [J]. ACI Structural Journal, 1998, 95(2): 96–106. DOI: 10.14359/530. [13] SULAIMAN M F, MA C K, APANDI N M, et al. A review on bond and anchorage of confined high-strength concrete [J]. Structures, 2017, 11: 97–109. DOI: 10.1016/j.istruc.2017.04.004. [14] GIURIANI E, SCHUMM C, PLIZZARI G. Role of stirrups and residual tensile strength of cracked concrete on bond [J]. Journal of Structural Engineering, 1991, 117(1): 1–18. DOI: 10.1061/(ASCE)0733-9445(1991)117:1(1). [15] AHMED K, SIDDIQI Z A, ASHRAF M, et al. Effect of rebar cover and development length on bond and slip in high strength concrete [J]. Pakistan Journal of Engineering and Applied Sciences, 2008, 2: 79–87. [16] 郑晓燕, 吴胜兴. 动荷载下锈蚀钢筋混凝土粘结滑移特性的试验研究 [J]. 土木工程学报, 2006, 39(6): 42–46. DOI: 10.3321/j.issn:1000-131X.2006.06.007.ZHENG Xiaoyan, WU Shengxing. An experimental study on the bond-slip behavior of corroded steel bars in concrete under dynamic loads [J]. China Civil Engineering Journal, 2006, 39(6): 42–46. DOI: 10.3321/j.issn:1000-131X.2006.06.007. [17] ZHANG W P, CHEN H, GU X L. Bond behaviour between corroded steel bars and concrete under different strain rates [J]. Magazine of Concrete Research, 2015, 68(7): 1–15. DOI: 10.1680/macr.15.00174. [18] HANSEN R J, LIEPINS A A. Behavior of bond under dynamic loading [J]. ACI Structural Journal, 1959, 59(4): 563–584. DOI: 10.14359/7929. [19] WEATHERSBY J H. Investigation of bond slip between concrete and steel reinforcement under dynamic loading conditions [D]. Baton Rouge: Louisiana State University, 2003: 1−263. [20] VOS E. Influence of loading rate and radial pressure on bond in reinforced concrete [D]. Delft: Delft University of Technology, 1983: 1−263. [21] SOLOMOS G, BERRA M. Rebar pullout testing under dynamic Hopkinson bar induced impulsive loading [J]. Materials & Structures, 2010, 43(1-2): 247–260. DOI: 10.1617/s11527-009-9485-z. [22] YAN C. Bond between reinforcing bars and concrete under impact loading [D]. Vancouver: University of British, 1992. -






 下载:
下载: