Dynamic compressive response of metal orthogonal corrugated sandwich structure
-
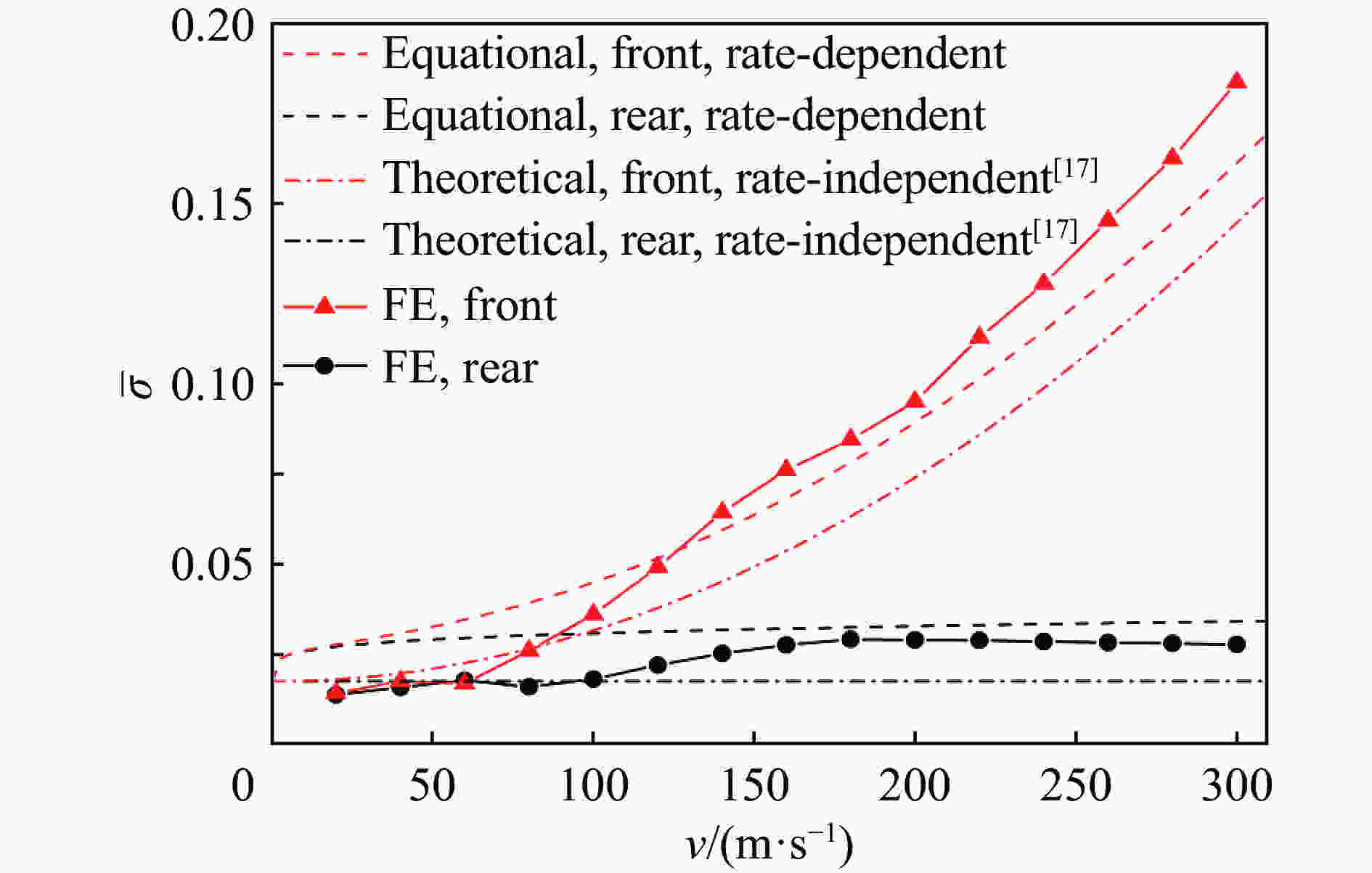
摘要: 通过理论和数值方法，对冲击载荷下金属正交波纹夹芯结构的动态压缩响应进行了研究。考虑材料应变率影响，建立了金属正交波纹夹芯结构动态响应的理论模型，同时对它的动态压缩响应进行了有限元模拟。结果表明，考虑材料应变率影响的理论模型的预测结果与有限元模拟结果吻合较好。进一步对多层正交波纹夹芯结构的动态压缩响应进行了数值模拟，获得了不同速度冲击下的变形模式，分析了层数对其动态响应的影响。研究发现，通过增加层数能够有效地增强结构的缓冲吸能能力，但层数超过4层以后增强效果不明显。Abstract: In this paper, dynamic compression response of metal orthogonal corrugated sandwich structures under impact loading is investigated theoretically and numerically. Considering the effect of strain rate of material, analytical models of dynamic response of metal orthogonal corrugated sandwich structure is developed. Finite element simulation of its dynamic compressive response is carried out. It is shown that there is a good agreement between the results based on the analytical model and finite element simulation. Furthermore, the dynamic compressive response of multi-layer orthogonal corrugated sandwich structure is studied using finite element method. Deformation modes under different impact velocities are obtained and the influence of the number of layers on the dynamic response is analyzed. It is found that the mitigation and energy absorption capacity of the sandwich structures can be effectively enhanced by increasing the number of layers while the number of layers have mild influence after exceeding four.
-
图 1 单层正交波纹夹芯结构
Figure 1. Sketch of single-layer orthogonal corrugated sandwich structure
图 2 多层正交波纹夹芯结构
Figure 2. Sketch of multi-layer orthogonal corrugated sandwich structure
图 3 单层正交波纹夹芯结构前、后面板的平均等效应力
Figure 3. Average stress of front and rear panels of single-layer orthogonal corrugated sandwich structure
图 4 冲击速度为20 m/s时单层正交波纹夹芯结构的动态响应
Figure 4. Dynamic response of single-layer orthogonal corrugated sandwich structure at shock velocity of 20 m/s
图 5 冲击速度为120 m/s时单层正交波纹夹芯结构的动态响应
Figure 5. Dynamic response of single-layer orthogonal corrugated sandwich structure at shock velocity of 120 m/s
图 6 冲击速度为300 m/s时单层正交波纹夹芯结构的动态响应
Figure 6. Dynamic response of single-layer orthogonal corrugated sandwich structure at shock velocity of 300 m/s
图 7 冲击速度为20 m/s时两层正交波纹夹芯结构的动态响应
Figure 7. Dynamic response of two-layer orthogonal corrugated sandwich structure at shock velocity of 20 m/s
图 8 冲击速度为60 m/s时两层正交波纹夹芯结构的动态响应
Figure 8. Dynamic response of two-layer orthogonal corrugated sandwich structure at shock velocity of 60 m/s
图 9 冲击速度为120 m/s时两层正交波纹夹芯结构的动态响应
Figure 9. Dynamic response of two-layer orthogonal corrugated sandwich structure at shock velocity of 120 m/s
图 10 冲击速度为300 m/s时两层正交波纹夹芯结构的动态响应
Figure 10. Dynamic response of two-layer orthogonal corrugated sandwich structure at shock velocity of 300 m/s
图 11 冲击速度为260 m/s时3层正交波纹夹芯结构的动态响应
Figure 11. Dynamic response of three-layer orthogonal corrugated sandwich structure at shock velocity of 260 m/s
图 12 不同层数正交波纹夹芯结构后面板的平均等效应力
Figure 12. Average stress of rear panel of orthogonal corrugated sandwich structure with different layers
图 13 夹芯层数对正交波纹夹芯结构比吸能的影响
Figure 13. Effect of number of layers on specific energy absorption of orthogonal corrugated sandwich structure
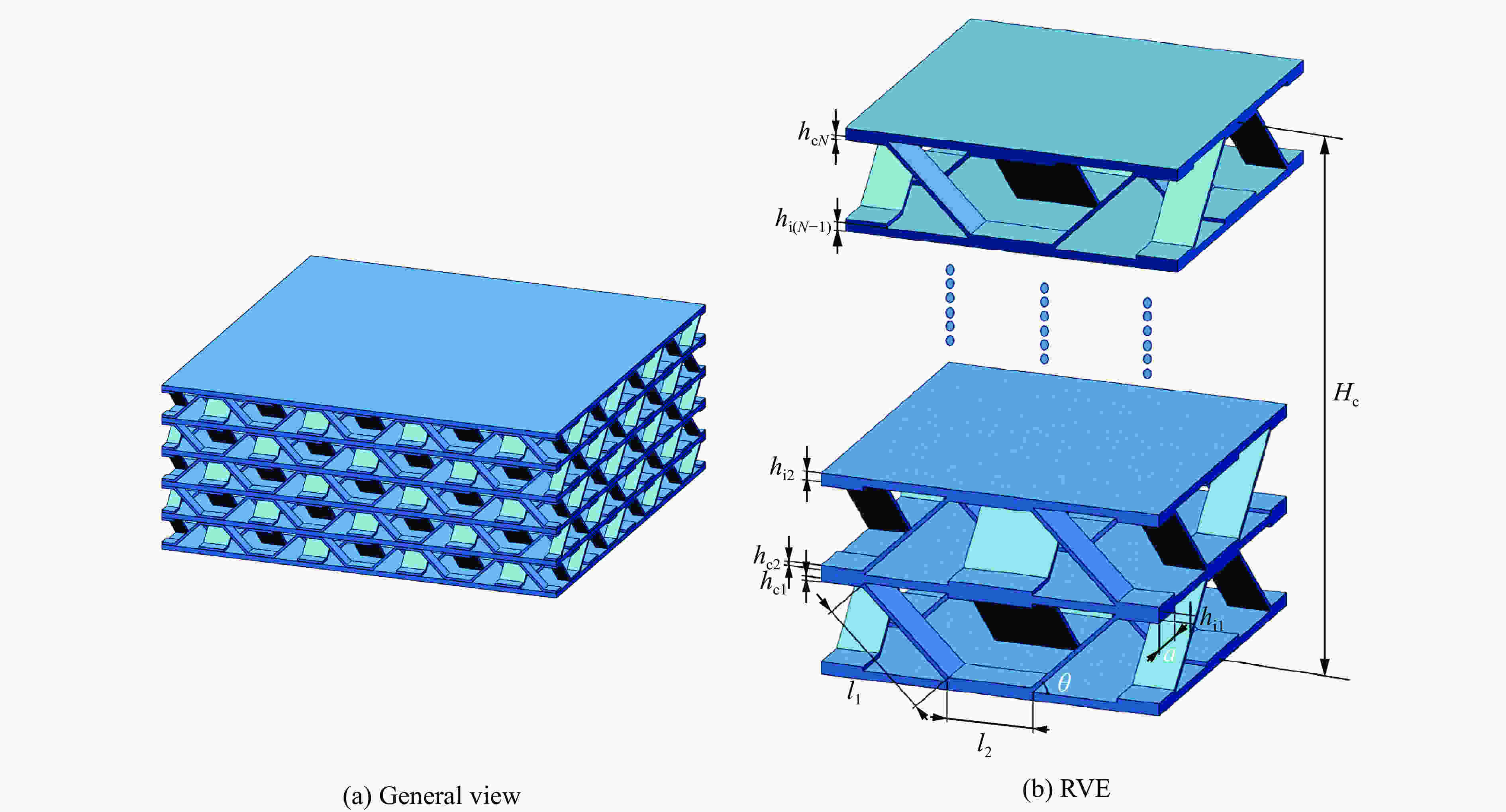
表 1 正交波纹夹芯结构的几何尺寸
Table 1. Geometric dimensions of orthogonal corrugated sandwich structure
l1/cm l2/cm θ/(°) a/cm hc/cm hi/cm $\sqrt{2}$ 1 45 1 0.05 0.1 
下载: 导出CSV
表 2 不同层数的正交波纹夹芯结构的相对密度
Table 2. Relative density of orthogonal corrugated sandwich structure with different layers
N ${\bar \rho _{\rm{c}}}$/% ${\bar \rho _{\rm{i}}}$/% ${\bar \rho _{\rm{m}}}$/% 1 5.75 0 5.75 2 5.49 4.55 10.04 3 5.41 5.97 11.38 4 5.37 6.67 12.04 5 5.34 7.07 12.41
下载: 导出CSV
表 3 正交波纹夹芯结构的变形模式
Table 3. Deformation modes of orthogonal corrugated sandwich structure
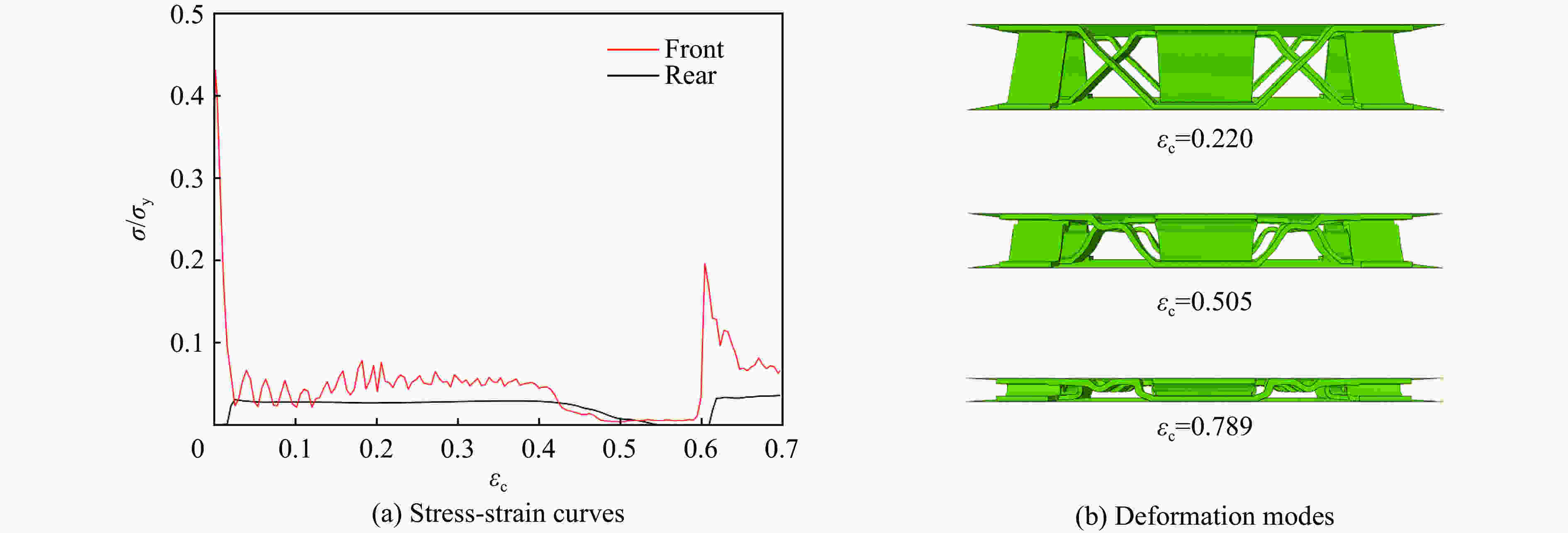
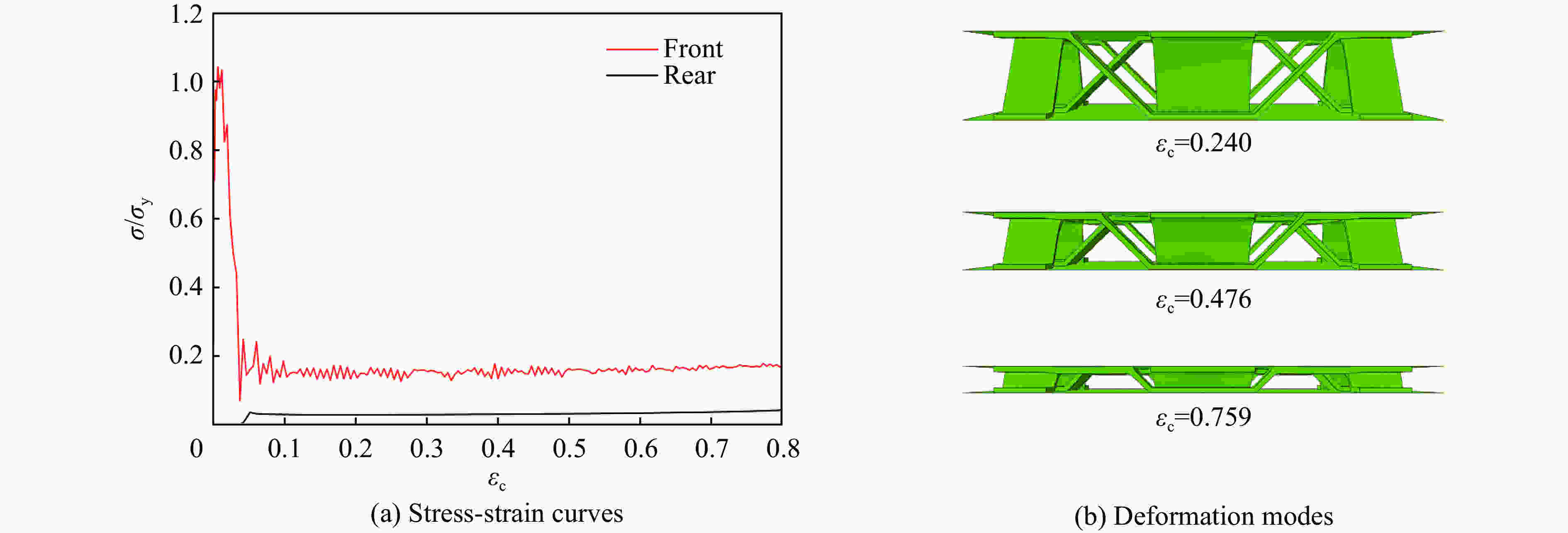
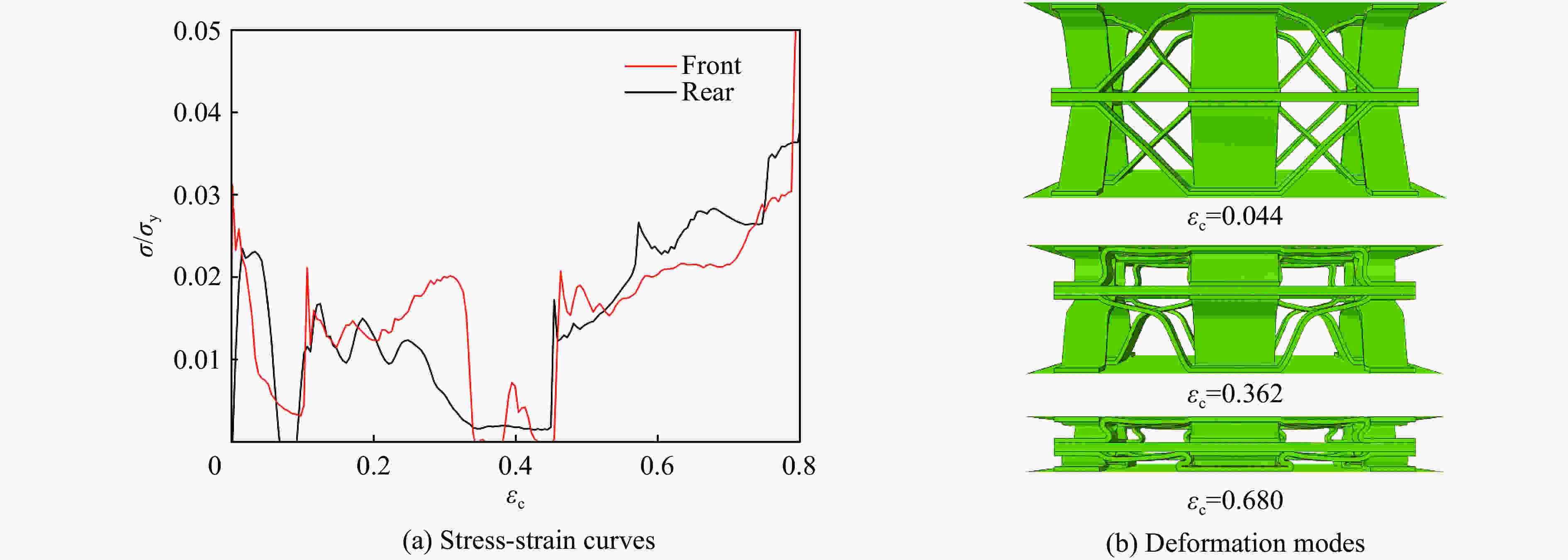
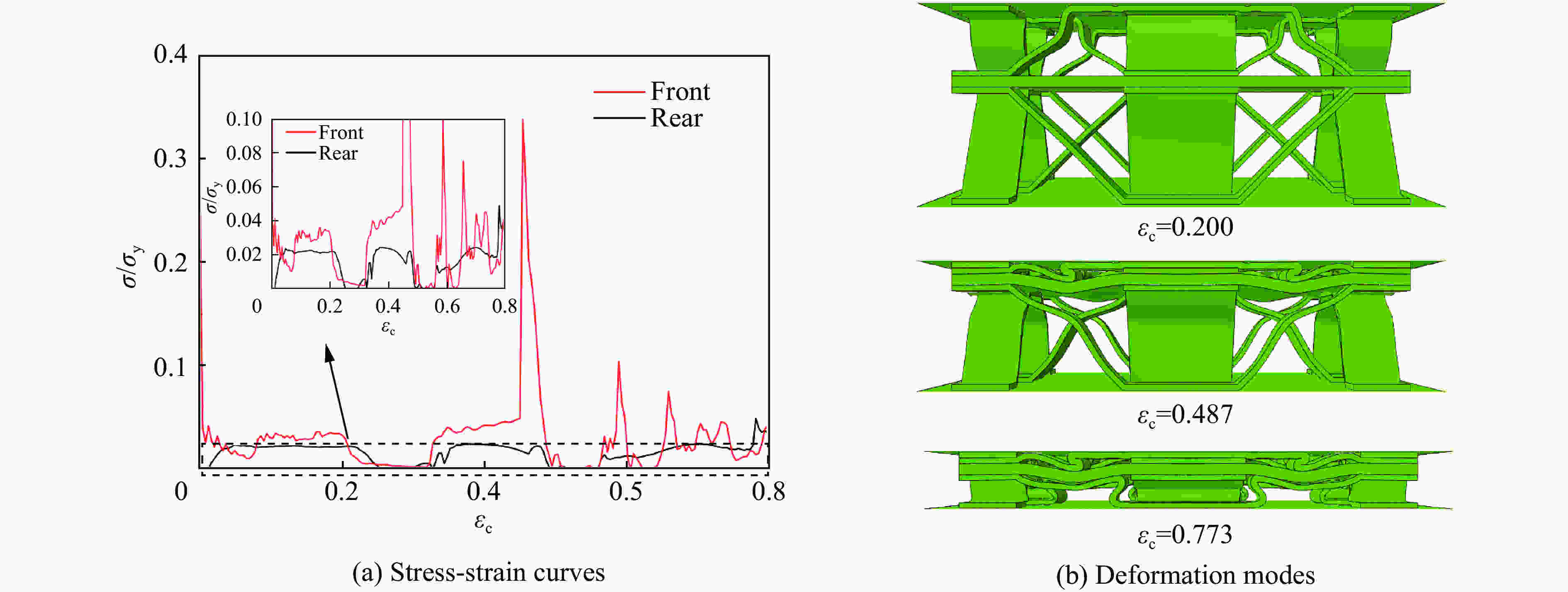
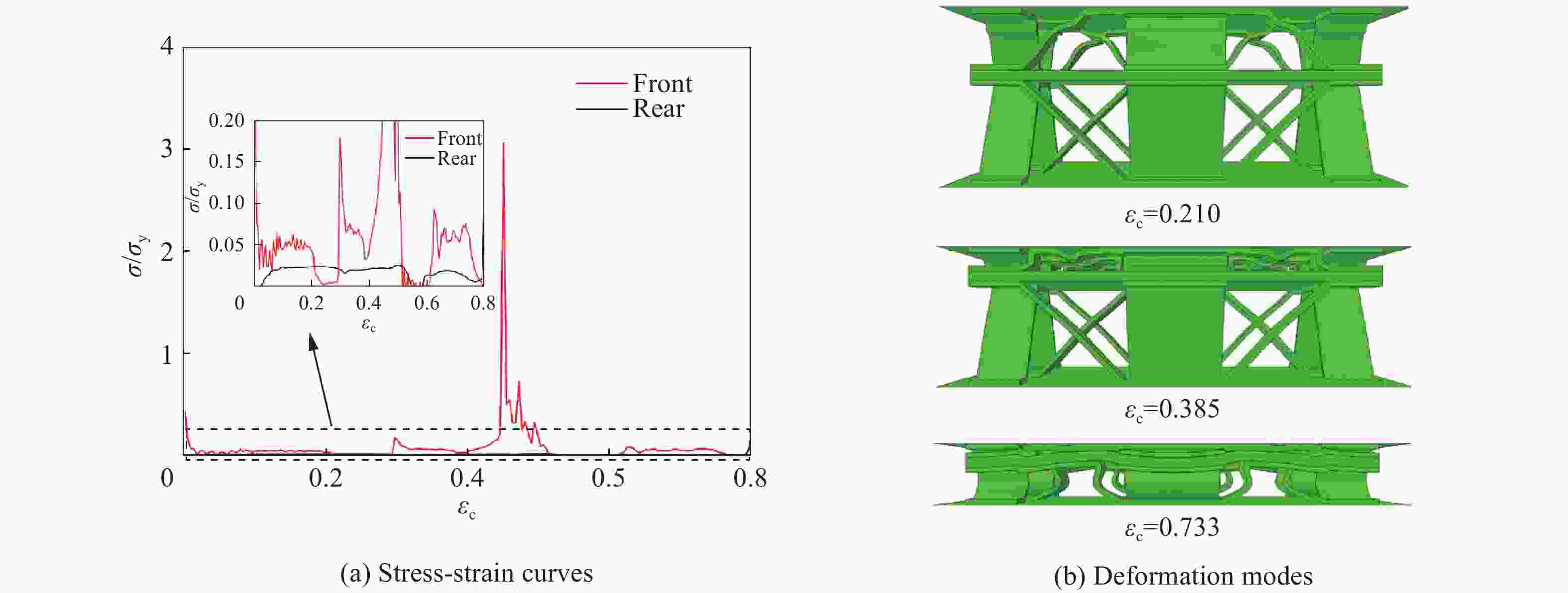
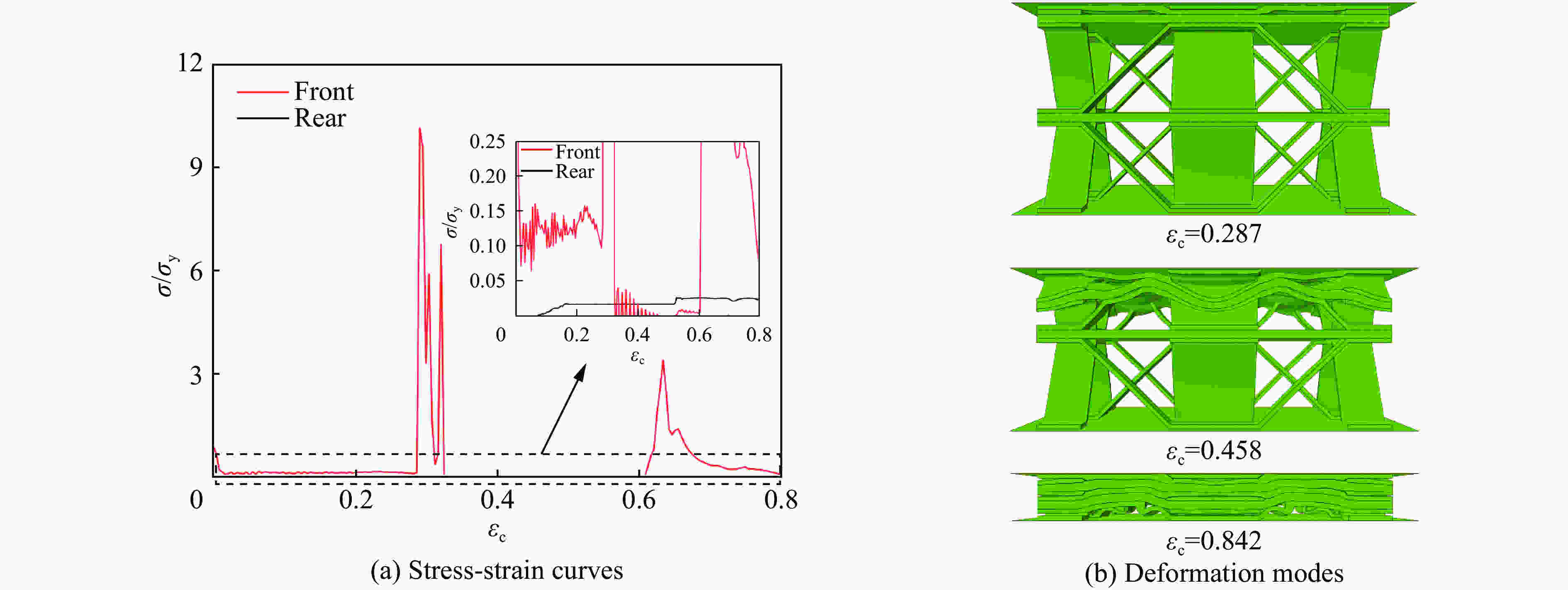
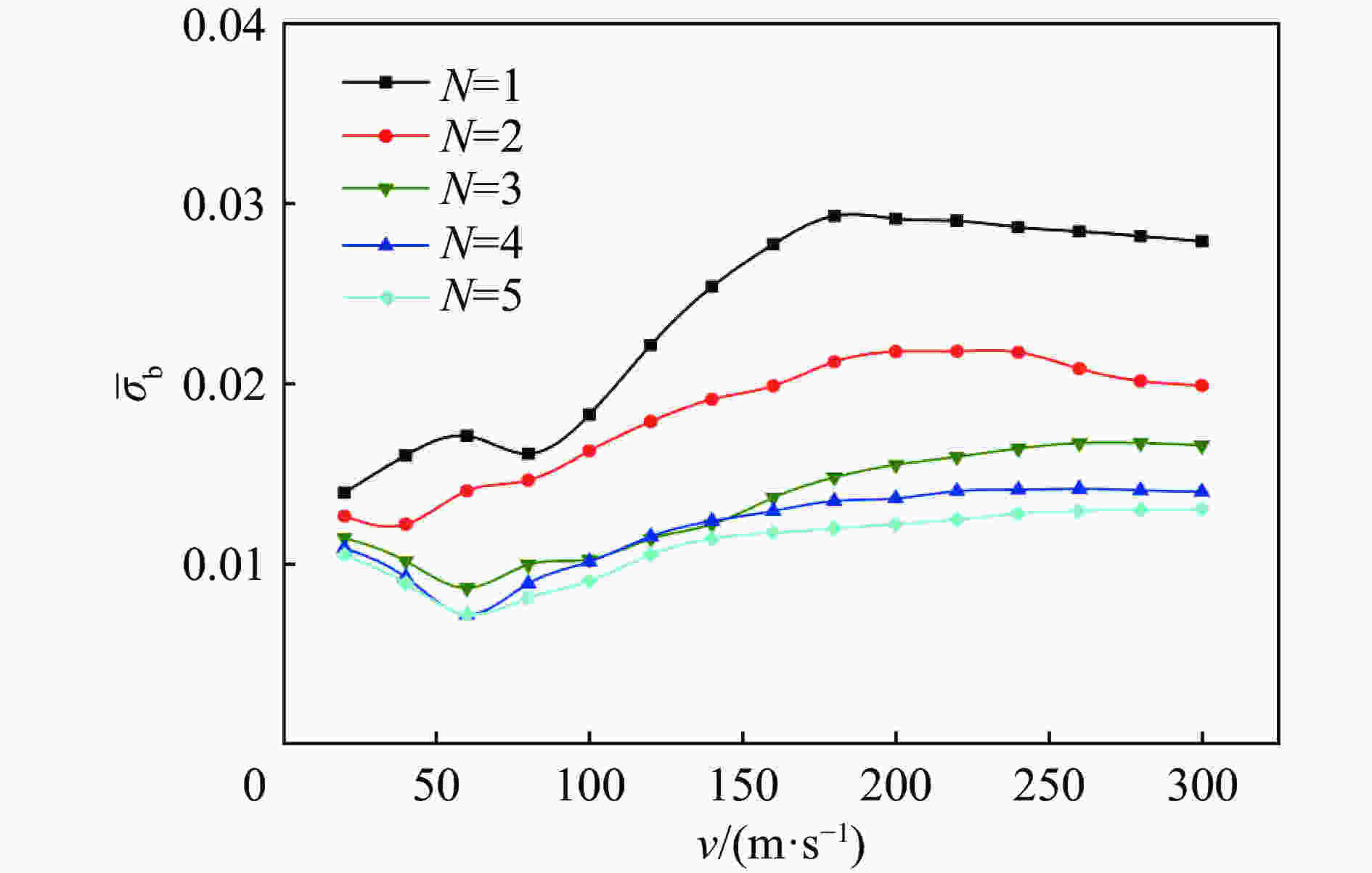
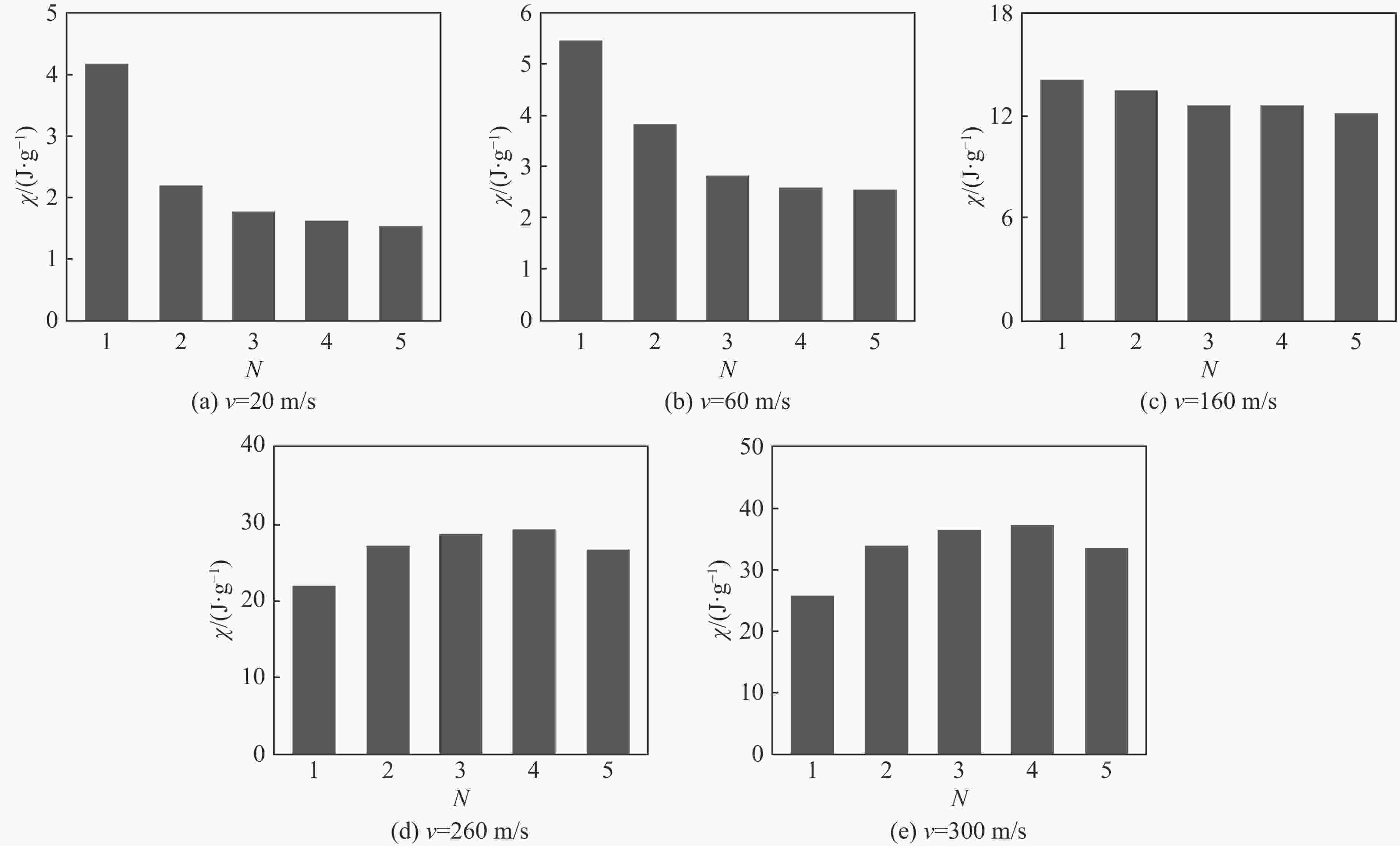
N 变形模式 v=20 m/s v=60 m/s v=160 m/s v=260 m/s v=300 m/s 1 B W W S S 2 B-B W-B W-W S-S S-S 3 B-B-B W-B-B W-W-W S-S-W S-S-S 4 B-B-B-B W-B-B-B W-W-W-W S-S-W-W S-S-S-S 5 B-B-B-B-B W-B-B-B-B W-W-W-W-W S-S-W-W-W S-S-S-S-S
下载: 导出CSV
-
[1] ASHBY M F, EVANS A, FLECK N A, et al. Metal foams: a design guide [M]. Oxford, UK: Butterworth-Heinemann, 2000. DOI: 10.1016/S0261-3069(01)00049-8. [2] GIBSON L J A A, ASHBY M F. Cellular solids: structure and properties [M]. Cambridge: Cambridge University Press, 1997. DOI: 10.1016/0921-5093(90)90295-E. [3] WANG A J, MCDOWELL D L. In-plane stiffness and yield strength of periodic metal honeycombs [J]. Journal of Engineering Materials & Technology, 2004, 126(2): 137–156. DOI: 10.1115/1.1646165. [4] DESHPANDE V S, FLECK N A, ASHBY M F. Effective properties of the octet-truss lattice material [J]. Journal of the Mechanics & Physics of Solids, 2001, 49(8): 1747–1769. DOI: 10.1016/s0022-5096(01)00010-2. [5] DESHPANDE V S, FLECK N A. Collapse of truss core sandwich beams in 3-point bending [J]. International Journal of Solids & Structures, 2001, 38(36): 6275–6305. DOI: 10.1016/S0020-7683(01)00103-2. [6] FAN H L, FANG D N, JING F N. Yield surfaces and micro-failure mechanism of block lattice truss materials [J]. Materials & Design, 2008, 29(10): 2038–2042. DOI: 10.1016/j.matdes.2008.04.013. [7] ASHBY M F, BRÉCHET Y J M. Designing hybrid materials [J]. Acta Materialia, 2003, 51(19): 5801–5821. DOI: 10.1016/S1359-6454(03)00441-5. [8] EBRAHIMI H, GHOSH R, MAHDI E, et al. Honeycomb sandwich panels subjected to combined shock and projectile impact [J]. International Journal of Impact Engineering, 2016, 95: 1–11. DOI: 10.1016/j.ijimpeng.2016.04.009. [9] RUBINO V, DESHPANDE V S, FLECK N A. The dynamic response of end-clamped sandwich beams with a Y-frame or corrugated core [J]. International Journal of Impact Engineering, 2008, 35(8): 829–844. DOI: 10.1016/j.ijimpeng.2007.10.006. [10] KOOISTRA G, DESHPANDE V, WADLEY H. Hierarchical corrugated core sandwich panel concepts [J]. Journal of Applied Mechanics, 2007, 74(2): 259–268. DOI: 10.1115/1.2198243. [11] KAZEMAHVAZI S, ZENKERT D. Corrugated all-composite sandwich structures. Part 1: Modeling [J]. Composites Science and Technology, 2009, 69(7/8): 913–919. DOI: 10.1016/j.compscitech.2008.11.030. [12] KAZEMAHVAZI S, TANNER D, DAN Z. Corrugated all-composite sandwich structures. Part 2: Failure mechanisms and experimental programme [J]. Composites Science and Technology, 2010, 69(7): 920–925. DOI: 10.1016/j.compscitech.2008.11.035. [13] CHEN M, PEI Y, FANG D. Computational method for radar absorbing composite lattice grids [J]. Computational Materials Science, 2009, 46(3): 591–594. DOI: 10.1016/j.commatsci.2008.12.011. [14] FOO C C, SEAH L K, CHAI G B. Low-velocity impact failure of aluminium honeycomb sandwich panels [J]. Composite Structures, 2008, 85(1): 20–28. DOI: 10.1016/j.compstruct.2007.10.016. [15] ZHANG J X, QIN Q H, WANG T J. The resistance of metallic sandwich plates to blast loading [J]. Key Engineering Materials, 2011, 462-463: 349–354. DOI: 10.4028/www.scientific.net/KEM.462-463.349. [16] ZHANG J, QIN Q, WANG T J. Compressive strengths and dynamic response of corrugated metal sandwich plates with unfilled and foam-filled sinusoidal plate cores [J]. Acta Mechanica, 2013, 224(4): 759–775. DOI: 10.1007/s00707-012-0770-5. [17] MCSHANE G J, PINGLE S M, DESHPANDE V S, et al. Dynamic buckling of an inclined strut [J]. International Journal of Solids and Structures, 2012, 49(19/20): 2830–2838. DOI: 10.1016/j.ijsolstr.2012.03.045. [18] XUE Z, HUTCHINSON J W. A comparative study of impulse-resistant metal sandwich plates [J]. International Journal of Impact Engineering, 2004, 30(10): 1283–1305. DOI: 10.1016/j.ijimpeng.2003.08.007. [19] HOU S, SHU C, ZHAO S, et al. Experimental and numerical studies on multi-layered corrugated sandwich panels under crushing loading [J]. Composite Structures, 2015, 126: 371–385. DOI: 10.1016/j.compstruct.2015.02.039. [20] WADLEY H, DHARMASENA K, CHEN Y, et al. Compressive response of multilayered pyramidal lattices during underwater shock loading [J]. International Journal of Impact Engineering, 2008, 35(9): 1102–1114. DOI: 10.1016/j.ijimpeng.2007.06.009. [21] DHARMASENA K, QUEHEILLALT D, WADLEY H, et al. Dynamic response of a multilayer prismatic structure to impulsive loads incident from water [J]. International Journal of Impact Engineering, 2009, 36(4): 632–643. DOI: 10.1016/j.ijimpeng.2008.06.002. [22] FAN H L, MENG F H, YANG W. Mechanical behaviors and bending effects of carbon fiber reinforced lattice materials [J]. Archive of Applied Mechanics, 2006, 75(10/11/12): 635–647. DOI: 10.1007/s00419-006-0032-x. [23] 秦庆华, 郝文乾, 郭奕蓉, 等. 一种轻质正交波纹夹芯复合结构及其制备方法: 中国, ZL201510117807.8 [P]. 2015-03-17. [24] LEEKITWATTANA M, BOYD S W, SHENOI R A. Evaluation of the transverse shear stiffness of a steel bi-directional corrugated-strip-core sandwich beam [J]. Journal of Constructional Steel Research, 2011, 67(2): 248–254. DOI: 10.1016/j.jcsr.2010.07.010. [25] HU Y, LI W, AN X, et al. Fabrication and mechanical behaviors of corrugated lattice truss composite sandwich panels [J]. Composites Science and Technology, 2016, 125: 114–122. DOI: 10.1016/j.compscitech.2016.02.003. [26] LI W, SUN F, WANG P, et al. A novel carbon fiber reinforced lattice truss sandwich cylinder: fabrication and experiments [J]. Composites Part A: Applied Science and Manufacturing, 2016, 81: 313–322. DOI: 10.1016/j.compositesa.2015.11.034. [27] HSU S S, JONES N. Quasi-static and dynamic axial crushing of thin-walled circular stainless steel, mild steel and aluminium alloy tubes [J]. International Journal of Crashworthiness, 2004, 9(2): 195–217. DOI: 10.1533/ijcr.2004.0282. [28] KILIÇASLAN C, GÜDEN M, ODACI İ K, et al. The impact responses and the finite element modeling of layered trapezoidal corrugated aluminum core and aluminum sheet interlayer sandwich structures [J]. Materials & Design, 2013, 46: 121–133. -
计量
- 文章访问数: 4797
- HTML全文浏览量: 1400
- PDF下载量: 109
- 被引次数: 0