一种散体材料SHPB被动围压试验体应力修正方法

魏久淇; 张春晓; 曹少华; 王世合; 李磊

doi:10.11883/bzycj-2019-0411

一种散体材料SHPB被动围压试验体应力修正方法

doi: 10.11883/bzycj-2019-0411

魏久淇^{1, 2,},
张春晓^{1, 2, ,},
曹少华^{1, 2},
王世合^{1, 2},
李磊^{1, 2}

1.
军事科学院国防工程研究院工程防护研究所，河南洛阳 471023
2.
河南省特种防护材料重点实验室，河南洛阳 471023

详细信息

作者简介:
魏久淇（1990－　），男，硕士，工程师，weijiuqi61489@163.com

通讯作者:
张春晓（1980－　），男，硕士，副研究员，cxz_007@163.com

中图分类号: O341; O344
计量
- 文章访问数: 1503
- HTML全文浏览量: 770
- PDF下载量: 73
- 被引次数: 0
出版历程
- 收稿日期: 2019-10-24
- 修回日期: 2020-01-19
- 刊出日期: 2020-12-05

A volume stress correction method for SHPB passiveconfined pressure of granular materials

WEI Jiuqi^{1, 2
,},
ZHANG Chunxiao^{1, 2
, ,},
CAO Shaohua^{1, 2},
WANG Shihe^{1, 2},
LI Lei^{1, 2}

1.
Institute of Engineering Protection, IDE, AMS, PLA, Luoyang 471023, Henan, china
2.
Henan Key Laboratory of Special Protective Materials, Luoyang 471023, Henan, China

摘要

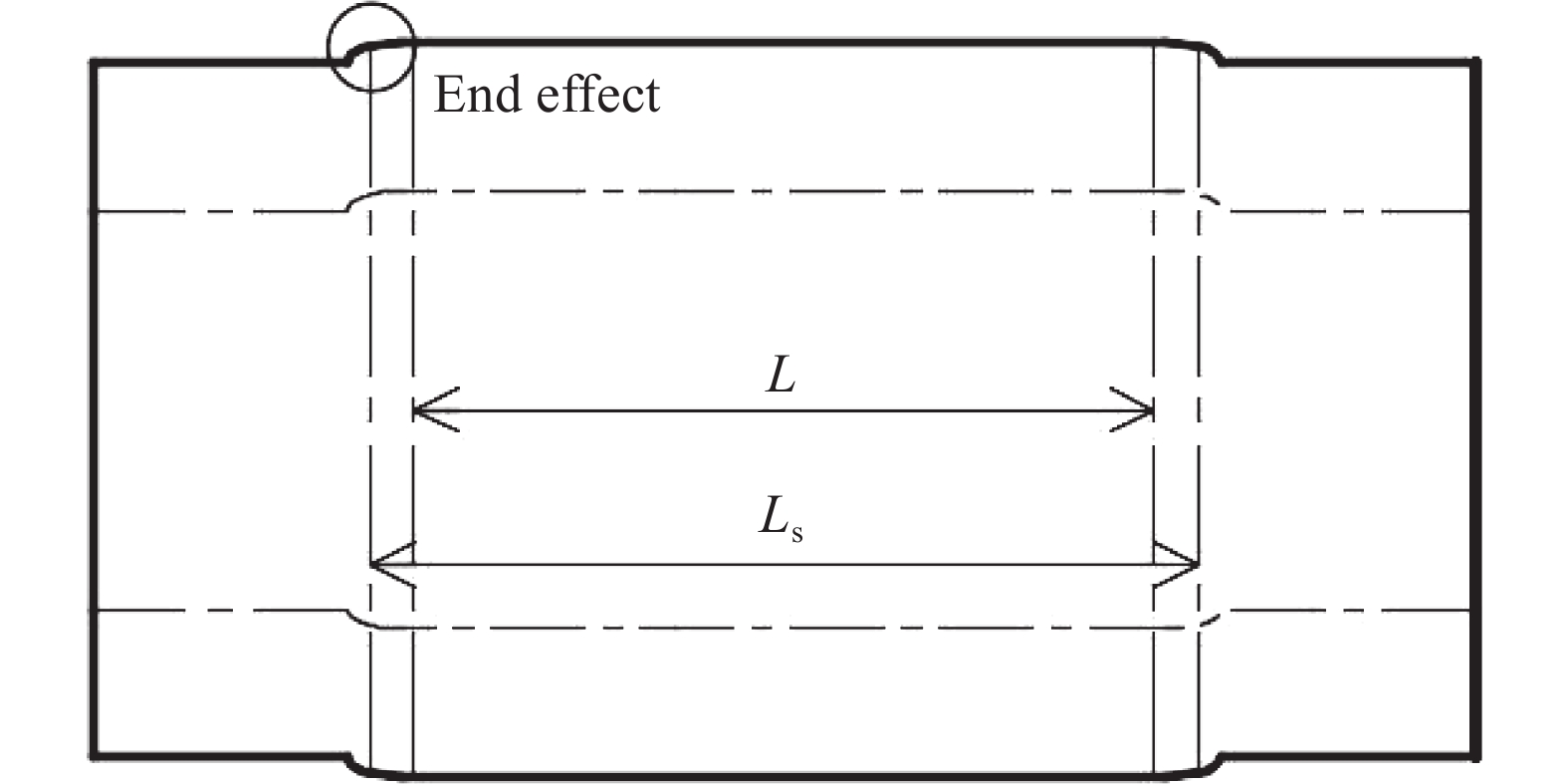
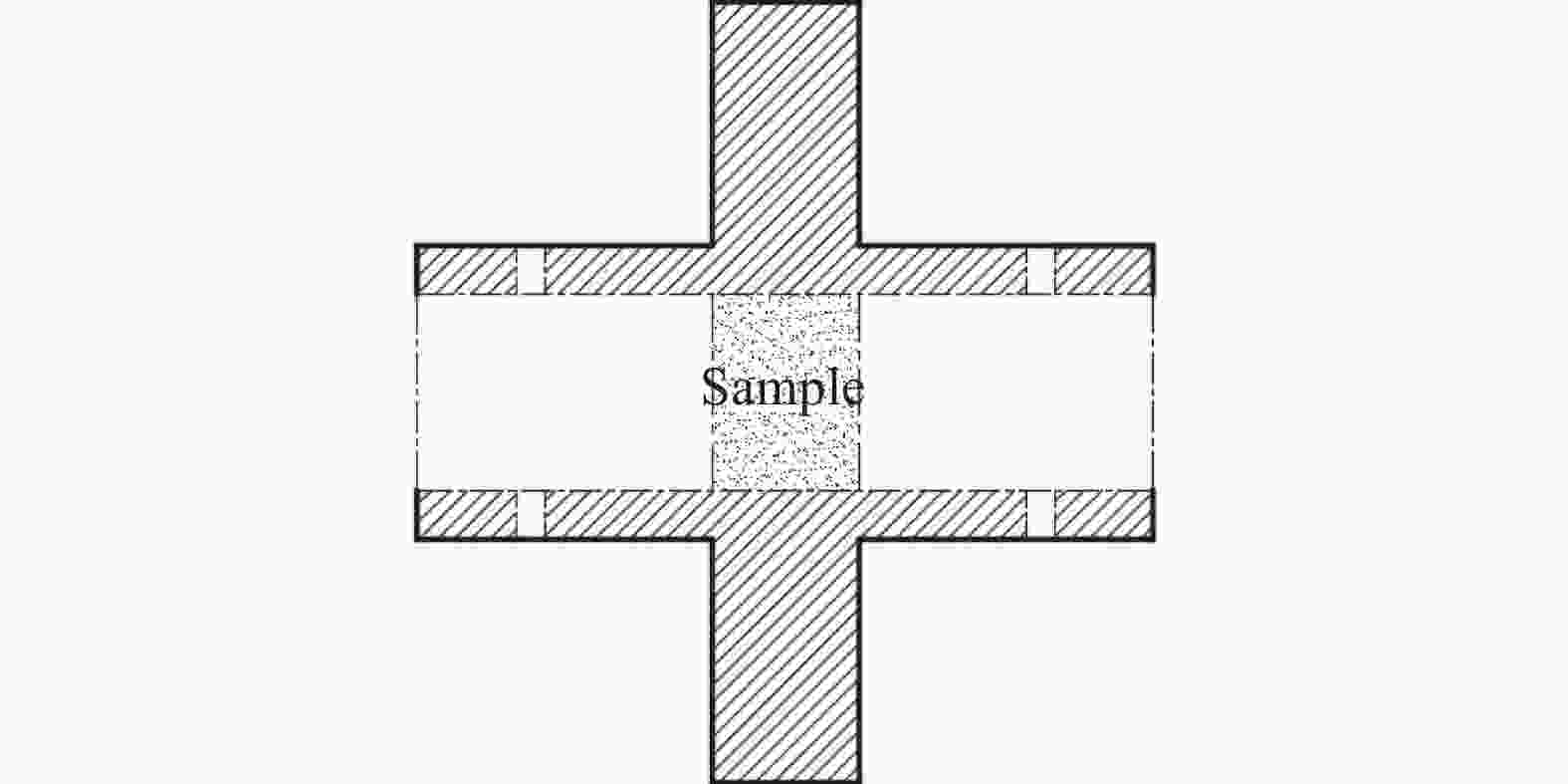
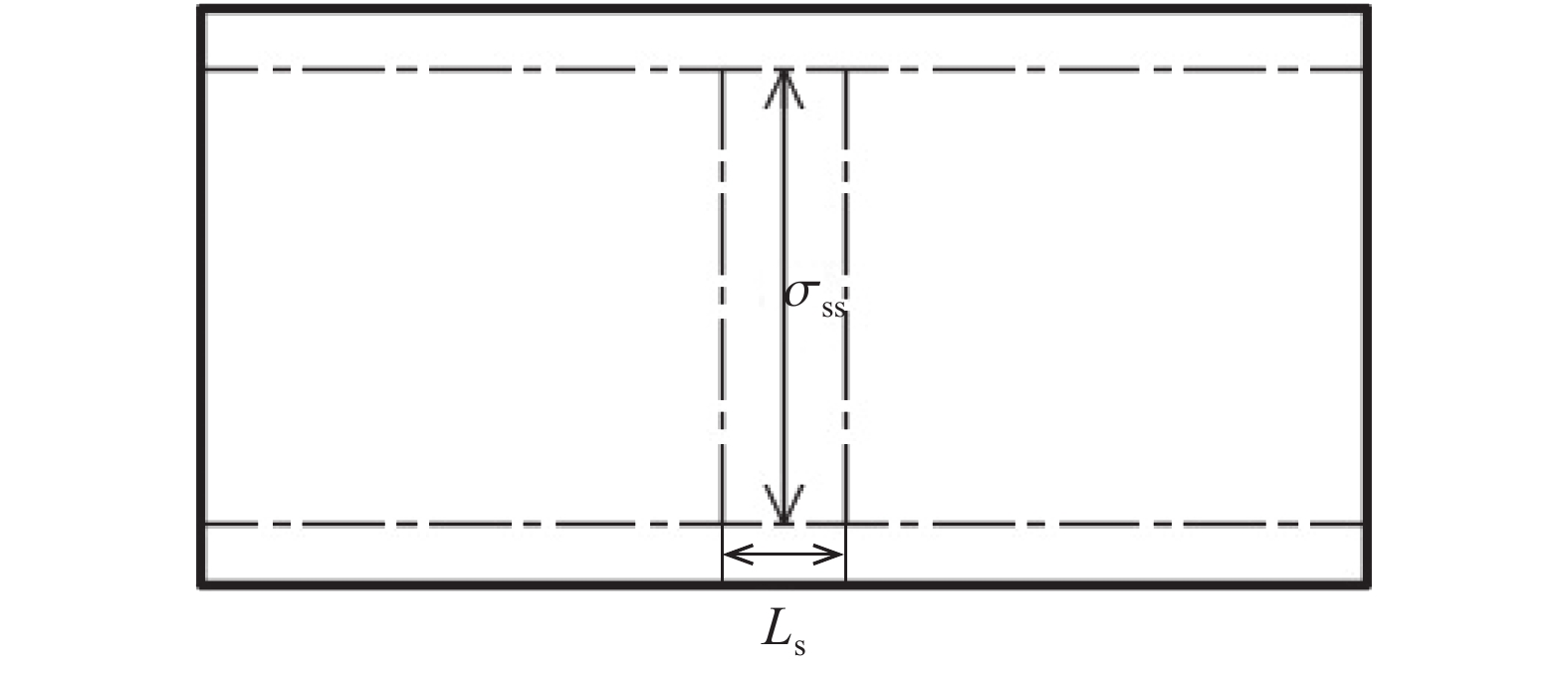
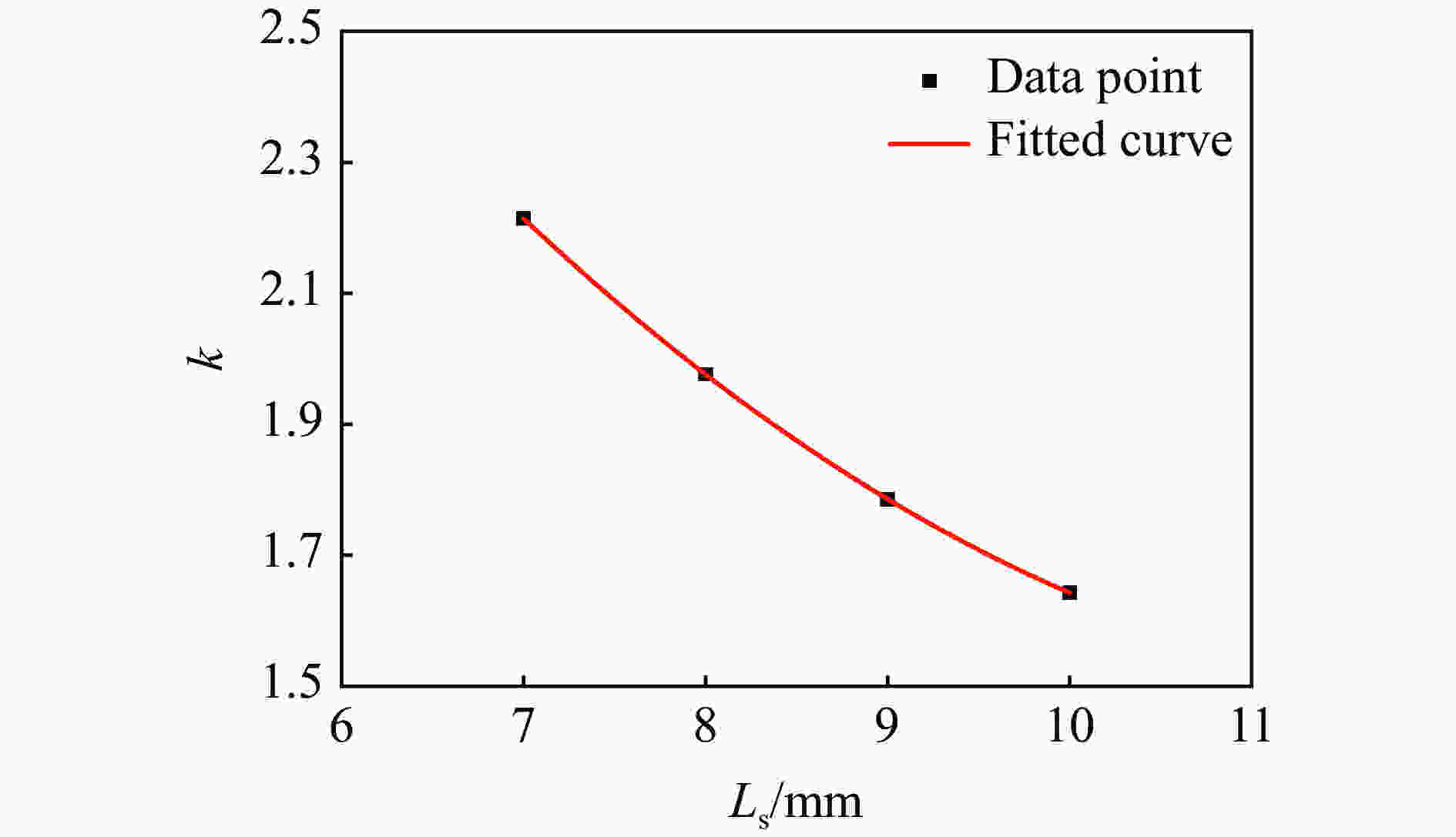
摘要: 本文利用有限元仿真给出了一种修正方法，并用数值仿真和试验验证了该方法的可靠性。研究表明：散体材料SHPB被动围压试验中，试样厚度远小于厚壁圆筒长度时，端部效应会导致厚壁圆筒不均匀凸出变形，计算材料的体应力-应变关系不能将厚壁圆筒应力状态简化为平面应力问题；厚壁圆筒处于弹性状态下，通过厚壁圆筒理论计算出的径向力与真实径向力存在一定比例关系，在一定范围内，折算系数与试样实时厚度呈二次函数关系。
- 散体材料 /
- SHPB试验 /
- 体应力 /
- 折算系数
Abstract: Aiming to overcome the disadvantages and demerits in the stress calculation in the passive confinement pressure SHPB tests of granular materials, a numerical modified approach is proposed in the present paper. The modified approach is also verified by finite element numerical simulation and experimental results. The results show that when the length of specimen is much shorter than the length of thick-walled hollow cylinder, the edge effects will lead to a non-uniform distribution of deformation along the length of hollow cylinder. Therefore, the configuration of thick-walled cannot be simplified as a plain stress problem when calculating the stress and deformation state of granular material. Due to the fact that the thick-walled hollow cylinder is elastic, the real radial stress in the hollow cylinder is proportional to the theoretical predictions. The proportionality coefficient has a quadratic function relation with the length of specimen.
- granular materials /
- SHPB test /
- volume stress /
- conversion coefficient

HTML全文

图 1 散体材料受约束的几何结构

Figure 1. Geometric structure constrained by SHPB test for bulk material

下载: 全尺寸图片幻灯片

图 2 试验时厚壁圆筒的几何变形图

Figure 2. Geometric deformation diagram of thick-walled cylinder in test

下载: 全尺寸图片幻灯片

图 3 阶梯型套筒^[15]

Figure 3. Ladder sleeve^[15]

下载: 全尺寸图片幻灯片

图 4 厚壁圆筒受力分析

Figure 4. Force analysis of thick-walled cylinder

下载: 全尺寸图片幻灯片

图 5 厚壁圆筒模型

Figure 5. Thick-walled cylinder model

下载: 全尺寸图片幻灯片

图 6 径向力${\sigma _{\rm{ss}}}$时程曲线

Figure 6. Time-history curve of radial force ${\sigma _{\rm{ss}}}$

下载: 全尺寸图片幻灯片

图 7 应变公式值（ε_c）与数值计算值（ε_s(L_c, L_s)）的对比

Figure 7. Comparison diagram between strain by fomula (ε_c) and that by simulation (ε_s(L_c, L_s))

下载: 全尺寸图片幻灯片

图 8 折算系数与试样实时厚度的关系图

Figure 8. relation diagram between conversion coefficient and real-time thickness of samples

下载: 全尺寸图片幻灯片

图 9 验证性模拟

Figure 9. Verification simulation

下载: 全尺寸图片幻灯片

图 10 试验砂样

Figure 10. Sand specimens tested

下载: 全尺寸图片幻灯片

图 11 砂样颗粒级配曲线

Figure 11. Grain size distribution

下载: 全尺寸图片幻灯片

图 12 试验设备

Figure 12. Test equipment

下载: 全尺寸图片幻灯片

图 13 试验原始波形

Figure 13. Test the original waveform

下载: 全尺寸图片幻灯片

图 14 砂样动态应力平衡

Figure 14. Dynamic stress equilibrium in the sand specimens

下载: 全尺寸图片幻灯片

图 15 含水率25%、30%钙质砂的应力应变

Figure 15. Stress and strain of calcareous sand with 25%, 30% water content

下载: 全尺寸图片幻灯片

表 1 试验工况表

Table 1. Summary of SHPB tests

编号	试验材料	含水率/%	砂质量/g	装样厚度/mm	干密度/(g∙cm⁻³)	相对密实度/%	气压/MPa
G60-0.2-01	钙质砂	25	13.90	10.02	1.29	58.73	0.2
G60-0.2-02		25		10.00	1.29	60
G60-0.2-03		25		9.98	1.30	61.31
G60-0.2-04		30		10.02	1.29	58.73
G60-0.2-05		30		10.00	1.29	60
G60-0.2-06		30		10.02	1.29	58.73

下载: 导出CSV

参考文献(20)

[1]	钱七虎, 王明洋. 三相介质饱和土自由场中爆炸波的传播规律 [J]. 爆炸与冲击, 1994, 14(2): 97–104. QIAN Q H, WANG M Y. Propagation of explosive wave in the free-field of three-phase saturated soil [J]. Explosion and Shock Waves, 1994, 14(2): 97–104.
[2]	SONG B, CHEN W, LUK V. Impact compressive response of dry sand [J]. Mechanics of Materials, 2009, 41(6): 777–785. DOI: 10.1016/j.mechmat.2009.01.003.
[3]	赵章泳, 邱艳宇, 紫民, 等. 含水率对非饱和钙质砂动力特性影响的试验研究 [J]. 爆炸与冲击, 2019, 40(2): 023102. DOI: 10.11883/bzycj-2019-0066. ZHAO Z Y, QIU Y Y, ZI Min, et al. Experimental study on dynamic compression of unsaturated calcareous sand [J]. Explosion and Shock Waves, 2019, 40(2): 023102. DOI: 10.11883/bzycj-2019-0066.
[4]	魏久淇, 王明洋, 邱艳宇, 等. 钙质砂动态力学特性试验研究 [J]. 振动与冲击, 2018, 37(24): 7–12. DOI: 10.13465/j.cnki.jvs.2018.24.002. WEI J Q, WANG M Y, QIU Y Y, et al. Impact compressive response of calcareous sand [J]. Journal of Vibration and Shock, 2018, 37(24): 7–12. DOI: 10.13465/j.cnki.jvs.2018.24.002.
[5]	魏久淇, 吕亚茹, 刘国权, 等. 钙质砂一维冲击响应及吸能特性试验 [J]. 岩土力学, 2019, 40(1): 191–198, 206. DOI: 10.16285/j.rsm.2017.1235. WEI J Q, LÜ Y R, LIU G Q. et al One-dimensional impact responses and energy absorption of calcareous sand [J]. Rock and Soil Mechanics, 2019, 40(1): 191–198, 206. DOI: 10.16285/j.rsm.2017.1235.
[6]	文祝, 邱艳宇, 紫民, 等. 钙质砂的准一维应变压缩试验研究 [J]. 爆炸与冲击, 2019, 39(3): 033103. DOI: 10.11883/bzycj-2018-0015. WEN Z, QIU Y Y, ZI M, et al. Experimental study on quasi-one-dimensional strain compression of calcareous sand [J]. Explosion and Shock Waves, 2019, 39(3): 033103. DOI: 10.11883/bzycj-2018-0015.
[7]	于潇, 陈力, 方秦. 珊瑚砂中应力波衰减规律的实验研究 [J]. 岩石力学与工程学报, 2018, 37(6): 1520–1529. DOI: 10.13722/j.cnki.jrme.2018.0147. YU X, CHEN L, FANG Q. Experimental study on the attenuation of stress wave in coral sand [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(6): 1520–1529. DOI: 10.13722/j.cnki.jrme.2018.0147.
[8]	BARR A D, CLARKE S D, TYAS A, et al. Effect of moisture content on high strain rate compressibility and particle breakage in loose sand [J]. Experimental Mechanics, 2018, 58(8): 1331–1334. DOI: 10.1007/s11340-018-0405-4.
[9]	ROSS C A, THOMPSON P Y, CHARLIE W A, et al. Transmission of pressure waves in partially saturated soils [J]. Experimental Mechanics, 1989, 29(1): 80–83. DOI: 10.1007/BF02327786.
[10]	MARTIN B E, KABIR Md E, CHEN W. Undrained high-pressure and high strain-rate response of dry sand under triaxial loading [J]. International Journal of Impact Engineering, 2013, 54: 51–63. DOI: 10.1016/j.ijimpeng.2012.10.008.
[11]	LUO H Y, COOPER W L, LU H B. Effects of particle size and moisture on the compressive behavior of dense Eglin sand under confinement at high strain rates [J]. International Journal of Impact Engineering, 2014, 65: 40–55. DOI: 10.1016/j.ijimpeng.2013.11.001.
[12]	OMIDVAR M, ISKANDER M, BLESS S. Stress-strain behavior of sand at high strain rates [J]. International Journal of Impact Engineering, 2012, 49: 192–213. DOI: 10.1016/j.ijimpeng.2012.03.004.
[13]	YAMAMURO J A, ABRANTES A E, LADE P V. Effect of strain rate on the stress-strain behavior of sand [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(12): 1169–1178. DOI: 10.1061/(ASCE)GT.1943-5606.0000542.
[14]	MARTIN B E, CHEN W N, SONG B, et al. Moisture effects on the high strain-rate behavior of sand [J]. Mechanics of Materials, 2009, 41(6): 786–798. DOI: 10.1016/j.mechmat.2009.01.014.
[15]	BRAGOV A M, LOMUNOV A K, SERGEICHEV I V, et al. Determination of physicomechanical properties of soft soils from medium to high strain rates [J]. International Journal of Impact Engineering, 2008, 35(9): 967–976. DOI: 10.1016/j.ijimpeng.2007.07.004.
[16]	BRAGOV A M, GRUSHEVSKY G M, LOMUNOV A K. Use of the Kolsky method for confined tests of soft soils [J]. Experimental Mechanics, 1996, 36(3): 237–242. DOI: 10.1007/BF02318013.
[17]	RAVI-CHANDAR K, Ma Z. Inelastic deformation in polymers under multiaxial compression [J]. Mechanics of Time-Dependent Materials, 2000, 4(4): 333–357. DOI: 10.1023/a:1026570826226.
[18]	FORQUIN P, GARY G, GATUINGT F. A testing technique for concrete under confinement at high rates of strain [J]. International Journal of Impact Engineering, 2008, 35(6): 425–446. DOI: 10.1016/j.ijimpeng.2007.04.007.
[19]	徐秉业. 应用弹塑性力学[M]. 北京: 清华大学出版社, 1995.
[20]	国家质量技术监督局, 中华人民共和国建设部. GBT/50123 土工试验方法标准[S]. 北京: 中国计划出版社, 1999.