Deformation behavior of WELDOX 700E steel subjected to TNT air-blast loading
-
摘要: 以WELDOX 700E钢为研究对象，研究了8 mm钢在6 kg球形TNT空爆载荷、12 mm钢在10 kg球形TNT空爆载荷下的抗爆轰变形行为，结合ABAQUS模拟计算软件建立了WELDOX 700E钢抗爆轰变形模拟计算模型。结果表明：材料强度是影响WELDOX 700E钢抗爆轰变形行为的关键因素之一，高强度WELDOX 700E钢在球形TNT空爆载荷条件下呈现均匀的拱形变形。在6 kg球形TNT空爆载荷下，8 mm WELDOX 700E钢板中点的最大动态位移为144 mm，永久挠度为124 mm，回弹为21 mm；在10 kg球形TNT空爆载荷下，12 mm WELDOX 700E钢板中点的最大动态位移为166 mm，永久挠度为143 mm，回弹为23 mm。在不考虑实验工装整体偏移的条件下，球形TNT空爆载荷下钢的抗爆轰变形模拟计算结果可准确反映WELDOX 700E钢的抗爆轰变形行为。WELDOX 700E钢在抗爆轰形变过程中存在显著的厚度减薄现象并伴随一定的应变硬化行为，应变硬化行为主要为WELDOX 700E钢马氏体晶粒内部位错増殖的表现，8 mm和12 mm WELDOX 700E钢中心区域的位错密度较边部分别增加80.31%和151.76%。
-
关键词:
- WELDOX 700E钢 /
- 球形TNT /
- 高强钢 /
- 变形
Abstract: The deformation behavior of 8 mm and 12 mm WELDOX 700E steel, at stand-off distance 250 mm, subjected to air-blast loading by 6 kg and 10 kg spherical TNT, was investigated. The simulation model of WELDOX 700E steel subjected to air-blast loading is established using ABAQUS. The results indicate that strength is one of key factors affecting the deformation behavior of WELDOX 700E steel. High strength WELDOX 700E steel presents uniform arch deformation under spherical TNT air blast loading. The maximum dynamic displacement, permanent deflection and rebound of 8 mm WELDOX 700E steel midpoint subjected to 6 kg TNT are 144 mm, 124 mm and 21 mm, respectively. The maximum dynamic displacement, permanent deflection and rebound of 12 mm WELDOX 700E steel midpoint subjected to 10 kg TNT are 166 mm, 143 mm and 23 mm, respectively. Without considering the overall deviation of experimental setup, the simulation results can accurately reflect the deformation behavior of WELDOX 700E steel subjected to spherical TNT air blast loading. Under air-blast loading, the thickness of WELDOX 700E steel decreases significantly, accompanied by strain hardening behavior. Strain hardening behavior is the dislocation growth in martensite of WELDOX 700E steel. Compared with the edge, the dislocation density in the center of 8 mm and 12 mm WELDOX 700E steel plate increases by 80.31% and 151.76%, respectively.-
Key words:
- WELDOX 700E steel /
- spherical TNT /
- high strength steel /
- deformation
-
图 2 WELDOX 700E钢爆炸实验高速摄像
Figure 2. Snapshots of WELDOX 700E steel subjected to explosion taken by high-speed camera at different times
图 4 WELDOX 700E钢爆轰变形模拟计算结果
Figure 4. Simulation of detonation deformation of WELDOX 700E steel
图 5 爆轰载荷下WELDOX 700E钢中点的位移曲线
Figure 5. Midpoint displacement of WELDOX 700E steel subjected to blast shock wave
图 6 WELDOX 700E钢抗爆轰球形形变曲线
Figure 6. Deformation curves of WELDOX 700E steel subjected to blast shock wave
图 7 WELDOX 700E钢抗爆轰厚度变化曲线
Figure 7. Thickness variation of WELDOX 700E steel subjected to blast shock wave
图 8 WELDOX 700E钢在爆轰变形后不同区域金相组织
Figure 8. Microstructure of WELDOX 700E steel subjected to blast shock wave
-
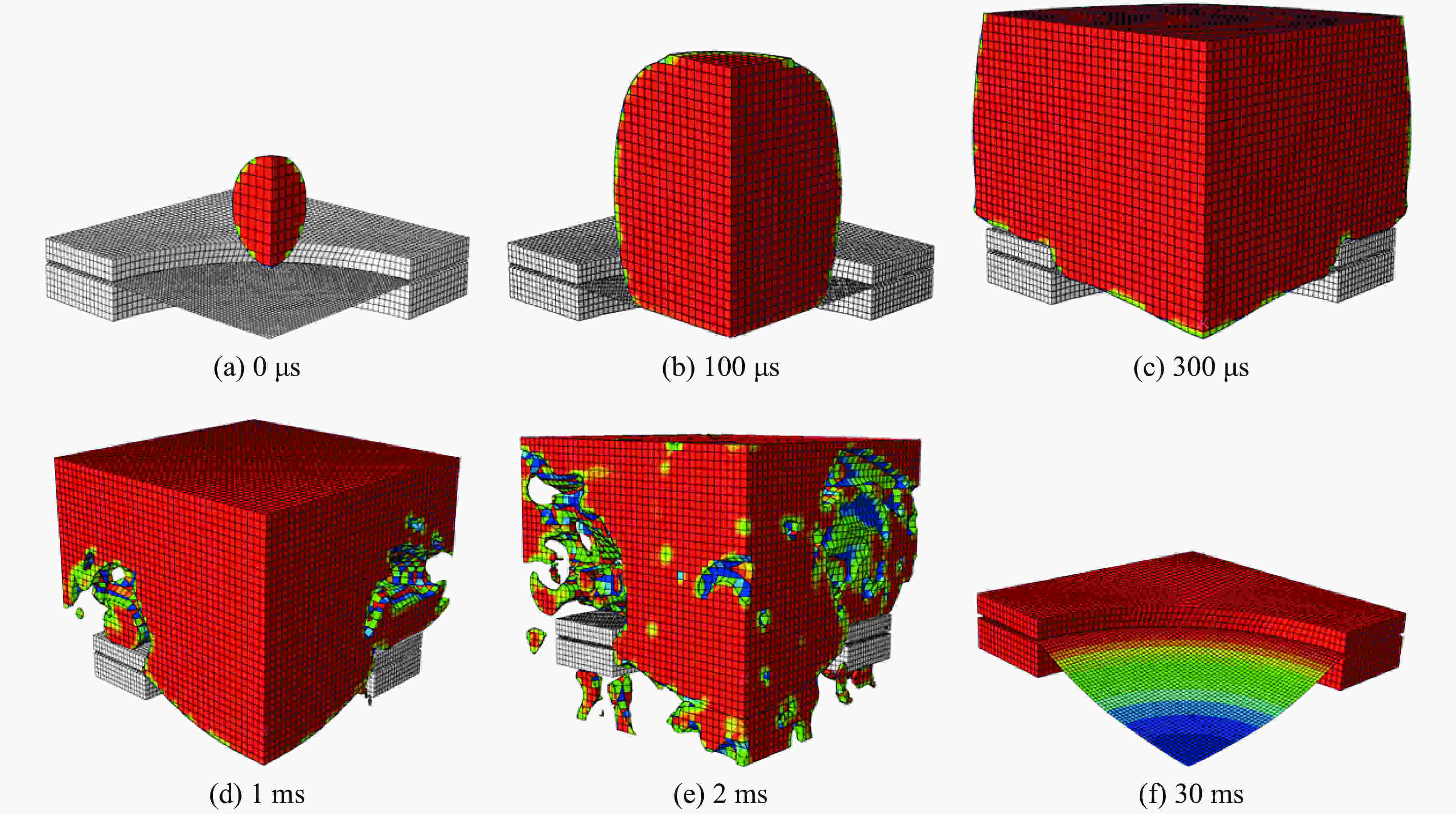
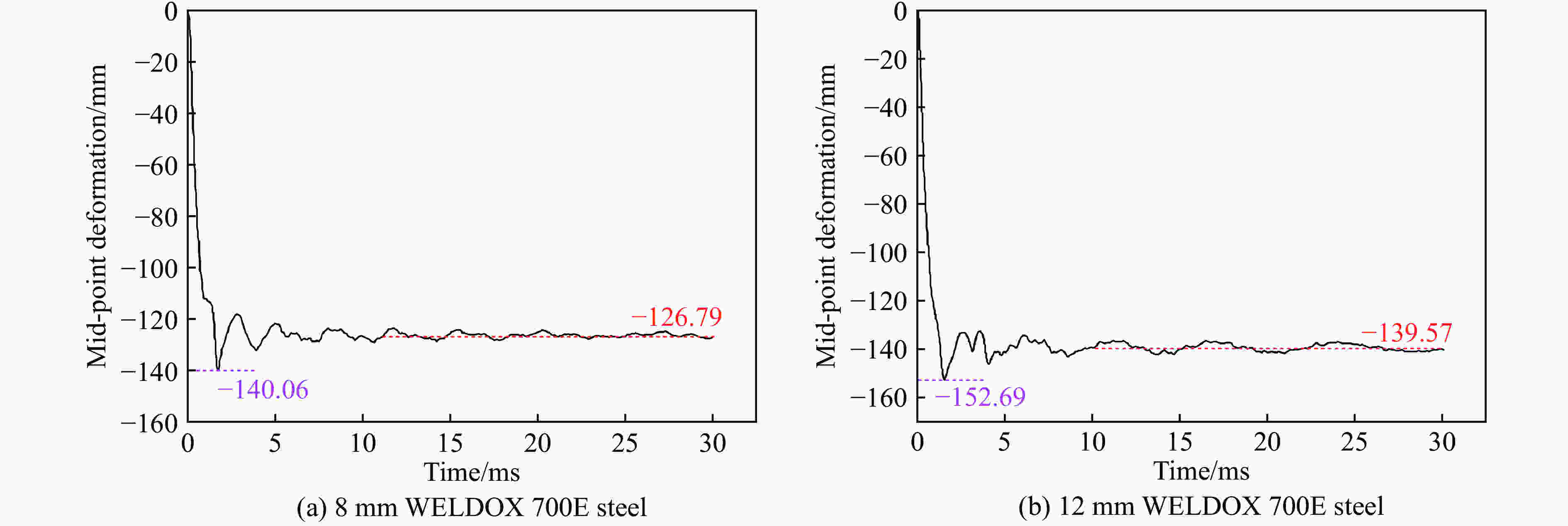
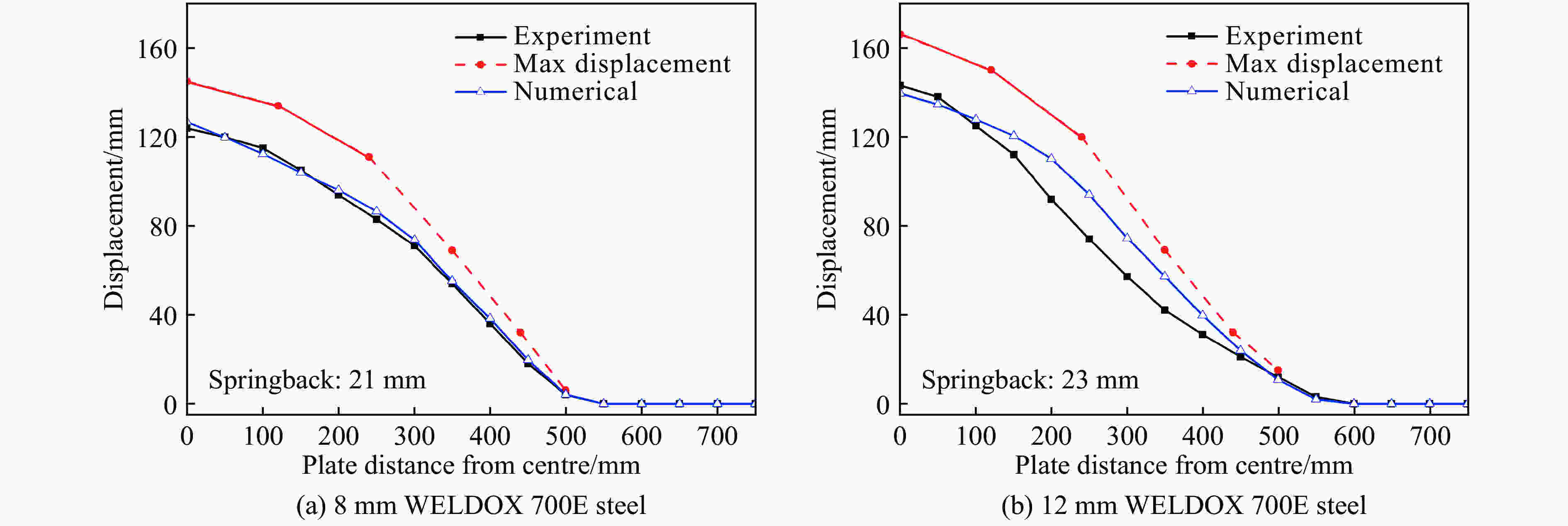
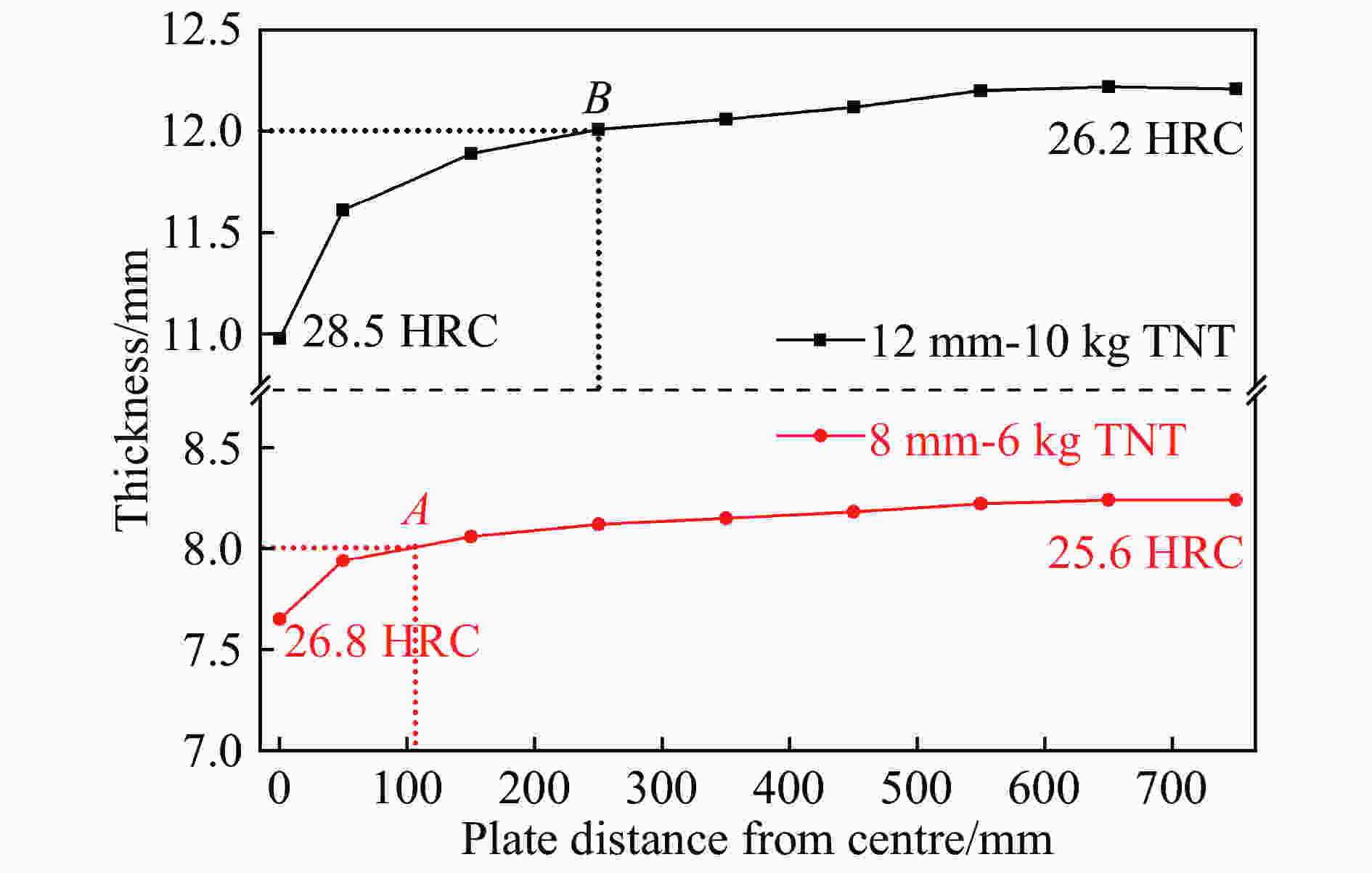
[1] RAHMAAN T, BARDELCIK A, IMBERT J, et al. Effect of strain rate on flow stress and anisotropy of DP600, TRIP780, and AA5182-O sheet metal alloys [J]. Impact Engineering, 2016, 88(2): 72–90. DOI: 10.1016/j.ijimpeng.2015.09.006. [2] 韩守红, 吕振华. 铝泡沫夹层结构抗爆炸性能仿真分析及优化 [J]. 兵工学报, 2010, 11(31): 1468–1474. DOI: 10.3184/030823410X12680741110954.HAN S H, LV Z H. Numerical simulation of blast-resistant performance of aluminum foam sandwich structures and optimization [J]. Acta Armamentarii, 2010, 11(31): 1468–1474. DOI: 10.3184/030823410X12680741110954. [3] 陈学军, 杨学文, 张永珍. 地雷爆炸作用下装甲车辆底部防护结构优化仿真研究 [J]. 兵工学报, 2014, 2(35): 353–357. DOI: CNKI: SUN: BIGO. 0. 2014-S2-066.CHEN X J, YANG X W, ZHANG Y Z. A simulation study of structural optimization of armor vehicle bottomprotection under the landmine explosion [J]. Acta Armamentarii, 2014, 2(35): 353–357. DOI: CNKI: SUN: BIGO. 0. 2014-S2-066. [4] 张钱城, 郝方楠, 李裕春,等. 爆炸冲击载荷作用下车辆和人员的损伤与防护 [J]. 力学与实践, 2014, 5(36): 527–539. DOI: 10.6052/1000-0879-13-539.ZHANG Q C, HAO F N, LI Y C, et al. Research progress in the injury and protection on vehicle and passengers under explosive shock loading [J]. Mechanics in Engineering, 2014, 5(36): 527–539. DOI: 10.6052/1000-0879-13-539. [5] CHUNG K Y S, LANGDON G S, NURICK G N, et al. Response of V-shape plates to localised blast load: experiments and numerical simulation [J]. Impact Engineering, 2012, 2(46): 97–109. DOI: 10.1016/j.ijimpeng.2012.02.007. [6] BORVIK T, OLOVSSON L, HANSSEN A G, et al. A discrete particle approach to simulate the combined effect of blast and sand impact loading of steel plates [J]. Mechanics and Physics of Solids, 2011, 3(59): 940–958. DOI: 10.1016/j.jmps.2011.03.004. [7] JUHO P, HAE-JIN C. Experiments and numerical analyses of HB400 and aluminum foam sandwich structure under landmine explosion [J]. Composite Structures, 2015, 11(134): 726–739. DOI: 10.1016/j.compstruct.2015.08.133. [8] MENKES S B, OPAT H J. Broken beams-tearing and shear failures in explosively loaded clamped beams [J]. Experimental Mechanics, 1973, 13(11): 480–486. DOI: 10.1007/BF02322734. [9] TEELING S, NURICK G N. The deformation and tearing of thin circular paltes subjected to impulsive loads [J]. Impact Engineering, 1991, 11(1): 77–91. DOI: 10.1016/0734-743X(91)90032-B. [10] BRODE H L. Blast wave from a spherical charge [J]. Physics of Fluids, 1959, 2(2): 217–229. DOI: 10.1063/1.1705911. [11] SEUNG H K, YOON S C, YONG J C. Parametric analyese of major nuclear components and reinforced concrete structures under FCI-induced explosive condition [J]. Nuclear Engineering and Design, 2017, 3(322): 148–158. DOI: 10.1016/j.nucengdes.2017.06.029. [12] JACON N, NURICK G N, LANGDON G S. The effect of stand-off distance on the failure of fully clamped circular mild steel plates subjected to blast loads [J]. Engineering Structures, 2007, 3(29): 2723–2736. DOI: 10.1016/j.engstruct.2007.01.021. [13] LING Z, NOBUAKI S, TAKAHITO O. Real time correlation between flow stress and dislocation density in steel during deformation [J]. Materials Science & Engineering A, 2014, 4(611): 188–193. DOI: 10.1016/j.msea.2014.05.073. [14] AMRITA K, DAVID P F. Influence of plastic deformation heterogeneity on development of geometrically necessary dislocation density in dual phase steel [J]. Materials Science & Engineering A, 2016, 5(667): 435–443. DOI: 10.1016/j.msea.2016.05.022. -
下载:
计量
- 文章访问数: 3091
- HTML全文浏览量: 1389
- PDF下载量: 81
- 被引次数: 0