Experimental research in damage effects of high-piled wharf under underwater explosion
-
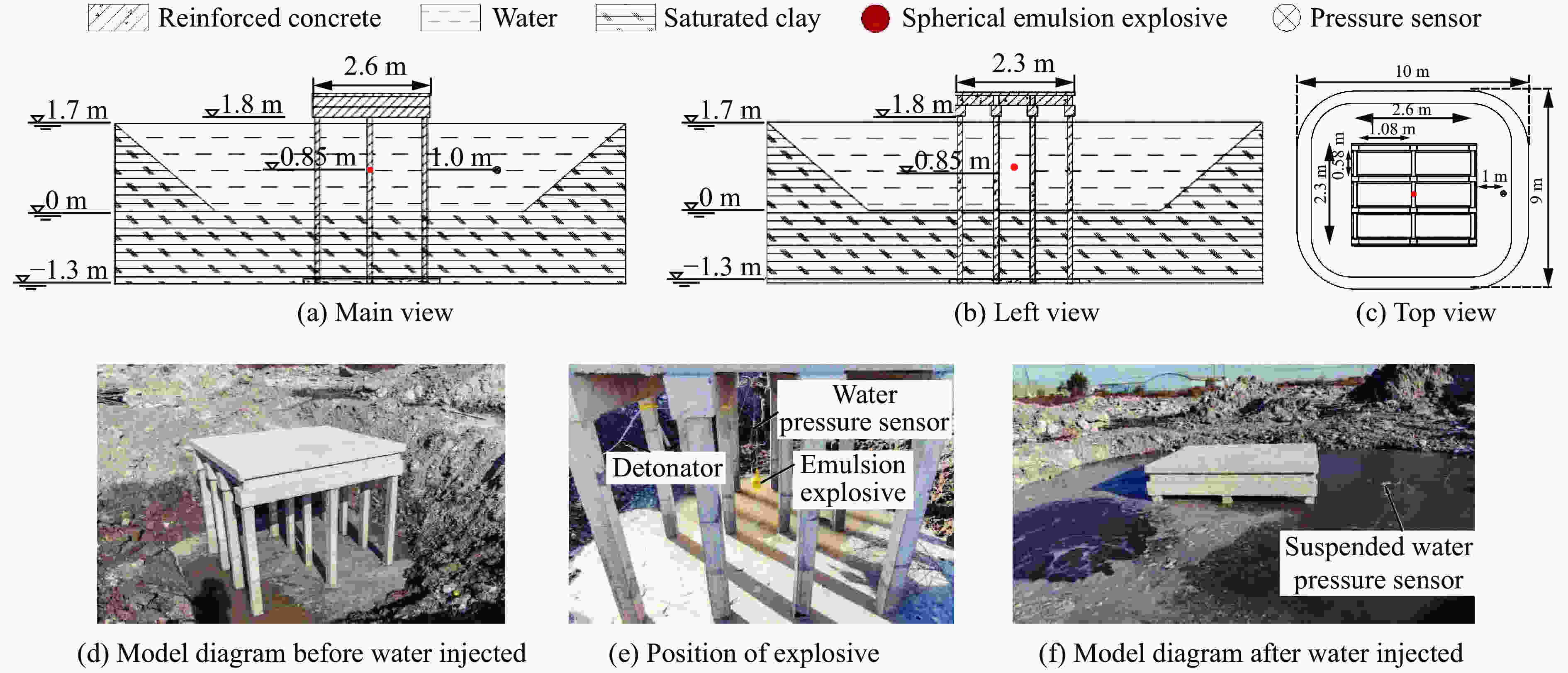
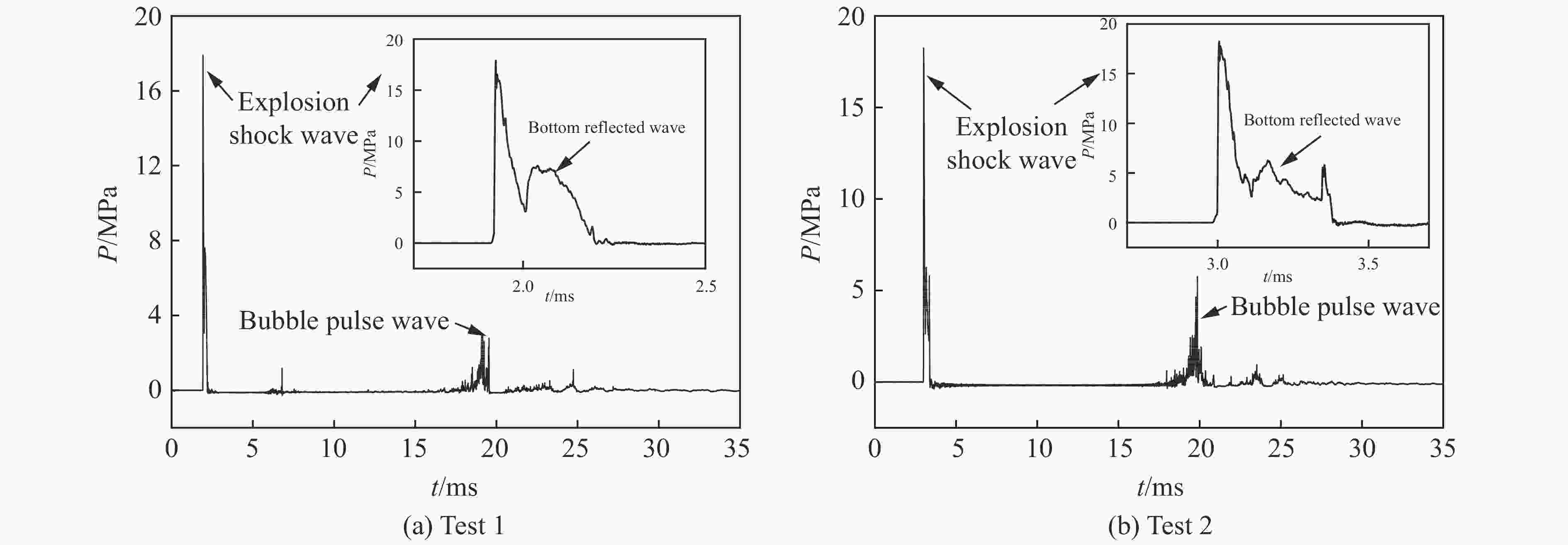
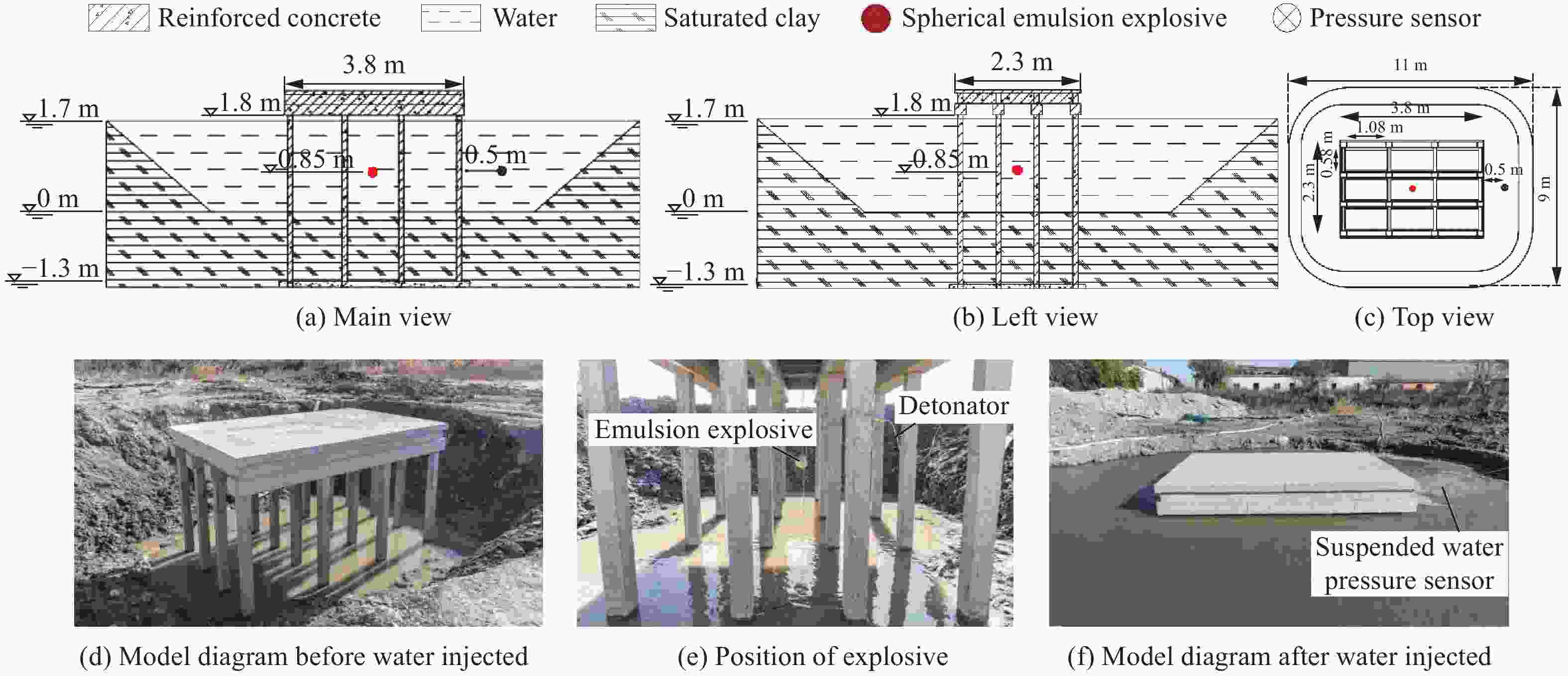
摘要: 为了研究水下爆炸作用下高桩码头的破坏模式和毁伤机理，考虑不同炸药位置，设计制作2个高桩码头模型，进行水下爆炸试验，记录了水下荷载数据和码头模型毁伤现象，探析了炸药位置对高桩码头毁伤效应和破坏机理的影响。研究表明：水下爆炸作用下码头受到2次超压荷载，分别为初始冲击波、水底反射波组成的冲击波载荷和气泡脉动载荷；水下爆炸作用下，高桩码头的主要毁伤部位为桩基的中部和顶部、面板、纵梁以及面板与纵、横梁连接处；炸药位置直接影响高桩码头破坏模式，减小爆距会加剧桩基毁伤效应，当炸药位于面板下方时，码头上部梁板结构的毁伤程度较大。Abstract: In order to study the failure mode and damage mechanism of a high-piled wharf subjected to underwater explosion, the experimental study on two models of the high-piled wharf under different explosive positions was conducted. The data collection and analysis for underwater loads and damage phenomenon of wharf models were recorded. The influence of explosive position on the damage effect and damage mechanism of high-piled wharf was analyzed. The results show the followings: The wharf is subjected to two times of loads under underwater explosive, which are the shock wave load composed of initial shock wave and underwater reflected wave, and bubble pulse load. The main damaged parts of the high-piled wharf are the middle and top of the piles, panel, longitudinal beams and the connection of the panel and beams. The explosive position directly affects the damage form of the wharf. Reducing the distance between the explosive and pile will increase the damage of the pile. When the explosive is located under the panel, the beams and panel of the high-piled wharf is seriously damaged.
-
Key words:
- underwater explosion /
- high-piled wharf /
- damage effect /
- explosive position
-
如何有效拦截来袭导弹，一直是反导弹药研究的热点问题。悬浮弹幕协同反导弹药是利用其多个子弹药战斗部协同作用产生的高速破片场毁伤来袭导弹[1]，此破片场由成百上千个飞散方向任意的破片（预制破片或爆炸成型弹丸）组成。应用具有一定分布密度的破片撞击来袭导弹并引发导弹战斗部起爆是毁伤导弹最有效的方法之一。
针对破片冲击起爆战斗部的问题，大多数学者是将其等效为单破片或多破片冲击起爆平板装药的问题进行研究。单破片冲击起爆平板装药的问题，学者们已通过理论、数值模拟和试验等方法进行了大量研究[2-8]。在单破片冲击起爆平板装药的基础上，一些学者也曾开展了多破片冲击起爆平板装药的研究。其中李文彬等[9]研究了双破片冲击起爆裸装药的机理；Lueck等[10]利用4组不同的参数，论证了Lee-Tarver点火增长模型模拟多破片冲击起爆炸药的可行性；贾宪振等[11]、梁斌等[12]通过数值模拟研究了多破片撞击平板装药的情况，得到了起爆速度阈值的变化规律。
然而，现实中战斗部多为圆柱结构，一些学者曾在试验和数值模拟过程中考虑了战斗部为圆柱结构的情况，但都是采用单破片进行研究。其中宋浦等[13]针对某型破片式战斗部对带壳柱装药模拟靶的撞击毁伤试验研究，得到柱壳装药的毁伤阈值范围；江增荣等[14]通过数值模拟得到重金属材料破片可以提高毁伤战斗部的能力；辛建国等[15]研究得到破片及破碎的柱面薄壳对壳内装药的撞击、摩擦等机械作用是引燃/引爆薄壳装药的主要原因;王昕等[16]通过数值模拟分析了单个破片冲击起爆柱壳装药的规律，得到命中位置和装药曲率半径对柱壳装药冲击起爆的影响。
在实战环境中，战斗部很有可能受到多个破片的累积毁伤作用，从现有文献可以看出，关于多破片冲击起爆柱壳装药问题的研究尚不深入全面，因此本文中将采用数值模拟的方法研究多钨球破片对柱壳装药的冲击起爆问题。采用AUTODYN-3D数值模拟软件，在单钨球破片撞击柱壳装药模型的基础上，建立多钨球破片撞击柱壳装药的模型，分析当存在一定空间间隔（撞击角、轴向球心距）和时间间隔的条件下，多钨球破片冲击柱壳装药的起爆过程，得到相关参数（钨球个数、装药半径、撞击角、轴向球心距和时间间隔）对起爆柱壳装药速度阈值的影响规律。研究结果可为反导弹药战斗部的设计和多破片累积毁伤评估提供参考。
1. 数值模拟模型
1.1 单钨球冲击起爆柱壳装药模型
为了建立多钨球破片撞击柱壳装药的模型，先建立单个钨合金球破片冲击起爆带钢壳的圆柱B炸药的模型，如图1(a) 所示，进行数值模拟。其中钨球质量为m，半径为r；炸药装药半径为R，长度为L；壳体厚度为H。假设钨球垂直于带壳装药轴线入射。
图 1 单钨球冲击柱壳装药的物理模型和有限元模型Figure 1. Physical model and finite element model of single tungsten fragment impacting on cylindrical charge with steel casing采用AUTODYN-3D程序，简化计算，建立1/2模型，通过对称性实现全模型，如图1(b) 所示。其中，钨球、钢壳和B炸药均采用Lagrange网格，网格数量分别为2 048、28 800、192 000。
钨球、钢壳和B炸药的材料参数均从AUTODYN材料库[17]选取。B炸药的状态方程采用Lee-Tarver三项反应过程炸药起爆模型，该模型可以很好地模拟非均质炸药的冲击起爆特性：
∂F∂t=I(1−F)b(ρρ0−1−a)x+G1(1−F)cFdpy+G2(1−F)eFgpz (1) 式中：F为反应比（炸药气体质量与炸药总质量比），ρ和ρ0为炸药当前密度和初始密度，p为炸药爆轰压力，其余参数为常数。式（1）中右边第1项为点火项，描述了热点燃烧阶段；第2项为成长项，描述了燃烧从热点向内部和外部的颗粒传递阶段；第3项为快反应项，描述了燃烧快速向爆轰转变的过程。炸药反应物和未反应物均采用JWL状态方程。B炸药材料参数见表1。破片和柱壳的材料状态方程、强度模型和失效方程见表2。
表 1 B炸药材料参数Table 1. Material parameters of composition BI/μs−1 b a x G1 c d y G2 e g z 44 0.222 0.01 4 414 0.222 0.667 2.0 0 0 0 0 表 2 破片、壳体材料模型Table 2. Material model of fragment and casing部件 材料 状态方程 强度模型 失效模型 破片 钨合金 Shock Johnson-Cook Geometric strain 壳体 4340合金钢 Linear Johnson-Cook Geometric strain 1.2 多钨球冲击起爆带壳装药模型
在单破片冲击起爆柱壳装药模拟模型的基础上，增加钨球破片数量，建立如图2所示的双钨球撞击柱壳装药的简化模型，其中双钨球完全相同，质量均为m=3 g；两球间平行于装药轴线方向的球心距即轴向球心距为l。假设钨球均垂直于带壳装药轴线入射。图3为任意一个钨球碰撞点的截面示意图。其中，AA′、BB′为圆柱装药相互垂直的两个对称面，双破片撞击时，假设碰撞点在AA′面的同一侧；O0、Oi0（i=1，2，···，最大值为钨球总个数）分别为装药的轴心和初始钨球球心，Oi为碰撞瞬间的钨球球心；钨球的初始速度为vi，钨球从初始位置运动到碰撞点的距离为hi，忽略钨球在飞行过程中的速度衰减，即碰撞速度亦为vi；O0Oi0的连线与vi的夹角为撞击角θi；设θi在∠AO0B范围内取正值，以步长为5°，从0°到60°设置一系列观测序列，列号设为θi-j(j=0～12)，在每列上设置间距为5 mm的观测点θi-j-k（k=1～9）；设θi在∠A′O0B范围内取负值，以步长为−5°，从0°到−60°设置一系列观测序列，列号设为θi-j(j=0～−12)，在每列上设置间距为5 mm的观测点θi-j-k（k=1～9），其中点θi-j-1在装药表面，点θi-j-9与O0重合。
图 2 双钨球撞击柱壳装药的简化模型Figure 2. Simplified model of double tungsten fragments impacting on cylindrical charge with casing综上，通过l/r和θi表征两钨球的空间碰撞位置间隔，hi/r表征两钨球的时间间隔。
2. 数值模拟结果与分析
为了研究多钨球累积冲击起爆柱壳装药的问题，先对单钨球在不同位置冲击起爆柱壳装药的情况进行数值模拟，以10 m/s为步长，得到装药半径R=40 mm时，单钨球起爆柱壳装药的速度阈值随撞击角θ的变化如图4所示。由图4可以看出，当0°≤θ＜25°时，起爆装药的速度阈值随θ的增大而缓慢增长；当25°≤θ＜55°时，起爆装药的速度阈值随θ的增大而迅速增长；当θ≥55°时，钨球发生跳飞，本文中不考虑跳飞的情况。简单来说，起爆速度阈值随撞击角增大呈指数增长是因为钨球破片速度方向上的壳体厚度的不同引起的。撞击角度越大，钨球速度方向上的壳体越厚，因此需要更大的起爆速度。
本文中采用的单钨球模型的撞击角度与起爆柱壳装药的速度阈值间的变化关系，采用最小二乘法得到拟合公式为：
vi=2809+60.93eθ/18.10∘≤θ＜55∘ (2) 式(2)可作为研究多钨球起爆柱壳装药的基础，方便获得其中任意一个钨球的碰撞位置对应此位置的单钨球冲击起爆柱壳装药的速度阈值。
当θ=0°时，钨球沿柱壳装药的径向碰撞时的起爆速度阈值为2 840 m/s，与文献[16]中数值的误差为0.5%，表明本文中采用的模拟模型具有较好的吻合性，采用冲击起爆机制开展引爆机理研究是合理的。当d=7.6 mm、H=6 mm时，数值模拟得到起爆速度阈值为2 700 m/s，对比文献[14]的试验值2 676 m/s，误差为0.9%，表明在改变钨球尺寸时，该模型仍有较好的适用性。因此可在单破片冲击起爆柱壳装药模拟模型的基础上，增加钨球破片数量，分析多钨球破片对柱壳装药冲击起爆的影响。
2.1 钨球个数的影响
在实战环境中，导弹战斗部可能受到多个高速破片的同时打击，图5展示了1、2、3、4、6个钨球的撞击位置方案，钨球关于柱壳装药的法线成轴对称，两两钨球间的球心距为2r。图6为5种方案下多钨球同时冲击柱壳装药的起爆速度阈值的变化曲线，可以看出当钨球个数从1个增加到4个时,起爆柱壳装药的速度阈值变化明显，4个钨球作用时的速度阈值约是单个的55%；当从4个增加到6个时速度阈值的变化曲线趋于平缓，6个钨球作用时的速度阈值约是单个的50%。随着钨球个数的增加，钨球撞击柱壳装药产生的冲击波数量增加，使得多道冲击波作用下更容易叠加成更强的冲击波，所以随着钨球个数的增加，起爆速度阈值逐渐减小。而随着钨球个数的增加，钨球球心距离撞击位置的轴对称中心更远，在到达叠加位置时每道冲击波衰减得更多，所以钨球个数从4个增加到6个时，个数对速度阈值的影响已经不明显。
2.2 装药半径的影响
由于柱壳装药柱面的存在，在研究双钨球紧靠在一起的情况时分为两种情况：一是关于BB′平面对称，并沿着平行此平面的方向撞击柱壳装药的情况；二是双钨球同时碰撞柱壳装药同一母线的情况。得到这两种情况下的柱壳装药起爆速度阈值随装药半径倒数的变化，如图7所示。由于选取的计算步长为10 m/s，可以看出针对不同的装药半径，起爆柱壳装药的速度阈值没有明显差异，这是由于在双钨球紧靠在一起时，不同装药半径的带壳装药在两种对称情况下的钨球速度方向的壳体厚度与H近似相等，因此可以认为此时装药半径对速度阈值没影响。
2.3 碰撞位置的影响
2.3.1 双钨球撞击的情况
双钨球冲击起爆柱壳装药时，双钨球的空间碰撞位置可分为两种情形：一是两个碰撞位置关于柱壳装药的任意对称面而对称；二是两个碰撞位置不关于柱壳装药的任意对称面对称。
当双钨球同时撞击柱壳装药，碰撞位置关于平面BB′对称（双钨球的撞击角θ1=−θ2、双钨球轴向球心距l =l12=0）时，装药起爆速度阈值随撞击角的增大而增大，起爆速度阈值的最小值约为对应位置单个钨球作用的76%，如图8所示。当|θ1|=|θ2|≥20°时，随着撞击角的增大起爆速度阈值已近似等于单个钨球的速度阈值。
图 8 双钨球起爆速度阈值随撞击角的变化Figure 8. Critical velocity vs. impact angle θ (double tungsten sphere fragments)双钨球同时碰撞柱壳装药同一母线（θ1=θ2=0°）时，装药起爆速度阈值随钨球球心距离的变化如图9所示。由前文知，当双钨球紧靠在一起时（即l=2r），柱壳装药与平板装药具有相同的阈值起爆速度。随着间隔距离的增大，速度阈值增大，并最终趋近于单个钨球的速度阈值，起爆速度阈值的最小值约为单个钨球作用的77%。当球心距在7倍钨球半径范围内，即速度小于单个钨球撞击柱壳装药的起爆速度阈值时，相同的球心距条件下，起爆柱壳装药的速度阈值不小于平板装药，即柱壳装药相对于同厚度的平板装药更难以起爆，这是由于此时冲击波在柱壳装药中传播的损耗比在平板装药中多。对于柱壳装药，球心距为4倍钨球半径时，双钨球的起爆速度阈值约为单个的92%，即l＜4r时双钨球起爆柱壳装药的叠加作用明显。
图 9 柱壳装药和平板装药起爆速度阈值随球心距的变化Figure 9. Critical velocities of cylindrical and plate charge而当双钨球碰撞位置不关于柱壳装药的任意对称面而对称时，选取双钨球分别以撞击角0°和20°撞击柱壳装药时，装药起爆速度阈值随球心距的变化如图10所示，双钨球的起爆速度阈值的最小值约为单钨球以0°撞击时的95%。可以看出当|θ1|≠|θ2|、l≠0时，即当两个钨球撞击角度一定时，圆柱装药的起爆速度阈值随球心距的增加而增大，最终趋于撞击角度绝对值更小的钨球起爆装药的速度阈值。
图 10 双钨球起爆速度阈值随轴向球心距的变化Figure 10. Critical velocity vs. axial ball center distance l/r(double tungsten sphere fragments)2.3.2 4个钨球撞击的情况
4个钨球同时撞击柱壳装药位置的方案如图11所示，假设4个钨球同时撞击，撞击形状近似为“矩形”和“菱形”。
图12是4个钨球呈“矩形”撞击柱壳装药在不同的空间间隔作用下，装药的起爆速度阈值随轴向球心距（钨球1、2的轴向球心距与钨球3、4的轴向球心距相等时，即l=l12=l34）的变化。当撞击角度相同时，随着轴向球心距l的增大，起爆速度阈值增大。而当钨球轴向球心距l相同时，随着撞击角的增大，起爆速度阈值增大。由图6、图12可以得出，4个钨球以“矩形”撞击时的起爆速度阈值的最小值约为撞击角度绝对值最小的单钨球作用时的54%。
图 12 “矩形”结构起爆速度阈值随轴向球心距的变化Figure 12. Critical velocity vs. axial ball center distance l/r (rectangle)图13是4个钨球呈“菱形”撞击柱壳装药在不同的空间间隔作用下，装药的起爆速度阈值随钨球2、4轴向球心距（l=l24）的变化。当撞击角度相同时，随着轴向球心距l的增大，起爆速度阈值增大；而当钨球间轴向球心距l相同时，随着撞击角的增大，起爆速度阈值增大。可以看出，4个钨球间排得越紧密，即空间间隔越小，装药的起爆速度阈值越小，4个钨球以“菱形”撞击时的起爆速度阈值的最小值约为撞击角度绝对值最小的单钨球作用时的55%。
图 13 “菱形”结构起爆速度阈值随轴向球心距的变化Figure 13. Critical velocity vs. axial ball center distance l/r (rhombus)因此，当多钨球破片同时撞击柱壳装药时，起爆速度阈值随空间碰撞位置间隔的增大而增大，这是由于间隔的增大造成每个破片产生的冲击波到达叠加位置时衰减得更多。
2.4 时间间隔的影响
为了研究时间间隔对起爆速度阈值的影响，也可分为两种情况分析：一是双钨球破片的球心在同一个圆柱截面；二是双钨球破片的球心不在同一个圆柱截面。
假设双钨球的球心在同一个圆柱截面，即l12=0。分别研究不同撞击角下，速度阈值随时间间隔（即h2/r）的变化；当2个钨球碰撞位置相同、而碰撞顺序不同时，速度阈值随h2/r的变化。
由图14可以看出，3种情况均是钨球1先碰撞柱壳装药，钨球2后碰撞，当双钨球撞击角分别为θ1=0°、θ2=10°时，装药起爆速度阈值随撞击时间间隔的增大而增大，最后达到单个钨球的速度阈值；而在θ1=0°、θ2=20°时，装药起爆速度阈值随碰撞时间间隔的增大先减小后增大；在θ1=20°、θ2=0°时，装药起爆速度阈值随碰撞时间间隔的增大先减小后增大。θ1=0°、θ2=20°与θ1=20°、θ2=0°的2条变化曲线的趋势基本保持一致，都是先减小后增大，最小的起爆速度阈值约为同时撞击的97%。
当θ1=0°、θ2=10°时，由于两个钨球距离较近，钨球2撞击瞬间，钨球1已经侵彻一段距离，而钨球1对于钨球2的侵彻过程造成干扰，所以随着撞击时间间隔的增大需要更高的起爆速度阈值。本文不侧重研究这种互相干扰的情况。当θ1=0°、θ2=20°、v=2 800 m/s时，选取h2=7，9，14 mm，提取不同计算文件中同一观测点θ2-5-2的压力-时间曲线，如图15所示。可以看出，当h2=9 mm时，峰值压力最大，其次是h2=7 mm，而h2=14 mm时压力最小，即随着h2的增大，峰值压力先增大后减小。当θ1=20°、θ2=0°、v=2 800 m/s时，同样选取h2=7，9，14 mm，提取不同计算文件中同一观测点θ2-0-2的压力-时间曲线，如图16所示。从图16可以看出，当h2=9 mm时峰值压力也是最大，同样可以得到随着h2的增大，峰值压力先增大后减小。对比图15和图16，在相同时间间隔下，图16中观测点的峰值压力均高于图15中对应点的峰值压力。因此，采用相同的撞击速度v=2 800 m/s时，无论钨球撞击的先后顺序怎样，随着时间间隔的增大，炸药内同一位置的压力值均先增大后减小，因此，起爆装药的速度阈值随时间间隔的增大先减小后增大。考虑钨球撞击先后顺序时，在|θ2|＜|θ1|的情况下更容易起爆柱壳装药，产生这种变化趋势的原因，可以借鉴一维平面冲击波的相互作用来解释。先减小是由于第2个钨球破片撞击时，第1个钨球破片的冲击波没扫过第2个钨球的撞击区域，所以两道冲击波迎面相遇发生叠加。后增大是由于第2个钨球破片撞击时，第1个钨球破片的冲击波扫过第2个破片的撞击区域，而冲击波的传播相对于波前介质是超音速的，而相对于波后介质是亚音速的，因此第2个钨球破片形成的冲击波必定追赶上第1道冲击波，叠加成更强的一道冲击波。而追赶过程相较于迎面相遇过程，两破片的冲击波衰减得更多，所以就需要更高的起爆速度阈值。在考虑撞击先后顺序时，以相同速度撞击时，后撞击的撞击角小于先撞击的角度时，后一个钨球速度方向的壳体厚度更薄，冲击波传播过程衰减相对少，更容易与前一道冲击波叠加成更强的一道冲击波，所以|θ2|＜|θ1|时更容易起爆柱壳装药。
图 15 观测点θ2-5-2的压力时间曲线Figure 15. Pressure-time curves at observation point θ2-5-2 (v=2 800 m/s)当两个钨球球心不在同一圆柱截面时，选取l12/r=2进行研究，钨球1先碰撞柱壳装药，钨球2后碰撞。当θ1=0°、θ2=20°、l12/r=2与θ1=20°、θ2=0°、l12/r=2时，装药起爆速度阈值均随碰撞时间间隔的增大先减小后增大，最小的起爆速度阈值约为同时撞击的95%，如图17所示。当2个钨球的撞击位置相同、撞击顺序不同时，曲线的整体趋势是相同的，都是先减小后增大。在h/r＜7范围内，|θ2|＜|θ1|时的起爆速度阈值小于|θ2|＞|θ1|时的速度阈值，即当2个钨球撞击角度一定时，后撞击的撞击角小于先撞击的角度时，更容易起爆柱壳装药。
3. 结 论
通过AUTODYN-3D软件对多钨球破片冲击起爆柱壳装药特性的研究，得到以下结论。
（1）相同球心距情况下，以柱壳装药的法线为对称轴，随着钨球个数的增加，起爆柱壳装药的速度阈值明显减小，4个钨球作用时的速度阈值约是单个钨球以0°撞击的55%，6个钨球作用时的速度阈值约是单个钨球以0°撞击的50%。
（2）双钨球紧靠在一起撞击柱壳装药时，装药半径对装药起爆速度阈值影响不明显。当以θ1=θ2=0°撞击时，柱壳装药和平板装药有明显的差别，当l≤7r时，柱壳装药相较于平板装药更难以起爆，且l＜4r时双钨球起爆柱壳装药的叠加作用明显。
（3）多钨球同时撞击柱壳装药的起爆速度阈值均随着撞击角、轴向球心距的增大而增大，最终趋近于多钨球破片中撞击角绝对值最小的那枚破片碰撞位置对应的单钨球起爆装药的速度阈值。双钨球作用时起爆速度阈值的最小值约为撞击角绝对值最小的单钨球作用的76%，4个钨球作用时起爆速度阈值的最小值约为撞击角绝对值最小的单钨球作用时的54%。
（4）双钨球间隔撞击柱壳装药的起爆速度阈值均随撞击时间间隔的增大而先减小后增大，最小起爆速度阈值约为同时撞击的95%，且|θ2|＜|θ1|的方案更容易起爆柱壳装药。
-
图 1 试验场地、炸药及传感器布设方案（HW1）
Figure 1. Experimental site, explosive and sensor position arrangement (HW1)
图 2 试验场地、炸药及传感器布设方案（HW2）
Figure 2. Experimental site, explosive and sensor position arrangement (HW2)
图 4 水下爆炸高桩码头模型破坏现象（HW1）
Figure 4. The damage phenomena of the high-piled wharf model under underwater explosion (HW1)
图 5 水下爆炸高桩码头模型破坏现象（HW2）
Figure 5. The damage phenomena of the high-piled wharf model under underwater explosion (HW2)
表 1 主要构件参数（单位为mm）
Table 1. Matching bar condition of main members (unit in mm)
构件 尺寸 配筋情况 保护层厚度 面板（HW1） 3800×2300×100 双层双向配筋∅6@200 20 面板（HW2） 2600×2300×100 双层双向配筋∅6@200 20 横梁 肋部纵筋2∅8
翼缘纵筋6∅8
箍筋∅6@20020 纵梁 纵筋4∅8
箍筋∅6@12520 桩 120×120×3100 纵筋4∅10
上部箍筋∅6@200，下部箍筋∅6@40020 注：纵梁箍筋仅在纵、横梁交界处布置；桩基为预制，码头面板、横梁、纵梁为现场整体浇筑。 
下载: 导出CSV
表 2 1 kg乳化炸药与1 kg TNT水下爆炸荷载比较
Table 2. Comparison of underwater explosion load between 1 kg emulsion explosive and 1 kg TNT
Pm/MPa I/(Pa·s) pm/MPa i/(Pa·s) T/s 乳化炸药 (HW1) 17.91 1 782.09 3.02 822.80 0.017 TNT 19.48 2 695.31 3.02 13 892.07 0.280 δ/% −8.06 −33.82 0 −94.08 −93.930 乳化炸药 (HW2) 18.25 2 066.17 5.76 1 026.39 0.017 TNT 20.44 2 799.48 3.15 14 496.07 0.280 δ/% −10.71 −26.20 82.86 −92.92 −93.930
下载: 导出CSV
表 3 高桩码头模型毁伤效应
Table 3. Damage effect of high-piled wharf
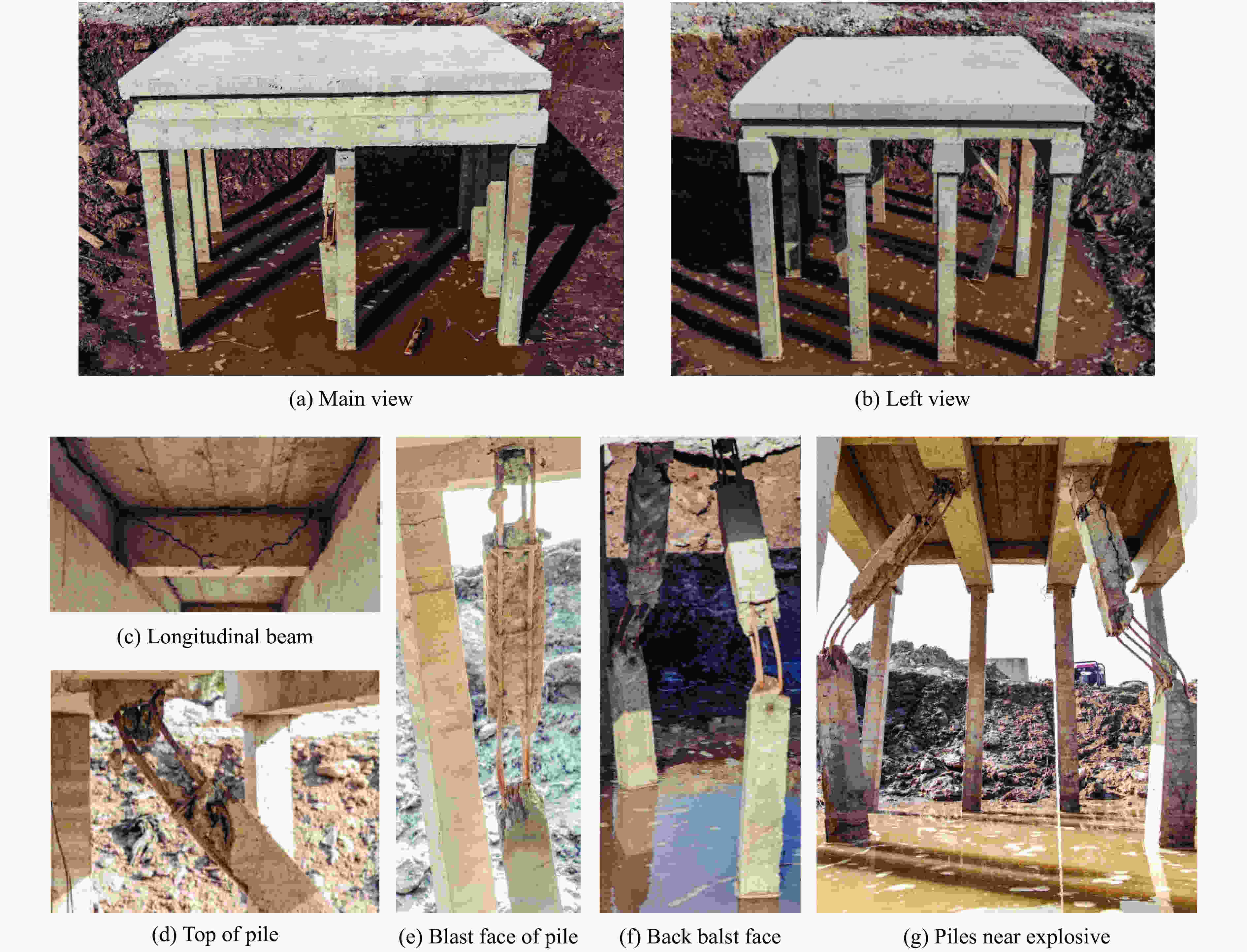
码头部位 毁伤效应 HW1
炸药位于4个桩基之间，面板下方，爆距0.61 mHW2
炸药位于2个桩基中间，纵梁下方，爆距0.29 m桩基 1. 桩中迎爆棱边形成爆坑，桩中背爆面形成水平裂缝；
2. 桩顶迎爆面与横梁连接处剪切破坏，桩顶背爆面混凝土压坏；
3. 桩底产生轻微位移。1. 桩中混凝土贯穿破坏，钢筋裸露向外侧变形；
2. 桩顶混凝土破坏严重，破坏贯通或形成塑性铰；
3. 桩底产生明显位移，出现水平裂缝。面板 1. 面板向上弯曲隆起，顶部形成裂缝；
2. 面板顶部长边侧混凝土破坏，钢筋裸露；
3. 面板底部与纵横梁连接处混凝土撕裂破坏，钢筋裸露。1. 面板向上弯曲隆起，顶部形成细微裂缝；
2. 面板底部与纵横梁连接处形成水平裂缝。横梁 横梁与面板连接处混凝土撕裂破坏，钢筋裸露向上拔起。 横梁与面板连接处形成水平裂缝。 纵梁 1. 纵梁与面板连接处混凝土撕裂破坏，钢筋裸露向上拔起；
2. 纵梁形成轻微斜裂缝。1. 纵梁与面板连接处形水平成裂缝；
2. 纵梁形成对称斜裂缝。
下载: 导出CSV
-
[1] 高勇军, 王伟策, 陈小波, 等. 浅层水中爆炸冲击波压力的测试与分析 [J]. 爆破, 1999(1): 9–13. DOI: CNKI:SUN:BOPO.0.1999-01-002.GAO Y J, WANG W C, CHEN X B, et al. Testing and analysis on shock wave pressure generated by explosion under shallow water [J]. Blasting, 1999(1): 9–13. DOI: CNKI:SUN:BOPO.0.1999-01-002. [2] 顾文彬, 叶序双, 张朋祥, 等. 浅层水中爆炸水底影响的试验研究 [J]. 解放军理工大学学报(自然科学版), 2001, 2(2): 55–58. DOI: 10.3969/j.issn.1009-3443.2001.02.013.GU W B, YE X S, ZHANG P X, et al. Experimental studies of bottom influence in shallow-layer water explosion [J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2001, 2(2): 55–58. DOI: 10.3969/j.issn.1009-3443.2001.02.013. [3] 顾文彬, 孙百连, 阳天海, 等. 浅层水中沉底爆炸冲击波相互作用数值模拟 [J]. 解放军理工大学学报(自然科学版), 2003, 4(6): 64–68. DOI: 10.7666/j.issn.1009-3443.20030615.GU W B, SUN B L, YANG T H, et al. Numerical simulation of explosive shockwave interaction in shallow-layer water [J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2003, 4(6): 64–68. DOI: 10.7666/j.issn.1009-3443.20030615. [4] WARDLAW A B, LUTON J A. Fluid-structure interaction mechanisms for close-in explosions [J]. Shock & Vibration, 2015, 7(5): 265–275. DOI: 10.1155/2000/141934. [5] 张阿漫, 姚熊亮. 复杂边界附近气泡的动态特性研究 [J]. 力学季刊, 2008, 29(1): 24–32.ZHANG A M, YAO X L. Dynamic of bubble near complex boundary [J]. Chinese Quarterly of Mechanics, 2008, 29(1): 24–32. [6] 朱锡, 白雪飞, 黄若波, 等. 船体板架在水下接触爆炸作用下的破口试验 [J]. 中国造船, 2003, 44(1): 46–52. DOI: CNKI:SUN:ZGZC.0.2003-01-007.ZHU X, BAI X F, HUANG R B, et al. Crevasse experiment research of plate membrance in vessels subjected to underwater contact explosion [J]. Shipbuilding of China, 2003, 44(1): 46–52. DOI: CNKI:SUN:ZGZC.0.2003-01-007. [7] 朱锡, 张振华, 刘润泉, 等. 水面舰艇舷侧防雷舱结构模型抗爆试验研究 [J]. 爆炸与冲击, 2004, 24(2): 133–139.ZHU X, ZHANG Z H, LIU R Q, et al. Experimental study on the explosion resistance of cabin near shipboard of surface warship subjected to underwater contact explosion [J]. Explosion and Shock Waves, 2004, 24(2): 133–139. [8] 李海涛, 朱锡, 张振华. 船体梁在近距爆炸冲击波作用下动态响应的相似律研究 [J]. 振动与冲击, 2010, 29(9): 28–32. DOI: CNKI:SUN:ZDCJ.0.2010-09-008.LI H T, ZHU X, ZHANG Z H. Similarity law of dynamic response of hull girder subjected to underwater explosion in near field [J]. Journal of Vibration and Shock, 2010, 29(9): 28–32. DOI: CNKI:SUN:ZDCJ.0.2010-09-008. [9] 李海涛, 张永坤, 张振海. 近场水下爆炸作用下箱形梁整体损伤特性研究 [J]. 兵工学报, 2012, 33(5): 611–616.LI H T, ZHANG Y K, ZHANG Z H. Damage characteristics of box-like beam as a bulk subjected to underwater explosion in near-field [J]. Acta Armamentarii, 2012, 33(5): 611–616. [10] 黄晓明, 朱锡, 牟金磊, 等. 圆柱壳在水下爆炸作用下鞭状响应试验研究 [J]. 哈尔滨工程大学学报, 2010, 31(10): 1278–1285. DOI: 10.3969/j.issn.1006-7043.2010.10.002.HUANG X M, ZHU X, MU J L, et al. Study on whipping response of a stiffened cylindrical shell in an underwater explosion [J]. Journal of Harbin Engineering University, 2010, 31(10): 1278–1285. DOI: 10.3969/j.issn.1006-7043.2010.10.002. [11] 刘美山, 吴新霞, 张恒伟. 混凝土水下爆破炸药单耗试验分析 [J]. 爆破, 2007, 24(1): 10–13. DOI: 10.3963/j.issn.1001-487X.2007.01.003.LIU M S, WU X X, ZHANG H W. Experimental analysis on specific charge of underwater explosion of concrete [J]. Blasting, 2007, 24(1): 10–13. DOI: 10.3963/j.issn.1001-487X.2007.01.003. [12] 李裕春, 程克明, 沈蔚, 等. 水中冲击波对混凝土结构破坏的实验研究 [J]. 材料工程, 2010, 16(1): 1–5. DOI: 10.3969/j.issn.1001-4381.2008.12.005.LI Y C, CHENG K P, CHEN W, et al. Damage analysis of concrete structure by underwater shock [J]. Engineering of Material, 2010, 16(1): 1–5. DOI: 10.3969/j.issn.1001-4381.2008.12.005. [13] 李建阳, 李永池, 高光发, 等. 混凝土水下径向不耦合爆破特性研究 [J]. 工程爆破, 2010, 16(1): 1–5. DOI: 10.3969/j.issn.1006-7051.2010.01.001.LI J Y, LI Y C, GAO G F, et al. Study on blasting characteristics of underwater concrete with decoupling charge [J]. Engineering Blasting, 2010, 16(1): 1–5. DOI: 10.3969/j.issn.1006-7051.2010.01.001. [14] 董琪, 韦灼彬, 唐廷,等. 水下爆炸对沉箱重力式码头毁伤效应 [J]. 爆炸与冲击, 2019, 39(6): 065101. DOI: 10.11883/bzycj-2018-0090.DONG Q, WEI Z B, TANG T, et al. Damage effects of caisson gravity wharf under underwater explosion [J]. Explosion and Shock Waves, 2019, 39(6): 065101. DOI: 10.11883/bzycj-2018-0090. [15] 李凌锋, 韦灼彬, 唐廷, 等. 爆炸荷载下沉箱重力式码头模型毁伤效应 [J]. 爆炸与冲击, 2019, 39(1): 012202. DOI: 10.11883/bzycj-2017-0406.LI L F, WEI Z B, TANG T, et al. Damage effects of the caisson gravity wharf model subjected to explosion [J]. Explosion and Shock Waves, 2019, 39(1): 012202. DOI: 10.11883/bzycj-2017-0406. [16] 韦灼彬. 钢筋混凝土桩基梁板码头爆炸毁伤及抢修技术研究[D]. 天津: 天津大学, 2005: 8-68. DOI: 10.7666/d.y850662. [17] 闫秋实, 宁素瑜, 杜修力, 等. 水中近场爆炸作用下钢筋混凝土桩毁伤效应研究 [J]. 北京工业大学学报, 2019, 45(2): 55–61. DOI: 10.11936/bjutxb2017110011.YAN Q S, NING S Y, DU X L, et al. Damage effect for a typical reinforced concrete pile under the near field explosion in water [J]. Journal of Beijing University of Technology, 2019, 45(2): 55–61. DOI: 10.11936/bjutxb2017110011. [18] RAJENDRAN R, NARASIMHAN K. Deformation and fracture behaviour of plate specimens subjected to underwater explosion: a review [J]. International Journal of Impact Engineering, 2006, 32(12): 1945–1963. DOI: 10.1016/j.ijimpeng.2005.05.013. [19] COLE R H. Underwater explosions[M]. Princeton: Princeton University Press, 1948: 118-127. -
下载:
计量
- 文章访问数: 3217
- HTML全文浏览量: 1355
- PDF下载量: 102
- 被引次数: 0