基于EMD改进算法的爆破振动信号去噪

易文华; 刘连生; 闫雷; 董斌斌

doi:10.11883/bzycj-2019-0471

基于EMD改进算法的爆破振动信号去噪

doi: 10.11883/bzycj-2019-0471

江西理工大学资源与环境工程学院，江西赣州 341000

基金项目: 国家自然科学基金（51404111）；江西省自然科学基金（20192BAB206017）；江西理工大学清江优秀人才支持计划（JXUSTQJYX2016007）

详细信息

作者简介:
易文华（1996－　），男，硕士研究生，yiwenhua0918@163.com

通讯作者:
刘连生（1979－　），男，博士，教授，lianshengliu@jxust.edu.cn

中图分类号: O389
计量
- 文章访问数: 4017
- HTML全文浏览量: 1368
- PDF下载量: 87
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-16
- 修回日期: 2020-03-10
- 网络出版日期: 2020-07-25
- 刊出日期: 2020-09-01

Vibration signal de-noising based on improved EMD algorithm

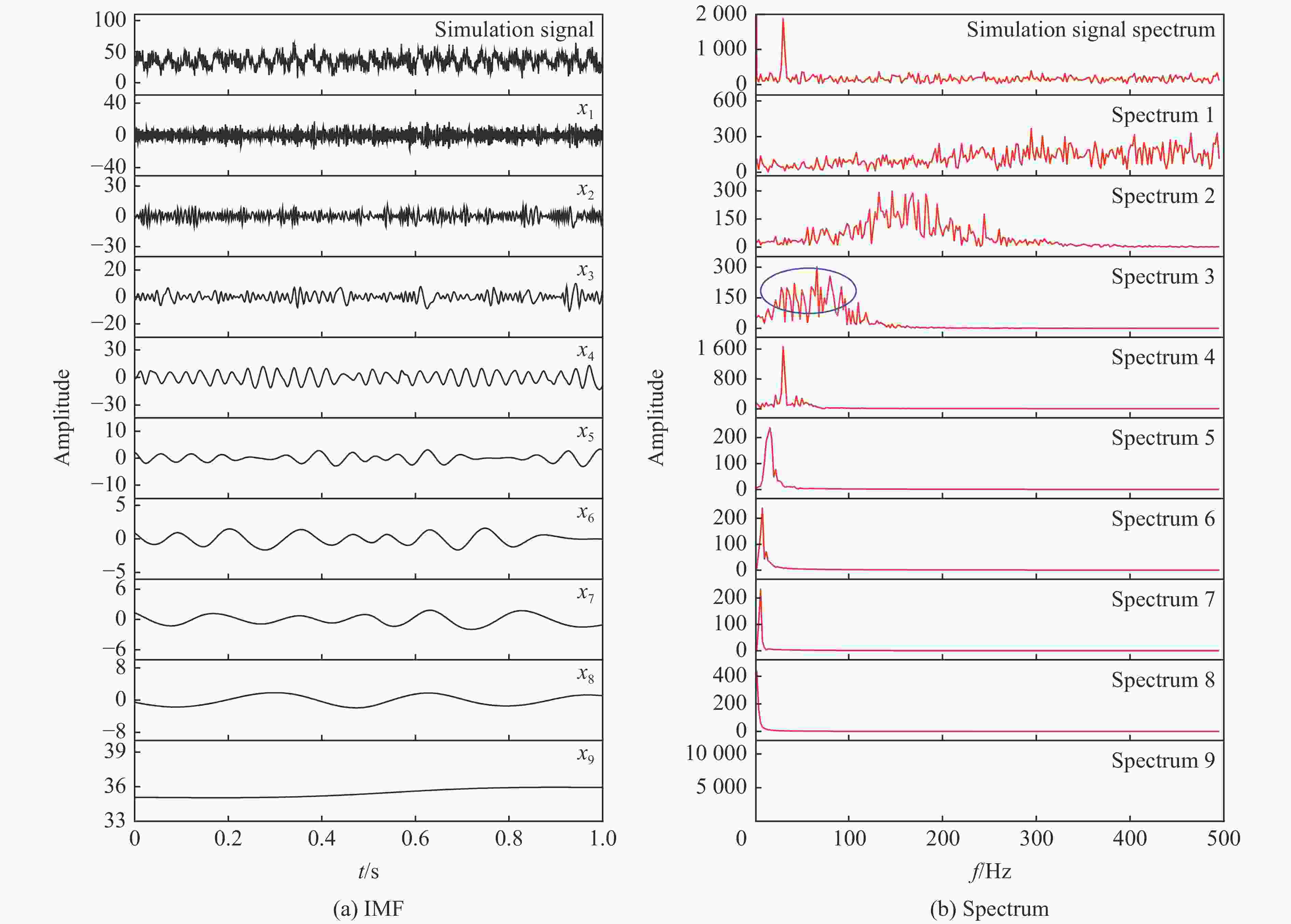
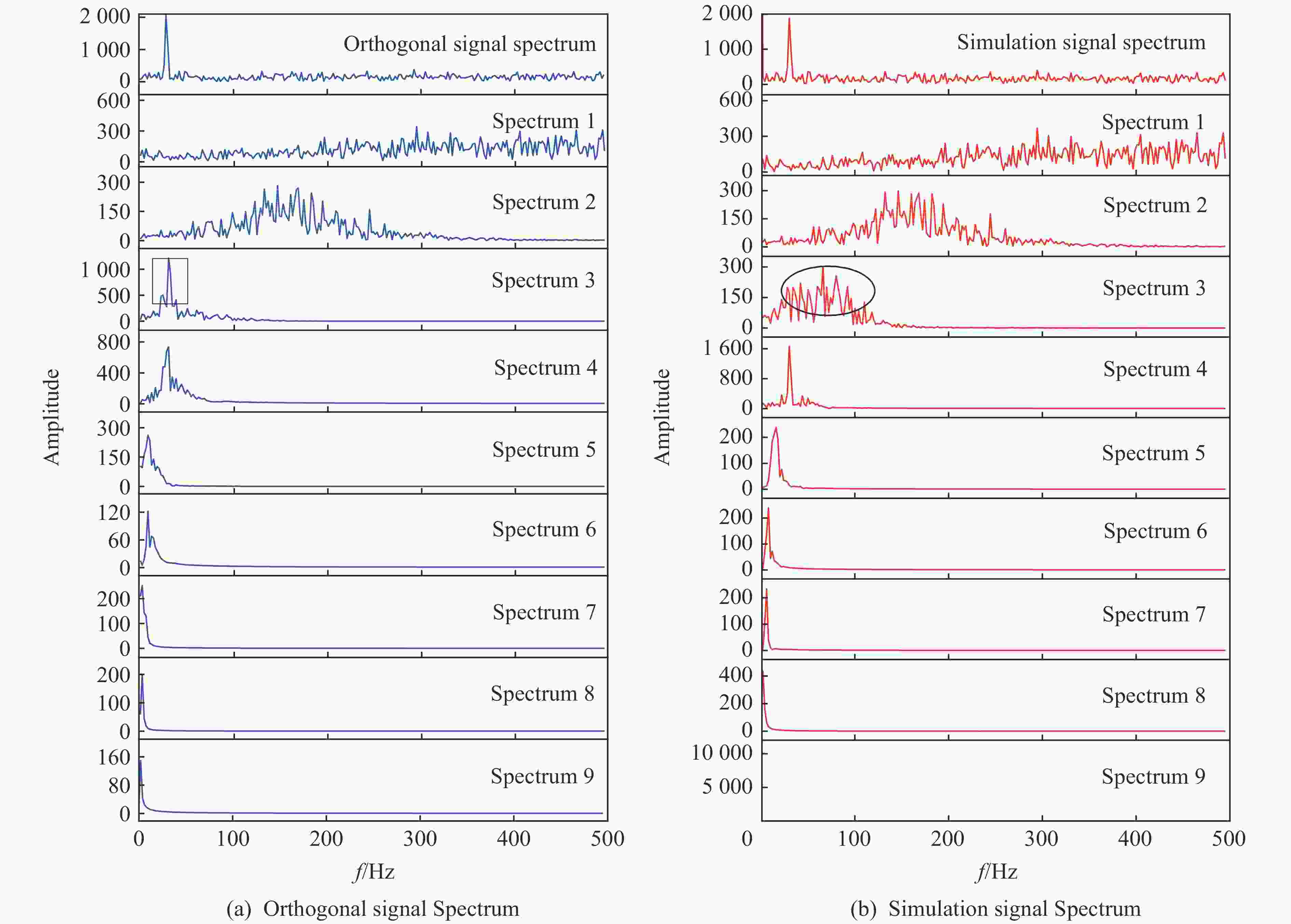
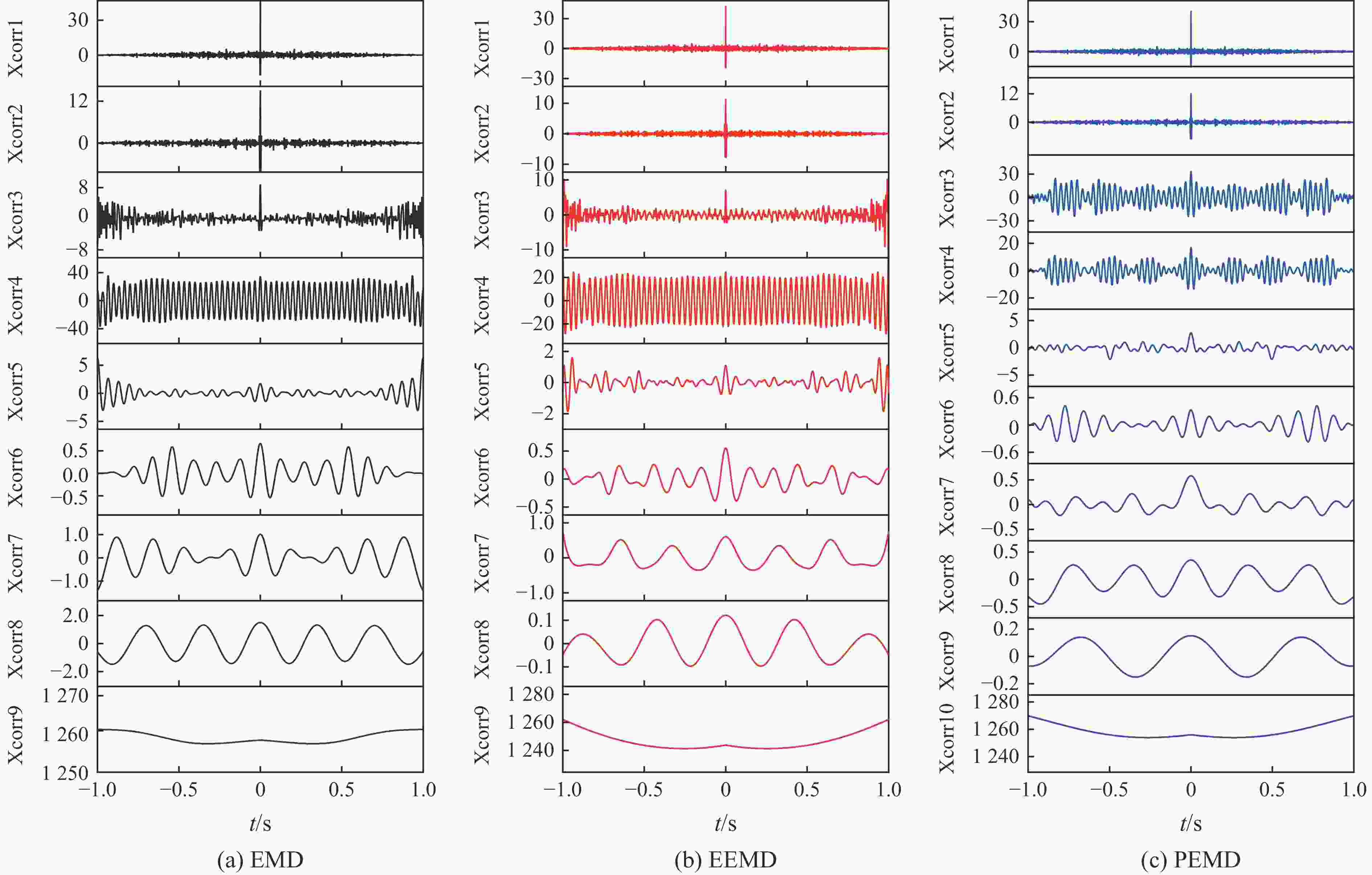
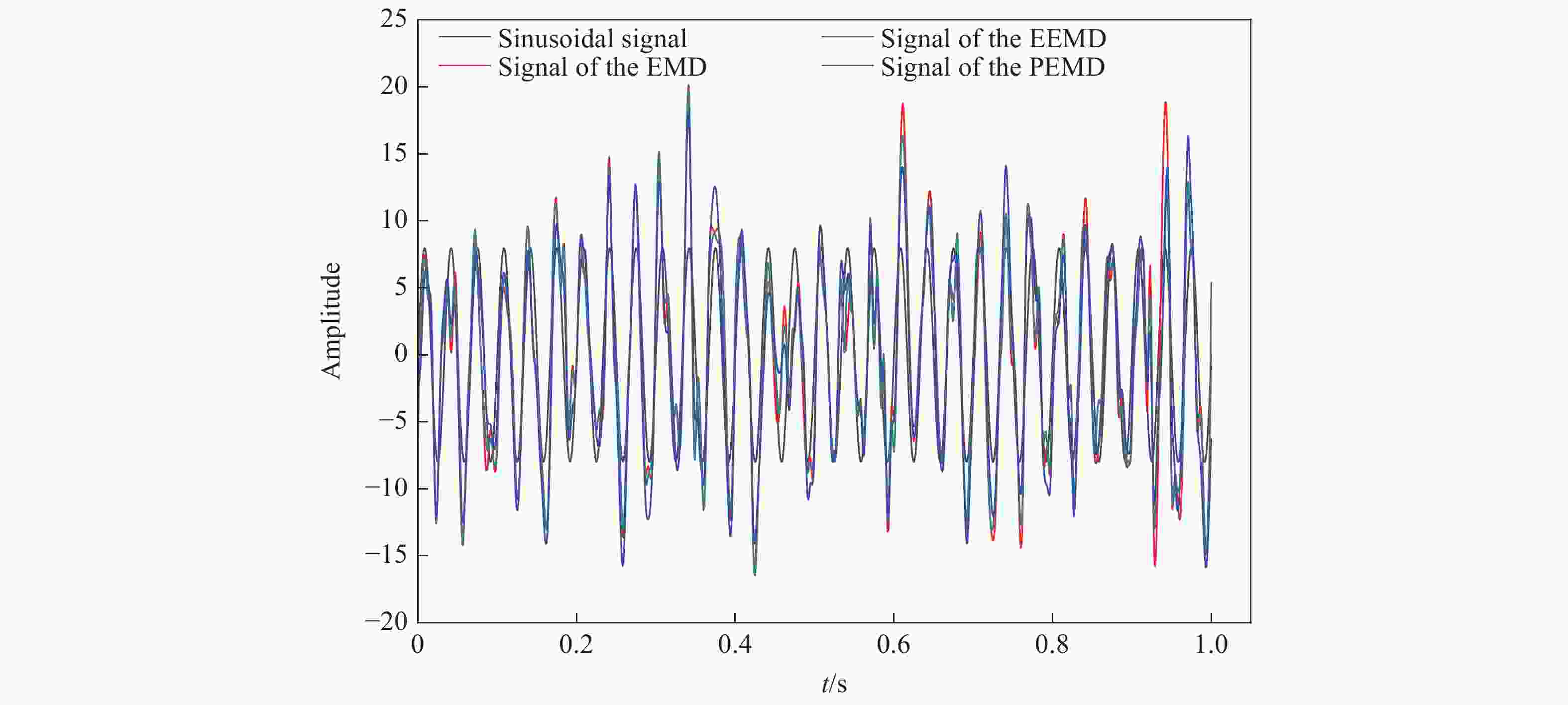
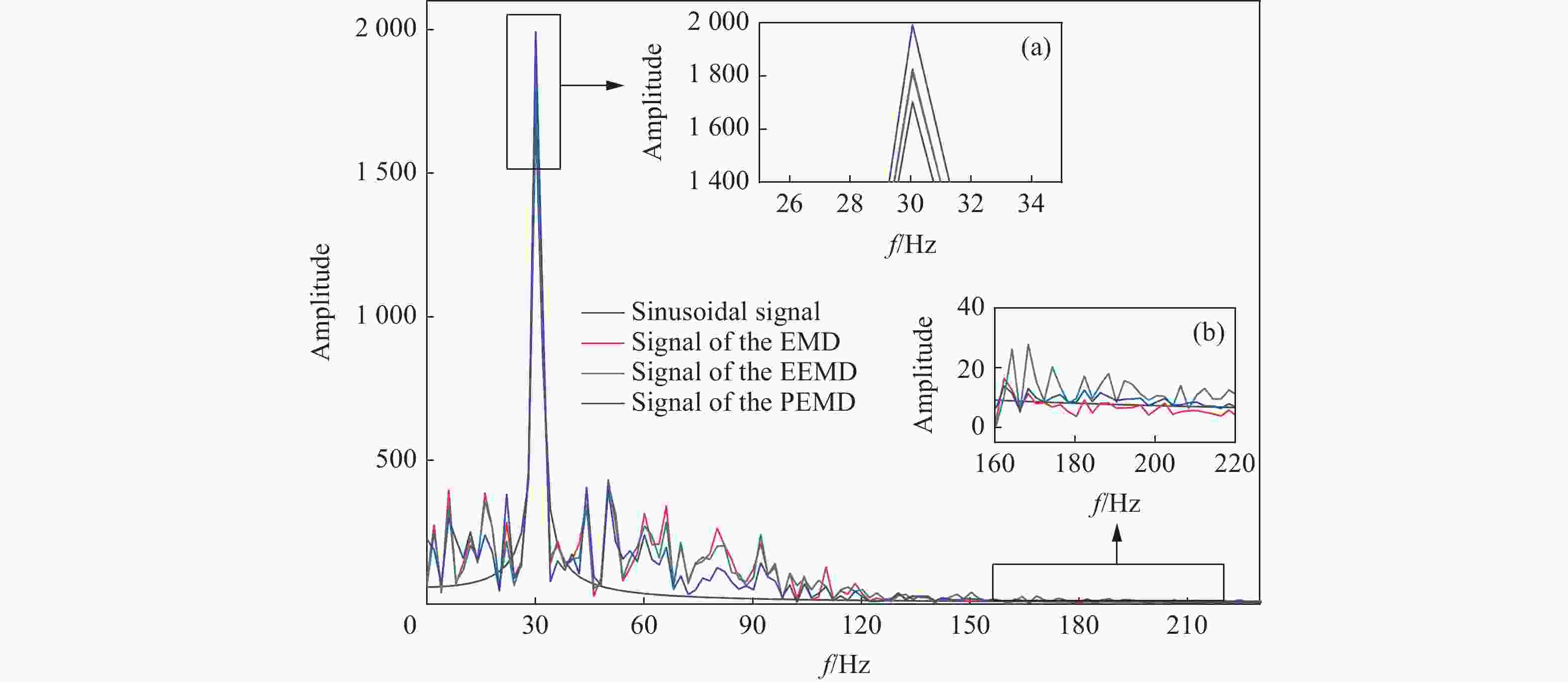
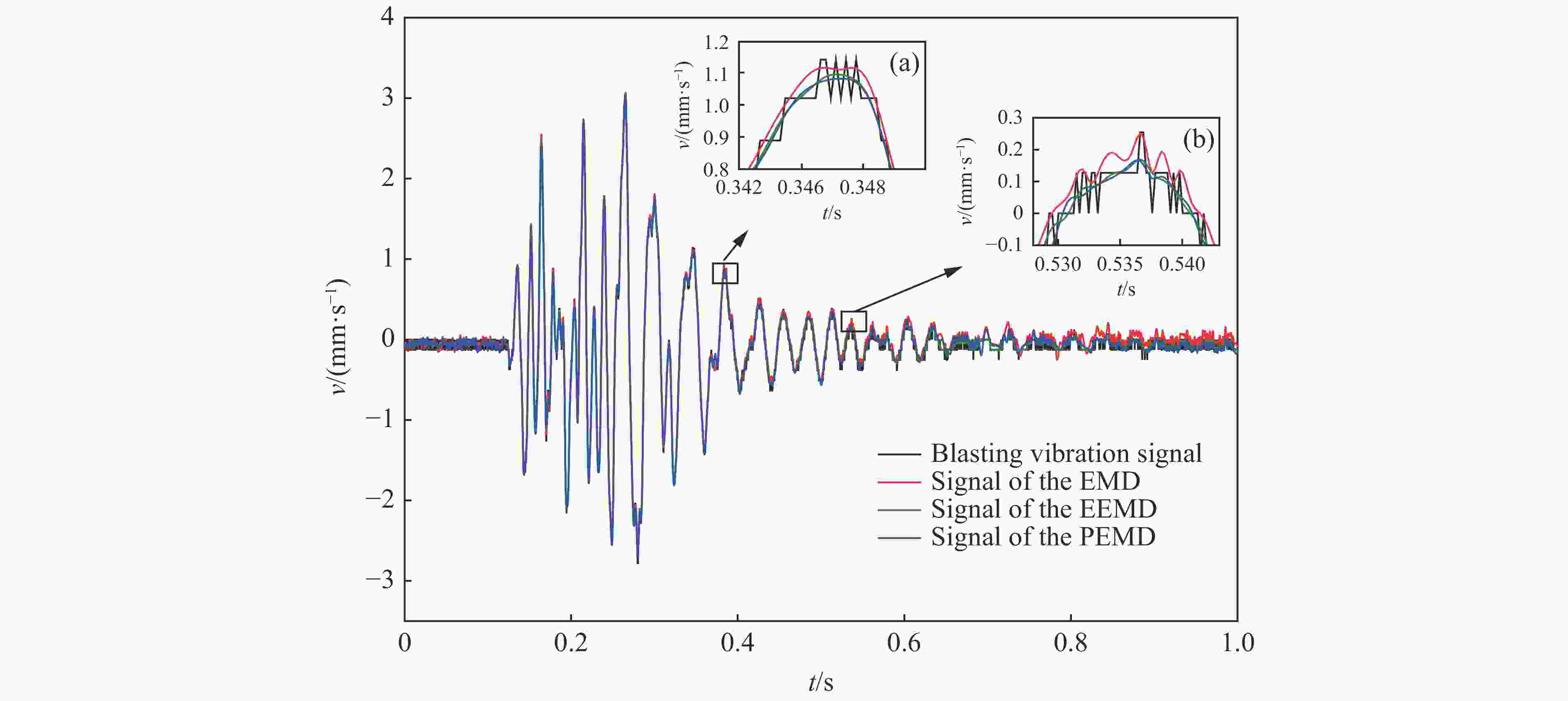
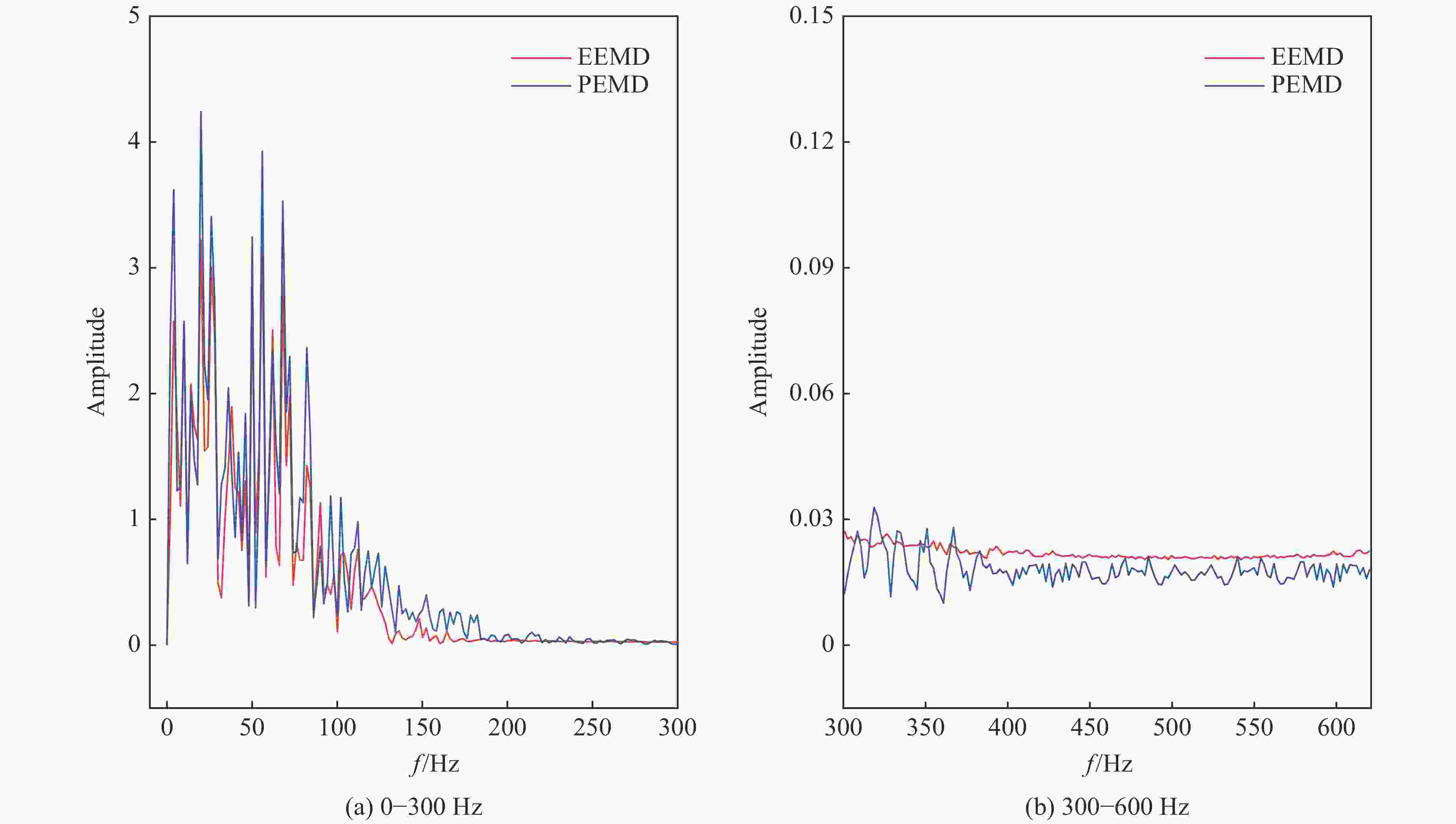
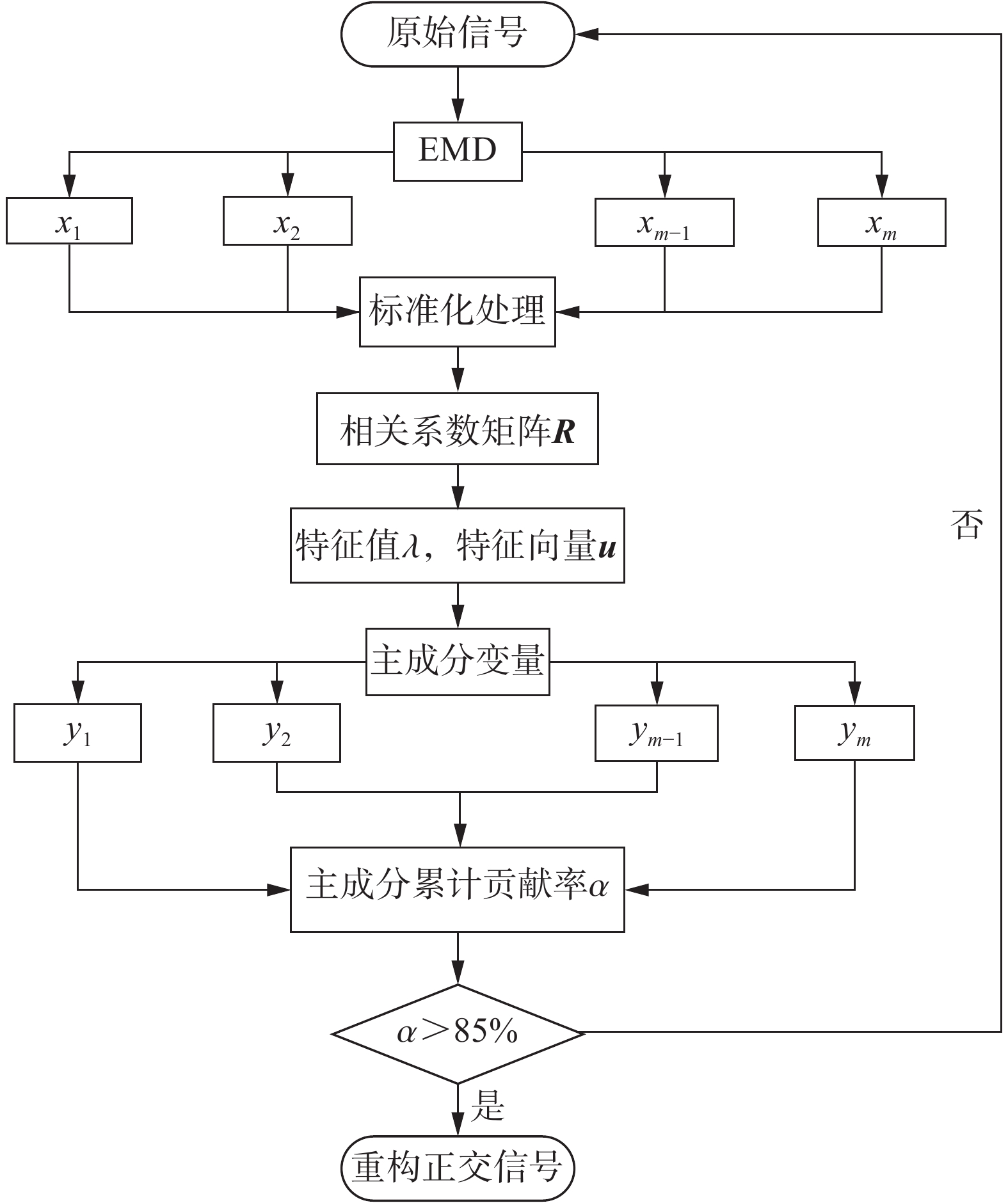
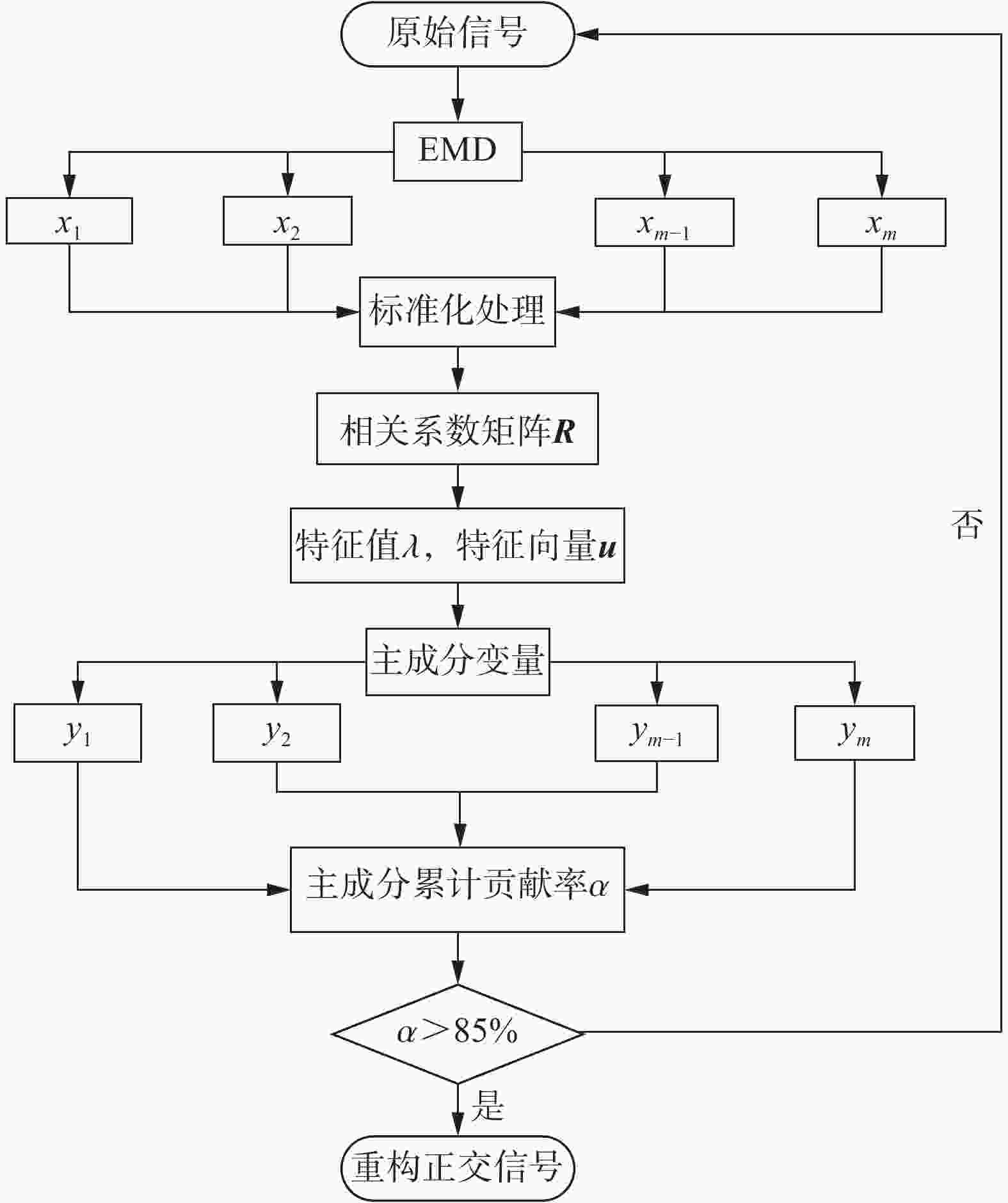
School of Resource and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China

摘要

摘要: 为了解决振动信号经验模态分解(empirical mode decomposition, EMD)滤波去噪效果不佳的问题，提出一种自适应性正交经验模态分解(principal empirical mode decomposition, PEMD)的信号去噪方法。该算法融合了EMD分解的自适应性和主成分分析(principal component analysis，PCA)的完全正交性特点，对信号EMD分解过程中产生的模态混叠现象进行消除，得到了最佳的去噪效果。分析表明：PEMD在仿真模拟试验中相比于传统EMD算法和集总经验模态分解(ensemble empirical mode decomposition, EEMD) 算法，信噪比分别提高了1.15 dB和0.38 dB，且均方根误差最小；频域上PEMD对仿真信号频率(30 Hz)识别的灵敏度最高，30 Hz之外的噪声滤除效果最好。在爆破振动试验中，PEMD和EEMD去除噪声毛刺的效果较为理想，且PEMD在0～300 Hz的中低频振动信号保存效果最好，300 Hz以上的高频噪声滤除效果最好。
- 爆破振动 /
- 去噪 /
- 模态混叠 /
- 主成分分析 /
- 经验模态分解 /
- 集总经验模态分解
Abstract: In order to solve the problem of poor performance of EMD (empirical mode decomposition） filter de-noising for vibration signal, an adaptive orthogonal decomposition signal de-noising method PEMD (principal empirical mode decomposition) is proposed. This algorithm combines the self-adaptability of EMD decomposition and the complete orthogonality of principal component analysis (PCA), eliminates the phenomenon of mode aliasing in the process of signal EMD decomposition, and obtains the best de-noising effect. The results showed that compared with EMD and EEMD (ensemble empirical mode decomposition）, PEMD (principal component analysis) improved 1.15 dB and 0.38 dB respectively in the simulation test, and the root-mean-square error was the smallest. In frequency domain, PEMD has the highest sensitivity to the frequency of simulation signal (30 Hz), and the noise filtering effect is the best outside 30 Hz. In the blasting vibration test, PEMD and EEMD had better performance in removing burrs, and PEMD had the best performance in preserving medium and low frequency vibration signals at 0−300 Hz, and the best performance in filtering high frequency noises above 300 Hz.
- blasting vibration /
- de-noising /
- mode aliasing /
- PCA（principal component analysis） /
- EMD(empirical mode decomposition） /
- EEMD (ensemble empirical mode decomposition）

HTML全文

图 1 PEMD算法流程图

Figure 1. PEMD algorithm flow chart

下载: 全尺寸图片幻灯片

图 2 仿真信号IMF分量与频谱

Figure 2. IMF component and spectrum of simulation signal

下载: 全尺寸图片幻灯片

图 3 正交信号与仿真信号频谱对比

Figure 3. Spectrum comparison between orthogonal signal and simulated signal

下载: 全尺寸图片幻灯片

图 4 IMF分量自相关函数特性曲线

Figure 4. Characteristic curves of IMF component autocorrelation function

下载: 全尺寸图片幻灯片

图 5 EMD、EEMD和PEMD去噪信号时域对比

Figure 5. Comparison of EMD, EEMD and PEMD de-noising signal time domain

下载: 全尺寸图片幻灯片

图 6 EMD、EEMD和PEMD去噪信号频谱对比

Figure 6. Comparison of EMD, EEMD and PEMD de-noising signal spectrum

下载: 全尺寸图片幻灯片

图 7 地质地形及监测点布置图

Figure 7. Geological topography and layout of the monitoring site

下载: 全尺寸图片幻灯片

图 8 EMD、EEMD和PEMD去噪信号时域对比

Figure 8. Comparison of EMD, EEMD and PEMD de-noising signal time domain

下载: 全尺寸图片幻灯片

图 9 EEMD与PEMD去噪信号频谱对比

Figure 9. Comparison of EEMD and PEMD de-noising signal spectrum

下载: 全尺寸图片幻灯片

表 1 主成分变量信息贡献率

Table 1. Principal component variable information contribution rate

主成分变量 ${y_1}$ ${y_2}$ ${y_3}$ ${y_4}$ ${y_5}$ ${y_6}$ ${y_7}$ ${y_8}$ ${y_9}$

信息贡献率/% 14.88 13.63 11.97 11.44 10.49 10.43 9.80 9.16 8.21

下载: 导出CSV

表 2 去噪效果评价指标

Table 2. Evaluation index of de-noising effect

去噪算法 γ $\sigma $

EMD 2.83 2.04
EEMD 3.60 1.87
PEMD 3.98 1.79

下载: 导出CSV

表 3 不同测点的爆破参数

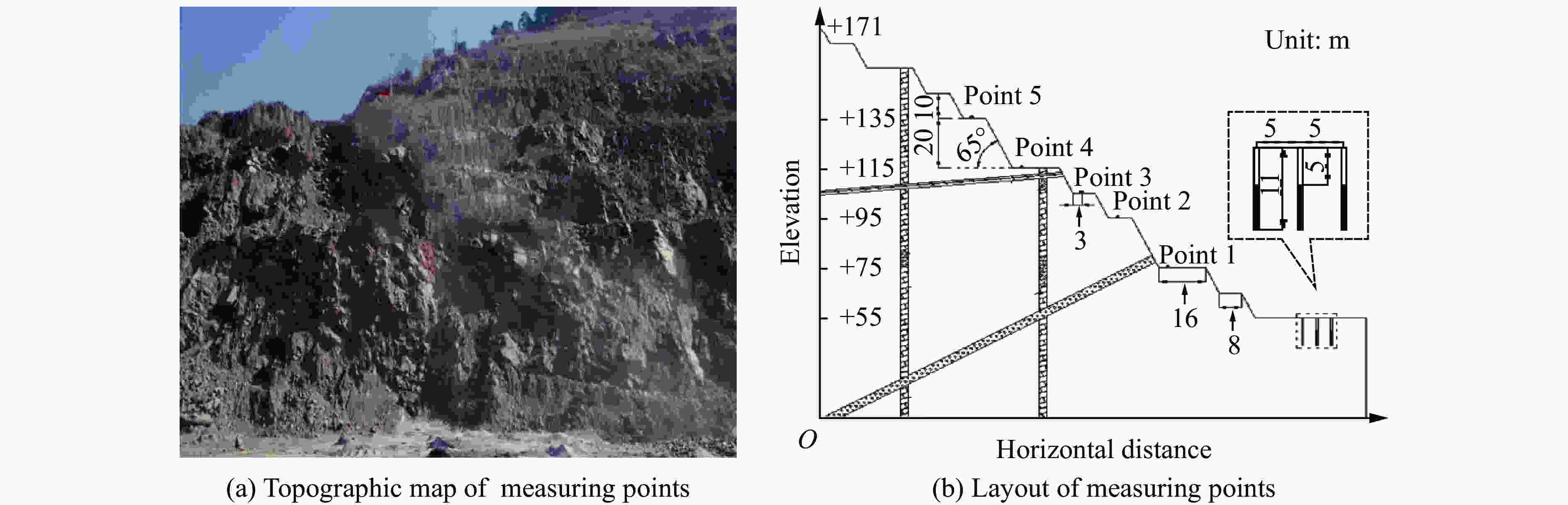
Table 3. Blasting parameters of different measuring points

测点最大段药量/kg 水平距离/m 高程差/m

1 3 172 190 20
2 3 172 286 40
3 3 172 311 50
4 3 172 330 60
5 3 172 350 80

下载: 导出CSV

参考文献(22)

[1]	ZHAI M Y. Seismic data de-noising based on the fractional Fourier transformation [J]. Journal of Applied Geophysics, 2014, 109: 62–70. DOI: 10.1016/j.jappgeo.2014.07.012.
[2]	李夕兵, 凌同华, 张义平. 爆破震动信号理论与技术[M]. 北京: 科学出版社, 2009: 60−63.
[3]	中国生, 徐国元, 赵建平. 基于小波变换的爆破地震信号阈值去噪的应用研究 [J]. 岩土工程学报, 2005, 27(9): 1055–1059. DOI: 10.3321/j.issn:1000-4548.2005.09.016. ZHONG G S, XU G Y, ZHAO J P. Study and application of threshold de-noising in seismic signals of blasting based on wavelet transform [J]. Chinese Journal of Geotechnical Engineering, 2005, 27(9): 1055–1059. DOI: 10.3321/j.issn:1000-4548.2005.09.016.
[4]	王志超, 夏虹, 朱少民, 等. 基于改进小波包的堆内构件振动信号去噪方法研究 [J]. 应用科技, 2018, 46(6): 74–79. DOI: 10.11991/yykj.201804005. WANG Z C, XIA H, ZHU S M, et al. Research on vibration signal de-noising method of PWR internals based on improved wavelet packet [J]. Applied Science and Technology, 2018, 46(6): 74–79. DOI: 10.11991/yykj.201804005.
[5]	马宏伟, 张大伟, 曹现刚, 等. 基于EMD的振动信号去噪方法研究 [J]. 振动与冲击, 2016, 35(22): 38–40. DOI: 10.13465/j.cnki.jvs.2016.22.006. MA H W, ZHANG D W, CAO X G, et al. Vibration signal de-noising method based on empirical mode decomposition [J]. Journal of Vibration and Shock, 2016, 35(22): 38–40. DOI: 10.13465/j.cnki.jvs.2016.22.006.
[6]	曹莹, 段玉波, 刘继承, 等. 多尺度形态滤波模态混叠抑制方法 [J]. 电机与控制学报, 2016, 20(9): 110–116. DOI: 10.15938/j.emc.2016.09.016. CAO Y, DUAN Y B, LIU J C, et al. Multi-scale morphological filtering method for mode mixing suppression [J]. Electric Machines and Control, 2016, 20(9): 110–116. DOI: 10.15938/j.emc.2016.09.016.
[7]	WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1–41. DOI: 10.1142/S1793536909000047.
[8]	李晓斌. HHT中EMD方法正交性的研究[D]. 昆明: 昆明理工大学, 2010: 27−45.
[9]	司守奎, 孙兆亮, 数学建模算法与应用[M]. 北京: 国防工业出版社, 2017: 231−239.
[10]	LIU B, FU A Q, YAO Z G, et al. SO₂, Concentration retrieval algorithm using EMD and PCA with application in CEMS based on UV-DOAS [J]. Optik-International Journal for Light and Electron Optics, 2018, 158: 273–282. DOI: 10.1016/j.ijleo.2017.12.057.
[11]	JAVED E, FAYE I, MALIK A S, et al. Removal of BCG artefact from concurrent fMRI-EEG recordings based on EMD and PCA [J]. Journal of Neuroscience Methods, 2017, 291: 150–165. DOI: 10.1016/j.jneumeth.2017.08.020.
[12]	MACKIEWICZ A, RATAJCZAK W. Principal components analysis (PCA) [J]. Computers & Geosciences, 1993, 19(3): 303–342. DOI: 10.1016/0098-3004(93)90090-R.
[13]	王志亮, 陈贵豪, 黄佑鹏. EEMD修正爆破加速度零漂信号中的最优白噪声系数 [J]. 爆炸与冲击, 2019, 39(8): 084201. DOI: 10.11883/bzycj-2019-0154. WANG Z L, CHEN G H, HUANG Y P. Optimal white noise coefficient in EEMD corrected zero drift signal of blasting acceleration [J]. Explosion and Shock Waves, 2019, 39(8): 084201. DOI: 10.11883/bzycj-2019-0154.
[14]	胡厅. 机械系统多点耦合非线性振动信号降噪方法研究[D]. 长沙: 湖南科技大学, 2016: 8−10.
[15]	韩亮, 刘殿书, 辛崇伟, 等. 深孔台阶爆破近区振动信号趋势项去除方法 [J]. 爆炸与冲击, 2018, 38(5): 1006–1012. DOI: 10.11883/bzycj-2016-0194. HAN L, LIU D S, XIN C W, et al. A method to remove the trend term of vibration signal near the deep hole step blasting [J]. Explosion and Shock Waves, 2018, 38(5): 1006–1012. DOI: 10.11883/bzycj-2016-0194.
[16]	钟建军, 宋健, 由长喜, 等. 基于信噪比评价的阈值优选小波去噪法 [J]. 清华大学学报(自然科学版), 2014, 54(2): 259–263. DOI: 10.16511/j.cnki.qhdxxb.2014.02.022. ZHONG J J, SONG J, YOU C X, et al. Wavelet de-noising method with threshold selection rules based on SNR evaluations [J]. Journal of Tsinghua University (Science & Technology), 2014, 54(2): 259–263. DOI: 10.16511/j.cnki.qhdxxb.2014.02.022.
[17]	司祯祯. 傅里叶变换与小波变换在信号去噪中的应用 [J]. 电子设计工程, 2011, 19(4): 155–157. DOI: 10.3969/j.issn.1674-6236.2011.04.045. SI Z Z. Application of Fourier transform and wavelet transform in signal de-noising [J]. Electronic Design Engineering, 2011, 19(4): 155–157. DOI: 10.3969/j.issn.1674-6236.2011.04.045.
[18]	张声辉, 刘连生, 钟清亮, 等. 露天边坡爆破地震波能量分布特征研究 [J]. 振动与冲击, 2019, 38(7): 224–232. DOI: 10.13465/j.cnki.jvs.2019.07.032. ZHANG S H, LIU L S, ZHONG Q L, et al. Energy distribution characteristics of blast seismic wave on open pit slope [J]. Journal of Vibration and Shock, 2019, 38(7): 224–232. DOI: 10.13465/j.cnki.jvs.2019.07.032.
[19]	岳相臣. 经验模态分解算法应用研究[D]. 西安: 西安电子科技大学, 2013:17−19.
[20]	HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings A, 1998, 454(1971): 903–995. DOI: 10.1098/rspa.1998.0193.
[21]	KRISHNA E H, SIVANI K, REDDY K A. On the use of EMD based adaptive filtering for OFDM channel estimation [J]. AEU-International Journal of Electronics and Communications, 2018, 83: 492–500. DOI: 10.1016/j.aeue.2017.11.002.
[22]	CHEN B, YU S Y, YU Y, et al. Nonlinear active noise control system based on correlated EMD and Chebyshev filter [J]. Mechanical Systems and Signal Processing, 2019, 130: 74–86. DOI: 10.1016/j.ymssp.2019.04.059.