回转体高速倾斜入水的流场特性及结构响应

高英杰; 孙铁志; 张桂勇; 尤天庆; 殷志宏; 宗智

doi:10.11883/bzycj-2020-0014

回转体高速倾斜入水的流场特性及结构响应

doi: 10.11883/bzycj-2020-0014

高英杰^1,,
孙铁志^{1, 2, ,},
张桂勇^{1, 2, 3},
尤天庆⁴,
殷志宏¹,
宗智^{1, 2, 3}

1.
大连理工大学船舶工程学院辽宁省深海浮动结构工程实验室，辽宁大连 116024
2.
大连理工大学工业装备结构分析国家重点实验室，辽宁大连 116024
3.
高新船舶与深海开发装备协同创新中心，上海 200240
4.
北京宇航系统工程研究所，北京 100076

基金项目: 国家自然科学基金（51639003，51709042）；中央高校基本科研业务费专项（DUT2017TB05）；中国博士后科学基金（2018M631791，2019T120211）；工信部高技术船舶科研项目（2017-614）；辽宁省自然科学基金（20180550619）；辽宁省“兴辽英才计划”（XLYC1908027）；海洋工程国家重点实验室开放基金（1803）

详细信息

作者简介:
高英杰（1994－　），男，硕士研究生，yingjie_gao@foxmail.com

通讯作者:
孙铁志（1986－　），男，博士，副教授，suntiezhi@dlut.edu.cn

中图分类号: O352
计量
- 文章访问数: 1401
- HTML全文浏览量: 754
- PDF下载量: 87
- 被引次数: 0
出版历程
- 收稿日期: 2020-01-13
- 修回日期: 2020-05-27
- 刊出日期: 2020-12-05

Flow characteristics and structure response of high-speed oblique water-entry for a revolution body

GAO Yingjie^1
,,
SUN Tiezhi^{1, 2
, ,},
ZHANG Guiyong^{1, 2, 3},
YOU Tianqing⁴,
YIN Zhihong¹,
ZONG Zhi^{1, 2, 3}

1.
Liaoning Engineering Laboratory for Deep-Sea Floating Structures, School of Naval Architecture,Dalian University of Technology, Dalian 116024, Liaoning, China
2.
State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology, Dalian 116024, Liaoning, China
3.
Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
4.
Beijing Aerospace System Engineering Research Institute, Beijing 100076, China

摘要

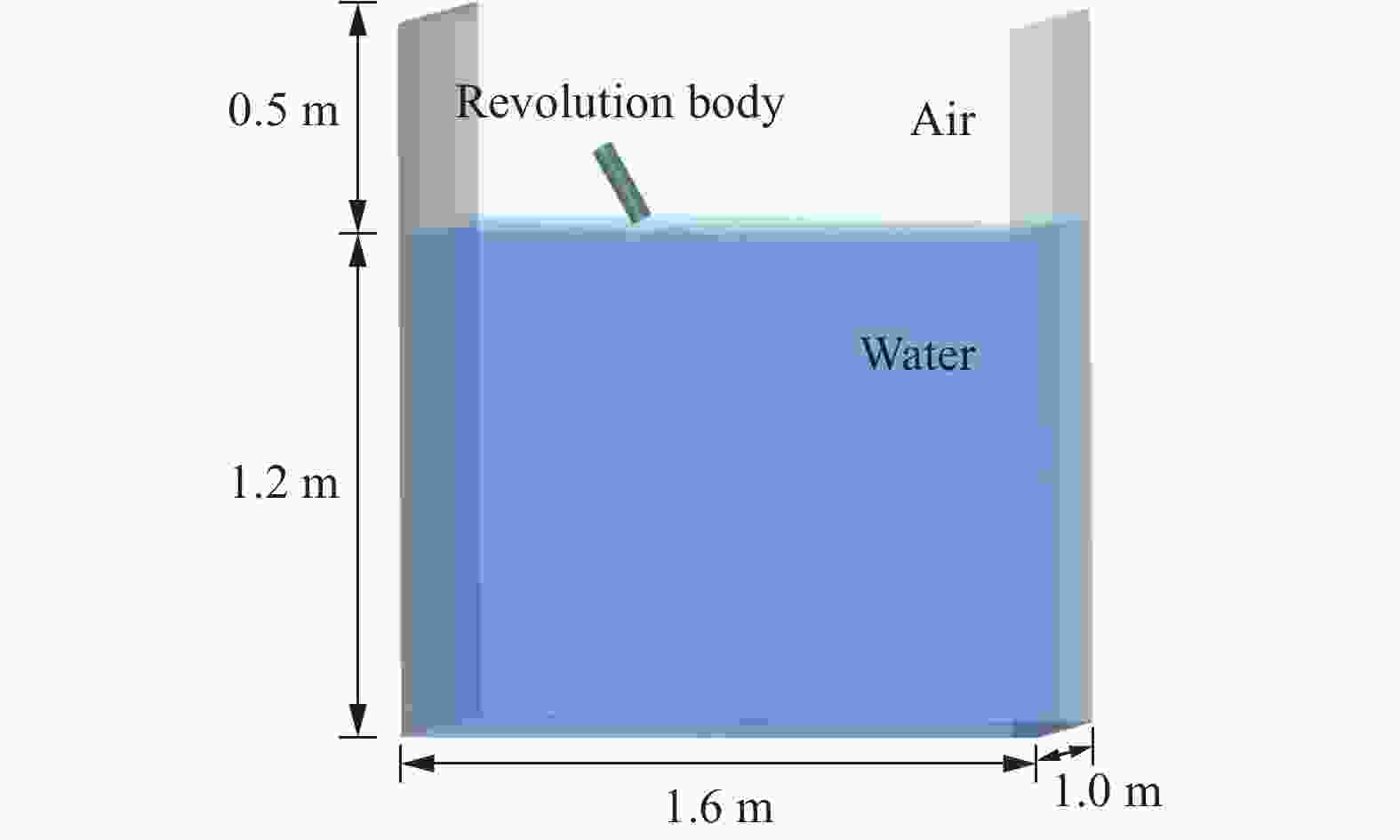
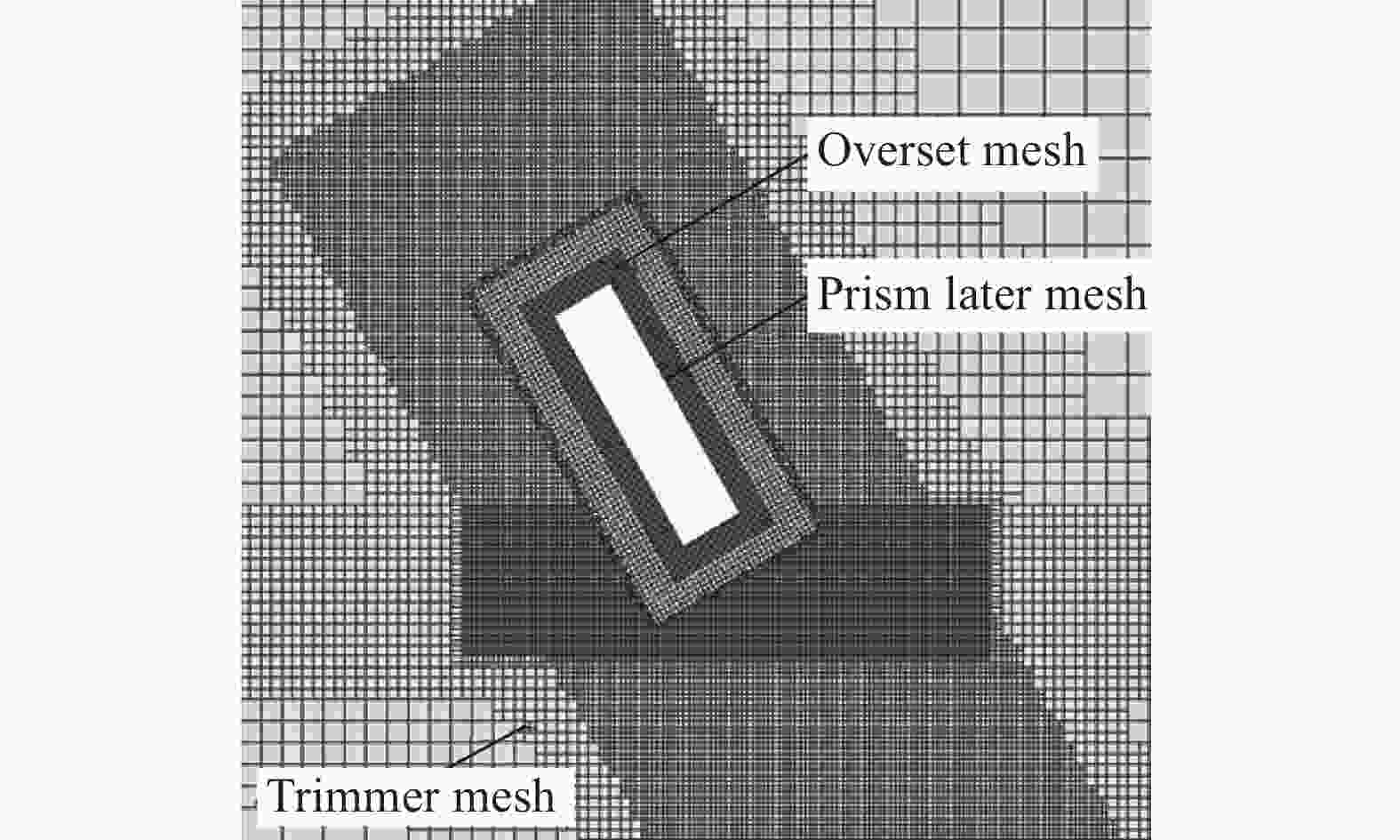
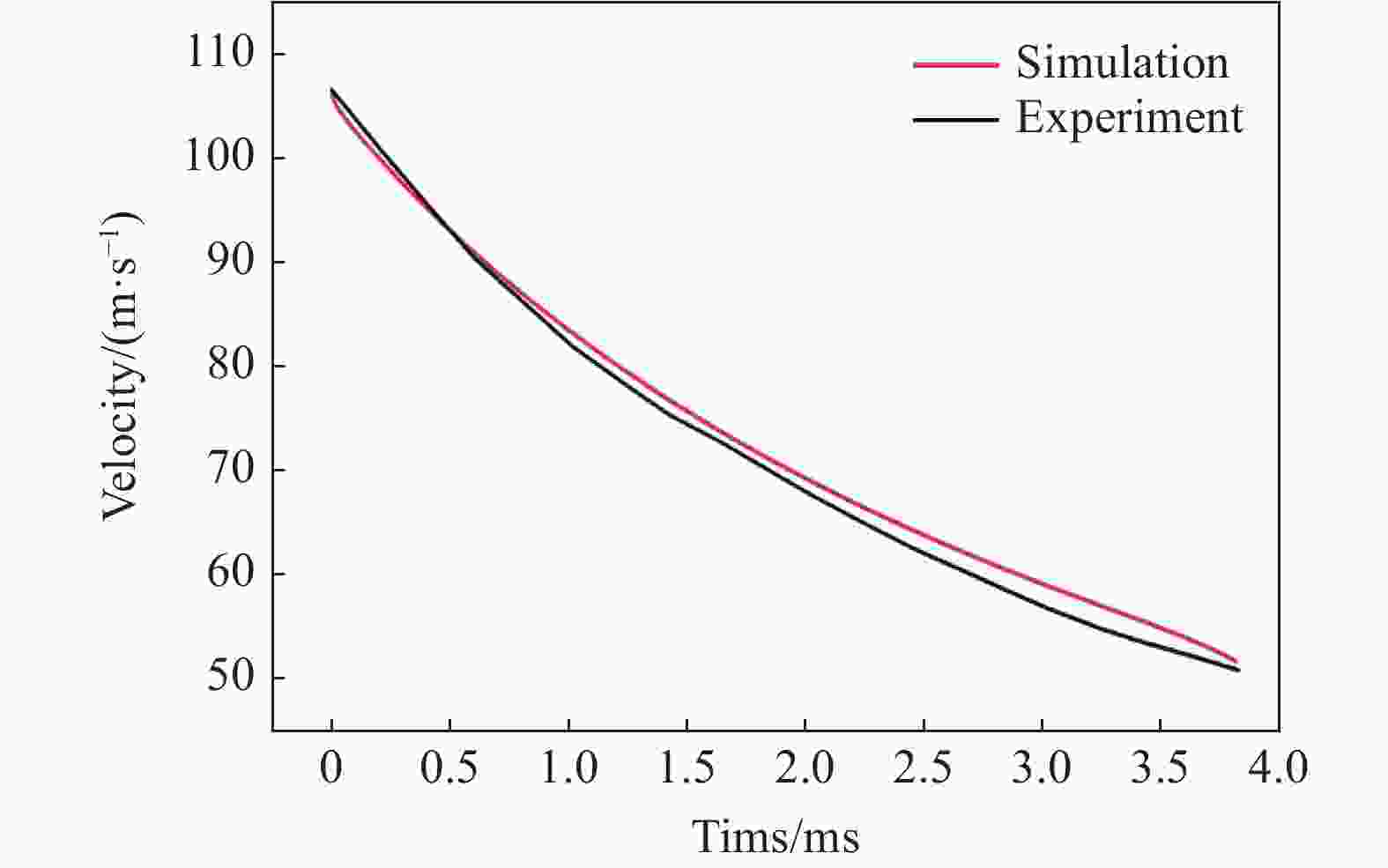
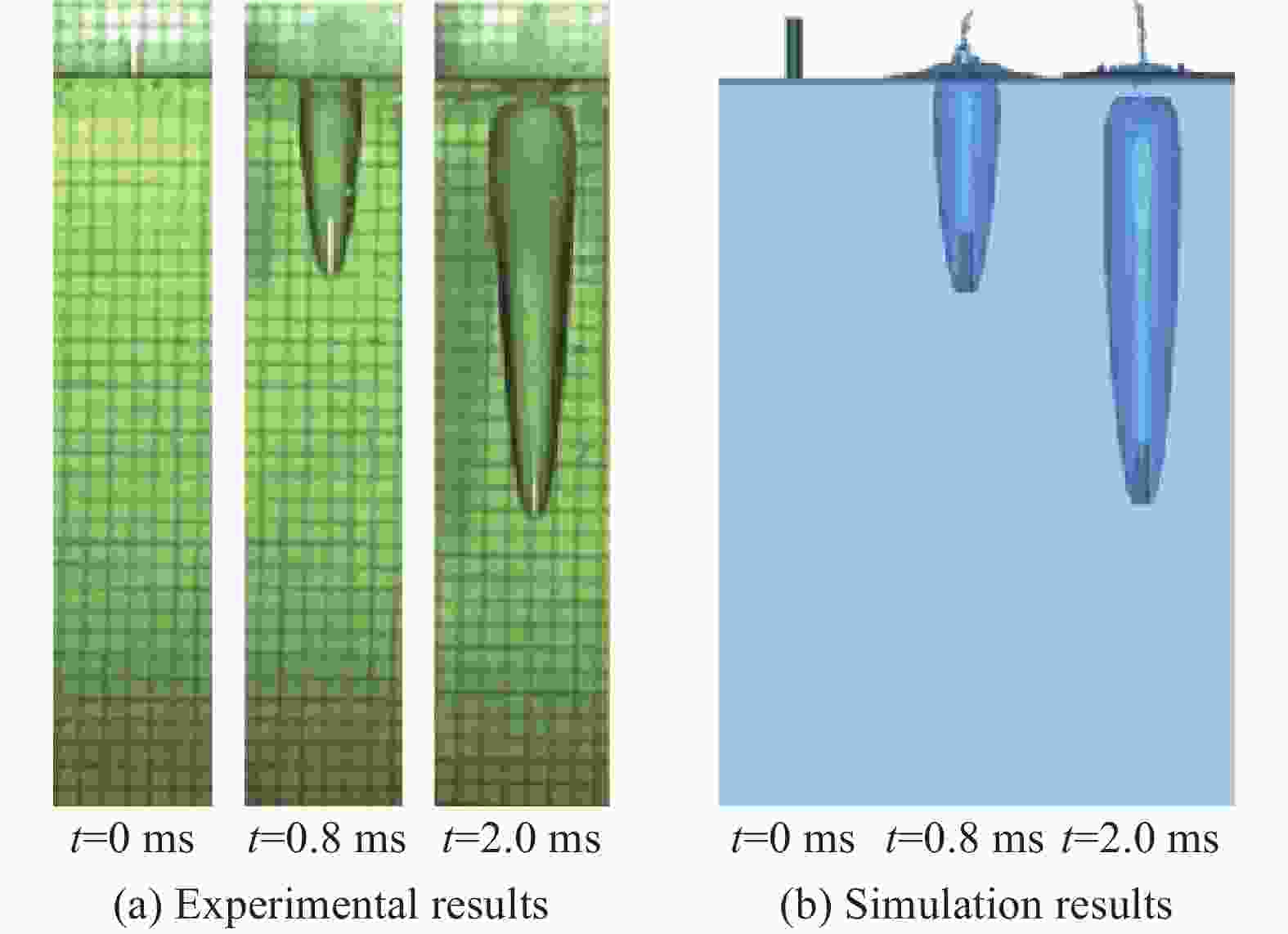
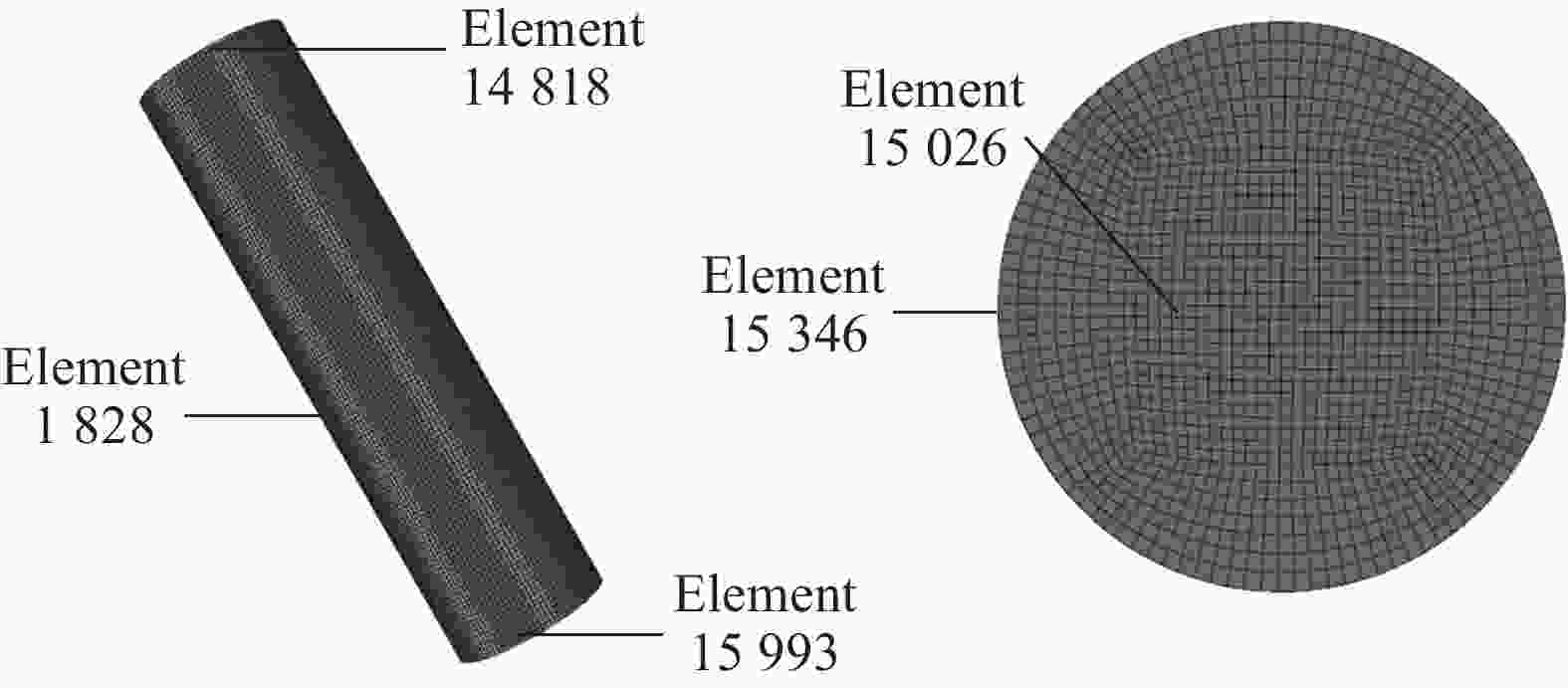
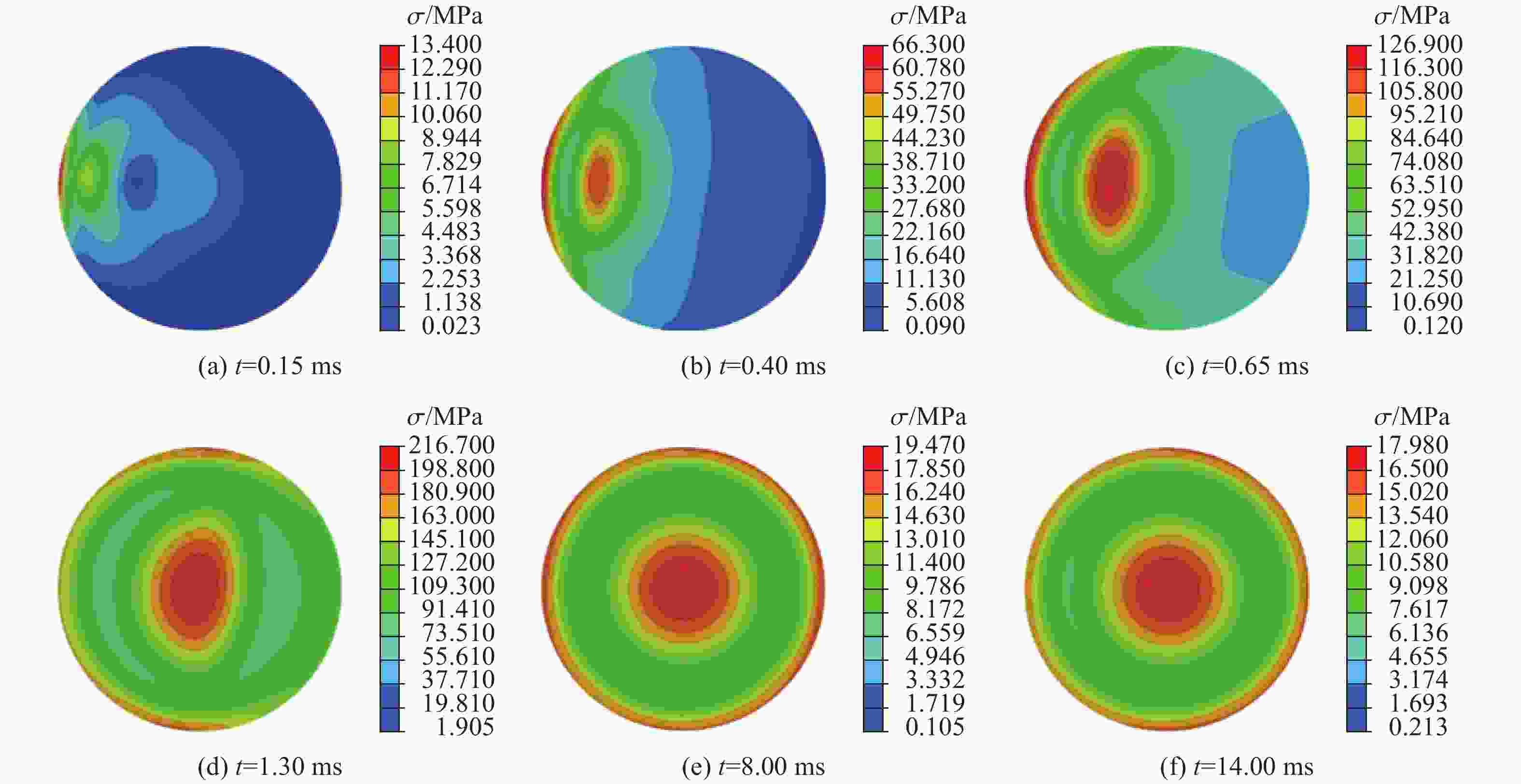
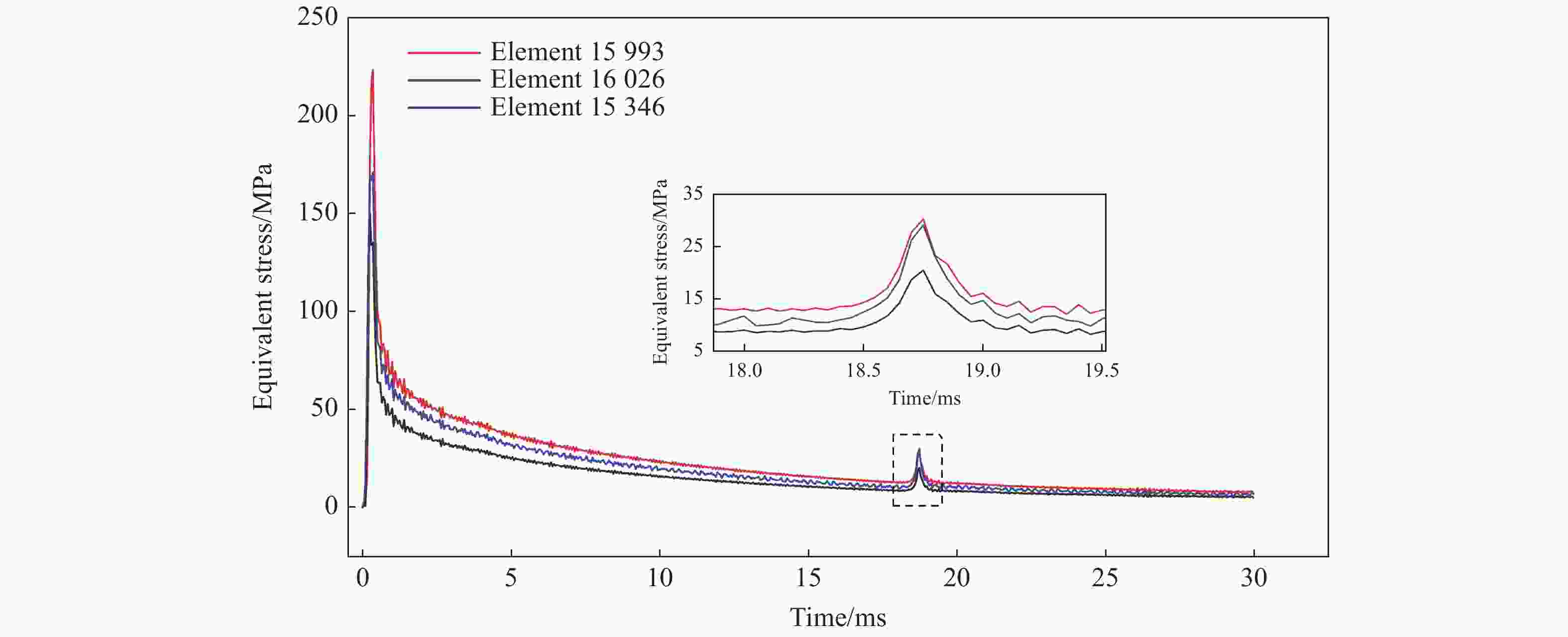
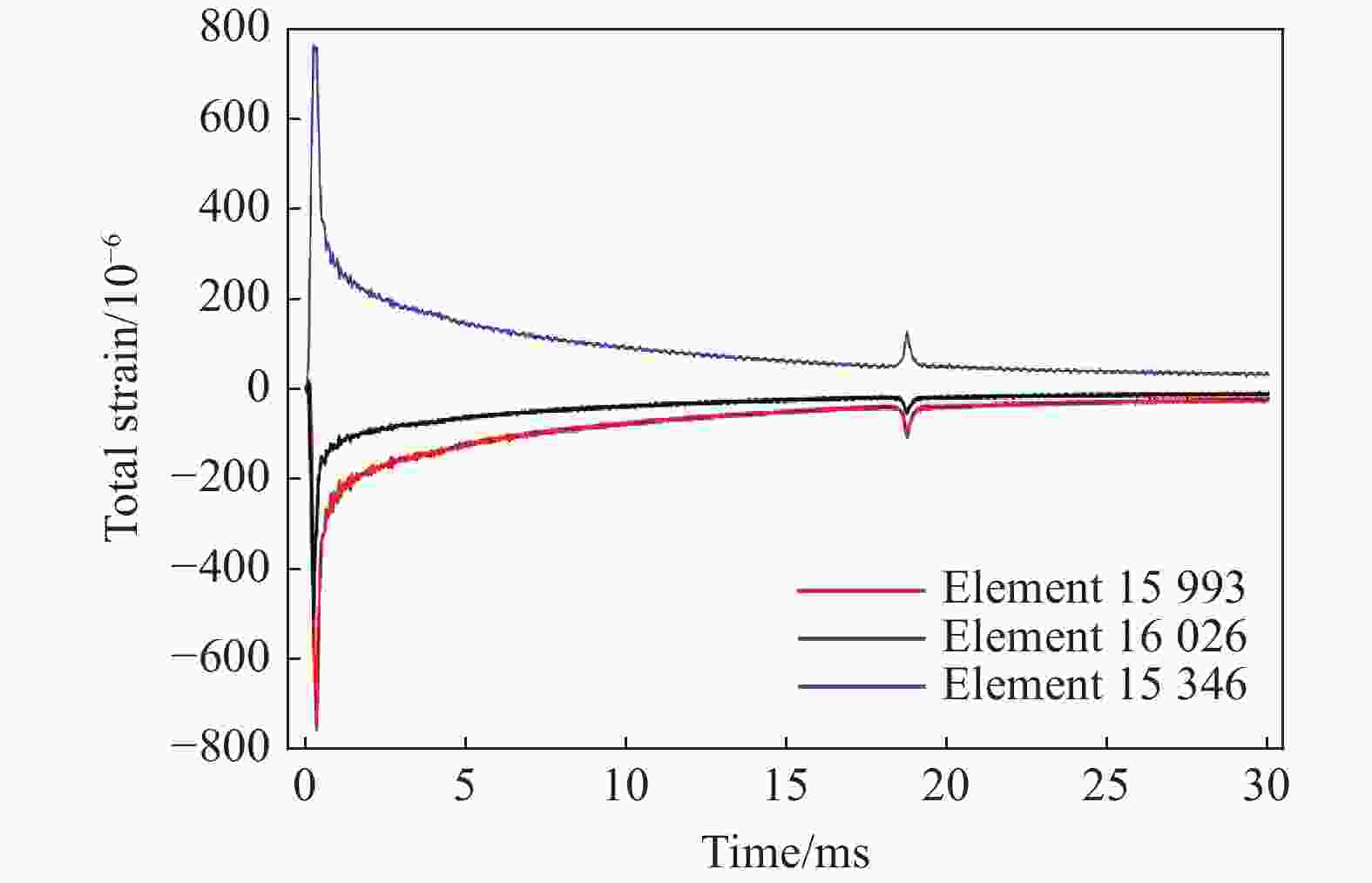
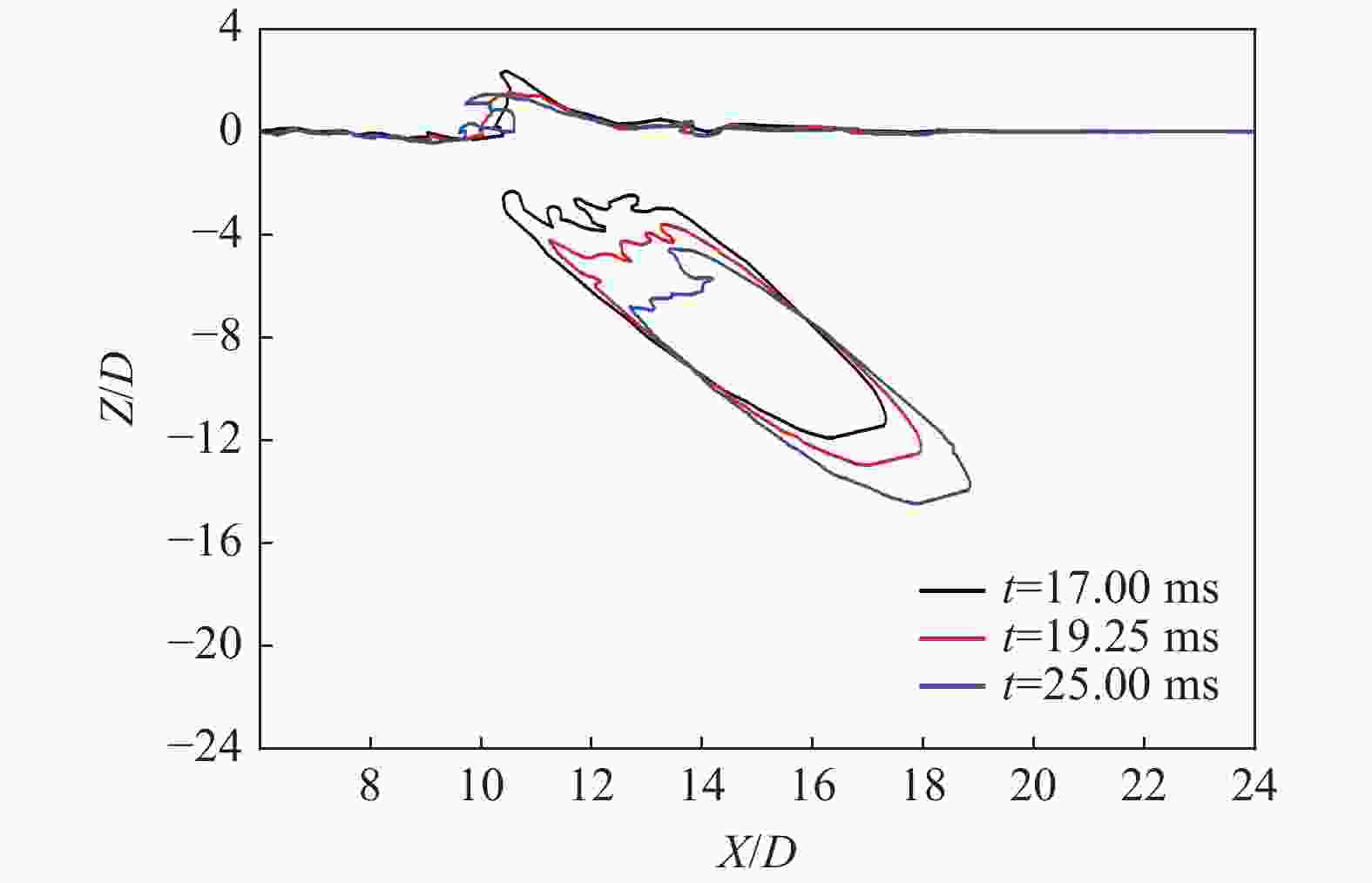
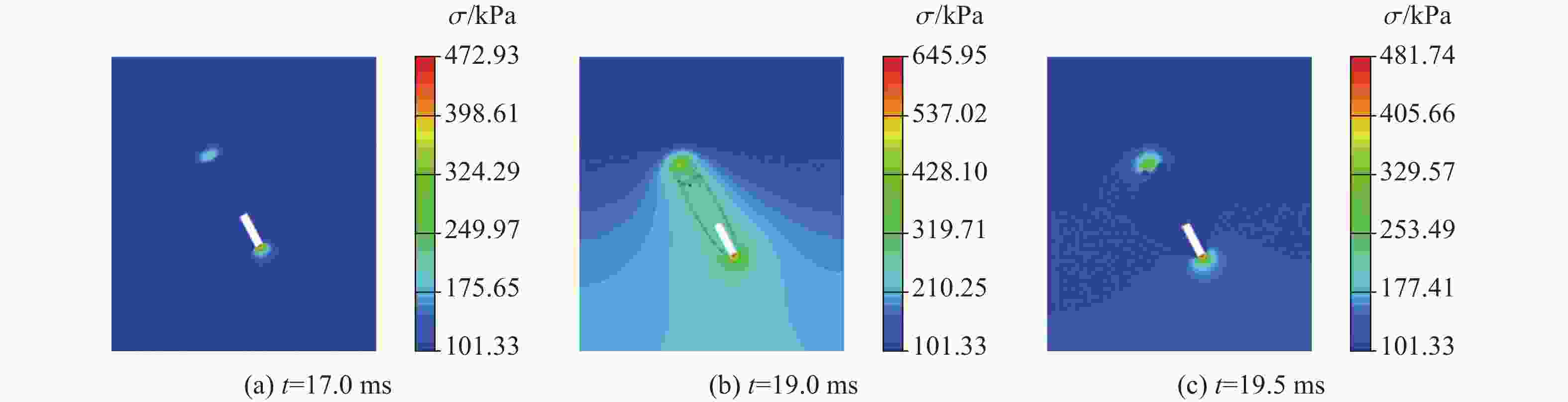
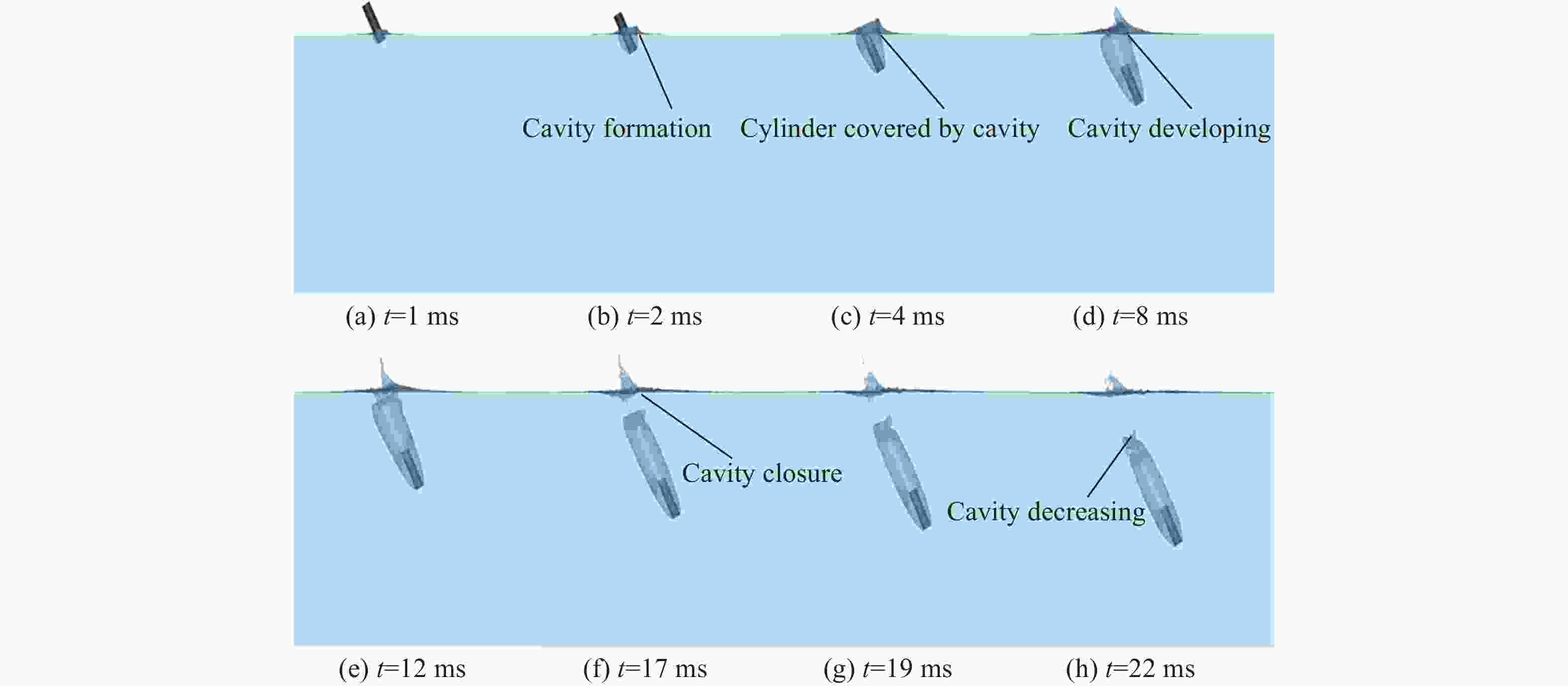
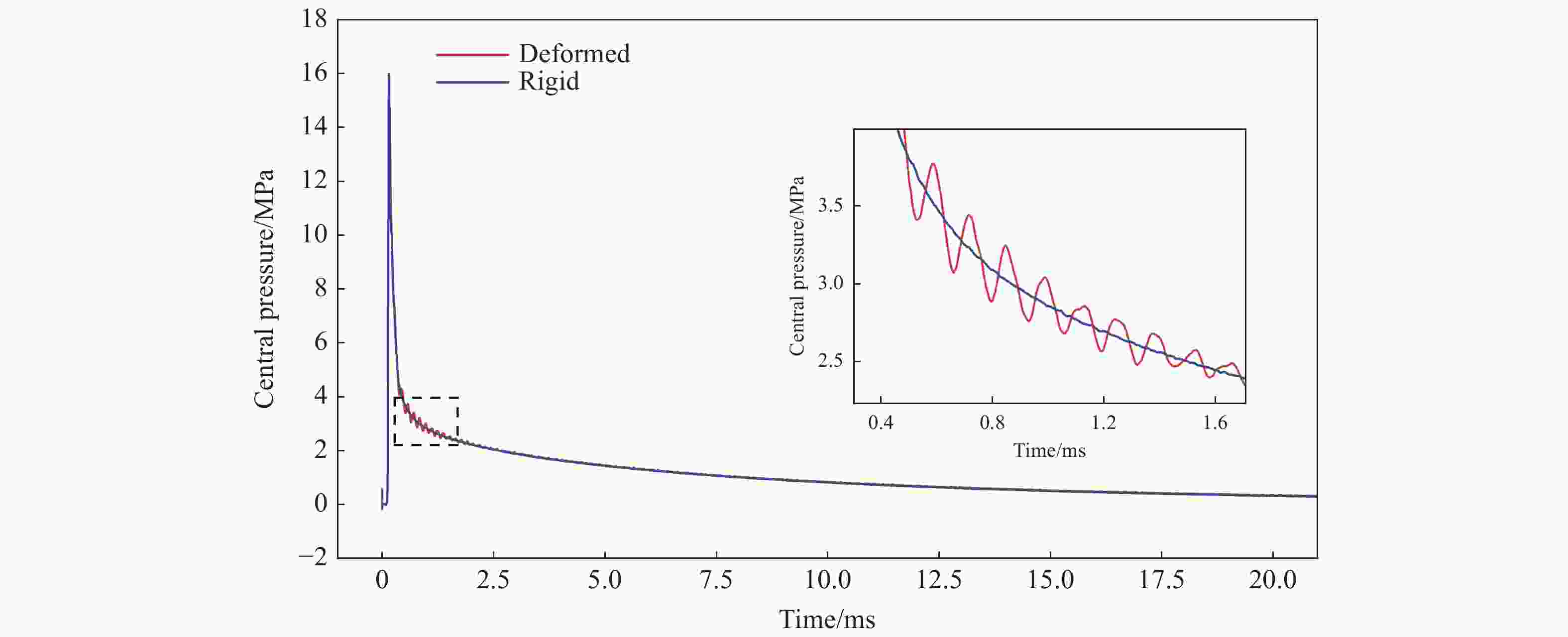
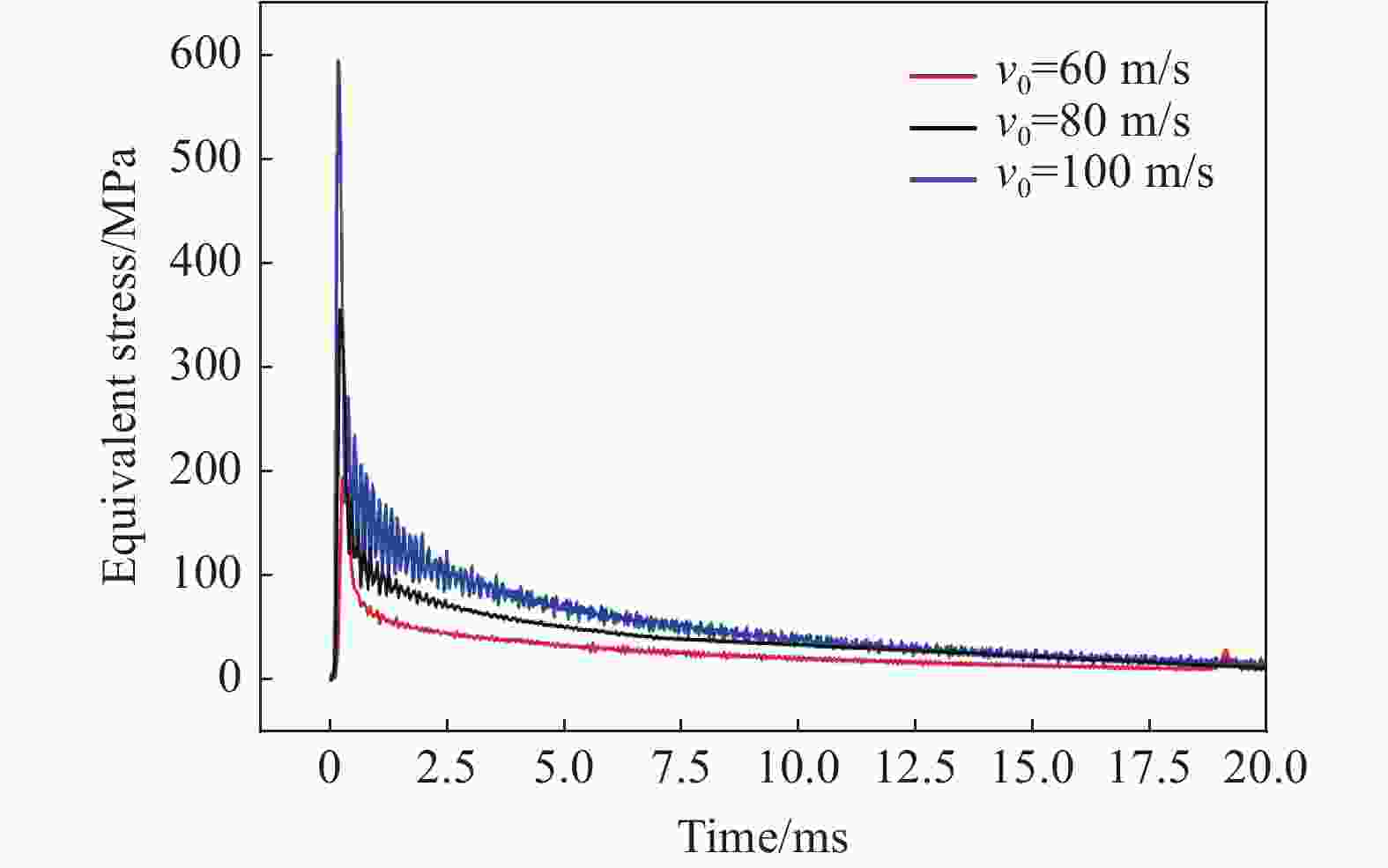
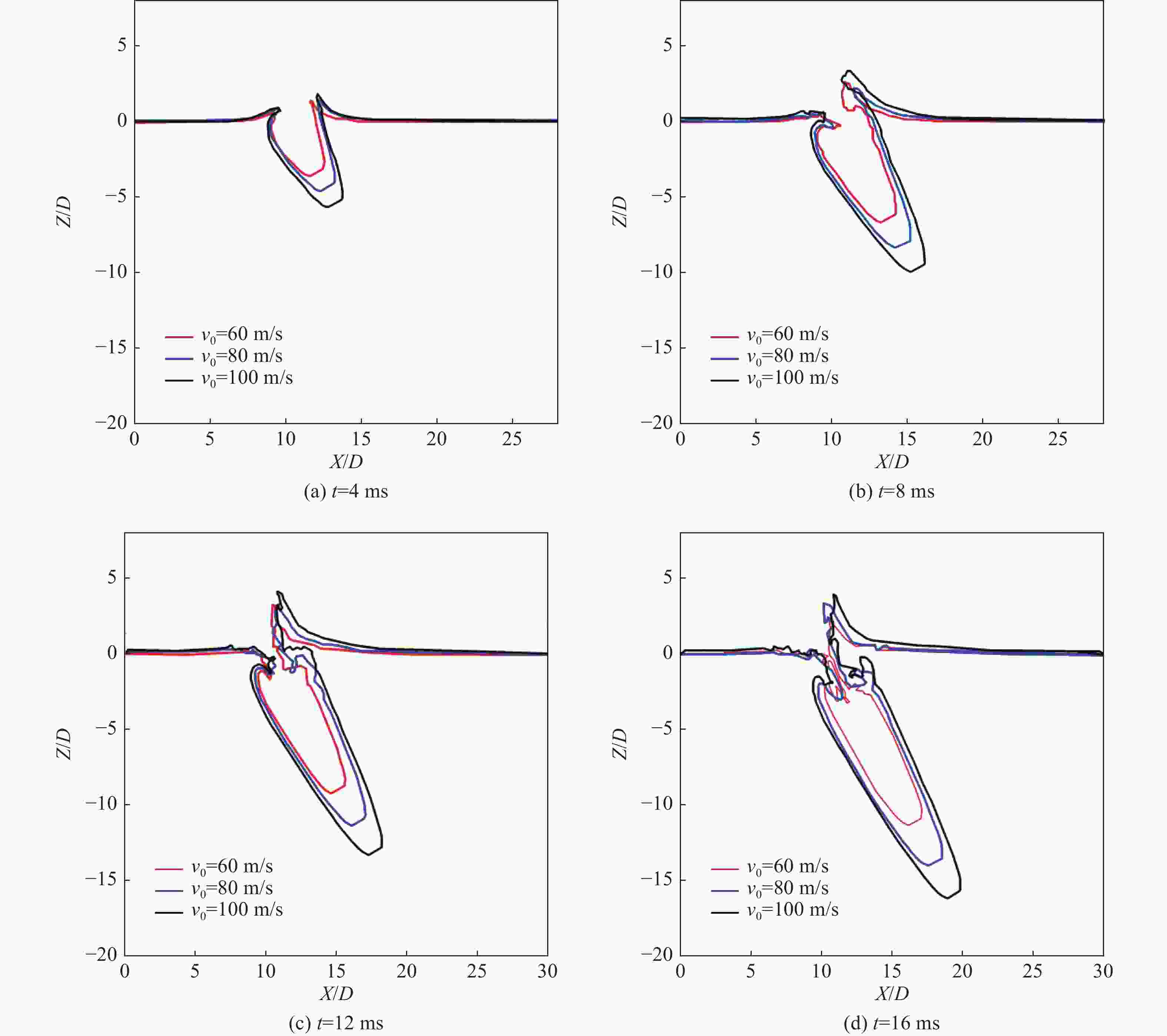
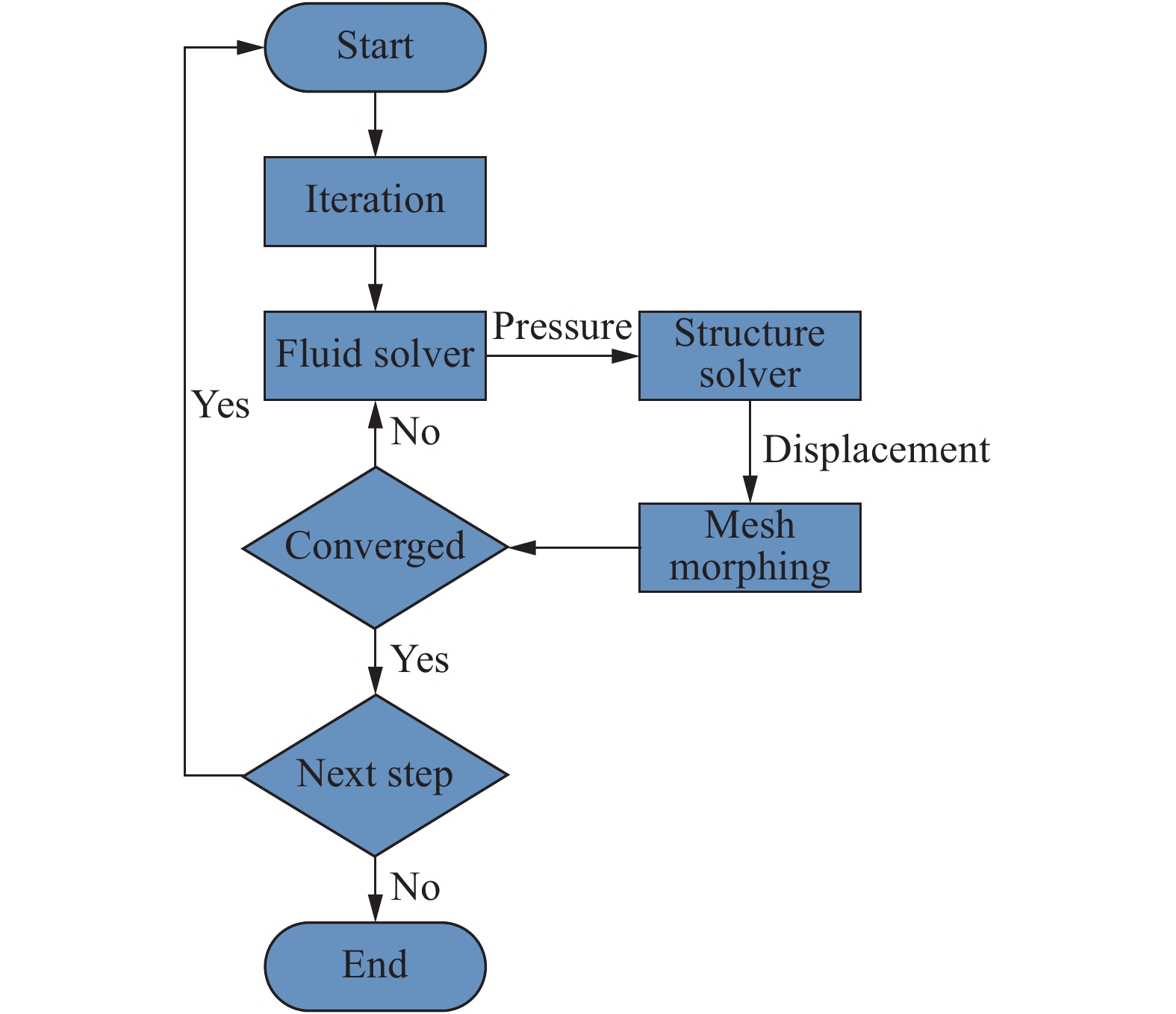
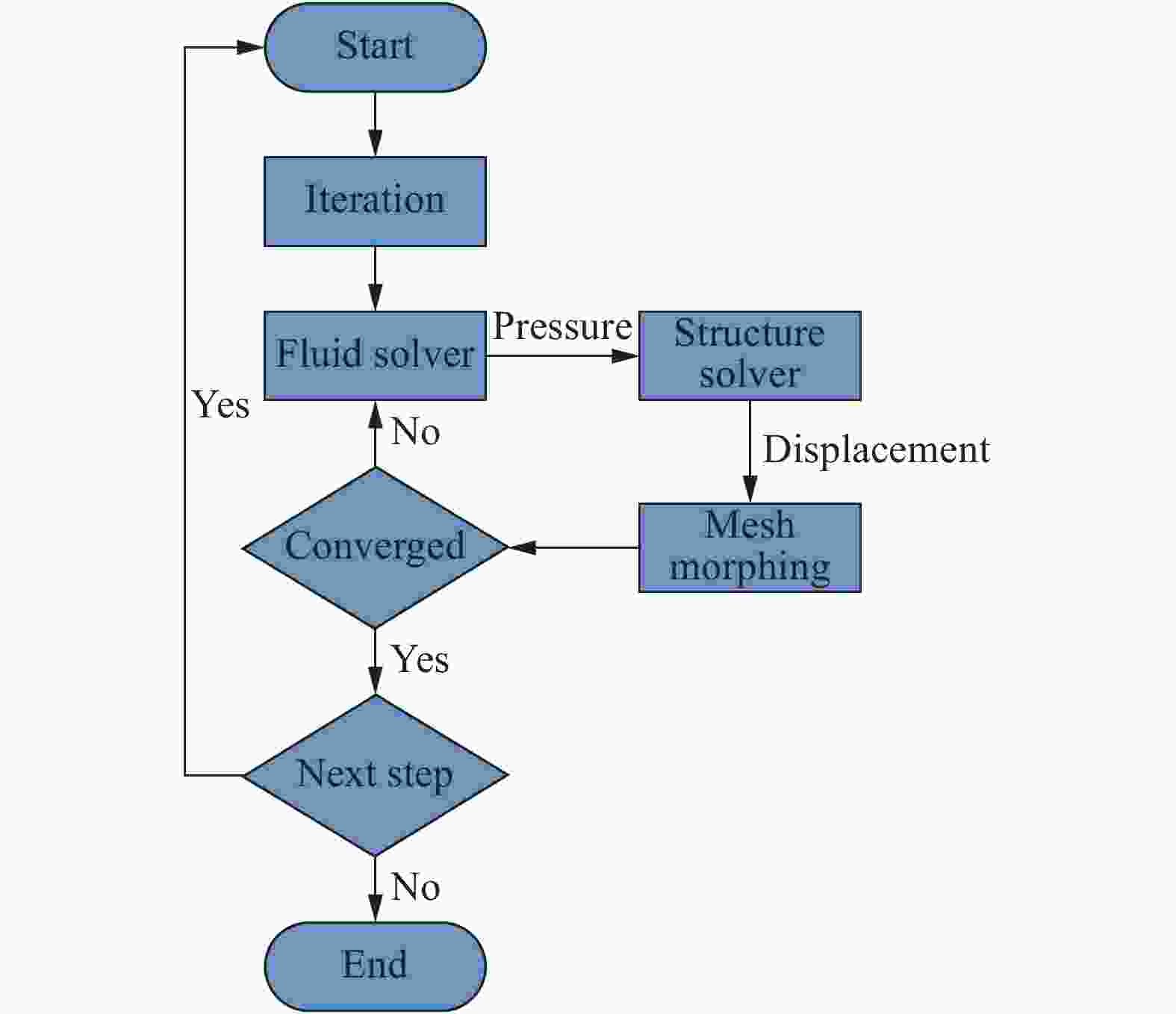
摘要: 回转体高速入水过程涉及液体和固体的耦合作用，是一个复杂的非线性、非定常过程。为研究回转体高速入水的结构动响应及流场演变规律，本文中基于STAR-CCM+和ABAQUS平台，建立了回转体高速入水的双向流固耦合数值模型，开展了不同入水速度的回转体高速倾斜入水流固耦合数值计算。结果表明：数值计算的入水速度、位移曲线和空泡形态与实验结果良好吻合，验证了流固耦合方法的有效性；回转体倾斜高速入水的载荷先集中在触水部分边缘处，后集中于回转体底部中心处；流固耦合方法的入水冲击载荷峰值小于刚体的，弹性回转体的载荷曲线产生明显波动；撞水阶段，回转体空泡呈现不对称形态，随着入水加深，空泡不对称性变弱；入水速度60 m/s下，空泡发生表面闭合，回转体入水初速度越快，空泡表面闭合越晚；冲击载荷与入水速度有关，入水速度越大，峰值出现越早，震荡越明显，速度超过100 m/s时，回转体产生塑性形变。
- 回转体 /
- 高速入水 /
- 流固耦合 /
- 流场 /
- 载荷
Abstract: The high-speed water-entry process of a revolution body involves fluid and structure interaction, which is a complex nonlinear and unsteady process. The revolution body with high speed is subjected to extreme impact load at the moment of hitting water surface which would cause great deformation or even damage to the structure. In order to investigate the physical understanding of the structural strength of revolution bodies and the mechanism of the cavity dynamics during high-speed water-entry process, a fluid-structure interaction (FSI) model based on a co-simulation progress between STAR-CCM+ and ABAQUS was adopted. The model performed a two-way interaction analysis which can consider the influence of the deformation of structure to fluid into. In the form of CFD analysis, a three-dimensional simulation with a six-degree-of-freedom model was carried out, in which the Shear Stress Transfer (SST) turbulence model and the volume of fluid (VOF) technique were used for turbulence computation and air-liquid interface tracking, respectively. In the part of FEM research, the shell mesh form with a whole Johnson-Cook material model was implemented to give a full consideration of deformation process and the accuracy of structure computation, which can effectively reflect the plastic deformation of structure. Firstly, a comparison between FSI result and experimental result of the high-speed water-entry process was conducted. The results show that the velocity attenuation, displacement and the cavity features are in good agreement with the experimental result, which proves two-way FSI method can be effectively applied into the research of high-speed water-entry problem. Then a numerical simulation of revolution body oblique water-entry with different velocity was carried out. The results show that the stress initially focuses on the edge of the bottom side of the revolution body, then it transports to the central area, remaining steady in the end. Compared with the results of rigid body, the peak value of impact load of the flexible body appears smaller due to the repeated deformation for buffer, which also causes the fluctuation of the load curve. After the initial water impacting, the cavity presents an asymmetric shape. As water-entry time increases, the asymmetry of cavity becomes weaker. In the process of 60 m/s oblique water-entry, surface closure of the cavity occurs. With the increase of water-entry velocity, the time of cavity surface closure takes longer. The peak value of the impact load whose period is quite short appears immediately at very beginning of water-entry process. After entering the water surface, the impact load of the revolution body decreases dramatically and rapidly and fluctuates slightly. The peak value of the impact load is related to water-entry velocity. The higher the velocity is, the earlier peak value of the impact load occurs and more obviously it fluctuates. As water-entry velocity exceeds 100 m/s, plastic deformation appears in the central area of bottom of revolution body.
- revolution body /
- high-speed water entry /
- fluid-structure interaction /
- fluid field /
- load

HTML全文

图 1 双向耦合求解过程

Figure 1. Computing process of fluid-structure interaction method

下载: 全尺寸图片幻灯片

图 2 计算域

Figure 2. Computational domain

下载: 全尺寸图片幻灯片

图 3 流体网格模型

Figure 3. Mesh of fluid domain

下载: 全尺寸图片幻灯片

图 4 速度衰减曲线

Figure 4. Velocity attenuation curves

下载: 全尺寸图片幻灯片

图 5 侵蚀位移曲线

Figure 5. Erosion displacement curves

下载: 全尺寸图片幻灯片

图 6 不同时刻的空泡形态

Figure 6. Cavity features at different times

下载: 全尺寸图片幻灯片

图 7 回转体轴向、底部径向的单元分布

Figure 7. Element distribution of revolution body

下载: 全尺寸图片幻灯片

图 8 回转体的应力沿轴向分布曲线

Figure 8. Equivalent stress curves of elements along axis

下载: 全尺寸图片幻灯片

图 9 不同时刻回转体底部应力分布

Figure 9. Stress distributions of revolution body bottom at different times

下载: 全尺寸图片幻灯片

图 10 回转体底部的应力沿径向分布曲线

Figure 10. Equivalent stress curves of bottom elements along radius

下载: 全尺寸图片幻灯片

图 11 回转体底部的应变沿径向分布曲线

Figure 11. Strain curves of bottom elements along radius

下载: 全尺寸图片幻灯片

图 12 不同时刻的空泡演变

Figure 12. Cavity features at different times

下载: 全尺寸图片幻灯片

图 13 不同时刻的应力分布

Figure 13. Stress distributions at different times

下载: 全尺寸图片幻灯片

图 14 速度60 m/s倾斜入水的空泡演变

Figure 14. Cavity features for oblique water-entry at v₀=60 m/s

下载: 全尺寸图片幻灯片

图 15 入水速度80 m/s时回转体底部中心点压力曲线

Figure 15. Pressure curve of bottom central point at v₀=80 m/s

下载: 全尺寸图片幻灯片

图 16 速度80 m/s入水时速度曲线

Figure 16. Velocity curves at v₀=80 m/s

下载: 全尺寸图片幻灯片

图 17 归一化的速度衰减曲线

Figure 17. Normalized velocity attenuation curves

下载: 全尺寸图片幻灯片

图 18 回转体中心单元的有效应力曲线

Figure 18. Equivalent stress curves of central elements

下载: 全尺寸图片幻灯片

图 19 空泡形态对比

Figure 19. Comparisons of cavity features

下载: 全尺寸图片幻灯片

表 1 不同入水速度的压力峰值

Table 1. Peak pressures at different initial water entry velocities

入水速度/(m·s⁻¹) 压力峰值/MPa
CFD FSI

60 9.93 9.42
80 16.03 15.59
100 27.92 25.12

下载: 导出CSV

参考文献(24)

[1]	王永虎, 石秀华. 入水冲击问题研究的现状与进展 [J]. 爆炸与冲击, 2008, 28(3): 276–282. DOI: 10.11883/1001-1455(2008)03-0276-07. WANG Y H, SHI X H. Review on research and development of water-entry impact problem [J]. Explosion and Shock Waves, 2008, 28(3): 276–282. DOI: 10.11883/1001-1455(2008)03-0276-07.
[2]	Von KARMAN T H. The impact on seaplane floats during landing [R]. Washington DC: National Advisory Committee on Aeronautics, 1929: 309−313. DOI: 10.1115/1.4023571.
[3]	WAGNER H. Über stoß-und gleitvorgänge an der oberfläche von flüssigkeiten [J]. Zeitschrift für Angewandte Mathematik und Mechanik, 1932, 12(4): 193–215. DOI: 10.1002/zamm.19320120402.
[4]	GAVRILENKO V N, KUBENKO V D. Plane problem of rigid body penetration into a compressible fluid [J]. Soviet Applied Mechanics, 1985, 21(4): 345–352. DOI: 10.1007/BF00886581.
[5]	WORTHINGTON A M, COLE R S. Impact with a liquid surface studied by the aid of instantaneous photography. Paper Ⅱ [J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1900, 194: 175–199. DOI: 10.1098/rsta.1900.0016.
[6]	MAY A. Effect of surface condition of a sphere on its water-entry cavity [J]. Journal of Applied Physics, 1951, 22(10): 1219–1222. DOI: 10.1063/1.1699831.
[7]	MAY A, WOODHULL J C. The virtual mass of a sphere entering water vertically [J]. Journal of Applied Physics, 1950, 21(12): 1285–1289. DOI: 10.1063/1.1699592.
[8]	ABELSON H I. Pressure measurements in the water-entry cavity [J]. Journal of Fluid Mechanics, 1970, 44(1): 129–144. DOI: 10.1017/S0022112070001738.
[9]	PANAHI R. Simulation of water-entry and water-exit problems using a moving mesh algorithm [J]. Journal of Theoretical and Applied Mechanics, 2012, 42(2): 79–92.
[10]	ERFANIAN M R, ANBARSOOZ M, RAHIMI N, et al. Numerical and experimental investigation of a three dimensional spherical-nose projectile water entry problem [J]. Ocean Engineering, 2015, 104: 397–404. DOI: 10.1016/j.oceaneng.2015.05.024.
[11]	NEAVES M D, EDWARDS J R. All-speed time-accurate underwater projectile calculations using a preconditioning algorithm [J]. Journal of Fluids Engineering, 2006, 128(2): 284–296. DOI: 10.1115/1.2169816.
[12]	孙辉, 卢炽华, 何友声. 二维楔形体冲击入水时的流固耦合响应的实验研究 [J]. 水动力学研究与进展, 2003, 18A(1): 104–109. DOI: 10.3969/j.issn.1000-4874.2003.01.018. SUN H, LU C H, HE Y S. Experimental research on the fluid-structure interaction in water entry of 2D elastic wedge [J]. Journal of Hydrodynamics, 2003, 18A(1): 104–109. DOI: 10.3969/j.issn.1000-4874.2003.01.018.
[13]	张伟, 郭子涛, 肖新科, 等. 弹体高速入水特性实验研究 [J]. 爆炸与冲击, 2011, 31(6): 579–584. DOI: 10.11883/1001-1455(2011)06-0579-06. ZHANG W, GUO Z T, XIAO X K, et al. Experimental investigations on behaviors of projectile high-speed water entry [J]. Explosion and Shock Waves, 2011, 31(6): 579–584. DOI: 10.11883/1001-1455(2011)06-0579-06.
[14]	郭子涛, 张伟, 郭钊, 等. 截卵形弹水平入水的速度衰减及空泡扩展特性 [J]. 爆炸与冲击, 2017, 37(4): 727–733. DOI: 10.11883/1001-1455(2017)04-0727-07. GUO Z T, ZHANG W, GUO Z, et al. Characteristics of velocity attenuation and cavity expansion induced by horizontal water-entry of truncated-ogive nosed projectiles [J]. Explosion and Shock Waves, 2017, 37(4): 727–733. DOI: 10.11883/1001-1455(2017)04-0727-07.
[15]	陈诚, 袁绪龙, 党建军, 等. 超空泡航行器20°角倾斜入水冲击载荷特性试验研究 [J]. 兵工学报, 2018, 39(6): 1159–1164. DOI: 10.3969/j.issn.1000-1093.2018.06.016. CHEN C, YUAN X L, DANG J J, et al. Experimental investigation into impact load during oblique water-entry of a supercavitating vehicle at 20° [J]. Acta Armamentarii, 2018, 39(6): 1159–1164. DOI: 10.3969/j.issn.1000-1093.2018.06.016.
[16]	YAN G X, PAN G, SHI Y, et al. Experimental and numerical investigation of water impact on air-launched AUVs [J]. Ocean Engineering, 2018, 167: 156–168. DOI: 10.1016/j.oceaneng.2018.08.044.
[17]	钱铖铖, 余春华, 穆青, 等. 发射速度和发射角度对射弹高速入水流动的影响 [J]. 兵器装备工程学报, 2019, 40(7): 35–39; 50. DOI: 10.11809/bqzbgcxb2019.07.008. QIAN C C, YU C H, MU Q, et al. Numerical research of effects of launch speed and launch angle on water entry of high-speed projectile [J]. Journal of Ordnance Equipment Engineering, 2019, 40(7): 35–39; 50. DOI: 10.11809/bqzbgcxb2019.07.008.
[18]	张佳悦, 李达钦, 吴钦, 等. 航行体回收垂直入水空泡流场及水动力特性研究 [J]. 力学学报, 2019, 51(3): 803–812. DOI: 10.6052/0459-1879-18-364. ZHANG J Y, LI D Q, WU Q, et al. Numerical investigation on cavity structures and hyrodynamics of the vehicle during vertical water-entry [J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(3): 803–812. DOI: 10.6052/0459-1879-18-364.
[19]	何春涛, 王聪, 闵景新, 等. 回转体匀速垂直入水早期空泡数值模拟研究 [J]. 工程力学, 2012, 29(4): 237–243. HE C T, WANG C, MIN J X, et al. Numerical simulation of early air-cavity of cylinder cone with vertical water-entry [J]. Engineering Mechanics, 2012, 29(4): 237–243.
[20]	侯昭, 孙铁志, 张桂勇, 等. 回转体倾斜入水空泡试验及六自由度数值计算研究 [J]. 宇航总体技术, 2017, 1(4): 38–45. HOU Z, SUN T Z, ZHANG G Y, et al. Experimental investigation and 6-DOF simulation of oblique water-entry cavity of revolution body [J]. Astronautical Systems Engineering Technology, 2017, 1(4): 38–45.
[21]	黄志刚, 孙铁志, 杨碧野, 等. 平头锥型回转体高速入水结构强度数值分析 [J]. 爆炸与冲击, 2019, 39(4): 043201. DOI: 10.11883/bzycj-2017-0330. HUANG Z G, SUN T Z, YANG B Y, et al. Numerical analysis on structural strength of a cone-shaped flatted revolution body during high-speed water-entry [J]. Explosion and Shock Waves, 2019, 39(4): 043201. DOI: 10.11883/bzycj-2017-0330.
[22]	陈宇, 曹红松, 王智军, 等. 一种新型防空MEFP的设计与仿真 [J]. 现代防御技术, 2013, 41(2): 202–206; 211. DOI: 10.3969/j.issn.1009-086x.2013.02.037. CHEN Y, CAO H S, WANG Z J, et al. New type of air defense MEFP [J]. Modern Defense Technology, 2013, 41(2): 202–206; 211. DOI: 10.3969/j.issn.1009-086x.2013.02.037.
[23]	AGMELL M, AHADI A, STÅHL J E. A numerical and experimental investigation of the deformation zones and the corresponding cutting forces in orthogonal cutting [J]. Advanced Materials Research, 2011, 223: 152–161. DOI: 10.4028/www.scientific.net/AMR.223.152.
[24]	CHEN T, HUANG W, ZHANG W, et al. Experimental investigation on trajectory stability of high-speed water entry projectiles [J]. Ocean Engineering, 2019, 175: 16–24. DOI: 10.1016/j.oceaneng.2019.02.021.