Blast resistance property of concrete shear wall with single-side steel plate
-
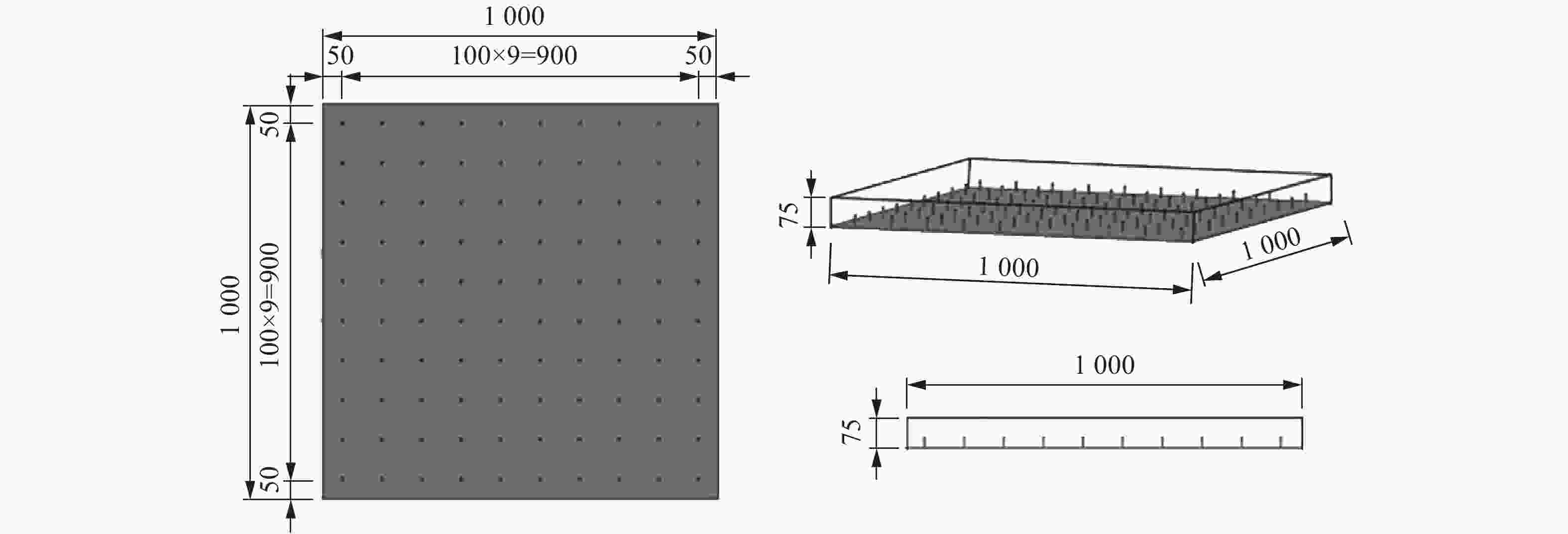
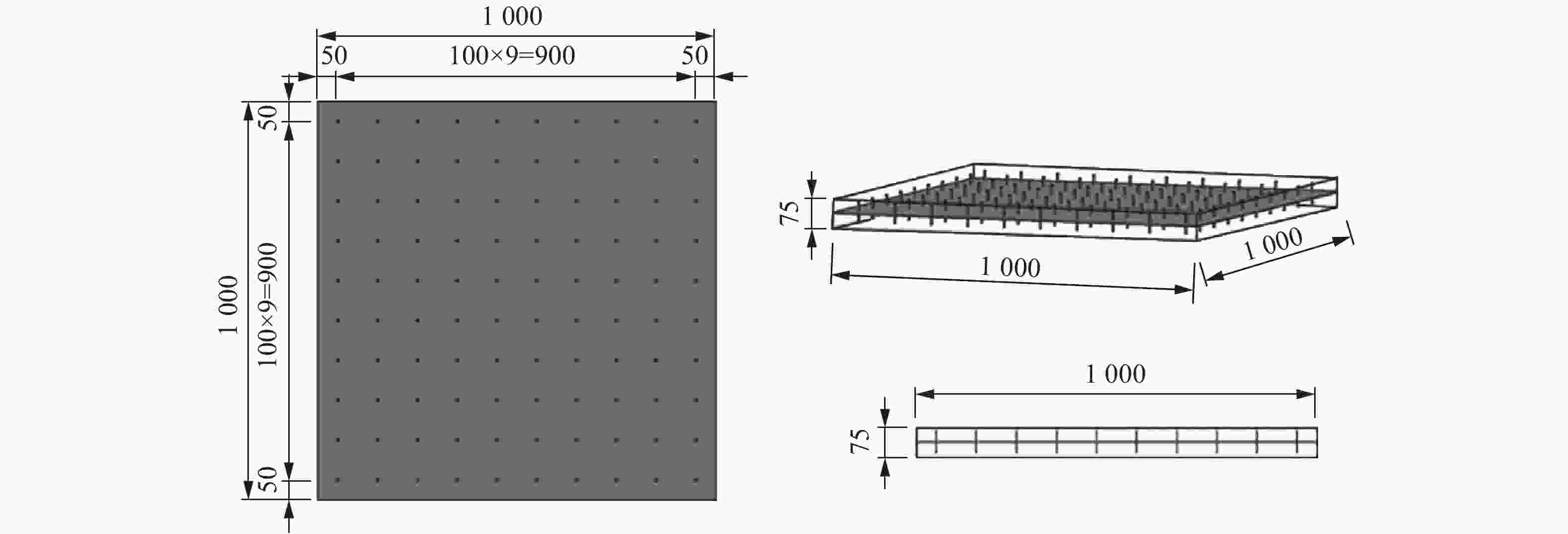
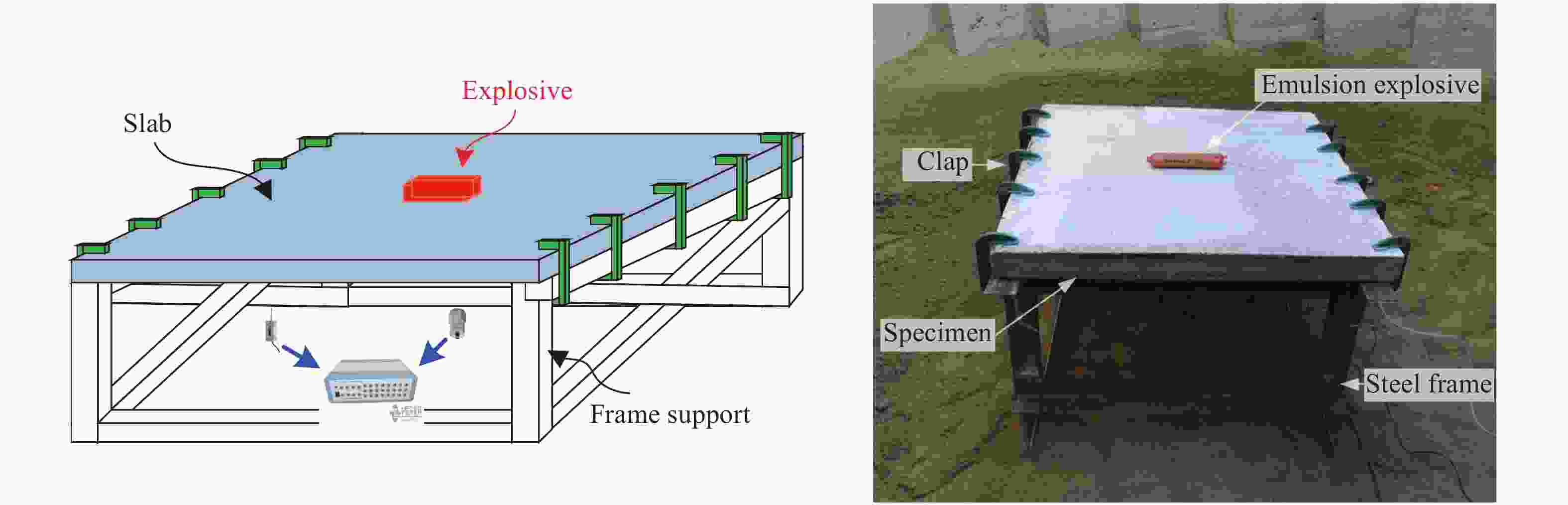
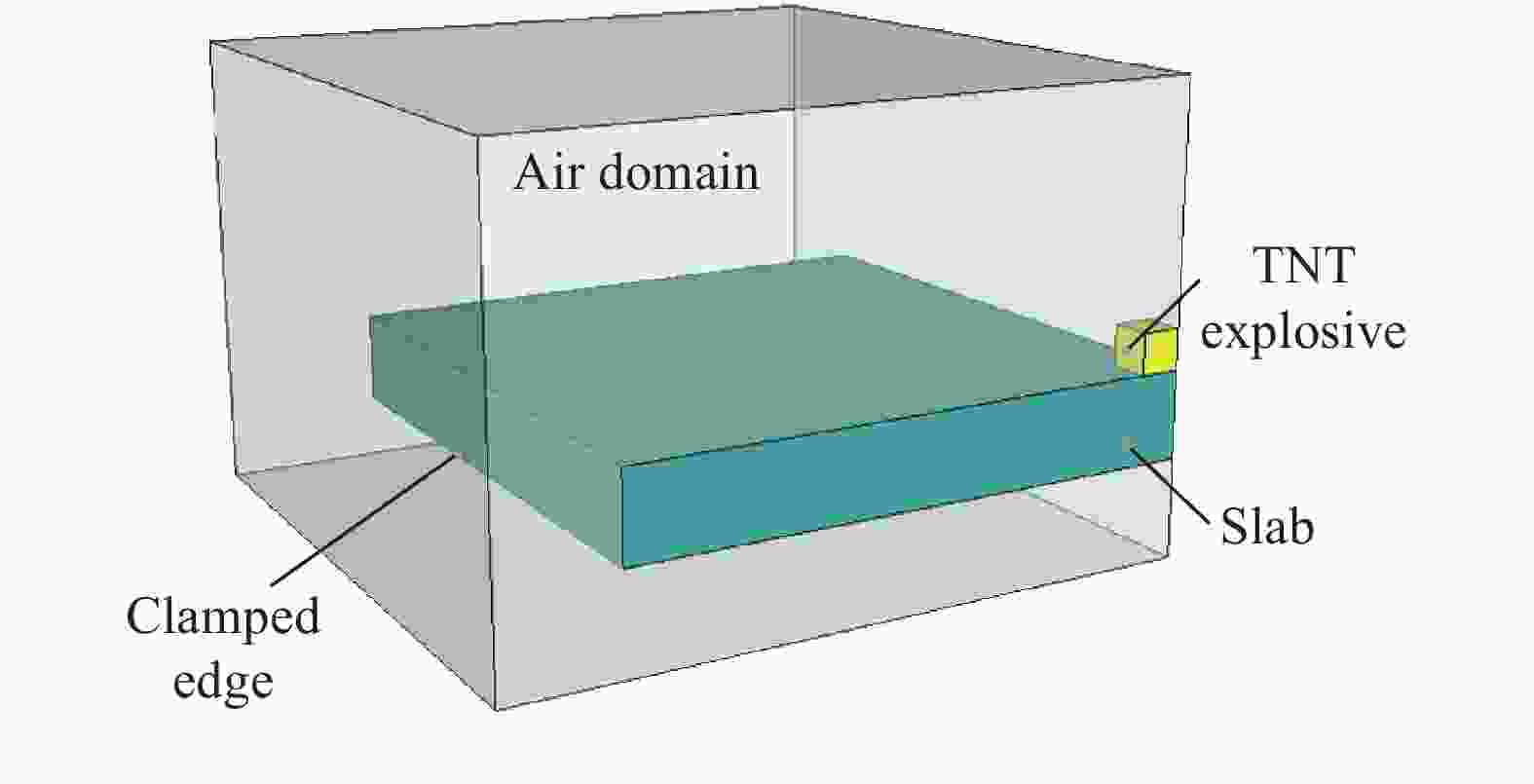
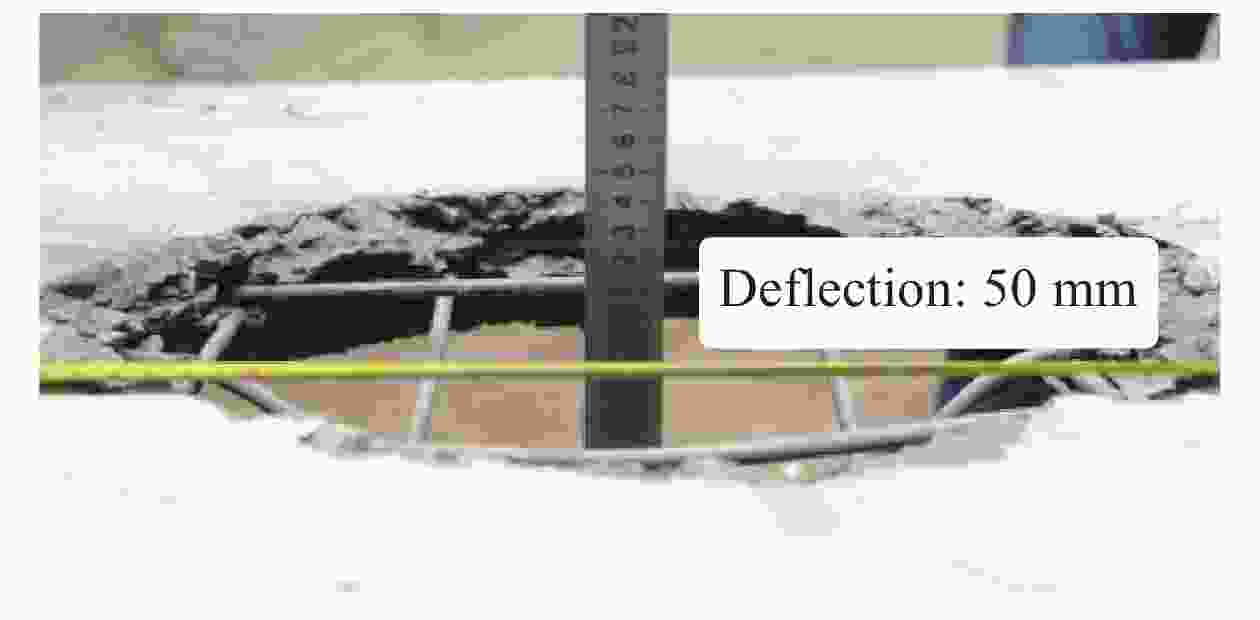
摘要: 钢板混凝土剪力墙作为一种新型的抗侧力构件，具有良好的耗能能力和抗冲击性能，已逐渐应用于建筑工程结构的抗震和防护结构的抗爆设计。设计了3个试件，分别为普通钢筋混凝土板、单侧钢板混凝土板和夹心钢板混凝土板，开展了钢板混凝土剪力墙的接触爆炸试验，并通过非线性程序LS-DYNA建立了3个钢板混凝土剪力墙试件的数值模型，对比分析了不同试件在接触爆炸作用下的动态响应、破坏模式和抗爆性能。试验和数值分析结果表明：接触爆炸作用下，试验设计的3种试件呈现3种破坏模式；普通钢筋混凝土板中部发生混凝土贯穿破坏，钢筋发生较大弯曲变形；单侧钢板混凝土板由于栓钉拔出发生钢板和混凝土分离，丧失整体性和继续承载能力；夹心钢板混凝土板发生上层混凝土压碎，夹心钢板、上层和下层混凝土板连接性能较强，整体性较好，具有继续承载的能力，且夹心钢板混凝土板跨中挠度和混凝土碎块飞溅距离较小。单侧钢板混凝土板和夹心钢板混凝土板配置钢筋网可以显著增强混凝土层和钢板的连接性能，有效减小上下层混凝土的碎裂和剥落，增强其整体性和抗爆性能。Abstract: As a lateral resisting component, the single-side steel plate shear wall (SPSW) has a favorable capacity of energy dissipation and impact resistance, it has been gradually applied into the anti-seismic design of building and the anti-explosion design of protective structures. In this paper, three specimens of reinforced concrete slab (RCS), side steel plate shear wall slab (SSPSWS) and center steel plate shear wall slab (CSPWS) were designed and casted, the contact explosion experiment of SPSW were carried out in the field, and the nonlinear program LS-DYNA was used to establish finite model of SPSWS specimens, the dynamic response, failure models and anti-blast capacity of SPSWs subjected to contact explosion loads were compared and analyzed. The experimental results and numerical analysis show that there are three types of failure models occurred in the SPSWs, The midspan concrete of RCS occurrs penetration failure, and the reinforcement bar of RCS had larger bending deformation; while the concrete and steel plate of SSPSWS separate with the state of shear studs pulling out, losting its integrity and resistance capacity. The specimen of CSPWS is failure under upper concrete crushing, but the CSPWS specimen is still integrity and bearing capacity with strong connection performance. The midspan deflection of concrete slab and the splashing distance of concrete fragments are small. In addition, the capacity of bonding performance between concrete and steel plate of SSPSWS and CSPWS can be enhanced through equipping with reinforcing fabric, it can effectively reduce the cracking and peeling of the upper and lower layers of concrete and improve the integrity and anti-explosion capacity either .
-
图 1 RCS几何尺寸及配筋方式（单位：mm）
Figure 1. Dimensions of RCS and reinforcement layout (unit in mm)
图 2 SSPSWS几何尺寸和结构形式（单位：mm）
Figure 2. Dimensions and structural style of SSPSWS (unit in mm)
图 3 CSPWS的几何尺寸和结构形式（单位：mm）
Figure 3. Dimensions and structural style of CSPWS (unit in mm)
图 7 RCS的试验与数值结果（单位：mm）
Figure 7. Experimental and numerical results of RCS (unit in mm)
图 13 试件SSPSWS试验及数值分析结果（单位：mm）
Figure 13. Experimental and numerical results of SSPSWS (unit in mm)
图 16 钢板及栓钉试验与数值分析结果
Figure 16. Experimental and numerical results of steel plate and weld studs
图 19 试件CSPWS试验及数值结果（单位：mm）
Figure 19. Experimental and numerical results of CSPWS specimen (unit in mm)
表 1 材料力学性能参数
Table 1. Mechanical properties of materials
材料类别 强度等级 弹性模量/GPa 抗压强度/MPa 屈服强度/MPa 抗拉强度/MPa 混凝土 C30 30 30 — — 钢筋 HRB335 200 — 341 472 钢板 Q235 200 — 235 370 焊钉 A2-50 200 — 210 500 
下载: 导出CSV
表 2 试件破坏尺寸对比
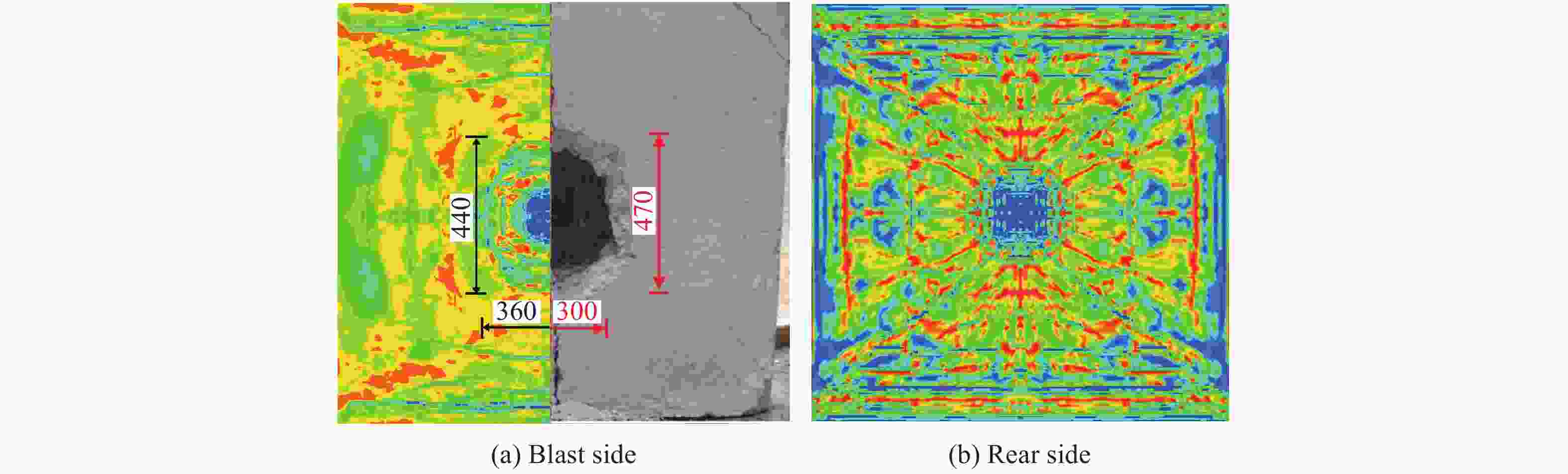
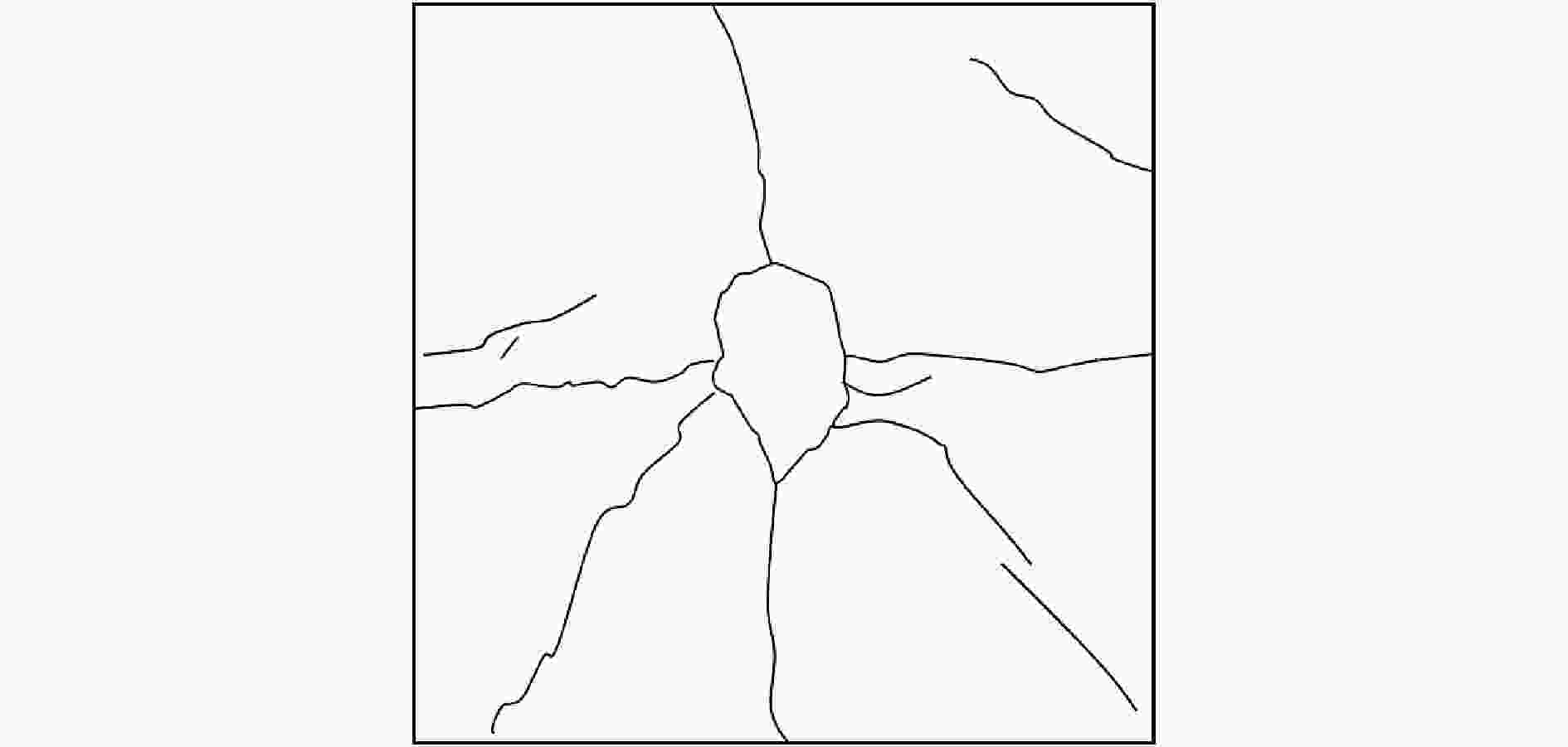
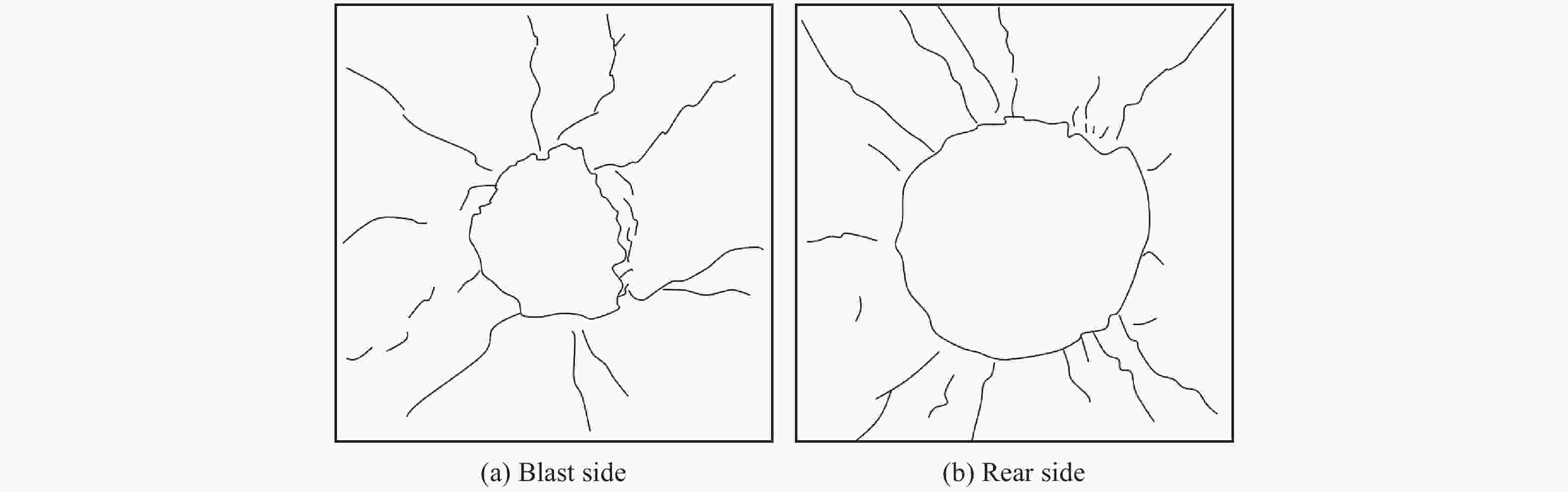
Table 2. Comparison of damage area for different specimens
类型 损伤尺寸 误差/% 迎爆面（试验） 背爆面（试验） 迎爆面（数值模拟） 背爆面（数值模拟） 迎爆面 背爆面 RCS 360 mm×300 mm 410 mm×400 mm 300 mm×300 mm 380 mm×360 mm 16.7 16.6 SSPSWS 470 mm×300 mm 440 mm×360 mm 12.3 CSPWS 400 mm×350 mm 560 mm×520 mm 350 mm×330 mm 520 mm×480 mm 17.5 14.3
下载: 导出CSV
-
[1] ZHAO C F, CHEN J Y. Damage mechanism and mode of square reinforced concrete slab subjected to blast loading [J]. Theoretical and Applied Fracture Mechanics, 2013, 63−64: 54–62. DOI: 10.1016/j.tafmec.2013.03.006. [2] ZHAO C F, WANG Q, LU X, et al. Numerical study on dynamic behaviors of NRC slabs in containment dome subjected to close-in blast loading [J]. Thin-Walled Structures, 2019, 135: 269–284. DOI: 10.1016/j.tws.2018.11.013. [3] 李利莎, 谢清粮, 郑全平, 等. 基于Lagrange、ALE和SPH算法的接触爆炸模拟计算 [J]. 爆破, 2011, 28(1): 18–22. DOI: 10.3963/j.issn.1001-487X.2011.01.005.LI L S, XIE Q L, ZHENG Q P, et al. Numerical simulation of contact explosion based on Lagrange ALE and SPH [J]. BLASTING, 2011, 28(1): 18–22. DOI: 10.3963/j.issn.1001-487X.2011.01.005. [4] 张想柏, 杨秀敏, 陈肇元, 等. 接触爆炸钢筋混凝土板的震塌效应 [J]. 清华大学学报(自然科学版), 2006(6): 765–768. DOI: 10.3321/j.issn:1000-0054.2006.06.004.ZHANG X B, YANG X M, CHEN Z Y, et al. Explosion spalling of reinforced concrete slabs with contact detonations [J]. Journal of Tsinghua University (Science and Technology), 2006(6): 765–768. DOI: 10.3321/j.issn:1000-0054.2006.06.004. [5] 刘云, 卢红标, 周布奎, 等. 高强RC板的抗接触爆试验分析 [J]. 江南大学学报(自然科学版), 2012(5): 571–574. DOI: 10.3969/j.issn.1671-7147.2012.05.015.LIU Y, LU H B, ZHOU B K, et al. Experimental study on the contact explosion resistance performance of high strength RC slabs [J]. Journal of Jiangnan University (Nature Science Edition), 2012(5): 571–574. DOI: 10.3969/j.issn.1671-7147.2012.05.015. [6] JUN L, WU C Q, HONG H, et al. Experimental investigation of ultra-high performance concrete slabs under contact explosions [J]. International Journal of Impact Engineering, 2016, 93(7): 62–75. DOI: 10.1016/j.ijimpeng.2016.02.007. [7] 王威, 张龙旭, 苏三庆, 等. 波形钢板剪力墙抗震性能试验研究 [J]. 建筑结构学报, 2018, 39(5): 36–44. DOI: 10.14006/j.jzjgxb.2018.05.005.WANG W, ZHANG L X, SU S Q, et al. Experimental research on seismic behavior of corrugated steel plate shear wall [J]. Journal of Building Structures, 2018, 39(5): 36–44. DOI: 10.14006/j.jzjgxb.2018.05.005. [8] 聂建国, 樊健生, 黄远, 等. 钢板剪力墙的试验研究 [J]. 建筑结构学报, 2010, 31(9): 1–8. DOI: 10.14006/j.jzjgxb.2010.09.015.NIE J G, FAN J S, HUANG Y, et al. Experimental research on steel plate shear wall [J]. Journal of Building Structures, 2010, 31(9): 1–8. DOI: 10.14006/j.jzjgxb.2010.09.015. [9] ZHAO C F, LU X, WANG Q, et al. Experimental and numerical investigation of steel-concrete (SC) slabs under contact blast loading [J]. Engineering Structures, 2019, 196: 109337. DOI: 10.1016/j.engstruct.2019.109337. [10] ZHAO C F, WANG Q, LU X, et al. Blast resistance of small-scale RCS in experimental test and numerical analysis [J]. Engineering Structures, 2019, 199: 109610. DOI: 10.1016/j.engstruct.2019.109610. [11] SOHEL K M A, LIEW J Y R. Behavior of steel-concrete-steel sandwich slabs subject to impact load [J]. Journal of Constructional Steel Research, 2014, 100: 163–175. DOI: 10.1016/j.jcsr.2014.04.018. [12] LIEW J, WANG T. Novel steel-concrete-steel sandwich composite Plates subject to impact and blast load [J]. Advances in Structural Engineering, 2011, 14(4): 673–688. DOI: 10.1260/1369-4332.14.4.673. [13] 中华人民共和国住房和城乡建设部.钢板剪力墙技术规程: JGJ/T 380—2015[S]. 北京: 中国建筑工业出版社, 2015. [14] 赵春风, 王强, 王静峰, 等. 近场爆炸作用下核电厂安全壳穹顶钢筋混凝土板的抗爆性能 [J]. 高压物理学报, 2019, 33(2): 025101. DOI: 10.11858/gywlxb.20180598.ZHAO C F, WANG Q, WANG J F, et al. Blast resistance of containment dome reinforced concrete slab in NPP under close-in explosion [J]. Chinese Journal of High Pressure Physics, 2019, 33(2): 025101. DOI: 10.11858/gywlxb.20180598. [15] HALLQUIST J O. LS-DYNA keyword user’s manual [M]. Livermore Software Technology Corporation, 2007. [16] BISCHOFF P H, PERRY S H. Compressive behavior of concrete at high strain rates [J]. Materials and Structures, 1991, 24(6): 425–450. DOI: 10.1007/BF02472016. [17] MALYAR L, CRAWFORD J, MORRILL K. K&C concrete material model release III: automated generation of material model input: TR-99-243 [R]. Karagozian and Case Structural Engineers, 2000. -
点击查看大图
计量
- 文章访问数: 1515
- HTML全文浏览量: 632
- PDF下载量: 109
- 被引次数: 0