斜波压缩下HMX晶体的弹塑性行为

种涛; 莫建军; 郑贤旭; 傅华; 蔡进涛

doi:10.11883/bzycj-2020-0071

斜波压缩下HMX晶体的弹塑性行为

doi: 10.11883/bzycj-2020-0071

中国工程物理研究院流体物理研究所，四川绵阳 621999

基金项目: 国家自然科学基金（11702276）；国防科技重点实验室基金（6142A03192007）

详细信息

作者简介:
种　涛（1986－　），男，博士，助理研究员，maoda318@163.com

通讯作者:
蔡进涛（1984－　），男，博士，副研究员，goldennoon@163.com

中图分类号: O347.5
计量
- 文章访问数: 706
- HTML全文浏览量: 289
- PDF下载量: 79
- 被引次数: 0
出版历程
- 收稿日期: 2020-03-19
- 修回日期: 2020-12-04
- 网络出版日期: 2021-03-18
- 刊出日期: 2021-05-05

Elastic-plastic transition behaviors of HMX crystal under ramp wave compression

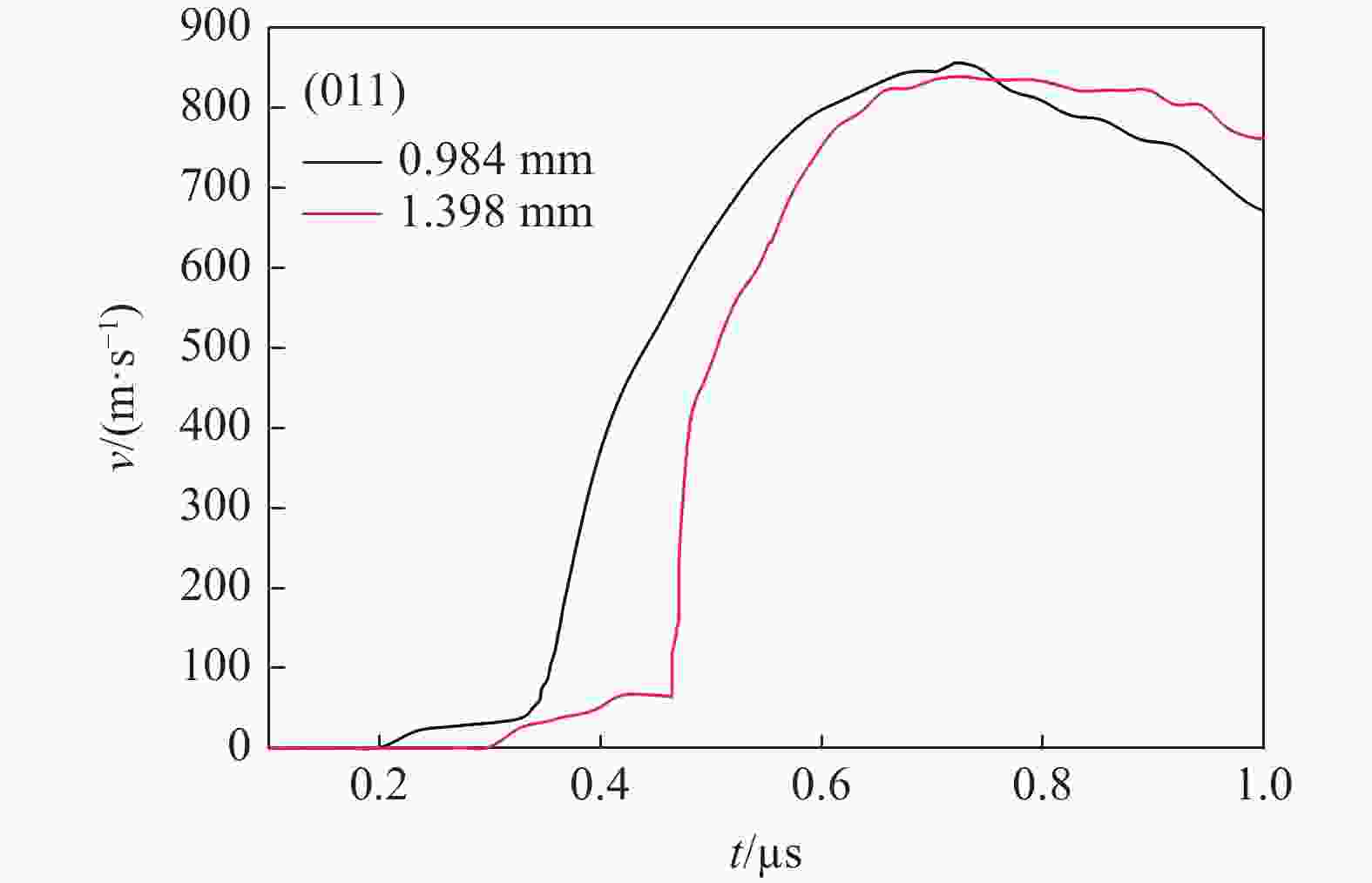
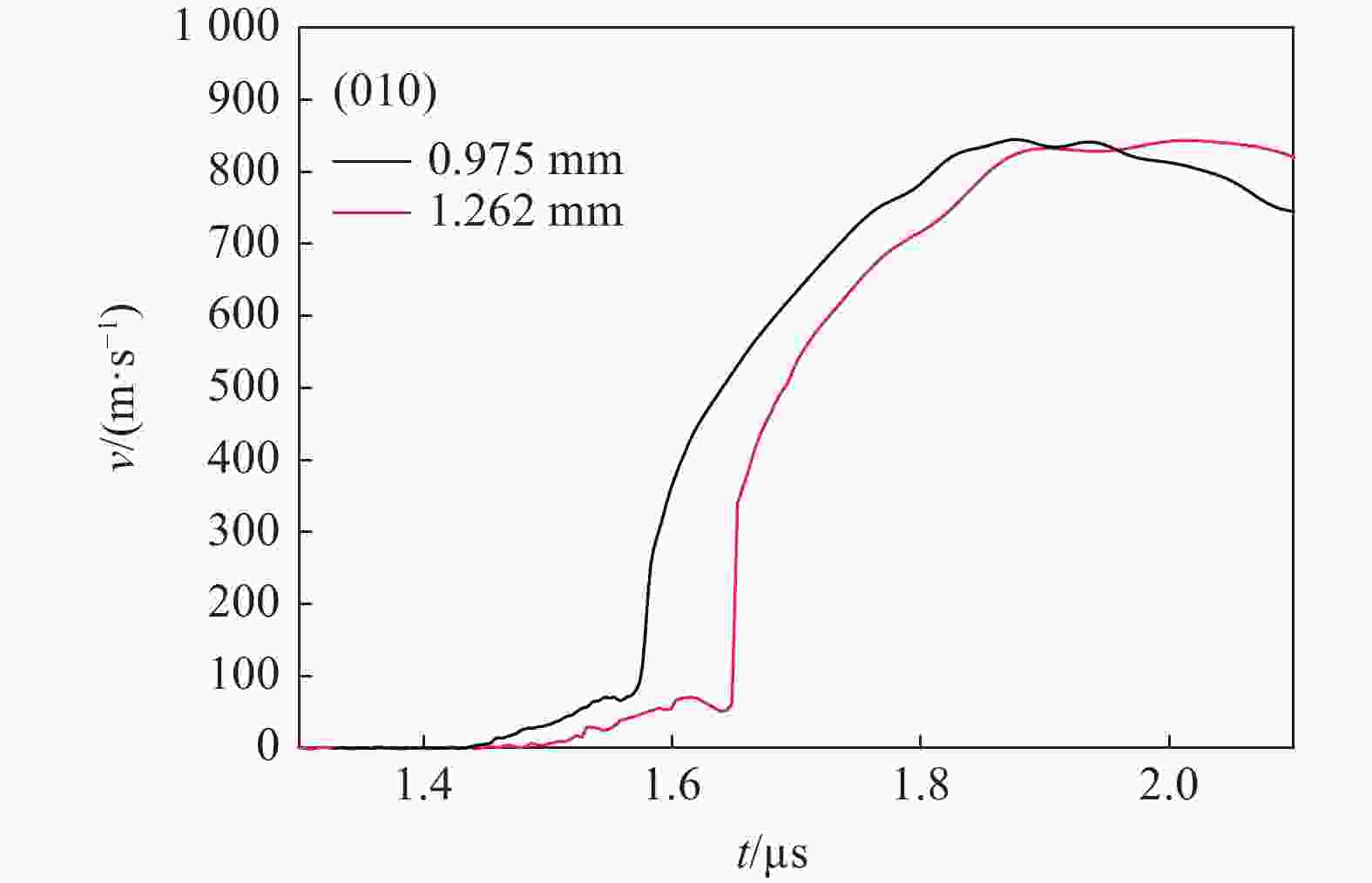
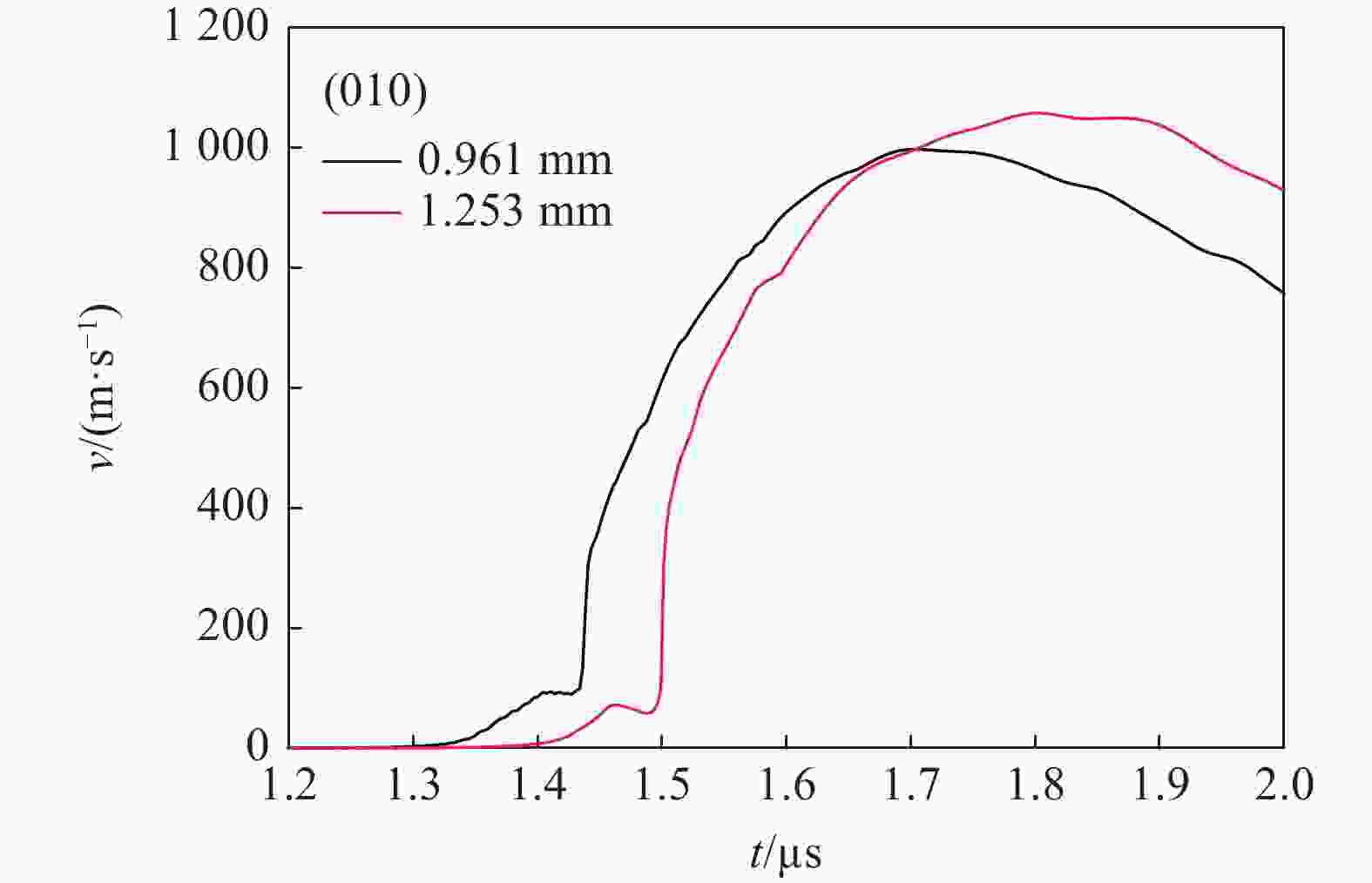
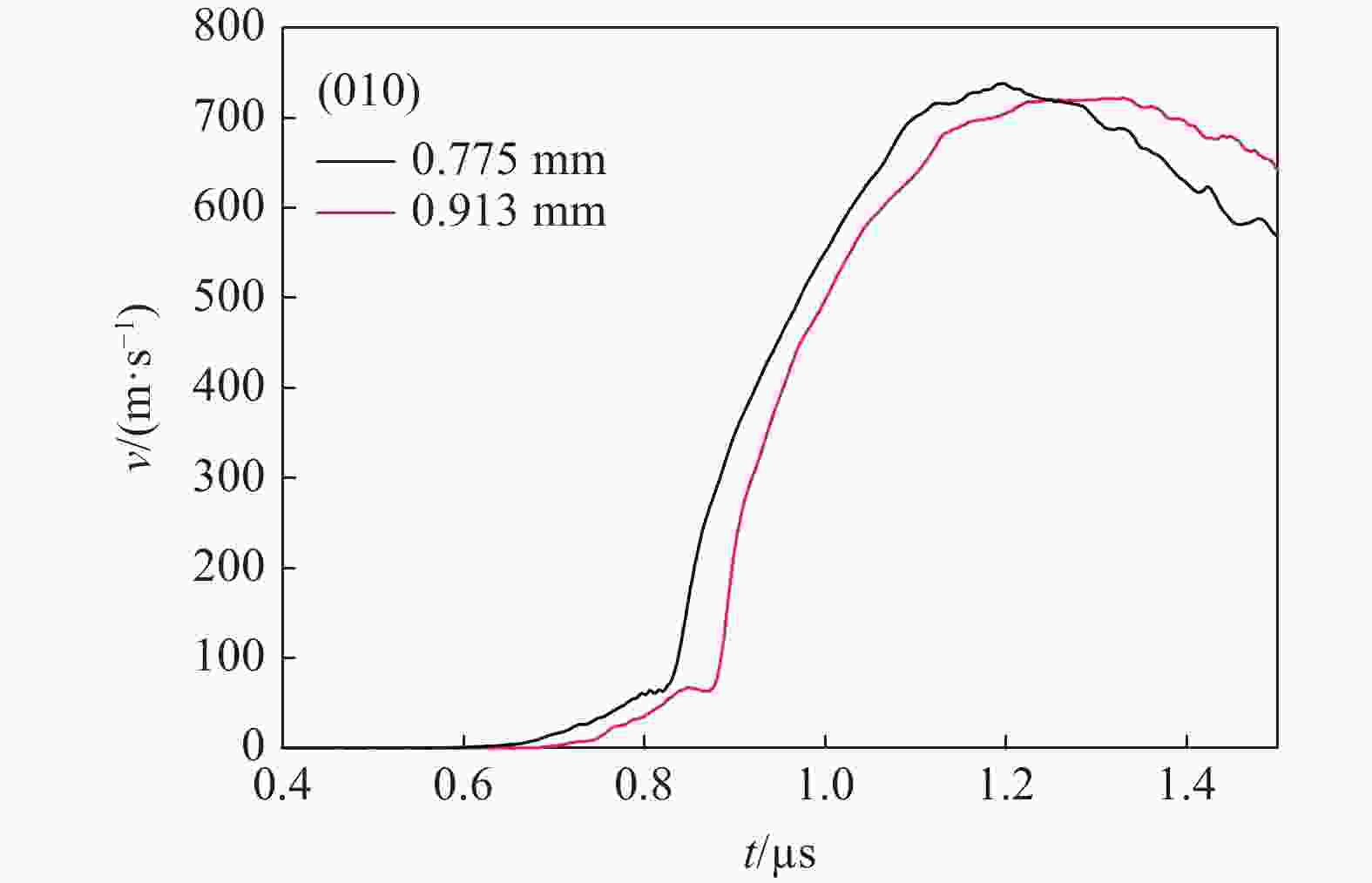
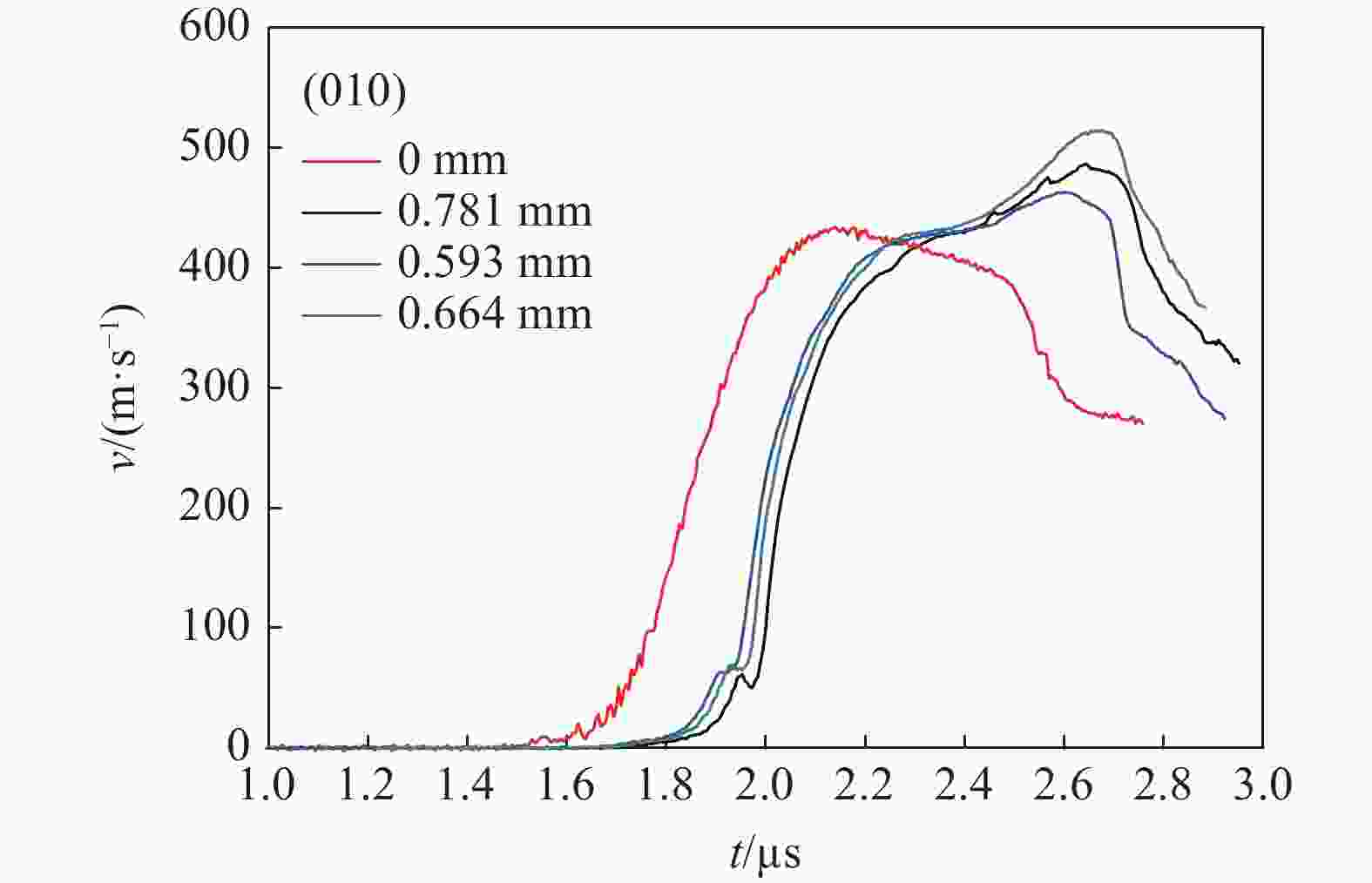
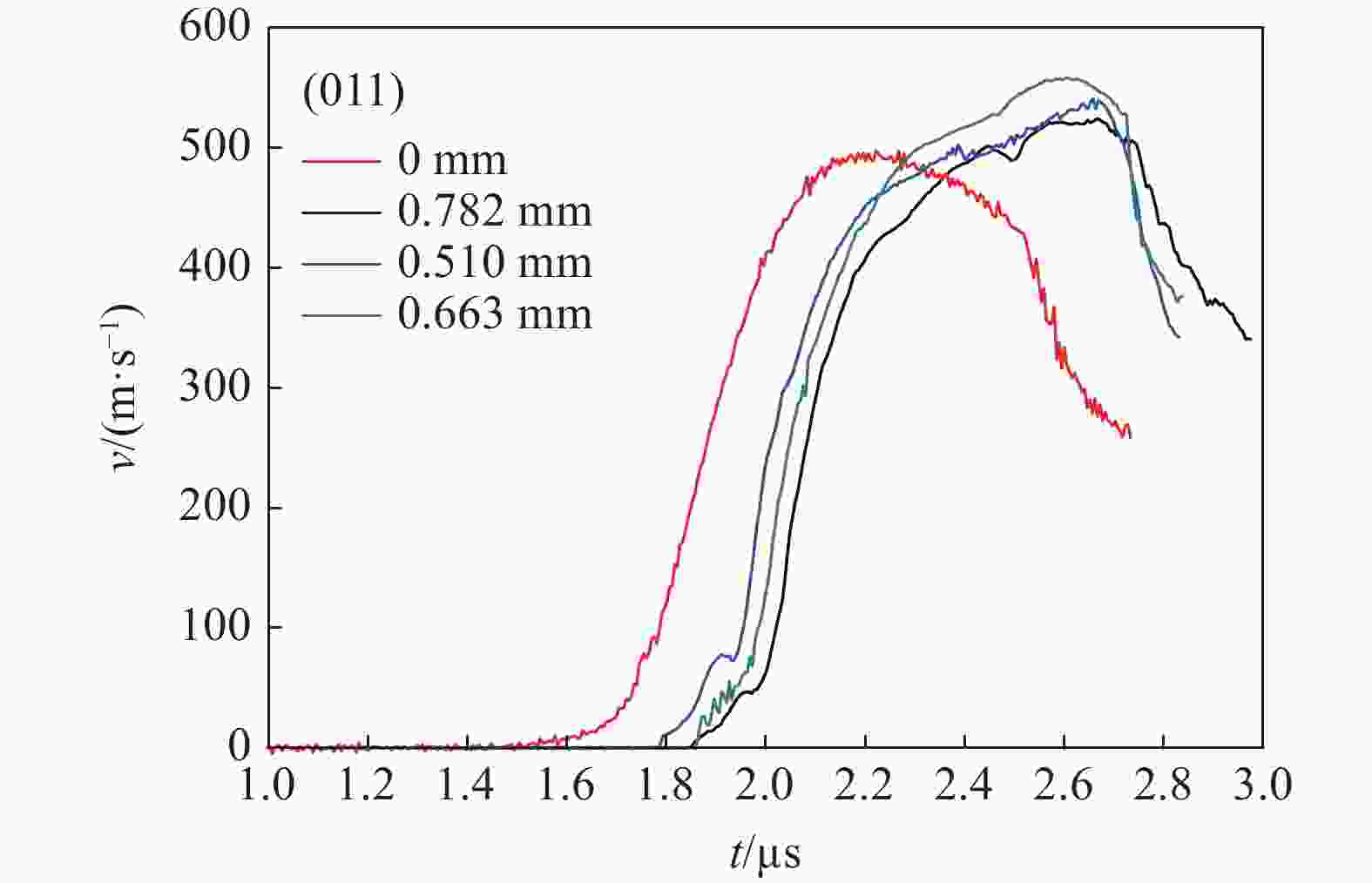
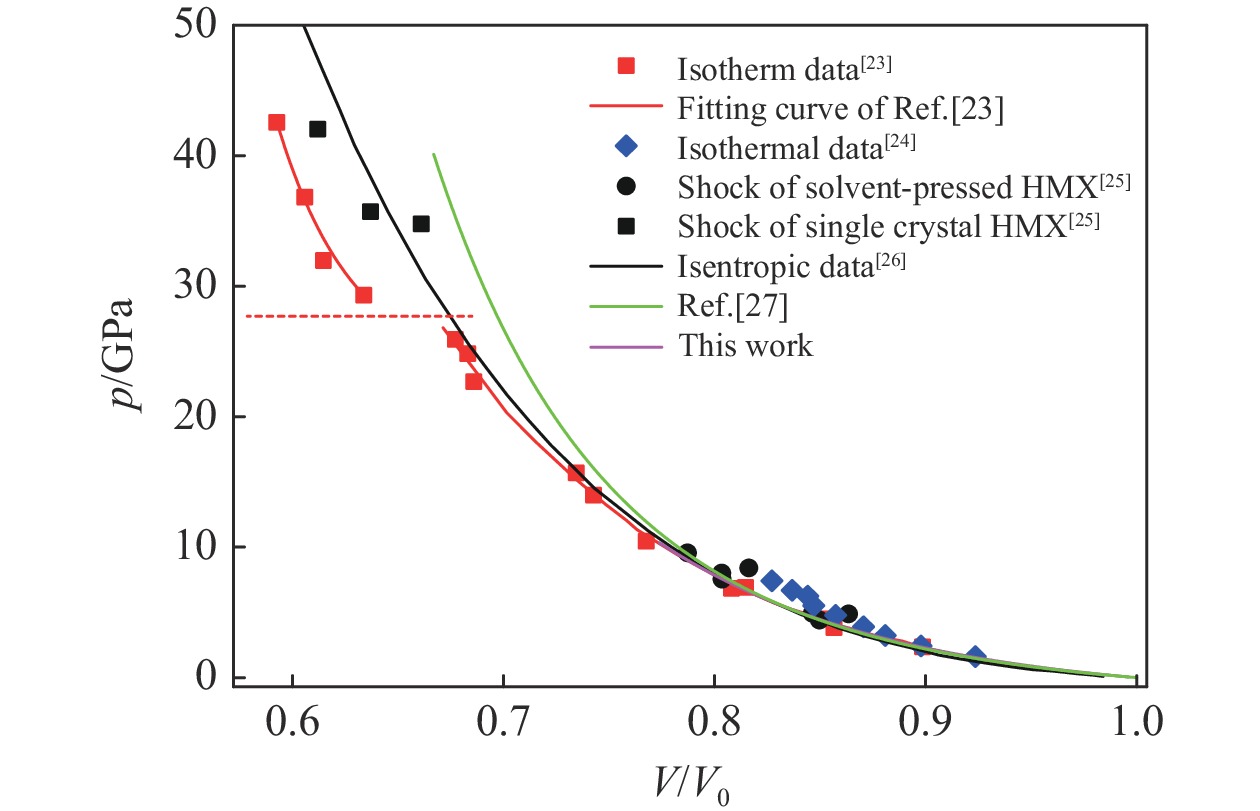
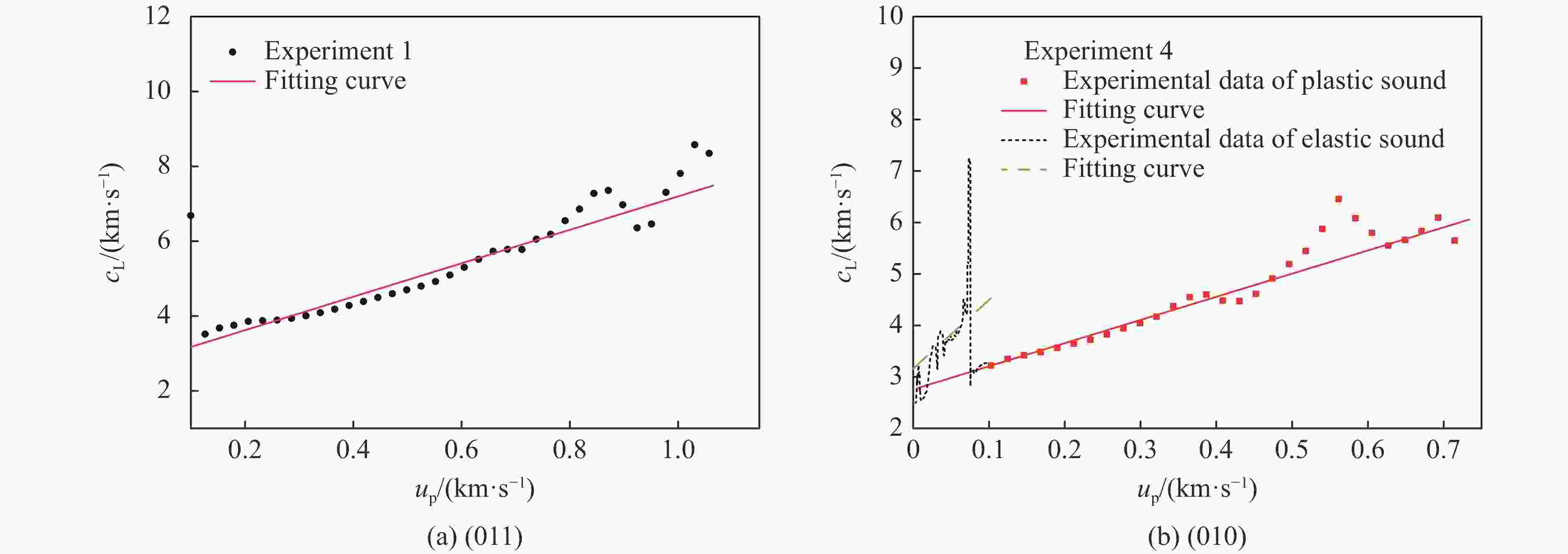
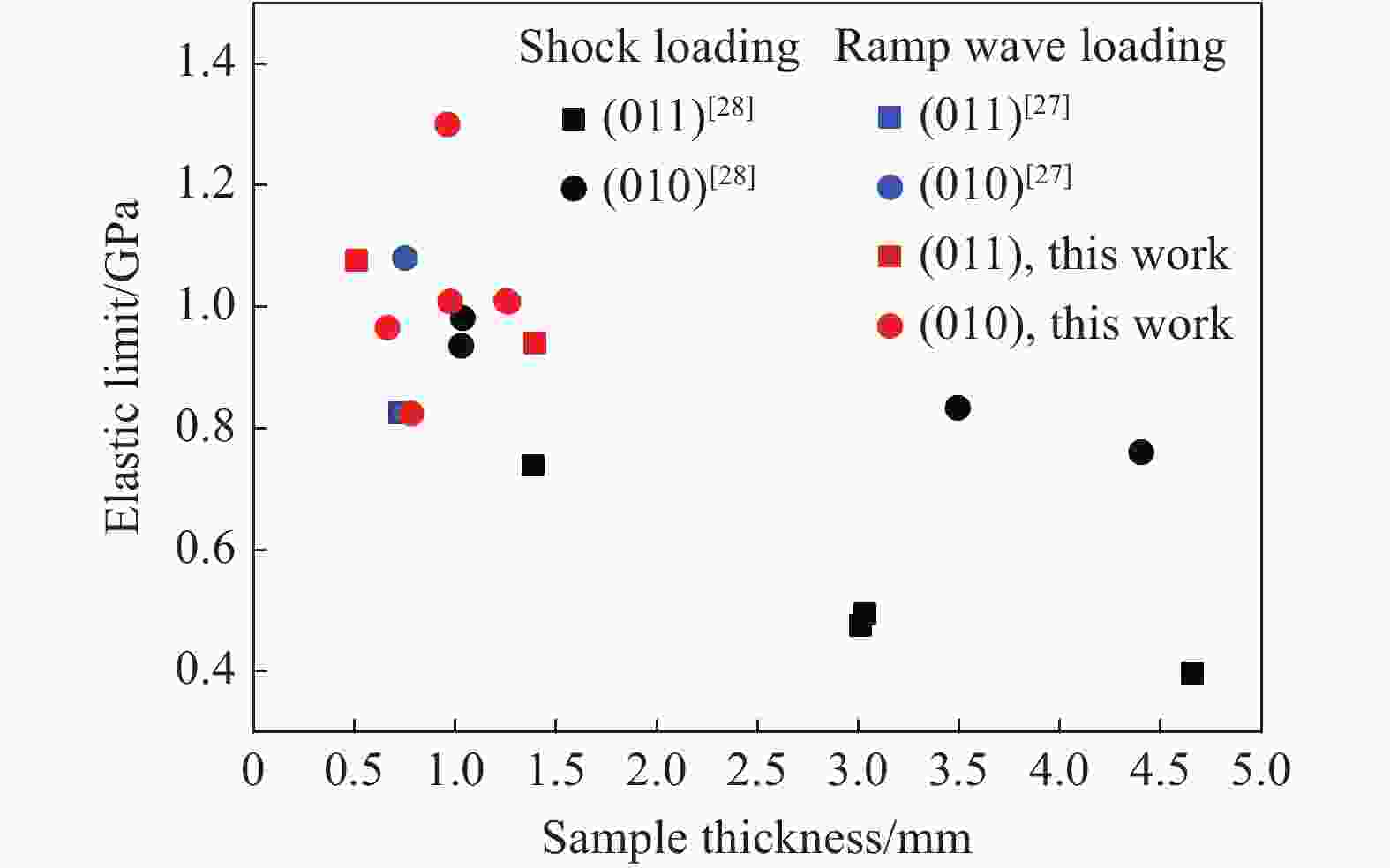
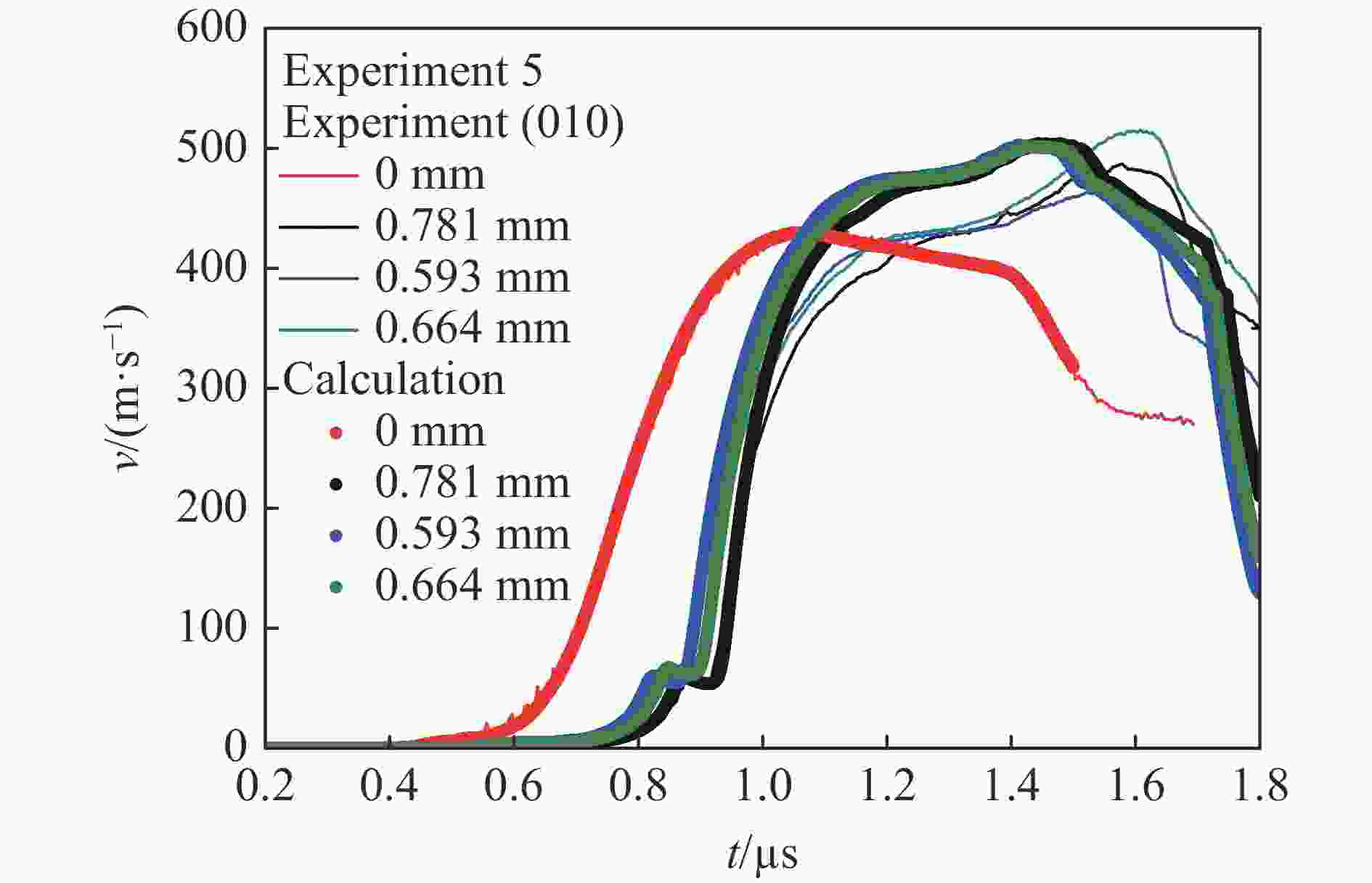
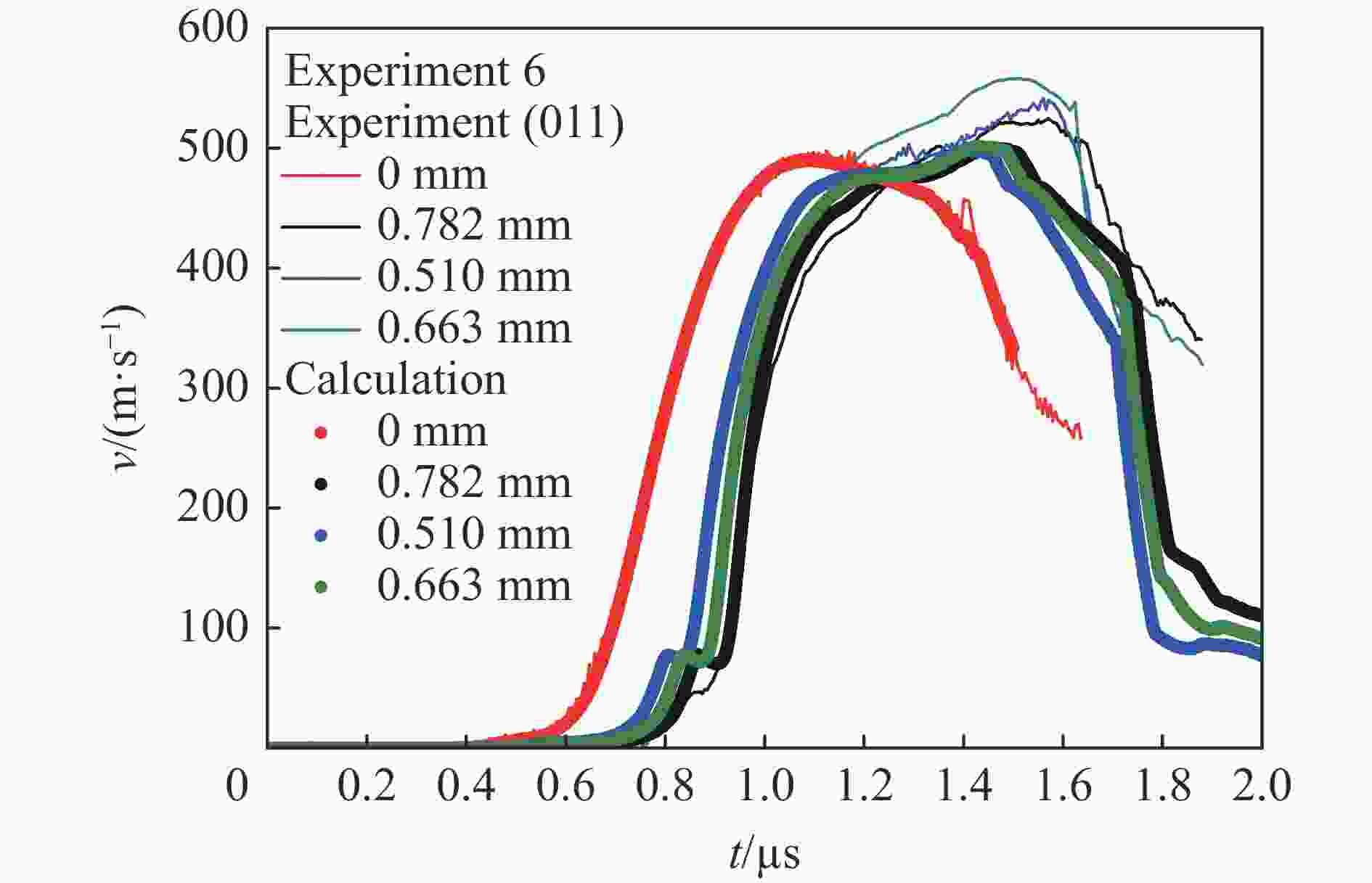
Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621999, Sichuan, China

摘要

摘要: 开展了（010）、（011）晶向HMX晶体的斜波压缩实验，获得了约15 GPa压力下的速度响应剖面。实验结果表明，HMX单晶存在明显弹塑性转变行为，且速度波形有下降趋势，这是材料的黏性效应导致，材料的弹性极限随着样品厚度增加而变化，不同晶向的材料动力学特性存在差异。结合Hobenemser-Prager黏弹塑性本构关系和三阶Birch-Murnaghan物态方程开展了HMX晶体斜波压缩物理过程的数值模拟，计算结果可以很好地描述HMX晶体的弹塑性转变这一物理过程。
- HMX晶体 /
- 弹塑性转变 /
- 斜波压缩 /
- 状态方程
Abstract: The dynamics of HMX single crystals under ramp wave loading was studied experimentally and numerically. The ramp wave compression experiments of (010) and (011) crystal oriented HMX crystals within 15 GPa were carried out with the magnetic driven device CQ-4, which can provide a loading pressure with a rising time of 450−600 ns. The velocity curves of the interface between the HMX single crystal and the LiF single crystal were obtained with dual laser heterodyne velocimetry (DLHV). The experimental results show that there is an obvious elastic-plastic transition behavior in the loading section. The velocity waveforms have a downward trend in the elastic-plastic transition section, which is caused by the viscous effect of the HMX single crystal. The elastic limit of the HMX single crystal changes with the increase of the sample thickness. The Lagrange sound speed-particle velocity data and pressure-specific volume curves of (010) and (011) crystal oriented HMX crystals were obtained with the iterative Lagrange data processing method for dynamic impedance mismatch. The Lagrange sound speed-particle velocity relationships in the different crystal directions are different. The pressure-specific volume curve is close to isentropic experimental data by Sandia laboratory. The numerical simulation of the physical process of ramp wave compression of the HMX crystal was carried out with the viscoelastic plastic constitutive relation of Hobnemser-Prager and the third-order Birch-Murnaghan equation of state. The calculation results can well describe the physical process of the elastic-plastic transformation of HMX crystal.
- HMX crystal /
- elastic-plastic transition /
- ramp wave compression /
- equation of state

HTML全文

图 1 HMX晶体

Figure 1. An HMX crystal

下载: 全尺寸图片幻灯片

图 2 实验1的速度响应曲线

Figure 2. Velocity profiles in experiment 1

下载: 全尺寸图片幻灯片

图 3 实验2的速度响应曲线

Figure 3. Velocity profiles in experiment 2

下载: 全尺寸图片幻灯片

图 4 实验3的速度响应曲线

Figure 4. Velocity profiles in experiment 3

下载: 全尺寸图片幻灯片

图 5 实验4的速度响应曲线

Figure 5. Velocity profiles in experiment 4

下载: 全尺寸图片幻灯片

图 6 实验5速度响应曲线

Figure 6. Velocity profiles in experiment 5

下载: 全尺寸图片幻灯片

图 7 实验6的速度响应曲线

Figure 7. Velocity profiles in experiment 6

下载: 全尺寸图片幻灯片

图 8 p-V/V₀曲线与文献数据结果

Figure 8. p-V/V₀ curve and literature data

下载: 全尺寸图片幻灯片

图 9 Lagrange声速与粒子速度关系曲线

Figure 9. Lagrange sound speed-particle velocity

下载: 全尺寸图片幻灯片

图 10 弹性极限与样品厚度关系

Figure 10. Relationship between elastic limit and sample thickness

下载: 全尺寸图片幻灯片

图 11 （010）晶向模拟计算结果与实验结果对比

Figure 11. Calculated and experimental data of (010) crystal direction

下载: 全尺寸图片幻灯片

图 12 （011）晶向模拟计算结果与实验结果对比

Figure 12. Calculated and experimental data of (011) crystal direction

下载: 全尺寸图片幻灯片

表 1 实验条件

Table 1. Experimental condition

实验编号	晶向	样品厚度/mm
1	（011）	1.398
1	（011）	0.984
2	（010）	1.262
2	（010）	0.975
3	（010）	1.253
3	（010）	0.961
4	(010)	0.775
4	(010)	0.913
5	(010)	0.593
		0.664
		0.781
6	(011)	0.510
		0.663
		0.782

下载: 导出CSV

表 2 HMX晶体的屈服

Table 2. Yield of HMX crystals

HMX晶向	厚度/mm	屈服速度/(m·s⁻¹)	弹性极限 /GPa
(011)	1.398	67.05	0.927
(011)	0.510	77.63	1.076
(010)	0.975	69.80	0.966
	1.262	70.30	0.973
	0.961	63.90	1.263
	1.253	71.50	0.990
	0.775	63.90	0.883
	0.913	67.10	0.928
	0.664	69.78	0.966
	0.781	59.69	0.824

下载: 导出CSV

表 3 模拟计算所用的模型参数

Table 3. Model parameters used in simulation

晶向	σ_y/GPa	G/GPa	η/(Pa·s)	K_T0/GPa	$K_{T0}'$
（010）	0.55	7	110	9.75	15.0
（011）	0.60	11	90	13.00	10.5

下载: 导出CSV

参考文献(32)

[1]	谭武军. 含能晶体力学性能研究[D]. 绵阳: 中国工程物理研究院, 2008. TAN W J. Studies on the mechanical properties of energetic crystals [D]. Mianyang: China Academy of Engineering Physics, 2008.
[2]	李明, 陈天娜, 黄明, 等. RDX晶体的破碎与细观断裂行为 [J]. 含能材料, 2013, 21(2): 200–204. DOI: 10.3969/j.issn.1006-9941.2013.02.008. LI M, CHEN T N, HUANG M, et al. Rupture and mesoscale fracture behaviors of RDX crystals [J]. Chinese Journal of Energetic Materials, 2013, 21(2): 200–204. DOI: 10.3969/j.issn.1006-9941.2013.02.008.
[3]	王国栋, 刘玉存. 神经网络在炸药晶体密度预测中的应用 [J]. 火炸药学报, 2007, 30(1): 57 –59. DOI: 10.3969/j.issn.1007-7812.2007.01.016. WANG G D, LIU Y C. Application of artificial neural network in predicting the density of explosives [J]. Chinese Journal of Explosives and Propellants, 2007, 30(1): 57 –59. DOI: 10.3969/j.issn.1007-7812.2007.01.016.
[4]	花成, 傅华, 田勇, 等. 冲击波作用下HMX晶体的细观响应 [J]. 火炸药学报, 2010, 33(3): 5– 8. DOI: 10.3969/j.issn.1007-7812.2010.03.002. HUA C, FU H, TIAN Y, et al. Mesoscale response of HMX crystal under the shock war effect [J]. Chinese Journal of Explosives and Propellants, 2010, 33(3): 5– 8. DOI: 10.3969/j.issn.1007-7812.2010.03.002.
[5]	黄明, 李洪珍, 徐容, 等. 高品质 RDX 的晶体特性及冲击波起爆特性 [J]. 含能材料, 2011, 19(6): 621–626. HUANG M, LI H Z, XU R, et al. Evaluation of crystal properties and initiation characteristics of decreased sensitivity RDX [J]. Chinese Journal of Energetic Materials, 2011, 19(6): 621–626.
[6]	HOWE P M. Effects of microstructure on explosive behavior [J]. Progress in Astronomics and Aeronautics, 2000, 185: 141.
[7]	JOHANSEN Ø H, KRISTIANSEN J D, GJERSØE R, et al. RDX and HMX with reduced sensitivity towards shock initiation-RS-RDX and RS-HMX [J]. Propellants, Explosives, Pyrotechnics, 2008, 33(1): 20–24. DOI: 10.1002/prep.200800203.
[8]	VAN DER HEIJDEN A E D M, BOUMA R H B, VAN DER STEEN A C. Physicochemical parameters of nitramines influencing shock sensitivity [J]. Propell. Explos. Pyrotech, 2004, 29(5): 304–313. DOI: 10.1002/prep.200400058.
[9]	WALLEY S M, FIELD J E, GREENAWAY M W. Crystal sensitivities of energetic materials [J]. Materials Science and Technology, 2006, 22(4): 402–413. DOI: 10.1179/174328406X91122.
[10]	CAULDER S M, MILLER P J, GIBSON K D, et al. Effect of particle size and crystal quality on the critical shock initiation pressure of RDX/HTPB formulations [C]// Proceedings of 13th Symposium (International) on Detonation. Norfolk, VA, USA, 2006: 656–661.
[11]	VANDER STEEN A C, VERBEEK H, MEULENBRUGGE J J. Influence of RDX crystal shape on the shock sensitivity of PBXs [C]// Proceedings of 9th Symposium (International) on Detonation. Portland, Oregon, USA, 1989: 83–88.
[12]	花成, 张盛国, 高大元. 冲击波作用下炸药安全性QMU评估 [J]. 火炸药学报, 2015, 38(4): 31–34. HUA C, ZHANG S G, GAO D Y. QMU evaluation of explosive safety under shock wave effect [J]. Chinese Journal of Explosives and Propellants, 2015, 38(4): 31–34.
[13]	GOETZ F, BRILL T B, FERRARO J R. Pressure dependence of the raman and infrared spectra of α-, β-, γ-, and δ-octahydro-1, 3, 5, 7-tetranitro-1, 3, 5, 7-tetrazocine [J]. Journal of Physics Chemistry B, 1978, 82(17): 1912–1917. DOI: 10.1021/j100506a011.
[14]	CHOI C S, BOUTIN H P. A study of the crystal structure of β-cyclotetramethylene tetranitramine by neutron diffraction [J]. Acta Crystallographica Section B, 1970, 26(9): 1235–1240. DOI: 10.1107/S0567740870003941.
[15]	HORST J H, KRAMER H J M, ROSMALEN G M, et al. Molecular modelling of the crystallization of polymorphs: Part Ⅰ: the morphology of HMX polymorphs [J]. Journal of Crystal growth, 2002, 237: 2215–2220.
[16]	CLEMENTS B E, MAS E M. A theory for plastic-bonded materials with a bimodal size distribution of filler particles [J]. Modelling and Simulation in Materials Science and Engineering, 2004, 12(3): 407–421. DOI: 10.1088/0965-0393/12/3/004.
[17]	MENIKOFF R, DICK J J, HOOKS D E. Analysis wave profiles for single-crystal cyclotetramethylene tetranitramine [J]. Journal of Applied Physics, 2005, 97(2): 023529. DOI: 10.1063/1.1828602.
[18]	DICK J J, HOOKS D E, MENIKOFF R, et al. Elastic-plastic wave profiles in cyclotetramethylene tetranitramine crystals [J]. Journal of Applied Physics, 2004, 96(1): 374–379.
[19]	JARAMILLO E, SEWELL T D. Inelastic Deformation in shock loaded: HMX LA-UA-06-3716 [R]. Los Alamos National Laboratory Report, 2005.
[20]	SEWELL T D, BEDROV D, MENIKOFF R, et al. Elastic properties of HMX [J]. AIP Conference Proceedings, 2002, 620(1). DOI: 10.1063/1.1483562.
[21]	ZAUG J M. Elastic constants of β-HMX and tantalum, equation of state of supercritical fluids and fluid mixtures and thermal transport determinations [C]//The 11th International Detonation Symposium. Snowmass Conference Center. Snowmass Village, Colorado. 1998: 498−509.
[22]	HALL C A, ASAY J R, KNUDSON M D, et al. Experimental configuration for isentropic compression of solids using pulsed magnetic loading [J]. Review of Scientific Instruments, 2001, 72(9): 3587–3595. DOI: 10.1063/1.1394178.
[23]	YOO C S, CYNN H. Equation of state, phase transition, decomposition of β-HMX (octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine) at high pressures [J]. The Journal of Chemical Physics, 1999, 111(22): 10229. DOI: 10.1063/1.480341.
[24]	OLINGER B, ROOF B and CADY H H. The linear and volume compression of β-HMX and RDX [C]//Actes du Symposium International sur le Comportement des Milieux Denses Sous Hautes Pressions Dynamiques, Commissariat a l’Energie Atomique, Paris, 1978: 3−8.
[25]	MARSH S. LASL shock Hugoniot data [M]. Berkeley: University of California Press, 1980.
[26]	DANIEL, HOOK E and HAYES D B. Isentropic compression of cyclotetramethylene tetranitramine (HMX) single crystals to 50 GPa [J]. The Journal of Applied Physics, 2006, 99(12): 124901. DOI: 10.1063/1.2203411.
[27]	苏锐, 龙瑶, 姜胜利, 等. 外部压力下β相奥克托金晶体弹性性质变化的第一性原理研究 [J]. 物理学报, 2012, 16(20): 336–341. SU R, LONG Y, JIANG S L, et al. Elastic properties of β–HMX under extra pressure: a first principle study [J]. Acta Physica Sinica, 2012, 16(20): 336–341.
[28]	罗斌强, 张红平, 种涛, 等. 磁驱动斜波压缩实验结果的不确定度分析 [J]. 高压物理学报, 2017, 31(3): 295–300. DOI: 10.11858/gywlxb.2017.03.011. LUO B Q, ZHANG H P, CHONG T, et al. Experimental uncertainty analysis of magnetically driven ramp wave compression [J]. Chinese Journal of High Pressure Physics, 2017, 31(3): 295–300. DOI: 10.11858/gywlxb.2017.03.011.
[29]	BAER M, ROOT S, DATTELBAUM D, et al. Shockless compression studies of HMX-based and TATB-based explosives [C] // The 16th APS Topical Conference on Shock Compression of Condensed Matter. Nashville, Tennessee, 2009:699–702.
[30]	贾乃文. 粘塑性力学及工程应用 [M]. 北京: 地震出版社, 2000.
[31]	HRBEK G M. Invariant functional forms for the second, third, and fourth order Birch-Murnaghan equation of state for materials subject to hydrodynamic shock. [J]. Aip Conference Proceedings, 2000, 505(1): 169–173. DOI: 10.1063/1.1303448.
[32]	郭昕, 南海, 齐晓飞, 等. RDX和HMX晶体力学性能的分子动力学模拟及其撞击加载响应 [J]. 含能材料, 2013, 21(4): 485–489. DOI: 10.3969/j.issn.1006-9941.2013.04.016. GUO X, NAN H, QI X F, et al. Molecular dynamics simulation on mechanical properties of RDX and HMX crystals and their impacting loading response [J]. Chinese Journal of Energetic Materials, 2013, 21(4): 485–489. DOI: 10.3969/j.issn.1006-9941.2013.04.016.