Numerical simulation of pre-shock desensitization in TATB-based heterogeneous explosive
-
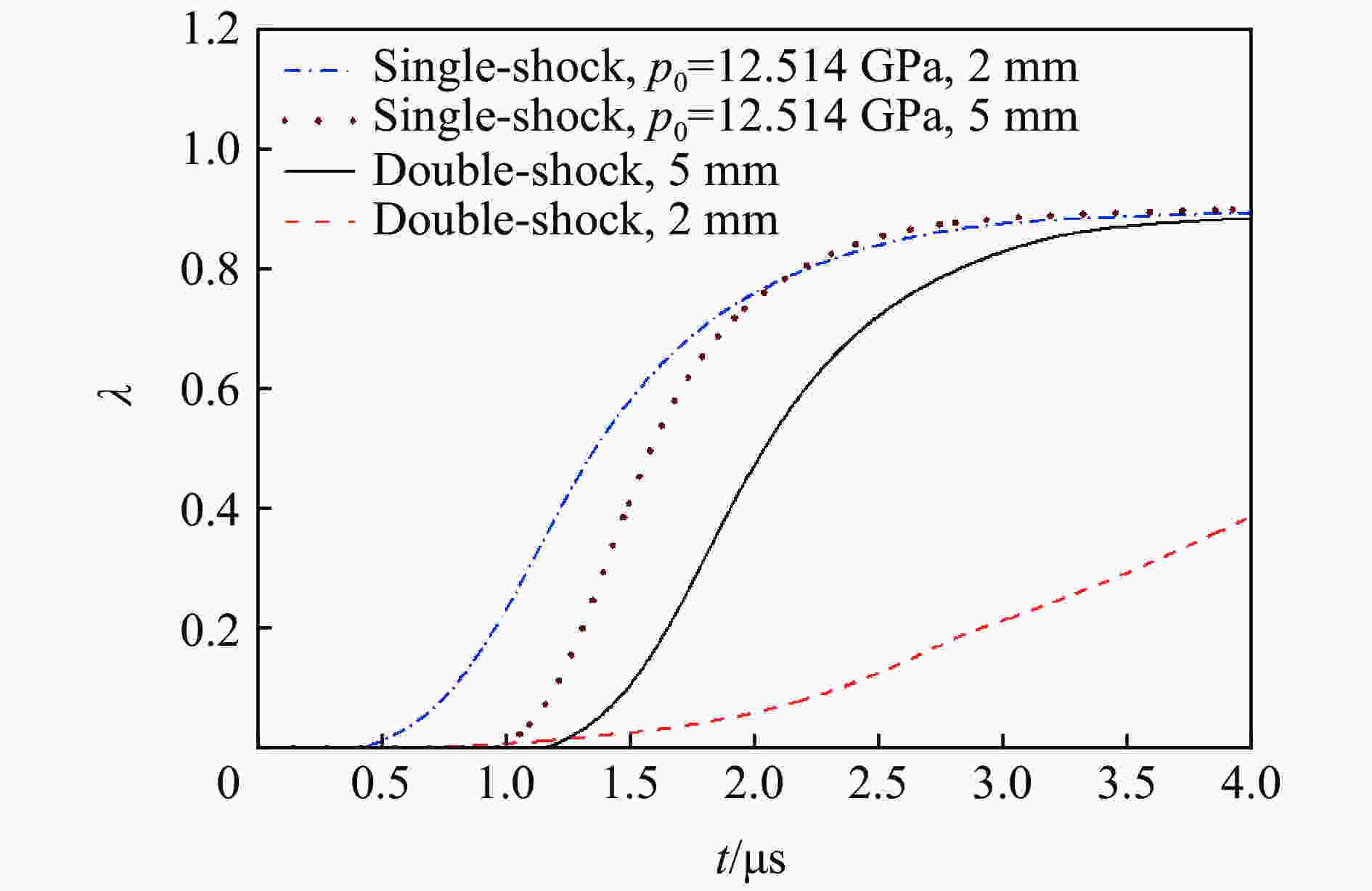
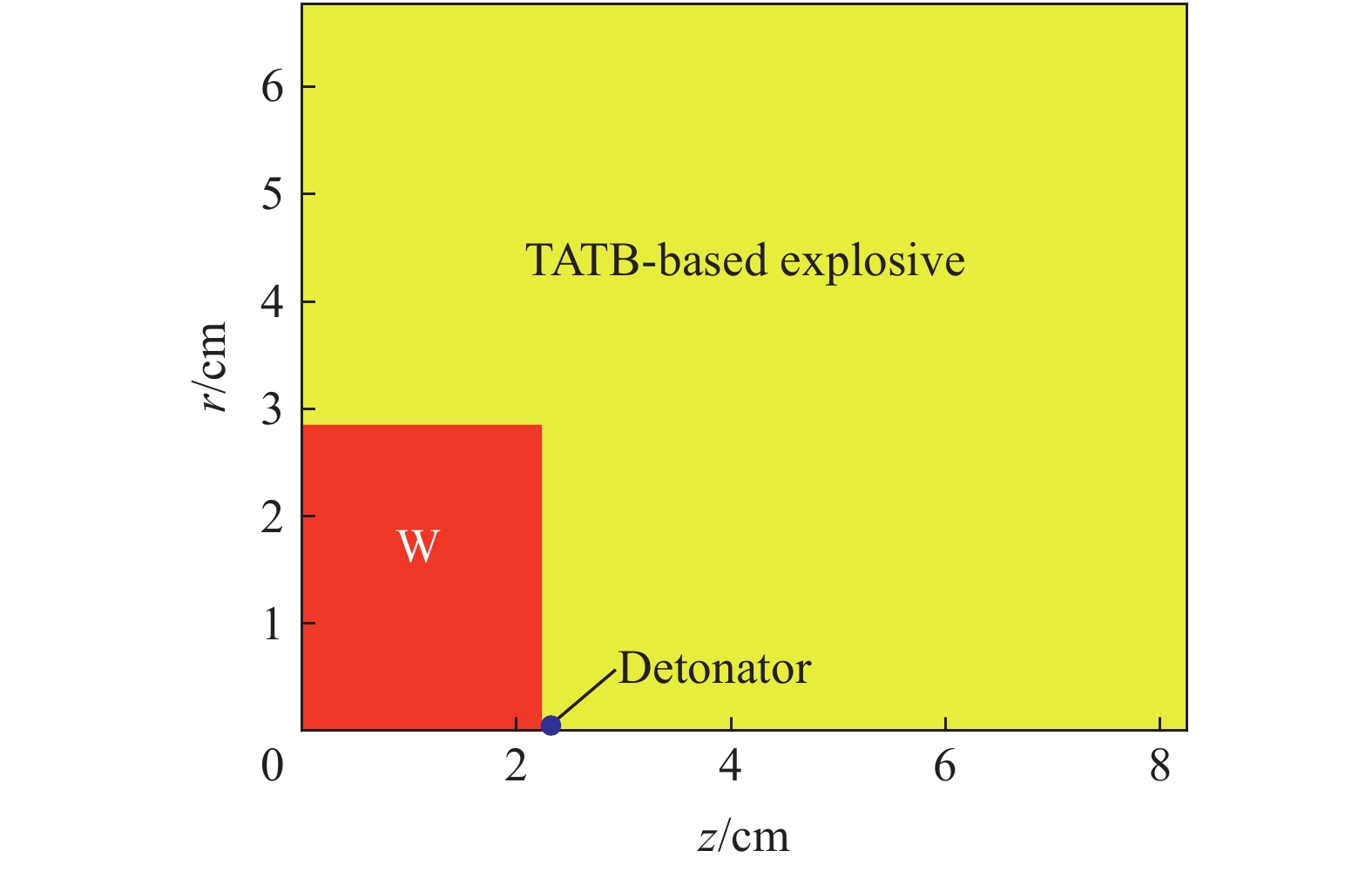
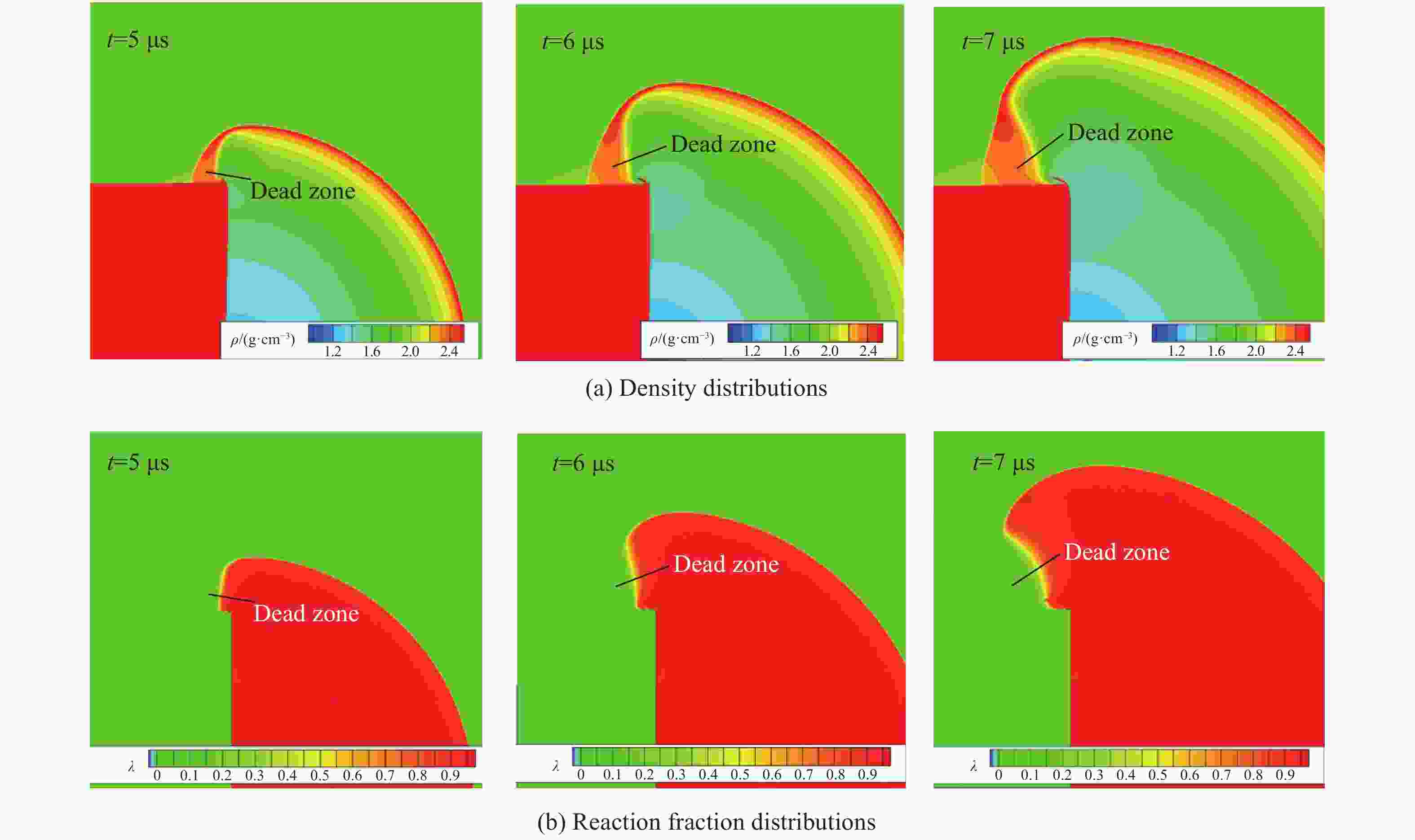
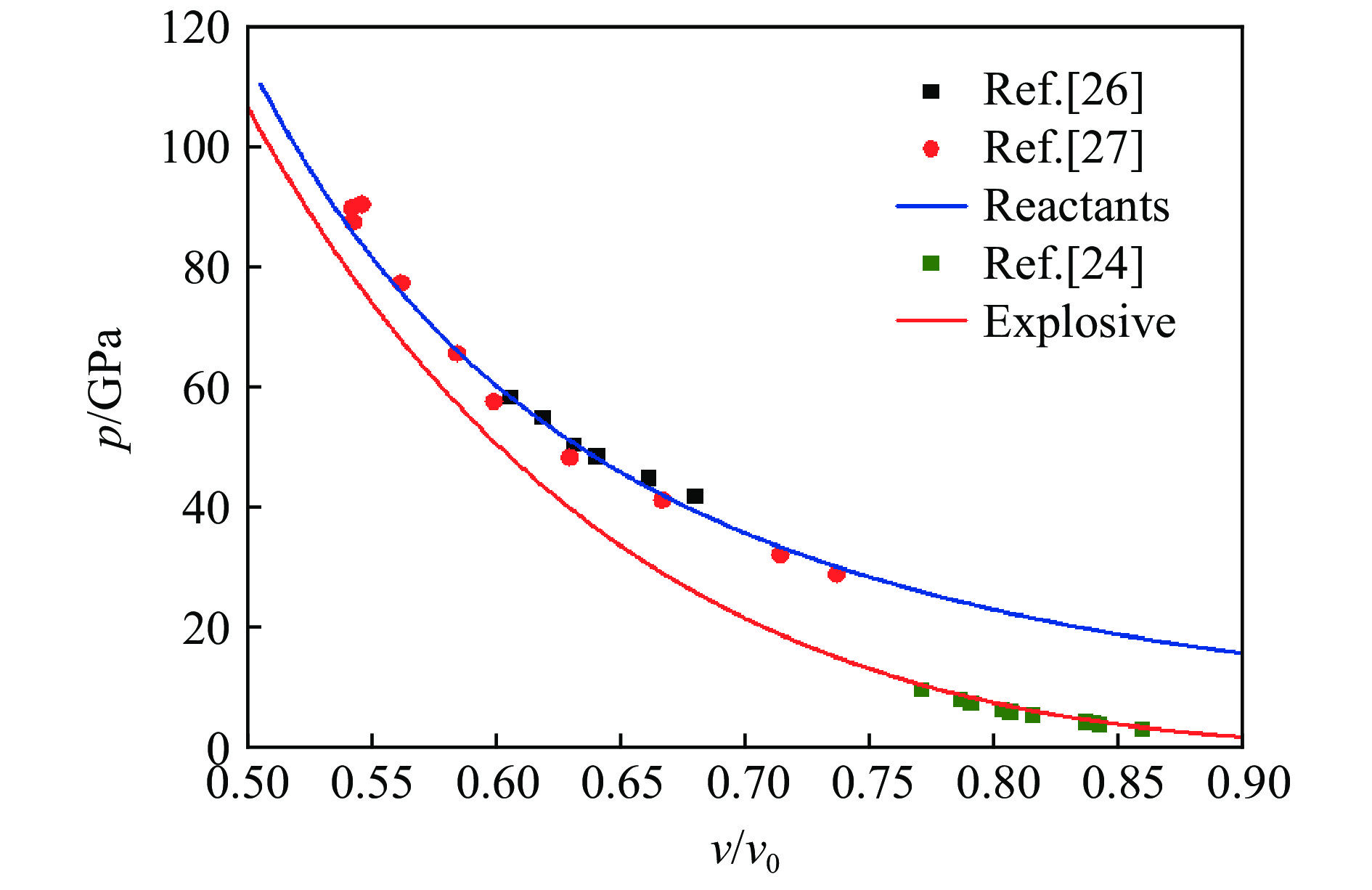
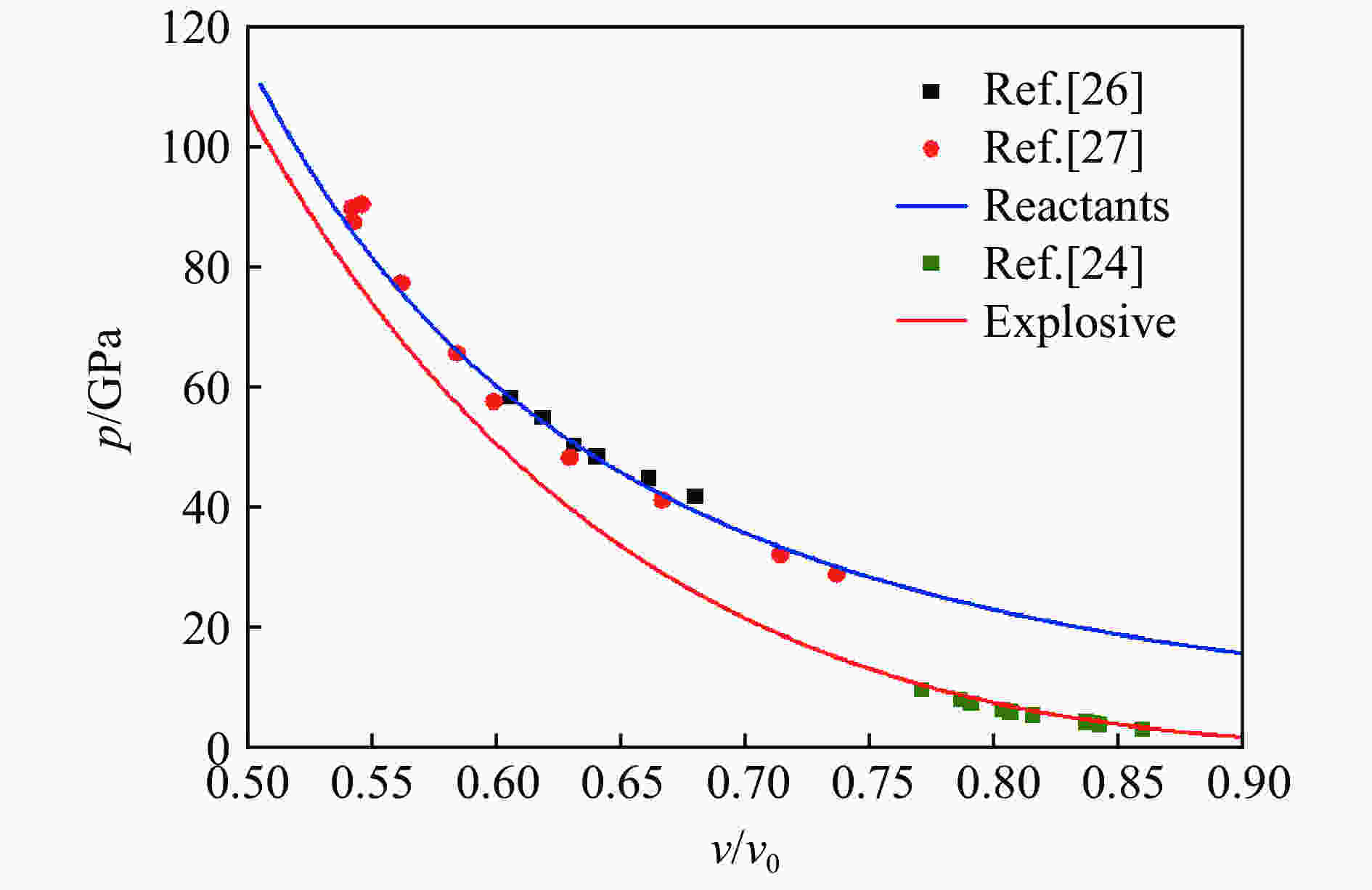
摘要: 为了对一种TATB基非均质炸药的预冲击起爆现象展开数值模拟研究，将基于冲击温度及压力的AWSD反应率模型耦合进二维结构网格拉氏弹塑性流体力学程序。利用炸药及其产物的冲击雨贡纽实验数据校验了未反应炸药及产物的状态方程参数，通过一维冲击起爆的模拟，标定了反应速率模型参数。模拟了炸药在弱冲击0.45 μs后跟随的强冲击波的二次冲击实验，结果表明，受预压缩区域的炸药反应变慢，到爆轰距离增长了约1 mm，与该炸药二次冲击实验减敏现象相符。模拟拐角效应时，爆轰波经过拐角后，在拐角附近形成稳定的不起爆区域，与主要成分相同的LX-17炸药的拐角效应实验的死区特征相符。数值模拟结果表明，基于冲击温度及压力的AWSD反应率模型可以较好地模拟非均质炸药预冲击减敏问题。Abstract: To study and simulate the pre-shock desensitization in the TATB-based heterogeneous explosive, the impact temperature and pressure based AWSD reaction flow model was implemented in a 2D structured mesh Lagrangian elastoplastic hydrodynamics program. The reactant and product EOS parameters were calibrated against the Hugoniot experimental data. To calibrate the parameters of the reaction flow model, one-dimensional numerical simulations of the shock initiation experiments were carried out. We simulated the double-shock experiments in which a first weak shock was followed by a second strong shock with a time interval of 0.45 μs. The results indicate the reaction becomes slower in the precompressed region and the run-to-detonation distance is about 1 mm longer than that in the uncompressed region, which is consistent with the desensitization in double-shock experiments. When simulating the corner-turning, the detonation wave passes through the corner and forms a stable non-initiation region near the corner, which is consistent with the dead zone characteristics of the corner-turning experiment of the LX-17 explosive with the same main composition. The numerical simulation results show that the AWSD reaction rate model based on the impact temperature and pressure can well simulate the pre-shock desensitization of heterogeneous explosives.
-
Key words:
- TATB-based /
- heterogeneous explosive /
- pre-shock /
- desensitization /
- AWSD model
-
地下化学爆炸过程中一氧化碳等有害气体在岩体中的渗漏行为研究对人员安全防护有重要参考意义, 不少学者对气体渗漏行为进行过数值模拟和现场监测。在以往的地下爆炸实验中, 对气体渗漏行为进行过大量的监测[1-2]。J.J.Nitao[3]开发的NUFT、B.J.Travis[4]开发的TRACR3D都是多孔介质中流体运动和输运程序, 应用于地下爆炸实验围岩和堵塞段中气体渗漏的模拟及示踪气体渗漏监测结果的分析。乔登江[5]分别用井筒一维多孔介质渗透模型、单一裂缝渗漏模型估算过花岗岩中封闭爆炸气体渗漏的速度和时间。王铁良等采用双孔隙度双渗透率模型对裂隙岩体中封闭爆炸气体渗漏行为进行过数值模拟[6], 在模型中考虑了渗透、扩散、热传导、热辐射等因素[7]。张建鑫等[8]用商业软件对高压驱动下非均匀介质内气体输运行为进行了数值模拟研究。
数值模拟中计算参数的选取与介质有关, 往往要根据同一场地或类似介质中已经进行过的爆炸实验气体渗漏监测结果反演参数, 再利用反演得到的参数对将要进行的爆炸实验气体渗漏行为进行数值模拟。如果相同介质中不同药量爆炸气体渗漏行为有一定的规律, 就可以直接用以往爆炸实验的气体渗漏监测结果, 估算将要进行的爆炸实验气体渗漏行为。
王铁良等[9]假设不同当量爆炸的埋深满足缩比关系, 即不同当量实验的L/W2/3是相同的, L表示埋深, W表示爆炸当量。分别针对3种渗漏机理:(1)气体通过均匀多孔介质渗漏, (2)气体通过非均匀多孔介质渗漏, (3)气体通过贯通裂缝渗漏, 通过理论分析和数值模拟研究了缩比化学爆炸实验气体渗漏时间、渗漏量与药量的关系。结论是, 不论哪种渗漏机理, 气体渗漏出介质的时间近似与W2/3成正比, 气体最终的渗漏份额基本一致。
本文中, 设计相同介质中的缩比实验, 监测CO的渗漏时间和渗漏份额, 与理论分析结果[9]对比。
1. 实验设计
文献[9]的理论研究结果显示, 如果相同介质中不同当量实验的埋深满足缩比关系, 则气体渗漏时间与L2或W2/3成正比, 渗漏份额基本一致。根据理论研究结果, 在不同尺寸花岗岩试样中进行缩比实验, 在实验中监测CO渗漏情况, 对监测结果进行总结分析。
选择陕西粗颗粒黑云母花岗岩, 采集完整的未风化无裂缝的花岗岩石块, 加工成立方体试样(见图 1)。由国土资源部西安矿产资源监督检测中心对岩石样品化学成分进行了检测, 分别为:w(SiO2)=69.2%, w(Si2O3)=15.06%, w(TFe2O3)=2.65%, w(FeO)=1.42%, w(K2O)=4.00%, w(Na2O)=4.25%, w(CaO)=2.12%。由贝士德仪器科技有限公司对花岗岩样品密度和孔隙度进行了测量, 测得平均密度为2 665.7 kg/m3, 平均孔隙度为1.3%。花岗岩的抗压强度和抗拉强度分别为154和12.2 MPa[10]。
花岗岩的试样尺寸、爆室尺寸、爆炸当量设计如表 1所示。表中, ag为花岗岩试样的边长, dc和lc分别为爆室的直径和高度, WTNT为炸药的TNT当量。根据理论计算, 按本文中设计的比例爆室半径, 化爆在岩石中产生的应力小于花岗岩的抗压强度, 同时, 爆后空腔内的静态压力小于花岗岩的抗拉强度, 爆后不会出现试样破碎破裂现象。
表 1 实验设计Table 1. Design of experimentsNo. ag/mm dc/mm lc/mm WTNT/g 1 500 80 80 1.25 2 500 80 80 1.25 3 1 000 160 160 10.00 4 1 000 160 160 10.00 装药孔和爆室设计如图 2所示。为了增加回填物与孔壁的摩擦力, 并有利于封闭, 在装药孔的孔壁设置数个环形嵌槽, 如图 3所示。炸药固定在特制的钢支架中心(见图 4), 连同支架放入爆室后炸药在爆室中心。装药后用花岗岩芯和环氧树脂对装药孔密实回填。
装药后, 将花岗岩试样放入1.2 m×1.2 m×2.0 m的矩形透明密闭室内, 实验中监测密闭室内的CO浓度, 并观察爆后现象。
各次实验之后, 花岗岩试样外观与爆炸前一样, 未见到花岗岩试样破裂现象, 无喷发性泄漏, 气体是通过花岗岩孔隙慢慢渗漏出来的。
2. CO浓度监测结果
各次实验密闭室内CO浓度随时间的变化曲线如图 5所示。由图可见, 爆后初期CO浓度有所起伏, 原因是爆后初期渗漏出来的CO并未在密闭室内混合均匀, 后来起动密闭室内的搅动设备将密闭室内的气体混合均匀。实验1~4中气体渗漏出来的时间分别为537、533、2 040和1 980 s。
3. 实验结果分析
3.1 气体渗漏时间
根据文献[9]的理论研究结果, 如果介质相同, 药量越小, 气体渗漏越早。边长0.5 m花岗岩中, 1.25 g TNT实验与边长1 m花岗岩中10 g TNT实验之间有1:2的缩比关系, 10 g TNT实验与1.25 g TNT实验气体渗漏时间有约4倍的关系。由实验结果, 10 g TNT实验与1.25 g TNT实验CO渗漏出来的时间倍数为约4, 实验结果与理论分析结果基本一致。
3.2 密闭室内CO浓度基本稳定时间
如果把密闭室内CO浓度基本稳定的时间看作气体渗漏基本停止的时间, 2次1.25 g TNT实验在爆后约200 min时CO浓度基本稳定, 而2次10 g TNT实验在约800 min时CO浓度基本稳定。10 g TNT实验与1.25 g TNT实验气体停止渗漏时间有约4倍关系。
3.3 气体渗漏份额
实验所用的炸药为黑索金。根据黑索金的反应方程式可知, 1 g黑索金爆炸产生的CO在标准状态下约300 ml。由于1 g黑索金相当于1.5 g TNT当量, 所以, 计算出1.25 g TNT当量实验和10 g TNT当量实验CO的产生量分别为250和2 000 ml。
密闭室内部体积为2.88 m3, 气体搅动设备体积为0.33 m3, CO变送器体积为0.05m3, 10 g TNT实验花岗岩试样体积1 m3, 1.25 g TNT实验花岗岩试样体积0.125 m3。由此算出, 1.25 g TNT实验密闭室内空间体积为2.47 m3, 10 g TNT实验密闭室内空间体积为1.5 m3。
根据各次实验炸药爆炸CO生成量、密闭室浓度稳定值及密闭室内空间体积, 计算出实验1~4中渗漏到密闭室内的CO占炸药爆炸生成的CO的份额分别为:1.06、1.15、0.59和0.56。
由实验结果, 对于缩比实验来说, 小药量实验气体渗漏份额大于大药量实验气体渗漏份额。而且, 部分实验CO渗漏份额已经大于1, 说明实验中除了炸药产生CO之外, 还有其他物质产生CO。
爆室内除了炸药之外, 还有其他一些物质, 如塑料袋、胶带、电缆皮等。实验研究显示, 聚乙烯的半分解温度(在真空中加热30 min后重量损失一半所需的温度)为414 ℃, 在800 ℃的高温下, 质量约1 g的聚乙烯仅需1~2 min就能完全分解。由于炸药爆炸后爆室内高温会持续一段时间, 所以, 会将一些物质分解为气体。
文献[9]的理论研究结果显示, 不同药量缩比实验的气体渗漏份额基本相同, 而本文中实验结果是小药量实验气体渗漏份额大于大药量实验气体渗漏份额。可认为在实验中爆室内安装炸药所用的塑料袋、胶带等物质分解产生一定量的非冷凝气体, 这就改变了爆室内非冷凝气体及CO的初始条件。1.25 g TNT实验和10 g TNT实验药量不同, 但爆室内可分解材料绝对量相差不大, 小药量实验因材料分解而增加的非冷凝气体相对量大于大药量实验。由监测结果推导渗漏份额时并未考虑材料分解增加的非冷凝气体, 所以, 推出的小药量实验气体渗漏份额大于大药量实验的气体渗漏份额。
本文中认为, 药量越大, 材料分解产生的气体与炸药爆炸所产生的气体之比越小, 所以可以推测, 当炸药质量远大于胶带和电缆皮的质量之后, 缩比实验的气体渗漏份额将基本相同。这方面还需要进一步的实验验证。
聚乙烯分解产生的气体改变了不同药量实验气体渗漏份额的关系, 但气体渗漏时间的关系仍与理论分析结果基本一致。原因是材料分解时吸收热量, 虽然爆室内气体增加了, 但温度降低了, 二者对压力的贡献有一定的抵消作用, 而气体渗漏速度决定于压力梯度, 所以对气体渗漏速度影响不大。上面只是定性的分析, 定量分析还需要进一步开展工作。
4. 总结
为研究花岗岩中不同药量缩比爆炸实验气体渗漏行为之间的关系, 设计了满足缩比关系的当量分别为10 g TNT和1.25 g TNT的化学爆炸实验, 监测了渗漏出来的CO浓度历程。通过研究得到如下结论:
(1) 相同介质中缩比实验气体渗漏出来的时间大约与药量的三分之二次方成正比, 渗漏停止时间也大约与药量的三分之二次方成正比;
(2) 封闭化学爆炸在爆室内产生的高温能够使爆室内一些物质分解产生非冷凝气体;
(3) 对于不同药量的缩比实验, 理论分析认为气体渗漏份额基本相同, 但在实验中, 由于胶带、电缆皮等材料的分解产生非冷凝气体, 这些气体对于较小药量实验的影响较大, 所以较小药量实验的气体渗漏份额大于较大药量实验的气体渗漏份额。
-
图 2 冲击压力与到爆轰距离的关系
Figure 2. Relationships between impact pressure and run-to-detonation distance
图 4 二次冲击压缩炸药粒子速度曲线的实验结果
Figure 4. Experimental particle velocity curves of explosive by double-shock compression
图 5 二次冲击压缩炸药粒子速度曲线的数值模拟结果
Figure 5. Simulated particle velocity curves of explosive by double-shock compression
图 6 不同位置计算单元的反应份额
Figure 6. Reaction fractions of numerical elements at different positions
图 10 AWSD模型的拐角效应特征时刻密度和反应份额分布
Figure 10. Density and reaction fraction distributions at character times for corner-turning by the AWSD model
图 11 WSD模型的拐角效应特征时刻密度和反应份额分布
Figure 11. Density and reaction fraction distributions at character times for corner-turning by the WSD model
表 1 未反应TATB基炸药的Davis状态方程参数
Table 1. Davis EOS parameters of unreacted TATB-based explosive
A/(mm·μs−1) B C Z Γ0s E0/(kJ·g−1) αst cVs/(kJ·g−1·K−1) 1.93 4.26 0.30 0 0.56 3.80 0.757 0 0.000 967 
下载: 导出CSV
表 2 TATB基炸药产物的Davis状态方程参数
Table 2. Davis EOS parameters of reaction products of TATB-based explosive
A k vc/(cm3·g−1) pc/GPa n b cVg/(kJ·g−1·K−1) 0.835 603 1.30 0.926 85 1.485 1 4.242 66 0.85 0.001 072
下载: 导出CSV
表 3 TATB基炸药AWSD模型参数
Table 3. Parameters of the AWSD model for the TATB-based explosive
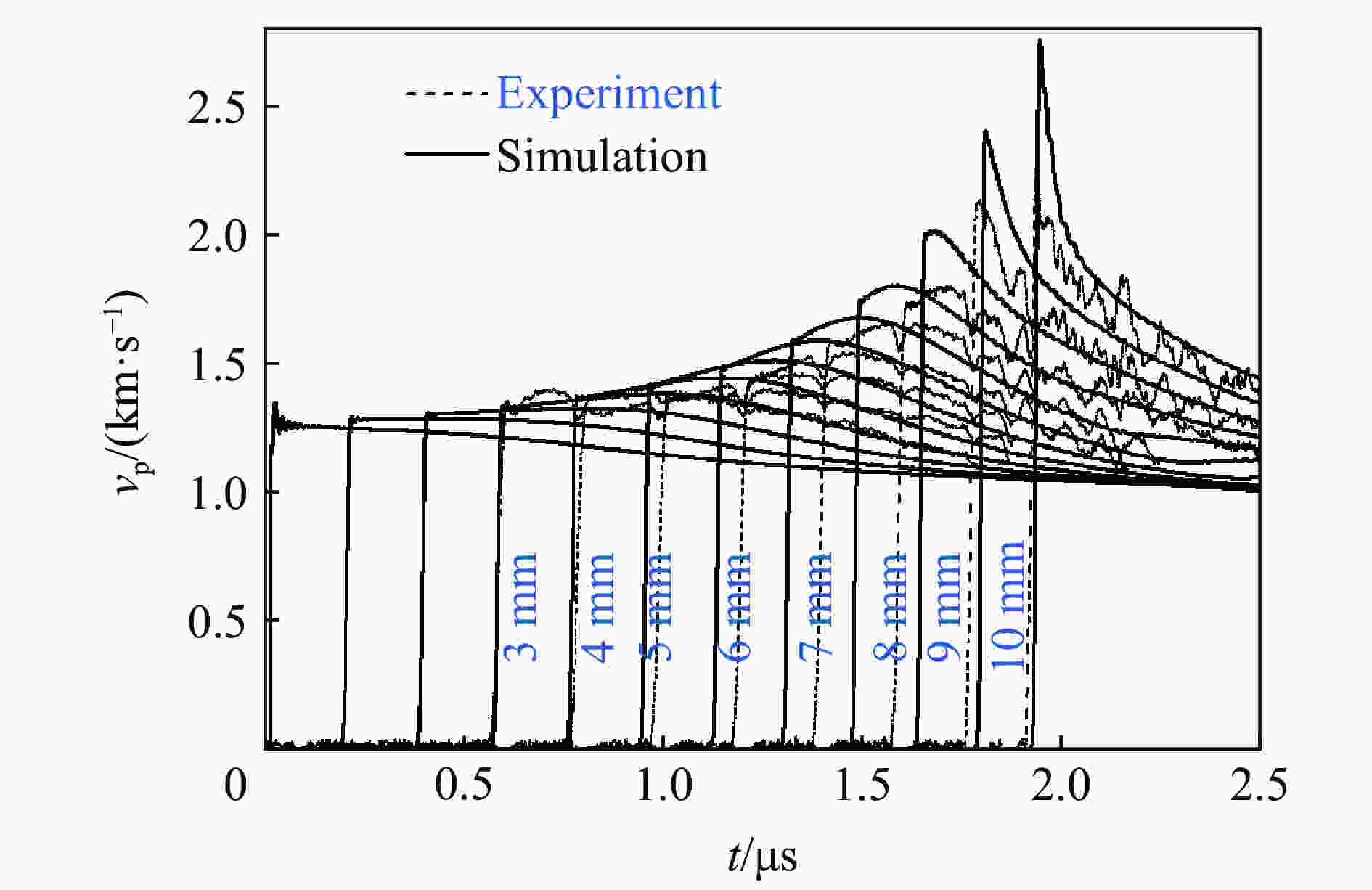
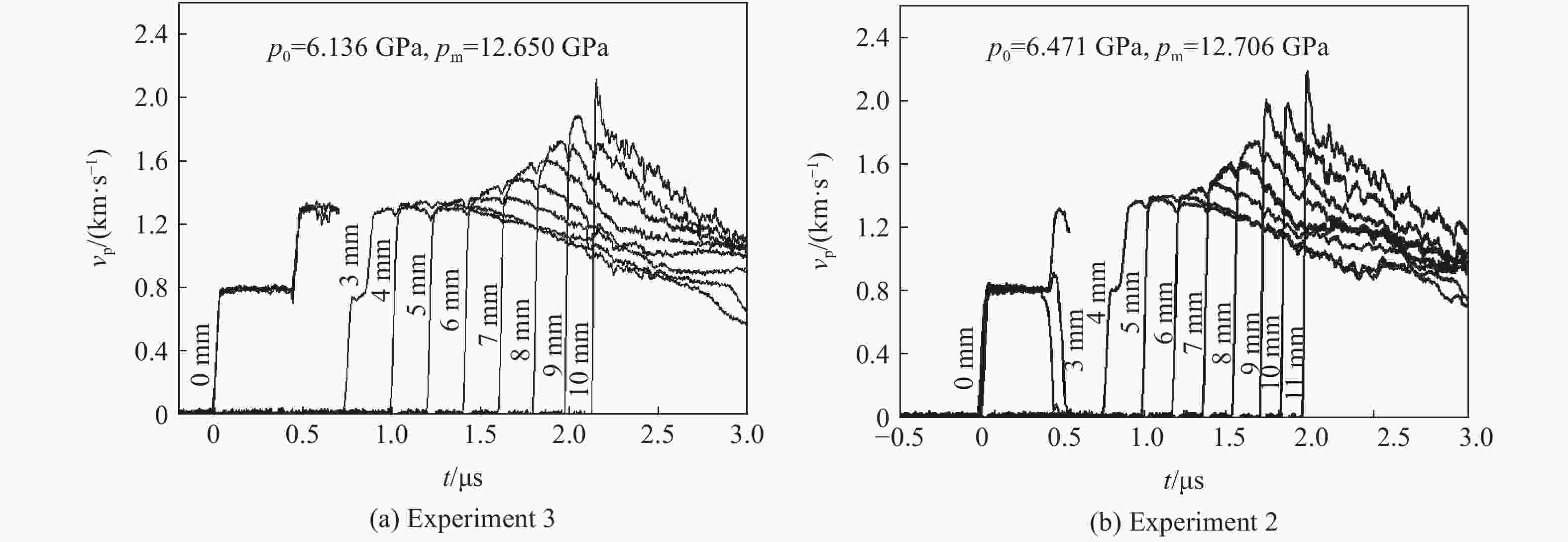
np ps/GPa k1/s−1 T1/K a1 b1 b2 k2/s−1 T2/K fs λc δλ 0.651 5 27.60 336 1 724 0.060 81 2.122 0.9 10 200 6 278 0.035 87 0.876 4 0.021 68
下载: 导出CSV
表 4 二次冲击起爆实验的到爆轰距离和到爆轰时间的实验和数值模拟结果
Table 4. Experimental and simulated results of distance and time of run to detonation by double-shock initiation
实验 方法 ρ0/(g·cm−3) v0/(km·s−1) p0/GPa pm/GPa L*/mm T*/μs 3 实验 1.881 1.669 6.135 6 12.649 9 9.845 1.716 数值模拟 10.141 1.679 2 实验 1.881 1.732 6.470 6 12.706 4 9.145 1.356 数值模拟 9.240 1.505
下载: 导出CSV
-
[1] CAMPBELL A W, DAVIS W C, RAMSAY J B, et al. Shock initiation of solid explosives [J]. Physics of Fluids, 1961, 4(4): 511. DOI: 10.1063/1.1706354. [2] CAMPBELL A W, TRAVIS J R. The shock desensitization of PBX-9404 and composition B-3 [C] // Proceedings of the 8th International Detonation Symposium. Albuquerque: Naval Surface Weapons Center, 1985: 1057−1068. [3] MULFORD R N, SHEFFIELD S A, ALCON R R. Preshock desensitization of PBX explosives [J]. AIP Conference Proceedings, 1994, 309(1): 1405–1408. DOI: 10.1063/1.46243. [4] TARVER C M, COOK T M, URTIEW P A, et al. Multiple shock initiation of LX-17 [C] // Proceedings of the 10th International Detonation Symposium. Boston: Office of Naval Research, 1993: 676−703. [5] BAT’KOV Y V, GLUSHAK B L, NOVIKOV S A. Desensitization of pressed explosive compositions based on TNT, RDX, and HMX under double shock-wave loading [J]. Combustion, Explosion and Shock Waves, 1995, 31(4): 482–485. DOI: 10.1007/BF00789372. [6] GUSTAVSEN R L, SHEFFIELD S A, ALCON R R, et al. Double shock initiation of the HMX based explosive EDC-37 [J]. AIP Conference Proceedings, 2002, 620(1): 999–1002. DOI: 10.1063/1.1483706. [7] MADER C L. Numerical modeling of explosives and propellants [M]. 3rd ed. Boca Raton: CRC Press, 2008. [8] HUSSAIN T, LIU Y, HUANG F L, et al. Modeling and simulation of preshock desensitization in heterogeneous explosives using a mesoscopic reaction rate model [J]. Simulation, 2015, 91(11): 980–988. DOI: 10.1177/0037549715608962. [9] BORDZILOVSKII S A, KARAKHANOV S M. Desensitization of pressed RDX/paraffin and HMX/paraffin compounds by multiple shock waves [J]. Combustion, Explosion and Shock Waves, 1995, 31(2): 227–235. DOI: 10.1007/BF00755754. [10] LEE E L, TARVER C M. Phenomenological model of shock initiation in heterogeneous explosives [J]. The Physics of Fluids, 1980, 23(12): 2362–2372. DOI: 10.1063/1.862940. [11] JOHNSON J N, TANG P K, FOREST C A. Shock-wave initiation of heterogeneous reactive solids [J]. Journal of Applied Physics, 1985, 57(9): 4323–4334. DOI: 10.1063/1.334591. [12] WESCOTT B L, STEWART D S, DAVIS W C. Equation of state and reaction rate for condensed-phase explosives [J]. Journal of Applied Physics, 2005, 98(5): 053514. DOI: 10.1063/1.2035310. [13] DEOLIVEIRA G, KAPILA A K, SCHWENDEMAN D W, et al. Detonation diffraction, dead zones and the ignition and growth model [C] // Proceedings of the 13th International Detonation Symposium. Norfolk: Office of Naval Research, 2006. [14] HUSSAIN T, LIU Y, HUANG F L, et al. Desensitization by pre-shocking in heterogeneous explosives and its numerical modelling [J]. Central European Journal of Energetic Materials, 2016, 13(2): 357–379. DOI: 10.22211/cejem/64990. [15] 郝鹏程, 冯其京, 洪滔, 等. 钝感炸药点火增长模型的欧拉数值模拟 [J]. 爆炸与冲击, 2012, 32(3): 243–250. DOI: 10.11883/1001-1455(2012)03-0243-08.HAO P C, FENG Q J, HONG T, et al. Eulerian simulation on insensitive explosives with the ignition-growth reactive model [J]. Explosion and Shock Waves, 2012, 32(3): 243–250. DOI: 10.11883/1001-1455(2012)03-0243-08. [16] STARKENBERG J. Shock-pressure and pseudo-entropic approaches to explosive initiation modeling [C] // Proceedings of the 15th International Detonation Symposium. San Francisco, 2014: 908−916. [17] STARKENBERG J. Modeling detonation propagation and failure using explosive initiation models in a conventional hydrocode [C] // Proceedings of the 12th International Detonation Symposium. Annapolis: Office of Naval Research, 2002. [18] HANDELEY C A. CREST reactive flow model [C] // Proceedings of the 13th International Detonation Symposium. Norfolk, 2006. [19] DESBIENS N, MATIGNON C, SORIN R. Temperature-based model for condensed-phase explosive detonation [J]. Journal of Physics: Conference Series, 2014, 500(15): 152004. DOI: 10.1088/1742-6596/500/15/152004. [20] ASLAM T D. Shock temperature dependent rate law for plastic bonded explosives [J]. Journal of Applied Physics, 2018, 123(14): 145901. DOI: 10.1063/1.5020172. [21] 裴红波, 刘俊明, 张旭, 等. 基于反向撞击法的JB-9014炸药Hugoniot关系测量 [J]. 爆炸与冲击, 2019, 39(5): 052301. DOI: 10.11883/bzycj-2017-0395.PEI H B, LIU J M, ZHANG X, et al. Measurement of Hugoniot relation for unreacted JB-9014 explosive with reverse-impact method [J]. Explosion and Shock Waves, 2019, 39(5): 052301. DOI: 10.11883/bzycj-2017-0395. [22] 刘俊明, 张旭, 裴红波, 等. JB-9014钝感炸药冲击Hugoniot关系测量 [J]. 高压物理学报, 2018, 32(3): 033202. DOI: 10.11858/gywlxb.20170669.LIU J M, ZHANG X, PEI H B, et al. Measurement of Hugoniot relation for JB-9014 insensitive explosive [J]. Chinese Journal of High Pressure Physics, 2018, 32(3): 033202. DOI: 10.11858/gywlxb.20170669. [23] 张旭, 池家春, 冯民贤. JB9014钝感炸药冲击绝热线测量 [J]. 高压物理学报, 2001, 15(4): 304–308. DOI: 10.11858/gywlxb.2001.04.011.ZHANG X, CHI J C, FENG M X. Hugoniot relation of JB9014 insensitive high explosive [J]. Chinese Journal of High Pressure Physics, 2001, 15(4): 304–308. DOI: 10.11858/gywlxb.2001.04.011. [24] 刘俊明. JB-9014炸药未反应状态方程研究[D]. 四川绵阳: 中国工程物理研究院, 2018. [25] 徐辉, 孙占峰. 钝感高能炸药JB-9014做功能力的实验研究 [J]. 高压物理学报, 2013, 27(4): 582–586. DOI: 10.11858/gywlxb.2013.04.018.XU H, SUN Z F. An experimental study on the capacity for work of insensitive high explosive [J]. Chinese Journal of High Pressure Physics, 2013, 27(4): 582–586. DOI: 10.11858/gywlxb.2013.04.018. [26] 曾代朋, 陈军, 谭多望. 超压爆轰产物冲击绝热线的实验研究 [J]. 高压物理学报, 2010, 24(1): 76–80. DOI: 10.11858/gywlxb.2010.01.014.ZENG D P, CHEN J, TAN D W. Experiment research on the Hugoniot of JB-9014 explosive over-driven detonation product [J]. Chinese Journal of High Pressure Physics, 2010, 24(1): 76–80. DOI: 10.11858/gywlxb.2010.01.014. [27] TANG P K, ANDERSON W W, FRITZ J N, et al. A study of the overdriven behaviors of PBX 9501 and PBX 9502 [C] // Proceedings of the 11th International Detonation Symposium. Snowmass, CO, 1998. [28] 张琪敏, 张旭, 赵康, 等. TATB基钝感炸药JB-9014的冲击起爆反应增长规律 [J]. 爆炸与冲击, 2019, 39(4): 041405. DOI: 10.11883/bzycj-2018-0050.ZHANG Q M, ZHANG X, ZHAO K, et al. Law of reaction growth of shock initiation on the TATB based insensitive explosive JB-9014 [J]. Explosion and Shock Waves, 2019, 39(4): 041405. DOI: 10.11883/bzycj-2018-0050. [29] 黄文斌, 文尚刚, 谭多望, 等. 在球面散心冲击波作用下JB-9014炸药冲击引爆过程实验研究 [J]. 爆炸与冲击, 2006, 26(4): 373–376. DOI: 10.11883/1001-1455(2006)04-0373-04.HUANG W B, WEN S G, TAN D W, et al. Experimental study on shock initiation process of JB-9014 under loading conditions of divergent spherical shock wave [J]. Explosion and Shock Waves, 2006, 26(4): 373–376. DOI: 10.11883/1001-1455(2006)04-0373-04. [30] 訾攀登, 陈军, 张蓉, 等. 二次压缩条件下JOB-9003炸药特性研究 [J]. 高压物理学报, 2017, 31(2): 155–161. DOI: 10.11858/gywlxb.2017.02.007.ZI P D, CHEN J, ZHANG R, et al. Characteristics of JOB-9003 in double shocks experiments [J]. Chinese Journal of High Pressure Physics, 2017, 31(2): 155–161. DOI: 10.11858/gywlxb.2017.02.007. [31] FERM E N, MORRIS C L, QUINTANA J P, et al. Proton radiography examination of unburned regions in PBX 9502 corner turning experiments [J]. AIP Conference Proceedings, 2002, 620(1): 966–969. DOI: 10.1063/1.1483699. [32] SOUERS P C, ANDRESKI H G, COOK Ⅲ C F, et al. LX-17 corner-turning [J]. Propellants, Explosives, Pyrotechnics, 2004, 29(6): 359–367. DOI: 10.1002/prep.200400067. [33] WHITWORTH N J. CREST modelling of PBX 9502 corner turning experiments at different initial temperatures [J]. Journal of Physics: Conference Series, 2014, 500(5): 052050. DOI: 10.1088/1742-6596/500/5/052050. 期刊类型引用(1)
1. 钟巍, 田宙, 王铁良. 基于量纲分析和达西定律的地下化学爆炸气体泄漏规律. 计算物理. 2019(04): 449-456 . 
百度学术其他类型引用(0)
-
下载:
百度学术
计量
- 文章访问数: 663
- HTML全文浏览量: 249
- PDF下载量: 99
- 被引次数: 1