Mechanism study of preventing crack propagation of fractured rockunder dynamic loads
-
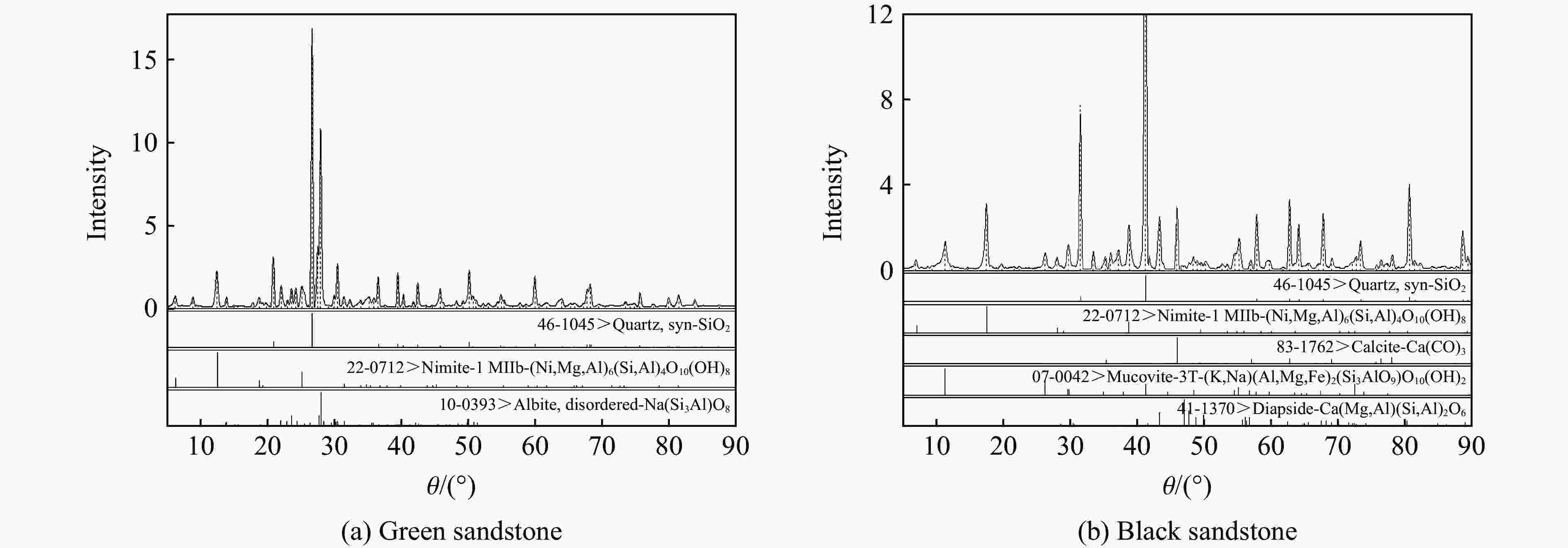
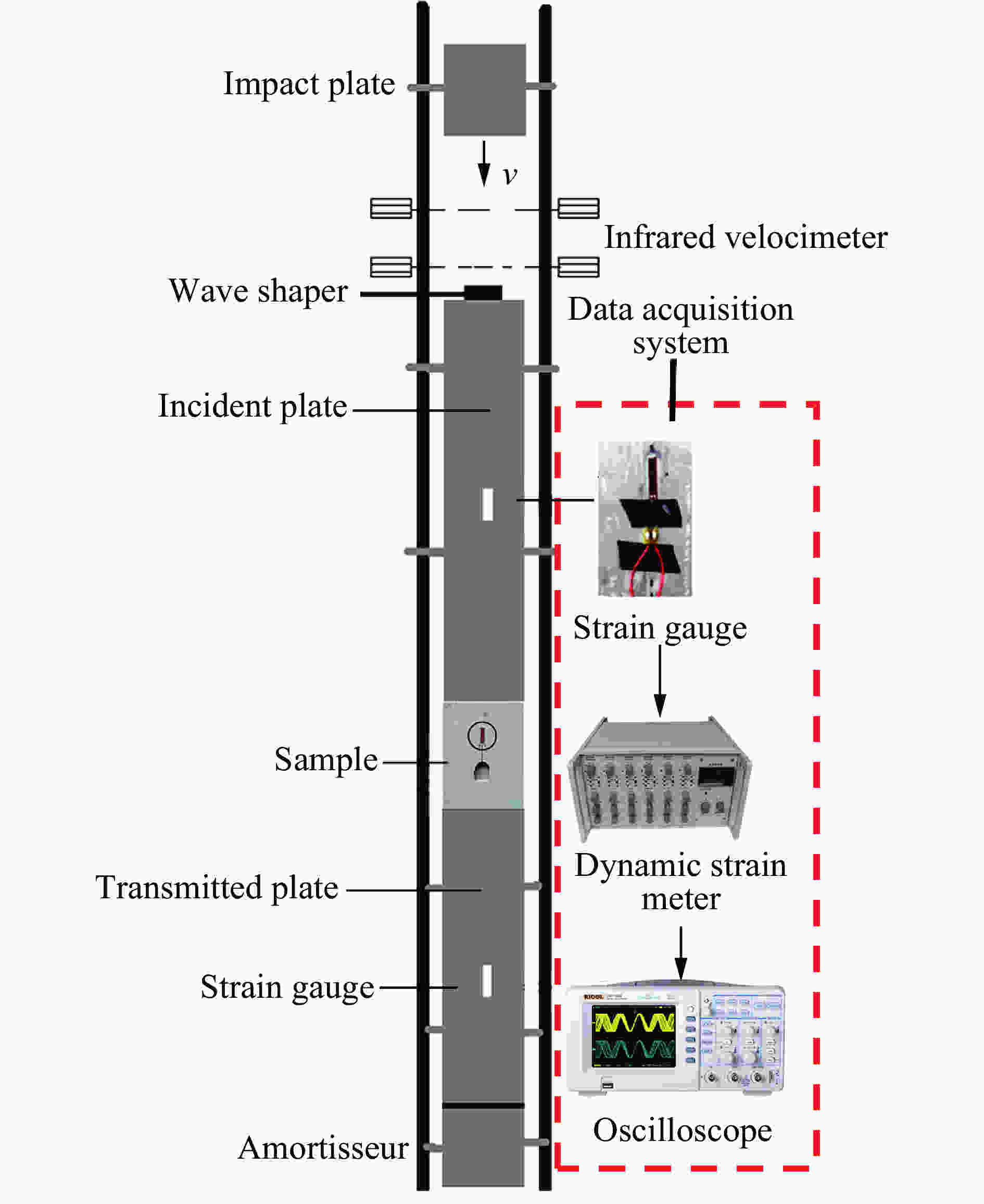
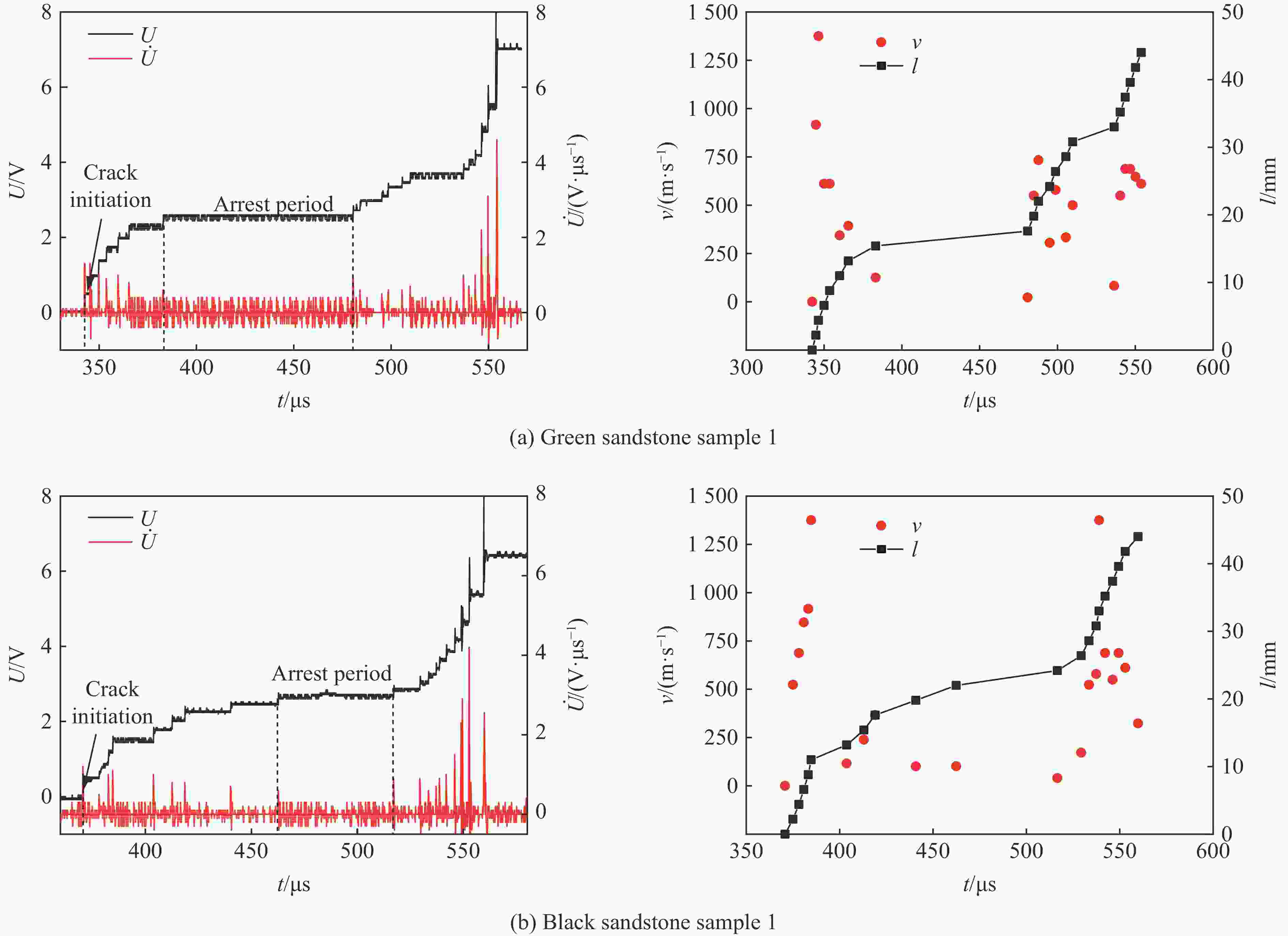
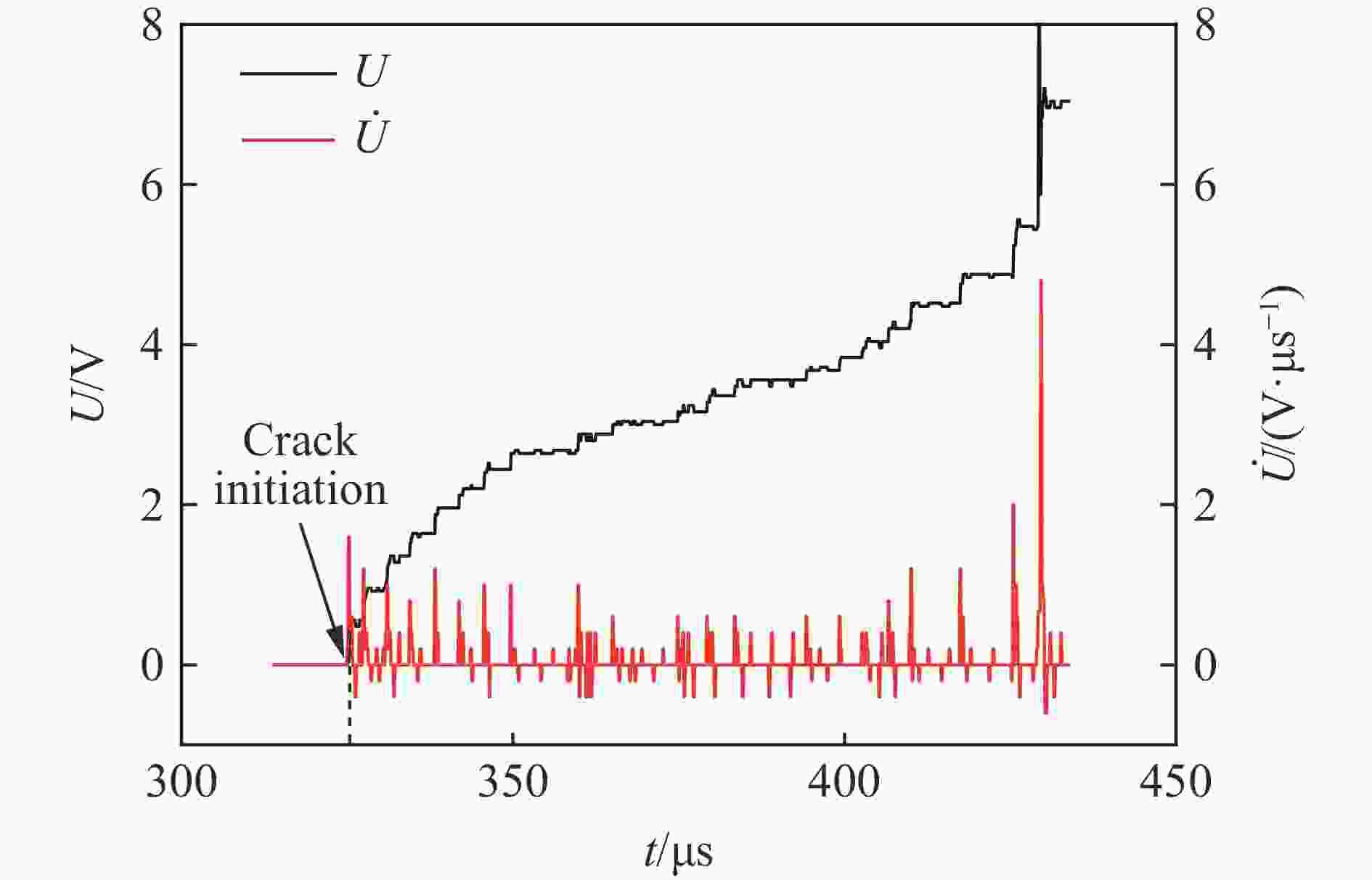
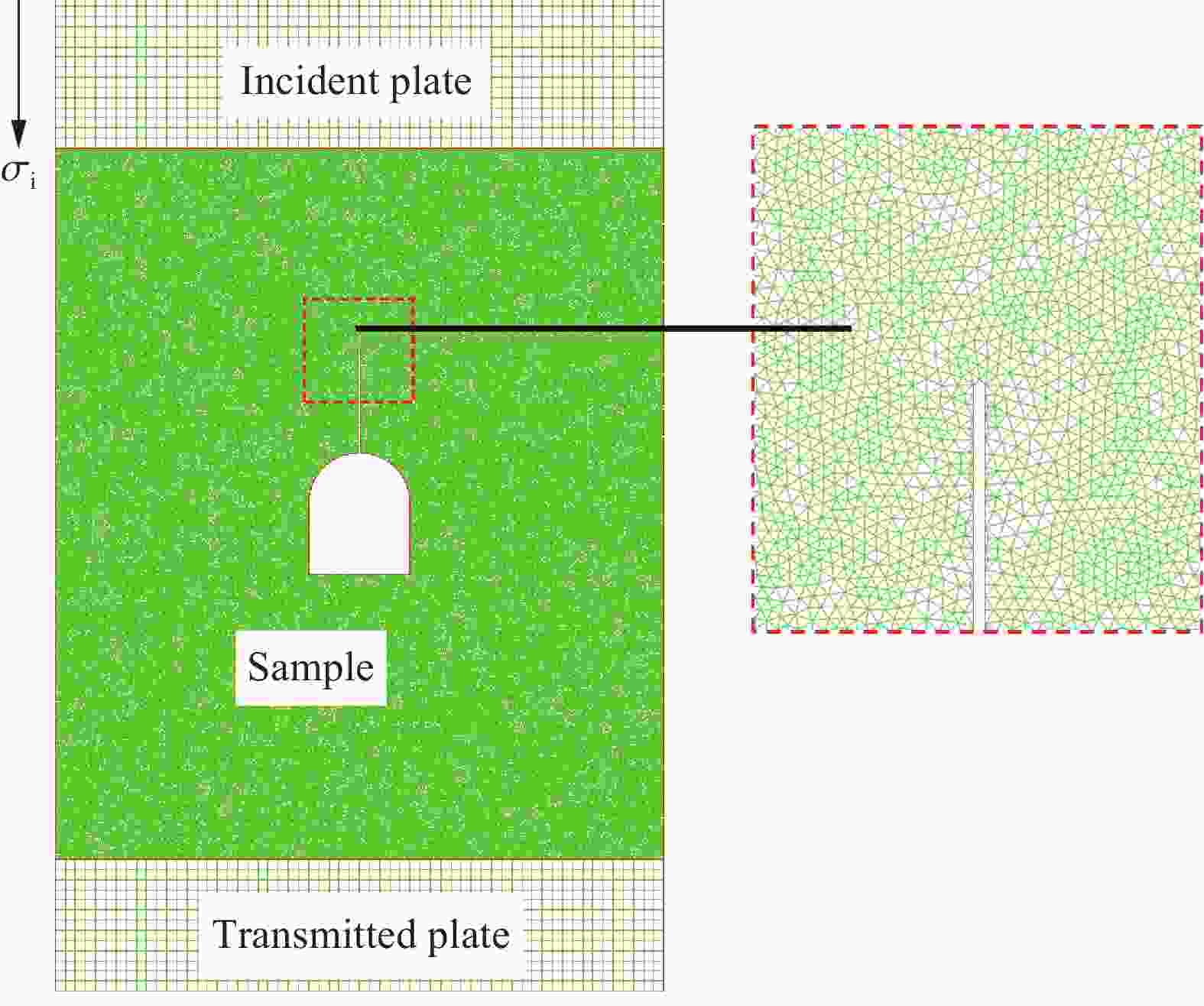
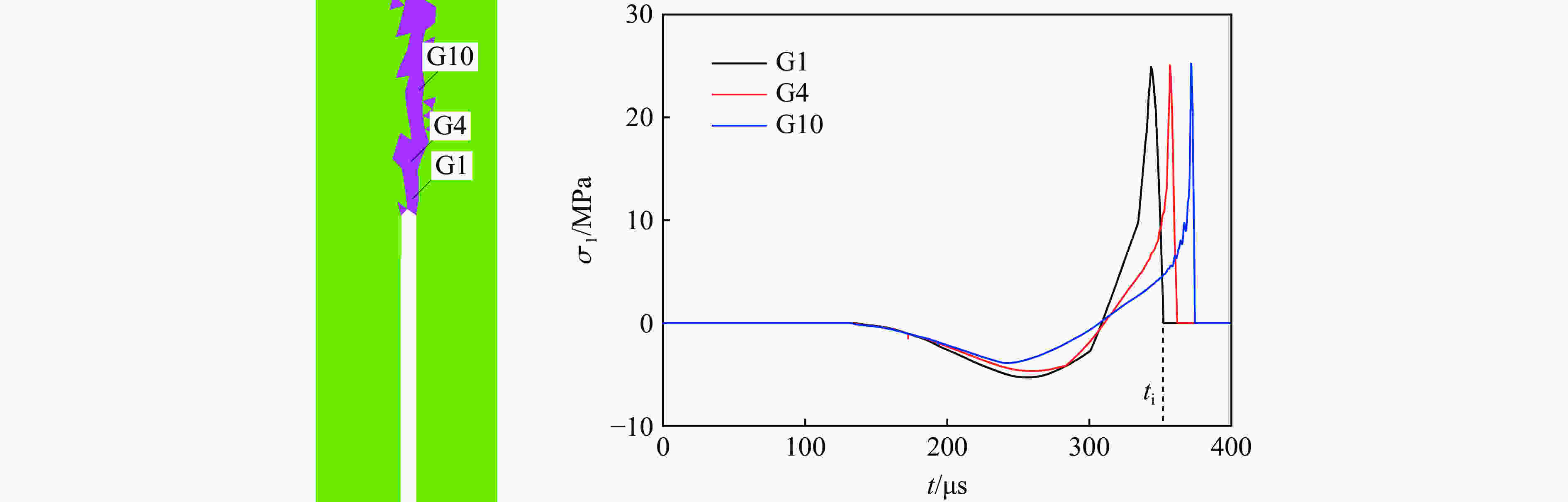
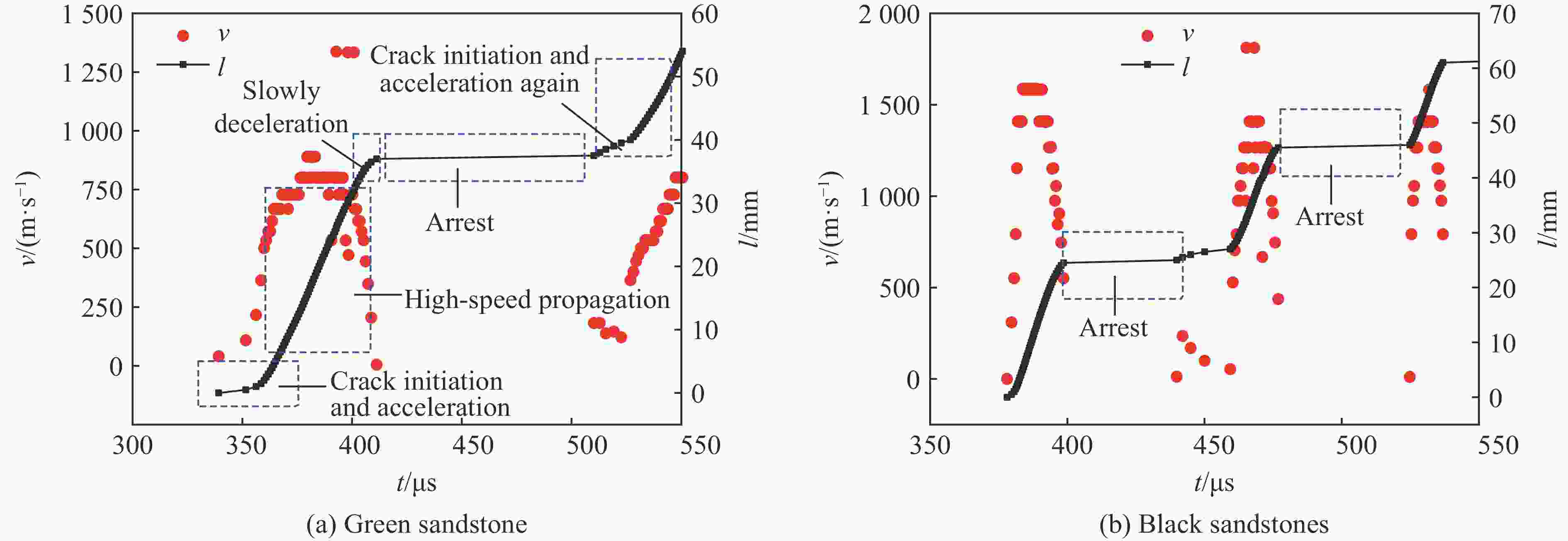
摘要: 为深层次了解裂隙岩体在动载荷作用下的动态断裂特性及止裂机理，采用TWSRC（tunnel with single radial crack）构型进行中低速冲击实验，选择砂岩作为原材料制作裂隙岩体试样，以落锤冲击试验装置与裂纹扩展计实验系统对裂纹的动态起裂、扩展及止裂过程进行全过程监测，重点研究动态破裂过程的破裂行为及止裂现象。使用有限差分法程序进行数值模拟，验证冲击实验结果的科学性与准确性。研究发现：裂隙岩体的动态断裂过程是由起裂加速-高速扩展-缓慢减速-止裂-再次起裂加速-再次高速扩展等多次循环的过程构成，且止裂区间尺寸为微秒量级；裂隙岩体止裂位置的穿晶断裂比例远小于初始起裂点，青砂岩动态断裂过程的穿晶断裂比例稍大于黑砂岩；裂隙岩体中止裂点再次起裂所需的能量，远小于预制裂纹初始起裂所需要的能量。Abstract: To deeply understanding dynamic fracture properties and preventing crack propagation of fractured rock mass under dynamic loads, impact experiments were conducted using TWSRC (tunnel with single radial crack) samples, and sandstone were selected as the raw material to manufacture fractured rock samples. The crack initiation, propagation and obstructing behavior were measured by using a drop hammer impact test device and crack propagation gauge measuring system. The mechanism of preventing crack propagation and failure behavior during dynamic fracturing process was focused, and then the corresponding numerical simulation was conducted by using the finite difference code, which can be used to accurately estimate the experiment result. The results indicate that the whole dynamic fracturing process of fractured rock under dynamic loads is composed of the cyclic process of crack initiation, high-speed crack propagation, slowly deceleration, preventing crack propagation. In addition, the period of crack obstruction was approximate the microsecond level. The ratio of transgranular (TG) fracture at the crack obstruction point of fractured rock was smaller than that of the crack initiation point, and the ratio of TG fracture of green sandstone during the dynamic fracturing process was larger than that of black sandstone. The fracture energy for crack initiation again after crack obstruction was much less than the fracture energy required for the initial initiation of pre-existing crack.
-
Key words:
- fractured rock mass /
- dynamic load /
- crack propagation velocity /
- crack arrest /
- energy evolution
-
地下化学爆炸过程中一氧化碳等有害气体在岩体中的渗漏行为研究对人员安全防护有重要参考意义, 不少学者对气体渗漏行为进行过数值模拟和现场监测。在以往的地下爆炸实验中, 对气体渗漏行为进行过大量的监测[1-2]。J.J.Nitao[3]开发的NUFT、B.J.Travis[4]开发的TRACR3D都是多孔介质中流体运动和输运程序, 应用于地下爆炸实验围岩和堵塞段中气体渗漏的模拟及示踪气体渗漏监测结果的分析。乔登江[5]分别用井筒一维多孔介质渗透模型、单一裂缝渗漏模型估算过花岗岩中封闭爆炸气体渗漏的速度和时间。王铁良等采用双孔隙度双渗透率模型对裂隙岩体中封闭爆炸气体渗漏行为进行过数值模拟[6], 在模型中考虑了渗透、扩散、热传导、热辐射等因素[7]。张建鑫等[8]用商业软件对高压驱动下非均匀介质内气体输运行为进行了数值模拟研究。
数值模拟中计算参数的选取与介质有关, 往往要根据同一场地或类似介质中已经进行过的爆炸实验气体渗漏监测结果反演参数, 再利用反演得到的参数对将要进行的爆炸实验气体渗漏行为进行数值模拟。如果相同介质中不同药量爆炸气体渗漏行为有一定的规律, 就可以直接用以往爆炸实验的气体渗漏监测结果, 估算将要进行的爆炸实验气体渗漏行为。
王铁良等[9]假设不同当量爆炸的埋深满足缩比关系, 即不同当量实验的L/W2/3是相同的, L表示埋深, W表示爆炸当量。分别针对3种渗漏机理:(1)气体通过均匀多孔介质渗漏, (2)气体通过非均匀多孔介质渗漏, (3)气体通过贯通裂缝渗漏, 通过理论分析和数值模拟研究了缩比化学爆炸实验气体渗漏时间、渗漏量与药量的关系。结论是, 不论哪种渗漏机理, 气体渗漏出介质的时间近似与W2/3成正比, 气体最终的渗漏份额基本一致。
本文中, 设计相同介质中的缩比实验, 监测CO的渗漏时间和渗漏份额, 与理论分析结果[9]对比。
1. 实验设计
文献[9]的理论研究结果显示, 如果相同介质中不同当量实验的埋深满足缩比关系, 则气体渗漏时间与L2或W2/3成正比, 渗漏份额基本一致。根据理论研究结果, 在不同尺寸花岗岩试样中进行缩比实验, 在实验中监测CO渗漏情况, 对监测结果进行总结分析。
选择陕西粗颗粒黑云母花岗岩, 采集完整的未风化无裂缝的花岗岩石块, 加工成立方体试样(见图 1)。由国土资源部西安矿产资源监督检测中心对岩石样品化学成分进行了检测, 分别为:w(SiO2)=69.2%, w(Si2O3)=15.06%, w(TFe2O3)=2.65%, w(FeO)=1.42%, w(K2O)=4.00%, w(Na2O)=4.25%, w(CaO)=2.12%。由贝士德仪器科技有限公司对花岗岩样品密度和孔隙度进行了测量, 测得平均密度为2 665.7 kg/m3, 平均孔隙度为1.3%。花岗岩的抗压强度和抗拉强度分别为154和12.2 MPa[10]。
花岗岩的试样尺寸、爆室尺寸、爆炸当量设计如表 1所示。表中, ag为花岗岩试样的边长, dc和lc分别为爆室的直径和高度, WTNT为炸药的TNT当量。根据理论计算, 按本文中设计的比例爆室半径, 化爆在岩石中产生的应力小于花岗岩的抗压强度, 同时, 爆后空腔内的静态压力小于花岗岩的抗拉强度, 爆后不会出现试样破碎破裂现象。
表 1 实验设计Table 1. Design of experimentsNo. ag/mm dc/mm lc/mm WTNT/g 1 500 80 80 1.25 2 500 80 80 1.25 3 1 000 160 160 10.00 4 1 000 160 160 10.00 装药孔和爆室设计如图 2所示。为了增加回填物与孔壁的摩擦力, 并有利于封闭, 在装药孔的孔壁设置数个环形嵌槽, 如图 3所示。炸药固定在特制的钢支架中心(见图 4), 连同支架放入爆室后炸药在爆室中心。装药后用花岗岩芯和环氧树脂对装药孔密实回填。
装药后, 将花岗岩试样放入1.2 m×1.2 m×2.0 m的矩形透明密闭室内, 实验中监测密闭室内的CO浓度, 并观察爆后现象。
各次实验之后, 花岗岩试样外观与爆炸前一样, 未见到花岗岩试样破裂现象, 无喷发性泄漏, 气体是通过花岗岩孔隙慢慢渗漏出来的。
2. CO浓度监测结果
各次实验密闭室内CO浓度随时间的变化曲线如图 5所示。由图可见, 爆后初期CO浓度有所起伏, 原因是爆后初期渗漏出来的CO并未在密闭室内混合均匀, 后来起动密闭室内的搅动设备将密闭室内的气体混合均匀。实验1~4中气体渗漏出来的时间分别为537、533、2 040和1 980 s。
3. 实验结果分析
3.1 气体渗漏时间
根据文献[9]的理论研究结果, 如果介质相同, 药量越小, 气体渗漏越早。边长0.5 m花岗岩中, 1.25 g TNT实验与边长1 m花岗岩中10 g TNT实验之间有1:2的缩比关系, 10 g TNT实验与1.25 g TNT实验气体渗漏时间有约4倍的关系。由实验结果, 10 g TNT实验与1.25 g TNT实验CO渗漏出来的时间倍数为约4, 实验结果与理论分析结果基本一致。
3.2 密闭室内CO浓度基本稳定时间
如果把密闭室内CO浓度基本稳定的时间看作气体渗漏基本停止的时间, 2次1.25 g TNT实验在爆后约200 min时CO浓度基本稳定, 而2次10 g TNT实验在约800 min时CO浓度基本稳定。10 g TNT实验与1.25 g TNT实验气体停止渗漏时间有约4倍关系。
3.3 气体渗漏份额
实验所用的炸药为黑索金。根据黑索金的反应方程式可知, 1 g黑索金爆炸产生的CO在标准状态下约300 ml。由于1 g黑索金相当于1.5 g TNT当量, 所以, 计算出1.25 g TNT当量实验和10 g TNT当量实验CO的产生量分别为250和2 000 ml。
密闭室内部体积为2.88 m3, 气体搅动设备体积为0.33 m3, CO变送器体积为0.05m3, 10 g TNT实验花岗岩试样体积1 m3, 1.25 g TNT实验花岗岩试样体积0.125 m3。由此算出, 1.25 g TNT实验密闭室内空间体积为2.47 m3, 10 g TNT实验密闭室内空间体积为1.5 m3。
根据各次实验炸药爆炸CO生成量、密闭室浓度稳定值及密闭室内空间体积, 计算出实验1~4中渗漏到密闭室内的CO占炸药爆炸生成的CO的份额分别为:1.06、1.15、0.59和0.56。
由实验结果, 对于缩比实验来说, 小药量实验气体渗漏份额大于大药量实验气体渗漏份额。而且, 部分实验CO渗漏份额已经大于1, 说明实验中除了炸药产生CO之外, 还有其他物质产生CO。
爆室内除了炸药之外, 还有其他一些物质, 如塑料袋、胶带、电缆皮等。实验研究显示, 聚乙烯的半分解温度(在真空中加热30 min后重量损失一半所需的温度)为414 ℃, 在800 ℃的高温下, 质量约1 g的聚乙烯仅需1~2 min就能完全分解。由于炸药爆炸后爆室内高温会持续一段时间, 所以, 会将一些物质分解为气体。
文献[9]的理论研究结果显示, 不同药量缩比实验的气体渗漏份额基本相同, 而本文中实验结果是小药量实验气体渗漏份额大于大药量实验气体渗漏份额。可认为在实验中爆室内安装炸药所用的塑料袋、胶带等物质分解产生一定量的非冷凝气体, 这就改变了爆室内非冷凝气体及CO的初始条件。1.25 g TNT实验和10 g TNT实验药量不同, 但爆室内可分解材料绝对量相差不大, 小药量实验因材料分解而增加的非冷凝气体相对量大于大药量实验。由监测结果推导渗漏份额时并未考虑材料分解增加的非冷凝气体, 所以, 推出的小药量实验气体渗漏份额大于大药量实验的气体渗漏份额。
本文中认为, 药量越大, 材料分解产生的气体与炸药爆炸所产生的气体之比越小, 所以可以推测, 当炸药质量远大于胶带和电缆皮的质量之后, 缩比实验的气体渗漏份额将基本相同。这方面还需要进一步的实验验证。
聚乙烯分解产生的气体改变了不同药量实验气体渗漏份额的关系, 但气体渗漏时间的关系仍与理论分析结果基本一致。原因是材料分解时吸收热量, 虽然爆室内气体增加了, 但温度降低了, 二者对压力的贡献有一定的抵消作用, 而气体渗漏速度决定于压力梯度, 所以对气体渗漏速度影响不大。上面只是定性的分析, 定量分析还需要进一步开展工作。
4. 总结
为研究花岗岩中不同药量缩比爆炸实验气体渗漏行为之间的关系, 设计了满足缩比关系的当量分别为10 g TNT和1.25 g TNT的化学爆炸实验, 监测了渗漏出来的CO浓度历程。通过研究得到如下结论:
(1) 相同介质中缩比实验气体渗漏出来的时间大约与药量的三分之二次方成正比, 渗漏停止时间也大约与药量的三分之二次方成正比;
(2) 封闭化学爆炸在爆室内产生的高温能够使爆室内一些物质分解产生非冷凝气体;
(3) 对于不同药量的缩比实验, 理论分析认为气体渗漏份额基本相同, 但在实验中, 由于胶带、电缆皮等材料的分解产生非冷凝气体, 这些气体对于较小药量实验的影响较大, 所以较小药量实验的气体渗漏份额大于较大药量实验的气体渗漏份额。
-
图 11 止裂点和再次起裂点的应力变化
Figure 11. Stress variations at crack arrest point and crack again point
图 12 起裂点、止裂点和再次起裂点的能量变化
Figure 12. Energy variations at crack point, crack arrest point and crack again point
表 1 砂岩的力学性能
Table 1. Mechanical properties of sandstone materials
材料 ρ/（kg·m−3） E/GPa μ fd/MPa cl/（m·s−1） ct /（m·s−1） 青砂岩 2 265 13.58 0.165 24.84 2 563 1 607 黑砂岩 2 650 33.67 0.205 52.96 3 678 2 239 
下载: 导出CSV
表 2 实验结果
Table 2. Experimental results
试件 vs/（m·s−1） ti/μs ta/μs va/（m·s−1） la/mm 青砂岩1 8.43 342.4 97.6 368.6 15.4 青砂岩2 8.40 356.1 79.6 363.7 24.2 青砂岩3 8.38 367.4 57.2 302.7 15.4 黑砂岩1 8.47 370.8 54.2 310.1 19.8 黑砂岩2 8.41 350.0 81.7 372.9 15.4 黑砂岩3 8.39 387.0 85.9 396.1 8.8
下载: 导出CSV
-
[1] 曹富, 杨丽萍, 李炼, 等. 压缩单裂纹圆孔板(SCDC)岩石动态断裂全过程研究 [J]. 岩土力学, 2017, 38(6): 1573–1582, 1588. DOI: 10.16285/j.rsm.2017.06.005.CAO F, YANG L P, LI L, et al. Research on whole dynamical fracture process of rock using single cleavage drilled compression (SCDC) specimen [J]. Rock and Soil Mechanics, 2017, 38(6): 1573–1582, 1588. DOI: 10.16285/j.rsm.2017.06.005. [2] 张盛, 鲁义强, 王启智. 用P-CCNBD试样测定岩石动态扩展韧度和观察动态止裂现象 [J]. 岩土力学, 2017, 38(11): 3095–3105. DOI: 10.16285/j.rsm.2017.11.003.ZHANG S, LU Y Q, WANG Q Z. Measurement of dynamic fracture propagation toughness of rock and observation of dynamic arrest phenomenon using P-CCNBD specimens [J]. Rock and Soil Mechanics, 2017, 38(11): 3095–3105. DOI: 10.16285/j.rsm.2017.11.003. [3] 周辉, 徐荣超, 张传庆, 等. 预应力锚杆锚固止裂效应的试验研究 [J]. 岩石力学与工程学报, 2015, 34(10): 2027–2037. DOI: 10.13722/j.cnki.jrme.2015.0983.ZHOU H, XU R C, ZHANG C Q, et al. Experimental study of crack prevention effect of pre-stressed bolt anchoring [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(10): 2027–2037. DOI: 10.13722/j.cnki.jrme.2015.0983. [4] FENG P, DAI F, LIU Y, et al. Coupled effects of static-dynamic strain rates on the mechanical and fracturing behaviors of rock-like specimens containing two unparallel fissures [J]. Engineering Fracture Mechanics, 2019, 207: 237–253. DOI: 10.1016/j.engfracmech.2018.12.033. [5] ZHANG Q B, ZHAO J. Determination of mechanical properties and full-field strain measurements of rock material under dynamic loads [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60: 423–439. DOI: 10.1016/j.ijrmms.2013.01.005. [6] 郭东明, 刘康, 胡久羡, 等. 爆生气体对邻近硐室背爆侧预制裂纹影响机理 [J]. 煤炭学报, 2016, 41(1): 265–270. DOI: 10.13225/j.cnki.jccs.2015.1249.GUO D M, LIU K, HU J X, et al. Experimental study on the effect mechanism of the explosion gas on the precrack in the back-blasting of adjacent tunnel [J]. Journal of China Coal Society, 2016, 41(1): 265–270. DOI: 10.13225/j.cnki.jccs.2015.1249. [7] XU Y, YAO W, ZHAO G L, et al. Evaluation of the short core in compression (SCC) method for measuring mode Ⅱ fracture toughness of rocks [J]. Engineering Fracture Mechanics, 2020, 224: 106747. DOI: 10.1016/j.engfracmech.2019.106747. [8] LI D Y, HAN Z Y, SUN X L, et al. Dynamic mechanical properties and fracturing behavior of marble specimens containing single and double flaws in SHPB tests [J]. Rock Mechanics and Rock Engineering, 2019, 52(6): 1623–1643. DOI: 10.1007/s00603-018-1652-5. [9] 李地元, 韩震宇, 孙小磊, 等. 含预制裂隙大理岩SHPB动态力学破坏特性试验研究 [J]. 岩石力学与工程学报, 2017, 36(12): 2872–2883. DOI: 10.13722/j.cnki.jrme.2017.0488.LI D Y, HAN Z Y, SUN X L, et al. Characteristics of dynamic failure of marble with artificial flaws under split Hopkinson pressure bar tests [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(12): 2872–2883. DOI: 10.13722/j.cnki.jrme.2017.0488. [10] HUANG Y H, YANG S Q, TIAN W L. Crack coalescence behavior of sandstone specimen containing two pre-existing flaws under different confining pressures [J]. Theoretical and Applied Fracture Mechanics, 2019, 99: 118–130. DOI: 10.1016/j.tafmec.2018.11.013. [11] WANG M, WANG F, ZHU Z M, et al. Modelling of crack propagation in rocks under SHPB impacts using a damage method [J]. Fatigue & Fracture of Engineering Materials & Structures, 2019, 42(8): 1699–1710. DOI: 10.1111/ffe.13012. [12] 杨仁树, 苏洪, 龚悦, 等. 爆炸荷载下不对称Y型裂纹扩展规律的试验研究 [J]. 岩土力学, 2017, 38(8): 2175–2181. DOI: 10.16285/j.rsm.2017.08.003.YANG R S, SU H, GONG Y, et al. Study on the regularity of asymmetric Y-shaped cracks propagation under blast loading [J]. Rock and Soil Mechanics, 2017, 38(8): 2175–2181. DOI: 10.16285/j.rsm.2017.08.003. [13] ZHOU L, ZHU Z M, LIU R F, et al. Investigation on fracture properties of single-flawed tunnel model under medium-to-low-speed impacts [J]. Acta Mechanica Solida Sinica, 2020, 33(2): 205–225. DOI: 10.1007/s10338-019-00124-4. [14] ZHOU Q, ZHU Z M, WANG X, et al. The effect of a pre‐existing crack on a running crack in brittle material under dynamic loads [J]. Fatigue & Fracture of Engineering Materials & Structures, 2019, 42(11): 2544–2557. DOI: 10.1111/ffe.13105. [15] 岳中文, 宋耀, 陈彪, 等. 冲击载荷下层状岩体动态断裂行为的模拟试验研究 [J]. 振动与冲击, 2017, 36(12): 223–229. DOI: 10.13465/j.cnki.jvs.2017.12.036.YUE Z W, SONG Y, CHEN B, et al. Study on behaviors of dynamic fracture in layered rock under impact loading [J]. Journal of Vibration and Shock, 2017, 36(12): 223–229. DOI: 10.13465/j.cnki.jvs.2017.12.036. [16] WANG Q Z, YANG J R, ZHANG C G, et al. Sequential determination of dynamic initiation and propagation toughness of rock using an experimental-numerical-analytical method [J]. Engineering Fracture Mechanics, 2015, 141: 78–94. DOI: 10.1016/j.engfracmech.2015.04.025. [17] GAO G, HUANG S, XIA K, et al. Application of digital image correlation (DIC) in dynamic notched semi-circular bend (NSCB) tests [J]. Experimental Mechanics, 2015, 55(1): 95–104. DOI: 10.1007/s11340-014-9863-5. [18] 李地元, 成腾蛟, 周韬, 等. 冲击载荷作用下含孔洞大理岩动态力学破坏特性试验研究 [J]. 岩石力学与工程学报, 2015, 34(2): 249–260. DOI: 10.13722/j.cnki.jrme.2015.02.004.LI D Y, CHENG T J, ZHOU T, et al. Experimental study of the dynamic strength and fracturing characteristics of marble specimens with a single hole under impact loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 249–260. DOI: 10.13722/j.cnki.jrme.2015.02.004. [19] 郭东明, 刘康, 杨仁树, 等. 动静荷载对邻近巷道裂纹缺陷扰动的模拟实验 [J]. 爆炸与冲击, 2016, 36(3): 297–304. DOI: 10.11883/1001-1455(2016)03-0297-08.GUO D M, LIU K, YANG R S, et al. Simulated experiment of disturbance effect on crack defects of adjacent tunnel under dynamic and static load [J]. Explosion and Shock Waves, 2016, 36(3): 297–304. DOI: 10.11883/1001-1455(2016)03-0297-08. [20] 王蒙, 朱哲明, 王雄. 冲击荷载作用下的Ⅰ/Ⅱ复合型裂纹扩展规律研究 [J]. 岩石力学与工程学报, 2016, 35(7): 1323–1332. DOI: 10.13722/j.cnki.jrme.2015.1260.WANG M, ZHU Z M, WANG X. The growth of mixed-mode Ⅰ/Ⅱ crack under impacting loads [J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(7): 1323–1332. DOI: 10.13722/j.cnki.jrme.2015.1260. [21] 邓帅, 朱哲明, 王磊, 等. 原岩应力对裂纹动态断裂行为的影响规律研究 [J]. 岩石力学与工程学报, 2019, 38(10): 1989–1999. DOI: 10.13722/j.cnki.jrme.2019.0347.DENG S, ZHU Z M, WANG L, et al. Study on the influence of in-situ stresses on dynamic fracture behaviors of cracks [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(10): 1989–1999. DOI: 10.13722/j.cnki.jrme.2019.0347. [22] 万端莹, 朱哲明, 刘瑞峰, 等. 基于RPC试件的爆炸应力波作用下Ⅰ型裂纹扩展行为的研究 [J]. 岩石力学与工程学报, 2019, 38(12): 2478–2490. DOI: 10.13722/j.cnki.jrme.2019.0573.WAN D Y, ZHU Z M, LIU R F, et al. Study of propagation behaviors of mode Ⅰ cracks under blasting stress wave based on RPC specimens [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(12): 2478–2490. DOI: 10.13722/j.cnki.jrme.2019.0573. [23] ZHANG Q B, ZHAO J. Quasi-static and dynamic fracture behaviour of rock materials: phenomena and mechanisms [J]. International Journal of Fracture, 2014, 189(1): 1–32. DOI: 10.1007/s10704-014-9959-z. [24] ZHOU L, ZHU Z M, DONG Y Q, et al. Study of the fracture behavior of mode I and mixed mode Ⅰ/Ⅱ cracks in tunnel under impact loads [J]. Tunnelling and Underground Space Technology, 2019, 84: 11–21. DOI: 10.1016/j.tust.2018.10.018. [25] 李夕兵. 岩石动力学基础与应用[M]. 北京: 科学出版社, 2014: 1-66. [26] JU M H, LI J C, YAO Q L, et al. Rate effect on crack propagation measurement results with crack propagation gauge, digital image correlation, and visual methods [J]. Engineering Fracture Mechanics, 2019, 219: 106537. DOI: 10.1016/j.engfracmech.2019.106537. [27] WU Q H, WENG L, ZHAO Y L, et al. On the tensile mechanical characteristics of fine-grained granite after heating/cooling treatments with different cooling rates [J]. Engineering Geology, 2019, 253: 94–110. DOI: 10.1016/j.enggeo.2019.03.014. [28] 谢和平. 分形-岩石力学导论[M]. 北京: 科学出版社, 1996: 168-261. [29] WONG L N Y, LI H Q. Numerical study on coalescence of two pre-existing coplanar flaws in rock [J]. International Journal of Solids and Structures, 2013, 50(22–23): 3685–3706. DOI: 10.1016/j.ijsolstr.2013.07.010. [30] HE C L, YANG J. Experimental and numerical investigations of dynamic failure process in rock under blast loading [J]. Tunnelling and Underground Space Technology, 2019, 83: 552–564. DOI: 10.1016/j.tust.2018.08.047. [31] JIANG H X, DU C L, LIU Z H. Theoretical and numerical investigation on rock fragmentation under high-pressure water-jet impact [J]. Iranian Journal of Science and Technology, Transactions of Civil Engineering, 2017, 41(3): 305–315. DOI: 10.1007/s40996-017-0065-0. [32] JIANG H X, DU C L, LIU S Y, et al. Numerical simulation of rock fragmentation under the impact load of water jet [J]. Shock and Vibration, 2014, 2014: 219489. DOI: 10.1155/2014/219489. 期刊类型引用(1)
1. 钟巍, 田宙, 王铁良. 基于量纲分析和达西定律的地下化学爆炸气体泄漏规律. 计算物理. 2019(04): 449-456 . 
百度学术其他类型引用(0)
-
下载:
百度学术
计量
- 文章访问数: 597
- HTML全文浏览量: 272
- PDF下载量: 137
- 被引次数: 1