晶粒尺寸对高纯铝板材层裂特性的影响

陈伟; 谢普初; 刘东升; 史同亚; 李治国; 王永刚

doi:10.11883/bzycj-2020-0130

晶粒尺寸对高纯铝板材层裂特性的影响

doi: 10.11883/bzycj-2020-0130

1.
宁波大学冲击与安全工程教育部重点实验室，浙江宁波 315211
2.
中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川绵阳 621999

基金项目: 国家自然科学基金（11972202）；科学挑战专题（TZ2018001）；冲击波物理与爆轰物理重点实验室稳定支持项目（JCKYS2019212009）

详细信息

作者简介:
陈　伟（1993－　），男，硕士研究生，1172957504@qq.com

通讯作者:
王永刚（1976－　），男，博士，教授，wangyonggang@nbu.edu.cn

中图分类号: O347.3
计量
- 文章访问数: 535
- HTML全文浏览量: 235
- PDF下载量: 75
- 被引次数: 0
出版历程
- 收稿日期: 2020-05-06
- 修回日期: 2020-06-26
- 网络出版日期: 2021-03-05
- 刊出日期: 2021-04-14

Effects of grain size on the spall behaviors of high-purity aluminum plates

1.
Key Laboratory of Impact and Safety Engineering, Ministry of Education, Ningbo University, Ningbo 315211, Zhejiang, China
2.
National Key Laboratory of Shock Wave and Detonation Physics, Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621999, Sichuan, China

摘要

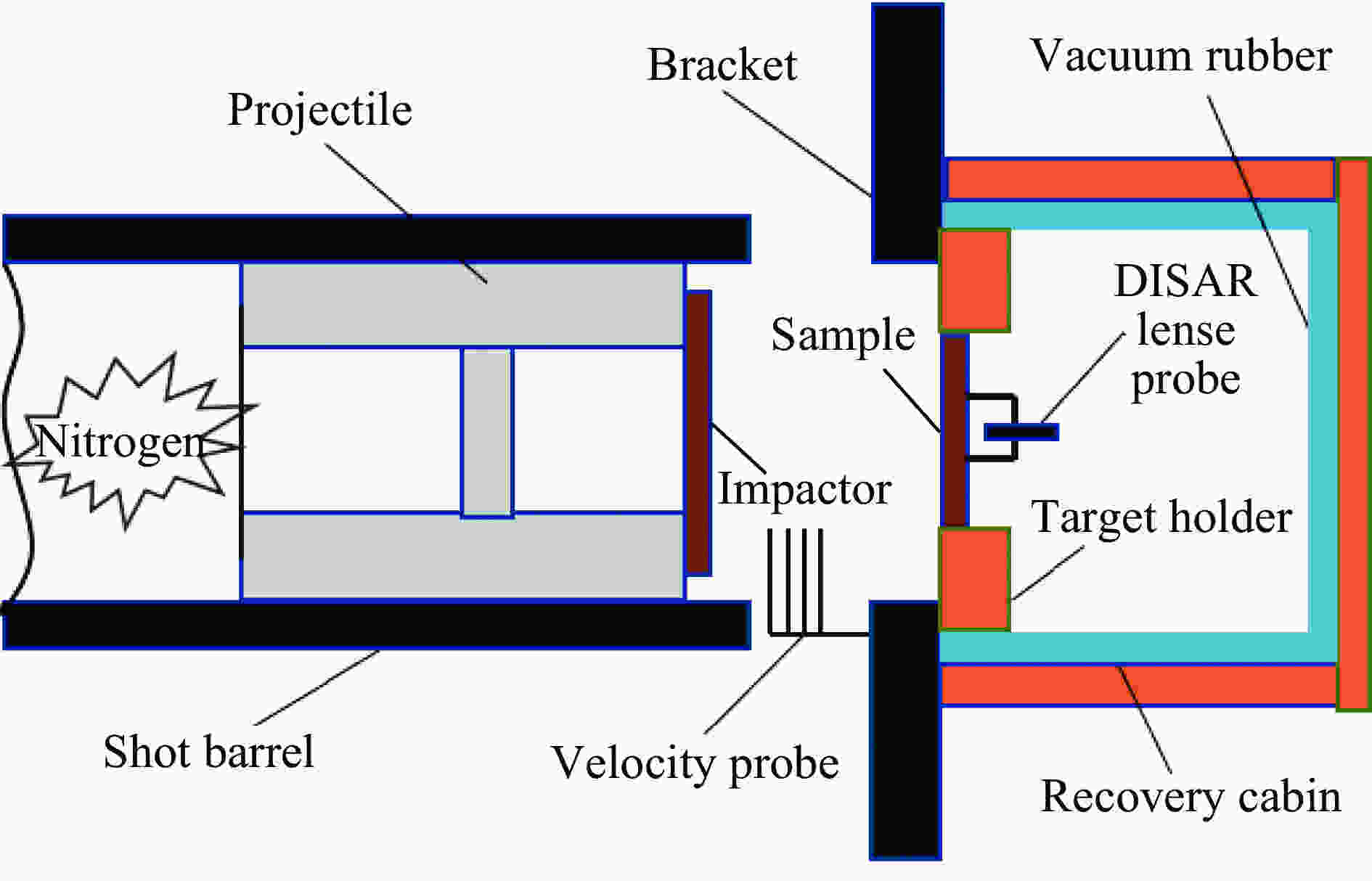
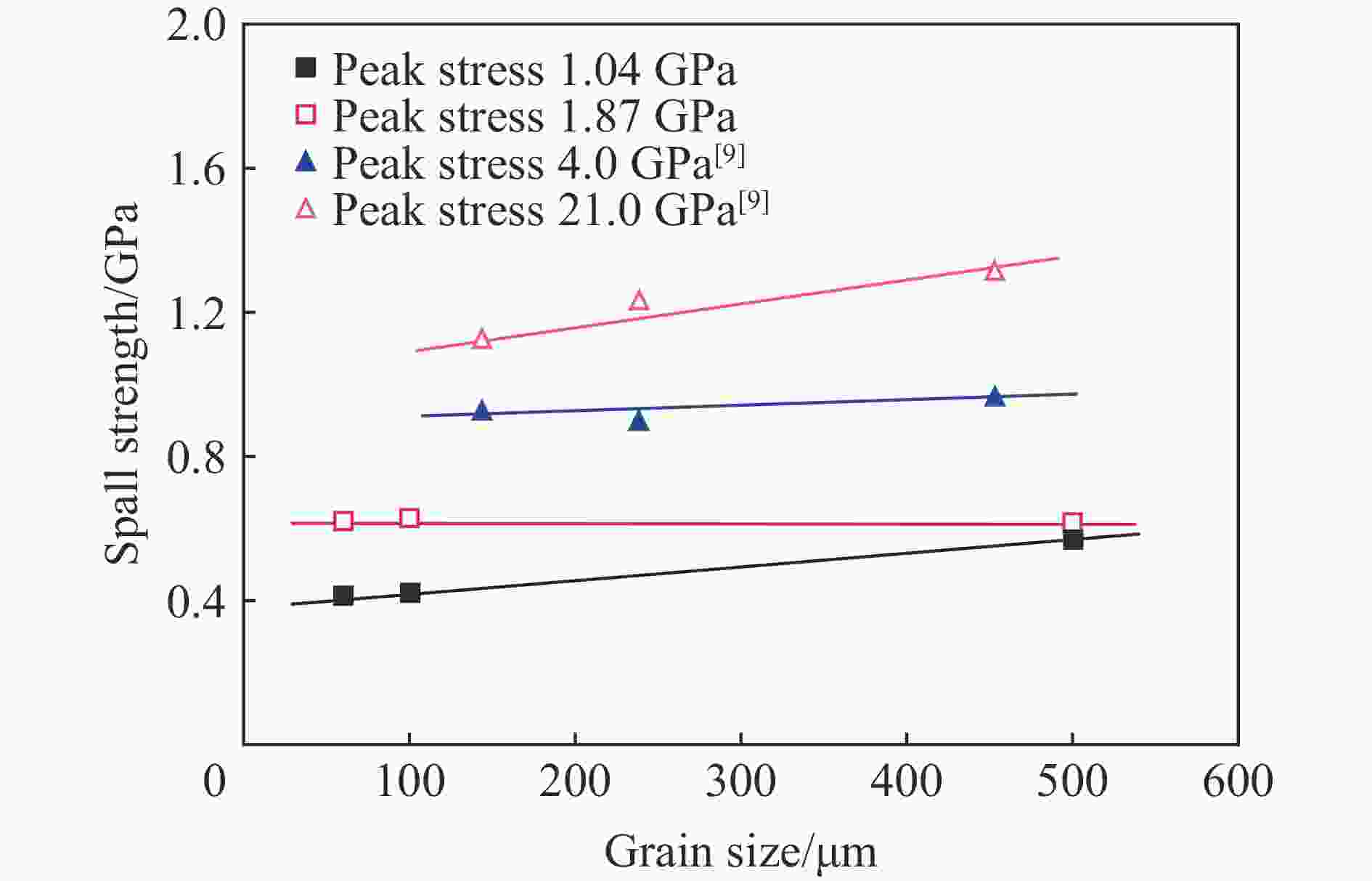
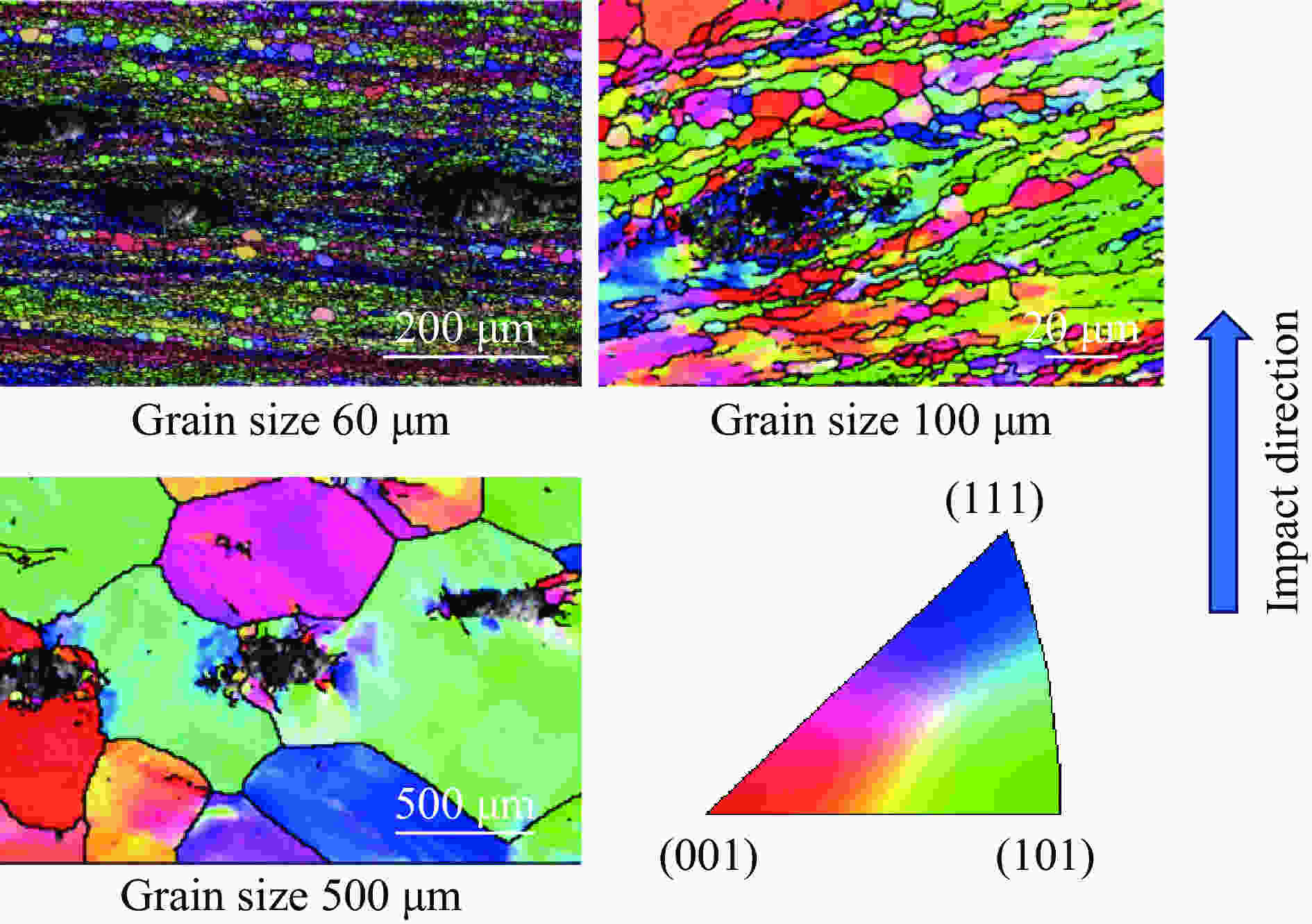
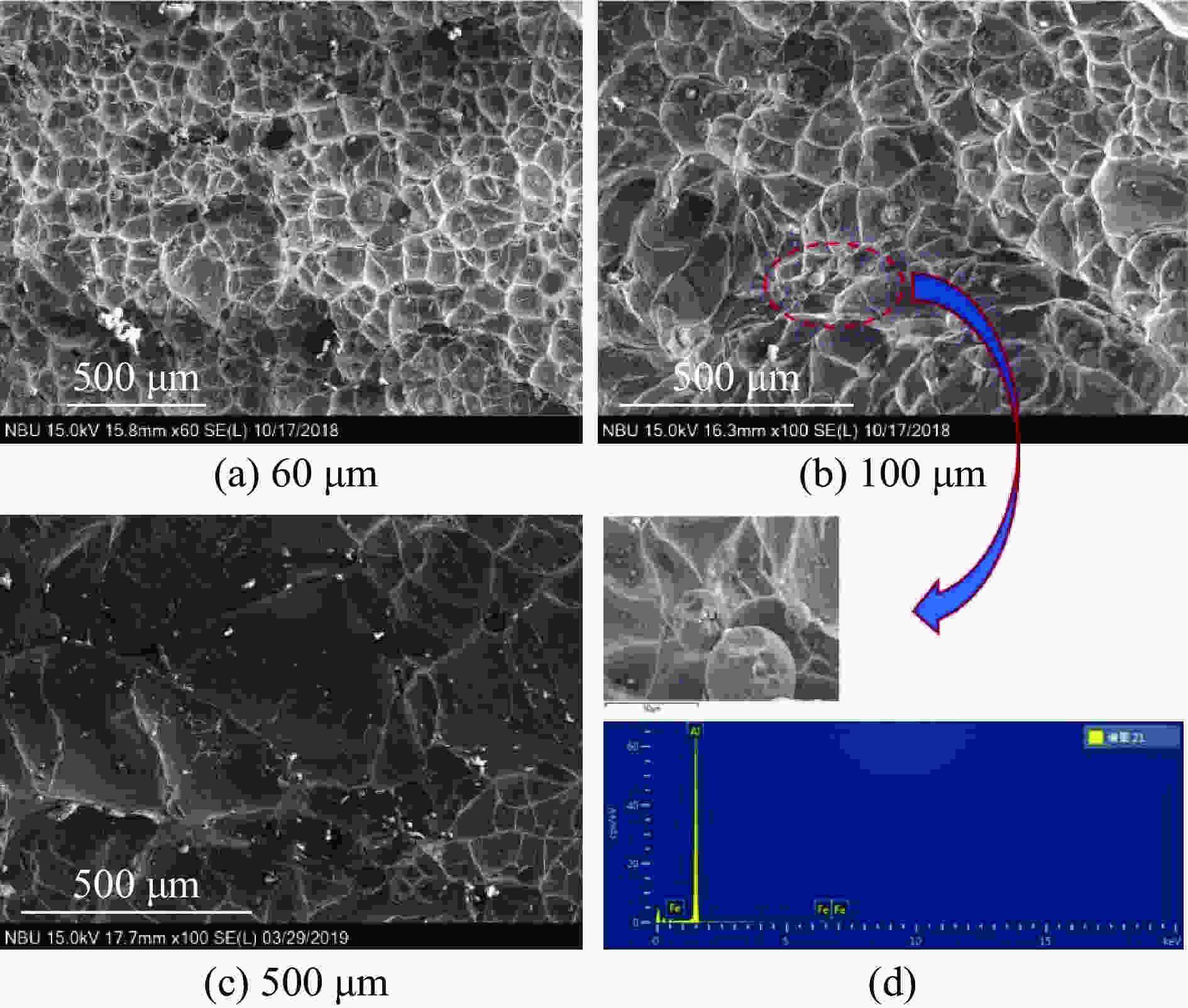
摘要: 采用不同热处理工艺制备了3种晶粒尺寸（60、100、500 μm）的高纯铝板材，利用平板撞击实验研究了其层裂行为。通过改变飞片击靶速度，在靶板中实现初始层裂状态和完全层裂状态。基于自由面速度时程曲线和微损伤演化及断口显微形貌分析，讨论了晶粒尺寸对高纯铝板材层裂特性的影响规律。实验结果显示：（1）晶粒尺寸对高纯铝板材层裂特性的影响强烈依赖于冲击加载应力幅值，在低应力条件下，层裂强度与晶粒尺寸之间表现出反Hall-Petch关系，而在高应力条件下，晶粒尺寸对层裂强度几乎没有影响；（2）随着晶粒尺寸的增大，靶板损伤区微孔洞的尺寸和分布范围均增大，但数量显著减少，在微孔洞周围还发现比较严重的晶粒细化现象；（3）随着晶粒尺寸的增大，层裂微观机制从韧性沿晶断裂向准脆性沿晶断裂转变，且在断口上观察到少量随机分布的小圆球，归因于微孔洞长大和聚集过程中严重塑性变形引起的热效应。
- 晶粒尺寸 /
- 层裂强度 /
- 损伤演化 /
- 高纯铝板材
Abstract: High-purity (HP) aluminum plates were cold rolled and heat treated to produce recrystallized samples with average grain sizes of 60, 100 and 500 μm, respectively. The effects of grain size on the spall response of HP aluminum plates were investigated by plate impact experiments including real-time measurements of the free surface velocity profiles by a compact all-fiber displacement interferometer system for any reflector, and post-impact fractography of soft-recovered samples by optical microscopy and scanning electron microscopy. The effect of grain size on the spall strength depends on the amplitude of peak stress. At lower peak stress loading, the dependence of the spall strength on the grain size is an inverse Hall-Petch relationship, but at higher peak stress loading, the spall strength is nearly constant with little effect of grain size. With the increase of grain size, the distribution range and size of micro-voids in the damaged sample increase, but the number of micro-voids decreases, and the grain refinement caused by the shock compression process is observed. On the other hand, with the increase of grain size, the mechanism of spallation changes from ductile intergranular fracture to quasi-brittle intergranular fracture. Some randomly distributed small metal balls are observed on the fracture surface, which is attributed to the thermal effect due to the serious plastic deformation during the growth and coalescence of micro-voids.
- grain size /
- spall strength /
- damage evolution /
- high-purity aluminum plate

HTML全文

图 1 板材轧制方向指示和层裂靶板取样示意图

Figure 1. Schematic showing the three principal orthogonal directions ofrolled plate and sample preparation

下载: 全尺寸图片幻灯片

图 2 不同热处理工艺得到的高纯铝微结构EBSD表征照片

Figure 2. Microstructures of high-purity (HP) aluminum by EBSD at different heat-treatment temperatures

下载: 全尺寸图片幻灯片

图 3 300 ℃条件下高纯铝微结构EBSD表征的三维照片

Figure 3. 3D microstructure of HP aluminum by EBSD at the heat-treatment temperature of 300 °C

下载: 全尺寸图片幻灯片

图 4 层裂实验装置示意图

Figure 4. Schematic diagram of spall experiments

下载: 全尺寸图片幻灯片

图 5 软回收靶板照片

Figure 5. Images of soft recovery HP aluminum samples

下载: 全尺寸图片幻灯片

图 6 不同撞击速度下3种晶粒尺寸的高纯铝靶板实测自由面速度曲线

Figure 6. Free-surface velocity profiles of HP aluminum with different grain sizes at different impact velocities

下载: 全尺寸图片幻灯片

图 7 不同冲击应力条件下高纯铝层裂强度随晶粒尺寸的变化关系

Figure 7. Relationship between spallation strength and grain size of HP aluminum under different impact stress conditions

下载: 全尺寸图片幻灯片

图 8 不同晶粒尺寸高纯铝板材的准静态应力应变曲线

Figure 8. Stress strain curves of HP aluminum with different grain sizes

下载: 全尺寸图片幻灯片

图 9 软回收不同晶粒尺寸靶板中微孔洞分布光学照片

Figure 9. Micro-void distribution in the HP aluminum plate samples with different grain sizes

下载: 全尺寸图片幻灯片

图 10 不同晶粒尺寸靶板中微孔洞尺寸统计结果

Figure 10. Statistical distribution of micro-void size in the HP aluminum plate samples with different grain sizes

下载: 全尺寸图片幻灯片

图 11 不同晶粒尺寸高纯铝损伤后靶板微观结构的EBSD表征照片

Figure 11. EBSD characterization of HP aluminum samples with different grain sizes after damage

下载: 全尺寸图片幻灯片

图 12 纯冲击压缩后不同初始晶粒尺寸的高纯铝靶板微观结构EBSD表征照片

Figure 12. EBSD characterization of HP aluminum sampleswith different grain sizes under shock compression

下载: 全尺寸图片幻灯片

图 13 高纯铝靶板原始的和冲击压缩后的晶粒尺寸分布

Figure 13. Grain size distribution of original and shocked high-purity aluminum plate.

下载: 全尺寸图片幻灯片

图 14 不同晶粒尺寸靶板的断口SEM表征照片

Figure 14. SEM micrographs of fracture surface of HP aluminum with different grain sizes

下载: 全尺寸图片幻灯片

表 1 高纯铝板材层裂实验条件和结果

Table 1. Conditions and results of spall experiment for high-purity aluminum plate

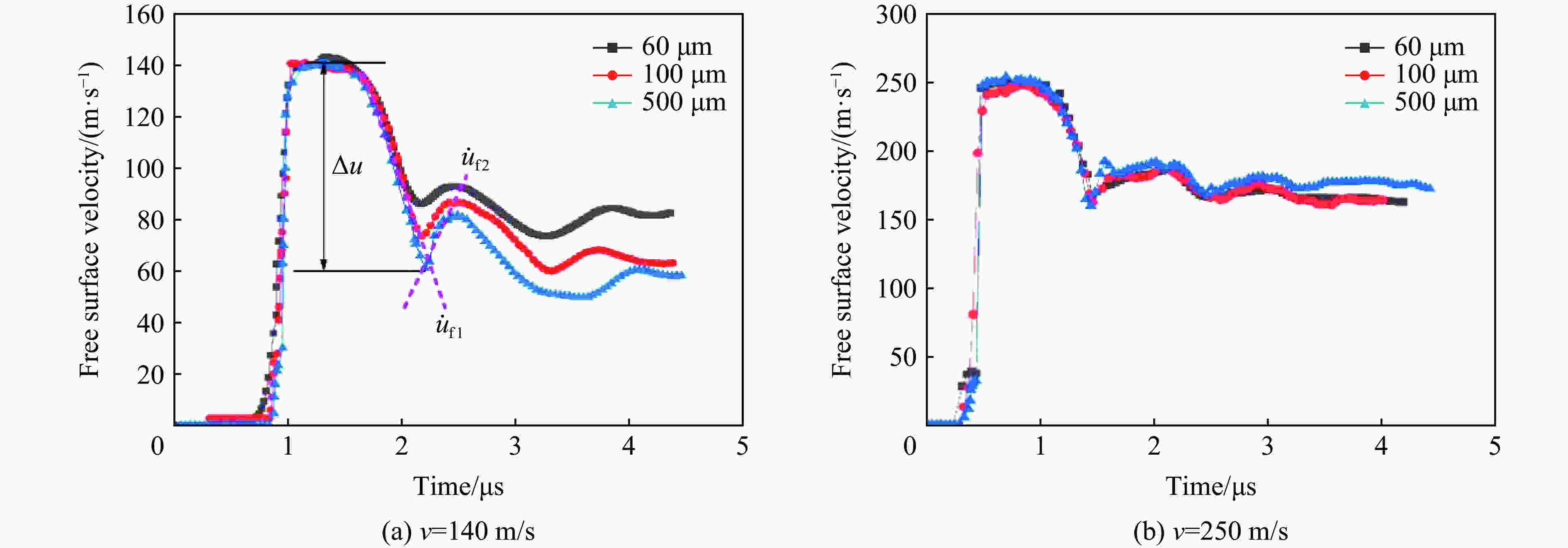
No.	D/μm	v/(m·s⁻¹)	$\sigma_{\rm{p}} $/GPa	Δu/(m·s⁻¹)	$\sigma_{\rm{s}} $/GPa	${\dot{u} }_{ {\rm{f} }1}$/(m·s⁻²)	$ \dot{\varepsilon } $/s⁻¹	${\dot{u} }_{ {\rm{f} }2}$/(m·s⁻²)
1	60	142	1.05	56.8	0.41	1.05×10⁸	0.98×10⁴	2.70×10⁷
2	100	139	1.03	58.8	0.42	1.23×10⁸	1.14×10⁴	4.16×10⁷
3	500	140	1.04	78.9	0.57	1.30×10⁸	1.21×10⁴	7.35×10⁷
4	60	250	1.87	85.1	0.62	2.68×10⁸	2.49×10⁴	2.80×10⁷
5	100	246	1.84	86.9	0.63	2.61×10⁸	2.43×10⁴	5.16×10⁷
6	500	252	1.89	86.1	0.62	2.58×10⁸	2.40×10⁴	7.92×10⁷

下载: 导出CSV

参考文献(24)

[1]	WANG Y M, CHEN M W, ZHOU F H, et al. High tensile ductility in a nanostructured metal [J]. Nature, 2002, 419(6910): 912–915. DOI: 10.1038/nature01133.
[2]	FANG T H, LI W L, TAO N R, et al. Revealing extraordinary intrinsic tensile plasticity in gradient nano-grained copper [J]. Science, 2011, 331(6024): 1587–1590. DOI: 10.1126/science.1200177.
[3]	VALIEV R. Nanostructuring of metals by severe plastic deformation for advanced properties [J]. Nature Materials, 2004, 3(8): 511–516. DOI: 10.1038/nmat1180.
[4]	HAHN E N, MEYERS M A. Grain-size dependent mechanical behavior of nanocrystalline metals [J]. Materials Science and Engineering: A, 2015, 646: 101–134. DOI: 10.1016/j.msea.2015.07.075.
[5]	ESTRIN Y, VINOGRADOV A. Extreme grain refinement by severe plastic deformation: a wealth of challenging science [J]. Acta Materialia, 2013, 61(3): 782–817. DOI: 10.1016/j.actamat.2012.10.038.
[6]	REMINGTON T P, HAHN E N, ZHAO S. et al Spall strength dependence on grain size and strain rate in tantalum [J]. Acta Materialia, 2018, 158: 313–329. DOI: 10.1016/j.actamat.2018.07.048.
[7]	MINICH R W, CAZAMIAS J U, KUMAR M, et al. Effect of microstructural length scales on spall behavior of copper [J]. Metallurgical and Materials Transactions A, 2004, 35(9): 2663–2673. DOI: 10.1007/s11661-004-0212-7.
[8]	兰胜威, 曾新吾. 晶粒度对纯铝动态力学性能的影响 [J]. 爆炸与冲击, 2008, 28(5): 462–466. DOI: 10.11883/1001-1455(2008)05-0462-05. LAN S W, ZENG X W. Effect of grain size on dynamic mechanical properties of pure aluminum [J]. Explosion and Shock Waves, 2008, 28(5): 462–466. DOI: 10.11883/1001-1455(2008)05-0462-05.
[9]	TRIVEDI P B, ASAY J R, GUPTA Y M, et al. Influence of grain size on the tensile response of aluminum under plate-impact loading [J]. Journal of Applied Physics, 2007, 102(8): 083513. DOI: 10.1063/1.2798497.
[10]	CHEN X, ASAY J R, DWIVEDI S K, et al. Spall behavior of aluminum with varying microstructures [J]. Journal of Applied Physics, 2006, 99(2): 023528. DOI: 10.1063/1.2165409.
[11]	ESCOBEDO J P, DENNIS-KOLLER D, CERRETA E K, et al. Effects of grain size and boundary structure on the dynamic tensile response of copper [J]. Journal of Applied Physics, 2011, 110(3): 033513. DOI: 10.1063/1.3607294.
[12]	CHEN T, JIANG Z X, PENG H, et al. Effect of grain size on the spall fracture behaviour of pure copper under plate-impact loading [J]. Strain, 2015, 51(3): 190–197. DOI: 10.1111/str.12132.
[13]	WHELCHEL R L, KENNEDY G B, DWIVEDI S K, et al. Spall behavior of rolled aluminum 5083-H116 plate [J]. Journal of Applied Physics, 2013, 113(23): 233506. DOI: 10.1063/1.4811452.
[14]	WILLIAMS C L, RAMESH K T, DANDEKAR D P. Spall response of 1100-O aluminum [J]. Journal of Applied Physics, 2012, 111(12): 123528. DOI: 10.1063/1.4729305.
[15]	WENG J D, TAN H, WANG X, et al. Optical-fiber interferometer for velocity measurements with picosecond resolution [J]. Applied Physics Letters, 2006, 89(11): 111101. DOI: 10.1063/1.2335948.
[16]	裴晓阳, 彭辉, 贺红亮, 等. 延性金属层裂自由面速度曲线物理涵义解读 [J]. 物理学报, 2015, 64(3): 034601. DOI: 10.7498/aps.64.034601. PEI X Y, PENG H, HE H L, et al. Discussion on the physical meaning of free surface velocity curve in ductile spallation [J]. Acta Physica Sinica, 2015, 64(3): 034601. DOI: 10.7498/aps.64.034601.
[17]	ANTOUN T, SEAMAN L, CURRAN D R, et al. Spall fracture [M]. New York, USA: Springer, 2003: 90−92. DOI: 10.1007/b97226.
[18]	KANEL G I, RAZORENOV S V, UTKIN A V, et al. Simulation of spall fracture of aluminum and magnesium over a wide range of load duration and temperature [J]. International Journal of Impact Engineering, 1997, 20(6–10): 467–478. DOI: 10.1016/S0734-743X(97)87435-0.
[19]	AHN D C, SOFRONIS P, KUMAR M, et al. Void growth by dislocation-loop emission [J]. Journal of Applied Physics, 2007, 101(6): 063514. DOI: 10.1063/1.2710346.
[20]	祁美兰. 高纯铝拉伸型动态破坏的临界行为研究[D]. 武汉: 武汉理工大学, 2007: 34–46. DOI: 10.7666/d.y1174895. QI M L. Critical behavior in dynamic tensile fracture of high purity aluminum [D]. Wuhan: Wuhan University of Technology, 2007: 34–46. DOI: 10.7666/d.y1174895.
[21]	QI M L, LUO C, HE H L, et al. Damage property of incompletely spalled aluminum under shock wave loading [J]. Journal of Applied Physics, 2012, 111(4): 043506. DOI: 10.1063/1.3681301.
[22]	SENCER B H, MALOY S A, GARY III G T. The influence of shock-pulse shape on the structure/property behavior of copper and 316L austenitic stainless steel [J]. Acta Materialia, 2005, 53(11): 3293–3303. DOI: 10.1016/j.actamat.2005.03.037.
[23]	张凤国, 周洪强. 晶粒尺度对延性金属材料层裂损伤的影响 [J]. 物理学报, 2013, 62(16): 164601. DOI: 10.7498/aps.62.164601. ZHANG F G, ZHOU H Q. Effects of grain size on the dynamic tensile damage of ductile polycrystalline metal [J]. Acta Physica Sinica, 2013, 62(16): 164601. DOI: 10.7498/aps.62.164601.
[24]	LIAO Y, XIANG M Z, ZENG X G, et al. Molecular dynamics studies of the roles of microstructure and thermal effects in spallation of aluminum [J]. Mechanics of Materials, 2015, 84: 12–27. DOI: 10.1016/j.mechmat.2015.01.007.