Mechanical behaviors of bi-directional gradient bio-inspired circular sandwich plates under blast loading
-
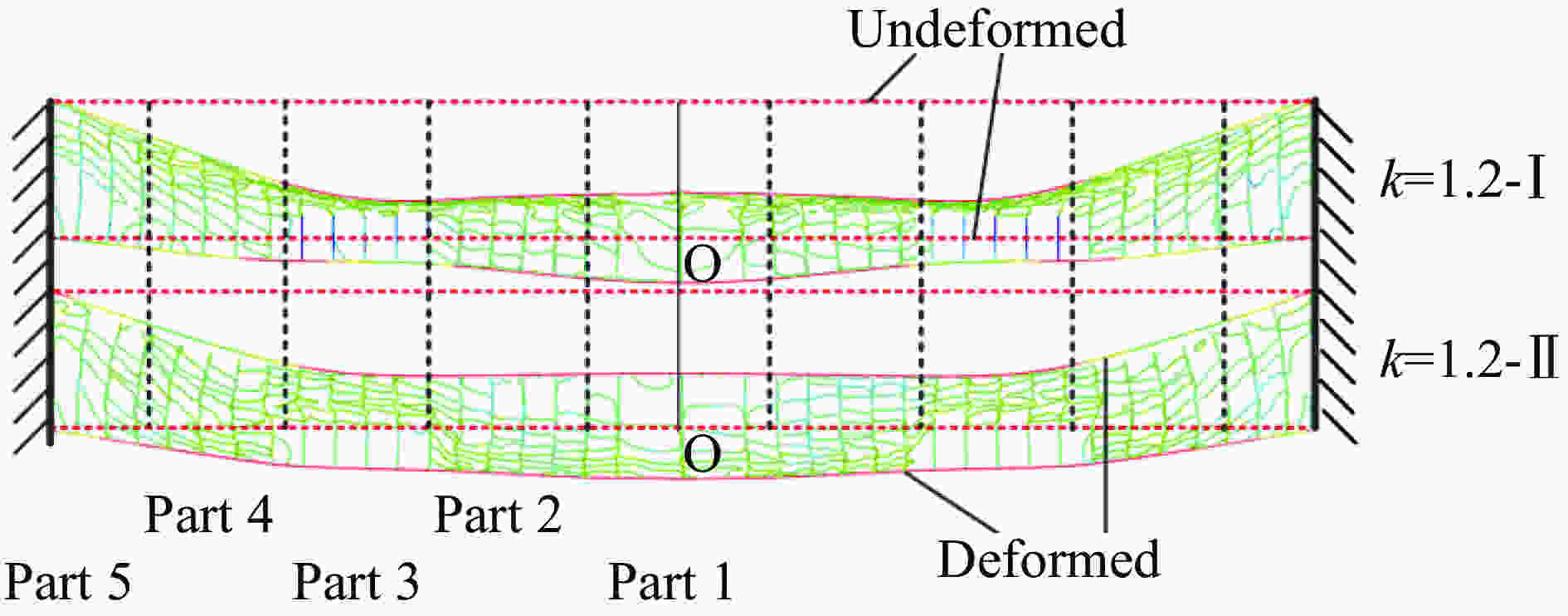
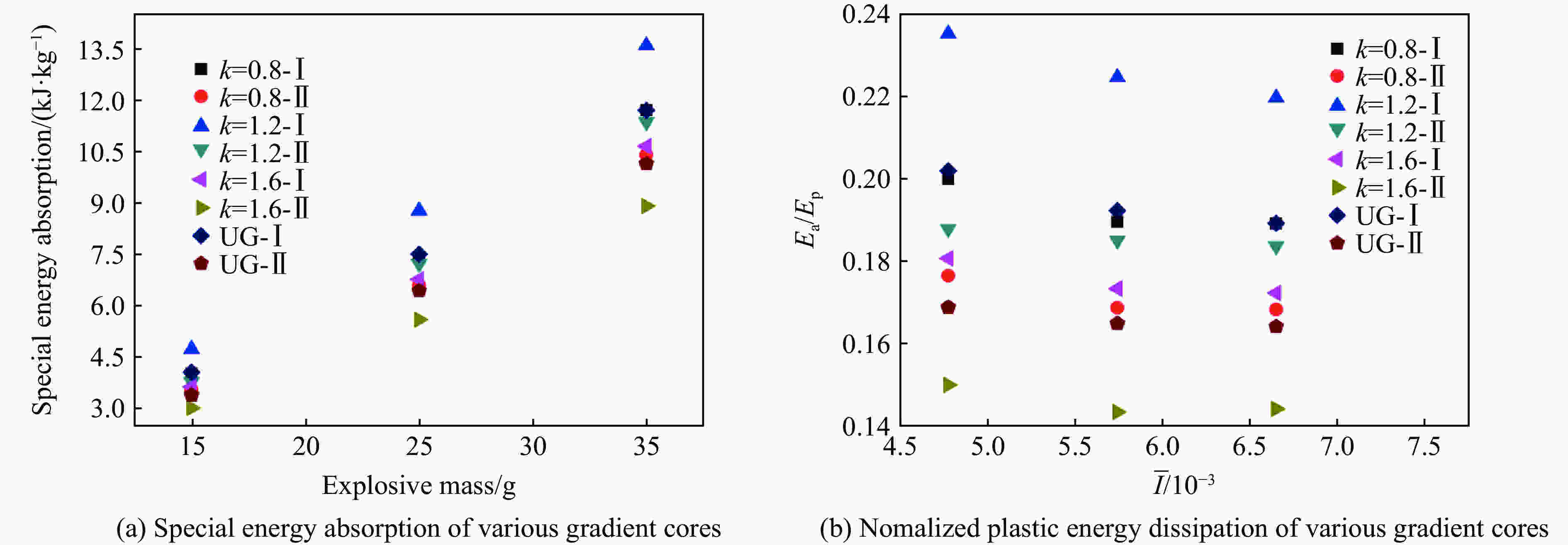
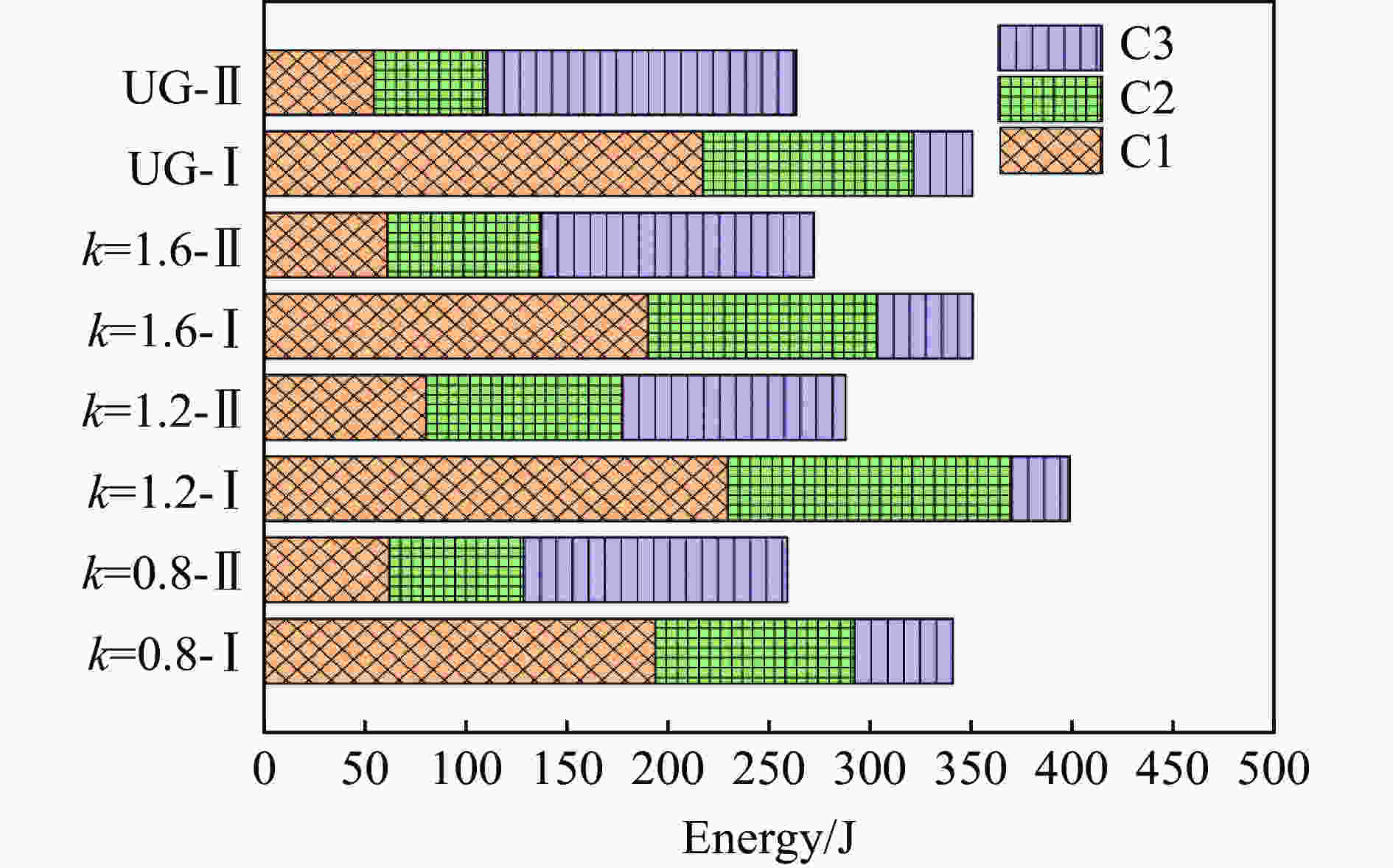
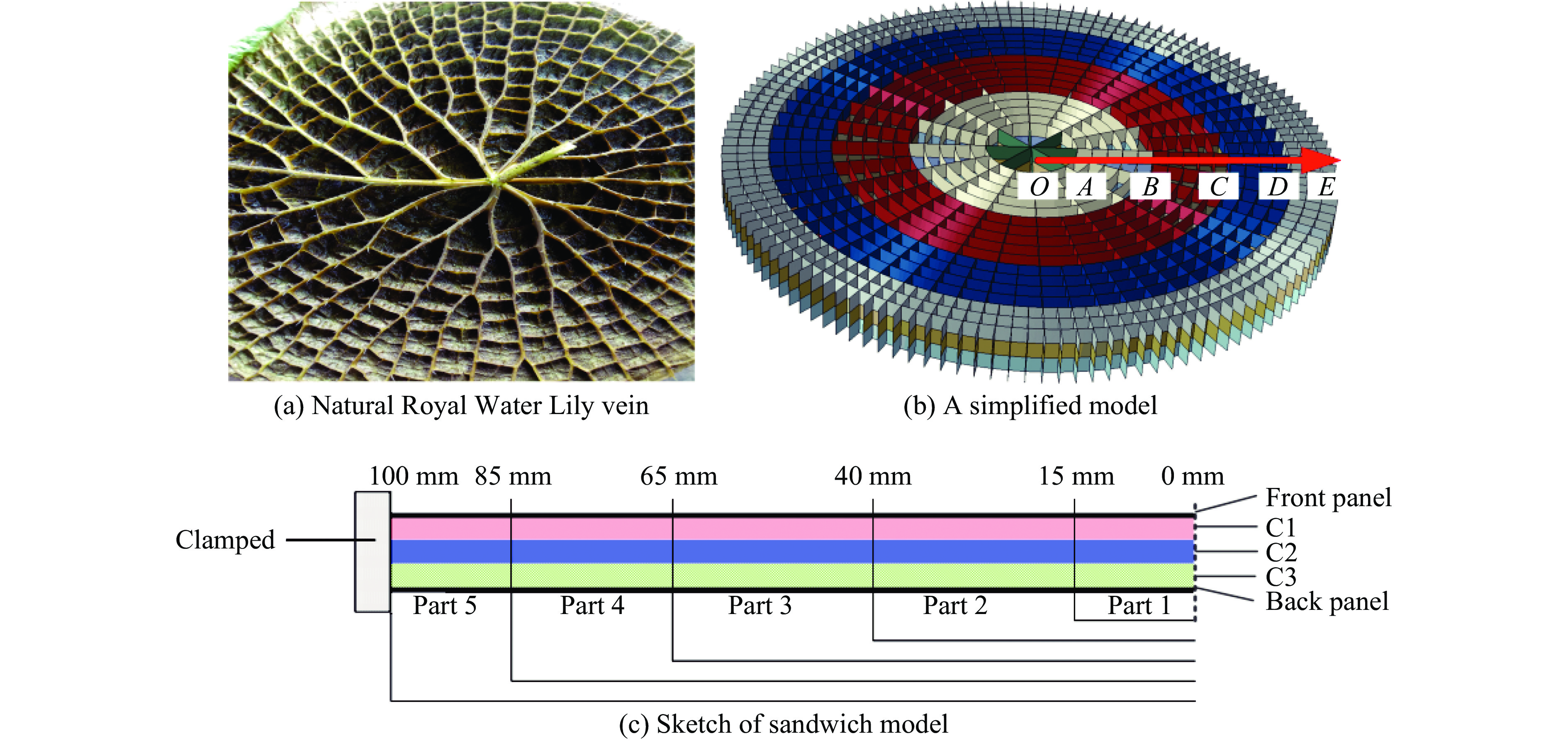
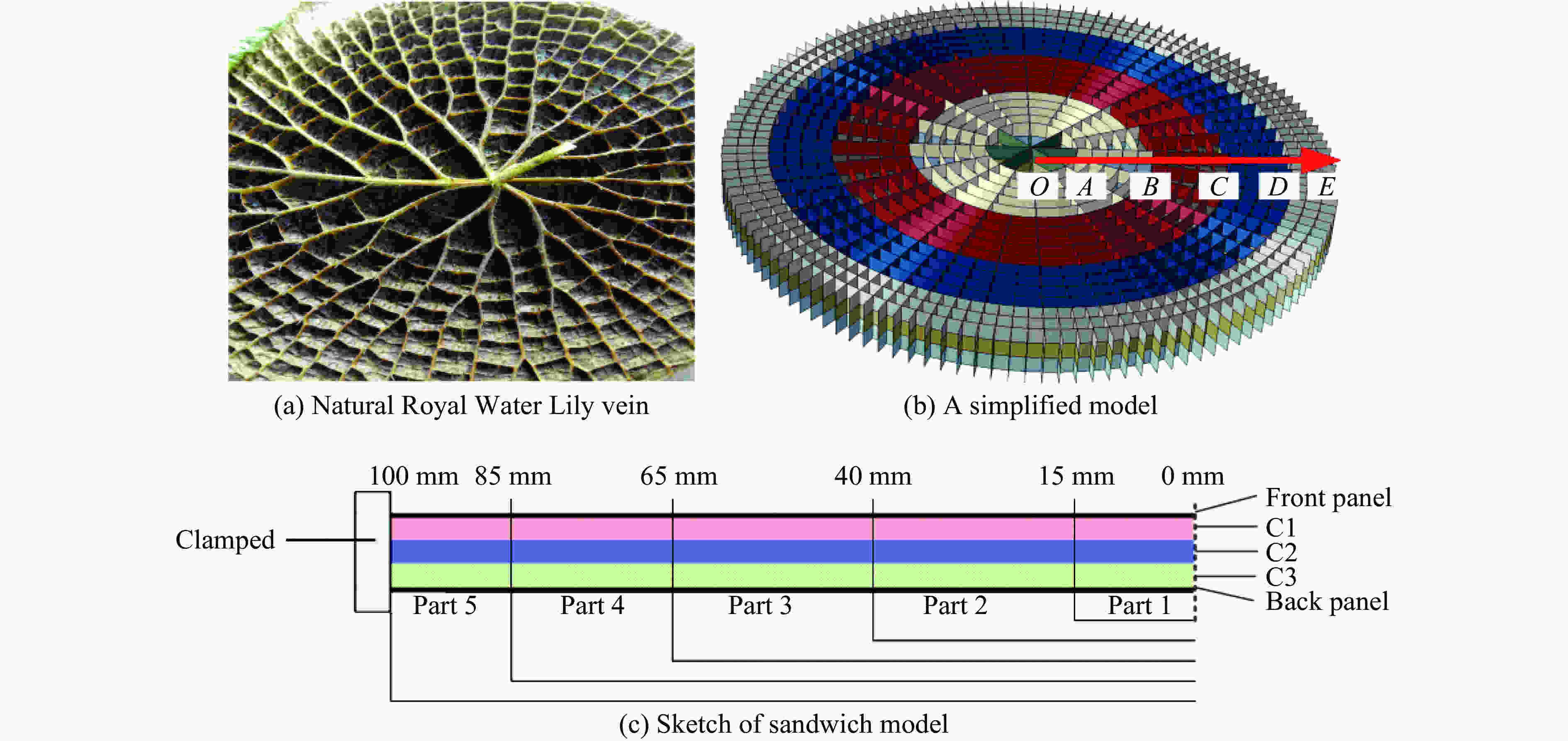
摘要: 基于王莲仿生面内梯度芯层,通过引入面外梯度,设计了一种双向梯度仿生夹芯圆板。在此基础上,运用ABAQUS有限元软件,对不同排列方式的双向梯度夹芯圆板在不同爆炸载荷作用下的响应进行了数值仿真,着重分析了不同仿生夹芯圆板的前后面板挠度、芯层压缩量、变形模式和能量吸收等特性,得到了一种抗爆性能较好的芯层排列方式。结果表明:相较于单一的面外梯度夹芯圆板,合理设计的双向梯度仿生夹芯圆板可以有效降低后面板挠度,并提高芯层的能量吸收。Abstract: A bi-directional gradient bionic circular sandwich plate was designed by introducing out-of-plane gradient into in-plane gradient core on the basis of Royal Water-Lily. Based on this, the responses of various bi-directional gradient circular sandwich plates under different blast loadings were simulated by using the finite element software of ABAQUS. The deflections of front and back panels, compression, deformation mode and energy absorption of different cores were analyzed emphatically, and a core arrangement mode with better blast resistant performance was obtained. The results show that: compared with a single out-of-plane gradient sandwich structure, the deflection of the back panel of bi-directional gradient sandwich structures can be effectively reduced, and the energy absorption capacity of the core can be improved through the reasonable bi-directional gradient arrangement.
-
表 1 铝合金的材料参数
Table 1. Material parameters of aluminum alloy
材料 ρ/(kg·m−3) E/GPa v σy/GPa Etan/GPa 5052铝合金 2 700 70 0.3 0.20 0.10 6060T4铝合金 2 700 70 0.3 0.08 0.07 表 2 模型类型与相关参数
Table 2. Model type and related parameters
模型 面内梯度 芯层C2各部分壁厚/mm 面外梯度 面外相对密度/% $\delta_1 $ $\delta_2 $ $\delta_3 $ $\delta_4 $ $\delta_5 $ C1 C2 C3 k=0.8- Ⅰ 负梯度 0.031 0.039 0.049 0.060 0.076 负梯度 1.30 2.00 2.70 k=0.8- Ⅱ 负梯度 0.031 0.039 0.049 0.060 0.076 正梯度 2.70 2.00 1.30 k=1.2- Ⅰ 混合梯度 0.100 0.082 0.068 0.057 0.048 负梯度 1.30 2.00 2.70 k=1.2- Ⅱ 混合梯度 0.100 0.082 0.068 0.057 0.048 正梯度 2.70 2.00 1.30 k=1.6- Ⅰ 正梯度 0.200 0.124 0.077 0.048 0.030 负梯度 1.30 2.00 2.70 k=1.6- Ⅱ 正梯度 0.200 0.124 0.077 0.048 0.030 正梯度 2.70 2.00 1.30 UG- Ⅰ 均匀 0.077 0.073 0.070 0.060 0.048 负梯度 1.30 2.00 2.70 UG- Ⅱ 均匀 0.077 0.073 0.070 0.060 0.048 正梯度 2.70 2.00 1.30 表 3 C2面内梯度模型各部分相对密度
Table 3. Relative density of in-plane gradient model C2
模型 相对密度/% $\overline \rho _1 $ $\overline \rho _2 $ $\overline \rho _3 $ $\overline \rho _4 $ $\overline \rho _5 $ k=0.8 0.80 1.06 1.39 2.00 3.13 k=1.0 1.55 1.65 1.72 1.97 2.48 k=1.2 2.56 2.26 1.97 1.88 1.97 k=1.6 5.14 3.41 2.22 1.59 1.25 UG 2.00 2.00 2.00 2.00 2.00 -
[1] ZHANG Q C, YANG X H, LI P, et al. Bioinspired engineering of honeycomb structure: using nature to inspire human innovation [J]. Progress in Materials Science, 2015, 74: 332–400. DOI: 10.1016/j.pmatsci.2015.05.001. [2] LIU Z, MEYERS M A, ZHANG Z, et al. Functional gradients and heterogeneities in biological materials: design principles, functions, and bioinspired applications [J]. Progress in Materials Science, 2017, 88: 467–498. DOI: 10.1016/j.pmatsci.2017.04.013. [3] CAI Z B, LI Z Y, DING Y, et al. Preparation and impact resistance performance of bionic sandwich structure inspired from beetle forewing [J]. Composites Part B: Engineering, 2019, 161: 490–501. DOI: 10.1016/j.compositesb.2018.12.139. [4] ZHANG Y, WANG J, WANG C H, et al. Crashworthiness of bionic fractal hierarchical structures [J]. Materials & Design, 2018, 158: 147–159. DOI: 10.1016/j.matdes.2018.08.028. [5] SONG J F, XU S C, WANG H X, et al. Bionic design and multi-objective optimization for variable wall thickness tube inspired bamboo structures [J]. Thin-Walled Structures, 2018, 125: 76–88. DOI: 10.1016/j.tws.2018.01.010. [6] 李世强, 李鑫, 吴桂英, 等. 梯度蜂窝夹芯板在爆炸荷载作用下的动力响应 [J]. 爆炸与冲击, 2016, 36(3): 333–339. DOI: 10.11883/1001-1455(2016)03-0333-07.LI S Q, LI X, WU G Y, et al. Dynamic response of functionally graded honeycomb sandwich plates under blast loading [J]. Explosion and Shock Waves, 2016, 36(3): 333–339. DOI: 10.11883/1001-1455(2016)03-0333-07. [7] ZHANG J J, WANG Z H, ZHAO L M. Dynamic response of functionally graded cellular materials based on the Voronoi model [J]. Composites Part B: Engineering, 2016, 85: 176–187. DOI: 10.1016/j.compositesb.2015.09.045. [8] WANG X K, ZHENG Z J, YU J L. Crashworthiness design of density-graded cellular metals [J]. Theoretical and Applied Mechanics Letters, 2013, 3(3): 9–13. DOI: 10.1063/2.1303101. [9] ZHENG J, QIN Q H, WANG T J. Impact plastic crushing and design of density-graded cellular materials [J]. Mechanics of Materials, 2016, 94: 66–78. DOI: 10.1016/j.mechmat.2015.11.014. [10] SHEN C J, YU T X, LU G. Double shock mode in graded cellular rod under impact [J]. International Journal of Solids and Structures, 2013, 50(1): 217–233. DOI: 10.1016/j.ijsolstr.2012.09.021. [11] SHEN C J, LU G, YU T X. Dynamic behavior of graded honeycombs: a finite element study [J]. Composite Structures, 2013, 98: 282–293. DOI: 10.1016/j.compstruct.2012.11.002. [12] YANG J, WANG S L, DING Y Y, et al. Crashworthiness of graded cellular materials: a design strategy based on a nonlinear plastic shock model [J]. Materials Science and Engineering: A, 2017, 680: 411–420. DOI: 10.1016/j.msea.2016.11.010. [13] LIANG M Z, LI Z B, LU F Y, et al. Theoretical and numerical investigation of blast responses of continuous-density graded cellular materials [J]. Composite Structures, 2017, 164: 170–179. DOI: 10.1016/j.compstruct.2016.12.065. [14] 于渤, 卢天健. 蜂窝夹芯结构的面内梯度设计 [C] // 中国力学大会-2015. 上海: 中国力学学会, 2015: 87. [15] YU B, HAN B, SU P B, et al. Graded square honeycomb as sandwich core for enhanced mechanical performance [J]. Materials & Design, 2016, 89: 642–652. DOI: 10.1016/j.matdes.2015.09.154. [16] TAO Y, DUAN S Y, WEN W B, et al. Enhanced out-of-plane crushing strength and energy absorption of in-plane graded honeycombs [J]. Composites Part B: Engineering, 2017, 118: 33–40. DOI: 10.1016/j.compositesb.2017.03.002. [17] WANG H R, LI S Q, LIU Z F, et al. Investigation on the dynamic response of circular sandwich panels with the bio-inspired gradient core [J]. Thin-Walled Structures, 2020, 149: 106667. DOI: 10.1016/j.tws.2020.106667. [18] 陶义, 王宗彦, 王珂, 等. 基于王莲叶脉分布的塔式起重机臂架结构仿生设计 [J]. 机械设计与制造, 2017(3): 36–39. DOI: 10.19356/j.cnki.1001-3997.2017.03.010.TAO Y, WANG Z Y, WANG K, et al. Structural bionic design for tower cranes boom based on King Lotus leaf vein branched structure [J]. Machinery Design & Manufacture, 2017(3): 36–39. DOI: 10.19356/j.cnki.1001-3997.2017.03.010. [19] VAZIRI A, HUTCHINSON J W. Metal sandwich plates subject to intense air shocks [J]. International Journal of Solids and Structures, 2007, 44(6): 2021–2035. DOI: 10.1016/j.ijsolstr.2006.08.038. [20] 强斌, 刘宇杰, 阚前华. 粘接界面泡沫铝夹芯板的三点弯曲失效数值模拟 [J]. 材料工程, 2014, 4(11): 97–101. DOI: 10.11868/j.issn.1001-4381.2014.11.017.QIANG B, LIU Y J, KAN Q H. Numerical simulation for three-point bending failure of aluminum foam sandwich panels with cohesive interface [J]. Journal of Materials Engineering, 2014, 4(11): 97–101. DOI: 10.11868/j.issn.1001-4381.2014.11.017. [21] LIU Z F, HAO W Q, XIE J M, et al. Axial-impact buckling modes and energy absorption properties of thin-walled corrugated tubes with sinusoidal patterns [J]. Thin-Walled Structures, 2015, 94: 410–423. DOI: 10.1016/j.tws.2015.05.002. [22] FLECK N A, DESHPANDE V S. The resistance of clamped sandwich beams to shock loading [J]. Journal of Applied Mechanics, 2004, 71(3): 386–401. DOI: 10.1115/1.1629109. -






 下载:
下载: