基于拓扑优化的车辆底部防护组件改进设计

毕政; 周云波; 吴凯; 李明星; 孙晓旺

doi:10.11883/bzycj-2020-0141

基于拓扑优化的车辆底部防护组件改进设计

doi: 10.11883/bzycj-2020-0141

南京理工大学机械工程学院，江苏南京 210094

基金项目: 国家自然科学基金（51405232,11802140）；中央高校基本科研业务费专项资金（30918011303）；道路交通安全公安部重点实验室开放基金（2018ZDSYSKFKT09）

详细信息

作者简介:
毕　政（1997－　），男，硕士研究生，koery806@163.com

通讯作者:
周云波（1980－　），男，博士，副教授，yunbo31983@163.com

中图分类号: O383; TJ81
计量
- 文章访问数: 623
- HTML全文浏览量: 271
- PDF下载量: 74
- 被引次数: 0
出版历程
- 收稿日期: 2020-05-11
- 修回日期: 2020-08-14
- 网络出版日期: 2021-04-14
- 刊出日期: 2021-04-14

Improved design of vehicle bottom protective components based on topology optimization

School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China

摘要

摘要: 为提升车辆底部防护组件的抗爆性能，降低车身底板变形对车内乘员的威胁，基于混合自动元胞机法对防护组件中的加强梁进行拓扑优化设计，得到了加强梁的最佳材料分布形式，随后根据拓扑优化结果进行了工程诠释和重新设计。为了进一步提升防护组件的抗爆性能，采用多目标优化的方法对加强梁进行优化设计，以基板的挠度峰值、基板的最大动能和防护组件质量为优化目标，防护组件的质量为约束条件，以及梁的厚度、截面尺寸为设计变量，得出加强梁各参数组合的最优方案。结果表明，相比于初始设计，该方案在不增加结构质量的情况下，防护组件的抗爆性能得到显著提升，改进后基板的挠度峰值降低了5%，基板的最大动能降低了11.58%。
- 防护组件 /
- 抗爆炸冲击 /
- 拓扑优化 /
- 多目标优化
Abstract: In order to improve the anti-explosion performance of the bottom protective components of the vehicle and reduce the threat of the body floor deformation to the occupants in the vehicle, topology optimization was conducted based on hybrid cellular automation (HCA) to design the stiffening beams in the protective components, the best material distribution form of the stiffening beams was obtained, the topology optimization results was interpreted and then the stiffening beams was redesigned. In order to further improve the anti-explosion performance of the protective components, the multi-objective optimization method was used to optimize the design of the stiffening beams, the optimal scheme for the parameter combination of the beams was obtained by selecting the peak deflection of test plate, the maximum kinetic energy of test plate and the mass of the protective components as objectives, the mass of the protective components as constraint, the thickness and cross-sectional dimensions of the beams as design variables. The results show that, compared with the original design, the scheme increase the anti-explosion performance of the protective components without increasing the structural mass. After optimization the peak deflection of test plate is reduced by 5%, and the maximum kinetic energy of test plate is reduced by 11.58%.
- protective components /
- anti-explosion impact /
- topology optimization /
- multi-objective optimization

HTML全文

图 1 爆炸冲击台架数值模型

Figure 1. Simulation model of explosive impact bench

下载: 全尺寸图片幻灯片

图 2 防护组件爆炸数值计算结果

Figure 2. Explosion simulation results of protective components

下载: 全尺寸图片幻灯片

图 3 台架爆炸试验结果与分析

Figure 3. Bench explosion test results and analysis

下载: 全尺寸图片幻灯片

图 4 台架模型简化及分析

Figure 4. Bench model simplification and analysis

下载: 全尺寸图片幻灯片

图 5 拓扑优化模型

Figure 5. Topology optimization model

下载: 全尺寸图片幻灯片

图 6 拓扑优化结果与工程解读

Figure 6. Topology optimization results and engineering interpretation

下载: 全尺寸图片幻灯片

图 7 设计变量位置图

Figure 7. Design variable position diagram

下载: 全尺寸图片幻灯片

图 8 帕累托解集

Figure 8. Pareto set

下载: 全尺寸图片幻灯片

图 9 改进后基板最大变形图

Figure 9. Maximum deflection of the test plate after optimization

下载: 全尺寸图片幻灯片

图 10 改进前后基板动能

Figure 10. Kinetic energy of test plate before and after optimization

下载: 全尺寸图片幻灯片

表 1 正交试验设计结果

Table 1. Results obtained by orthogonal test design

试验	T₁/mm	T₂/mm	T₃/mm	T₄/mm	T₅/mm	d/mm	K/kJ
1	7.2	5.4	3.6	3.6	0.288	134.4	39.1
2	7.2	5.4	3.6	4.4	0.352	130.5	38.7
3	7.2	6.6	4.4	3.6	0.288	126.6	35.4
4	7.2	6.6	4.4	4.4	0.352	122.1	35.3
5	8.8	5.4	4.4	3.6	0.352	128.7	37.2
6	8.8	5.4	4.4	4.4	0.288	127.3	35.8
7	8.8	6.6	3.6	3.6	0.352	123.5	32.2
8	8.8	6.6	3.6	4.4	0.288	123.1	32.8

下载: 导出CSV

表 2 基板挠度峰值及最大动能影响因素显著性分析

Table 2. Notability analysis of peak deflection and maximum kinetic energy of test plate influence factors

来源	基板挠度峰值/mm			基板最大动能/kJ
来源	平方和	均方	F	平方和	均方	F
T₁	15.125	15.125	88.971	13.781	13.781	26.956
T₂	81.920	81.920	481.882	28.501	28.501	55.748
T₃	5.780	5.780	34.000	0.101	0.101	0.198
T₄	13.005	13.005	76.500	0.211	0.211	0.413
T₅	5.445	5.445	32.029	0.011	0.011	0.022
误差	0.340	0.340		1.022	1.022

下载: 导出CSV

表 3 设计变量取值范围

Table 3. Design variable value range

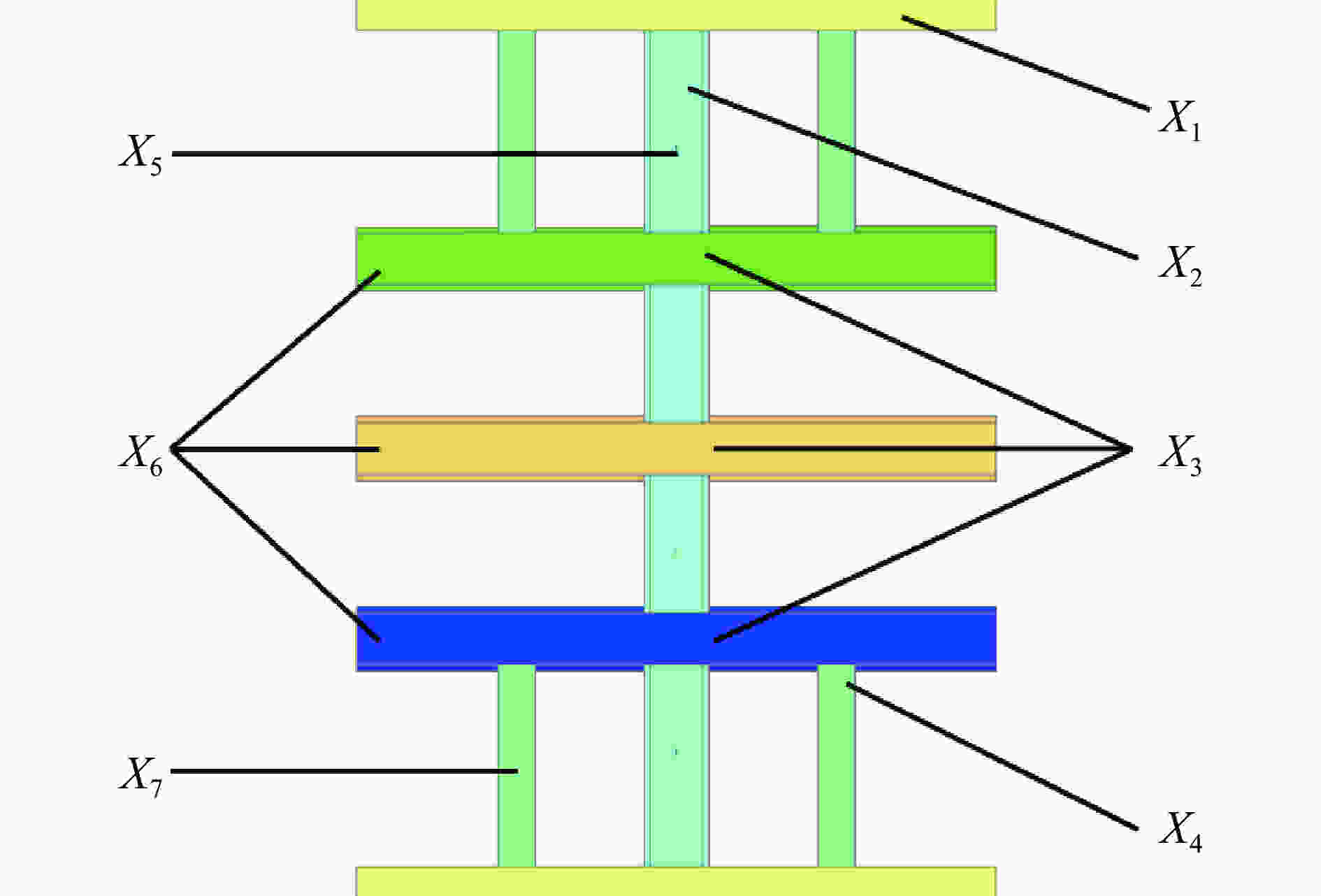
设计变量	变量描述	初始值	下限	上限
X₁/mm	边梁厚度	4	4	6
X₂/mm	原有纵梁厚度	4	3	6
X₃/mm	横梁厚度	4	2	6
X₄/mm	新增纵梁厚度	2	1	3
X₅/mm	原有纵梁宽度	100	80	120
X₆/mm	横梁宽度	100	80	120
X₇/mm	新增纵梁宽度	60	48	72

下载: 导出CSV

表 4 不同近似模型误差分析

Table 4. Error analysis of different approximate models

性能指标	样本	相对误差/%
性能指标	样本	RBF_MQ	kriging	SVR
基板的挠度峰值/mm	1	−1.24	0.61	1.53
	2	4.61	1.31	4.26
	3	1.12	3.24	−1.72
	4	1.23	−1.27	2.36
	5	1.57	1.06	4.87
	6	1.43	2.11	1.65
	7	1.58	4.71	−1.42
	8	2.02	−1.21	2.31
	平均相对误差	1.54	1.32	1.73
	最大相对误差	4.61	4.71	4.87
基板的最大动能/kJ	1	0.55	0.50	1.08
	2	1.03	4.03	1.51
	3	1.32	−1.52	2.65
	4	2.45	1.69	3.28
	5	2.60	2.37	−1.38
	6	2.32	1.86	2.19
	7	−2.36	1.17	2.52
	8	1.29	1.02	3.51
	平均相对误差	1.15	1.39	1.92
	最大相对误差	2.60	4.03	3.51
防护组件质量/kg	1	−0.022	0.019	0.31
	2	0.033	−0.024	0.61
	3	0.023	0.022	0.87
	4	0.018	0.035	0.98
	5	0.081	0.086	0.16
	6	0.032	0.057	0.52
	7	0.046	0.069	−0.21
	8	0.021	−0.016	0.12
	平均相对误差	0.029	0.031	0.42
	最大相对误差	0.081	0.086	0.98

下载: 导出CSV

表 5 优化前后设计变量取值

Table 5. Design variable values before and after optimization

设计变量	初始值	优化值
X₁/mm	4	4.85
X₂/mm	4	3.93
X₃/mm	4	2.00
X₄/mm	2	2.73
X₅/mm	100	108.20
X₆/mm	100	80.00
X₇/mm	60	62.52

下载: 导出CSV

表 6 优化解的预测值与计算值对比

Table 6. Comparison of the predicted and simulated values of the optimized solution

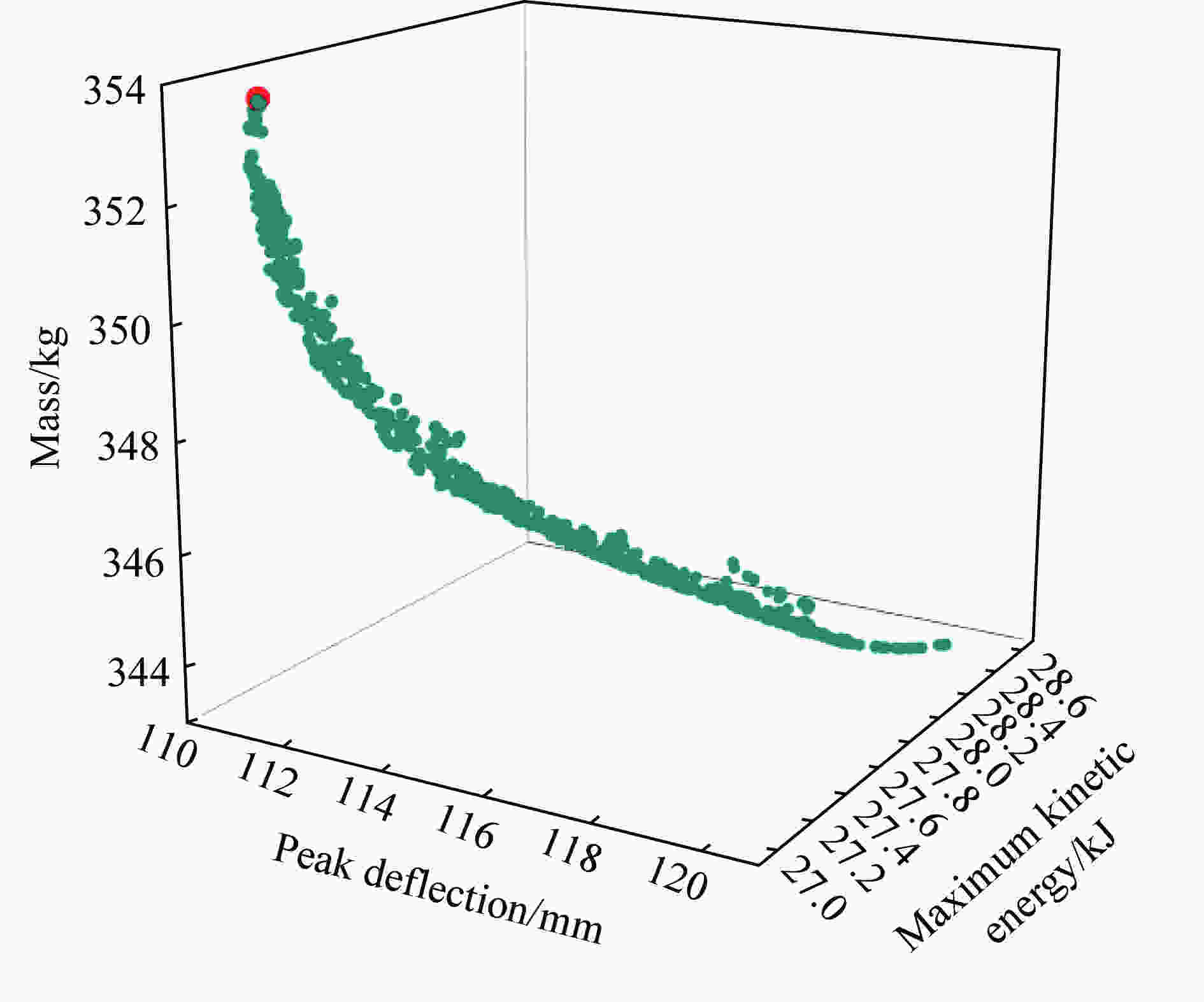
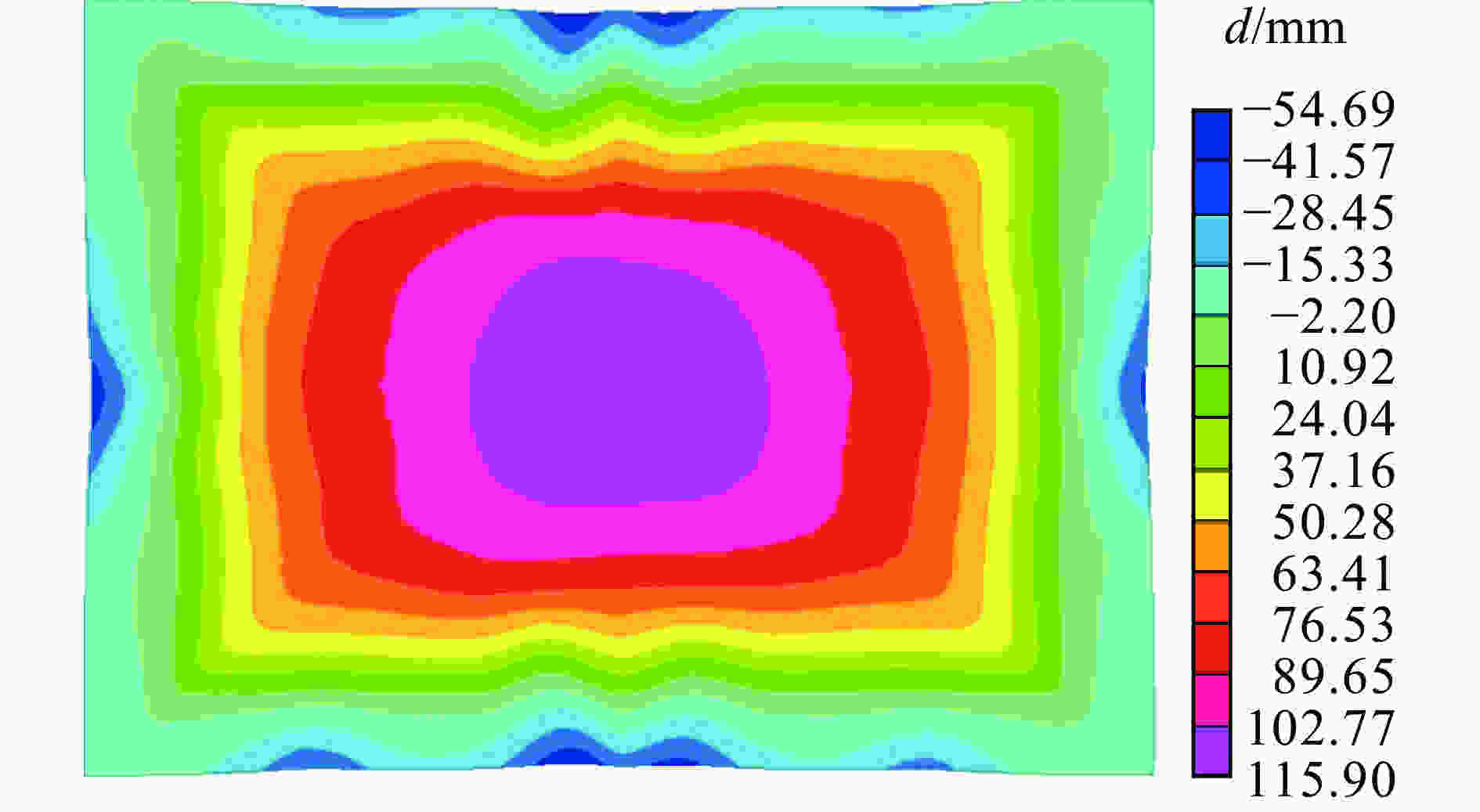
优化目标	预测值	计算值	相对误差/%
基板的挠度峰值/mm	111.36	115.90	4.08
基板的最大动能/kJ	27.03	27.10	0.26
防护组件质量/kg	353.71	354.12	0.12

下载: 导出CSV

表 7 改进前后各性能指标对比

Table 7. Comparison of performance indexes before and after optimization

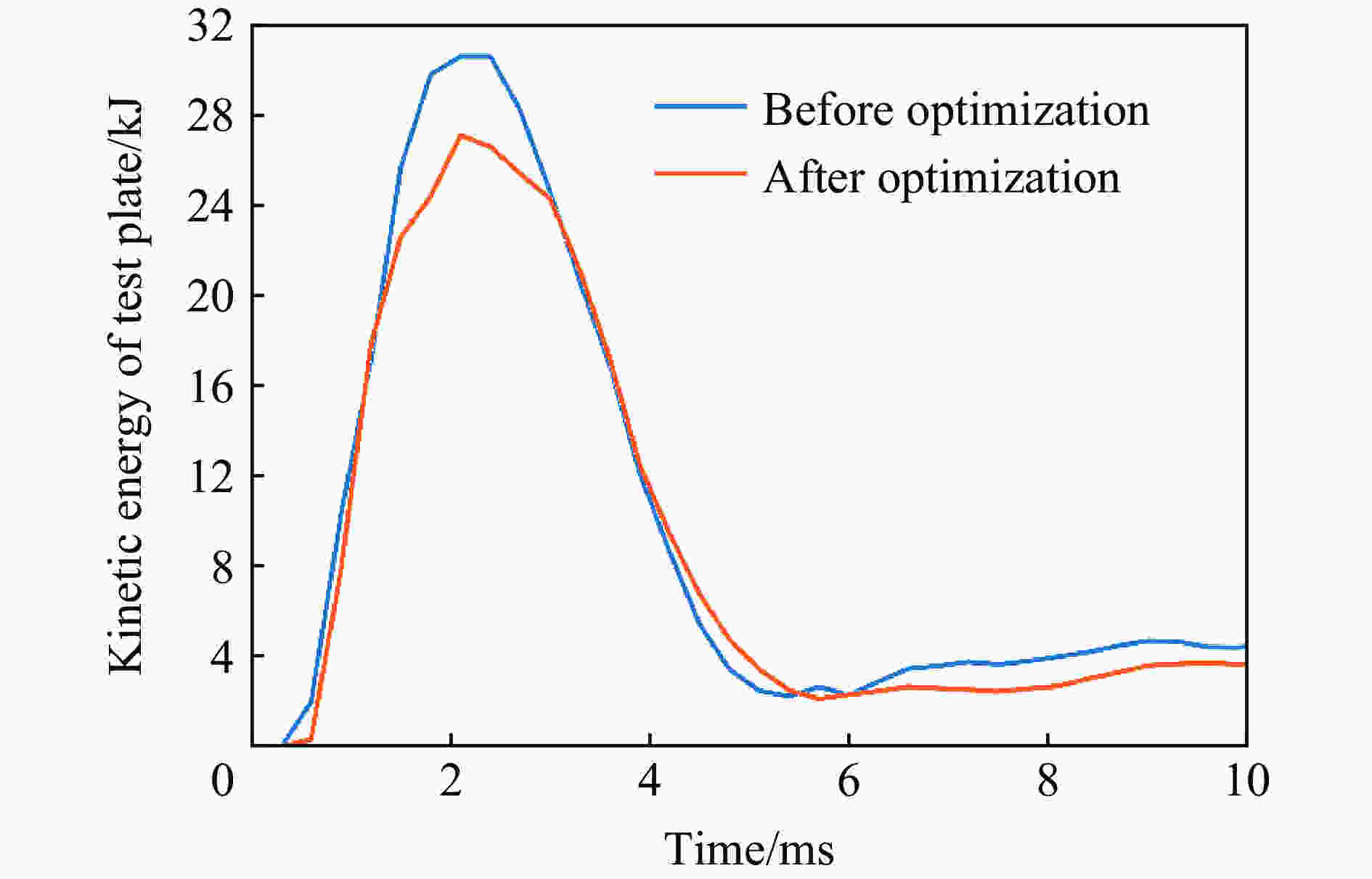
优化目标	改进前	改进后	变化量/%
基板的挠度峰值/mm	122	115.90	−5.00
基板的最大动能/kJ	30.65	27.10	−11.58
防护组件质量/kg	360	354.12	−1.63

下载: 导出CSV

参考文献(19)

[1]	李红勋, 谭柏春, 贾楠, 等. 美军战术轮式车辆发展策略研究 [J]. 军事交通学院学报, 2012, 14(10): 83–87. DOI: 10.3969/j.issn.1674-2192.2012.10.022. LI H X, TAN B C, JIA N, et al. Research on US military tactic wheeled vehicle strategy [J]. Journal of Military Transportation University, 2012, 14(10): 83–87. DOI: 10.3969/j.issn.1674-2192.2012.10.022.
[2]	张钱城, 郝方楠, 李裕春, 等. 爆炸冲击载荷作用下车辆和人员的损伤与防护 [J]. 力学与实践, 2014, 36(5): 527–539. DOI: 10.6052/1000-0879-13-539. ZHANG Q C, HAO F N, LI Y C, et al. Damage and protection of vehicles and personnel under blast loading [J]. Mechanics in Engineering, 2014, 36(5): 527–539. DOI: 10.6052/1000-0879-13-539.
[3]	韩辉, 焦丽娟, 徐平. 战车底部防雷技术研究 [J]. 四川兵工学报, 2007, 28(3): 11–13. DOI: 10.3969/j.issn.1006-0707.2007.03.004. HAN H, JIAO L J, XU P. Study on protection technology for combat vehicles against belly-attack anti-tank mine [J]. Journal of Sichuan Ordnance, 2007, 28(3): 11–13. DOI: 10.3969/j.issn.1006-0707.2007.03.004.
[4]	RAMASAMY A, HILL A M, HEPPER A E, et al. Blast mines: physics, injury mechanisms and vehicle protection [J]. Journal of the Royal Army Medical Corps, 2009, 155(4): 258–264. DOI: 10.1136/jramc-155-04-06.
[5]	SUN G, ZHANG J, LI S, et al. Dynamic response of sandwich panel with hierarchical honeycomb cores subject to blast loading [J]. Thin Walled Structures, 2019, 142: 499–515. DOI: 10.1016/j.tws.2019.04.029.
[6]	李明星, 王显会, 周云波, 等. 基于神经网络的车辆抗冲击防护组件优化 [J]. 爆炸与冲击, 2020, 40(2): 024203. DOI: 10.11883/bzycj-2019-0055. LI M X, WANG X H, ZHOU Y B, et al. Research on optimization of vehicle anti-shock protection components based on neural network [J]. Explosion and Shock Waves, 2020, 40(2): 024203. DOI: 10.11883/bzycj-2019-0055.
[7]	IMBALZANO G, LINFORTH S, NGO T, et al. Blast resistance of auxetic and honeycomb sandwich panels: comparisons and parametric designs [J]. Composite Structures, 2018, 183(1): 242–261. DOI: 10.1016/j.compstruct.2017.03.018.
[8]	陈震. 某SUV车架多目标拓扑优化设计[D]. 合肥: 合肥工业大学, 2014.
[9]	聂昕, 黄鹏冲, 陈涛, 等. 基于耐撞性拓扑优化的汽车关键安全件设计 [J]. 中国机械工程, 2013(23): 140–145. DOI: 10.3969/j.issn.1004-132X.2013.23.028. NIE X, HUANG P C, CHEN T, et al. Topology optimization of automotive key safety component design based on crashworthiness [J]. China Mechanical Engineering, 2013(23): 140–145. DOI: 10.3969/j.issn.1004-132X.2013.23.028.
[10]	高云凯, 张玉婷, 方剑光. 基于混合元胞自动机的铝合金保险杠横梁设计 [J]. 同济大学学报(自然科学版), 2014, 43(3): 0456–0461. DOI: 10.11908/j.issn.0253-374x.2015.03.021. GAO Y K, ZHANG Y T, FANG J G. Design of aluminum bumper beam based on hybrid cellular automata [J]. Journal of Tongji University (Natural Science), 2014, 43(3): 0456–0461. DOI: 10.11908/j.issn.0253-374x.2015.03.021.
[11]	DUDDECK F, HUNKELER S, LOZANO P, et al. Topology optimization for crashworthiness of thin-walled structures under axial impact using hybrid cellular automata [J]. Structural & Multidisciplinary Optimization, 2016, 54(3): 415–428. DOI: 10.1007/s00158-016-1445-y.
[12]	GOETZ J, TAN H, RENAUD J E, et al. Two-material optimization of plate armour for blast mitigation using hybrid cellular automata [J]. Engineering Optimization, 2012, 44(8): 985–1005. DOI: 10.1080/0305215x.2011.624182.
[13]	NATO. Protection levels for occupants of logistic and light armored vehicles: NSA/0533- LAND/4569 [S]. Brussels: NATO, 2004.
[14]	王春林, 胡蓓蓓, 冯一鸣, 等. 基于径向基神经网络与粒子群算法的双叶片泵多目标优化 [J]. 农业工程学报, 2019, 35(2): 25–32. DOI: 10.11975/j.issn.1002-6819.2019.02.004. WANG C L, HU B B, FENG Y M, et al. Multi-objective optimization of double vane pump based on radial basis neural network and particle swarm [J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(2): 25–32. DOI: 10.11975/j.issn.1002-6819.2019.02.004.
[15]	PATEL N M, KANG B, RENAUD J E, et al. Crashworthiness design using topology optimization [J]. Journal of Mechanical Design, 2009, 131(6): 061013–1-061013-12. DOI: 10.1115/1.3116256.
[16]	张颂安. 小型轻量化电动汽车正面碰撞响应及结构优化[D]. 北京: 清华大学, 2016.
[17]	甘宁. 基于耐撞性和刚度车辆端部底架的拓扑概念设计[D]. 长沙: 中南大学, 2014.
[18]	刘丰嘉. 机车车辆耐撞性仿真与端部结构拓扑优化设计[D]. 成都: 西南交通大学, 2018.
[19]	伍素珍, 郑刚, 李光耀, 等. 汽车车身结构安全部件材料匹配优化设计 [J]. 锻压技术, 2015, 40(11): 85–93. DOI: 10.13330/j.issn.1000-3940.2015.11.018. WU S Z, ZHENG G, LI G Y, et al. Optimization design of material matching for auto-body safety components [J]. Forging & Stamping Technology, 2015, 40(11): 85–93. DOI: 10.13330/j.issn.1000-3940.2015.11.018.