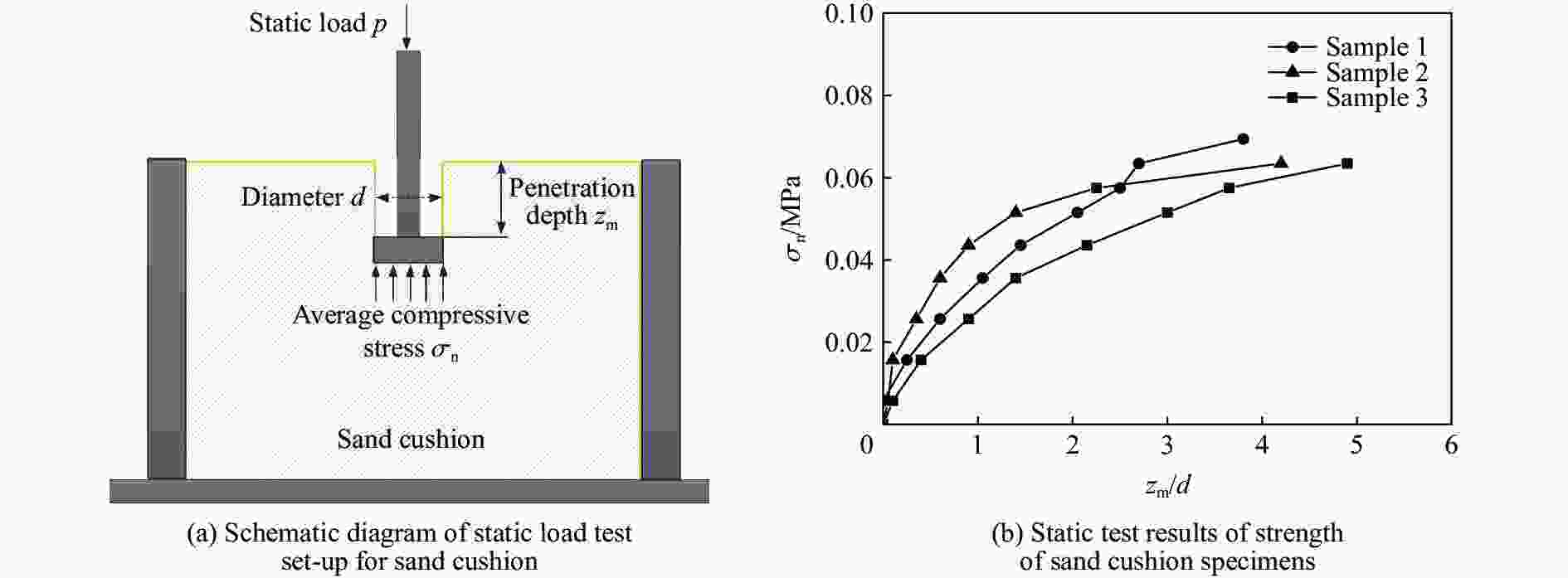
Experimental study of different typical shape falling-rocks impacting on the sand cushion and dimensionless analysis
-
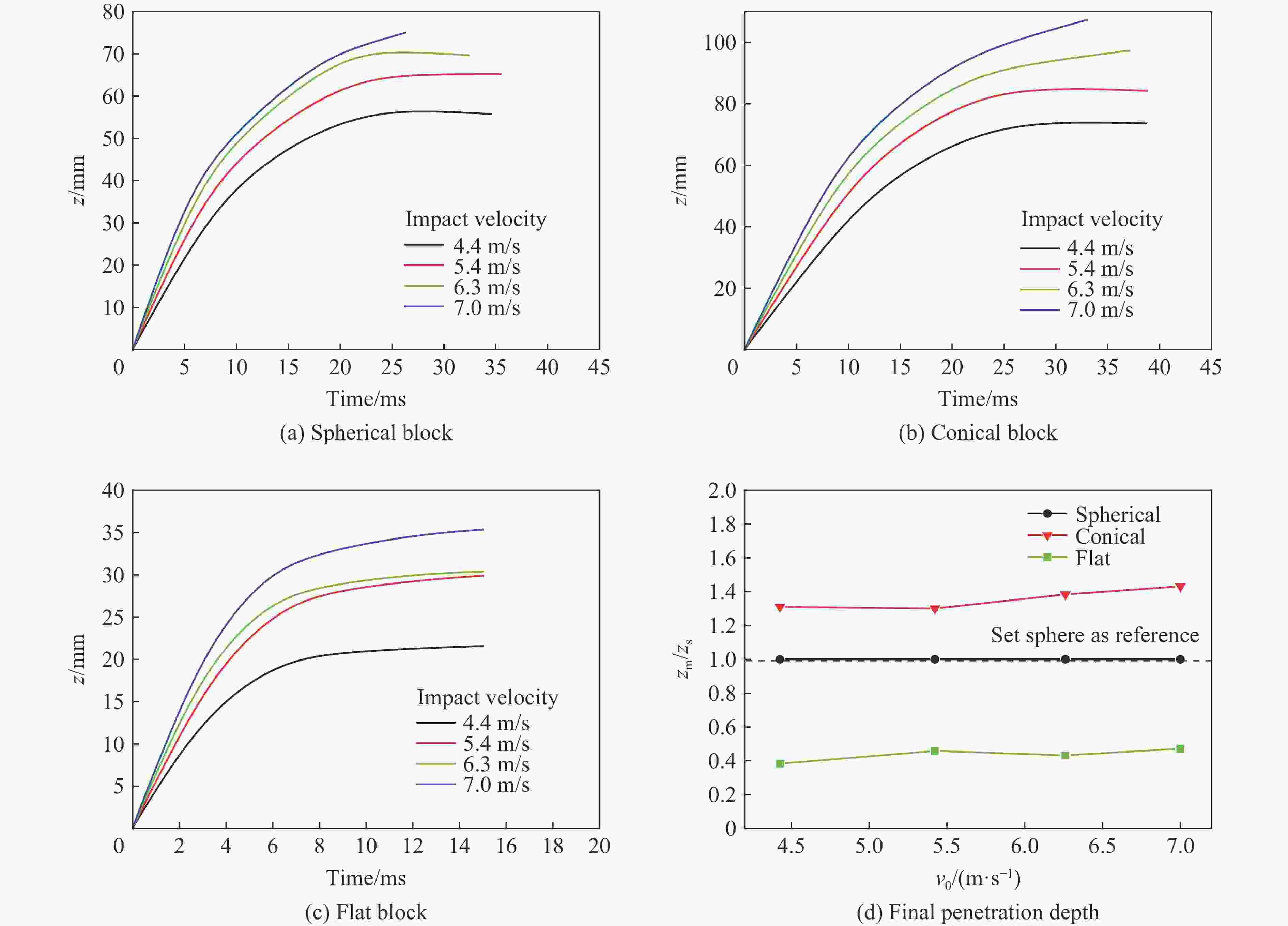
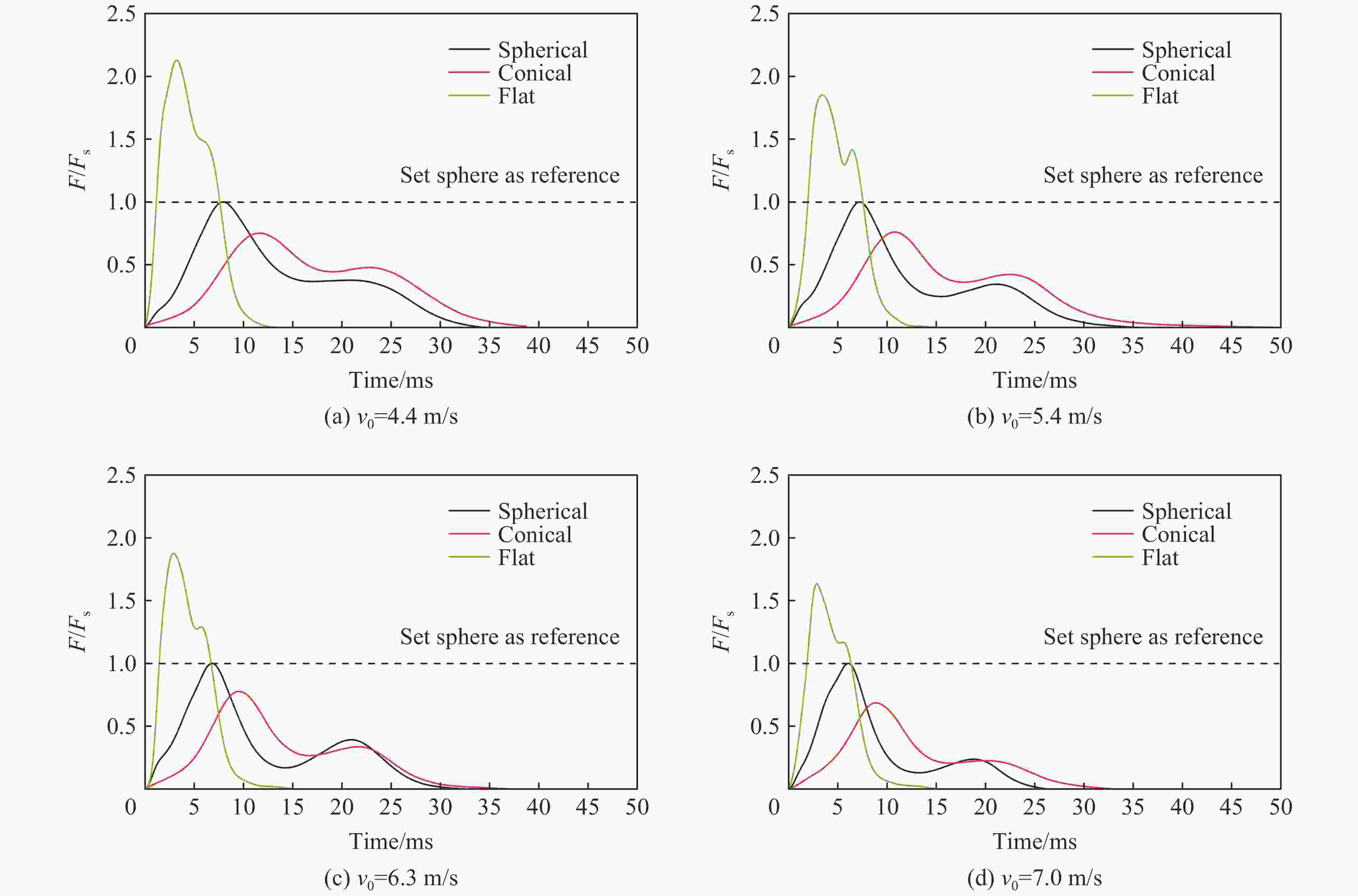
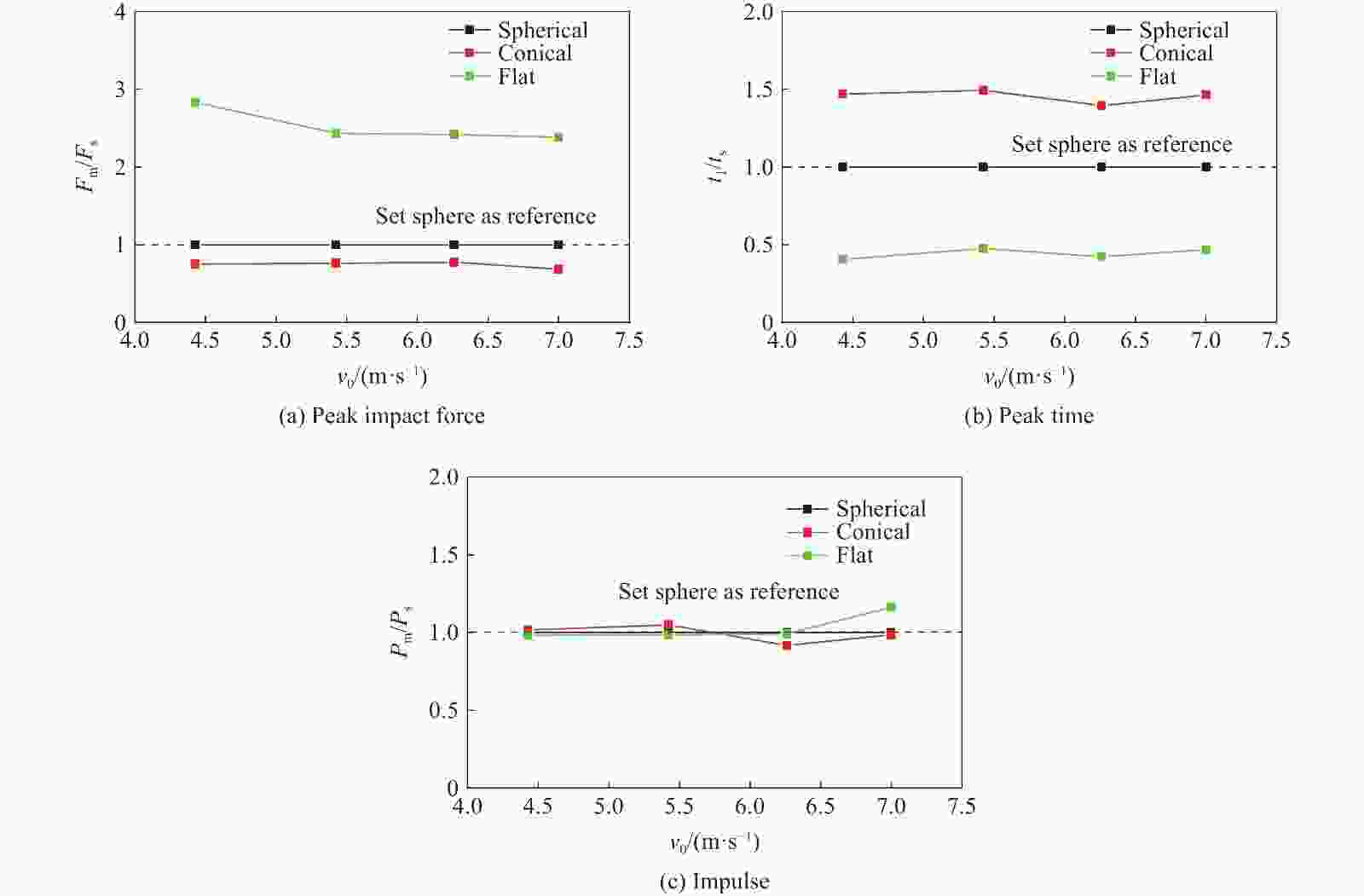
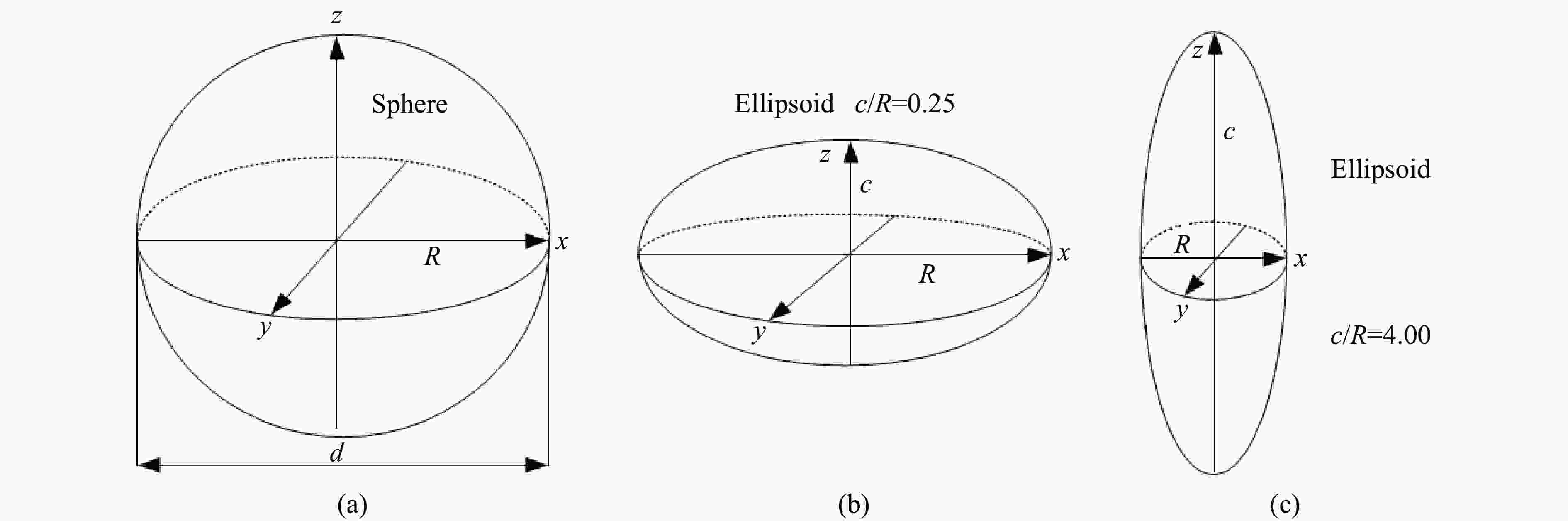
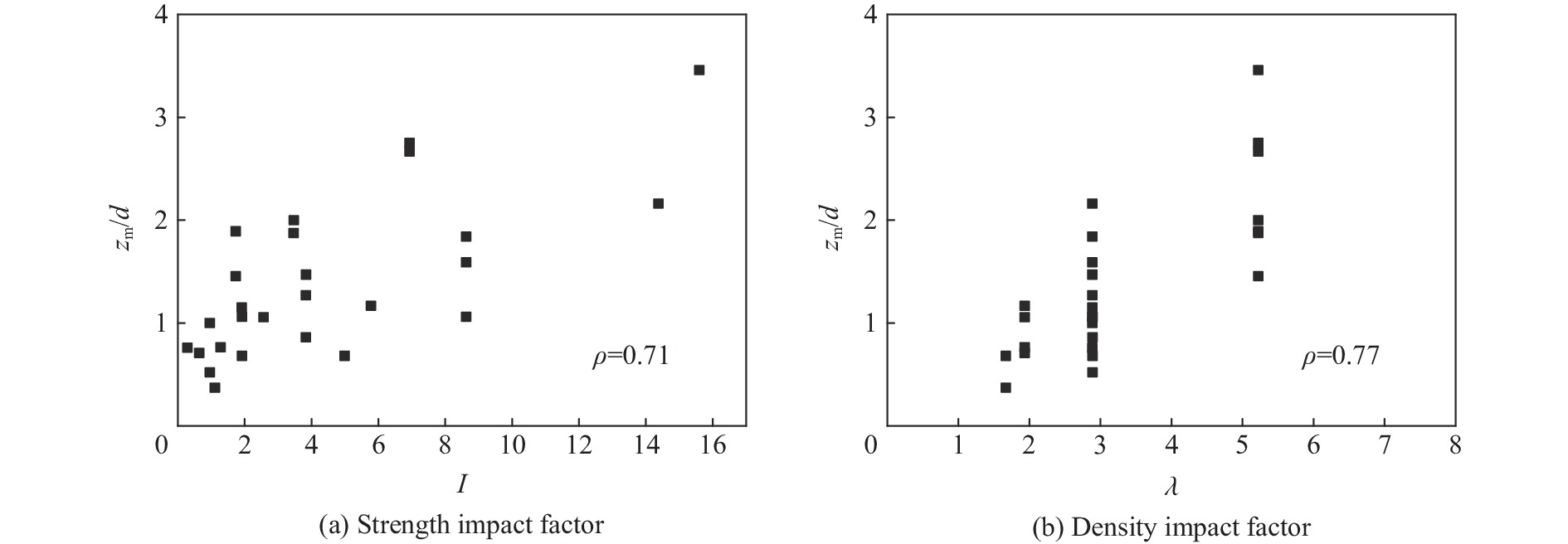
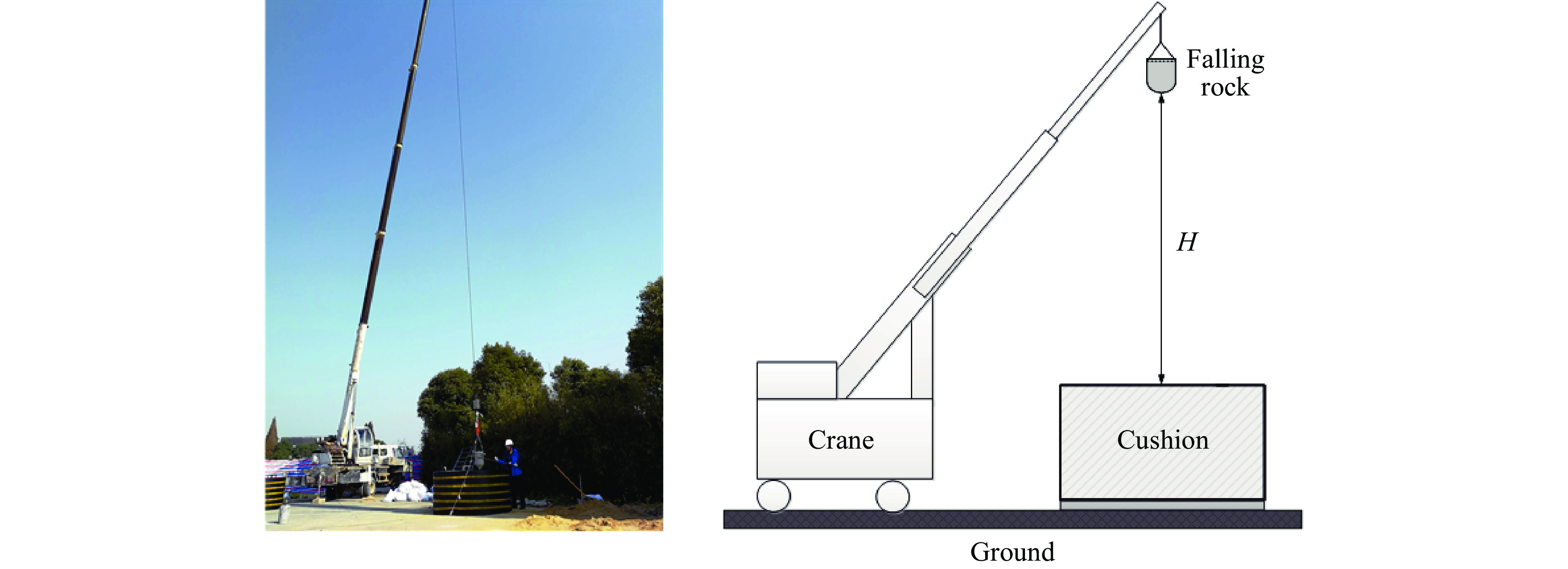
摘要: 开展了球形、锥形和平头3种典型形状落石撞击垫层的冲击力及侵入深度的试验研究。结果表明，落石形状对冲击试验结果有显著影响：相同条件下，平头落石的冲击力最大，侵入深度和冲击力峰值时间最短，锥形落石反之，而球形落石介于两者之间。采用无量纲化分析方法，将落石的质量、速度、形状、特征尺寸，垫层的强度、密度转换为无量纲强度冲击因子I、密度冲击因子λ和形状冲击因子ψ，并对冲击因子与侵入深度的试验数据进行了相关性分析，结果表明：（1）冲击因子I和λ在决定最终侵深zm/d 中所起到的作用比较相近；（2）冲击因子I和λ对侵入深度的影响分析表明，I和λ的相对独立性较强，相互影响较小，在不同的λ值下，I对侵入深度的影响规律基本一致。Abstract: An experimental study on the impact force and penetration of falling rocks with three typical shapes, including spherical, conical and flat shapes, against the cushion was carried out. The experimental results show that the shape of the falling rock has a significant influence on the impact results. Under the same conditions, the flat blocks have the highest impact force, the lowest penetration depth and the shortest peak impact time, and the opposite for the conical falling rocks, with spherical blocks are between the two. The dimensionless analysis method was adopted to convert the mass, velocity, shape, size of the falling rock, the strength and density of the cushion layer into the dimensionless strength impact factor I, density impact factor λ and shape impact factor ψ. The correlation analysis between the impact factors and penetration test data shows that: (1) The effects of the impact factors I and λ on the final depth of penetration zm/d are similar. (2) The analysis of the impact factors I and λ effects on penetration depth shows that I and λ are relatively independent. The pattern of the I effects on the depth of penetration is generally consistent for different λ values.
-
Key words:
- falling rock’s shape /
- impact force /
- penetration depth /
- dimensionless /
- cushion
-
水下爆炸主要包括三个阶段：装药的爆轰、冲击波的产生和传播、气泡的形成和脉动，各阶段的荷载效应和宏观行为各有特点又密切联系、相互影响。早期的研究多出于军事应用的目的，着重分析了水下爆炸现象及荷载效应，其中Cole[1]基于对二十世纪中叶前的水下爆炸研究成果的总结分析，对水下爆炸的物理现象、毁伤机理和基本定律进行了研究，形成了比较系统的理论体系。近年来，随着试验和数值模拟技术的发展，研究重心逐渐向复杂边界条件对荷载特性和气泡脉动规律的影响倾斜，对于水深[2]、水面环境[3-4]、水底条件[5-6]、临近结构[3,7]等因素影响下的爆炸荷载效应均有较成熟的研究，这为准确分析水下爆炸的荷载特性和对结构的毁伤机理提供了依据。
爆炸荷载作用下码头结构毁伤效应及毁伤机理研究是一个涉及爆炸荷载特性、多种材料动态本构模型、多介质瞬态动力耦合相互作用、钢筋混凝土结构动力破坏机理和动态性能等多方面的复杂课题，相关系统研究较少，现有研究多集中于钢筋混凝土构件毁伤机理和抗爆特性[8-11]。近年来，张社荣等[12]、王高辉等[13-14]和Li等[15]对水下爆炸下高混凝土坝的毁伤机理和毁伤特性进行了较为系统的研究。国内外就爆炸对码头的毁伤效应和抢修抢建问题已开展了一些研究，但研究对象多为高桩码头，荷载作用方式多为空爆和内爆，鲜见水下爆炸对沉箱重力式码头的毁伤效应的研究[16-18]。
本文通过开展不同爆距下水下爆炸对沉箱重力式码头模型毁伤效应的试验研究，对水下爆炸下水中荷载和码头毁伤情况进行了采集分析，得到了水下爆炸下沉箱重力式码头的主要毁伤因素和毁伤模式，系统分析了毁伤机理，初步研究了爆距对毁伤效应的影响。为进一步开展理论和数值模拟研究提供了参考和依据。
1. 试验设计
1.1 试验模型
以现有突堤式沉箱码头为参考，以真实反映沉箱重力式码头结构特性和材料特性为原则，依据设计规范，兼顾施工可行性和试验条件制作模型。模型长298 cm、宽162 cm、高219 cm。以封仓板为界，码头下部为沉箱结构，高180 cm，由外墙、沉箱底板、封舱板、内隔墙及其所围成的6个长86 cm、宽65 cm仓格和仓格内的饱和砂构成。码头上部结构高39 cm，由面板、外墙、管沟底板、管沟内壁及其所围成的前、后管沟和中间仓格以及仓格内的干砂构成。为便于描述，对码头竖向外墙进行编号，将码头外墙长度方向等分成3份、宽度方向外墙等分成2份，从迎爆面左端起，按逆时针依次编为1#～10#号墙。模型三视图及其剖面图如图1所示，本文图中长度单位均采用厘米（cm），高程单位均采用米（m），后文不再赘述。
混凝土设计强度C30，钢筋采用HPB335型号，填料为普通河砂，主要部位件混凝土厚度及配筋情况如表1所示。共制作3个模型。
表 1 主要部位混凝土厚度及配筋情况Table 1. Concrete thickness and matching bar condition of main members位置 混凝土厚度/cm 配筋情况 保护层厚度/cm 仓格外墙 12 双层双向配筋，钢筋直径 1.2 cm，间距 18 cm 2 仓格内隔墙 8 双层双向配筋，钢筋直径 0.8 cm，间距 9 cm 1.5 沉箱底板 25 双层双向配筋，钢筋直径 2 cm，间距 18 cm 4 管沟底板 13 双层双向配筋，钢筋直径 0.6 cm，间距 15 cm 2 管沟外壁 12 双层双向配筋，钢筋直径 0.6 cm，间距 15 cm 1.5 面板 6 管沟上部面板单层双向配筋，其他部位不配筋 1.5 封仓板 6 不配筋 1.2 试验方案
试验场地为直径8 m、深8 m的钢筋混凝土空心圆柱爆坑，内衬2 cm厚钢板。试验水深1.8 m，模型四面临水，底部无人为约束。炸药承台与沉箱吊环焊接定位。均采用1 kg TNT当量的圆柱状PENT炸药，药包轴线垂直于迎爆面，正对迎爆面外墙中点。炸药位于水深0.9 m处，工况1、2、3中离迎爆面水平距离分别为接触、0.5 m、1 m。试验方案如表2所示，试验场地及炸药布设方案如图2所示。
表 2 试验方案Table 2. Experimental schemes工况 爆炸类型 模型 药包编号 炸药位置 1 接触爆炸 UW2 c1 贴于迎爆面中间仓格外墙中点，水深 0.9 m 处 2 非接触爆炸 UW1 c2 正对中间仓格外墙中点，爆距 0.5 m，水深 0.9 m 处 3 非接触爆炸 UW3 c3 正对中间仓格外墙中点，爆距 1.0 m，水深 0.9 m 处 试验中采用PCB138A10水下激波传感器对水下冲击波荷载进行测量，传感器量程69 MPa，谐振频率≥1 MHz，采集器采集频率为1 MHz。通过钢丝绳和重锤将传感器固定于远离模型侧面与迎爆面平齐处，测点与药包同深。试验前对传感器实际位置进行量测，布设方案和各工况中传感器实际位置如图3所示。此外，以爆坑内壁为基准，试验前后通过人工量距对模型定位，得到码头整体滑移。
2. 水中荷载分析
本试验为有限水域浅水爆炸，现无被广泛认可的冲击波荷载经验计算公式[19]，采用基于大量实验得到的无限水域中爆炸的冲击波荷载经验计算公式：
Pm=52.16(W1/3S)1.13 (1) I=5 760W0.63S0.891 (2) Rmax=3.3(WH+10.33)1/3 (3) 式中：W为炸药装量，kg；H为炸药距离水面的深度，m；S为荷载传播距离，m；Pm为冲击波峰值压力，MPa；I为冲击波比冲量，Pa·s；Rmax为气泡膨胀的最大半径，m。表3为水下荷载测量值和理论计算值比较，对比发现峰值压力偏差较小，试验设置准确、有效；但各冲击波相互作用使得荷载的衰减规律发生了较大的变化，故比冲量偏差较大。
表 3 爆炸冲击波荷载验证Table 3. Verification of explosion shock wave pressure工况 冲击波峰值压力/MPa 冲击波比冲量/(kPa·s) 测量值 计算值 偏差% 测量值 理论计算值 偏差% 1 13.57 13.08 3.75 1.17 1.94 −39.69 2 13.58 13.27 2.34 1.00 1.96 −48.98 3 14.16 13.88 2.02 1.69 2.03 −16.75 根据式（3）可知本文试验中气泡的理论最大半径为1.47 m，而实际爆深为0.9 m。受气泡膨胀的推动，自由面会向上运动形成水冢直至破碎，水质点获得大量动能，出现垂直喷射和径向飞溅[20]。起爆后各工况均观察到十几米高的水柱。此外，因水面被顶开，爆轰产物大量外泄，试验中未形成完整的气泡脉动过程，因此本文工况下水下爆炸荷载作用主要发生于冲击波传播阶段。
图4为各工况测点压力时程曲线，起算时间为爆炸冲击波到达测点时。不同工况下测点位置荷载变化规律相似，各工况中均出现了3次较为明显的超压作用。爆炸冲击波到达测点时出现第1个峰值压力，亦是最大峰值压力，随后水底反射波到达测点位置，第2个峰值压力出现。最后一个峰值压力是由爆炸冲击波在爆坑侧壁产生的反射波引起的。3次荷载对比如表4所示，爆炸冲击波、水底反射波和侧壁反射波峰值压力、衰减时间和比冲量相近，均会对结构产生较大影响，是本文试验中水下爆炸冲击波传播阶段的主要毁伤因素。
表 4 冲击波荷载比较Table 4. Compasion of shock wave pressure工况 峰值压力/MPa 冲击波比冲量/(kPa·s) 爆炸冲击波 水底反射波 侧壁反射波 爆炸冲击波 水底反射波 侧壁反射波 1 13.57 6.05 7.83 1.17 0.16 0.37 2 13.58 5.73 9.58 1.00 0.15 0.36 3 14.16 8.68 6.13 1.69 0.26 0.63 3. 结构毁伤情况及分析
3.1 工况1结构毁伤模式及分析
接触爆炸下码头模型毁伤模式如图5所示。爆炸后结构向后整体滑移约35 cm。码头毁伤严重，迎爆面、侧面和顶面均出现较大毁伤。迎爆面外墙被炸穿，填料大量流出。背爆面出现多条较长裂缝，码头上部结构迎爆侧整体前倾，断裂为多块并被部分掀飞，底板无明显破坏现象。此外，在水下爆炸对迎爆面的冲切和通过仓格向上传播的冲击波共同作用下，仓格封仓板与竖向各墙连接处混凝土出现拉剪混合破坏，表现为在沉箱封仓板下缘出现横向通长裂缝，裂缝在迎爆面和侧面较宽，裂纹局部位置在墙的厚度方向贯穿。
图 5 水下接触爆炸码头模型毁伤模式Figure 5. The damage mode of the wharf under contact explosion in water3.1.1 面板
迎爆面管沟上部面板被掀飞，前后管沟之间面板断裂为多块，后管沟上部面板未出现较为明显的贯通裂缝。这是由于从结构内部传来的冲击波使面板向上弯曲，面板外部受拉严重，混凝土开裂，裂缝在厚度方向迅速发展贯穿，面板断裂为多块并继续向上运动导致的。而从内部传来的冲击波由迎爆侧到背爆侧逐渐衰减，对面板的作用效果逐渐减小，故后管沟上部面板的破坏较轻。此外，面板下侧与管沟侧壁连接位置的混凝土受拉断裂，面板下缘出现横向通长裂缝。
3.1.2 迎爆面
迎爆面外墙严重内凹，在沉箱底板上沿和封仓板下沿对应位置各有一条较深的横向贯通裂缝，裂缝由迎爆面延伸至背爆面。2#墙毁伤最严重，大部分混凝土破碎或剥落，外墙被炸穿，形成椭圆形爆坑，爆坑内窄外宽。爆坑边缘混凝土疏松。钢筋网架与爆坑周边混凝土向内弯曲，节点最大挠度为13 cm。爆坑边缘和内部残留的混凝土被大量径向、切向和环向裂缝分割成大小不等的碎块。
炸药爆炸后，高温高压的爆轰产物急剧膨胀，爆炸冲击波压力超过混凝土的动态抗压强度，2#墙大部分的外保护层混凝土被压碎，形成椭圆形粉碎区，粉碎区深度由起爆位置向四周逐渐变浅。钢筋网架受冲击波的应力作用突变，向内弯曲，在粉碎区外与存留的混凝土之间发生黏结破坏。粉碎区消耗了大部分的爆炸能量，冲击波迅速衰减为压缩应力波向结构内继续传播，此时混凝土虽不会直接被压碎，但引起的径向变形带来的切向拉伸将产生径向微裂纹，并在尖劈作用下向墙内发展形成较宽的径向裂缝。爆坑周边较为明显的环向通长裂缝是面板向内弯曲变形导致成的，环向裂缝在爆坑周边和墙体四周较密。直接作用于两侧墙体的爆炸冲击波荷载较小，毁伤模式以裂缝开展为主。1#和3#墙的毁伤模式相近，在靠近侧面位置，墙外表面存在大量的竖向通长裂缝；在靠近仓格底面和顶面位置存在大量横向通长裂缝。作用于迎爆面的荷载较大，内部纵向隔墙作用有限，迎爆面整体受弯内凹，在迎爆面边缘产生大量的环向裂缝。墙面其余位置未出现明显的通长裂缝。受外墙与填料接触面反射产生的拉伸波的作用，混凝土出现微裂缝，靠近墙体外表面混凝土骨料被拔出，迎爆面出现大量小坑洞。
此外，爆炸冲击波在水面反射产生的稀疏波与入射冲击波在近自由面区域叠加，产生气穴效应，使得结构出现气穴冲切损伤[14]。仓格封仓板与仓格墙体连接处即处于气穴作用区域，且该处混凝土抗拉和抗剪能力较弱，在气穴冲切的作用下易出现拉伸损伤甚至开裂。损伤沿封仓板下缘，从其迎爆面外墙交界处向结构内发展，形成薄弱面，随后在爆炸对迎爆面冲切作用下进一步发展，最终形成由迎爆面中间发展至背爆面的通长横向裂缝。
3.1.3 侧面及背爆面
侧面毁伤情况较迎爆面轻，毁伤主要出现在仓格封仓板以上部分，以4#和5#墙破坏为例说明。外墙下部毁伤以竖向通长裂纹为主。前管沟整体前倾，下部边缘混凝土被压碎。一条较宽的斜裂缝从面板下缘贯通至压碎区，在墙厚度方向裂缝上深下浅，局部贯穿。此外，斜裂缝在封仓板处发展出两条横向裂纹，局部混凝土破裂，钢筋露出。背爆面在侧面外墙和内隔墙对应位置有少量的竖向裂纹，这是由于纵向墙体受爆炸冲切作用向背爆面运动造成的。
3.1.4 内隔墙及封仓板
结构内部的毁伤主要分布于迎爆面中间仓格的隔墙和封仓板。封仓板破坏严重，多条横纵裂缝相互贯通，并在厚度方向贯穿。板与内隔墙的交界处混凝土断裂，钢筋拔出，板整体向上隆起。纵隔墙受压变形较大，与外墙接触位置混凝土被压碎。纵隔墙前部钢筋向外鼓曲，混凝土保护层碎裂，部分钢筋露出。隔墙向后弯曲变形，在迎爆面和背面均出现大量半环状裂缝，裂缝由下至上发展，背爆面出现竖向通长裂缝。背爆面裂缝开展较迎爆面严重。
3.2 工况2结构毁伤模式及分析
爆距0.5 m，水下非接触爆炸下码头模型毁伤模式如图6所示。爆炸后结构向后整体滑移约35 cm。码头迎爆面、侧面和顶面均有较大的毁伤，背爆面和底板无明显毁伤。迎爆面外墙被炸穿，中间仓格填料少量流出。
图 6 爆距0.5 m码头模型毁伤模式Figure 6. The damage mode of the wharf at the explosion distance of 0.5 m迎爆面沉箱底板上沿和封仓板对应位置下沿各有一条较深的横向贯通裂缝，裂缝由迎爆面延伸至背爆面。仓格封仓板与仓格墙体连接处出现横向通长裂缝，裂缝由迎爆面中间向背爆面发展，开裂程度逐渐变小。爆炸荷载以水下冲击波的形式作用于迎爆面，迎爆面整体内凹，2#墙凹陷程度最重，1#墙最轻，墙体边缘出现环状裂缝。2#墙体形成边长约20 cm的方形爆坑，爆坑中间墙体被炸穿。爆坑外围混凝土出现大范围冲切破裂，深度较浅，主要出现在外侧钢筋保护层，部分位置钢筋外露。2#墙内凹明显，钢筋网架亦明显弯曲，从爆坑到墙体边缘混凝土分布大量环状裂缝。环状裂缝与径向冲切作用和混凝土部分回弹引起的切向裂缝相互贯通，墙体外表面混凝土大范围龟裂。此外，由于冲击波在墙体与仓格填料交界面反射产生的强拉伸波传播至外表面时，部分靠外的混凝土骨料被附着动能拔出，使得整个迎爆面出现大量小坑洞。
模型其他部位毁伤模式和诱因与工况1基本相同，纵隔墙无明显毁伤。值得注意的是，工况2除迎爆面外，各部位毁伤程度较工况1基本一致。
3.3 工况3结构毁伤模式
爆距1 m，水下非接触爆炸下码头模型毁伤模式如图7所示。爆炸后结构向后整体滑移约30 cm。码头迎爆面、侧面和顶面出现明显毁伤，背爆面和底板无明显毁伤。
图 7 爆距1 m码头模型毁伤模式Figure 7. The damage mode of the wharf at the explosion distance of 1 m面板顶部出现两条明显的横向通长裂缝，其中远离迎爆面的一条在码头两侧与两侧墙面的斜裂缝相连贯通。面板与管沟侧壁连接位置出现横向通长裂缝，裂缝存在于迎爆面和侧面对应位置，未发展至背爆面，开裂程度从迎爆面到侧面逐渐减小。迎爆面毁伤以裂缝开展为主，未出现明显的混凝土破碎，在沉箱底板上沿和封仓板对应位置下沿各出现一条横向贯通裂缝，裂缝由迎爆面延伸至背爆面。迎爆面墙体内凹，2#墙凹陷程度最重，1#墙最轻，墙体边缘出现环状裂缝。爆炸冲击波到达结构前以球面波形式传播，2#墙体中部所受荷载较大，2#墙中间偏下一小块区域内凹明显，并出现较宽的局部环状裂缝。迎爆面出现大量混凝土粗骨料尺寸小坑洞。侧面毁伤主要出现在上部结构。前管沟整体前倾，管沟下侧出现一条斜裂缝，由面板下缘贯通至封仓板下沿，裂缝上深、宽，下浅、窄。侧面封仓板下部及背爆面除少量混凝土粗骨料抛出造成的小坑洞外无明显毁伤。剖开结构后发现，封仓板下表面有多条较浅的横纵裂缝出现，板与内隔墙的交界处出现较深裂缝，裂缝未贯穿板的厚度方向。横隔墙边缘有少量环状裂缝。纵隔墙无明显毁伤。
4. 水下爆炸码头结构毁伤模式及爆距的影响
沉箱码头内部结构复杂，介质种类较多，爆炸能量在结构内部传播情况复杂。在受到复杂荷载作用时，结构内部各构件之间相互影响，毁伤模式较为复杂。将可能出现的主要毁伤模式汇总于表5。
表 5 沉箱码头模型主要毁伤模式Table 5. Damage modes of caisson gravity wharf.毁伤部位 毁伤模式 整体 1.整体滑移；2.变形；3.混凝土外表面粗骨料拔出 面板 1.弯曲变形；2.裂缝开展；3.断裂抛出；4.与其他构件交界处拉剪断裂；5.钢筋混凝土粘结破坏 迎爆面外墙 1.爆炸成坑；2.混凝土冲切破裂；3混凝土破碎失效；4.弯曲破坏；5.钢筋网架挠曲；6.裂缝开展；7.钢筋混凝土粘结破坏 侧面外墙 1.混凝土局部破碎；2.裂缝开展 管沟 1.整体倾斜；2.上面板掀飞；3.裂缝开展 封仓板 1.整体和局部弯曲；2.裂缝开展；3.断裂；4.与其他构件交界处拉剪断裂；5.钢筋混凝土粘结破坏 仓格横隔墙 1.裂缝开展；2.受弯变形；3.整体位移 仓格纵隔墙 1.裂缝开展；2.混凝土破碎、剥落；3.钢筋网架鼓曲；4.整体位移 沉箱底板 无明显毁伤出现 爆距对整体滑移影响较小，对毁伤模式和毁伤程度影响较大。爆距较远时，毁伤以裂缝扩展为主，较少裂缝互相贯通，局部变形较小，结构完整性和承载能力受影响较小；爆距较近时，迎爆面、侧面和上部结构出现大面积变形、材料破坏失效，裂缝大量贯通、贯穿，结构完整性和承载能力严重下降。但当爆距过近时，爆炸能量被迎爆面结构变形大量吸收，迎爆面毁伤程度大幅增大，码头其他部位毁伤程度增幅放缓。
5. 结 论
本文通过开展水下爆炸对沉箱重力式码头毁伤效应的试验研究，得到如下结论：
（1）试验中未形成完整的气泡脉动过程，荷载超压主要出现在冲击波传播初始阶段，爆炸冲击波、水底反射波和侧壁反射波是主要的毁伤因素。
（2）水下爆炸对沉箱重力式码头造成的毁伤程度大、模式多、机理复杂。从整体来看，主要毁伤模式为结构整体滑移和变形。从局部来看，除底板外其余部位均有较大毁伤，迎爆面出现局部的爆炸成坑和混凝土破碎失效，墙体内凹明显，裂缝大量扩展，爆距较近时，外墙被炸穿，仓格内填料流出。前管沟整体前倾，造成通长斜裂缝开展和局部混凝土破碎。面板和封仓板裂缝的开展和贯通较严重，爆距较近时，大量裂缝贯穿，板断裂为多块，出现整体和局部的明显隆起，面板甚至会被大面积掀飞。面板、封仓板与其他构件的连接处较为薄弱，易出现拉、剪或拉剪混合破坏。仓格隔墙变形和裂缝开展较轻，当爆距较近时，纵向内隔墙出现较为明显的偏压破坏。
（3）同等条件下，爆距越近码头毁伤越严重，但当爆距过近时，爆炸能量被迎爆面结构变形大量吸收，迎爆面毁伤程度大幅增大，码头其他部位毁伤程度增幅放缓。
（4）码头主要毁伤部位为迎爆面外墙、迎爆侧管沟、封仓板和面板。主要毁伤部位多为码头的主要船岸界面和工作平台，沉箱整体滑移和仓格填料外漏亦会直接影响船舶靠泊环境。水下爆炸对沉箱重力式码头造成的毁伤会直接影响码头的正常运转。
-
图 4 砂土垫层强度静力载荷试验及结果
Figure 4. Static load test and results of strength of sand cushion
图 5 不同形状落石侵入深度对比
Figure 5. Comparison of the penetration depth of falling rocks with different shapes
图 6 不同形状下落石冲击力时程曲线
Figure 6. Time history curves of impact force for falling rocks with different shapes
图 7 不同形状落石相对冲击力时程曲线
Figure 7. Time history curves of relative impact force for falling rocks with different shapes
图 8 落石形状对冲击力、峰值时间和冲量的影响
Figure 8. Effects of falling rock’s shape on impact force, peak time and impulse
图 9 不同典型形状落石冲击成坑形状
Figure 9. Different impact craters formed by different typical falling rocks
图 10 椭球形落石的整体形状变化范围
Figure 10. Variation of the overall shape of the ellipsoid falling rocks
图 11 无量纲冲击因子与无量纲侵入深度之间的相关性
Figure 11. Correlation between dimensionless impact factors and penetration depths
图 12 不同形状落石无量纲侵入深度的拟合曲线
Figure 12. Fitting curves of the dimensionless penetration depths of the blocks
表 1 球形落石冲击砂垫层试验工况
Table 1. Conditions of impact test by spherical falling rocks
编号 m/kg v0/（m·s−1） H/m d/m I λ zm/d S-01 10 4.43 1.00 0.12 1.73 5.22 1.45 S-02 10 6.26 2.00 0.12 3.47 5.22 1.88 S-03 10 8.85 4.00 0.12 6.93 5.22 2.67 S-04 10 13.28 9.00 0.12 15.60 5.22 3.46 S-05 50 4.43 1.00 0.25 0.96 2.89 1.00 S-06 50 6.26 2.00 0.25 1.92 2.89 1.15 S-07 50 8.85 4.00 0.25 3.83 2.89 1.47 S-08 50 13.28 9.00 0.25 8.63 2.89 1.84 S-09 100 4.43 1.00 0.36 0.64 1.93 0.71 S-10 100 6.26 2.00 0.36 1.28 1.93 0.76 S-11 100 8.85 4.00 0.36 2.57 1.93 1.06 S-12 100 13.28 9.00 0.36 5.78 1.93 1.17 
下载: 导出CSV
表 2 锥形落石冲击砂垫层试验工况
Table 2. Conditions of impact test by conical falling rocks
编号 m/kg v0/（m·s−1） H/m d/m I λ zm/d C-01 10 4.40 1.00 0.12 1.73 5.22 1.89 C-02 10 6.30 2.00 0.12 3.47 5.22 2.00 C-03 10 8.90 4.00 0.12 6.93 5.22 2.75 C-04 50 2.40 0.30 0.25 0.29 2.89 0.76 C-05 50 6.30 2.00 0.25 1.92 2.89 1.06 C-06 50 8.90 4.00 0.25 3.83 2.89 1.27 C-07 50 13.30 9.00 0.25 8.63 2.89 1.59 C-08 50 17.10 15.00 0.25 14.38 2.89 2.16
下载: 导出CSV
表 3 平头落石冲击砂垫层试验工况
Table 3. Conditions of impact test by flat falling rocks
编号 m/kg v0/（m·s−1） H/m d/m I λ zm/d F-01 50 4.40 1.00 0.25 0.96 2.89 0.52 F-02 50 6.30 2.00 0.25 1.92 2.89 0.68 F-03 50 8.90 4.00 0.25 3.83 2.89 0.86 F-04 50 13.30 9.00 0.25 8.63 2.89 1.06 F-05 50 6.30 2.00 0.30 1.11 1.67 0.37 F-06 50 13.30 9.00 0.30 4.99 1.67 0.68
下载: 导出CSV
表 4 无量纲冲击因子之间及与侵入深度的相关性
Table 4. Correlation between dimensionless impact factors and penetration depths
冲击因子 I λ zm/d I 1.00 0.24 0.71 λ 0.24 1.00 0.77 zm/d 0.71 0.77 1.00
下载: 导出CSV
表 5 不同形状落石3种拟合公式的拟合参数比较
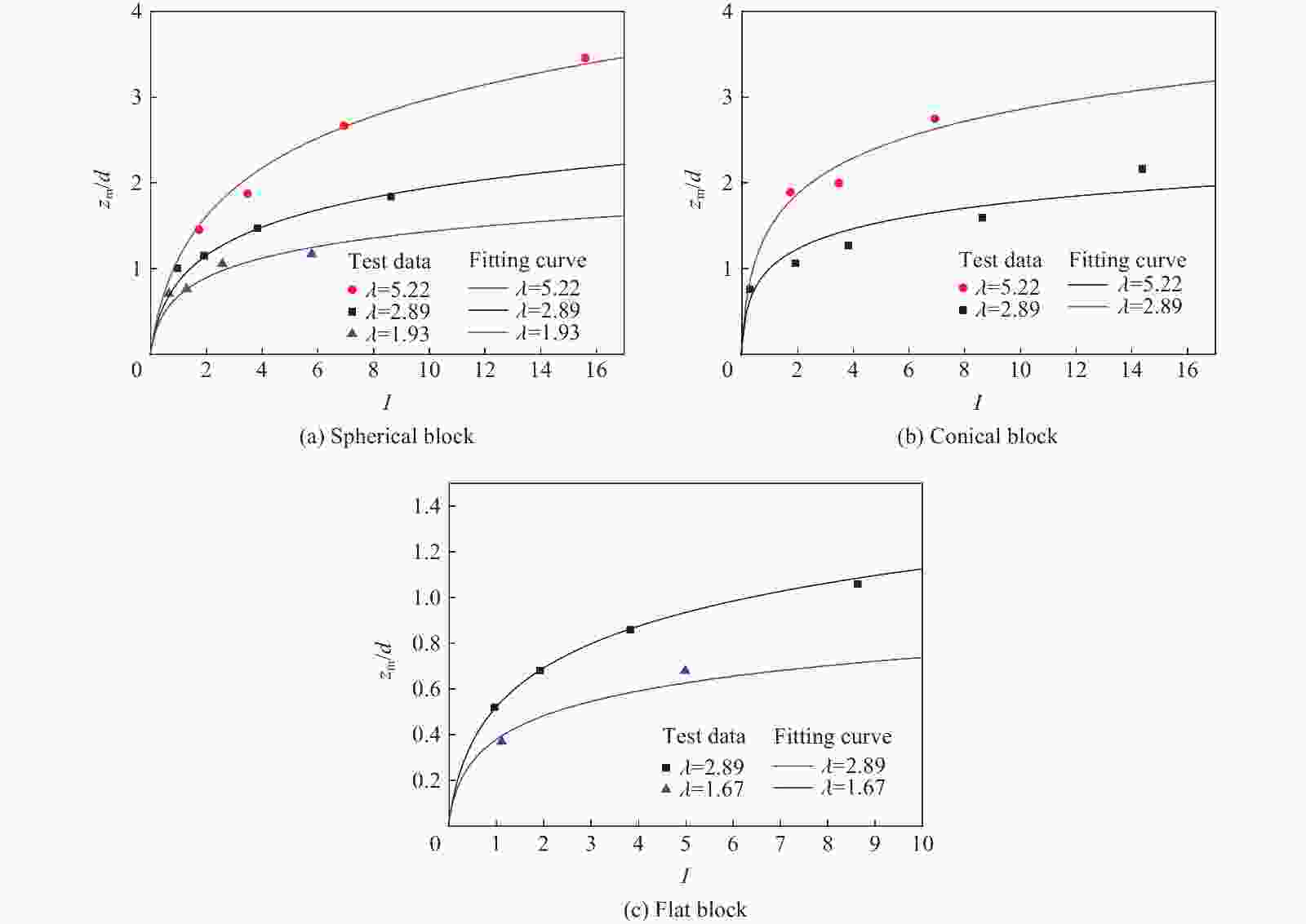
Table 5. Comparison of parameters of three fitting formulas for falling rocks with different shapes
落石形状 zm/d=Aλ ln(1+CI/λ)拟合参数 A C 球形 0.18 11.67 锥形 0.12 47.64 平头 0.10 15.09
下载: 导出CSV
-
[1] JACQUEMOUD J. Swiss guideline for the design of protection galleries: background, safety concept and case histories [C] // Impact Load by Rock Falls and Design of Protection Structures, Joint Japan-Swiss Scientific Seminar. Kanazawa, Japan: Kanazawa University, 1999. [2] 山口悟, 木幡行宏, 小室雅人, 等. 敷砂あるいは砕石緩衝材の緩衝特性に関する大型重錘落下衝撃実験 [C] // 構造工学論文集, 2014, 60: 983–995. [3] CALVETTI F, PRISCO C, VECCHIOTTI M. Experimental and numerical study of rock-fall impacts on granular soils [J]. Rivista Italiana di Geotecnica, 2005, 4: 95–109. [4] GERBER W, VOLKWEIN A. Impact loads of falling rocks on granular material [C] // Third Euro Mediterranean Symposium on Advances in Geomaterials and Structures, 2010, 10: 337–342. [5] 袁进科, 黄润秋, 裴向军. 滚石冲击力测试研究 [J]. 岩土力学, 2014, 35(1): 48–54. DOI: 10.16285/j.rsm.2014.01.011.YUAN J K, HUANG R Q, PEI X J. Test research on rockfall impact force [J]. Rock and Soil Mechanics, 2014, 35(1): 48–54. DOI: 10.16285/j.rsm.2014.01.011. [6] YU B, YI W, ZHAO H B. Experimental study on the maximum impact force by rock fall [J]. Landslides, 2018, 15(2): 233–242. DOI: 10.1007/s10346-017-0876-x. [7] 何思明, 沈均, 吴永. 滚石冲击荷载下棚洞结构动力响应 [J]. 岩土力学, 2011, 32(3): 781–788. DOI: 10.16285/j.rsm.2011.03.033.HE S M, SHEN J, WU Y. Rock shed dynamic response to impact of rock-fall [J]. Rock and Soil Mechanics, 2011, 32(3): 781–788. DOI: 10.16285/j.rsm.2011.03.033. [8] FITYUS S G, GIACOMINI A, BUZZI O. The significance of geology for the morphology of potentially unstable rocks [J]. Engineering Geology, 2013, 162: 43–52. DOI: 10.1016/j.enggeo.2013.05.007. [9] 重庆交通科研设计院. 公路隧道设计规范: JTG D70–2004 [S]. 北京: 人民交通出版社, 2004. [10] 铁道部第二设计院. 铁路工程设计技术手册（隧道） [M]. 北京: 人民铁道出版社, 1978. [11] 杨其新, 关宝树. 落石冲击力计算方法的试验研究 [J]. 铁道学报, 1996, 18(1): 101–106. DOI: 10.3321/j.issn:1001-8360.1996.01.017.YANG Q X, GUAN B S. Test and research on calculating method of falling stone impulsive force [J]. Journal of the China Railway Society, 1996, 18(1): 101–106. DOI: 10.3321/j.issn:1001-8360.1996.01.017. [12] Janpan Road Association. Manual for anti-impact structures against falling rocks [M]. Tokyo, Japan: Maruzen Publisher, 2000. [13] LABIOUSE V, DESCOEUDRES F, MONTANI S. Experimental study of rock sheds impacted by rock blocks [J]. Structural Engineering International, 1996, 6(3): 171–176. DOI: 10.2749/101686696780495536. [14] ASTRA S B B. Einwirkungen infolge Steinschlags auf Schutzgalerien [M]. Bern: Swiss Federal Roads Office and Swiss Federal Railways, 2008. [15] PICHLER B, HELLMICH C, MANG H A. Impact of rocks onto gravel design and evaluation of experiments [J]. International Journal of Impact Engineering, 2005, 31(5): 559–578. DOI: 10.1016/j.ijimpeng.2004.01.007. [16] MOUGIN J P, PERROTIN P, MOMMESSIN M, et al. Rock fall impact on reinforced concrete slab: an experimental approach [J]. International Journal of Impact Engineering, 2005, 31(2): 169–183. DOI: 10.1016/j.ijimpeng.2003.11.005. [17] SCHELLENBERG K, KHASRAGHY G S, VOGEL T, et al. Impact behavior of reinforced concrete slabs subjected to rock fall loading [C] // SUSI 2008. Southampton: WIT Press, 2008, 98: 25–34. [18] DELHOMME F, MOMMESSIN M, MOUGIN J P, et al. Simulation of a block impacting a reinforced concrete slab with a finite element model and a mass-spring system [J]. Engineering Structures, 2007, 29(11): 2844–2852. DOI: 10.1016/j.engstruct.2007.01.017. [19] CHIKATAMARLA R, LAUE J, SPRINGMAN S M. Rockfall impact on protection galleries [C] // The Second International Conference of Structural Engineering Mechanics and Computations. Cape Town, South Africa, 2004: 1139–1144. [20] PERERA S, LAM N, PATHIRANA M, et al. Deterministic solutions for contact force generated by impact of windborne debris [J]. International Journal of Impact Engineering, 2016, 91: 126–141. DOI: 10.1016/j.ijimpeng.2016.01.002. [21] 唐建辉. 落石冲击对隧道明洞结构的影响研究 [D]. 成都: 西南交通大学, 2013. [22] 陈驰, 刘成清, 陈林雅, 等. 落石作用于钢筋混凝土棚洞的冲击力研究 [J]. 公路交通科技, 2015, 32(1): 102–109. DOI: 10.3969/j.issn.1002-0268.2015.01.017.CHEN C, LIU C Q, CHEN L Y, et al. Study on impact force of rock-fall onto rock shed tunnel [J]. Journal of Highway and Transportation Research and Development, 2015, 32(1): 102–109. DOI: 10.3969/j.issn.1002-0268.2015.01.017. [23] SHEN W G, ZHAO T, DAI F, et al. DEM analyses of rock block shape effect on the response of rockfall impact against a soil buffering layer [J]. Engineering Geology, 2019, 249: 60–70. DOI: 10.1016/j.enggeo.2018.12.011. [24] CALVETTI F, DI PRISCO C. Rockfall impacts on sheltering tunnels: real-scale experiments [J]. Géotechnique, 2012, 62(10): 865–876. DOI: 10.1680/geot.9.p.036. [25] YAN P, ZHANG J, FANG Q, et al. Numerical simulation of the effects of falling rock’s shape and impact pose on impact force and response of RC slabs [J]. Construction and Building Materials, 2018, 160: 497–504. DOI: 10.1016/j.conbuildmat.2017.11.087. [26] KAWAHARA S, MURO T. Effects of dry density and thickness of sandy soil on impact response due to rockfall [J]. Journal of Terramechanics, 2006, 43(3): 329–340. DOI: 10.1016/j.jterra.2005.05.009. [27] 唐红梅, 鲜学福, 王林峰, 等. 基于小波变换的碎石土垫层落石冲击回弹系数试验 [J]. 岩土工程学报, 2012, 34(7): 1278–1282.TANG H M, XIAN X F, WANG L F, et al. Coefficient of resilience for rock fall onto gravel soil cushion based on wavelet transform theory [J]. Chinese Journal of Geotechnical Engineering, 2012, 34(7): 1278–1282. [28] JONES N. Structural impact [M]. London: Cambridge University Press, 1989. [29] BUCKINGHAM E. On physically similar systems; illustrations of the use of dimensional equations [J]. Physical Review, 1914, 4(4): 345–376. DOI: 10.1103/physrev.4.345. [30] SEGUIN A, BERTHO Y, MARTINEZ F, et al. Experimental velocity fields and forces for a cylinder penetrating into a granular medium [J]. Physical Review E, 2013, 87(1): 1–10. DOI: 10.1103/physreve.87.012201. [31] LI Q M, CHEN X W. Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile [J]. International Journal of Impact Engineering, 2003, 28(1): 93–116. DOI: 10.1016/s0734-743x(02)00037-4. [32] FORRESTAL M J, TZOU D Y. A spherical cavity-expansion penetration model for concrete targets [J]. International Journal of Solids and Structures, 1997, 34(31–32): 4127–4146. DOI: 10.1016/s0020-7683(97)00017-6. [33] FORRESTAL M J, LUK V K. Penetration into soil targets [J]. International Journal of Impact Engineering, 1992, 12(3): 427–444. DOI: 10.1016/0734-743x(92)90167-r. [34] WYLLIE D C. Rock fall engineering [M]. Boca Raton: CRC Press, 2015. [35] 铁道第二勘察设计院. 铁路隧道设计规范: TB 10003–2005 [S] 北京: 中国铁道出版社, 2005. -
下载:
计量
- 文章访问数: 526
- HTML全文浏览量: 292
- PDF下载量: 97
- 被引次数: 0