Numerical study on the fracture mechanism of electron beam controlled projectile based on micro modeling
-
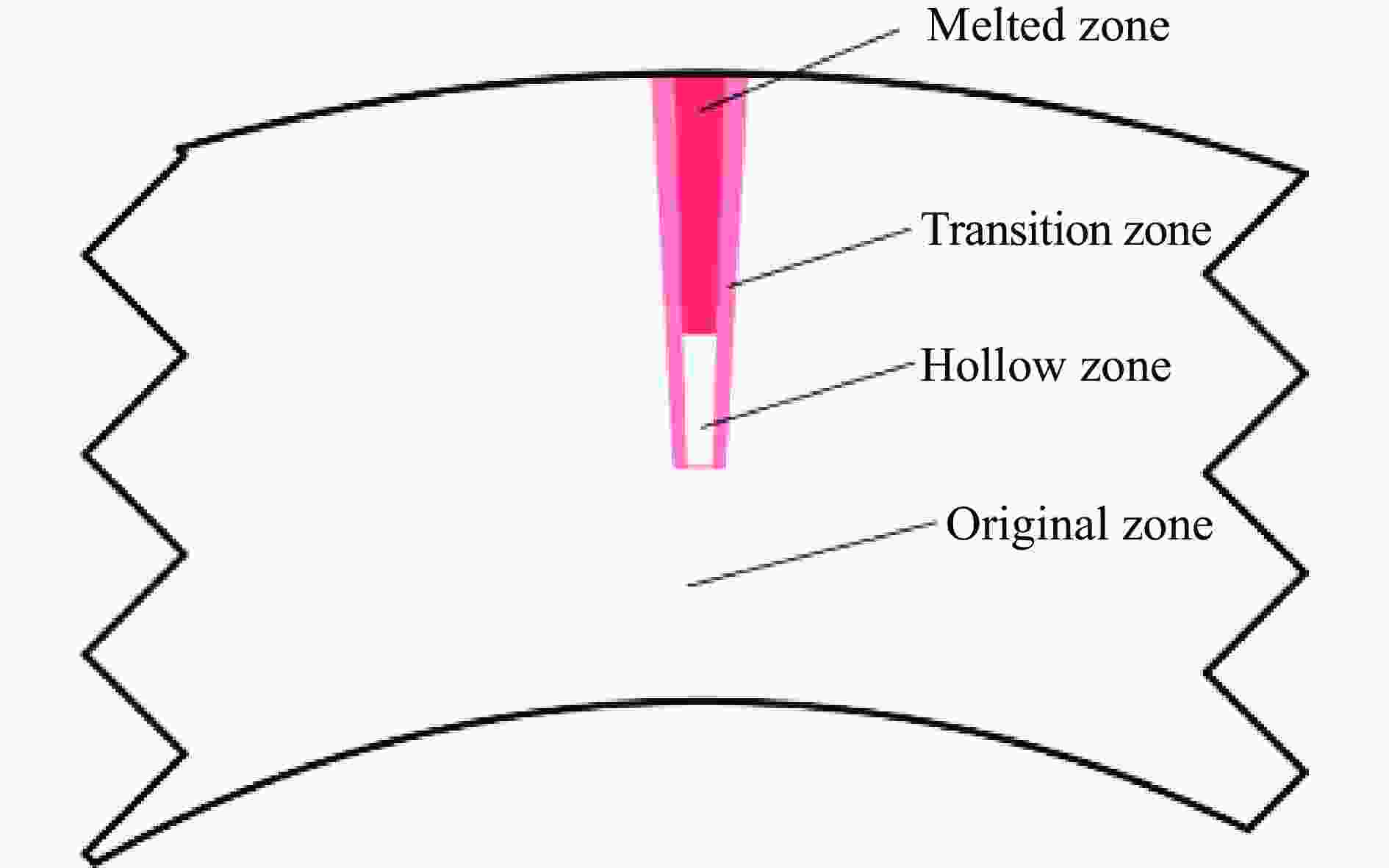
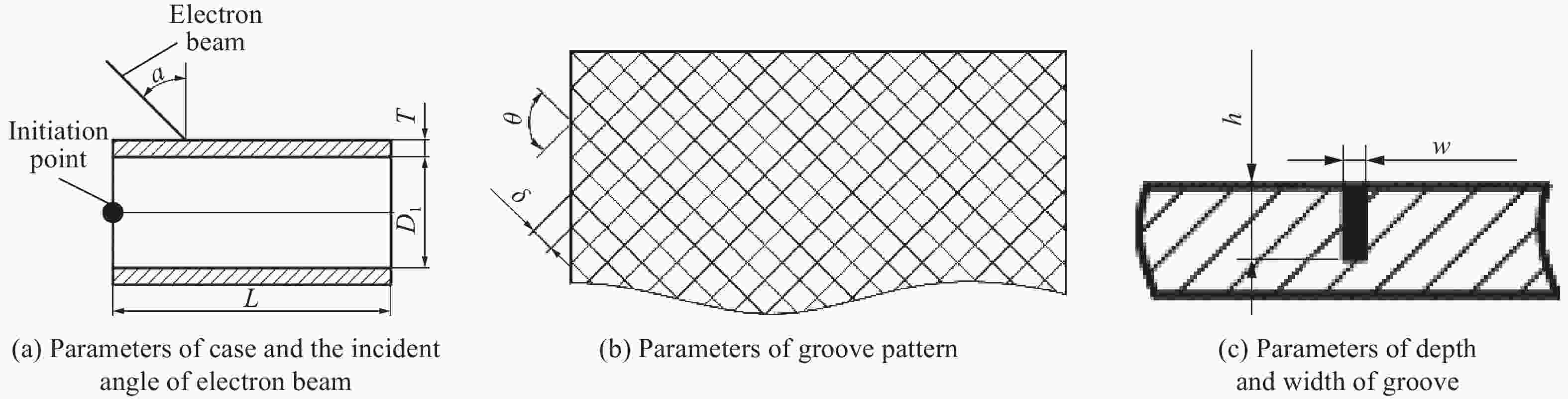
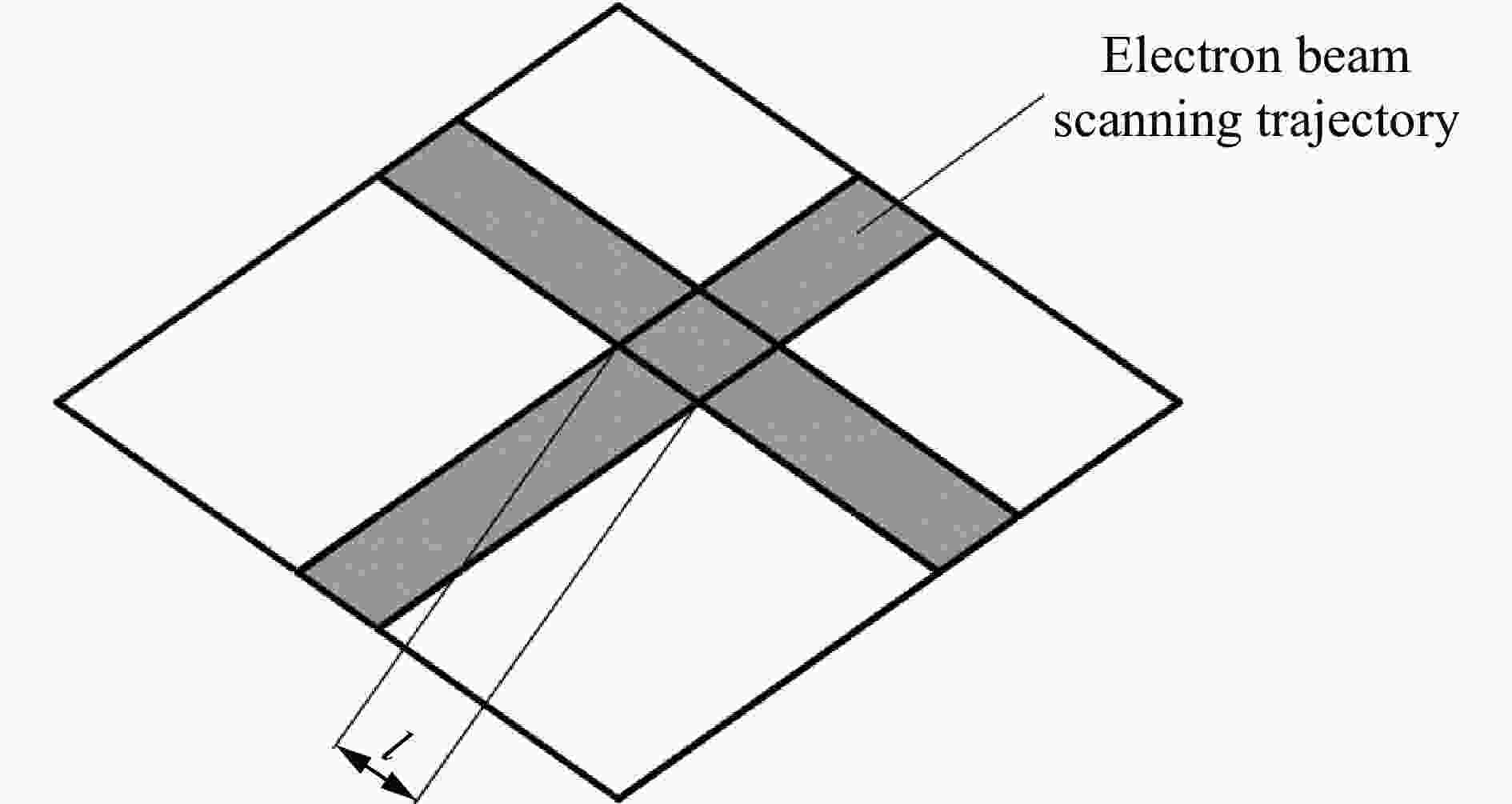
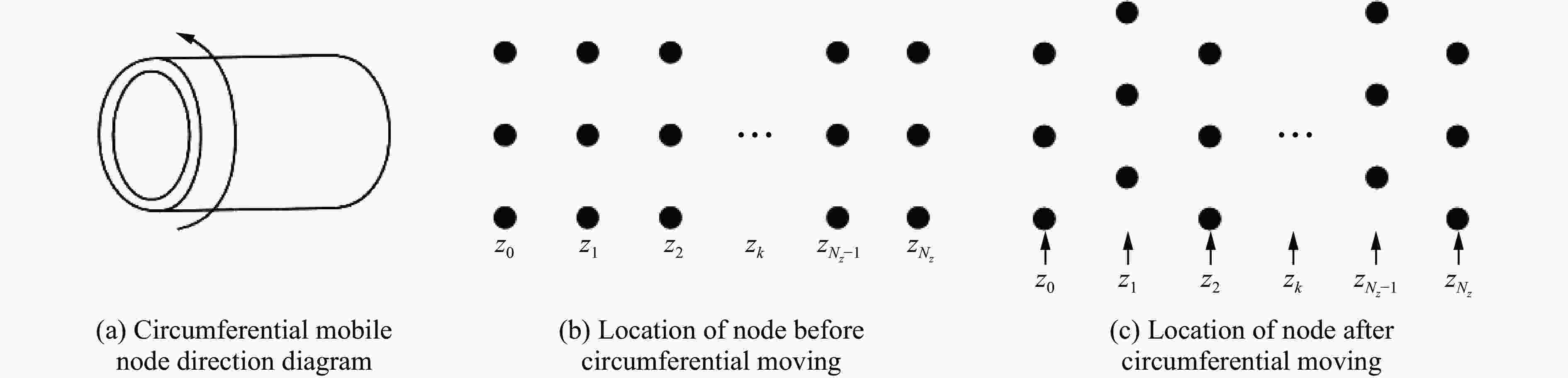
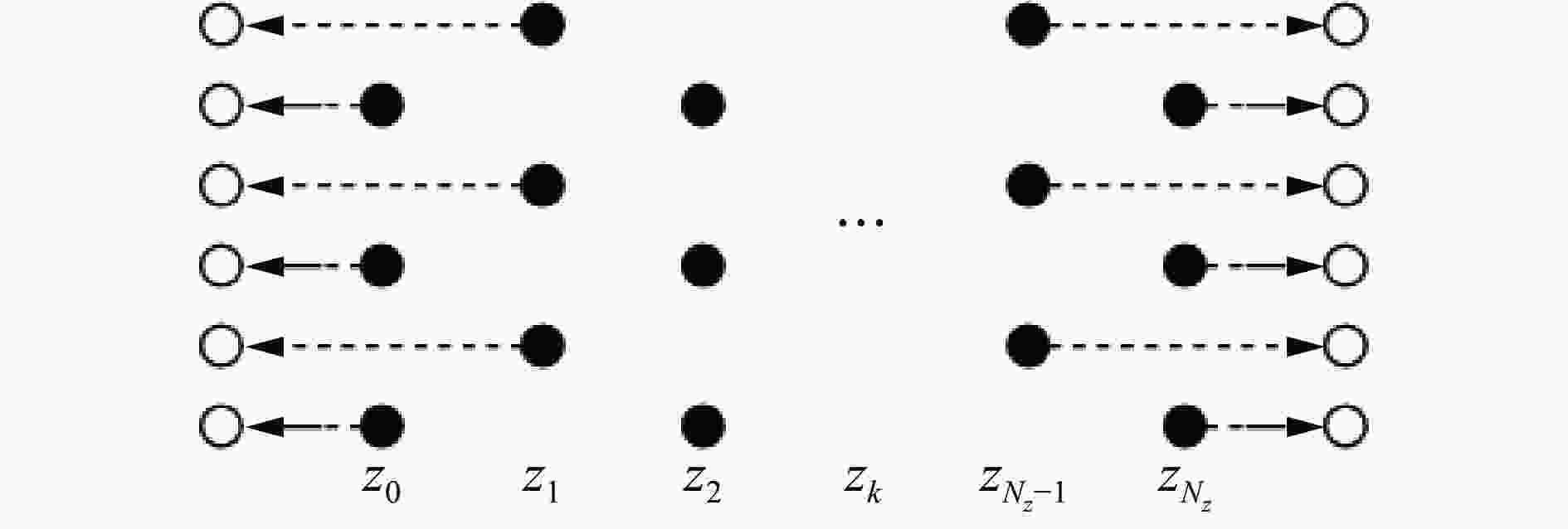
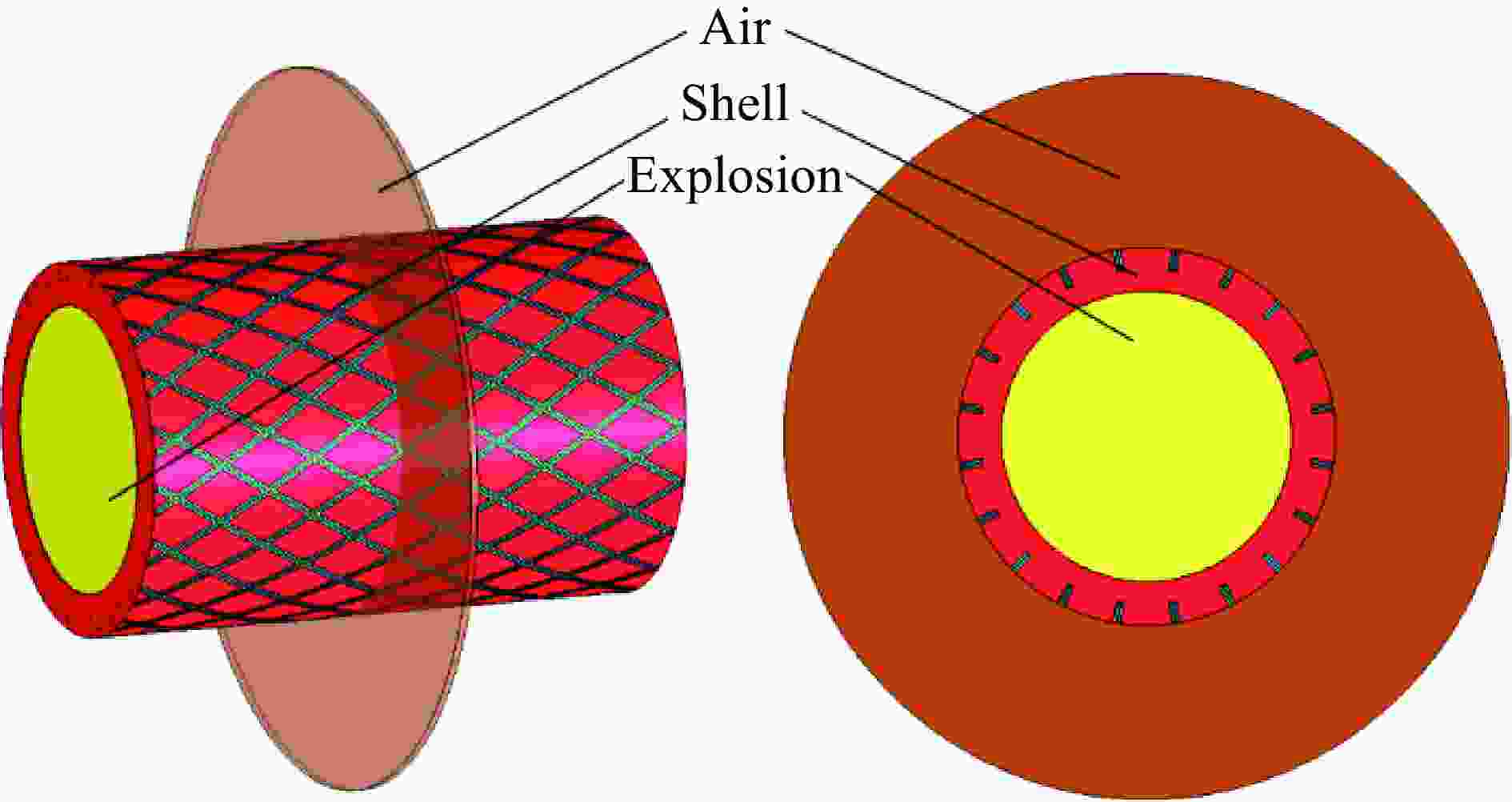
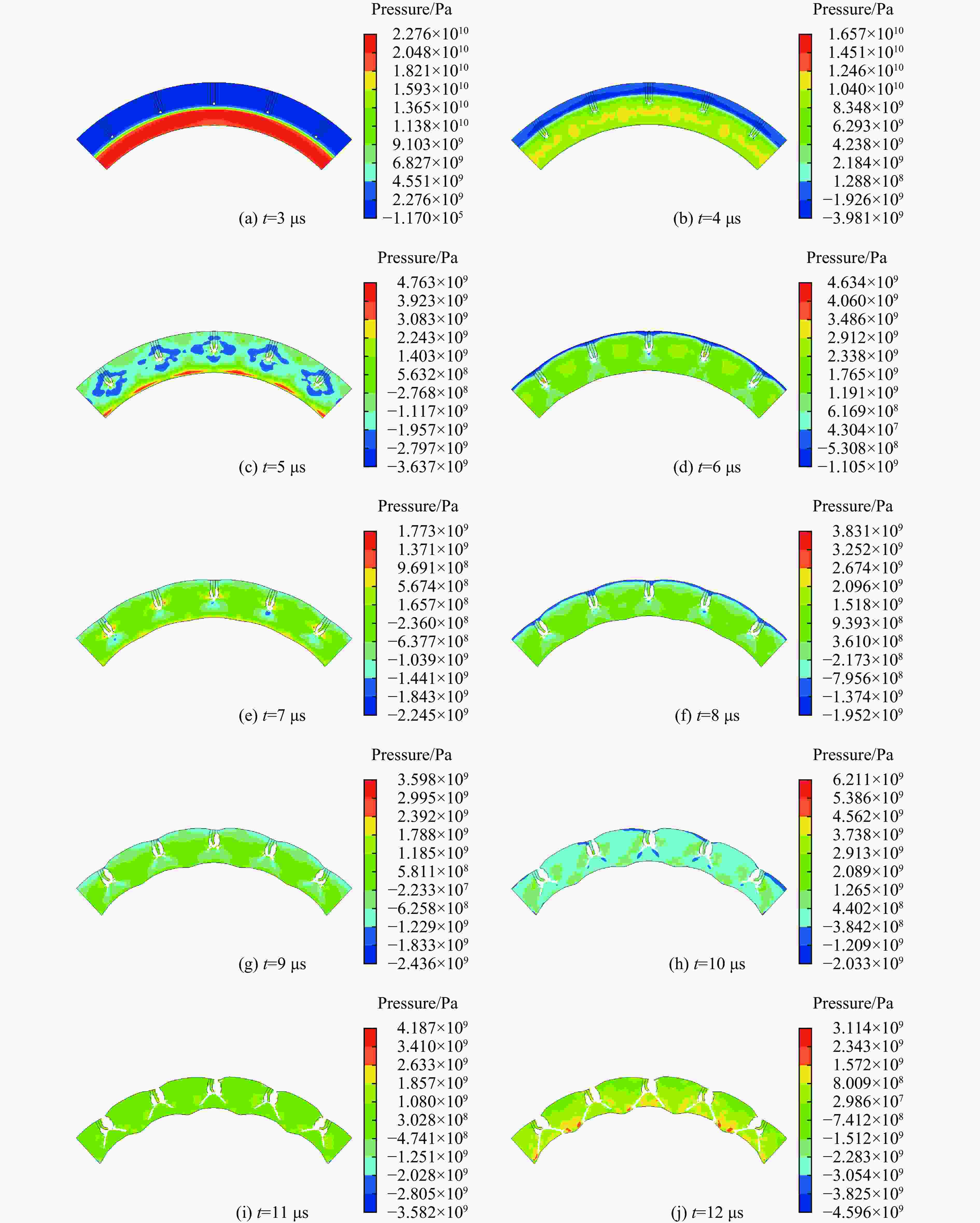
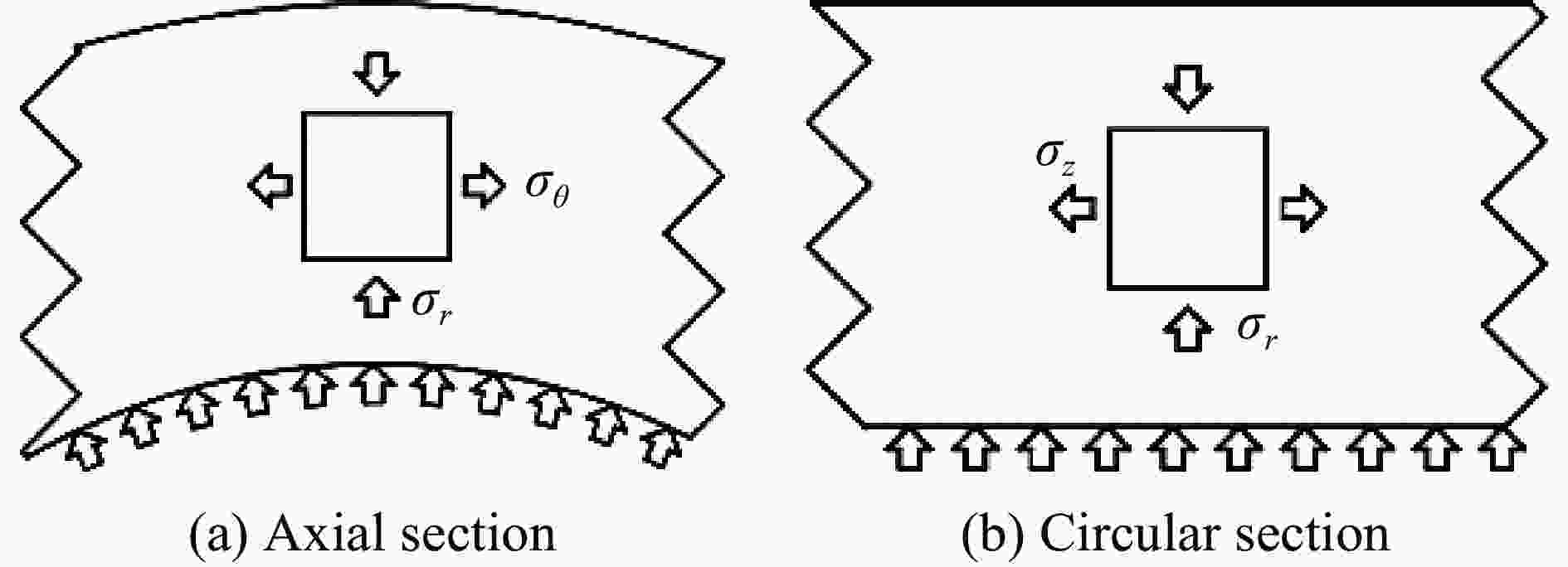
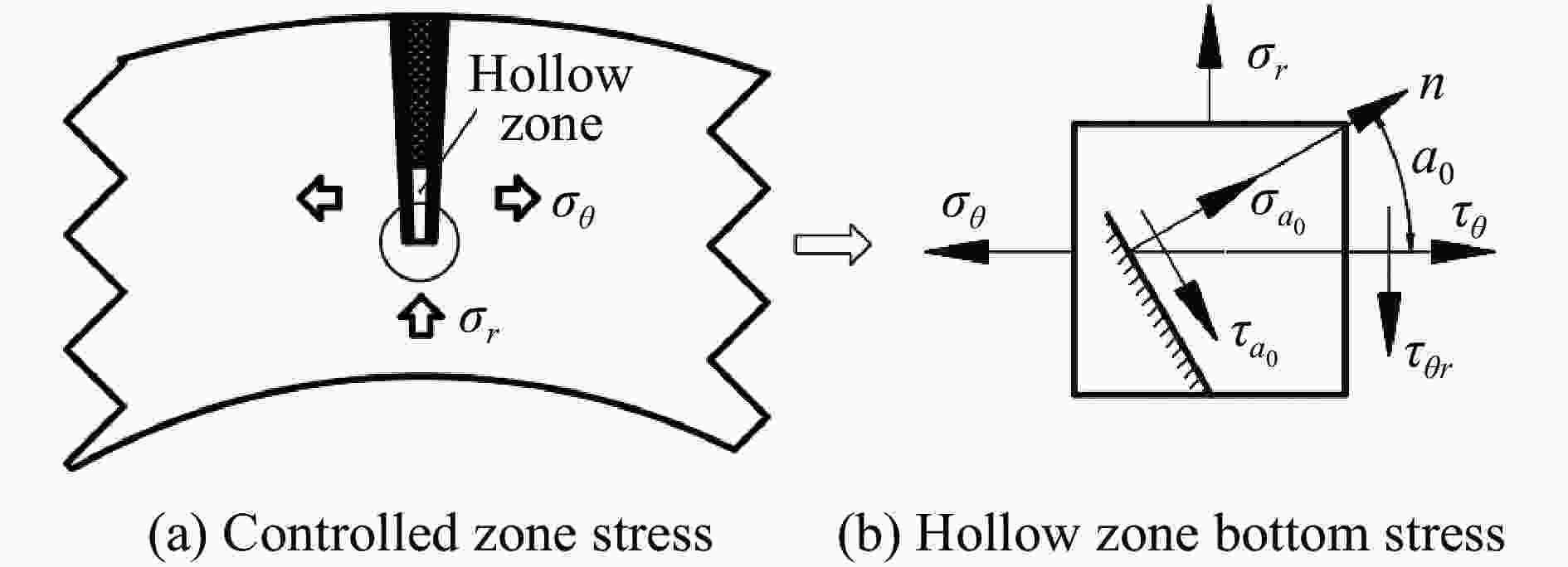
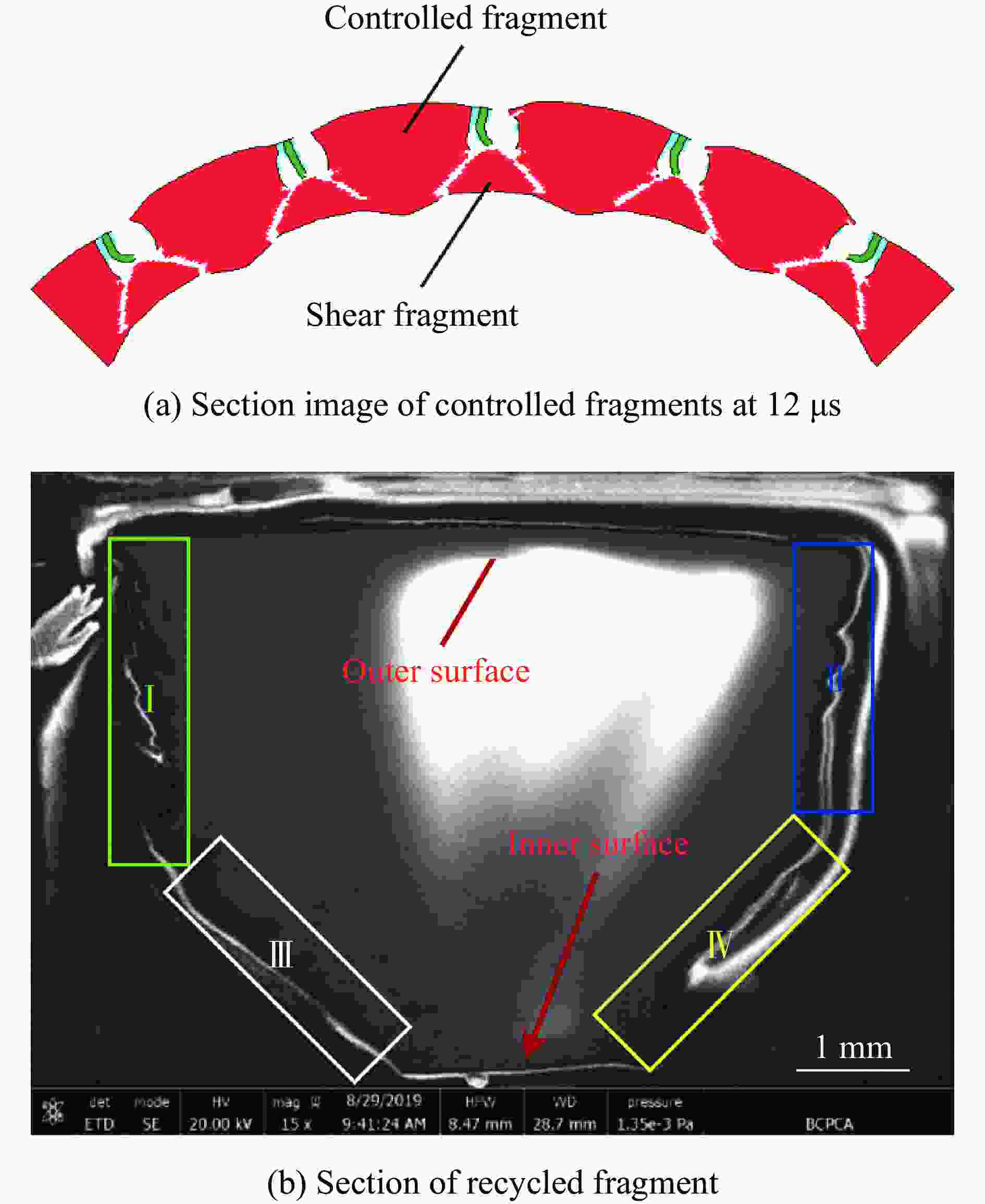
摘要: 为研究电子束预控弹体的破裂机理。提出了基于电子束预控弹体细观几何特性的参数化建模方法,建立了含基体、熔融区、过渡区和空腔区弹体的三维有限元模型,采用LS-DYNA软件对典型弹体的爆炸驱动和破裂过程进行了数值模拟分析。结果表明:电子束预控弹体破裂过程可分为:弹体膨胀后的空腔区在环向拉应力作用下产生拉伸断裂、过渡区产生裂纹扩展和拉伸断裂以及空腔区底部基体在两侧拉应力和底部压应力作用下产生与弹体内壁法线呈45°的剪切破坏3个阶段。数值模拟结果与回收的破片截面形状和破坏模式吻合较好。研究结果对电子束预控弹体破片成型控制具有参考价值。Abstract: In order to study the fracture mechanism of the projectile melted by the electron beam, a parameterized modeling method based on the micromechanical characteristics of the projectile was proposed. Scanning electron microscope and hardness tester were used to accurately obtain the characteristics of the electron beam melted zone. The typical electron beam controlled area was composed of the melting zone, the transition zone, the hollow zone and the matrix zone. Three hypotheses were proposed based on the mesoscopic characteristics of the electron beam controlled projectile. First, the structural characteristic parameters of the electron beam controlled projectile were summarized. Second, diamond-shaped finite element mesh elements were constructed through translation nodes. Third, the electron beam controlled pattern was constructed by combining diamond-shaped finite elements. Finally, the materials of melting zone and transition zone are defined, and finite elements of the hollow zone were deleted. A three-dimensional finite element model of the projectile with matrix, melting zone, transition zone and hollow zone was established. The explosion driving and fracture process of the typical projectile was simulated and analyzed by LS-DYNA software. The results show that the fracture process of the projectile can be divided into three stages: the tensile fracture in the hollow zone after the expansion of the projectile under the action of the circumferential tensile stress; the crack propagation and tensile fracture in the transition area; and the shear failure of the matrix at the bottom of the cavity area under the action of the tensile stress at both sides and the compressive stress at the bottom, which is 45° to the normal of the inner wall of the projectile. The numerical simulation results are in good agreement with the recovered fragment section shape and failure mode. The research results are of reference value to the forming control of projectile fragments by electron beam controlled.
-
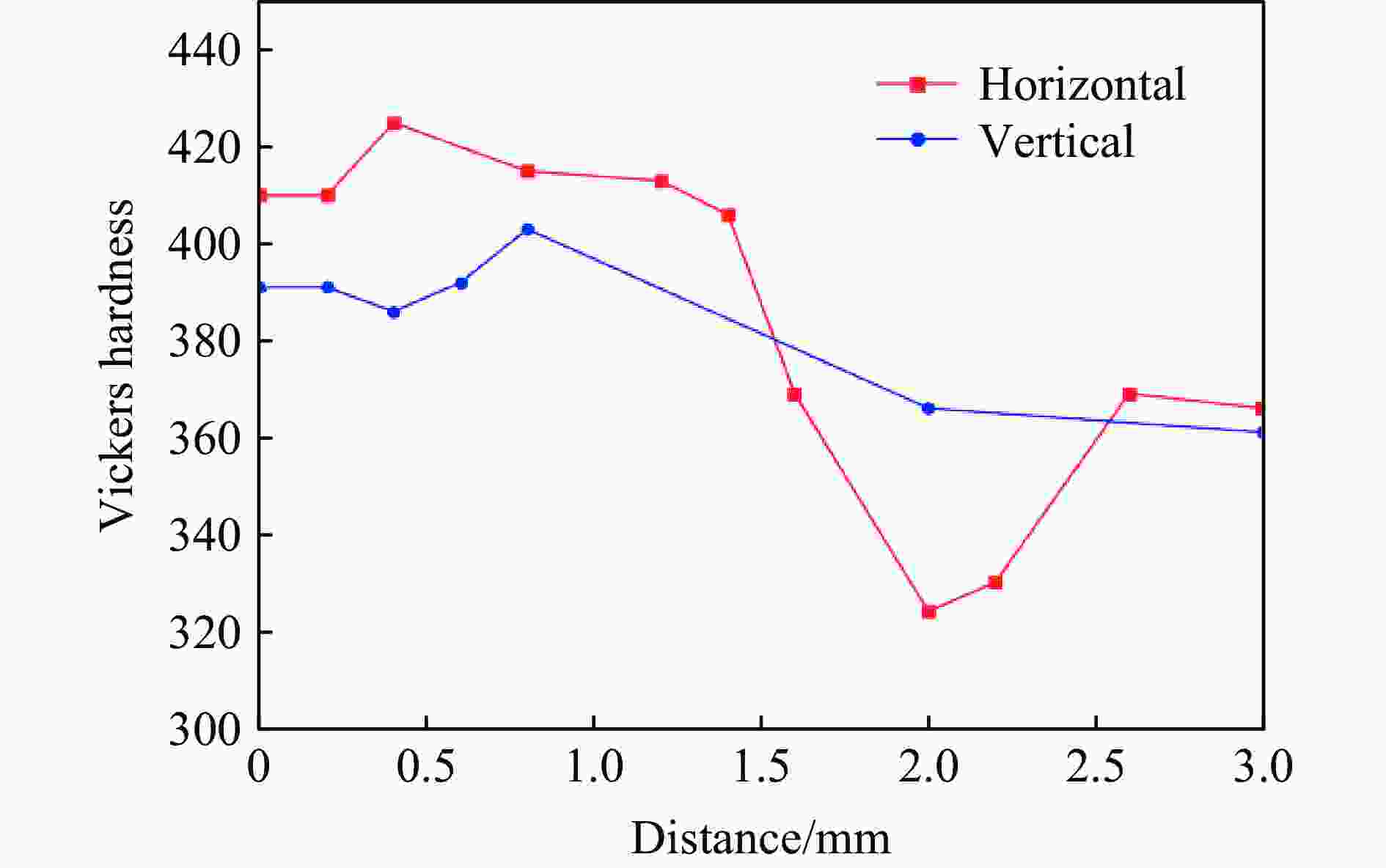
表 1 测量的硬度值
Table 1. Measured hardness value
区域 维氏硬度 横向 410 410 425 415 413 406 369 324 330 369 376 — 纵向 391 391 386 392 403 — 基体 366 361 372 — — — -
[1] 李超, 李德元, 万仁毅, 等. 激光和等离子弧加工弹体材料脆性带的对比 [J]. 成都工业学院学报, 2013, 16(1): 22–24. DOI: 10.3969/j.issn.1008-5440.2013.01.007.LI C, LI D Y, WAN R Y, et al. Comparison between the brittleness belts of shell materials treated by laser hardening and plasma-arc hardening [J]. Journal of Chengdu Technological University, 2013, 16(1): 22–24. DOI: 10.3969/j.issn.1008-5440.2013.01.007. [2] 赵力. 局部激冷处理弹壳材料破碎过程模拟 [D]. 沈阳: 沈阳工业大学, 2014.ZHAO L. Simulation of local chilling treatment shell material crushing process [D]. Shenyang: Shenyang University of Technology, 2014. [3] 石岩, 刘东炜, 刘佳, 等. 硬脆钢50SiMnVB激光预控裂纹工艺试验研究 [J]. 兵工学报, 2018, 39(10): 1997–2005. DOI: 10.3969/j.issn.1000-1093.2018.10.016.SHI Y, LIU D W, LIU J, et al. Research on laser crack-precontrolling technology for 50SiMnVB [J]. Acta Armamentarii, 2018, 39(10): 1997–2005. DOI: 10.3969/j.issn.1000-1093.2018.10.016. [4] 马宇宇, 李梅, 邱浩, 等. 电子束局部扫描对35CrMnSiA钢组织和力学性能的影响 [J]. 兵器装备工程学报, 2019, 40(9): 204–207. DOI: 10.11809/bqzbgcxb2019.09.042.MA Y Y, LI M, QIU H, et al. Effect of electron beam local scanning on microstructure and mechanical properties of 35CrMnSiA steel [J]. Journal of Ordnance Equipment Engineering, 2019, 40(9): 204–207. DOI: 10.11809/bqzbgcxb2019.09.042. [5] 刘峰涛, 袁书强, 陈炯, 等. 高能束控制破碎弹体威力对研究 [J]. 兵器材料科学与工程, 2008, 31(1): 67–70. DOI: 10.3969/j.issn.1004-244X.2008.01.018.LIU F T, YUAN S Q, CHENG J, et al. Comparative study on the shell power after high-energy-beam controlled fragmentation [J]. Ordnance Material Science and Engineering, 2008, 31(1): 67–70. DOI: 10.3969/j.issn.1004-244X.2008.01.018. [6] 李华, 李国昌, 陈炯, 等. 高能束控制破碎模拟弹体破片分布试验研究 [J]. 兵器材料科学与工程, 2009, 32(5): 81–83. DOI: 10.3969/j.issn.1004-244X.2009.05.024.LI H, LI G C, CHENG J, et al. Fragment distribution of high-energy-beam controlled fragmentation simulation shell [J]. Ordnance Material Science and Engineering, 2009, 32(5): 81–83. DOI: 10.3969/j.issn.1004-244X.2009.05.024. [7] 陈炯, 袁书强, 周春华, 等. 高能束控制破碎钨合金壳体破碎效果研究 [J]. 兵器材料科学与工程, 2010, 33(6): 62–64. DOI: 10.3969/j.issn.1004-244X.2010.06.019.CHEN J, YUAN S Q, ZHOU C H, et al. Fragment effect of tungsten alloy shells controlled by high-energy-beam [J]. Ordnance Material Science and Engineering, 2010, 33(6): 62–64. DOI: 10.3969/j.issn.1004-244X.2010.06.019. [8] 沈正祥, 袁书强, 陈炯, 等. 局部淬火金属柱壳破碎性的研究 [J]. 高压物理学报, 2015, 29(4): 293–298. DOI: 10.11858/gywlxb.2015.04.009.SHEN Z X, YUAN S Q, CHEN J, et al. Fragmentation of metal cylindrical shell treated by local quenching [J]. Chinese Journal of High Pressure Physics, 2015, 29(4): 293–298. DOI: 10.11858/gywlxb.2015.04.009. [9] 袁书强, 沈正详, 李亚哲, 等. 弹体材料性能对预控破片威力的影响 [J]. 科学技术与工程, 2016, 16(9): 195–195. DOI: 10.3969/j.issn.1671-1815.2016.09.034.YUAN S Q, SHEN Z X, LI Y Z, et al. Influence of case material on controlled fragmentation performance [J]. Science Technology and Engineering, 2016, 16(9): 195–195. DOI: 10.3969/j.issn.1671-1815.2016.09.034. [10] 沈正祥, 袁书强, 杨辉, 等. 电子束局部扫描对40CrMnSiB钢组织与冲击性能的影响 [J]. 金属热处理, 2017, 42(1): 87–90. DOI: 10.13251/j.issn.0254-6051.2017.01.020.SHEN Z X, YUAN S Q, YANG H, et al. Effect of electron beam local scanning on microstructure and impact property of 40CrMnSiB steel [J]. Heat Treatment of Metals, 2017, 42(1): 87–90. DOI: 10.13251/j.issn.0254-6051.2017.01.020. [11] 刘桂峰. 激光加工弹体破片形成及杀伤威力研究[D]. 南京: 南京理工大学, 2015.LIU G F. Study on the formation and lethality of fragments of laser processing casing [D]. Nanjing: Nanjing University of Science & Technology, 2015. [12] 陈帅. 弹体改性区对弹丸过载性能和破片形成的影响[D]. 南京: 南京理工大学, 2014.CHEN S. Influence of projectile property-changing zone to overloading capability and to form fragments [D]. Nanjing: Nanjing University of Science & Technology, 2014. [13] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, tempeatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31–48. DOI: 10.1016/0013-7944(85)90052-9. [14] 李硕. 强冲击载荷下35CrMnSi动态力学行为与断裂机理研究[D]. 太原: 中北大学, 2015.LI S. Research on dynamic mechanical behavior and fracture mechanisem of 35CrMnSi under strong impact load [D]. Taiyuan: North University of China, 2015. [15] MURPHY M J, LEE E L. Modeling shock initiation in Composition B [C]// 10th International Detonation Symposium. US: Lawrence Livermore National Laboratory, 1993, 963−970. [16] 隋树元, 王树山. 终点效应学 [M]. 北京: 国防工业出版社, 2000: 57−58.SUI S Y, WANG S S. Terminal effects [M]. Beijing: National Defense Industry Press, 2000: 57−58. [17] 刘鸿文. 材料力学 [M]. 北京: 高等教育出版社, 2010: 217−219.LIU H W. Material mechanics [M]. Beijing: Higher Education Press, 2010: 217−219. -







 下载:
下载: