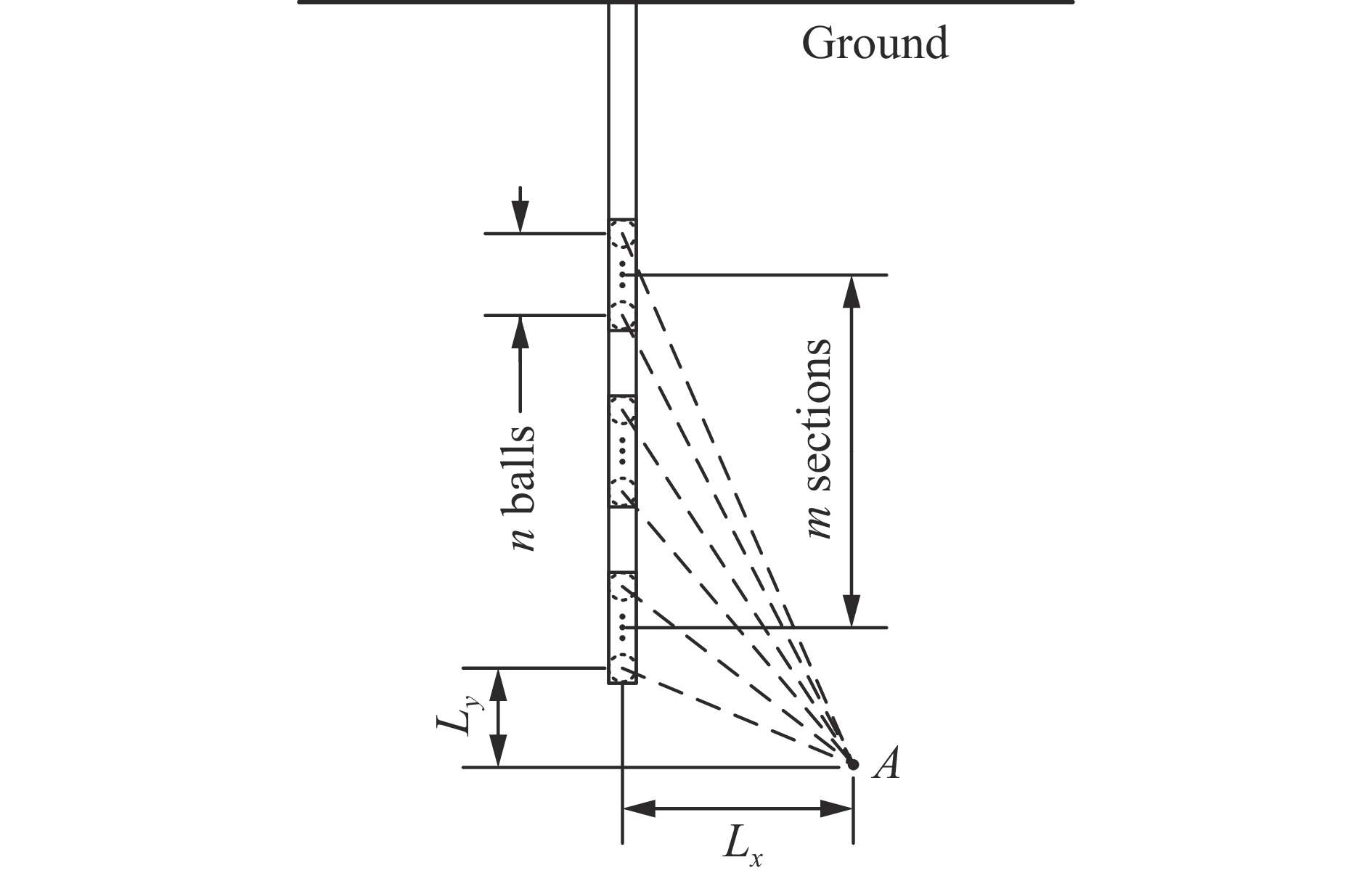
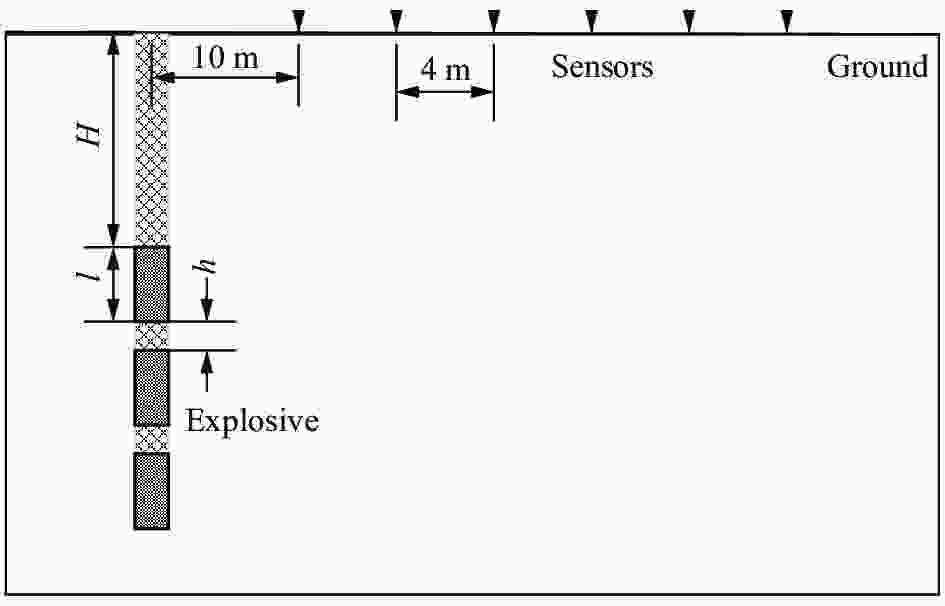
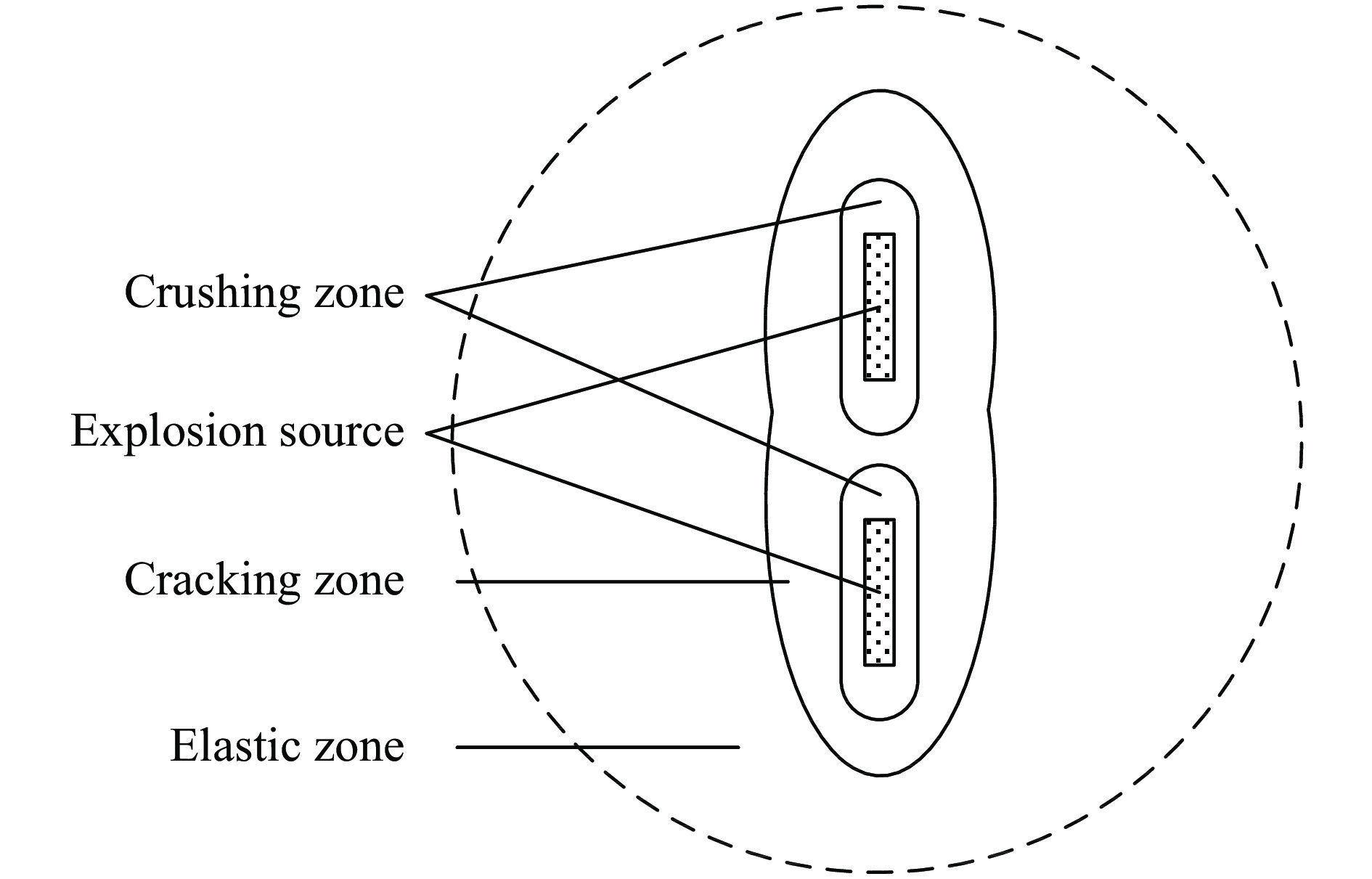
Model of seismic wave field excited by axially distributed explosive
-
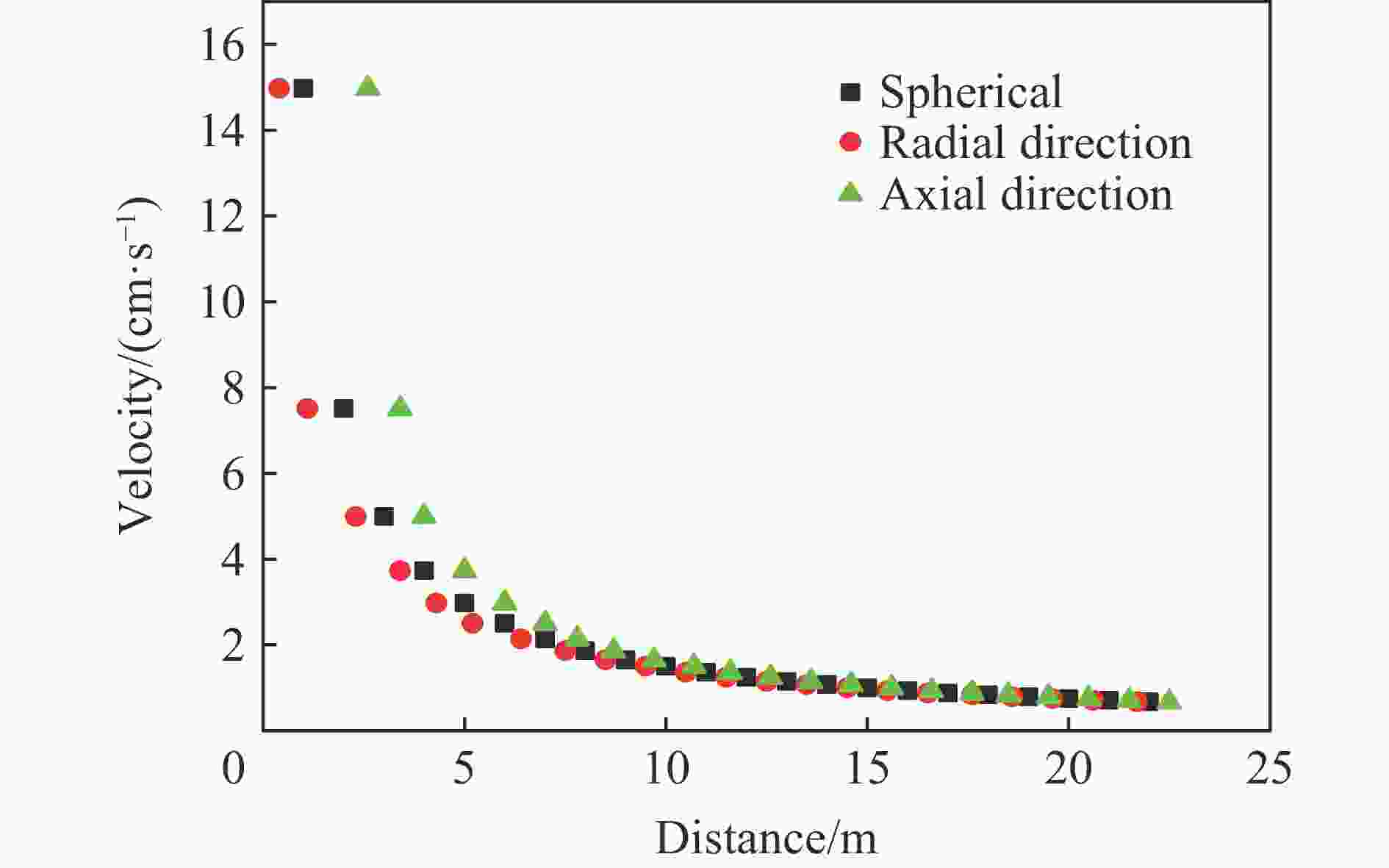
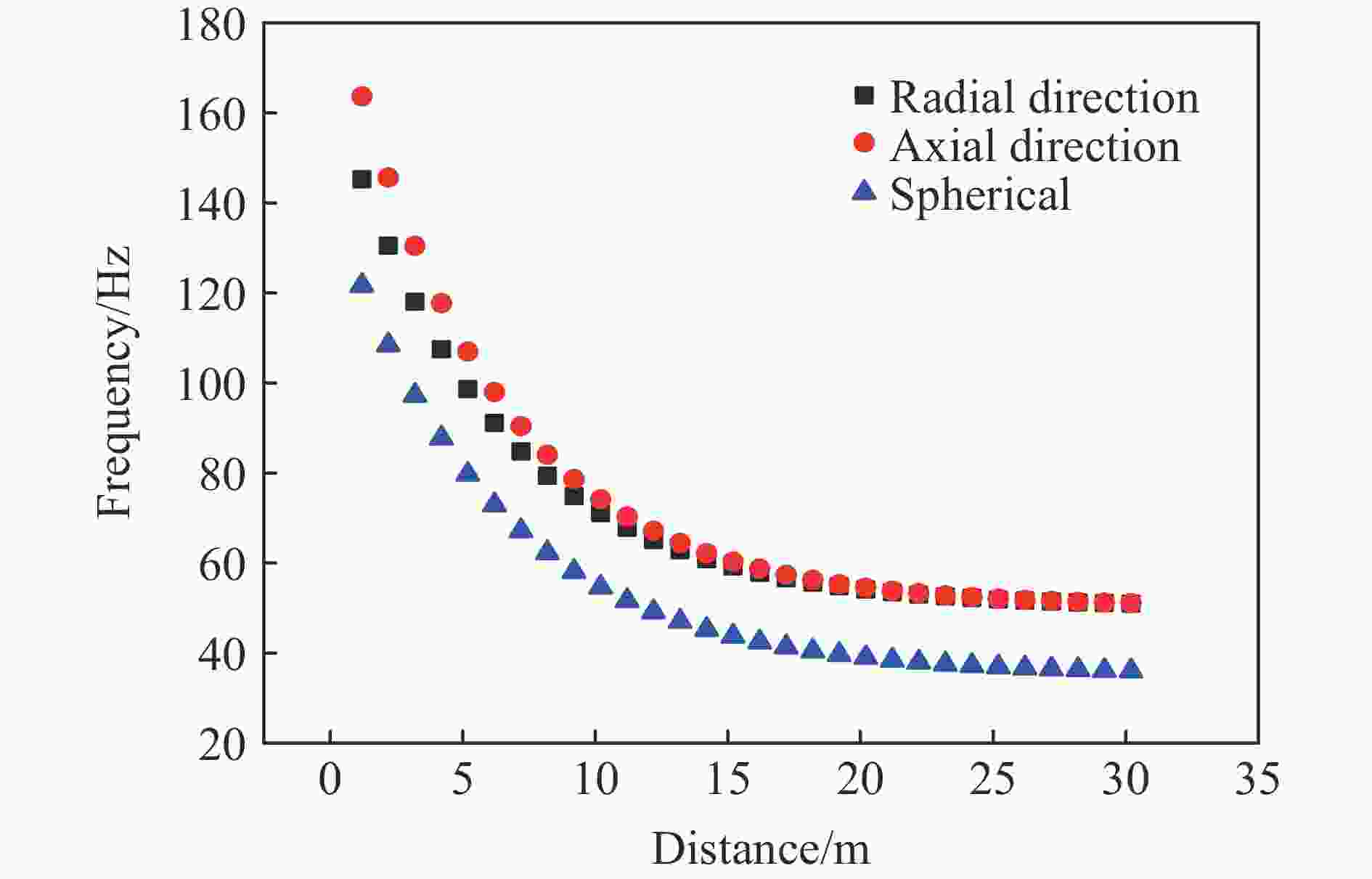
摘要: 炸药震源激发地震波场幅频特性直接影响地震勘探精度，本文通过计算研究轴向分布式药包激发地震波场幅频特征规律：以球形空腔震源模型为基础，采用叠加方法获得轴向分布式药包激发地震波场计算方法，并与数值模拟结果进行对比。研究表明：该方法误差在7%以内；在爆心距大于药柱总长度9.8倍时轴向分布式药包所激发地震波速度场与球形药包基本一致，但地震波的频率更高。Abstract: The amplitude-frequency characters of the seismic wave excited by the explosive source directly affect the seismic exploration accuracy. In order to reveal the characteristic law of the amplitude and frequency of the seismic wave field excited by an axially distributed explosive, the study on the calculation method of the seismic wave field of the axially distributed explosive was proposed. Based on the spherical cavity source model, the calculation method of the seismic wave field excited by the axially distributed explosive source was obtained by using the superposition method, and the seismic wave field model excited by the axially distributed charge was established. This model can describe the characteristics of the seismic wave field of distributed explosive sources in seismic exploration. Comparison with numerical simulation shows that the error between the theoretical model and the numerical model is within 5% in the radial direction, and the error between the theoretical model and the numerical model is within 3.4% in the axial direction. Compared with the field experiment results, the theoretical model seismic wave vibration velocity error is within 10% when the blast center distance is greater than 14 m. The calculation accuracy increases with the increase of the distance, and the error is less than 6% when the distance is greater than 24 m. When the blast center distance is the same, the vibration speed in the axial direction is greater than the vibration speed in the radial direction. The difference between the two decreases with the increase of the blast center distance. When the blast center distance is 9.8 times the total length of the charge, the axial direction is the vibration speed difference in the radial direction is within 5%, and the frequency of the seismic wave is higher. The research shows that the model can accurately describe the amplitude-frequency character of the seismic wave excited by the axially-distributed explosive.
-
Key words:
- seismic wave /
- seismic exploration /
- explosive source /
- axially distributed explosive
-
图 1 轴向分布式药包在岩土介质中爆炸分区
Figure 1. Explosive zoning of an axially distributed charge in geotechnical media
图 3 轴向分布式药包最大振动速度
Figure 3. Maximum vibration velocity at different locations of axial distributed excitation:
图 5 不同激发方案地震波的峰值粒子振动速度衰减规律
Figure 5. Peak particle vibration velocities of seismic waves with different excitation schemes
图 6 球形药包和轴向分布式药包地震波场
Figure 6. Seismic wave field of spherical explosive and axially-distributed explosive
图 7 相同质点振动速度时球形药包距离与柱形药包轴向、径向距离对比
Figure 7. Comparison of the distance between spherical explosives and different directions of axially distributed cylindrical explosives at the same particle vibration velocity
图 8 轴向分布式柱形药包和球形药包形成地震波主频对比
Figure 8. Comparison of frequency of spherical charge and axially distributed charge
表 1 轴向分布式炸药激发方案
Table 1. Excitation scheme of axially distributed explosives
方案 药柱数量 单药柱质量/kg 药柱间隔/mm 总药量/kg 延迟时间/s 激发方向 3 kg×2 2 3 400 6 0.3 由上而下 2 kg×3 3 2 400 6 0.3 由上而下 1.5 kg×4 4 1.5 400 6 0.3 由上而下 
下载: 导出CSV
表 2 土介质参数
Table 2. Parameters of soil
$ {\sigma }_{\mathrm{c}} $/MPa $ {\sigma }_{\mathrm{t}} $/MPa $G$/GPa $ \alpha $ $ \varphi /\mathrm{k}\mathrm{P}\mathrm{a} $ $ {\rho }_{\mathrm{s}} $/($ \mathrm{k}\mathrm{g} \cdot {\mathrm{m}}^{3} $) k/MPa G/MPa $ {\sigma }_{\mathrm{y}} $/MPa 13 2 0.147 0.115 11.8 1840 245 147 22
下载: 导出CSV
表 3 TNT炸药特性参数
Table 3. Parameters of TNT
C1/GPa C2/GPa R1 R2 ω ρe/（kg·m−3） D/（m·s−1） e/（J·m−3） pCJ/GPa p0/GPa 373.7 3.747 4.15 0.90 0.35 1650 6930 6.0$ \times {10}^{9} $ 21 9.82
下载: 导出CSV
表 4 检波器部分参数
Table 4. Parameters of sensors
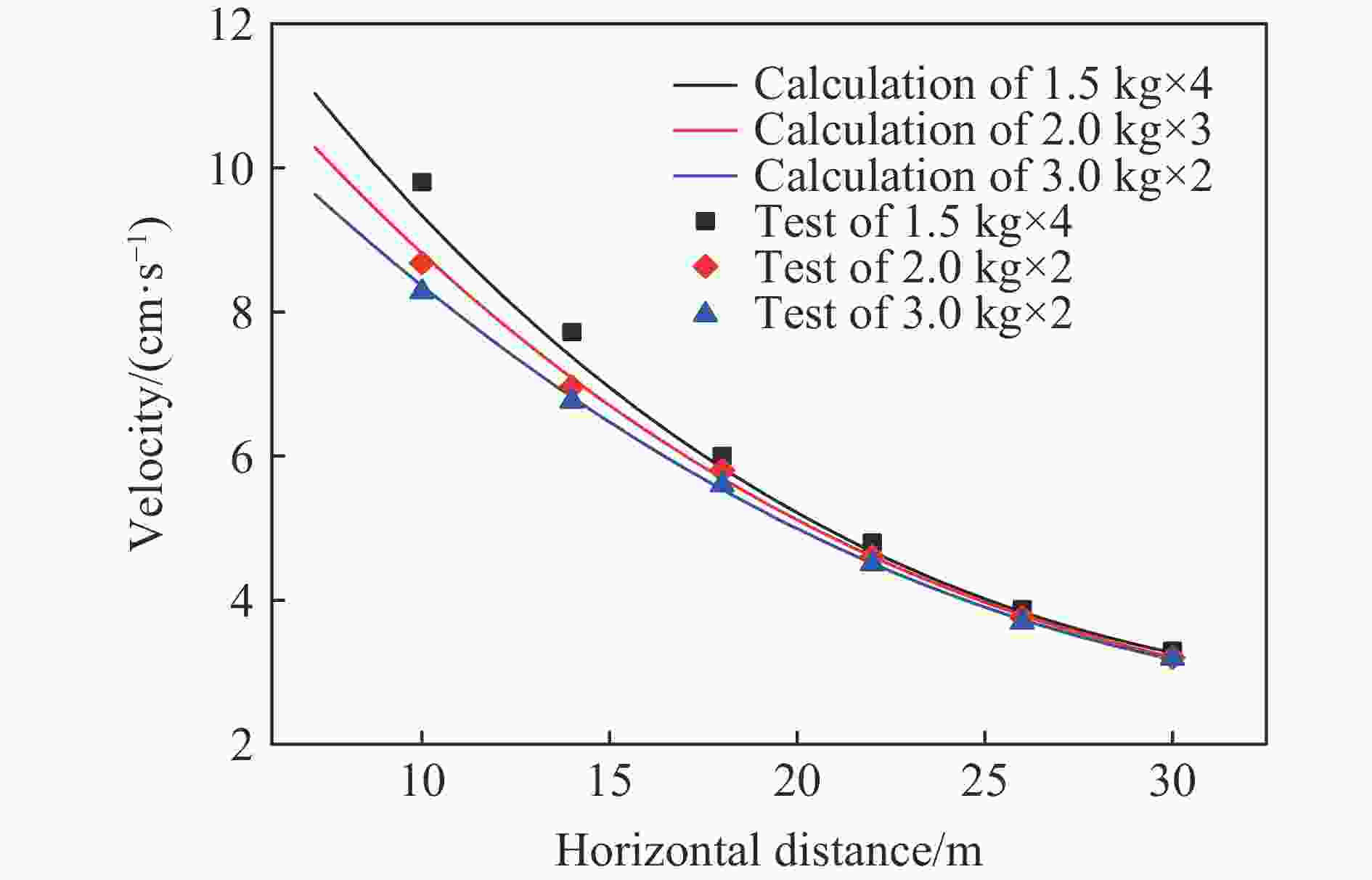
量程/V 灵敏度/[V·（m·s−1）−1] 通频带/Hz 误差范围/% 10 7 1～100 ＜0.05
下载: 导出CSV
表 5 不同位置(x)处峰值粒子速度实验结果相与计算结果的相对误差
Table 5. Table 6 Relative error of experimental results of peak paritcle velocity to the calculational ones at different position x
炸药激发方案 误差/% x=10 m x=14 m x=18 m x=22 m x=26 m x=30 m 3 kg×2 4.52 4.84 4.77 4.32 3.92 4.12 2 kg×3 4.56 4.63 4.32 3.93 4.12 3.93 1.5 kg×4 8.01 6.82 6.51 7.25 8.80 9.44
下载: 导出CSV
-
[1] 陆基孟, 王永刚. 地震勘探原理[M]. 青岛: 中国石油大学出版社, 2009: 3−5. [2] 钱七虎, 王明洋. 岩土中的冲击爆炸效应[M]. 北京: 国防工业出版社, 2010: 52−57. [3] JEFFREYS H. On the cause of oscillatory movement in seismograms [J]. Geophysical Journal International, 1931, 2(S8): 407–416. DOI: 10.1111/j.1365-246X.1931.tb04462.x. [4] SHARPE J A. The production of elastic waves by explosion pressures: I: theory and empirical field observations [J]. Geophysics, 1942, 7(2): 144–154. DOI: 10.1190/1.1445002. [5] BLAKE F G Jr. Spherical wave propagation in solid media [J]. The Journal of the Acoustical Society of America, 1952, 24(2): 211–215. DOI: 10.1121/1.1906882. [6] 肖建华, 孙文涛. 关于点爆炸震源产生的地震子波 [J]. 石油地球物理勘探, 1997, 32(6): 809–817. DOI: 10.3321/j.issn:1000-7210.1997.06.006.XIAO J H, SUN W T. Seismic wavelet generated by point explosive source [J]. Oil Geophysical Prospecting, 1997, 32(6): 809–817. DOI: 10.3321/j.issn:1000-7210.1997.06.006. [7] 肖建华. 论球面波波动方程 [J]. 石油地球物理勘探, 2001, 36(2): 160–172. DOI: 10.3321/j.issn:1000-7210.2001.02.004.XIAO J H. Argument on wave equation of spherical wave [J]. Oil Geophysical Prospecting, 2001, 36(2): 160–172. DOI: 10.3321/j.issn:1000-7210.2001.02.004. [8] 丁桦, 郑哲敏. 爆破震动等效载荷模型 [J]. 中国科学(E辑), 2003, 33(1): 82–90. DOI: 10.3969/j.issn.1674-7259.2003.01.011. [9] 林大超, 白春华. 爆炸地震效应[M]. 北京: 地质出版社, 2007. [10] YU C L, WANG Z Q, HAN W G. A prediction model for amplitude-frequency characteristics of blast-induced seismic waves [J]. GEOPHYSICS, 2018, 83: T159–T173. DOI: 10.1190/geo2017-0228.1. [11] HEELAN P A. Radiation from a cylindrical source of finite length [J]. Geophysics, 1953, 18(3): 685–696. DOI: 10.1190/1.1437923. [12] STARFIELD A M, PUGLIESE J M. Compression waves generated in rock by cylindrical explosive charges: a comparison between a computer model and field measurements [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1968, 5(1): 65–77. DOI: 10.1016/0148-9062(68)90023-5. [13] 龙源, 林学圣, 许连坡. 条形装药土中爆炸空腔发展过程的实验研究 [J]. 爆炸与冲击, 1988, 8(3): 227–235.LONG Y, LIN X S, XU L P. Experimental research on growth process of the cavity of a strip-shaped explosive charge exploding in soil [J]. Explosion and Shock Waves, 1988, 8(3): 227–235. [14] 李鹏毅, 王仲琦, 徐谦, 等. 有限长柱形药包土中爆腔特征尺寸的计算方法 [J]. 爆炸与冲击, 2019, 39(12): 124201. DOI: 10.11883/bzycj-2018-0416.LI P Y, WANG Z Q, XU Q, et al. Calculation methods for characteristic sizes of blasting cavities induced by finite-length cylindrical charges in soil [J]. Explosion and Shock Waves, 2019, 39(12): 124201. DOI: 10.11883/bzycj-2018-0416. [15] 于成龙, 王仲琦. 球形装药爆腔预测的准静态模型 [J]. 爆炸与冲击, 2017, 37(2): 249–254. DOI: 10.11883/1001-1455(2017)02-0249-06.YU C L, WANG Z Q. Quasi-static model for predicting explosion cavity with spherical charges [J]. Explosion and Shock Waves, 2017, 37(2): 249–254. DOI: 10.11883/1001-1455(2017)02-0249-06. [16] 胡立新, 杨德宽, 何兵寿, 等. 延迟爆炸法的理论分析 [J]. 石油地球物理勘探, 2002, 37(1): 33–38. DOI: 10.3321/j.issn:1000-7210.2002.01.007.HU L X, YANG D K, HE B S, et al. Theoretic analysis of delayed blast [J]. Oil Geophysical Prospecting, 2002, 37(1): 33–38. DOI: 10.3321/j.issn:1000-7210.2002.01.007. [17] 黄文尧, 颜事龙, 吕淑然, 等. 低爆速细长震源药柱的研究与应用 [J]. 爆破器材, 2005, 34(4): 18–22. DOI: 10.3969/j.issn.1001-8352.2005.04.007.HUANG W Y, YAN S L, LÜ S R, et al. The research and application of the low detonation velocity and elongated source charge [J]. Explosive Materials, 2005, 34(4): 18–22. DOI: 10.3969/j.issn.1001-8352.2005.04.007. [18] 牟杰. 炸药震源激发地震波近场特征试验研究[D]. 北京: 北京理工大学, 2015. -
计量
- 文章访问数: 477
- HTML全文浏览量: 357
- PDF下载量: 50
- 被引次数: 0