考虑摩擦因数变化的弹体高速侵彻混凝土质量侵蚀模型研究

刘均伟; 张先锋; 刘闯; 陈海华; 王季鹏; 熊玮

doi:10.11883/bzycj-2020-0250

考虑摩擦因数变化的弹体高速侵彻混凝土质量侵蚀模型研究

doi: 10.11883/bzycj-2020-0250

南京理工大学机械工程学院，江苏南京 210094

基金项目: 国家自然科学基金(11790292)；国家自然科学基金委员会与中国工程物理研究院联合基金(U1730101)；中央高校基本科研业务费专项(30919011401)

详细信息

作者简介:
刘均伟（1996－　），男，博士研究生，717904682@qq.com

通讯作者:
张先锋（1978－　），男，博士，教授，博士生导师，lynx@njust.edu.com

中图分类号: O385
计量
- 文章访问数: 588
- HTML全文浏览量: 272
- PDF下载量: 111
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-21
- 修回日期: 2020-11-29
- 网络出版日期: 2021-07-19
- 刊出日期: 2021-08-05

Study on mass erosion model of projectile penetrating concrete at high speed considering variation of friction coefficient

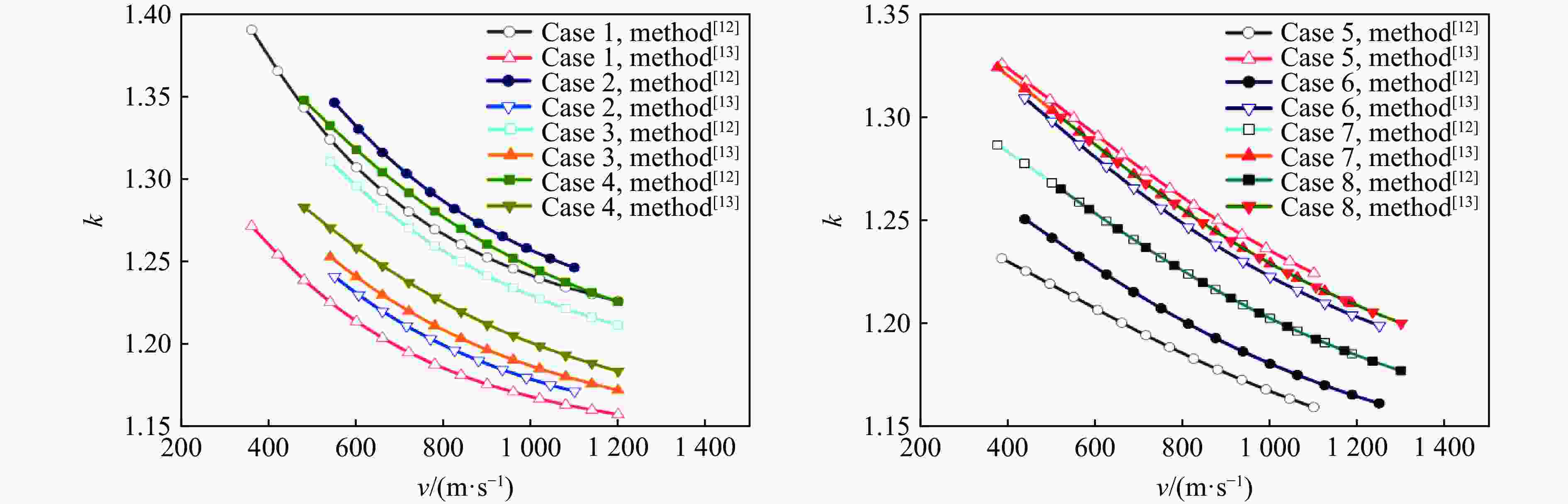
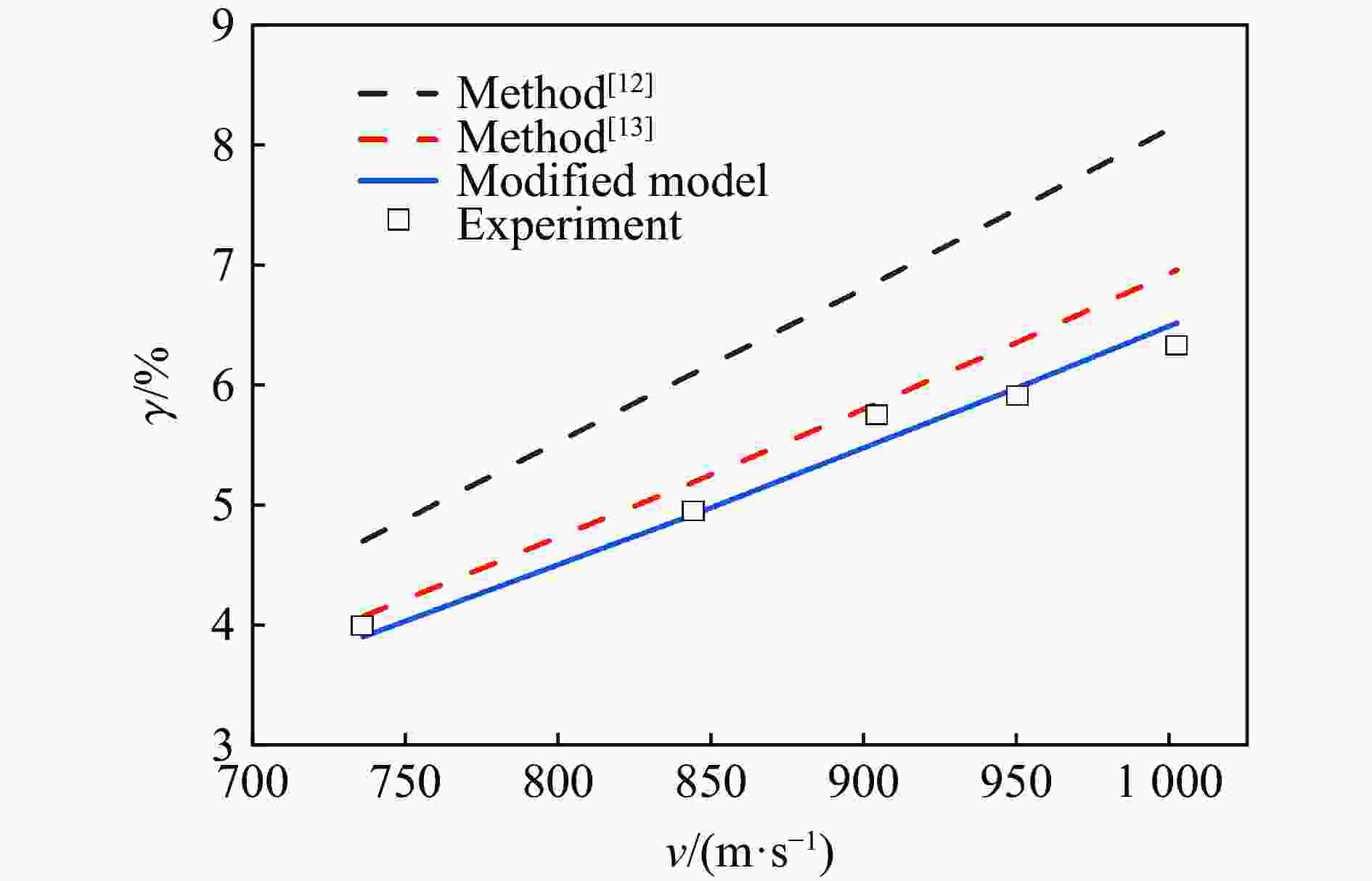
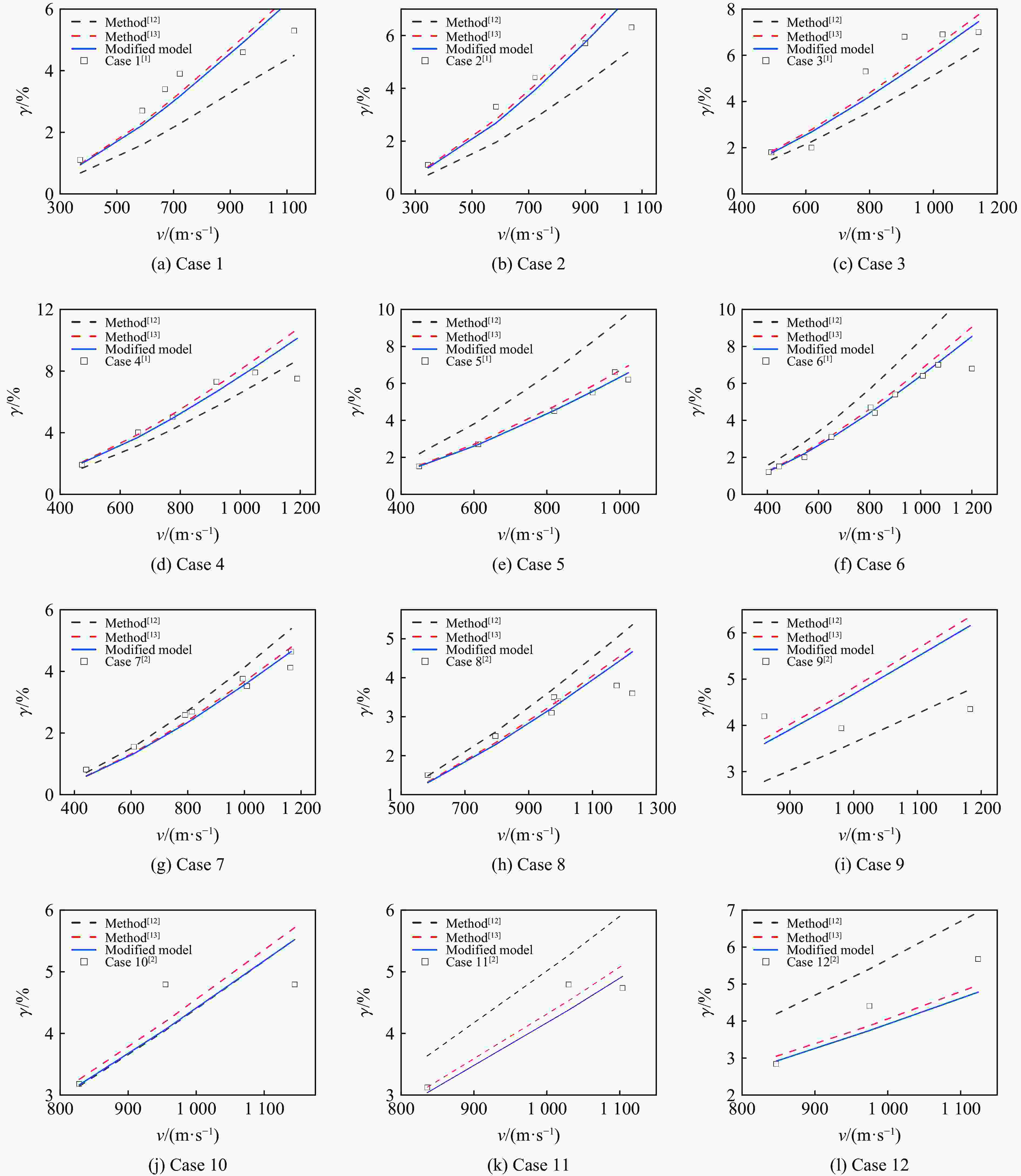
School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China

摘要

摘要: 弹体在高速侵彻混凝土介质时，由于弹靶之间强烈的局部作用，导致弹体发生质量损失和弹头钝化。为进一步探究弹体高速侵彻混凝土靶质量侵蚀效应及其影响因素，基于热熔化机制及变摩擦因数模型，考虑弹体侵彻过程中头部形状变化，修正了弹体高速侵彻混凝土质量侵蚀模型。为验证模型的可靠性，基于30 mm弹道炮平台，开展了卵形弹体高速(700～1 000 m/s)侵彻典型混凝土靶体实验，获得了弹体高速侵彻质量侵蚀结果。结合理论模型对本文实验及文献实验数据进行了对比分析计算，验证了本文修正模型的可靠性。结果表明：弹体侵彻过程中，滑动摩擦项占总摩擦力的10%～40%，它对弹体侵彻过程的影响不能被忽略；考虑摩擦因数变化的质量侵蚀模型预测结果与已有实验数据吻合得较好；与本文实验数据的最大误差不超过7%，能较准确地预测不同工况下弹体的质量损失。
- 高速侵彻 /
- 质量侵蚀 /
- 头部形状 /
- 摩擦因数
Abstract: When the projectile penetrates into the concrete medium at high speed, the mass loss and nose blunting occur due to the strong local interaction between the projectile and the target. In order to further explore the mass erosion effect of high-speed projectile penetrating concrete target and its influencing factors, based on the thermal melting mechanism and variable friction coefficient model, the mass erosion model of high-speed projectile penetrating concrete target was modified considering the change of projectile nose shape during penetration. In order to verify the reliability of the model, based on the 30 mm ballistic gun platform, the oval projectile penetrating typical concrete targets at high velocities ranging from 700 to 1000 m/s was carried out, and the mass erosion results of high-speed penetration were obtained. Combined with the theoretical model, the reliability of the modified model is verified by analyzing the test data in this paper and the literature. The results show that the sliding friction term accounts for 10%−40% of the total friction in the process of projectile penetration, and its influence on the penetration process can’t be ignored. The prediction results of mass erosion model considering the variation of friction coefficient are in good agreement with the existing test data, and the maximum error with the test data in this paper is less than 7%, which can accurately predict the mass loss of projectile under different working conditions.
- high speed penetration /
- mass loss /
- head shape /
- friction coefficient

HTML全文

图 1 侵彻过程中弹体头部受力

Figure 1. Force diagram projectile head during penetration

下载: 全尺寸图片幻灯片

图 2 计算流程

Figure 2. Flow chart of calculation

下载: 全尺寸图片幻灯片

图 3 摩擦力比值的计算结果

Figure 3. Calculation results of friction ratio

下载: 全尺寸图片幻灯片

图 4 实验弹靶

Figure 4. Projectile and target used in penetration experiments

下载: 全尺寸图片幻灯片

图 5 高速摄影记录的弹体撞击靶体过程

Figure 5. Process of projectile impacting target recorded by high speed photography

下载: 全尺寸图片幻灯片

图 6 实验前、后弹体轮廓对比

Figure 6. Projectile profiles before and after experiment

下载: 全尺寸图片幻灯片

图 7 弹体质量侵蚀预测结果与实验结果对比

Figure 7. Comparison of prediction results of projectile mass erosion with experimental results

下载: 全尺寸图片幻灯片

图 8 模型预测结果与实验回收弹体对比

Figure 8. Comparison between the predicted results of the model and the recovered projectile

下载: 全尺寸图片幻灯片

图 9 弹体质量侵蚀预测结果与实验结果对比

Figure 9. Comparison of prediction results of projectile mass erosion with test results

下载: 全尺寸图片幻灯片

表 1 实验弹靶参数

Table 1. Parameters of projectile and target

f_c/MPa	ρ_t/（kg·m⁻³）	骨料	弹体材料	Y_p/MPa	ρ_p/（kg·m⁻³）	m₀/kg	d/mm	L/d	φ
35	2 300	石灰石	30CrMnSiA	1 243	7 850	0.553	30	6	4

下载: 导出CSV

表 2 各工况弹靶参数

Table 2. Parameters of projectile and target

工况	f_c/MPa	ρ_t/（kg·m⁻³）	骨料	弹体材料	Y_p/MPa	ρ_p/（kg·m⁻³）	m₀/kg	d/mm	L/d	φ
1^[1]	13.5	2 000	石英石 7	4340钢	1 481	7 850	0.064	12.9	6.88	3.00
2^[1]	13.5	2 000	石英石 7	4340钢	1 481	7 850	0.064	12.9	6.88	4.25
3^[1]	21.6	2 000	石英石 7	4340钢	1 481	7 850	0.064	12.9	6.88	3.00
4^[1]	21.6	2 000	石英石 7	4340钢	1 481	7 850	0.064	12.9	6.88	4.25
5^[1]	62.8	2 300	石英石 7	4340钢	1 481	7 850	0.478	20.3	10.00	3.00
6^[1]	51.0	2 300	石英石 7	4340钢	1 481	7 850	1.600	30.5	10.00	3.00
7^[2]	58.4	2 320	石灰石 3	4340钢 AerMet100	1 481 1 820	7 850	0.478	20.3	10.00	3.00
8^[2]	58.4	2 320	石灰石 3	4340钢 AerMet100	1 481 1 820	7 850	1.620	30.5	10.00	3.00
9^[2]	34.8	2 300	石灰石 3	4340钢 Tc4	1 300 1 030	7 850	0.155	14.0	10.00	4.25
10^[2]	48.6	2 300	石灰石 3	60Si2Mn 20钢	1 300 450	7 850	0.155	14.0	10.00	4.25
11^[2]	61.3	2 300	石灰石 3	60Si2Mn 45钢	1 300 680	7 850	0.155	14.0	10.00	4.25
12^[2]	76.4	2 300	石灰石 3	60Si2Mn 35CrMnSi	1 300 1 540	7 850	0.155	14.0	10.00	4.25

下载: 导出CSV

表 3 不同速度下弹体的质量损失率与长度缩短率

Table 3. Mass loss rate and length shortening rate of projectile body at different speeds

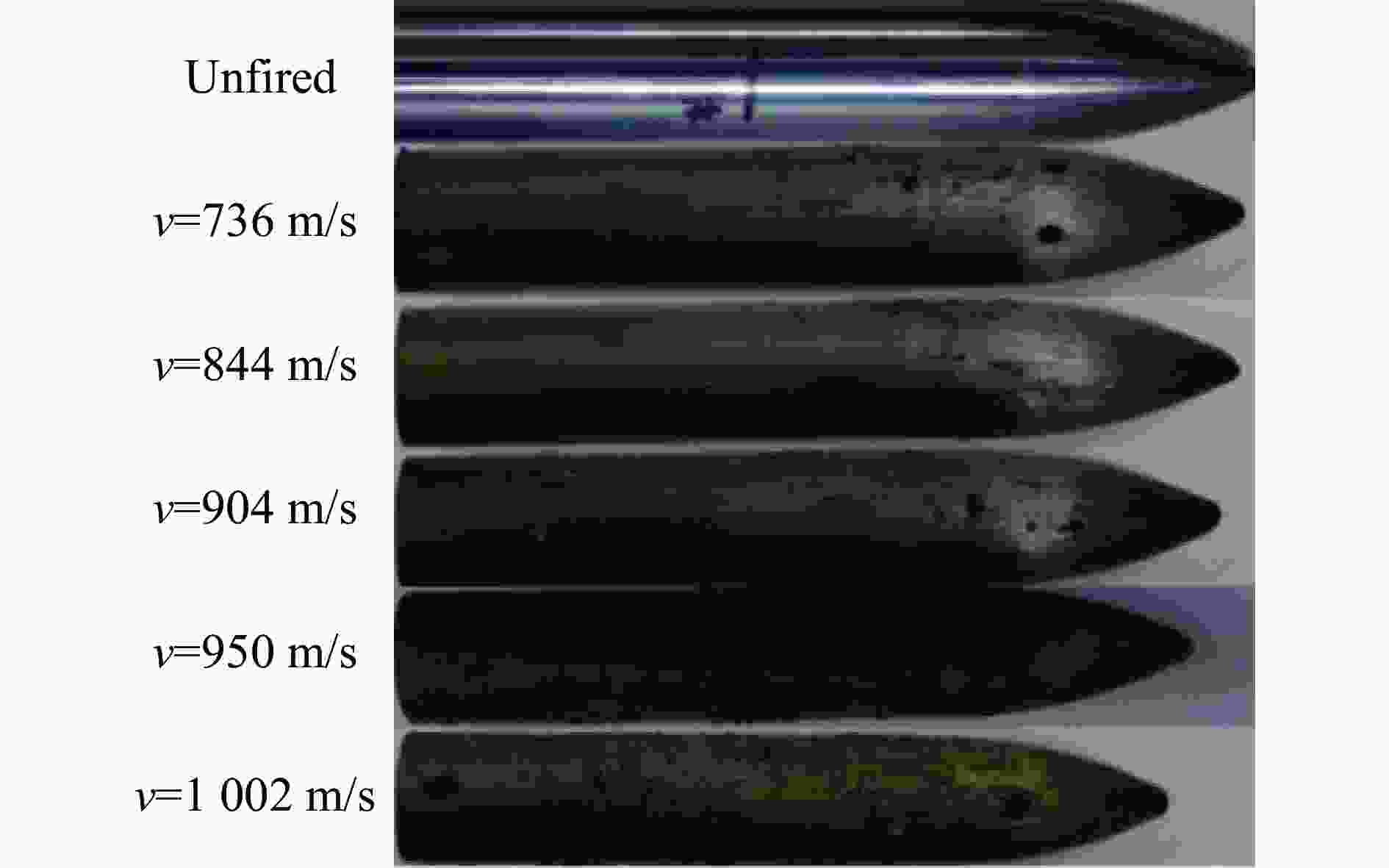
v/（m·s⁻¹）	γ/%	δ/%
730	3.99	1.50
844	4.95	1.55
904	5.75	1.72
950	5.91	1.88
1 002	6.33	2.17

下载: 导出CSV

表 4 弹体质量侵蚀预测结果与实验结果对比

Table 4. Comparison of prediction results of projectile mass erosion with experimental results

v/（m·s⁻¹）	γ/%
v/（m·s⁻¹）	实验	文献[12]方法	文献[13]方法	修正模型
736	3.99	4.70	4.06	3.90
844	4.95	6.09	5.19	4.92
904	5.75	6.86	5.85	5.52
950	5.91	7.47	6.36	5.98
1 002	6.33	8.17	6.96	6.52

下载: 导出CSV

参考文献(21)

[1]	FORRESTAL M J, FREW D J, HANCHAK S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectiles [J]. International Journal of Impact Engineering, 1996, 18(5): 465–476. DOI: 10.1016/0734-743x(95)00048-f.
[2]	FREW D J, HANCHAK S J, GREEN M L, et al. Penetration of concrete targets with ogive-nose steel rods [J]. International Journal of Impact Engineering, 1998, 21(6): 489–497. DOI: 10.1016/S0734-743X(98)00008-6.
[3]	何翔, 徐翔云, 孙桂娟, 等. 弹体高速侵彻混凝土的效应实验 [J]. 爆炸与冲击, 2010, 30(1): 1–6. DOI: 10.11883/1001-1455(2010)01-0001-06. HE X, XU X Y, SUN G J, et al. Experimental investigation on projectiles high-velocity penetration into concrete target [J]. Explosion and Shock Waves, 2010, 30(1): 1–6. DOI: 10.11883/1001-1455(2010)01-0001-06.
[4]	MU Z C, ZHANG W. An investigation on mass loss of ogival projectiles penetrating concrete targets [J]. International Journal of Impact Engineering, 2011, 38(8−9): 770–778. DOI: 10.1016/j.ijimpeng.2011.04.002.
[5]	武海军, 黄风雷, 王一楠, 等. 高速侵彻混凝土弹体头部侵蚀终点效应实验研究 [J]. 兵工学报, 2012, 33(1): 48–55. WU H J, HUANG F L, WANG Y N, et al. Experimental investigation on projectile nose eroding effect of high-velocity penetration into concrete [J]. Acta Armamentarii, 2012, 33(1): 48–55.
[6]	SILLING S A, FORRESTAL M J. Mass loss from abrasion on ogive-nose steel projectiles that penetrate concrete targets [J]. International Journal of Impact Engineering, 2007, 34(11): 1814–1820. DOI: 10.1016/j.ijimpeng.2006.10.008.
[7]	WU H J, HUANG F L, WANG Y N, et al. Mass loss and nose shape change on ogive-nose steel projectiles during concrete penetration [J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2012, 13(3−4): 273–280. DOI: 10.1515/ijnsns-2011-0047.
[8]	WEN H M, YANG Y, HE T. Effects of abrasion on the penetration of ogival-nosed projectiles into concrete targets [J]. Latin American Journal of Solids and Structures, 2010, 7(4): 413–422. DOI: 10.1590/S1679-78252010000400003.
[9]	ZHAO J, CHEN X W, JIN F N, et al. Depth of penetration of high-speed penetrator with including the effect of mass abrasion [J]. International Journal of Impact Engineering, 2010, 37(9): 971–979. DOI: 10.1016/j.ijimpeng.2010.03.008.
[10]	JONES S E, FOSTER J C, TONESS O A, et al. An estimate for mass loss from high velocity steel penetrators [C] // Proceedings of ASME 2002 Pressure Vessels and Piping Conference. Vancouver: ASME, 2002. DOI: 10.1115/PVP2002-1149.
[11]	陈小伟, 杨世全, 何丽灵. 动能侵彻弹体的质量侵蚀模型分析 [J]. 力学学报, 2009, 41(5): 739–747. DOI: 10.3321/j.issn:0459-1879.2009.05.017. CHEN X W, YANG S Q, HE L L. Modeling on mass abrasion of kinetic energy penetrator [J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(5): 739–747. DOI: 10.3321/j.issn:0459-1879.2009.05.017.
[12]	HE L L, CHEN X W, HE X. Parametric study on mass loss of penetrators [J]. Acta Mechanica Sinica, 2010, 26(4): 585–597. DOI: 10.1007/s10409-010-0341-8.
[13]	欧阳昊, 陈小伟. 混凝土骨料对高速侵彻弹体质量侵蚀的影响分析 [J]. 爆炸与冲击, 2019, 39(7): 073102. DOI: 10.11883/bzycj-2018-0068. OUYANG H, CHEN X W. Analysis of mass abrasion of high-speed penetrator influencedby aggregate in concrete target [J]. Explosion and ShockWaves, 2019, 39(7): 073102. DOI: 10.11883/bzycj-2018-0068.
[14]	OUYANG H, CHEN X W. Modeling on mass loss and nose blunting of high-speed penetrator into concrete target [J]. International Journal of Protective Structures, 2019, 10(1): 3–25. DOI: 10.1177/2041419618784749.
[15]	何丽灵, 陈小伟, 夏源明. 侵彻混凝土弹体磨蚀的若干研究进展 [J]. 兵工学报, 2010, 31(7): 950–966. HE L L, CHEN X W, XIA Y M. A review on the mass loss of projectile [J]. Acta Armamentarii, 2010, 31(7): 950–966.
[16]	LUK V K, FORRESTAL M J. Penetration into semi-infinite reinforced-concrete targets with spherical and ogival nose projectiles [J]. International Journal of Impact Engineering, 1987, 6(4): 291–301. DOI: 10.1016/0734-743X(87)90096-0.
[17]	DAVIS R N, NEELY A M, JONES S E. Mass loss and blunting during high-speed penetration [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2004, 218(9): 1053–1062. DOI: 10.1243/0954406041991189.
[18]	CHEN X W, HE L L, YANG S Q. Modeling on mass abrasion of kinetic energy penetrator [J]. European Journal of Mechanics-A: Solids, 2010, 29(1): 7–17. DOI: 10.1016/j.euromechsol.2009.07.006.
[19]	KLEPACZKO J R, HUGHES M L. Scaling of wear in kinetic energy penetrators [J]. International Journal of ImpactEngineering, 2005, 31(4): 435–459. DOI: 10.1016/j.ijimpeng.2004.02.006.
[20]	KLEPACZKO J R. Surface layer thermodynamics of steel penetrators at high and very high sliding velocities: A709014 [R]. Washington: Storming Media, 2001.
[21]	FORRESTAL M J, ALTMAN B S, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets [J]. International Journal of Impact Engineering, 1994, 15(4): 395–405. DOI: 10.1016/0734-743X(94)80024-4.