仿生波纹夹层结构耐撞性分析及优化

黄晗; 许述财; 陈姮

doi:10.11883/bzycj-2020-0275

仿生波纹夹层结构耐撞性分析及优化

doi: 10.11883/bzycj-2020-0275

黄晗^1,,
许述财^2, ,,
陈姮³

1.
南京航空航天大学航天学院，江苏南京 211106
2.
清华大学汽车安全与节能国家重点实验室，北京 100084
3.
陆军工程大学野战工程学院，江苏南京 210001

基金项目: 国家自然科学基金（11902157）；中国博士后科学基金（2018M641338）；南京航空航天大学校人才科研启动基金（1011-YAH20001）

详细信息

作者简介:
黄　晗（1989－　），男，博士，副研究员，huanghan@nuaa.edu.cn

通讯作者:
许述财（1978－　），男，博士，副研究员，xushc@tsinghua.edu.cn

中图分类号: O383
计量
- 文章访问数: 666
- HTML全文浏览量: 469
- PDF下载量: 147
- 被引次数: 0
出版历程
- 收稿日期: 2020-08-11
- 修回日期: 2020-10-12
- 网络出版日期: 2021-07-12
- 刊出日期: 2021-08-05

Crashworthiness analysis and optimization of bionic corrugated sandwich structures

HUANG Han^1
,,
XU Shucai^{2
, ,},
CHEN Heng³

1.
Academy of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, Jiangsu, China
2.
State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084, China
3.
Field Engineering College, Army Engineering University of PLA, Nanjing 210001, Jiangsu, China

摘要

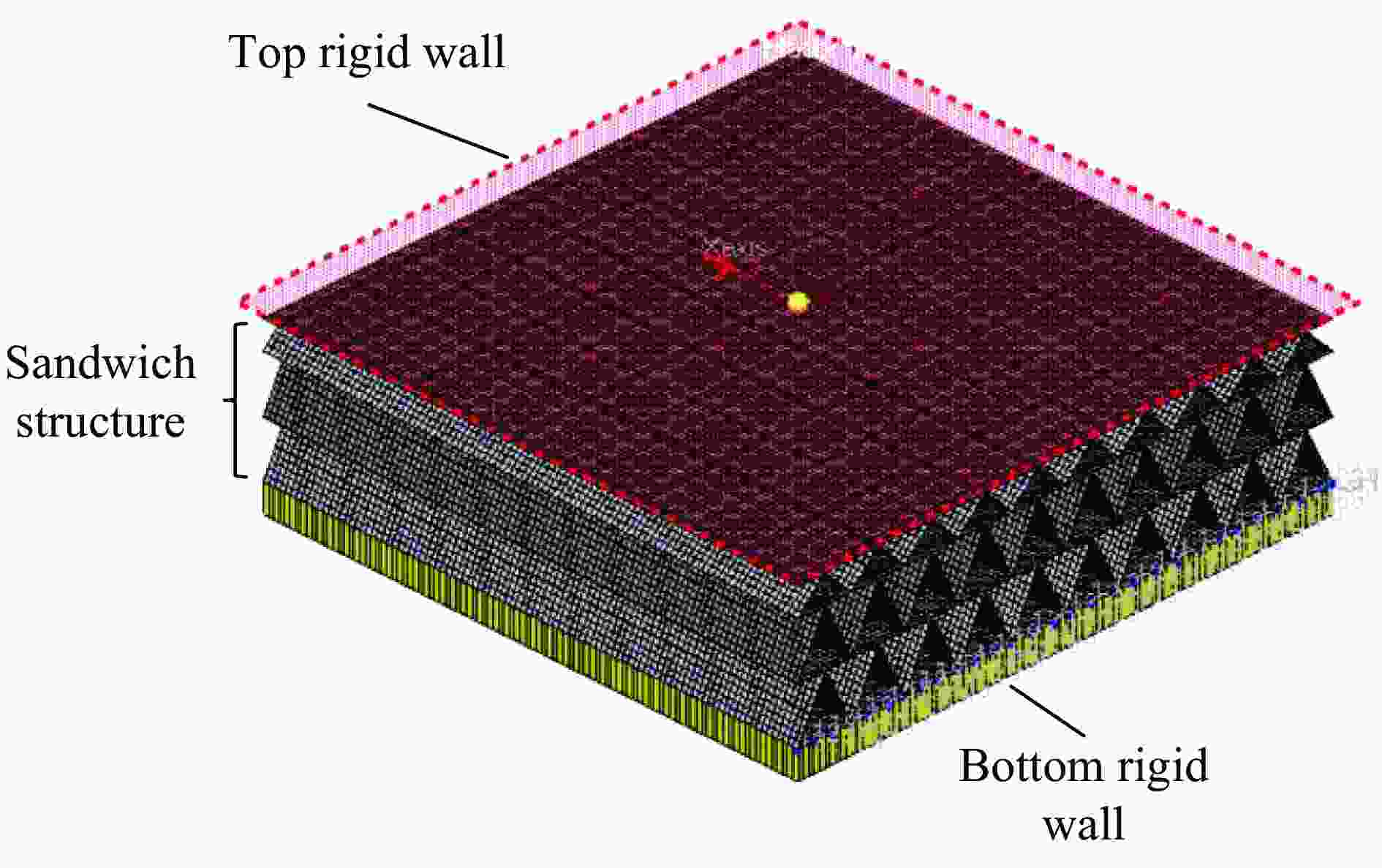
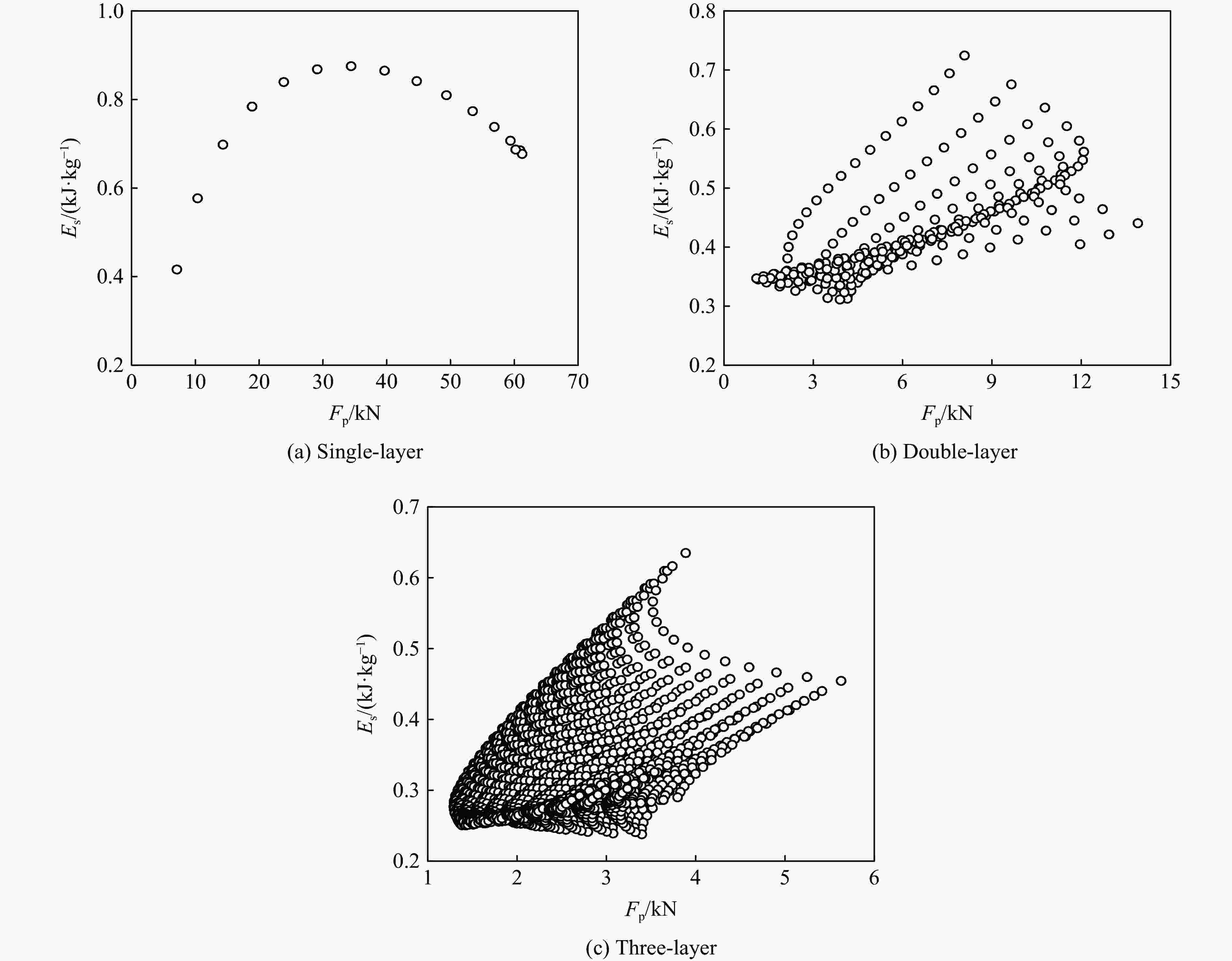
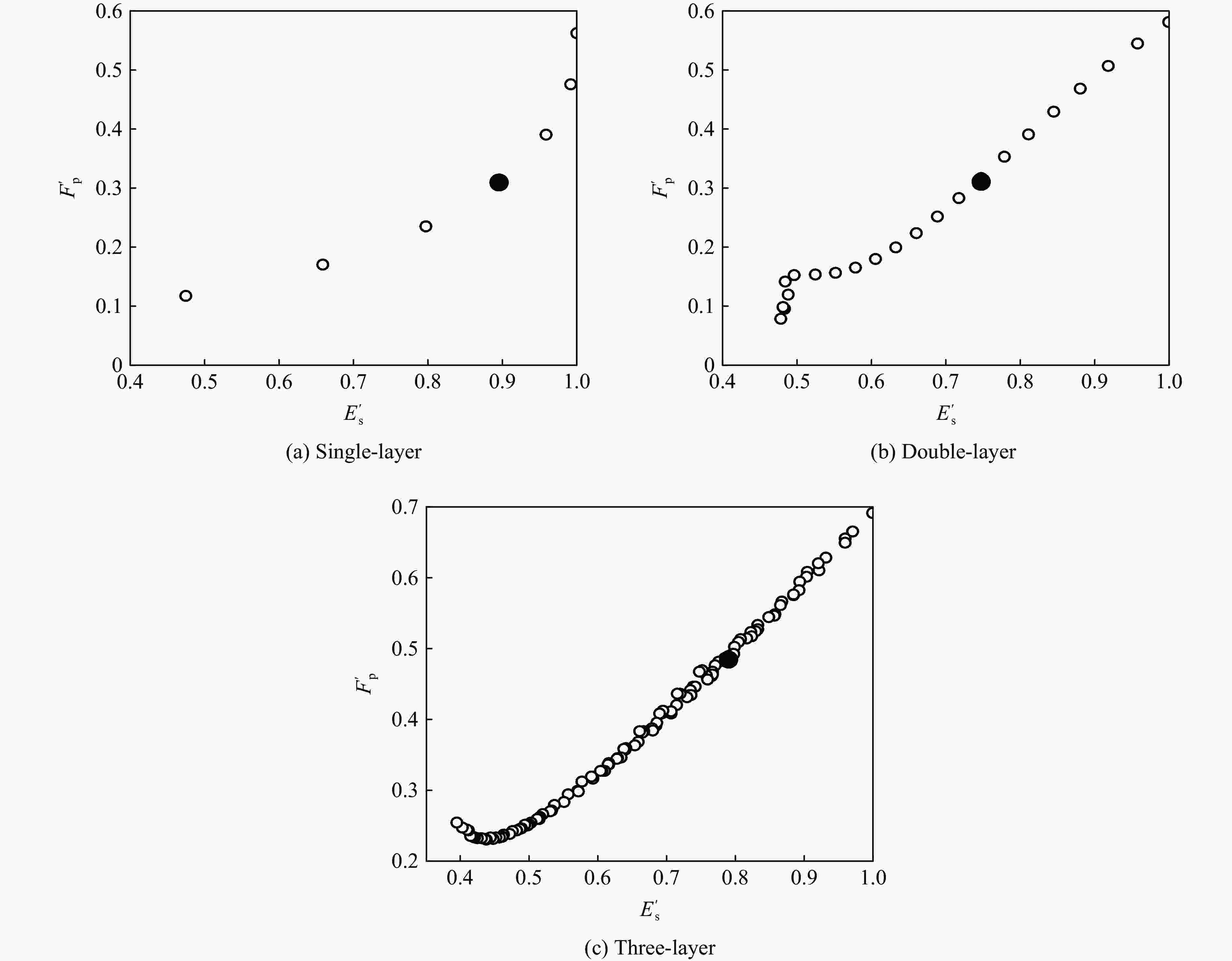
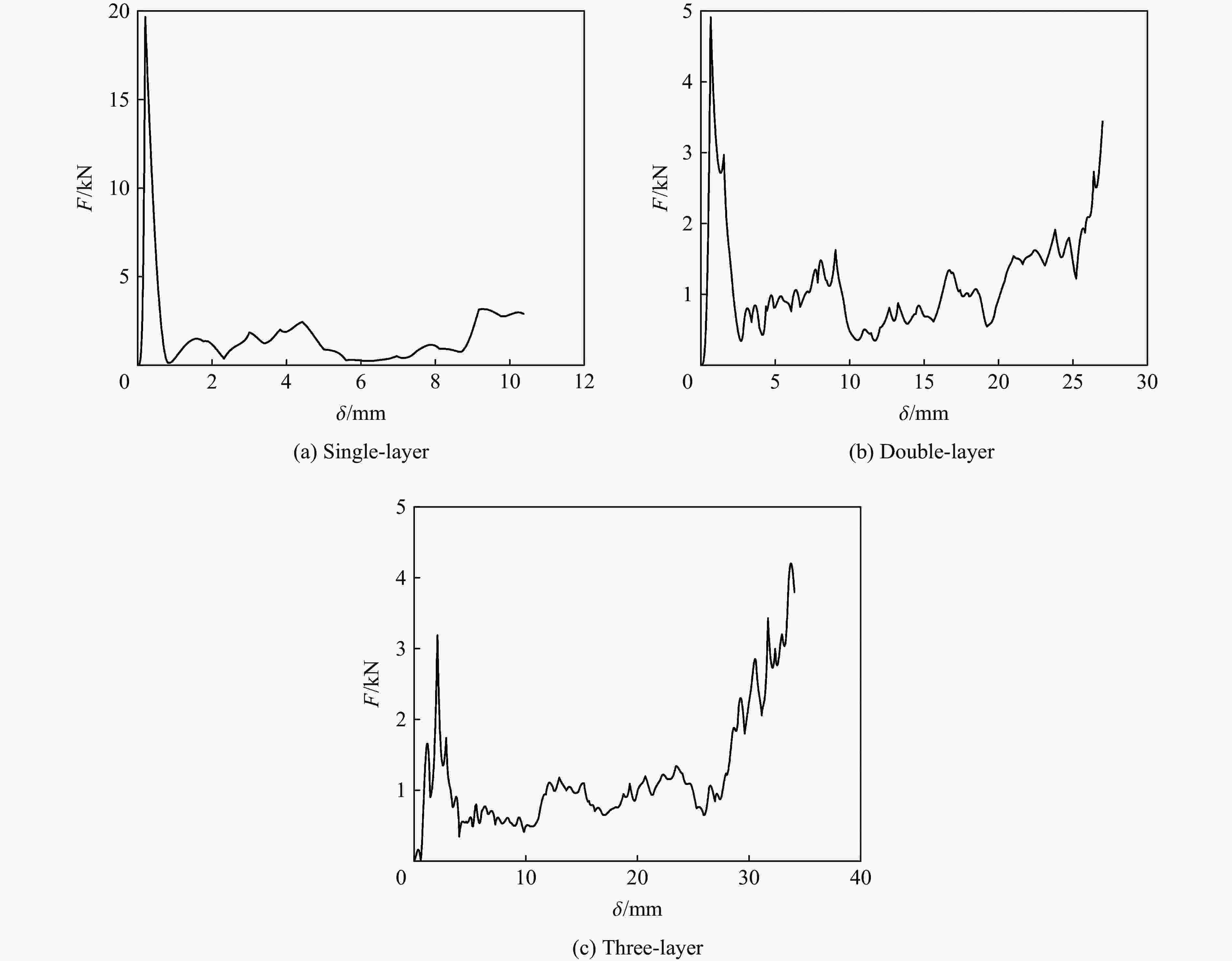
摘要: 为提高薄壁夹层结构耐撞性，以虾螯为仿生原型，设计梯度分布的仿生波纹形夹层结构，包括单层、双层和三层波纹结构。以初始峰值载荷F_p、比吸能E_s为耐撞性指标，利用有限元法分析了单元高宽比γ（γ₁、γ₂和γ₃分别为单元第1层、第2层和第3层的高宽比）对波纹夹层结构耐撞性的影响，采用多目标粒子群优化方法得到了夹层结构最优参数。结果表明，单层波纹结构耐撞性随单元高宽比γ的增大逐渐变差，双层波纹结构下层结构单元高宽比γ对耐撞性的影响大于上层结构单元高宽比γ对耐撞性的影响，较小的γ值有利于提高三层波纹结构的比吸能。结构优化结果表明：单层结构最优尺寸γ₁为0.8；双层结构最优尺寸为γ₁ = 0.5和γ₂ = 1.2；三层结构最优组合为γ₁ = 0.6，γ₂ = 0.6和γ₃ = 0.9。上述结果可为薄壁夹层结构轻量化设计提供新思路。
- 薄壁夹层结构 /
- 耐撞性 /
- 结构优化 /
- 工程仿生 /
- 冲击
Abstract: To improve the crashworthiness of thin-walled sandwich structures, a series of bionic corrugated sandwich structures with triangular elements (the height-to-width ratios of the elements are defined as γ) were designed inspired by the structures of shrimp chelas, including single-layer, double-layer and three-layer corrugated sandwich structures (γ₁, γ₂ and γ₃ denotes the height-to-width ratios of single-layer, double-layer and three-layer elements, respectively). To analyze the deformation and mechanical response of the bionic thin-walled structures, the finite element method was adopted based on LS-DYNA and HyperMesh. By taking the initial peak load F_p and specific energy absorption E_s as crashworthiness indexes, the influences of γ on the crashworthiness of the corrugated sandwich structures were discussed. The crashworthiness of the single-layer sandwich structures becomes worse gradually when the parameters γ exceed a certain value. For the double-layer sandwich structures, the influences of the parameters γ₂ in the lower layers on the crashworthiness is greater than that of the parameters γ₁ in the upper layers.. The F_p decreases by 37.8% with the increase of γ₂, which means the greater γ₂ of the lower layer is beneficial to improve the crashworthiness of the structure. For the three-layer sandwich structures, the influence of γ on crashworthiness indexes was investigated by range and variance analysis methods. The results show that the γ₃ has the most significant influence on E_s, and the significance level reaches 0.1. Finally, the optimal parameters of the bionic corrugated sandwich structures were obtained by using the multi-objective particle swarm optimization method based on a polynomial regression (PR) meta model. The optimal results show that the crashworthiness of the single-layer corrugated sandwich structures improves with the increase of γ. For the double-layer corrugated sandwich structures, The γ of the lower layer affects the crashworthiness more significantly than the γ of the upper layer. The three-layer corrugated sandwich structure with lower γ has higher E_s. The optimal dimensions of the single-layer, double-layer and three-layer structures are γ = 0.8; γ₁ = 0.5 and γ₂ = 1.2; γ₁ = 0.6, γ₂ = 0.6 and γ₃ = 0.9, respectively. The above results are helpful for the design of the thin-walled sandwich structures.
- thin-walled sandwich structure /
- crashworthiness /
- structure optimization /
- engineering bionics /
- impact

HTML全文

图 1 雀尾螳螂虾及其虾螯宏微观结构

Figure 1. Odontodactylus scyllarus and macro-micro structure of shrimp chela

下载: 全尺寸图片幻灯片

图 2 仿生波纹夹层结构（3层）

Figure 2. Bionic corrugated-core sandwich structure (three layers)

下载: 全尺寸图片幻灯片

图 3 仿生波纹夹层结构有限元模型

Figure 3. A finite element model for the bionic corrugated-core sandwich structure

下载: 全尺寸图片幻灯片

图 4 单层波纹结构峰值载荷和比吸能随高宽比变化关系

Figure 4. The initial peak load and specific energy absorption of single-layer structure versus with height-to-width ratios

下载: 全尺寸图片幻灯片

图 5 单层波纹结构变形

Figure 5. Deformation of single-layer structures

下载: 全尺寸图片幻灯片

图 6 双层波纹结构峰值载荷和比吸能随高宽比变化关系

Figure 6. The initial peak load and specific energy absorption of double-layer structure versus with height-to-width ratios

下载: 全尺寸图片幻灯片

图 7 不同结构的峰值载荷和比吸能模型预测值变化

Figure 7. The initial peak load and specific energy absorption predicted by the models for different structures

下载: 全尺寸图片幻灯片

图 8 优化结果粒子群边界

Figure 8. Particle swarm boundaries of optimization results

下载: 全尺寸图片幻灯片

图 9 最优结果验证

Figure 9. Validation for optimization results

下载: 全尺寸图片幻灯片

表 1 三层波纹结构耐撞性仿真结果

Table 1. Simulated crashworthiness of three-layer sandwich structures

试验号	γ₁	γ₂	γ₃	F_p/kN	E_s/（kJ·kg⁻¹）
1	0.5	0.5	0.5	3.88	0.65
2	0.5	1.0	1.0	1.99	0.38
3	0.5	1.5	1.5	2.01	0.32
4	0.5	2.0	2.0	3.06	0.29
5	1.0	0.5	2.0	1.90	0.29
6	1.0	1.0	1.5	1.56	0.35
7	1.0	1.5	1.0	1.53	0.31
8	1.0	2.0	0.5	1.72	0.28
9	1.5	0.5	1.0	3.10	0.39
10	1.5	1.0	0.5	3.46	0.40
11	1.5	1.5	2.0	1.65	0.24
12	1.5	2.0	1.5	1.64	0.26
13	2.0	0.5	1.5	3.25	0.28
14	2.0	1.0	2.0	3.58	0.28
15	2.0	1.5	0.5	3.73	0.34
16	2.0	2.0	1.0	3.58	0.28

下载: 导出CSV

表 2 极差分析结果

Table 2. Results of range analysis

参数	F_p/kN			E_s/（kJ·kg⁻¹）
参数	γ₁	γ₂	γ₃	γ₁	γ₂	γ₃
${\bar y_{j1}}$	2.732	3.031	3.196	0.410	0.400	0.415
${\bar y_{j2}}$	1.678	2.645	2.548	0.305	0.350	0.341
${\bar y_{j3}}$	2.462	2.233	2.116	0.321	0.302	0.300
${\bar y_{j4}}$	3.536	2.499	2.548	0.293	0.277	0.273
R_j	1.858	0.798	1.080	0.117	0.123	0.142

下载: 导出CSV

表 3 方差分析结果

Table 3. Results of variance analysis

因素	F_p		E_s
因素	P_j	显著性水平α	P_j	显著性水平α
γ₁	8.29	0.05	2.57	0.25
γ₂	1.57	＞0.25	2.69	0.25
γ₃	2.80	0.25	3.5	0.1

下载: 导出CSV

表 4 模型误差分析

Table 4. Error analysis of the model

波纹结构	F_p		E_s
波纹结构	ε_e/%	ζ/kN	ε_e /%	ζ/（kJ·kg⁻¹）
单层	7.87	1.94	4.68	0.0372
双层	10.27	0.67	0.71	0.0041
三层	8.07	0.25	3.67	0.0172

下载: 导出CSV

表 5 优化结果与验证

Table 5. Optimization results and validation

结构	γ₁	γ₂	γ₃	F_p /kN			E_s /（kJ·kg⁻¹）
结构	γ₁	γ₂	γ₃	预测值	实际值	误差 /%	预测值	实际值	误差 /%
单层	0.8	−	−	18.97	19.67	−3.56	0.78	0.86	−9.30
双层	0.5	1.2	−	4.42	4.91	−9.98	0.54	0.56	−3.57
三层	0.6	0.6	0.9	2.73	3.03	−9.90	0.50	0.46	8.70

下载: 导出CSV

参考文献(20)

[1]	周晓松, 梅志远, 张焱冰. 复合材料夹层结构在舰艇碰撞防护中的研究进展 [J]. 爆炸与冲击, 2018, 38(3): 696–706. DOI: 10.11883/bzycj-2016-0303. ZHOU X S, MEI Z Y, ZHANG Y B. Research progress of composite sandwich structure in ship collision protection [J]. Explosion and Shock Waves, 2018, 38(3): 696–706. DOI: 10.11883/bzycj-2016-0303.
[2]	张振华, 钱海峰, 王媛欣, 等. 球头落锤冲击下金字塔点阵夹芯板结构的动态响应实验 [J]. 爆炸与冲击, 2015, 35(6): 888–894. DOI: 10.11883/1001-1455(2015)06-0888-07. ZHANG Z H, QIAN H F, WANG Y X, et al. Experiment of dynamic response of multilayered pyramidal lattices during ball hammer collision loading [J]. Explosion and Shock Waves, 2015, 35(6): 888–894. DOI: 10.11883/1001-1455(2015)06-0888-07.
[3]	邓泽华, 郭锐, 周昊, 等. 梯度波纹夹层防护结构超高速碰撞特性仿真研究 [J]. 航天器环境工程, 2018, 35(1): 7–13. DOI: 10.3969/j.issn.1673-1379.2018.01.002. DENG Z H, GUO R, ZHOU H, et al. Simulation of hypervelocity impact characteristics of gradient corrugated-core sandwich plates [J]. Spacecraft Environment Engineering, 2018, 35(1): 7–13. DOI: 10.3969/j.issn.1673-1379.2018.01.002.
[4]	潘晋, 黄义飞, 徐荣康, 等. 波纹夹层结构耐撞性影响因素分析 [J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(2): 192–197. DOI: 10.3963/j.issn.2095-3844.2019.02.003. PAN J, HUANG Y F, XU R K, et al. Analysis of influencing factors on crashworthiness of corrugated sandwich structures [J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2019, 43(2): 192–197. DOI: 10.3963/j.issn.2095-3844.2019.02.003.
[5]	骆伟, 谢伟, 刘敬喜. 芯层几何构形对复合材料波纹夹层结构冲击特性的影响 [J]. 江苏科技大学学报(自然科学版), 2018, 32(1): 21–26. DOI: 10.3969/j.issn.1673-4807.2018.01.004. LUO W, XIE W, LIU J X. Research on dynamic characteristics of a sandwich structures with various core shapes under impact loads [J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2018, 32(1): 21–26. DOI: 10.3969/j.issn.1673-4807.2018.01.004.
[6]	HE W T, LIU J X, TAO B, et al. Experimental and numerical research on the low velocity impact behavior of hybrid corrugated core sandwich structures [J]. Composite Structures, 2016, 158: 30–43. DOI: 10.1016/j.compstruct.2016.09.009.
[7]	LIU J X, HE W T, XIE D, et al. The effect of impactor shape on the low-velocity impact behavior of hybrid corrugated core sandwich structures [J]. Composites Part B: Engineering, 2017, 111: 315–331. DOI: 10.1016/J.COMPOSITESB.2016.11.060.
[8]	HE W T, LIU J X, WANG S Q, et al. Low-velocity impact response and post-impact flexural behaviour of composite sandwich structures with corrugated cores [J]. Composite Structures, 2018, 189: 37–53. DOI: 10.1016/j.compstruct.2018.01.024.
[9]	杨欣, 范晓文, 许述财, 等. 仿虾螯结构薄壁管设计及耐撞性分析 [J]. 爆炸与冲击, 2020, 40(4): 043301. DOI: 10.11883/bzycj-2019-0280. YANG X, FAN X W, XU S C, et al. Design and crashworthiness analysis of thin-walled tubes based on a shrimp chela structure [J]. Explosion and Shock Waves, 2020, 40(4): 043301. DOI: 10.11883/bzycj-2019-0280.
[10]	秦诗牧, 秦俊奇, 杨玉良, 等. 枪虾夹螯的结构特性、运动特性与射流聚焦机理研究 [J]. 振动与冲击, 2019, 38(21): 202–209. DOI: 10.13465/j.cnki.jvs.2019.21.028. QIN S M, QIN J Q, YANG Y L, et al. Structure and motion characteristics as well as jet focusing mechanism of snapping shrimp claw [J]. Journal of Vibration and Shock, 2019, 38(21): 202–209. DOI: 10.13465/j.cnki.jvs.2019.21.028.
[11]	郭婷, 王跃方. 仿甲壳虫芯柱的缓冲吸能结构 [J]. 工程力学, 2011, 28(2): 246–251, 256. GUO T, WANG Y F. Energy absorbing structures imitating trabecular of beetle cuticles [J]. Engineering Mechanics, 2011, 28(2): 246–251, 256.
[12]	ZHANG X M, XIE J, CHEN J X, et al. The beetle elytron plate: a lightweight, high-strength and buffering functional-structural bionic material [J]. Scientific Reports, 2017, 7(1): 4440. DOI: 10.1038/s41598-017-03767-w.
[13]	YANG X F, MA J X, SHI Y L, et al. Crashworthiness investigation of the bio-inspired bi-directionally corrugated core sandwich panel under quasi-static crushing load [J]. Materials & Design, 2017, 135: 275–290. DOI: 10.1016/j.matdes.2017.09.040.
[14]	PATEK S N, KORFF W L, CALDWELL R L. Biomechanics: deadly strike mechanism of a mantis shrimp [J]. Nature, 2004, 428(6985): 819–820. DOI: 10.1038/428819a.
[15]	PATEK S N, CALDWELL R L. Extreme impact and cavitation forces of a biological hammer: strike forces of the peacock mantis shrimp Odontodactylus scyllarus [J]. Journal of Experimental Biology, 2005, 208(19): 3655–3664. DOI: 10.1242/jeb.01831.
[16]	WEAVER J C, MILLIRON G W, MISEREZ A, et al. The stomatopod dactyl club: a formidable damage-tolerant biological hammer [J]. Science, 2012, 336(6086): 1275–1280. DOI: 10.1126/science.1218764.
[17]	CLAVERIE T, CHAN E, PATEK S N. Modularity and scaling in fast movements: power amplification in mantis shrimp [J]. Evolution: International Journal of Organic Evolution, 2011, 65(2): 443–461. DOI: 10.1111/j.1558-5646.2010.01133.x.
[18]	QIU N, GAO Y K, FANG J G, et al. Crashworthiness analysis and design of multi-cell hexagonal columns under multiple loading cases [J]. Finite Elements in Analysis and Design, 2015, 104: 89–101. DOI: 10.1016/j.finel.2015.06.004.
[19]	HUANG H, XU S C. Crashworthiness analysis and bionic design of multi-cell tubes under axial and oblique impact loads [J]. Thin-Walled Structures, 2019, 144: 106333. DOI: 10.1016/J.TWS.2019.106333.
[20]	BARAKAT S, BANI-HANI K, TAHA M Q, et al. Multi-objective reliability-based optimization of prestressed concrete beams [J]. Structural Safety, 2004, 26(3): 311–342. DOI: 10.1016/j.strusafe.2003.09.001.