弹性楔形体入水砰击载荷及结构响应的理论计算与数值模拟研究

王一雯; 郑成; 吴卫国

doi:10.11883/bzycj-2020-0276

弹性楔形体入水砰击载荷及结构响应的理论计算与数值模拟研究

doi: 10.11883/bzycj-2020-0276

武汉理工大学绿色智能江海直达船舶与邮轮游艇研究中心，湖北武汉 430063

基金项目: 高技术船舶科研项目（2014[493]）；基础加强计划重点基础研究（2020-JCJQ-ZD-225-11）

详细信息

作者简介:
王一雯（1990－　），女，博士，讲师， yiwenwang90@whut.edu.cn

通讯作者:
郑　成（1991－　），男，博士，讲师，zhengchengyeep@whut.edu.cn

中图分类号: O352
计量
- 文章访问数: 460
- HTML全文浏览量: 368
- PDF下载量: 69
- 被引次数: 0
出版历程
- 收稿日期: 2020-08-12
- 修回日期: 2021-08-10
- 网络出版日期: 2021-11-01
- 刊出日期: 2021-11-23

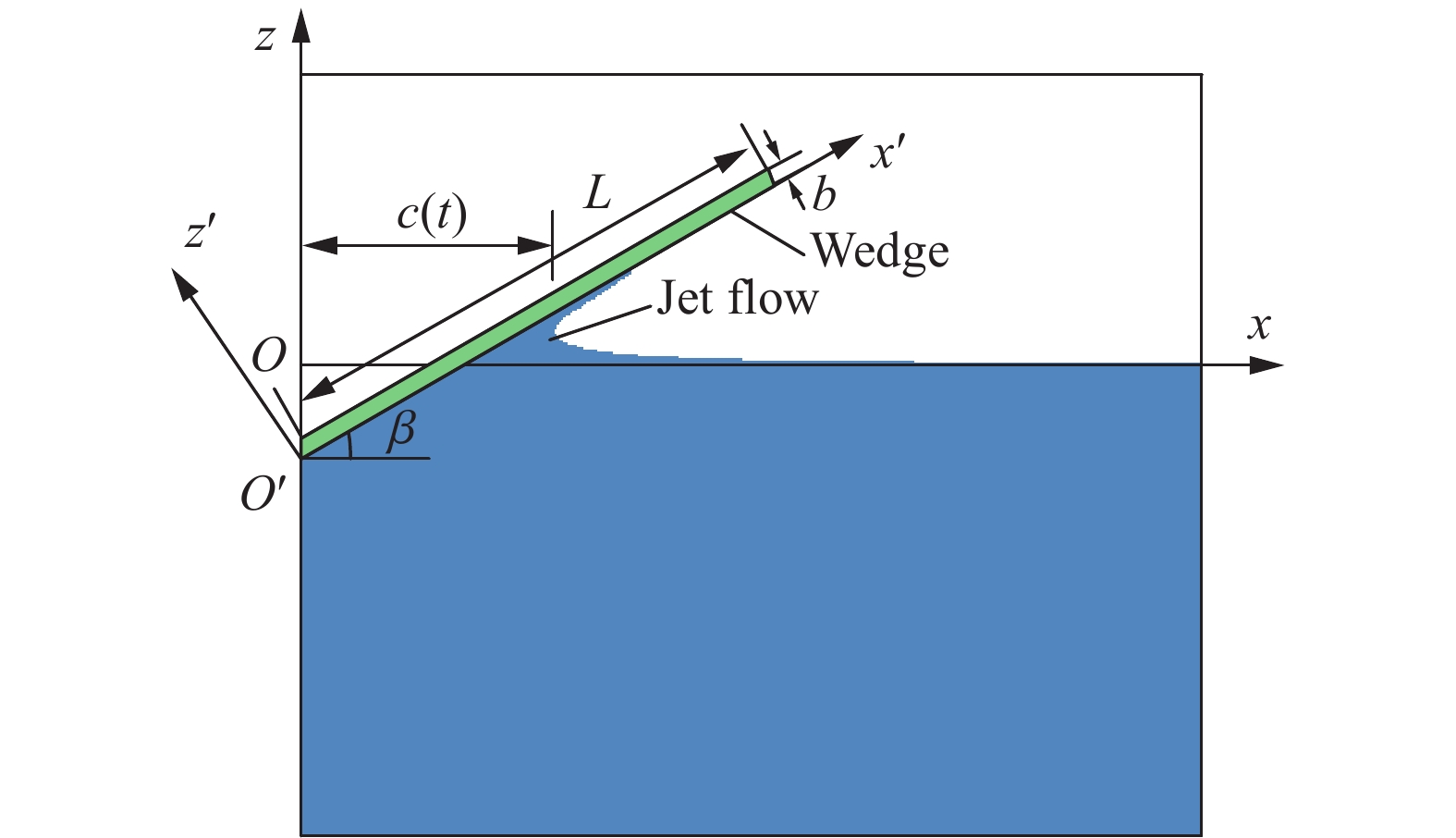
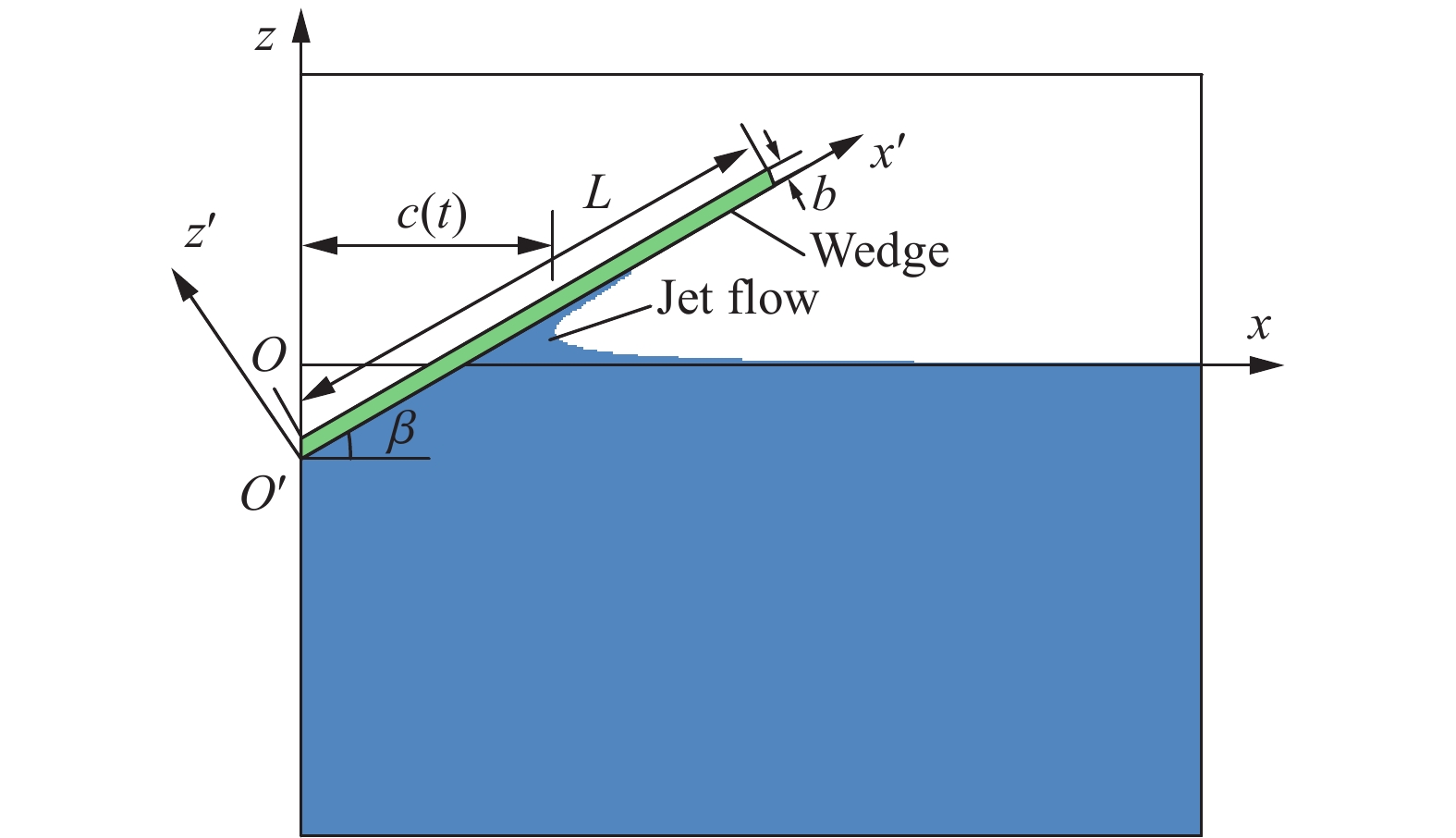
On slamming load and structural response of a flexible wedge via analytical methods and numerical simulations

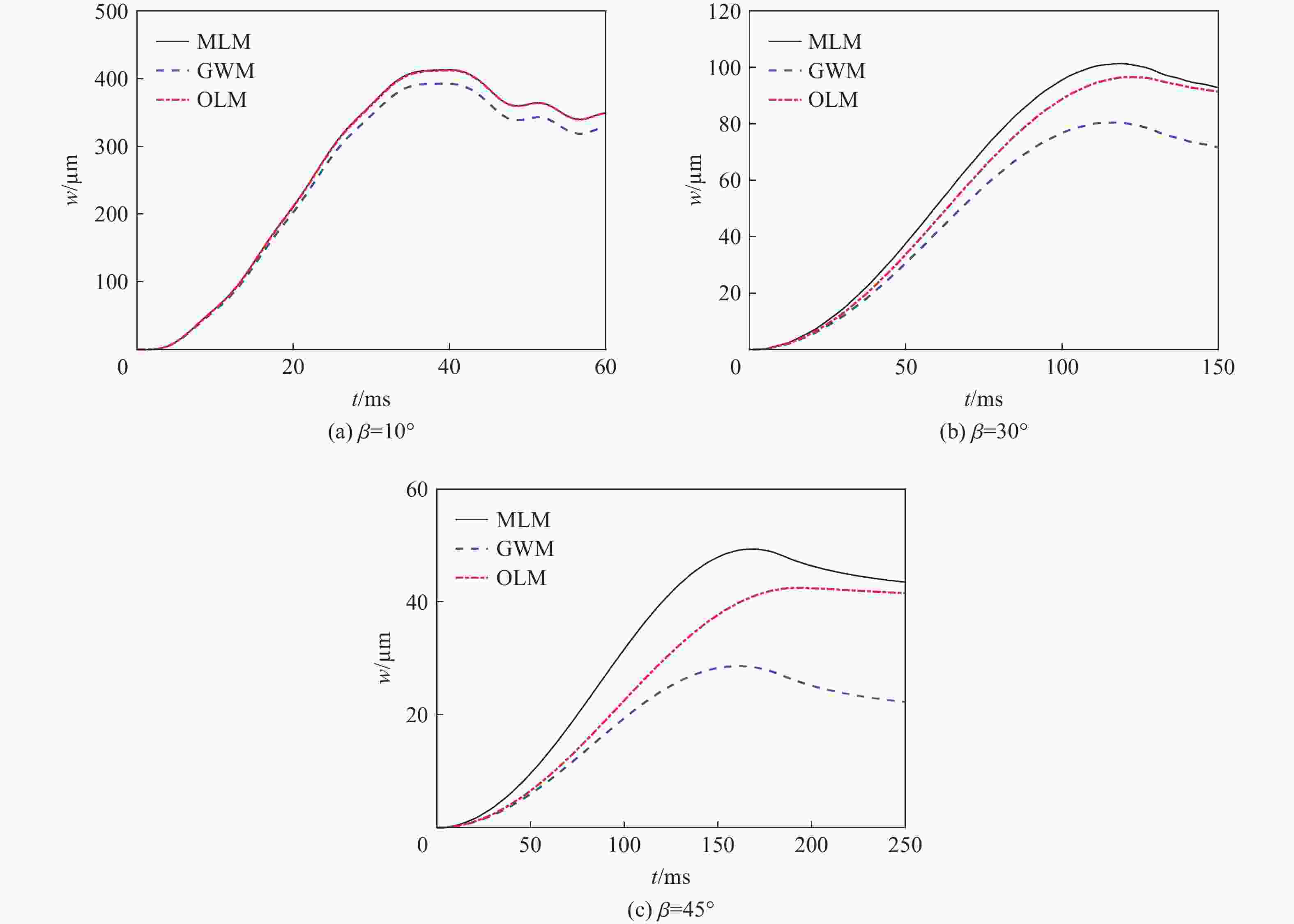
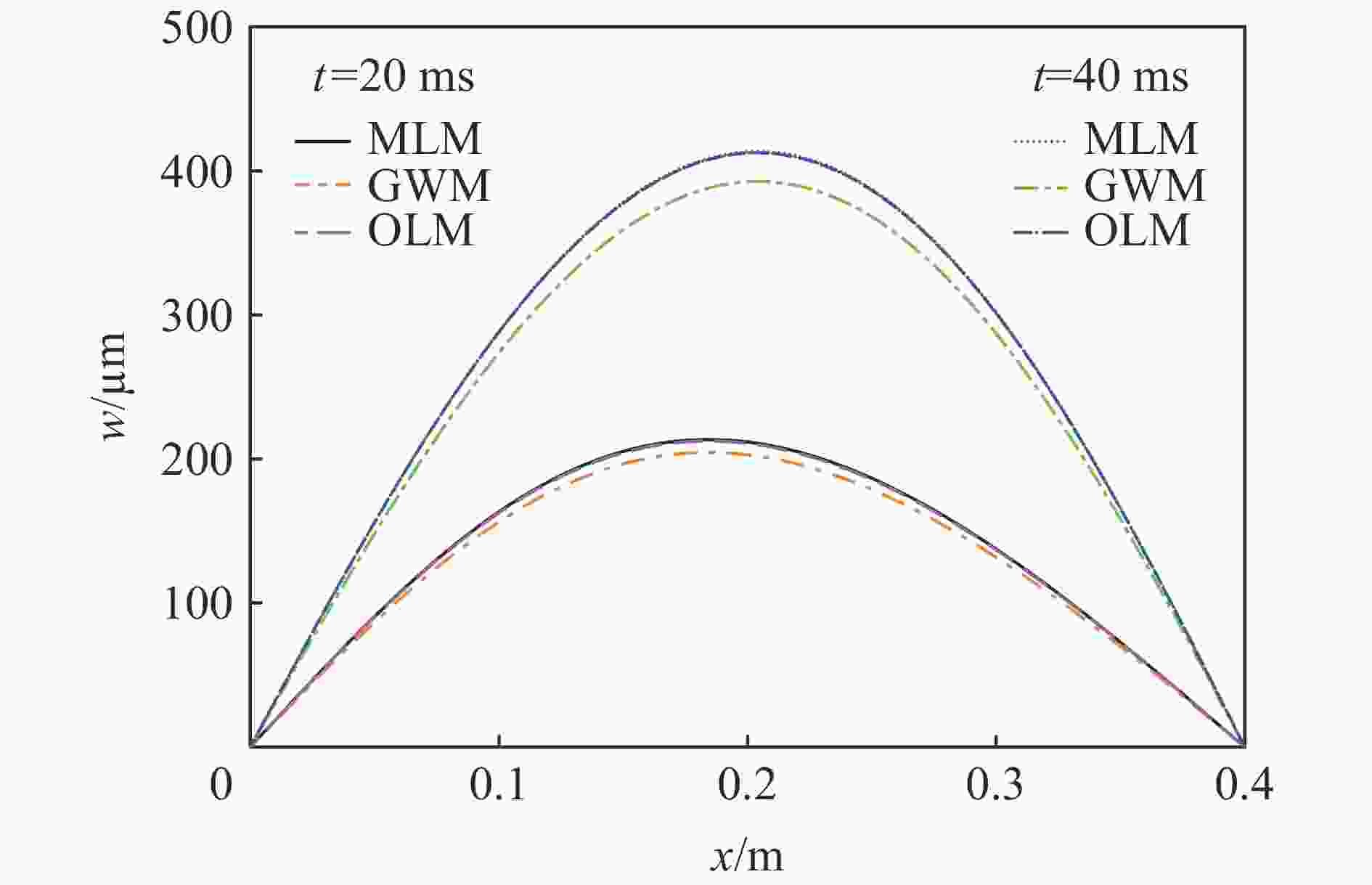
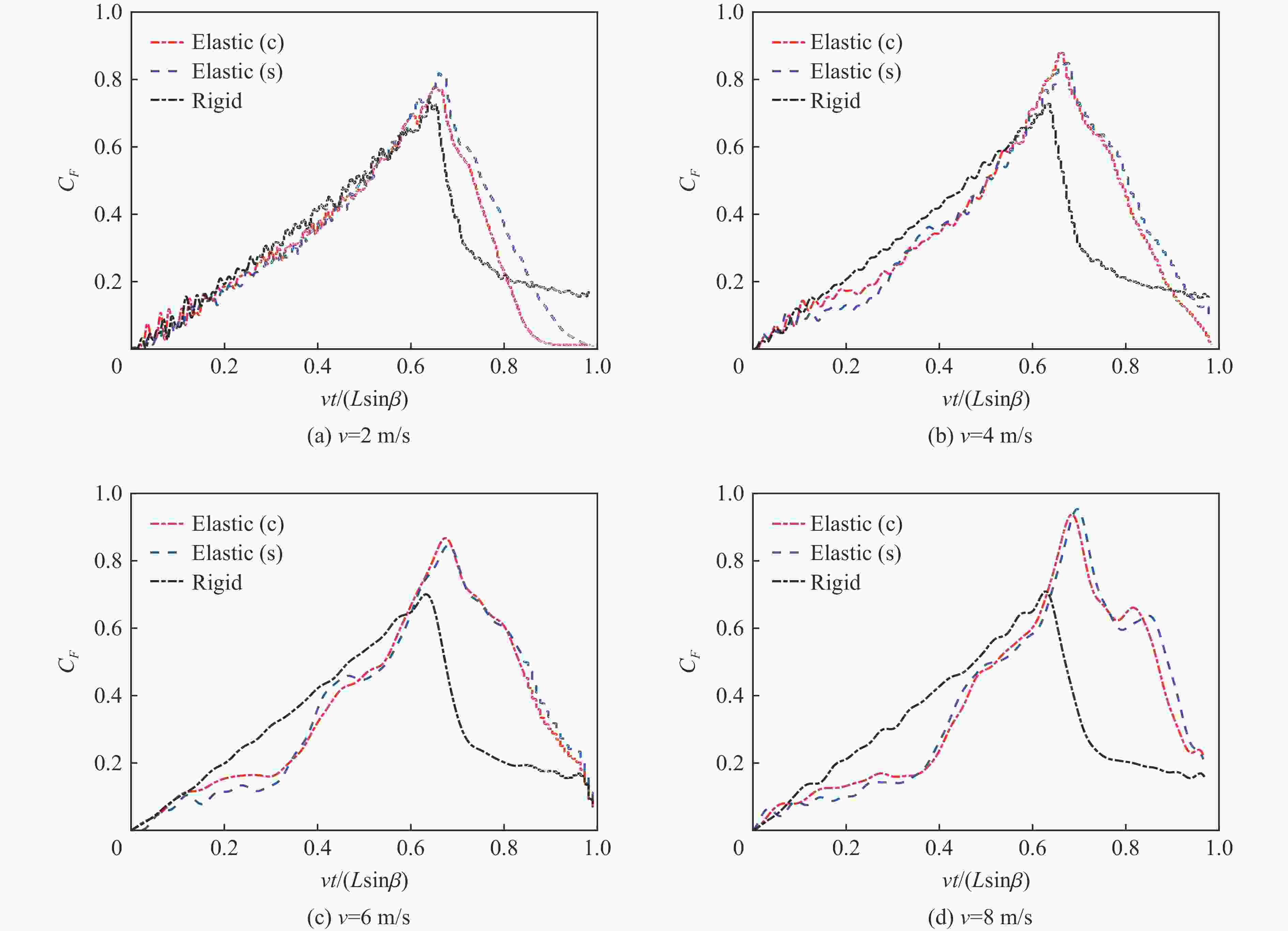
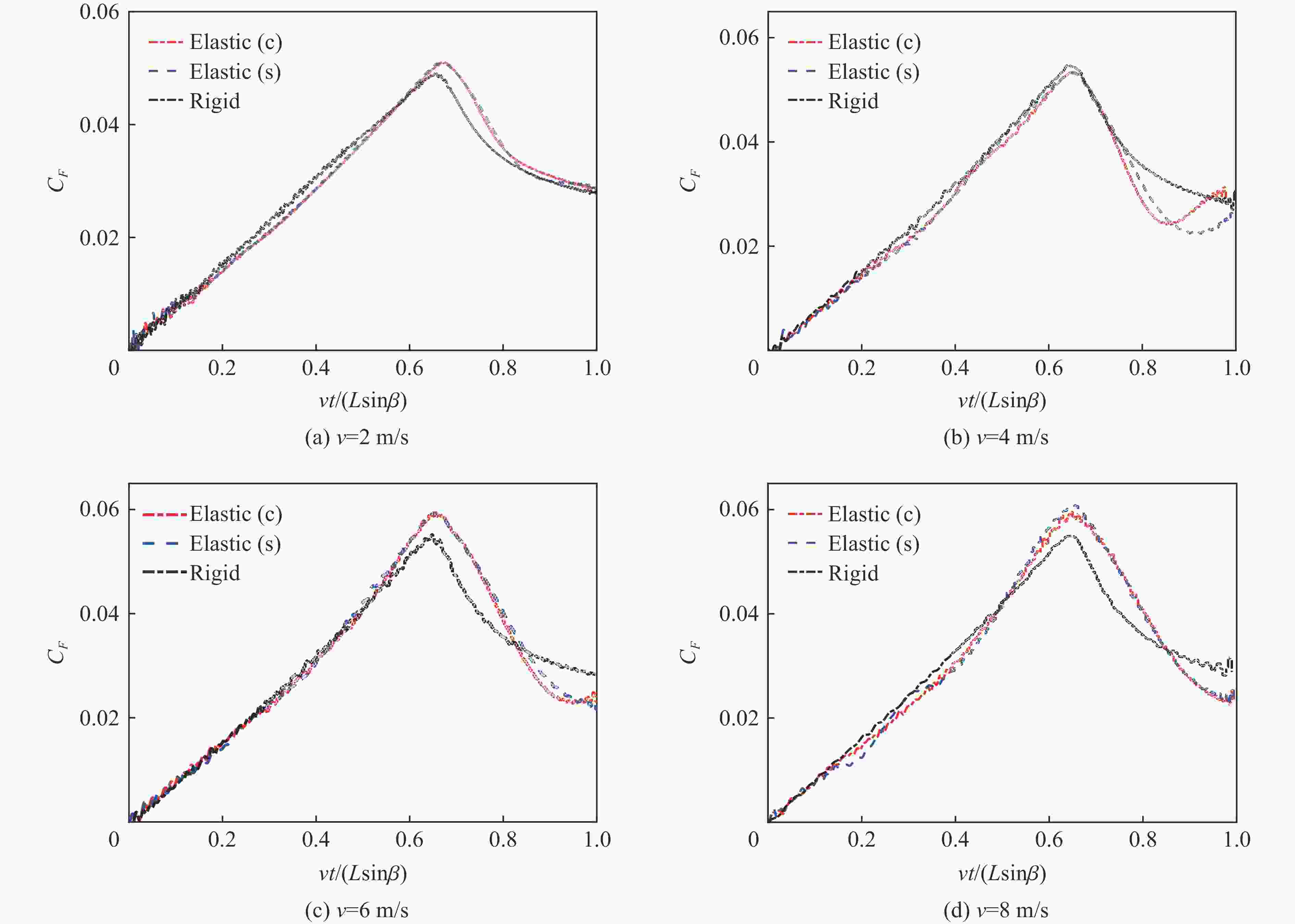
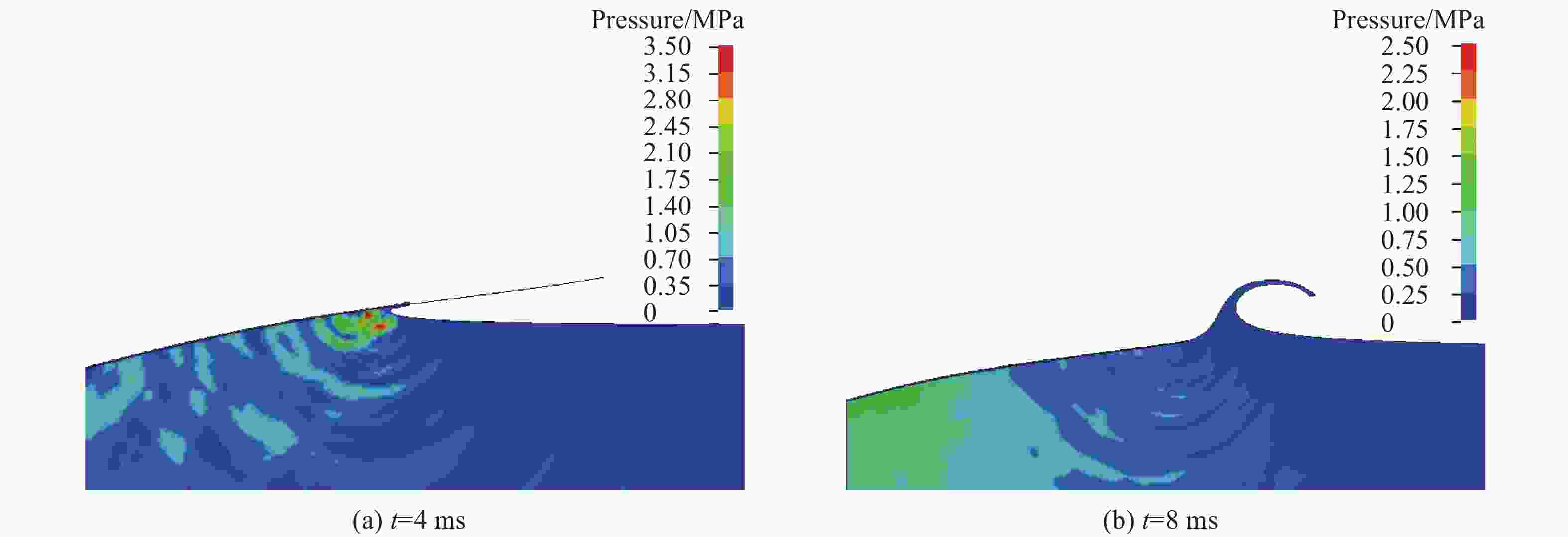
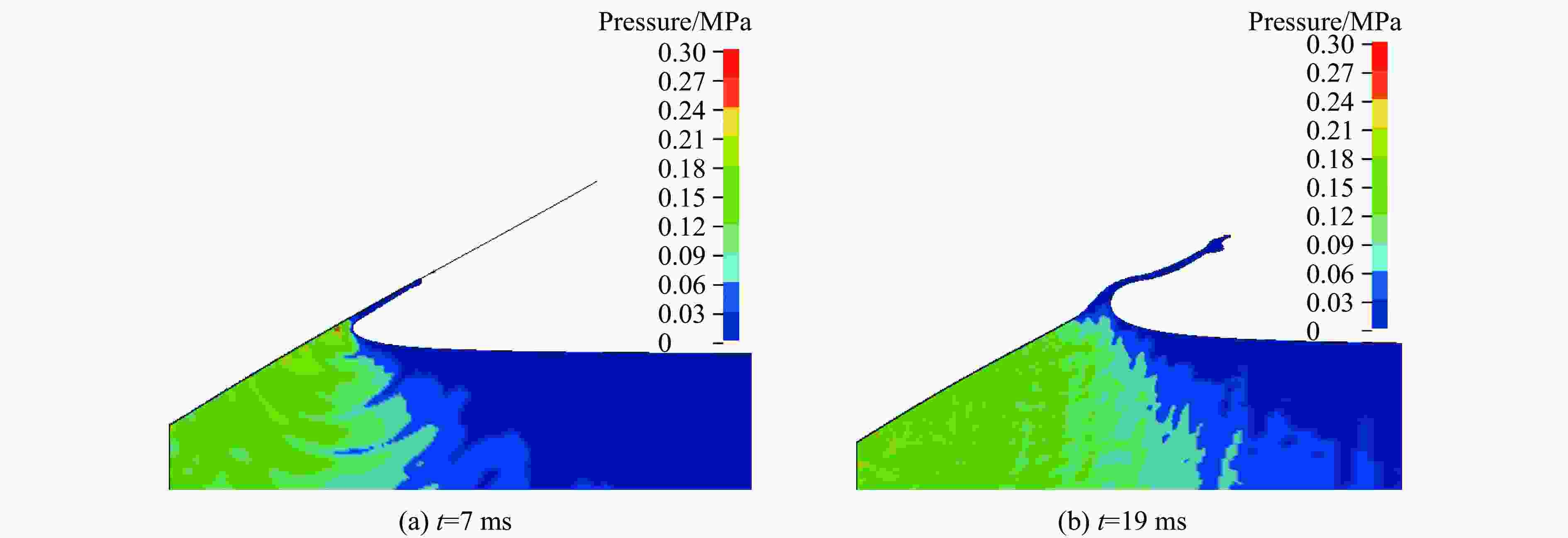
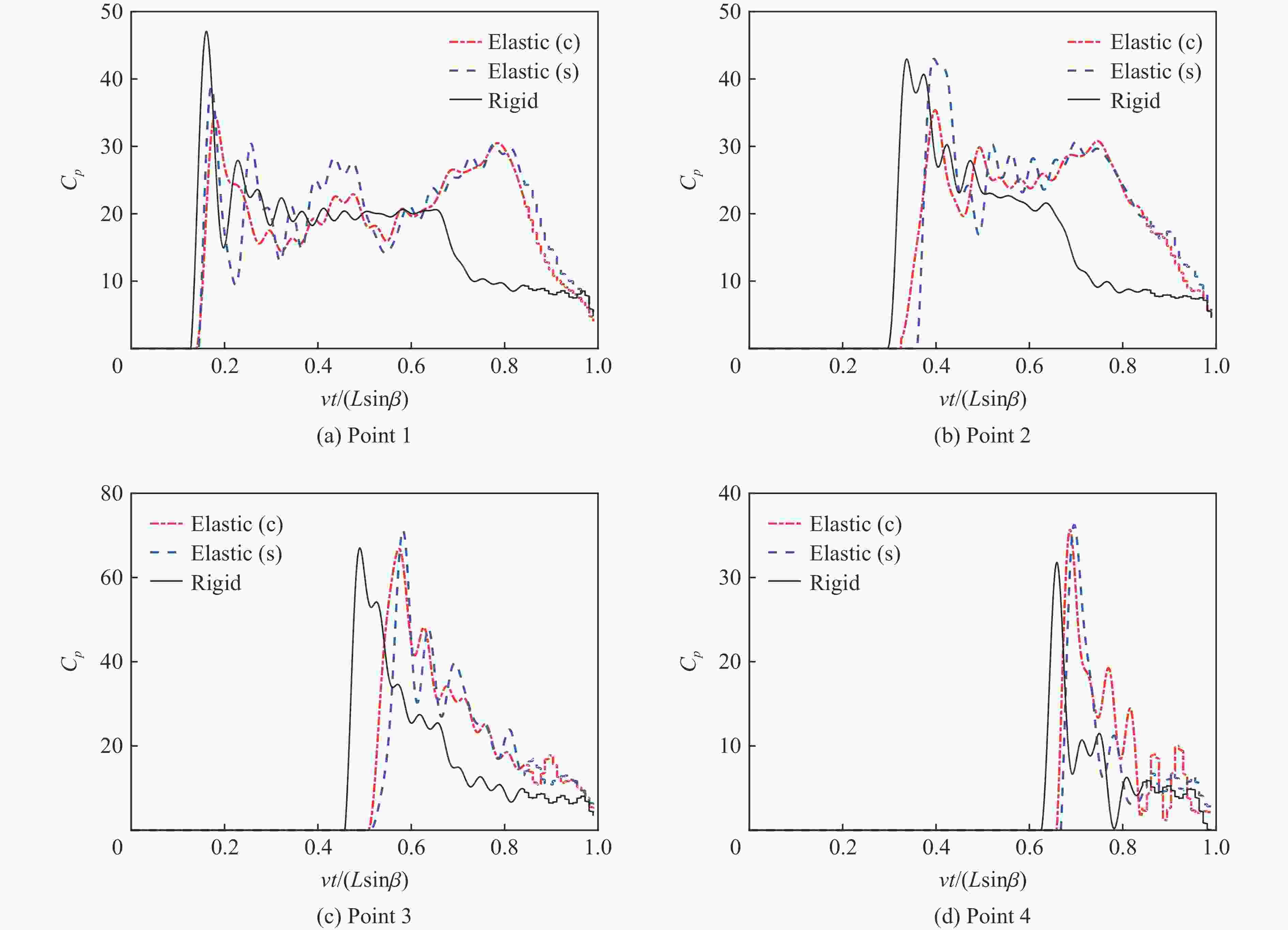
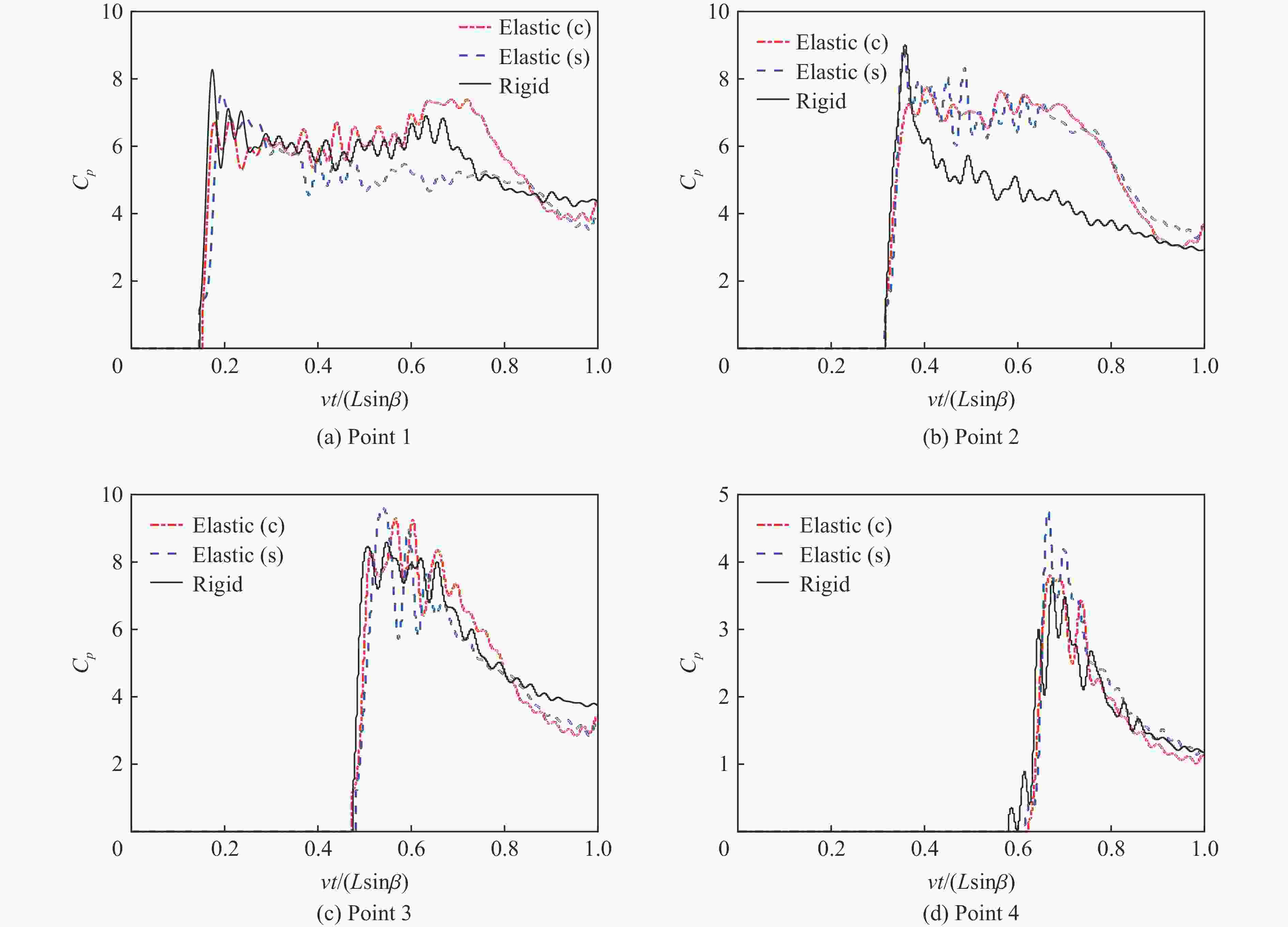
Green & Smart River-Sea-Going Ship, Cruise and Yacht Research Center, Wuhan University of Technology, Wuhan 430063, Hubei, China

摘要

摘要: 针对弹性楔形体砰击载荷及结构响应问题，采用理论解析计算方法以及任意拉格朗日-欧拉(arbitrary Lagrangian-Eulerian, ALE)流固耦合数值计算方法开展研究。分别分析不同边界条件、入水速度、板厚以及斜升角对弹性结构所受砰击力及结构响应的影响及变化规律，并探讨砰击载荷时间历程和物面分布特性。结果表明，通过增大斜升角可有效降低弹性楔形体砰击载荷和结构响应，斜升角自10°增大至30°，无量纲砰击力峰值减小至6.9%，结构变形极值减小至6.5%。可通过水弹性因数${ {R_{\text{F}}} = {C_{\text{B}}}\tan \beta \sqrt {EI/(\rho {L^3})} /v }$评估板厚、入水速度、斜升角以及边界条件对砰击载荷作用下结构水弹性效应的影响，在水弹性因数R_F＞1.71时，可采用理论解析方法高效高精度预报砰击载荷作用下弹性楔形体结构变形响应。
- 水弹性效应 /
- 弹性楔形体 /
- 砰击入水 /
- 流固耦合
Abstract: The slamming load and structural response of flexible wedges were investigated by both analytical methods and numerical simulations based on the ALE (arbitrary Lagrangian-Eulerian) coupled method. The cases with various boundary conditions, impact velocities, thicknesses and deadrise angles were simulated and the corresponding slamming loads and the structural responses were discussed as well. The slamming load and the structural response are susceptible to the variation of the deadrise angle. To increase the deadrise angles is an effective way to ensure the structural strength concerning about the impact load. With the increase of the deadrise angle from 10º to 30º, the dimensionless slamming load decreased to 6.9% and the structural response decreased to 6.5%. The hydroelastic effects of the response of the flexible structure under slamming load can be evaluated by the factor ${ {R_{\text{F}}} = {C_{\text{B}}}\tan \beta \sqrt {EI/(\rho {L^3})} /v }$ which combining with boundary condition, deadrise angle and rigidity of the structure. If the R_F＞1.71, the hydroelastic analytical method is an efficient and effective way to evaluate the response of the flexible structure under slamming load.
- hydroelastic effect /
- flexible wedge /
- water impact /
- fluid-structure interaction

HTML全文

图 1 弹性楔形体砰击载荷及结构响应示意图

Figure 1. Schematics of slamming load and structural response of a flexible wedge

下载: 全尺寸图片幻灯片

图 2 采用不同模型得到的板厚为8mm、以 1 m/s的速度垂直入水的弹性楔形体$ x' = 0.5L $处结构变形的时间历程

Figure 2. Time series of the structural response at $ x' = 0.5L $ of the flexible wedges with different deadrise angles and the plate thickness of 8 mm at the vertical water-entry velocity of 1 m/s calculated by different models

下载: 全尺寸图片幻灯片

图 3 t=20, 40 ms时沿弹性楔形体物面的结构变形分布（$ \ \beta $=10°, b=8 mm）

Figure 3. Response distribution along the wedge structure at t=20, 40 ms ($ \ \beta $=10°, b=8 mm)

下载: 全尺寸图片幻灯片

图 4 砰击入水计算模型

Figure 4. The water-entry impact computation model with mesh generation

下载: 全尺寸图片幻灯片

图 5 不同网格尺寸的楔形体模型所受结构砰击力

Figure 5. Comparison of slamming forces of wedge models with different mesh sizes

下载: 全尺寸图片幻灯片

图 6 刚性和弹性楔形体所受到的无量纲砰击力 (β=10°)

Figure 6. Dimensionless slamming forces on rigid and elastic wedges with β=10°

下载: 全尺寸图片幻灯片

图 7 刚性和弹性楔形体所受到的无量纲砰击力 (β=30°)

Figure 7. Dimensionless slamming forces on rigid and elastic wedges with β=30°

下载: 全尺寸图片幻灯片

图 8 10°斜升角弹性楔形体入水过程中自由液面变化及流场压力分布(v=8 m/s)

Figure 8. Fluid evolution and pressure distribution during the process of the elastic wedge with β=10° entering the water (v=8 m/s)

下载: 全尺寸图片幻灯片

图 9 30°斜升角弹性楔形体入水过程中自由液面变化及流场压力分布(v=8 m/s)

Figure 9. Fluid evolution and pressure distribution during the process of the elastic wedge with β=30° entering the water (v=8 m/s)

下载: 全尺寸图片幻灯片

图 10 刚性和弹性楔形体点1～4处的无量纲砰击压力-时间历程(β=10°，v=6 m/s)

Figure 10. Dimensionless slamming pressure-time history curves at points 1−4 of the rigid and elastic wedges (β=10°, v=6 m/s)

下载: 全尺寸图片幻灯片

图 11 刚性和弹性楔形体点1～4处的无量纲砰击压力时间历程($ \beta $=30°，v=6 m/s)

Figure 11. Dimensionless slamming pressure-time history curves at points 1−4 of the rigid and elastic wedges ($ \beta $=30°, v=6 m/s)

下载: 全尺寸图片幻灯片

图 12 不同板厚的楔形体x′ =0.5L处的结构变形 (β=30°)

Figure 12. Structural responses at x′=0.5L of the wedges with different thicknesses (β=30°)

下载: 全尺寸图片幻灯片

图 13 不同板厚的楔形体x′=0.5L处的结构变形(β=10°)

Figure 13. Structural responses at x′=0.5L of the wedges with different plate thickness (β=10°)

下载: 全尺寸图片幻灯片

图 14 不同板厚的楔形体x′=0.5L处的结构变形(β=45°)

Figure 14. Structural responses at x′=0.5L of the wedges with different plate thicknesses (β=45°)

下载: 全尺寸图片幻灯片

图 15 两端固支的不同板厚的弹性楔形体x′=0.5L处的结构变形(β=30°)

Figure 15. Structural responses at x′=0.5L of the clamped wedges with different plate thicknesses (β=30°)

下载: 全尺寸图片幻灯片

图 16 不同入水速度下两端简支楔形体的结构变形极值 (β=30°)

Figure 16. The maximum responses of the supported wedges at different impact velocities (β=30°)

下载: 全尺寸图片幻灯片

图 17 不同入水速度下两端固支楔形体的结构变形极值(β=30°)

Figure 17. The maximum responses of the clamped wedges at different impact velocities (β=30°)

下载: 全尺寸图片幻灯片

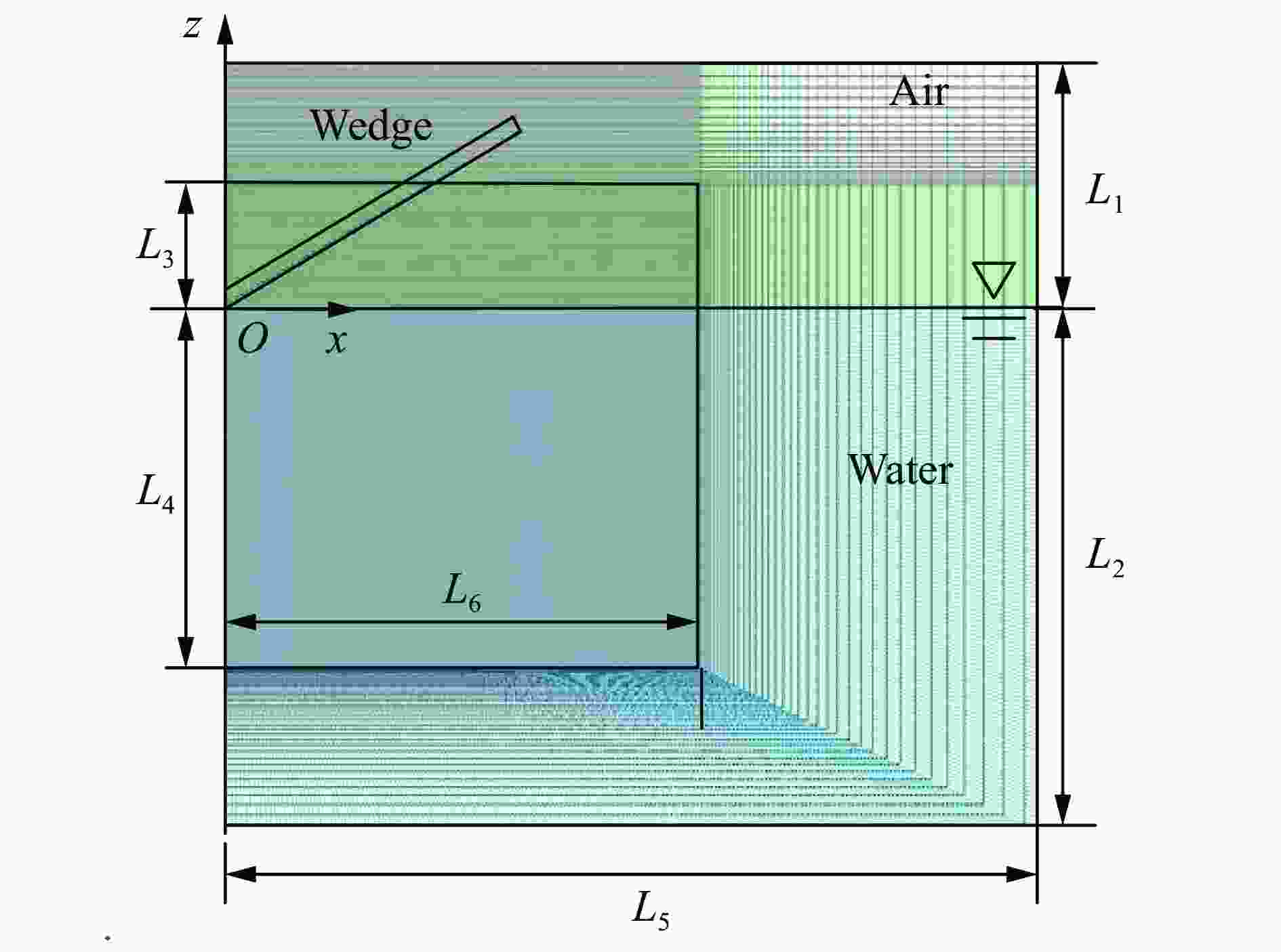
表 1 空气域及水域状态方程参数

Table 1. Parameters for equations of state of air and water

材料	ρ₀/（kg·m⁻³）	c/（m·s⁻¹）	C₄	C₅	S₁	S₂
空气	1.2	340	0.4	0.4
水	1 000	1 480			1.92	−0.096

下载: 导出CSV

表 2 不同网格尺寸模型信息

Table 2. Three models with different mesh sizes

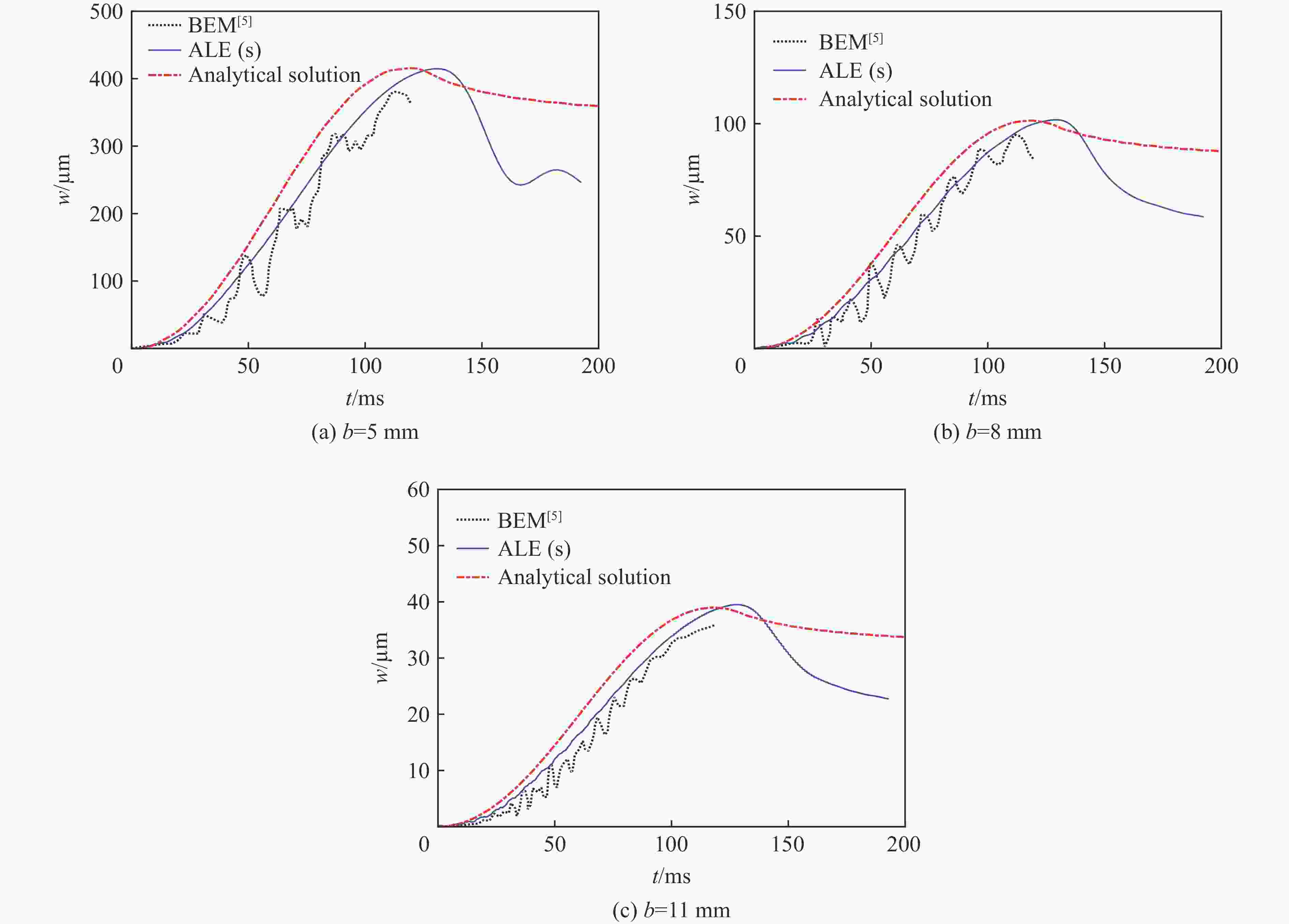
网格尺寸/mm	结构单元数量	流体单元数量	计算时长/min
4	100	24 000	57
2	200	55 800	440
1	400	223 500	5 142

下载: 导出CSV

表 3 两端简支的不同板厚的弹性楔形体$x' = 0.5L $处的结构变形峰值

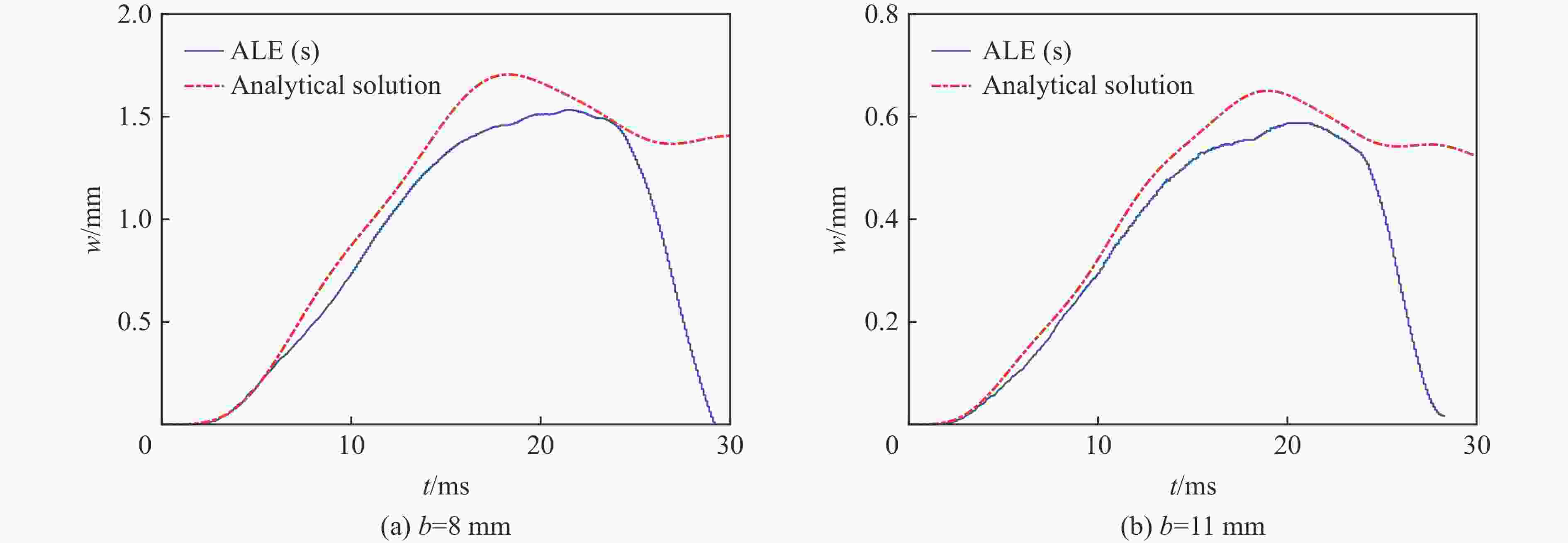
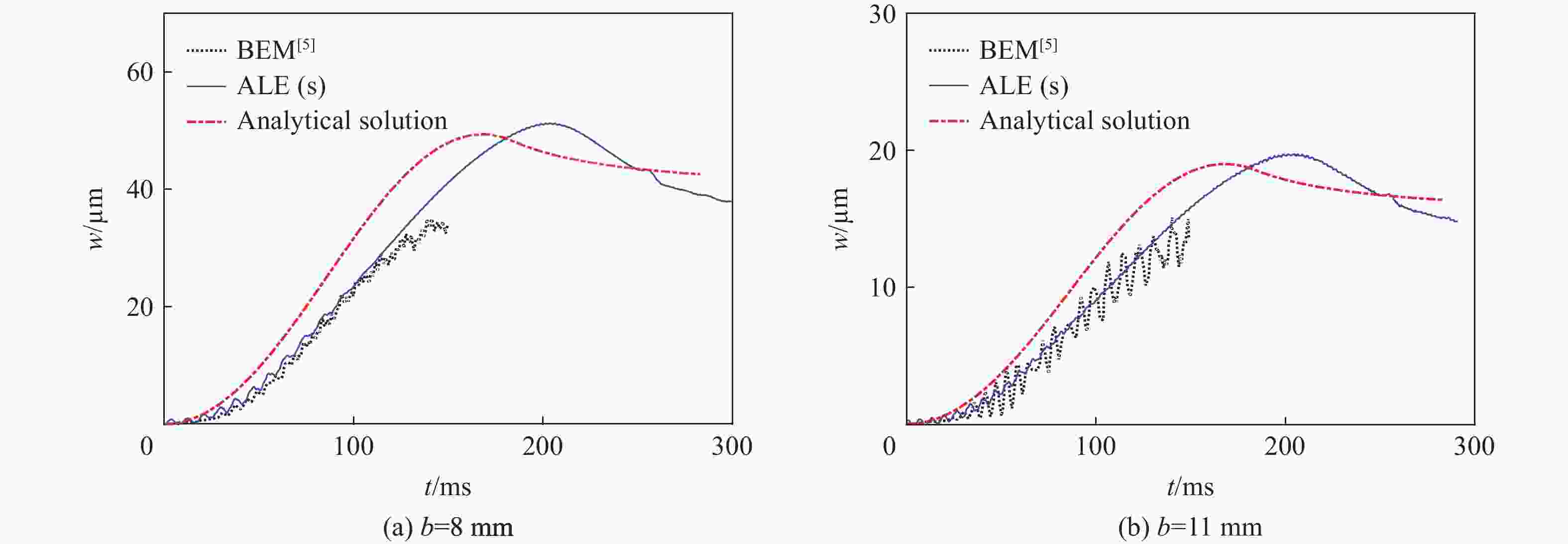
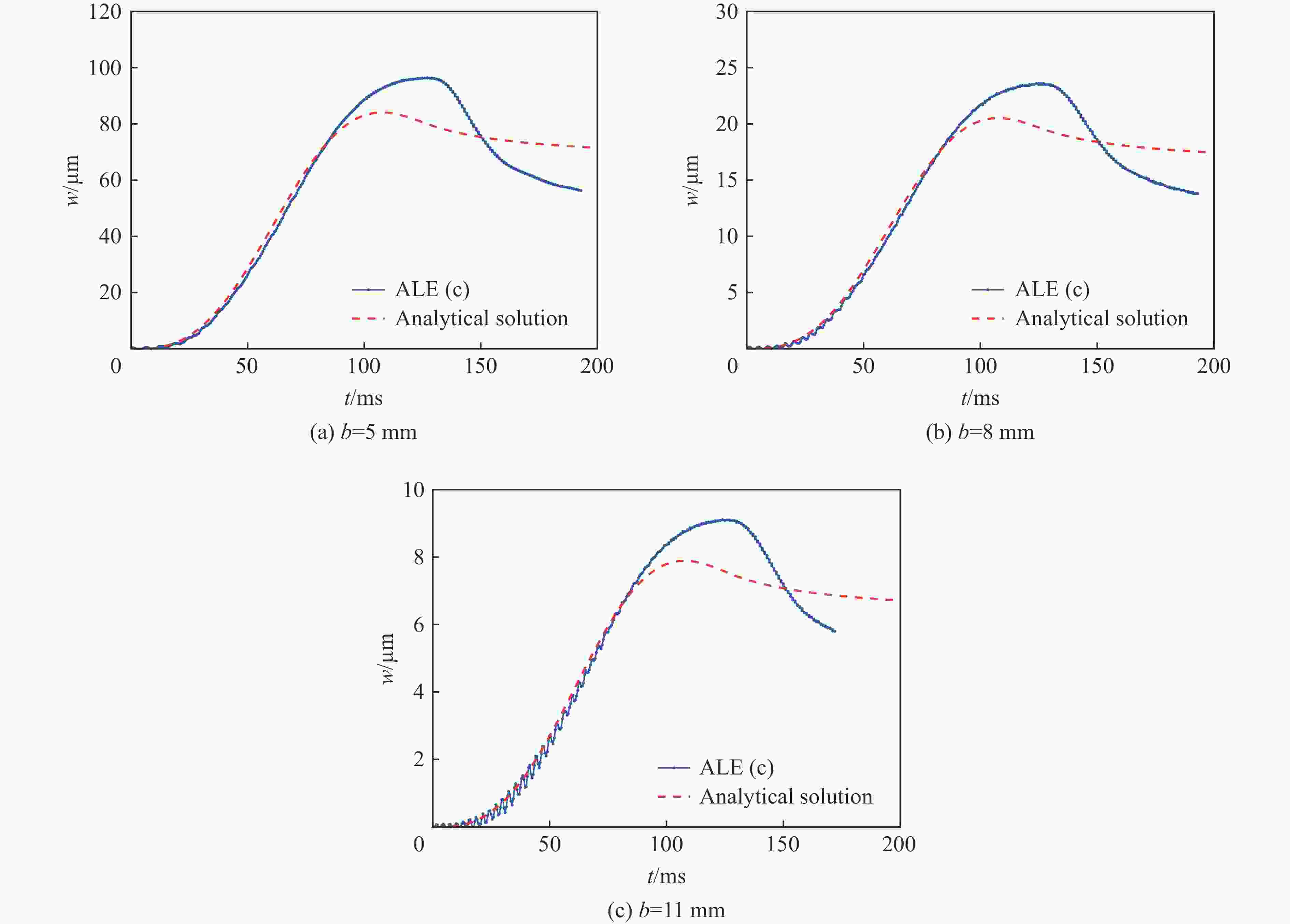
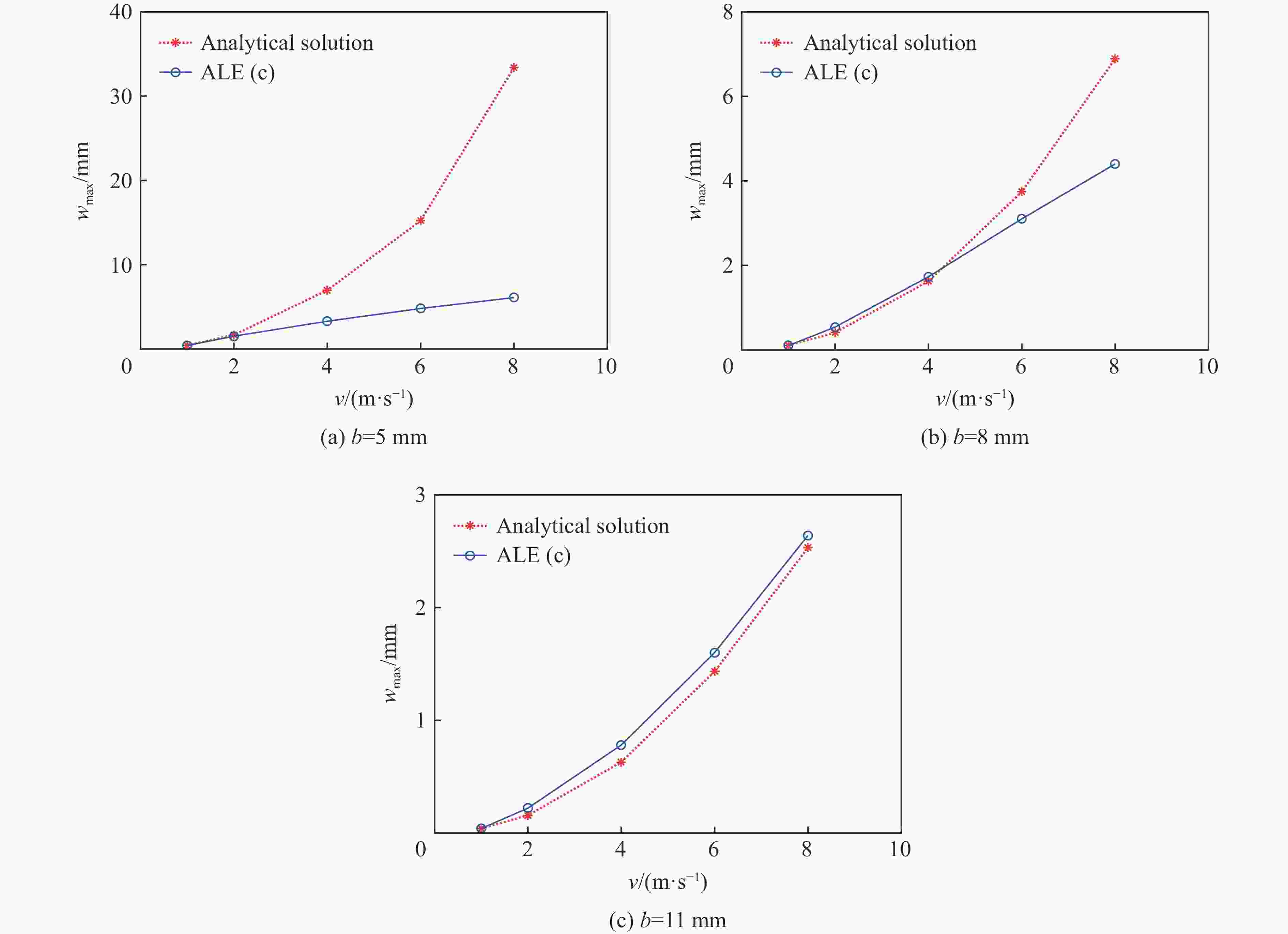
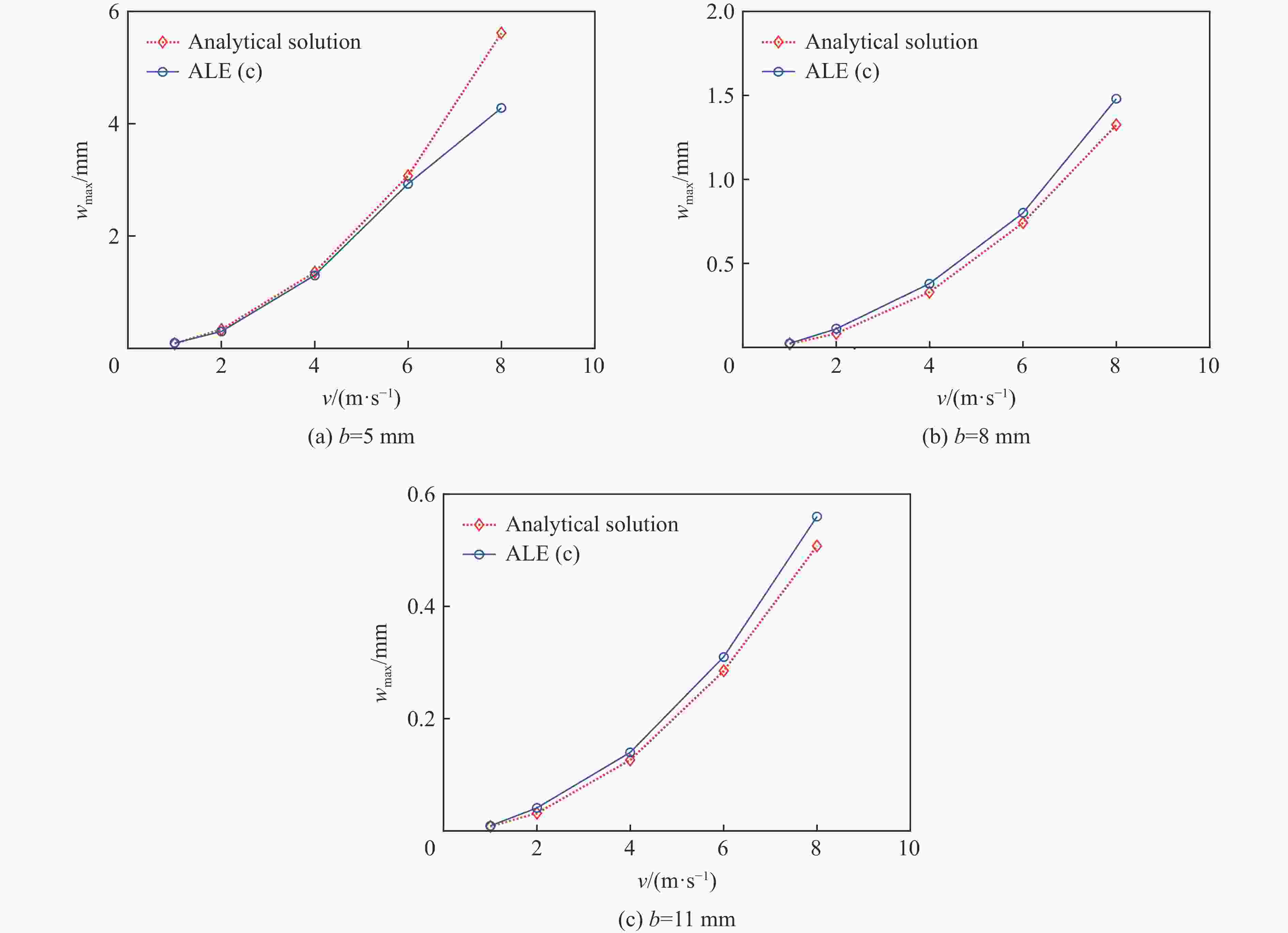
Table 3. The maximum structural responses at $x' = 0.5L $ of the supported wedges with different plate thickesses

b/mm	w_max/mm
	理论解析解			ALE			BEM^[5]
	β=10°	β=30°	β=45°	β=10°	β=30°	β=45°	β=30°	β=45°
5	6.970	0.420	0.200	4.320	0.410	0.210	0.380	0.150
8	1.710	0.100	0.049	1.530	0.100	0.051	0.095	0.035
11	0.660	0.039	0.019	0.590	0.400	0.020	0.036	0.015

下载: 导出CSV

表 4 $\ \beta=30^\circ $的不同板厚的弹性楔形体$x'=0.5L$处的结构变形峰值

Table 4. The maximum structural responses at $x'=0.5L$ of the wedges with $\ \beta=30^\circ $ and different plate thicknesses

b/mm	w_max/μm
	理论解析		ALE
	两端简支	两端固支	两端简支	两端固支
5	420	84.0	410	96.0
8	100	21.0	100	24.0
11	39	7.9	400	9.1

下载: 导出CSV

表 5 不同板厚的楔形体在不同入水速度下的水弹性因数

Table 5. The hydroelastic factors of the wedges with different plate thicknesses at different water-enter velocities

速度/(m·s^-1)	R_F
速度/(m·s^-1)	b=5 mm	b=8 mm	b=11 mm
1	3.38	6.83	11.01
2	1.69	3.42	5.51
4	0.84	1.71	2.75
6	0.56	1.14	1.84
8	0.42	0.85	1.38

下载: 导出CSV

参考文献(12)

[1]	KVALSVOLD J, FALTINSEN O M. Hydroelastic modeling of wet deck slamming on multihull vessels [J]. Journal of Ship Research, 1995, 39(3): 225–239. DOI: 10.5957/jsr.1995.39.3.225.
[2]	FALTINSEN O M, KVÅLSVOLD J, AARSNES J V. Wave impact on a horizontal elastic plate [J]. Journal of Marine Science and Technology, 1997, 2(2): 87–100. DOI: 10.1007/BF02491523.
[3]	KHABAKHPASHEVA T I, KOROBKIN A A. Elastic wedge impact onto a liquid surface: Wagner’s solution and approximate models [J]. Journal of Fluids and Structures, 2013, 36: 32–49. DOI: 10.1016/j.jfluidstructs.2012.08.004.
[4]	SHAMS A, PORFIRI M. Treatment of hydroelastic impact of flexible wedges [J]. Journal of Fluids and Structures, 2015, 57: 229–246. DOI: 10.1016/j.jfluidstructs.2015.06.017.
[5]	LU C H, HE Y S, WU G X. Coupled analysis of nonlinear interaction between fluid and structure during impact [J]. Journal of Fluids and Structures, 2000, 14(1): 127–146. DOI: 10.1006/jfls.1999.0257.
[6]	STENIUS I, ROSÉN A, KUTTENKEULER J. Hydroelastic interaction in panel-water impacts of high-speed craft [J]. Ocean Engineering, 2011, 38(2−3): 371–381. DOI: 10.1016/j.oceaneng.2010.11.010.
[7]	PANCIROLI R, ABRATE S, MINAK G, et al. Hydroelasticity in water-entry problems: comparison between experimental and SPH results [J]. Composite Structures, 2012, 94(2): 532–539. DOI: 10.1016/j.compstruct.2011.08.016.
[8]	PANCIROLI R. Water entry of flexible wedges: some issues on the FSI phenomena [J]. Applied Ocean Research, 2013, 39: 72–74. DOI: 10.1016/j.apor.2012.10.010.
[9]	HASSOON O H, TARFAOUI M, ALAOUI A E M, et al. Experimental and numerical investigation on the dynamic response of sandwich composite panels under hydrodynamic slamming loads [J]. Composite Structures, 2017, 178: 297–307. DOI: 10.1016/j.compstruct.2017.07.014.
[10]	HASSOON O H, TARFAOUI M, ALAOUI A E M, et al. Mechanical behavior of composite structures subjected to constant slamming impact velocity: an experimental and numerical investigation [J]. International Journal of Mechanical Sciences, 2018, 144: 618–627. DOI: 10.1016/j.ijmecsci.2018.05.035.
[11]	HASSOON O H, TARFAOUI M, ALAOUI A E M, et al. Mechanical performance evaluation of sandwich panels exposed to slamming impact: comparison between experimental and SPH results [J]. Composite Structures, 2019, 220: 776–783. DOI: 10.1016/j.compstruct.2019.04.051.
[12]	KOROBKIN A. Analytical models of water impact [J]. European Journal of Applied Mathematics, 2004, 15(6): 821–838. DOI: 10.1017/S0956792504005765.