基于SHPB实验的砂岩动态破坏过程及应变-损伤演化规律研究

张明涛; 王伟; 王奇智; 张思怡

doi:10.11883/bzycj-2020-0288

基于SHPB实验的砂岩动态破坏过程及应变-损伤演化规律研究

doi: 10.11883/bzycj-2020-0288

张明涛^{1, 2, 3,},
王伟^{1, 2, 3},
王奇智^4, ,,
张思怡¹

1.
石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄 050043
2.
河北省金属矿山安全高效开采技术创新中心，河北石家庄 050043
3.
石家庄铁道大学土木工程学院，河北石家庄 050043
4.
河北科技大学建筑工程学院，河北石家庄 050018

基金项目: 国家自然科学基金（51979170，U1967208）；河北省自然科学基金青年基金（E2020208071）

详细信息

作者简介:
张明涛（1994－　），男，硕士，2868992828@qq.com

通讯作者:
王奇智（1987－　），男，博士，讲师，wangqizhi118@126.com

中图分类号: O346.4；TU45
计量
- 文章访问数: 600
- HTML全文浏览量: 357
- PDF下载量: 123
- 被引次数: 24
出版历程
- 收稿日期: 2020-08-24
- 修回日期: 2020-11-14
- 网络出版日期: 2021-08-16
- 刊出日期: 2021-09-14

Dynamic failure process and strain-damage evolution law of sandstone based on SHPB experiments

ZHANG Mingtao^{1, 2, 3
,},
WANG Wei^{1, 2, 3},
WANG Qizhi^{4
, ,},
ZHANG Siyi¹

1.
State Key Laboratory of Mechanics Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang 050043, Hebei, China
2.
Hebei Metal Mine Safety and Efficient Mining Technology Center, Shijiazhuang 050043, Hebei, China
3.
School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, Hebei, China
4.
School of Civil Engineering, Hebei University of Science and Technology, Shijiazhuang 050018, Hebei, China

摘要

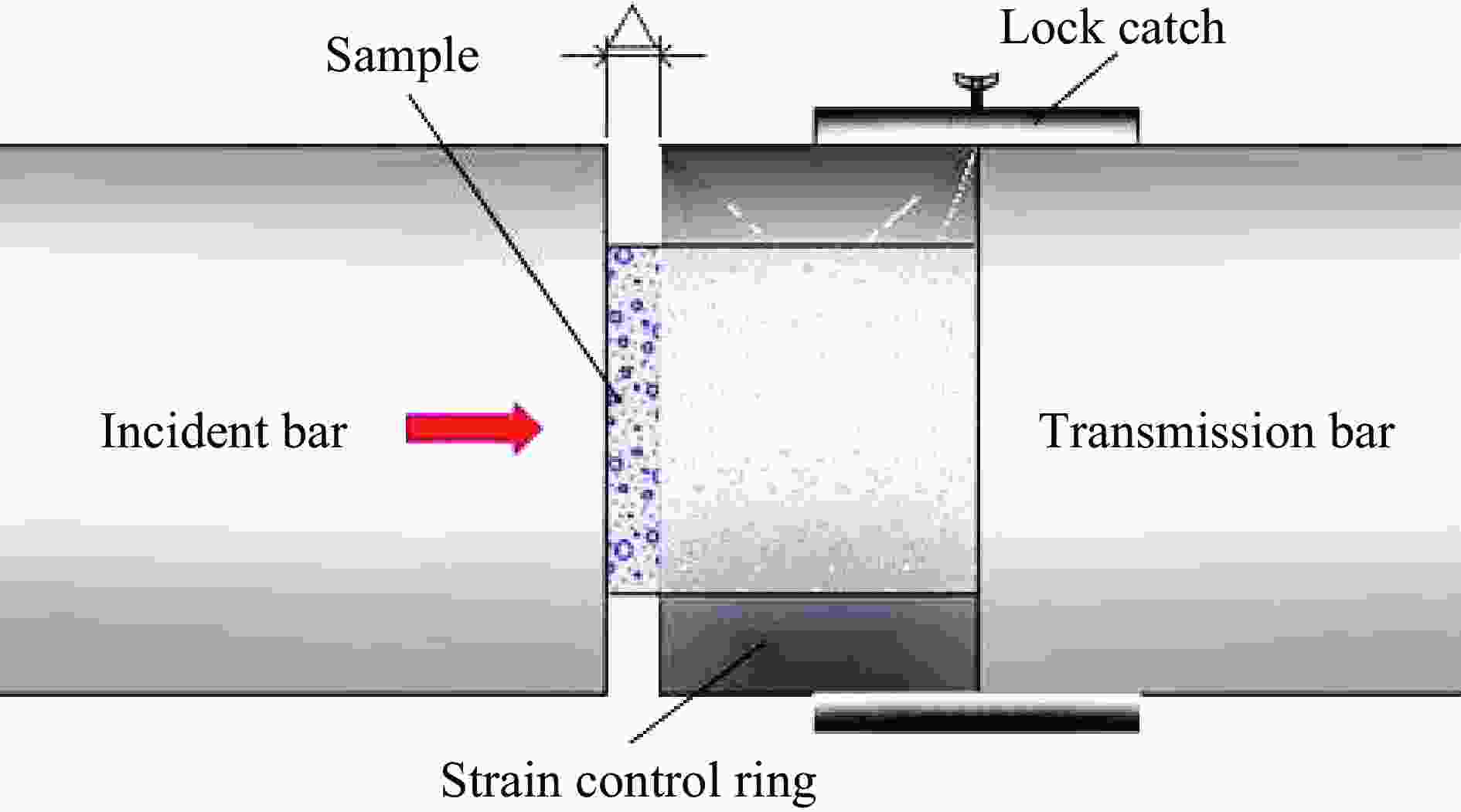
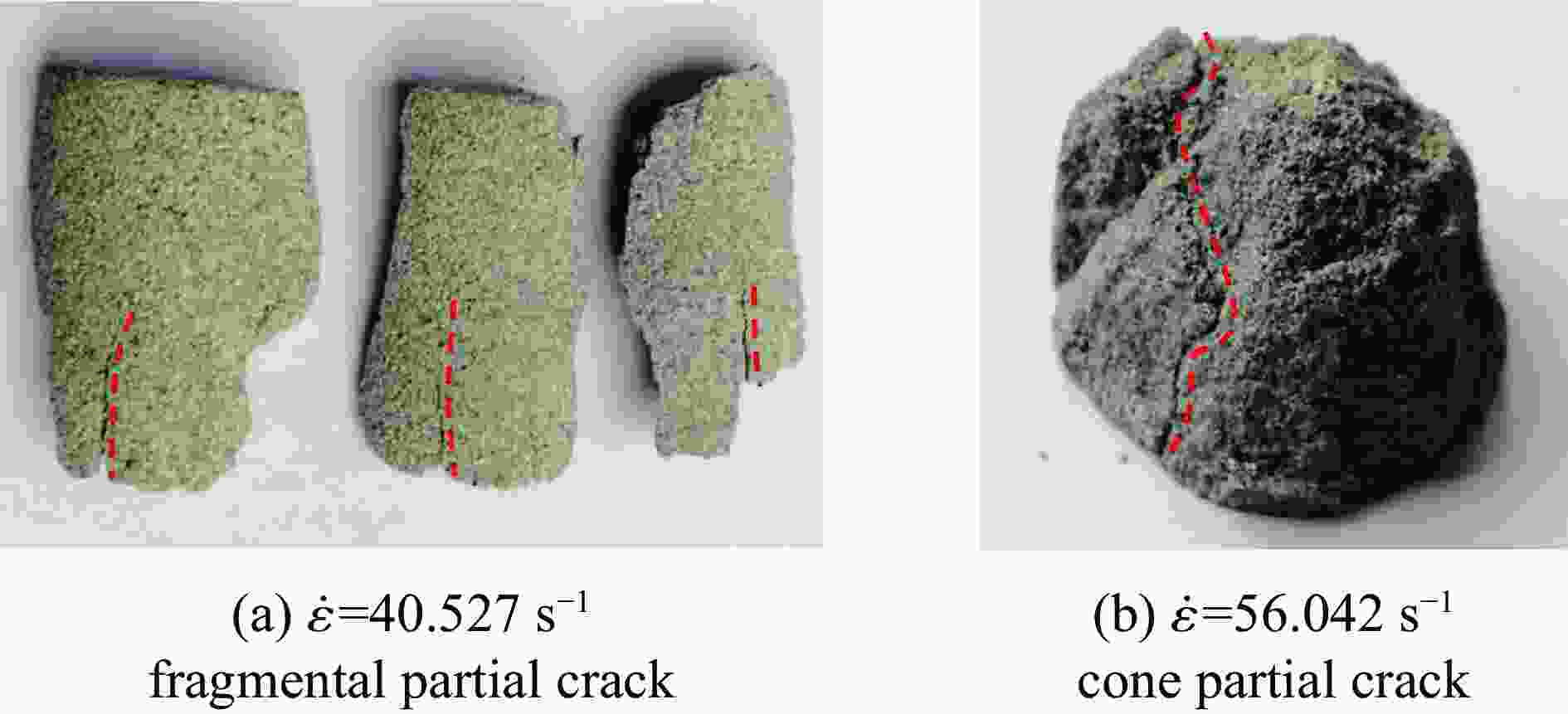
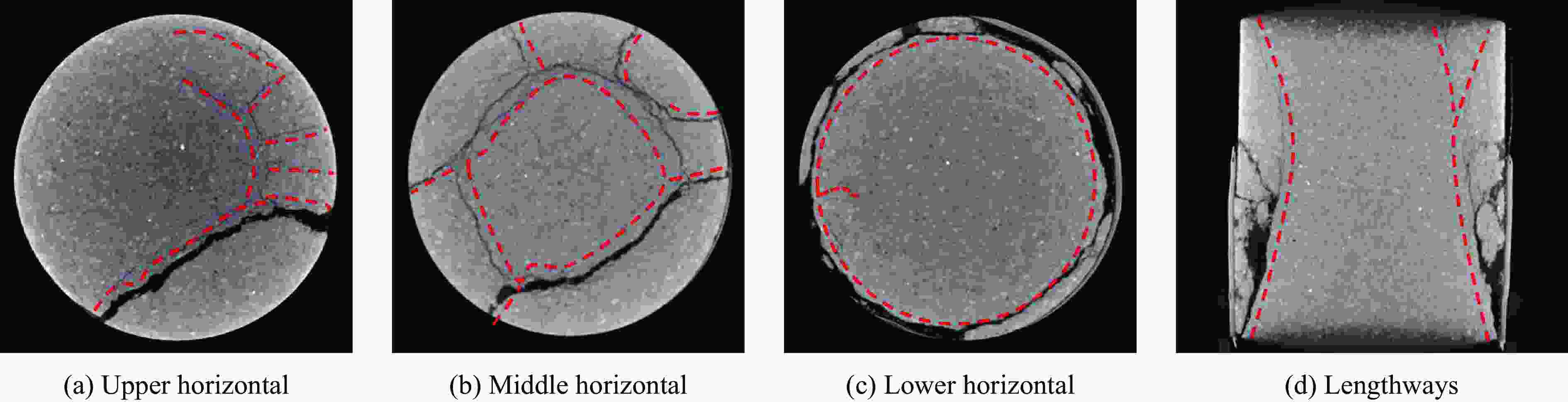
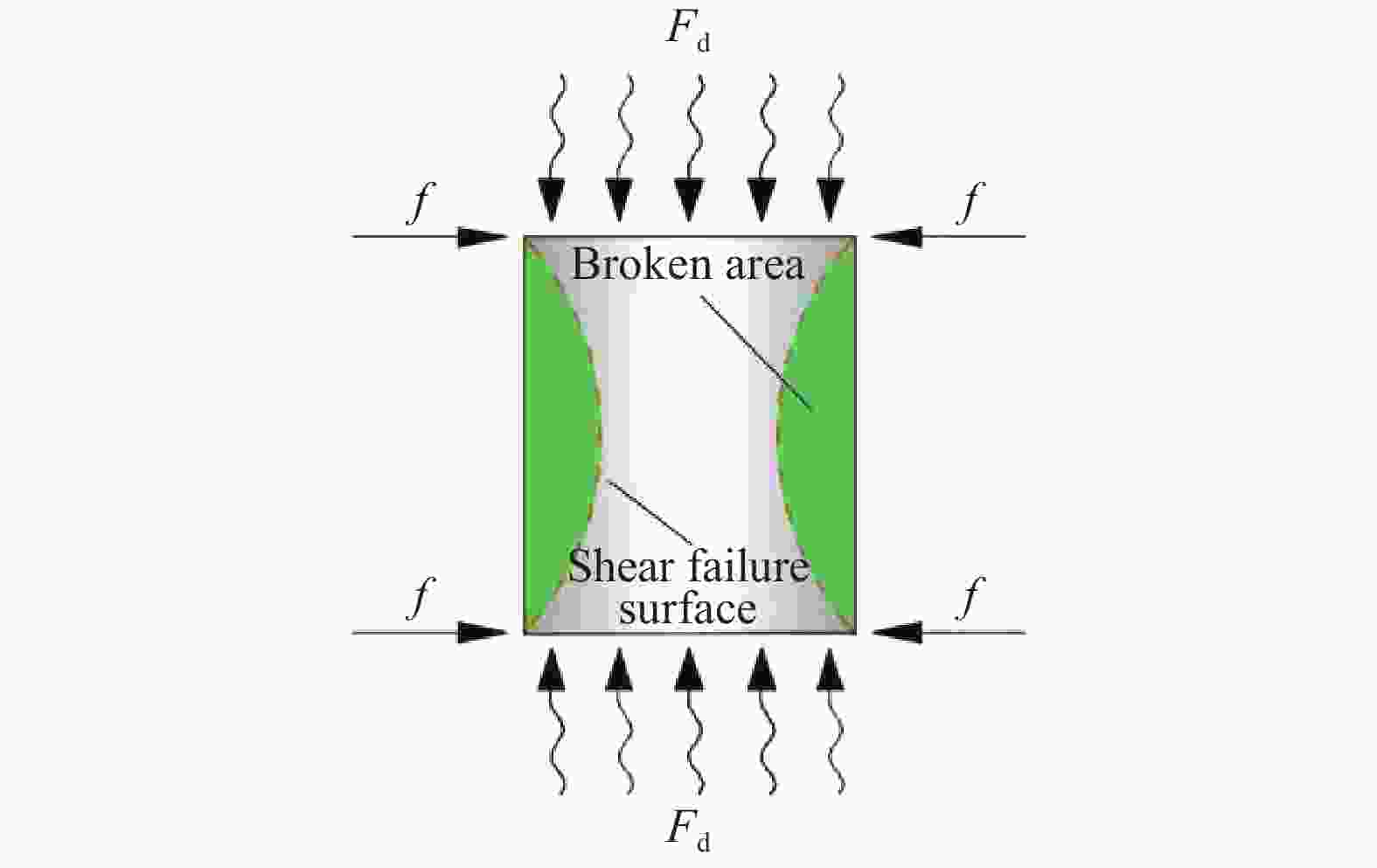
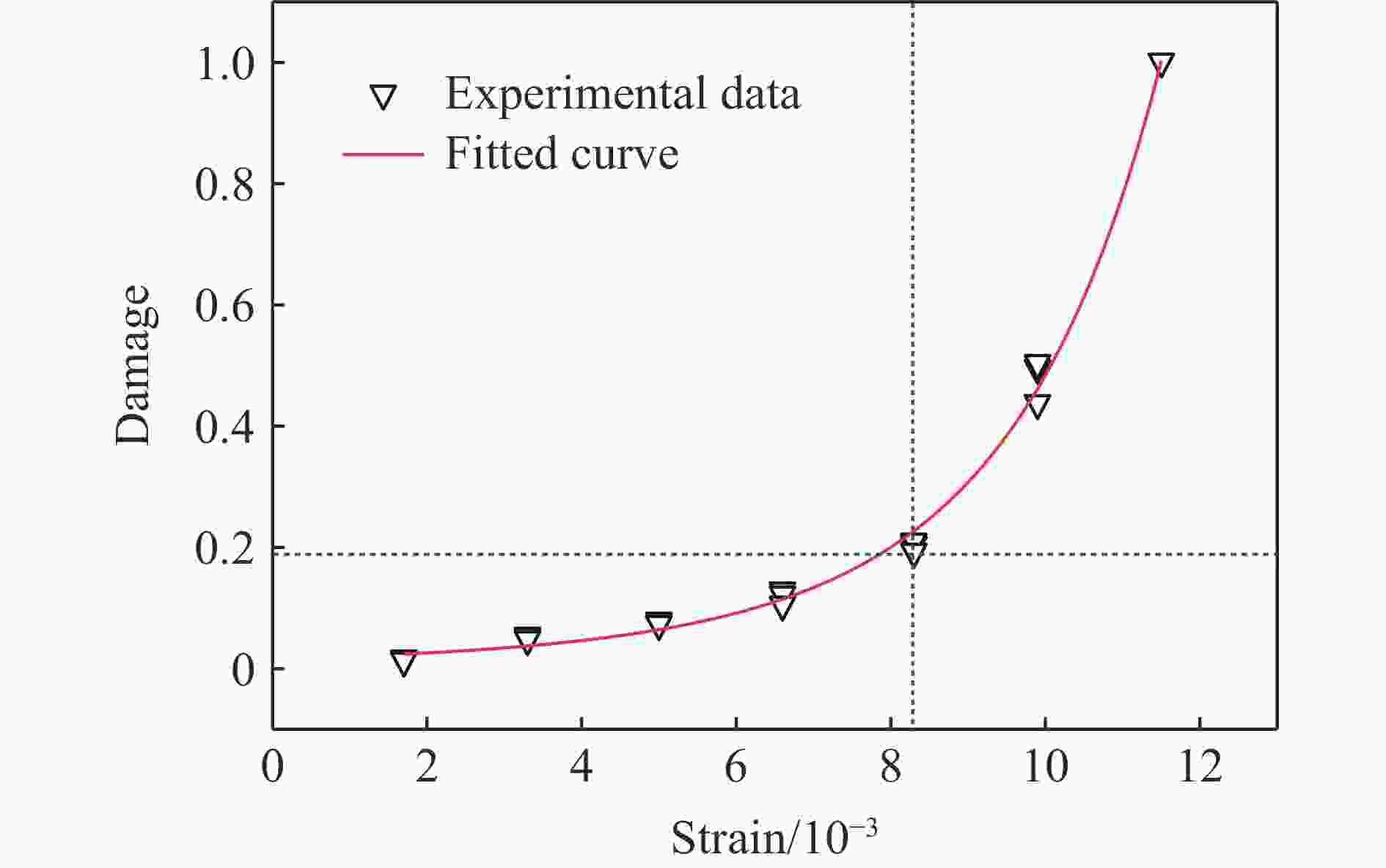
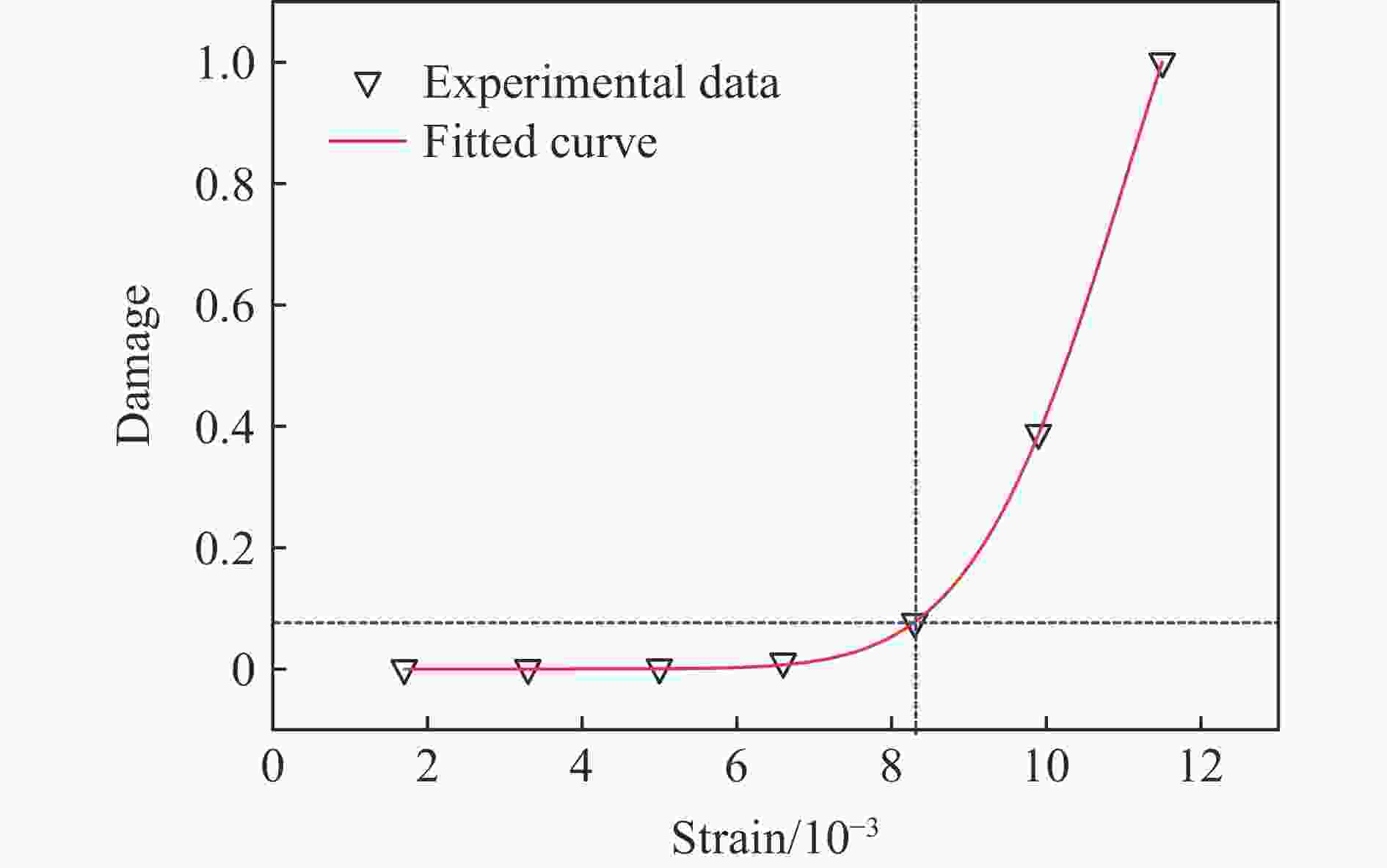
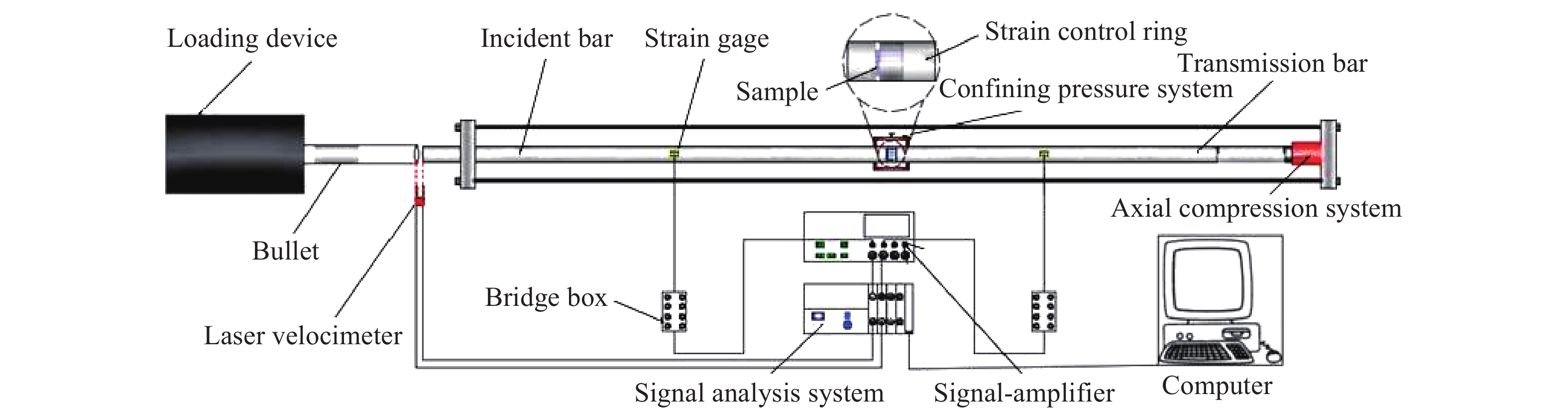
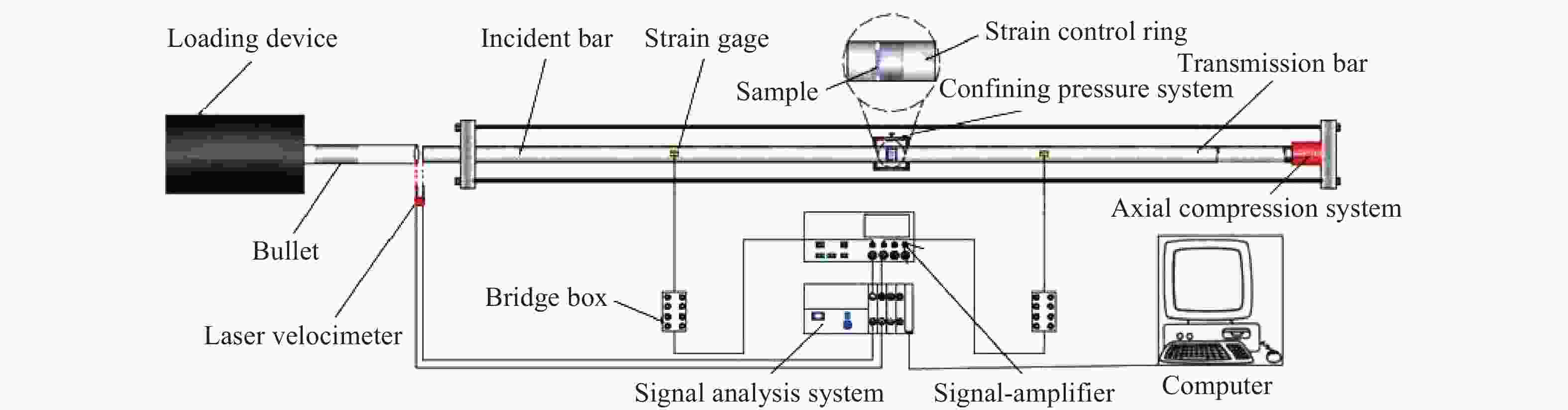
摘要: 为研究砂岩型铀矿爆破增渗地浸开采过程中赋矿岩层的破坏特征及损伤演化规律, 利用带有应变控制环的SHPB实验系统，对砂岩试样进行控制应变条件下的动态冲击实验，并结合波速测试实验和CT扫描实验，分析研究了砂岩试样的整体破坏过程、裂纹分布及应变-损伤演化规律。实验结果表明：在冲击荷载作用下，当应变值超过0.008 3时，砂岩试样会突然出现明显的整体破坏，整体破坏形式近似双锥形，其破坏模式为剪切-张拉混合破坏；随着应变的增加，裂纹的产生及扩展大致分为无裂纹阶段（0～0.003 3）、微裂纹起裂阶段（0.003 3～0.008 3）、裂纹贯通阶段（0.008 3～0.009 9）3个阶段，且裂纹分布区域主要集中在试样中间外围。分别从宏观、细观两方面建立了应变-损伤之间的定量关系式，损伤变量随应变的增长趋势大致分为两个阶段：平缓发展区（0～0.008 3）和迅速增长区（0.008 3～0.011 5），损伤变量随应变增加并非简单的线性增加，而是应变值超过应变损伤阈值之后损伤程度急剧增加，应变损伤阈值为0.008 3。
- SHPB /
- 砂岩 /
- 控制应变 /
- 破坏过程 /
- 损伤演化
Abstract: In order to study the failure characteristics and damage evolution law of sandstone type uranium ore by blasting, the SHPB experimental system with strain control loop is used to conduct dynamic impact experiment on sandstone samples under controlled strain conditions. Combined with the wave velocity experiment and CT scanning experiments, the whole failure process, crack distribution and strain damage evolution law of sandstone samples are analyzed and studied. The experimental results show that the sandstone sample will suddenly appear obvious overall failure when the strain value exceeds 0.008 3 under impact load, and that the overall failure form is approximately biconical and its failure mode is shear-tension mixed failure. With the increase of strain, the generation and propagation of cracks can be roughly divided into crack free stage (0−0.003 3), microcrack initiation stage (0.003 3−0.008 3) and crack through stage (0.008 3−0.009 9). The quantitative relationship between strain and damage is established from macroscopic and microscopic aspects. The growth trend of damage variable with strain can be roughly divided into two stages, i.e. the smooth development area (0−0.008 3) and the rapid growth area (0.008 3−0.011 5). The damage variable does not increase linearly with the increase of strain, but the damage degree increases sharply when the strain value exceeds the strain damage threshold (0.008 3).
- SHPB /
- sandstone /
- controlled strain /
- failure process /
- damage evolution

HTML全文

现代鱼雷可通过多种发射方式攻击敌对目标, 如飞机空投或舰载发射等, 但不管采用何种发射方式, 都要经过空中、入水、水下航行至命中目标的全弹道过程。入水是一个短暂、变化激烈而又复杂的力学过程, 在入水的整个过程中, 鱼雷将经历撞水、浸水、带空泡航行、全浸湿后转入受控运动等4个阶段。入水过程中雷体会激起周围流体介质的运动, 反过来, 流体介质对结构又施加各种反作用力。入水冲击力有2个分量相当重要:一个是轴向力或阻力, 会引起减加速度, 可能使雷头变形, 破坏鱼雷内部的仪表设备; 另一个是法向力或升力, 会形成力矩, 产生横向角速度, 影响弹道, 并可能使雷体皱折或断裂。因此研究空投鱼雷入水冲击力对鱼雷结构的总体设计以及水下弹道设计等方面具有重要的工程意义^[1]。

本文中拟基于鱼雷入水动力学模型、动态非线性有限原理论和耦合算法^[2], 计算计算鱼雷入水时受到的作用力, 建立空投鱼雷入水冲击有限元模型, 对不同工况进行数值模拟, 以期为预测鱼雷入水冲击载荷提供参考。

1. 鱼雷入水受力分析

作用在鱼雷上的力可以分成2类:鱼雷重力和流体反作用力, 流体反作用力中包括浮力和流体动力^[3]。重力和浮力的大小和方向都是明确的, 容易确定的。流体动力不仅取决于鱼雷的外形、流体的特性, 也取决于鱼雷入水运动状态参数(如速度、加速度、姿态角、姿态角速度)等。可以用适合于惯性参考系的牛顿运动定律来描述鱼雷斜入水时纵平面内的受力及运动。鱼雷入水时运动和几何参数如图 1所示。

图 1 鱼雷入水运动简图

Figure 1. Schematic of torpedo entry into water

下载: 全尺寸图片幻灯片

浮力及其力矩为:

$\begin{array}{c} F_{\mathrm{b}}=\rho g \int_{-L_{2}}^{L_{1}} A_{\mathrm{b}}(l) \mathrm{d} l \end{array}$

(1)

$\begin{array}{c} M_{\mathrm{b}}=F_{\mathrm{b}} \int_{L}^{L_{1}} \sin (\phi) L(l) \mathrm{d} l \end{array}$

(2)

式中:A_b为沾湿部分有效截面积。

轴向黏性阻力、法向黏性阻力及其对重心力矩为:

$\begin{aligned} F_{\mathrm{d}, \mathrm{a}} & =\frac{1}{2} \rho C_{\mathrm{d}, \mathrm{a}} A_{\mathrm{e}} v_{\mathrm{a}}\left|v_{\mathrm{a}}\right| \end{aligned}$

(3)

$\begin{aligned} F_{\mathrm{d}, \mathrm{n}} & =\rho C_{\mathrm{d}, \mathrm{n}} \int_{L}^{L_{1}} r v_{\mathrm{n}}\left|v_{\mathrm{n}}\right| \mathrm{d} l \end{aligned}$

(4)

$\begin{aligned} M_{\mathrm{d}, \mathrm{n}} & =\rho C_{\mathrm{d}, \mathrm{n}} \int_{l}^{L_{1}} r l v_{\mathrm{n}}\left|v_{\mathrm{n}}\right| \mathrm{d} l \end{aligned}$

(5)

式中:v_a、v_n分别为轴向、法向速度, 轴向黏性阻力系数C_{d, a}=0.3, 法向粘性阻力系数C_{d, n}=1.1, A_e为轴向有效面积, r为轴向截面半径。

轴向、法向附加力及其对重心的力矩为:

$\begin{array}{c} F_{\mathrm{m}, \mathrm{a}}=\frac{\mathrm{d} m_{\mathrm{a}}}{\mathrm{d} v} \frac{\mathrm{d} v}{\mathrm{~d} t}+m_{\mathrm{a}} A_{\mathrm{a}}\left(\frac{L}{L_{1}+L_{2}}\right) \end{array}$

(6)

$\begin{array}{c} F_{\mathrm{m}, \mathrm{n}}=\int_{-L_{2}}^{L_{1}}\left(v_{\mathrm{n}} \frac{\mathrm{d} m}{\mathrm{~d} t}+m \frac{\mathrm{d} v_{\mathrm{n}}}{\mathrm{d} t}\right) \mathrm{d} l \end{array}$

(7)

$\begin{array}{c} M_{\mathrm{m}, \mathrm{n}}=\int_{-L_{2}}^{L_{1}} l \mathrm{~d} F_{\mathrm{m}, \mathrm{n}} \end{array}$

(8)

式中:m_a为轴向附加质量, m为单位长度的横截面在浸深h处的附加质量, 其计算方法可由文献[4]确定。根据以上受力分析, 建立鱼雷入水过程中动力学方程:

$\left\{\begin{array}{l} M X^{\prime \prime}=F_{\mathrm{m}, \mathrm{n}} \cos \phi-F_{\mathrm{m}, \mathrm{a}} \sin \phi-F_{\mathrm{m}, \mathrm{a}} \sin \phi+F_{\mathrm{m}, \mathrm{n}} \cos \phi \\ M Z^{\prime \prime}=F_{\mathrm{m}, \mathrm{n}} \sin \phi+F_{\mathrm{m}, \mathrm{a}} \cos \phi+F_{\mathrm{m}, \mathrm{a}} \sin \phi+F_{\mathrm{m}, \mathrm{n}} \sin \phi-M g \\ I_{\phi}^{\prime \prime}=M_{\mathrm{b}}+M_{\mathrm{m}, \mathrm{n}}+M_{\mathrm{d}, \mathrm{n}} \end{array}\right.$

(9)

式中:M为鱼雷总质量, I为对重心的转动惯量。将上式转化成矩阵形式:

$\left(\begin{array}{ccc} M+m_{11} & m_{12} & m_{13} \\ m_{21} & M+m_{22} & m_{23} \\ m_{31} & m_{32} & M+m_{33} \end{array}\right)\left(\begin{array}{c} X^{\prime \prime} \\ Z^{\prime \prime} \\ \phi^{\prime \prime} \end{array}\right)=\left(\begin{array}{c} F_{x} \\ F_{z} \\ F_{\phi} \end{array}\right)$

(10)

式中:m_ij(i, j=1, 2, 3)对应于加速度的质量项。式(10)是一个二阶常微分方程组, 将其降阶转化为一阶方程组, 采用变步长Runge-Kutta法求解, 对于各积分项采用变步长辛普森法进行计算。取MK46鱼雷为计算目标, 入水角为45°, 入水速度为32m/s, 攻角为零, 通过使用Matlab进行数值计算, 计算结果如表 1所示。

表 1 鱼雷入水时力学参数

Table 1. Mechnical parameters for torpedo entry into water

t/ms	F_{m, a}/kN	F_{m, n}/kN	M_{m, n}/(kN·m)
0.34	28.5	19.7	121.6
1.00	10.1	6.3	38.9
2.00	2.1	1.7	10.5
3.00	3.6	2.3	14.2
4.00	2.1	2.0	12.3
5.00	1.8	1.2	7.4
6.00	1.6	1.1	6.8

下载: 导出CSV

| 显示表格

由表 1可以看出, 鱼雷在入水的瞬间就会受到很大的轴向以及法向冲击载荷, 从而也产生了很大的法向弯矩, 这都会对鱼雷的结果以及姿态产生很大的影响。但持续时间很短, 随着不断入水, 轴向力和法向力迅速衰减, 趋于某一常值。

2. 数值模型

以MK46鱼雷为算例, 依据所研究问题的侧重点, 对鱼雷和流体进行了必要的简化。由于主要研究对象为鱼雷入水冲击时的流体动力情况, 不考虑载荷下鱼雷壳体会不会发生塑性变形以及结构破坏, 故将鱼雷作为刚体建模, 且不考虑分段。对于鱼雷入水, 由于其入水速度高, 粘性仅仅表现在附着在耦合面边界层很薄的一部分, 对数值计算的结果影响很小, 在本文中不予考虑^[5-7]。

鱼雷结构采用刚体假设, 泊松比μ=0.3, 质量m=235kg, 空气和水选用可压缩理想流体本构材料关系, 水压力由多项式状态方程描述。

对于压缩状态:

$p=a_{1} \mu+a_{2} \mu^{2}+a_{3} \mu^{3}+\left(b_{0}+b_{1} \mu\right) \rho_{0} e$

(11)

对于拉伸状态:

$p=a_{1} \mu+\left(b_{0}+b_{1} \mu\right) \rho_{0} e$

(12)

空气的压力由Gamma状态方程来描述:

$p=(\gamma-1) \rho_{1} e$

(13)

水密度为ρ₀=1 000kg/m³, 体积模量K=2.2GPa, 质量内能e=83.95kJ/kg; 空气密度ρ₁=1.293kg/m³, 质量热容比γ=1.4, 质量内能e=212.65kJ/kg

雷体结构采用拉格朗日四节点四边形壳建模, 共有4 800个节点, 4 798个单元, 有限元模型如图 2所示。水和空气选用欧拉六面体实体单元, 考虑到入水问题的具体情况, 在近水面处网格较密, 远离水面采用等差网格, 逐渐稀疏。鱼雷的整个外表面为流固耦合面, 采用一般耦合算法。鱼雷头部距液面初始高度0.2m。鱼雷入水(45°入水角)模型如图 3所示。

图 2 鱼雷有限元网格模型

Figure 2. Finite element model of torpedo

下载: 全尺寸图片幻灯片

图 3 鱼雷入水有限元模型

Figure 3. Finite element model for torpedo entry into water

下载: 全尺寸图片幻灯片

3. 鱼雷入水冲击载荷分析

3.1 鱼雷入水载荷分析

选取初始入水速度为32m/s, 入水角度为45°, 初始步长为1μm, 总计算时间为0.06s。将结果文件导入MSC.Dytran计算后可以得到该工况下鱼雷入水的分析结果。如图 4所示为鱼雷入水过程中耦合面受到的作用力时间历程曲线。

图 4 鱼雷入水耦合面作用力时间历程曲线

Figure 4. Coupling force-time curve for torpedo entry into water

下载: 全尺寸图片幻灯片

由图 4中可以看出, 鱼雷在入水时, 会遭受极大的冲击载荷, 随着鱼雷不断入水, 冲击载荷迅速的衰减下去, 但还是会不断受到冲击力的作用, 3ms后冲击过程基本结束, 作用力趋于稳定。作用力峰值达到35.397kN, 时间约为0.32ms, 由于作用时间很短, 不会影响鱼雷入水的姿态以及运动。计算得到的不同时刻作用力大小也与相同工况下Matlab计算出的结果(表 1)比较接近, 从而从进一步验证了数值模型的可靠性。

图 5所示为入水1.8ms时鱼雷外壳以及水所受到的压力云图。根据鱼雷在入水过程中受到的压力变化情况可得出, 入水初始时接触面的压力最大, 峰值为25.8MPa, 向边缘逐渐减小。对于平头鱼雷入水情况, 其撞水瞬间是一种碰撞现象, 撞水初期可以假设其为一平板撞击可压缩水面。基于Von Karman一元碰撞理论, 刚性平板撞击压缩水面的撞击压力峰值可由下式估算^[8]:

图 5 入水时鱼雷及水的压力云图

Figure 5. Pressure contour for torpedo entry into water

下载: 全尺寸图片幻灯片

$p_{\max }=\rho c v_{\perp} \sin \varphi$

(14)

式中:ρ为水的密度, 入水角度φ=45°, 水的声速c=1 480m/s, 垂直入水速度v_⊥=22.6m/s。计算得最大理论压力峰值为33.45MPa, 较计算结果高。这主要是由于没有考虑到空气被压入水中的空气垫效应而减小了压力。对于一般雷头壳体, 选用的材料为硬铝合金, 其屈服应力为330MPa, 故壳体所受压力值不可能使壳体发生塑性变形或破坏。

3.2 入水速度对鱼雷入水的影响

为了进一步分析入水过程, 以入水角度为45°的工况下分别给鱼雷加以从10~40m/s范围内变化的轴向入水速度进行计算。根据数值模拟结果, 将不同速度下的鱼雷头部所受到的压力峰值进行曲线拟合, 如图 6所示。

图 6 不同速度下鱼雷头部所受到的压力峰值

Figure 6. The pressure peak of torpedo head at different water-entry velocities

下载: 全尺寸图片幻灯片

所得拟合二次曲线函数:

$F=223 x^{2}+3523 x+12480 \quad 10 \mathrm{~m} / \mathrm{s} \leqslant x \leqslant 40 \mathrm{~m} / \mathrm{s}$

(15)

将不同速度下的鱼雷入水弹道曲线进行比对分析, 如图 7所示, 可以得出, 当冲击力作用在鱼雷头部时, 由于不通过重心, 使得鱼雷产生俯仰角速度, 对弹道产生严重影响。随着鱼雷入水速度的增大, 弹道偏离现象逐渐减小, 说明入水速度越高, 越有利于消除法向力引起的弯矩对鱼雷带来的影响。

图 7 不同入水速度鱼雷弹道曲线图

Figure 7. Torpedo trajectory curves at different water-entry velocities

下载: 全尺寸图片幻灯片

3.3 入水角度对鱼雷入水的影响

取入水速度为40m/s, 改变入水角度, 得到不同角度下的冲击力峰值变化曲线, 如表 2所示。

表 2 不同角度入水时鱼雷所受最大冲击力

Table 2. The maximum impact force at different water-entry angles

ϕ/(°)	F_{m, a}/kN	F_{m, n}/kN
30	23.9	21.8
45	30.9	19.2
60	36.5	11.7
75	38.5	6.5
90	68.0	0

下载: 导出CSV

| 显示表格

由表 2可知, 入水轴向冲击力随着入水角度的增大而增大, 尤其在垂直入水时轴向力急剧增大, 这说明垂直入水是鱼雷入水最不安全的情况, 会对鱼雷的纵向结构强度提出了很高的要求, 应该尽量避免。

而法向力随着入水角度的增大而减小, 这说明当鱼雷以小角度入水时应该注意避免法向力太大而引起的忽扑现象。同时根据计算结果分析不同角度入水弹道轨迹, 发现随着入水角度的变小, 鱼雷运动轨迹偏离初始角度的情况变的更为严重, 这也同样说明法向作用力及其所引起的弯矩在小角度入水情况下大于大角度入水时的现象。

3.4 不同头型对雷体入水的影响

分别选取了截头锥形壳体, 尖头壳体以及半圆头壳体这3种头部壳体形状的结构, 以入水速度30m/s对鱼雷垂直入水工况进行计算, 其有限元模型如图 8所示。

图 8 不同头型鱼雷有限元模型

Figure 8. Finite element models for torpedo with different headtypes

下载: 全尺寸图片幻灯片

3种不同头型鱼雷垂直入水工况的入水耦合面作用力时间历程曲线如图 9所示。

图 9 不同头型入水耦合面作用力时程曲线

Figure 9. Coupling force-time curve for water-entry torpedoes with different head shapes

下载: 全尺寸图片幻灯片

由图 9可以看出, 鱼雷在开始入水时都会受到很大的冲击载荷, 但截头锥形的头部形状受到的压力峰值最大, 压力作用的时间也是最长的, 其次是圆头雷, 最小的是尖头雷。这说明鱼雷入水时, 如果减小头部与水的接触面积, 则可以有效地减小鱼雷所受到的冲击载荷。

4. 结论

分析了鱼雷入水时受到的流体动力, 应用MATLAB编程求解了鱼雷入水过程的流体动力参数, 并通过使用MSC.Dytran仿真模拟了空投鱼雷入水过程。通过建立鱼雷入水三维有限元模型, 对鱼雷入水过程雷体所遭受的冲击力及其在不同入水速度和角度下冲击压力峰值、不同头部形状冲击压力峰值特点、鱼雷入水弹道做了分析与讨论。得出如下结论:

(1) 空投鱼雷入水时会受到很高的冲击载荷, 存在明显的冲击载荷峰值, 对雷头部结构将造成极大的影响, 随着鱼雷不断进入水中, 冲击载荷逐渐趋于常值。因此, 在设计鱼雷壳体的时候有必要强化其前端面附近的强度设计或在头部加装缓冲头帽, 提高其耐冲击的性能, 以确保其入水时的安全性;

(2) 随着鱼雷入水速度的增加, 作用在鱼雷壳体上的冲击载荷也不断升高, 这对鱼雷雷体的强度提出了很高的要求, 所以应尽可能减小空投鱼雷在入水时的速度, 如在空投时雷身附有降落伞;

(3) 随着鱼雷入水角度的增加, 作用在鱼雷上的法向作用力不断减小, 但轴向力不断增大, 从而由于法向弯矩引起的忽扑现象逐渐消失。垂直入水时轴向作用力达到最高值, 这是鱼雷入水最危险的工况, 应该尽量避免;

(4) 对于垂直入水工况, 不同头型鱼雷的入水载荷各不相同, 减小鱼雷与水的接触面积会明显减小入水载荷峰值的大小。

图 1 SHPB实验系统组成

Figure 1. Diagram of SHPB experimental system

下载: 全尺寸图片幻灯片

图 2 SHPB实验系统照片

Figure 2. Photo of SHPB experimental system

下载: 全尺寸图片幻灯片

图 3 应变控制环与锁扣的照片

Figure 3. Photos of strain control ring and lock catch

下载: 全尺寸图片幻灯片

图 4 应变控制环组成

Figure 4. Diagram of strain control ring

下载: 全尺寸图片幻灯片

图 5 打磨后的砂岩试样

Figure 5. Sandstone samples after grinding and finishing

下载: 全尺寸图片幻灯片

图 6 不同应变率下砂岩的破坏特征

Figure 6. Failure characteristics of sandstones under different strain rates

下载: 全尺寸图片幻灯片

图 7 横向拉伸引起的裂纹

Figure 7. Cracks caused by transverse tension

下载: 全尺寸图片幻灯片

图 8 不同控制应变下砂岩试样的破坏状态

Figure 8. Failure states of sandstone samples under different controlled strains

下载: 全尺寸图片幻灯片

图 9 在ε=0.001 7冲击下试样CT扫描图

Figure 9. CT scans of the sample under impact at ε=0.001 7

下载: 全尺寸图片幻灯片

图 10 在ε=0.003 3冲击下试样CT扫描图

Figure 10. CT scans of the sample under impact at ε=0.003 3

下载: 全尺寸图片幻灯片

图 11 在ε=0.005 0冲击下试样CT扫描图

Figure 11. CT scans of the sample under impact at ε=0.005 0

下载: 全尺寸图片幻灯片

图 12 在ε=0.006 6冲击下试样CT扫描图

Figure 12. CT scans of the sample under impact at ε=0.006 6

下载: 全尺寸图片幻灯片

图 13 在ε=0.008 3冲击下试样CT扫描图

Figure 13. CT scans of the sample under impact at ε=0.008 3

下载: 全尺寸图片幻灯片

图 14 在ε=0.009 9冲击下试样CT扫描图

Figure 14. CT scans of the sample under impact at ε=0.009 9

下载: 全尺寸图片幻灯片

图 15 试样破坏示意图

Figure 15. Schematic diagram of sample failure

下载: 全尺寸图片幻灯片

图 16 自然界中双锥形破坏的照片

Figure 16. Photo of the biconical destruction in nature

下载: 全尺寸图片幻灯片

图 17 声波测速实验数据及其拟合曲线

Figure 17. Experimental data and fitting curve of acoustic velocity measurement

下载: 全尺寸图片幻灯片

图 18 微焦点3D计算机断层扫描系统

Figure 18. Microfocal 3D computed tomography system

下载: 全尺寸图片幻灯片

图 19 无损砂岩试样三维重构图

Figure 19. Three dimensional reconstruction of non-destructive sandstone samples

下载: 全尺寸图片幻灯片

图 20 三维可视化渲染图

Figure 20. Three dimensional visual rendering

下载: 全尺寸图片幻灯片

图 21 CT扫描实验数据及其拟合曲线

Figure 21. Experimental data and fitting curve of CT scanning

下载: 全尺寸图片幻灯片

表 1 砂岩基本物理力学参数

Table 1. Basic physical and mechanical parameters of gray sandstone

密度/（kg·m⁻³）	纵波波速/（m·s⁻¹）	抗压强度/MPa	弹性模量/GPa	泊松比
2 416	2 578	88.3	12.9	0.25

下载: 导出CSV

表 2 声波波速测试结果

Table 2. Experiment results of acoustic wave velocities

试样	应变	冲击速度/（m·s⁻¹）	冲击前纵波波速/（m·s⁻¹）	冲击后纵波波速/（m·s⁻¹）	损伤变量
30.05-1	0.001 7	6.325 0	3 237	3 212	0.015 387
30.05-2		6.526 6	3 307	3 286	0.012 660
30.05-3		6.331 3	3 103	3 084	0.012 209
30.10-1	0.003 3	6.556 2	3 079	3 003	0.048 757
30.10-2		6.259 4	3 285	3 197	0.052 859
30.10-3		6.680 5	3 279	3 201	0.047 010
30.15-1	0.005 0	6.317 2	3 316	3 193	0.072 810
30.15-2		6.698 9	3 414	3 279	0.077 522
30.15-3		6.167 4	3 395	3 270	0.072 282
30.20-1	0.006 6	6.643 5	3 322	3 103	0.127 502
30.20-2		6.533 6	3 084	2 892	0.120 638
30.20-3		6.503 8	3 084	2 919	0.104 141
30.25-1	0.008 3	6.923 1	3 345	2 986	0.203 130
30.25-2		6.252 2	3 137	2 791	0.208 428
30.25-3		6.612 0	3 291	2 959	0.191 585
30.30-1	0.009 9	6.309 1	3 123	2 220	0.494 685
30.30-2		6.282 7	3 123	2 202	0.502 846
30.30-3		6.394 3	3 130	2 349	0.436 781
30.35-1	0.011 5	6.514 1	3 323	0	1
30.35-2		6.355 9	3 402	0	1
30.35-3		6.545 4	3 171	0	1
30.40-1	0.013 1	6.439 7	3 155	0	1
30.40-2		6.320 2	3 080	0	1
30.40-3		6.720 2	3 121	0	1

下载: 导出CSV

表 3 CT扫描损伤测试结果

Table 3. CT scan damage experiment results

试样	应变	冲击速度/（m·s⁻¹）	损伤变量
30.05-3	0.001 7	6.526 6	0.000 02
30.10-1	0.003 3	6.556 2	0.000 09
30.15-2	0.005 0	6.317 2	0.001 14
30.20-3	0.006 6	6.533 6	0.010 86
30.25-3	0.008 3	6.923 1	0.076 38
30.30-1	0.009 9	6.309 1	0.387 60

下载: 导出CSV

参考文献(18)

[1]	苏学斌, 杜志明. 我国地浸采铀工艺技术发展现状与展望 [J]. 中国矿业, 2012, 21(9): 79–83. DOI: 10.3969/j.issn.1004-4051.2012.09.021. SU X B, DU Z M. Development and prospect of China uranium in-situ leaching technology [J]. China Mining Magazine, 2012, 21(9): 79–83. DOI: 10.3969/j.issn.1004-4051.2012.09.021.
[2]	梁卫国, 赵阳升, 徐素国, 等. 原位溶浸采矿理论研究 [J]. 太原理工大学学报, 2012, 43(3): 382–387. DOI: 10.3969/j.issn.1007-9432.2012.03.030. LIANG W G, ZHAO Y S, XU S G, et al. Theoretical study of in-situ solution mining [J]. Journal of Taiyuan University of Technology, 2012, 43(3): 382–387. DOI: 10.3969/j.issn.1007-9432.2012.03.030.
[3]	王伟, 李小春. 低渗透砂岩型铀矿床增渗方法及其可行性研究 [J]. 岩土力学, 2009, 30(8): 2309–2314. DOI: 10.16285/j.rsm.2009.08.002. WANG W, LI X C. Study of enhanced permeability methods and their feasibility in low-permeability sandstone-type uranium deposit [J]. Rock and Soil Mechanics, 2009, 30(8): 2309–2314. DOI: 10.16285/j.rsm.2009.08.002.
[4]	LUNDBERG B. A split Hopkinson bar study of energy absorption in dynamic rock fragmentation [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1976, 13(6): 187–197. DOI: 10.1016/0148-9062(76)91285-7.
[5]	宫凤强, 李夕兵, 刘希灵. 三维动静组合加载下岩石力学特性试验初探 [J]. 岩石力学与工程学报, 2011, 30(6): 1179–1190. GONG F Q, LI X B, LIU X L. Preliminary experimental study of characteristics of rock subjected to 3D coupled static and dynamic loads [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(6): 1179–1190.
[6]	宫凤强, 李夕兵, 刘希灵. 三轴SHPB加载下砂岩力学特性及破坏模式试验研究 [J]. 振动与冲击, 2012, 31(8): 29–32. DOI: 10.13465/j.cnki.jvs.2012.08.006. GONG F Q, LI X B, LIU X L, et al. Tests for sandstone mechnical properties and failure model under triaxial SHPB loading [J]. Journal of Vibration and Shock, 2012, 31(8): 29–32. DOI: 10.13465/j.cnki.jvs.2012.08.006.
[7]	金解放, 李夕兵, 王观石, 等. 循环冲击载荷作用下砂岩破坏模式及其机理 [J]. 中南大学学报(自然科学版), 2012, 43(4): 1453–1461. JIN J F, LI X B, WANG G S, et al. Failure modes and mechanisms of sandstone under cyclic impact loadings [J]. Journal of Central South University (Science and Technology), 2012, 43(4): 1453–1461.
[8]	刘希灵, 崔佳慧, 王金鹏, 等. 不同应变率下岩石冲击破坏的声发射特性研究 [J]. 爆破, 2018, 35(1): 1–8. DOI: 10.3963/j.issn.1001-487X.2018.01.001. LIU X L, CUI J H, WANG J P, et al. Acoustic emission characteristics analysis of rock under impact loading of different strain rate [J]. Blasting, 2018, 35(1): 1–8. DOI: 10.3963/j.issn.1001-487X.2018.01.001.
[9]	高文学. 岩石动态响应特性及损伤模型研究[D]. 北京: 北京理工大学, 1999.
[10]	LIU L Q, KATSABANIS P D. Development of a continuum damage model for blasting analysis [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(2): 217–231. DOI: 10.1016/S0148-9062(96)00041-1.
[11]	RAYNAUD S, FABRE D, MAZEROLLE F, et al. Analysis of the internal structure of rocks and characterisation of mechanical deformation by a non-destructive method: X-ray tomodensitometry [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1989, 26(6): 293–294. DOI: 10.1016/0148-9062(89)91486-1.
[12]	KAWAKATA H, CHO A, KIYAMA T, et al. Three-dimensional observations of faulting process in Westerly granite under uniaxial and triaxial conditions by X-ray CT scan [J]. Tectonophysics, 1999, 313(3): 293–305. DOI: 10.1016/S0040-51(99)00205-X.
[13]	KAWAKATA H, CHO A, YANAGIDANI T, et al. Gross structure of a fault during its formation process in Westerly granite [J]. Tectonophysics, 2000, 323(1−2): 61–76. DOI: 10.1016/S0040-1951(00)00088-3.
[14]	HUANG S, XIA K, ZHENG H. Observation of microscopic damage accumulation in brittle solids subjected to dynamic compressive loading [J]. Review of Scientific Instruments, 2013, 84(9): 093903. DOI: 10.1063/1.4821497.
[15]	王洪亮, 范鹏贤, 王明洋, 等. 应变率对红砂岩渐进破坏过程和特征应力的影响 [J]. 岩土力学, 2011, 32(5): 1340–1346. DOI: 10.16285/j.rsm.2011.05.008. WANG H L, FAN P X, WANG M Y, et al. Influence of strain rate on progressive failure process and characteristic stresses of red sandstone [J]. Rock and Soil Mechanics, 2011, 32(5): 1340–1346. DOI: 10.16285/j.rsm.2011.05.008.
[16]	金解放. 静载荷与循环冲击组合作用下岩石动态力学特性研究[D]. 长沙: 中南大学, 2012: 13−82. DOI: 10.7666/d.y2198002.
[17]	杨军, 高文学. 岩石冲击损伤特性的声波测试研究 [J]. 黑龙江矿业学院学报, 2000, 10(1): 50–53. DOI: 10.3969/j.issn.1671-0118.2000.01.015. YANG J, GAO W X. Experimental study on damage properties of rock under dynamic loading [J]. Journal of Helongjiang Mining Institute, 2000, 10(1): 50–53. DOI: 10.3969/j.issn.1671-0118.2000.01.015.
[18]	KAWAMOTO T, ICHIKAWA Y, KYOYA T. Deformation and fracturing behaviour of discontinuous rock mass and damage mechanics theory [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1988, 25(4): A178. DOI: 10.1016/0148-9062(88)91668-3.

施引文献

期刊类型引用(14)

1.	赵林海，吴功勇，聂兴信，李广齐，阮顺领，江松，李宗利，苟晓斌，王超. 矿山岩石动力学研究现状及展望. 黄金. 2025(01): 37-46 . 百度学术
2.	李嘉伟，郑永香，王伟，牛庆合. 非均质砂岩铀矿层爆破增渗裂纹扩展数值模拟. 铀矿冶. 2025(01): 18-29 . 百度学术
3.	杨尚，宁建国，王俊，高明涛，史新帅，张朝辉. 动载作用下锚固体动态失稳试验研究. 岩石力学与工程学报. 2025(02): 409-426 . 百度学术
4.	戴俊，刘博源. 冲击荷载下含孔洞花岗岩动态力学特性研究. 河南理工大学学报(自然科学版). 2025(03): 172-180 . 百度学术
5.	杨彦鑫，林子雲，吴建建，卢锋. 基于SHPB的切缝药包防护特性研究. 工程爆破. 2024(02): 19-26 . 百度学术
6.	王磊，陈礼鹏，刘怀谦，朱传奇，李少波，范浩，张帅，王安铖. 不同初始瓦斯压力下煤体动力学特性及其劣化特征. 岩土力学. 2023(01): 144-158 . 百度学术
7.	石浩，张后全，宋雷，李明，黎明镜，林钢，施鑫，龙伟，吴捷豪. 动载下含预制裂纹砂岩的力学特性及破裂过程研究. 振动与冲击. 2023(04): 28-38 . 百度学术
8.	雷学文，李浩明，孟庆山，洪胜男，周皓然，蒋雪. 冲击荷载下珊瑚礁灰岩动态力学特性及损伤特征. 长江科学院院报. 2023(05): 85-93 . 百度学术
9.	徐泽辉，何童，杜光钢，刘磊. 恒定动载下高温水冷后玄武岩的动力特性及本构模型. 爆炸与冲击. 2023(06): 62-75 . 本站查看
10.	耿昊，杨江坤，宋彦琦，马宏发，郑俊杰，杨俊涛. 泥岩动态冲击力学响应及裂纹演化试验研究. 金属矿山. 2023(10): 45-52 . 百度学术
11.	孟祥，安华明，刘磊. 高温作用下角砾岩动态力学特性研究. 化工矿物与加工. 2022(03): 49-52 . 百度学术
12.	孙晓元，李吉辉，丁浩，金廷旭，谢建林，梁磊. 基于SHPB动载过程的煤岩冲击破坏特征试验研究. 煤炭与化工. 2022(08): 1-5 . 百度学术
13.	潘博，汪旭光，郭连军，徐振洋，闫大洋. 组合静载条件下SHPB试件长径比优选研究. 爆破. 2022(03): 1-9 . 百度学术
14.	徐景龙，郭连军，王军祥，王雪松. 基于细观角度的岩石冲击动力学研究进展及展望. 矿业研究与开发. 2022(09): 68-78 . 百度学术

其他类型引用(10)

资源附件(0)

访问统计

图(21) / 表(3)

计量

文章访问数: 600
HTML全文浏览量: 357
PDF下载量: 123
被引次数: 24

1. 鱼雷入水受力分析
2. 数值模型
3. 鱼雷入水冲击载荷分析
3.1 鱼雷入水载荷分析
3.2 入水速度对鱼雷入水的影响
3.3 入水角度对鱼雷入水的影响
3.4 不同头型对雷体入水的影响
4. 结论

基于SHPB实验的砂岩动态破坏过程及应变-损伤演化规律研究

doi: 10.11883/bzycj-2020-0288

作者简介: 张明涛（1994－ ），男，硕士，2868992828@qq.com

通讯作者: 王奇智（1987－ ），男，博士，讲师，wangqizhi118@126.com

计量

出版历程

Dynamic failure process and strain-damage evolution law of sandstone based on SHPB experiments

1. 鱼雷入水受力分析

2. 数值模型

3. 鱼雷入水冲击载荷分析

3.1 鱼雷入水载荷分析

3.2 入水速度对鱼雷入水的影响

3.3 入水角度对鱼雷入水的影响

3.4 不同头型对雷体入水的影响

4. 结论

期刊类型引用(14)

其他类型引用(10)

计量

出版历程

目录

1. 鱼雷入水受力分析

2. 数值模型

3. 鱼雷入水冲击载荷分析

3.1 鱼雷入水载荷分析

3.2 入水速度对鱼雷入水的影响

3.3 入水角度对鱼雷入水的影响

3.4 不同头型对雷体入水的影响

4. 结论

作者简介:
张明涛（1994－　），男，硕士，2868992828@qq.com

通讯作者:
王奇智（1987－　），男，博士，讲师，wangqizhi118@126.com