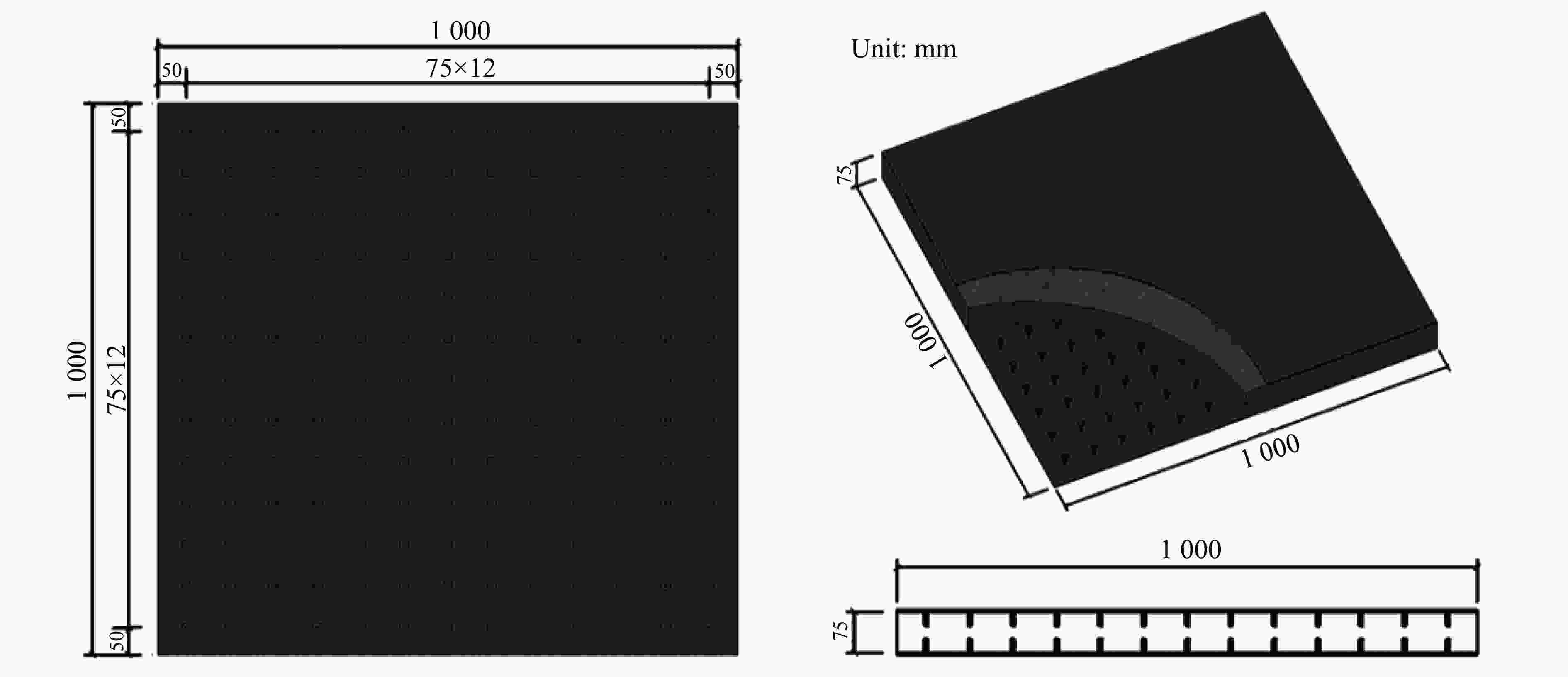
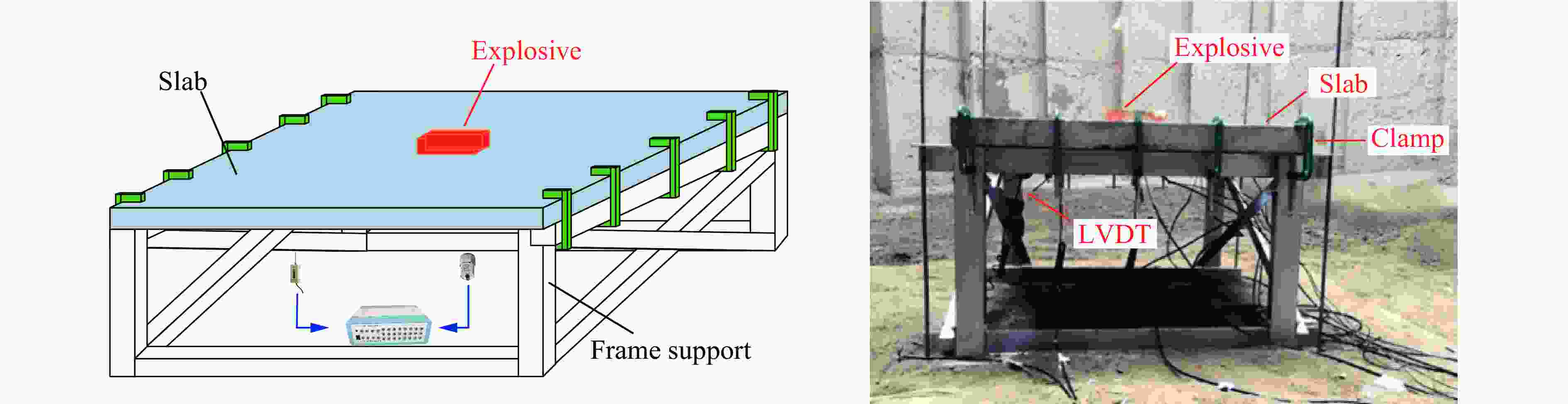
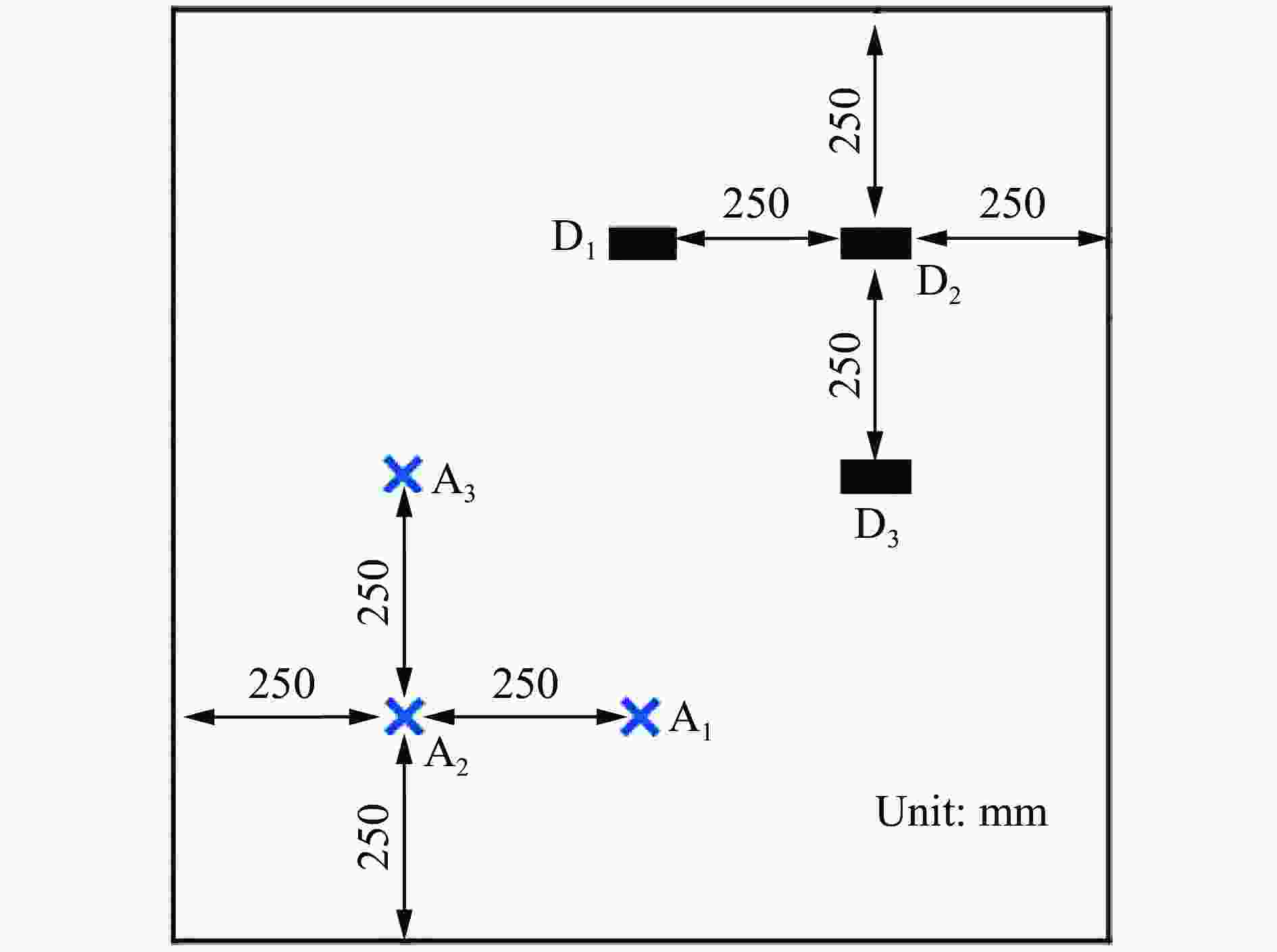
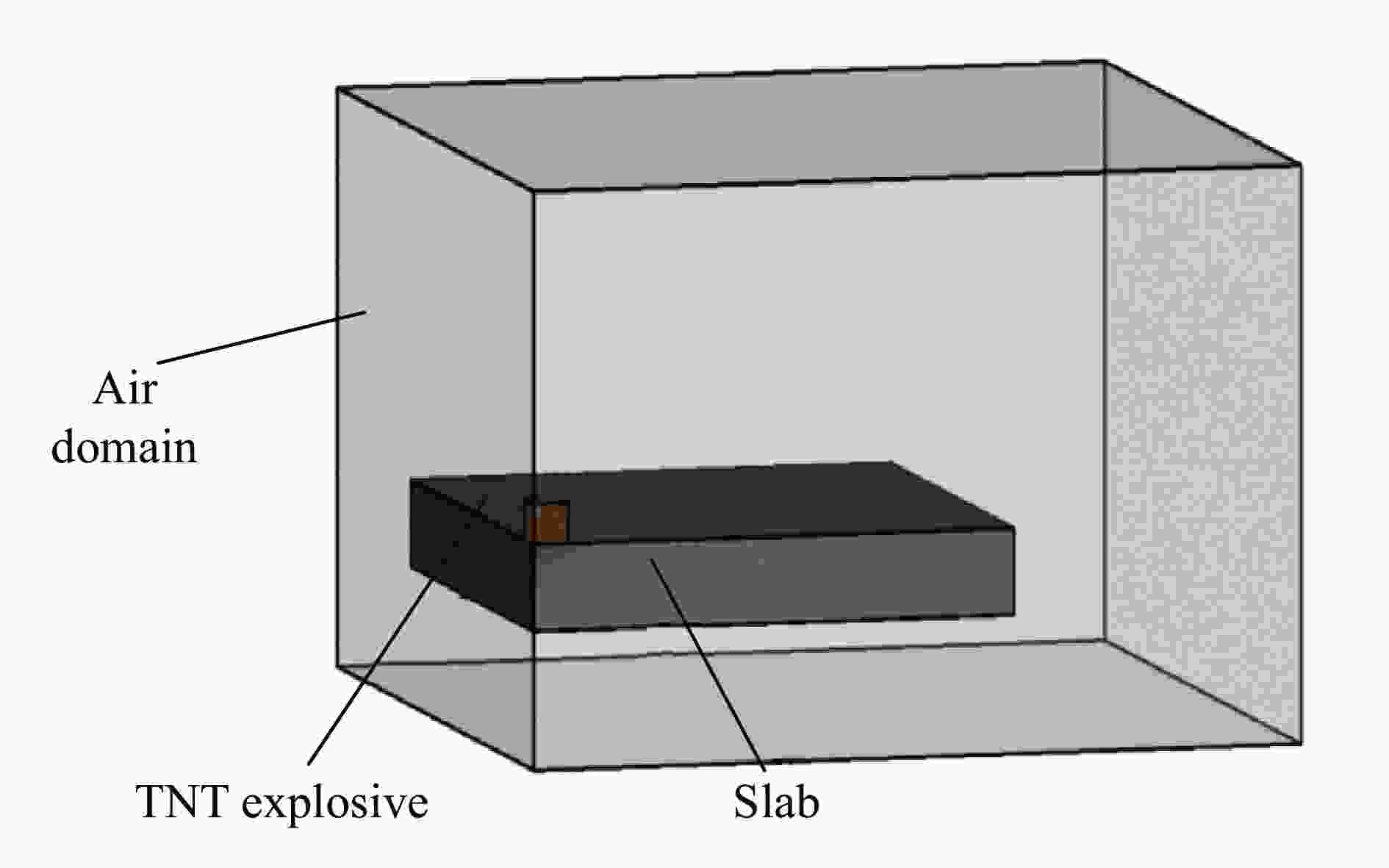
Analysis on the blast resistance of steel concrete composite slab
-
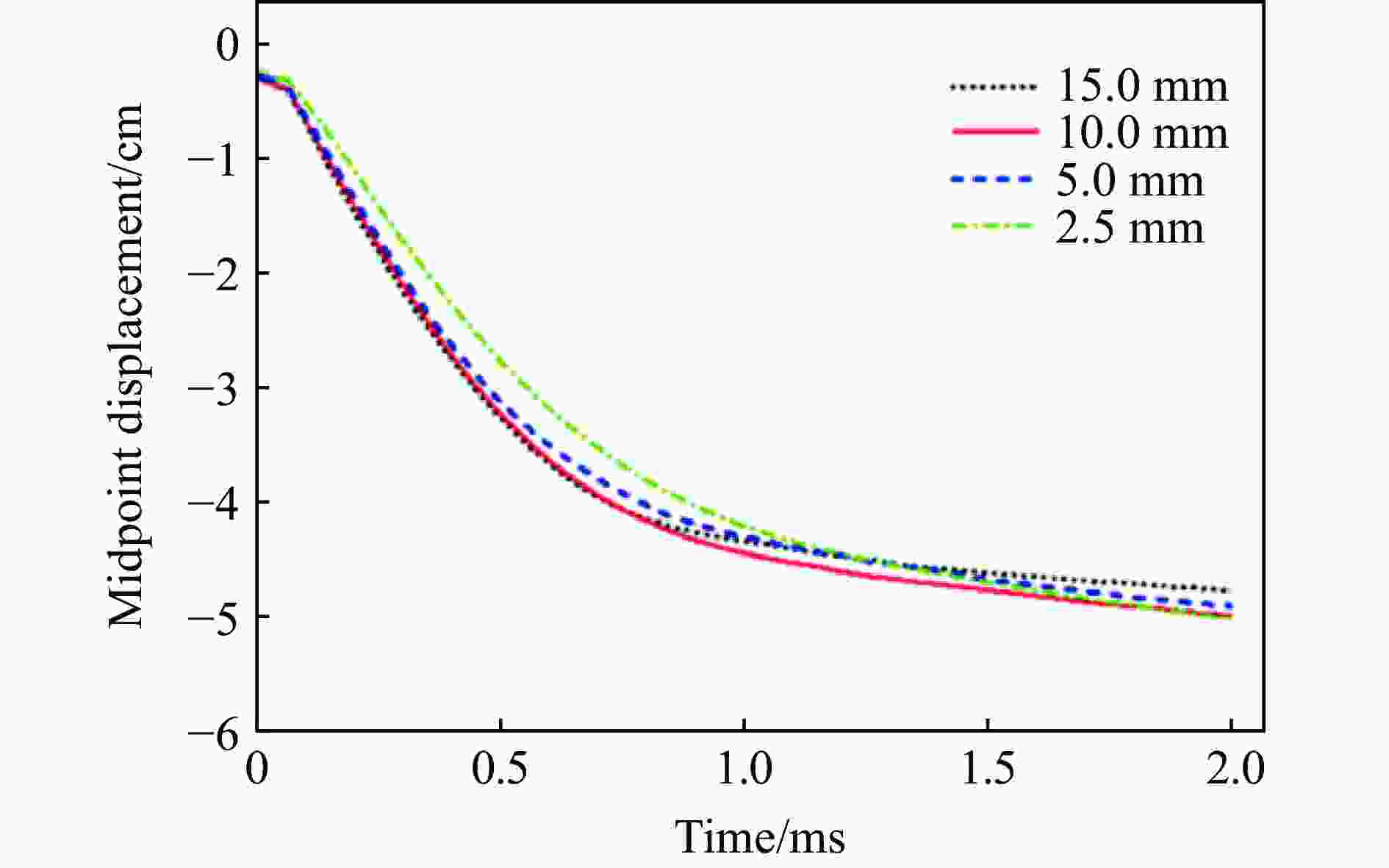
摘要: 钢-混凝土-钢组合板是一种新型的组合结构，与传统钢筋混凝土板相比，具有抗剪强度高、延性大、耗能能力强等特点，目前已经被广泛应用于核反应堆安全壳、海洋平台及储油罐等结构。本文中，设计并制作了缩尺的普通钢筋混凝土板和钢-混凝土-钢组合板，开展了在接触爆炸荷载作用下的实验研究，通过损伤分析、跨中最大挠度对比研究不同板的抗爆性能。基于ANSYS/LS-DYNA非线性有限元程序，研究了钢-混凝土-钢组合板的损伤模式、跨中最大挠度等，并与实验结果进行了对比分析，验证了有限元分析模型的准确性和适用性。参数化分析了炸药量、混凝土强度和钢板厚度等参数对钢-混凝土-钢组合板抗爆性能的影响规律。利用多参数回归分析方法，提出钢-混凝土-钢组合板跨中挠度的预测公式。结果表明：提高混凝土强度可以降低结构的塑性损伤, 增加钢板厚度可以有效降低钢-混凝土-钢组合板的跨中最大挠度。相对于普通钢筋混凝土板，钢-混凝土-钢组合板保持了良好的整体性，且具有继续承载的能力。拟合公式能够较好地预测钢-混凝土-钢组合板跨中挠度与药量和钢板厚度的关系。Abstract: Steel concrete steel composite slab is a new type of composite structure. It has the characteristics of high shear strength, high ductility and strong energy consumption compared with the traditional reinforced concrete slab. The new type composite slab has been widely used in nuclear reactor containment, offshore platform and oil storage tank. Two scaled reinforced concrete slabs (RCS) and steel-concrete-steel (SCS) composite slabs were designed and manufactured, and the experimental study was carried out under the contact explosion load. The anti-blast performance of different slabs was analyzed by damage analysis and displacement. Based on ANSYS/LS-DYNA nonlinear finite element program, the damage modes and the maximum deflection of the mid-span of the steel-concrete composite slab are numerically investigated, and the numerical damage modes and maximum deflection of the steel-concrete composite slabs are compared with the test results of the components, which verifies the accuracy and applicability of the finite element analysis model. In this study, the influences of parameters, such as explosive quantity, concrete strength and steel plate thickness on the anti-blast performance of steel-concrete composite plate are numerically analyzed by parametric analysis. Then, the prediction formula of mid-span deflection of SCS slab is proposed by using the method of multi parameter regression analysis. The results show that the plastic damage of the structure can be reduced by increasing the strength of concrete, and the maximum deflection of SCS can be effectively reduced by increasing the thickness of steel plate. It is indicated that the SCS maintains good integrity and owns the ability to continue to carry load compared with the RCS. Finally, the fitting formula can well predict the relationship between the mid span deflection of SCS plate and the charge amount and the thickness of steel plate.
-
图 9 RCS试件钢筋变形的实验和数值模拟结果
Figure 9. Experimental and numerical results of RCS’s rebar deformation
图 20 不同炸药量时SCS中混凝土的有效塑性应变
Figure 20. Effective plastic strains of concrete in SCS with different explosive charges
图 21 不同炸药量时SCS的跨中位移曲线
Figure 21. Mid-span displacement curves of SCS with different explosive charges
图 22 不同炸药量时SCS的跨中最大位移
Figure 22. Maximum displacements of SCS with different explosive charges
图 23 不同混凝土强度时SCS混凝土的有效塑性应变
Figure 23. Effective plastic strains of concrete in SCS with different concrete strengths
图 24 不同混凝土时SCS的跨中位移曲线
Figure 24. Mid-span displacement curves of SCS with different concrete strengths
图 25 不同混凝土时SCS的跨中最大位移
Figure 25. Maximum displacement of SCS with different concrete strengths
图 26 不同钢板厚度时SCS混凝土的有效塑性应变
Figure 26. Effective plastic strains of concrete in SCS with different thickness of steel plate
图 27 不同钢板厚度时SCS的跨中位移曲线
Figure 27. Mid-span displacement curves of SCS with different thicknesses of steel plates
图 28 不同钢板厚度时SCS的跨中最大位移
Figure 28. Maximum displacements of SCS with different thicknesses of steel plates
图 29 SCS跨中挠度与炸药量、钢板厚度的关系
Figure 29. Mid-span deflections of SCS versus explosive charges and thicknesses of steel plates
表 1 材料力学性能参数
Table 1. Mechanical properties of materials
材料 型号 弹性模量/GPa 抗压强度/MPa 屈服强度/MPa 抗拉强度/MPa 混凝土 C30 30 30 钢筋 HRB335 200 341 472 钢板 Q235 200 235 370 焊钉 A2-50 200 210 500 
下载: 导出CSV
表 2 试件的损伤和挠度
Table 2. Damages and deflections of specimens
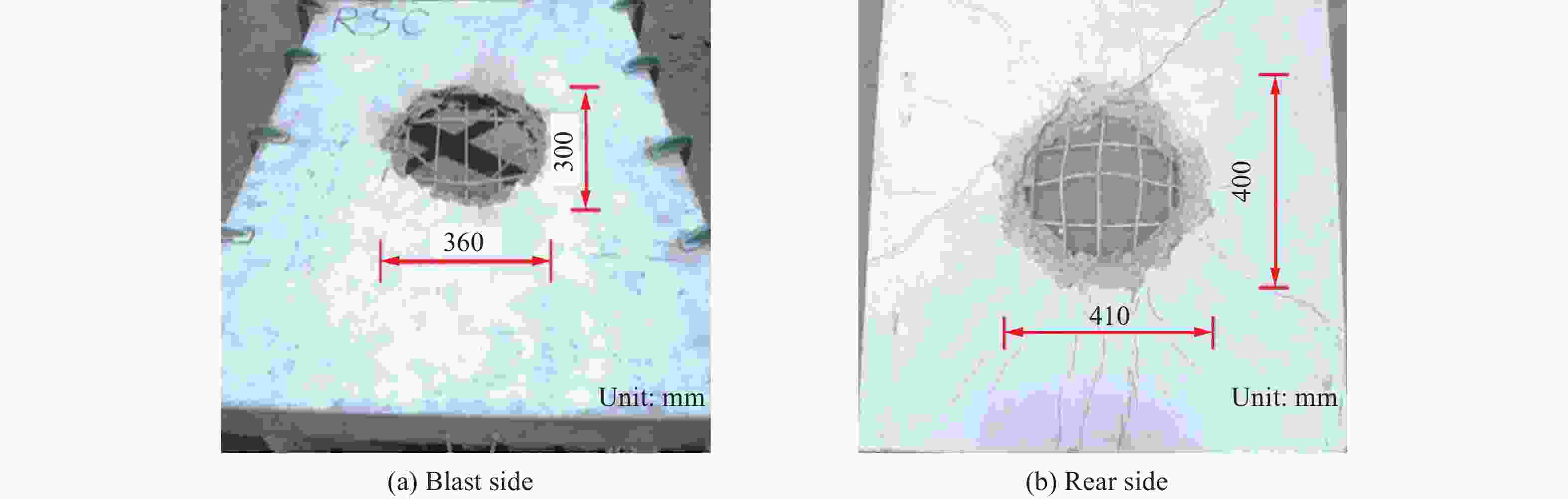
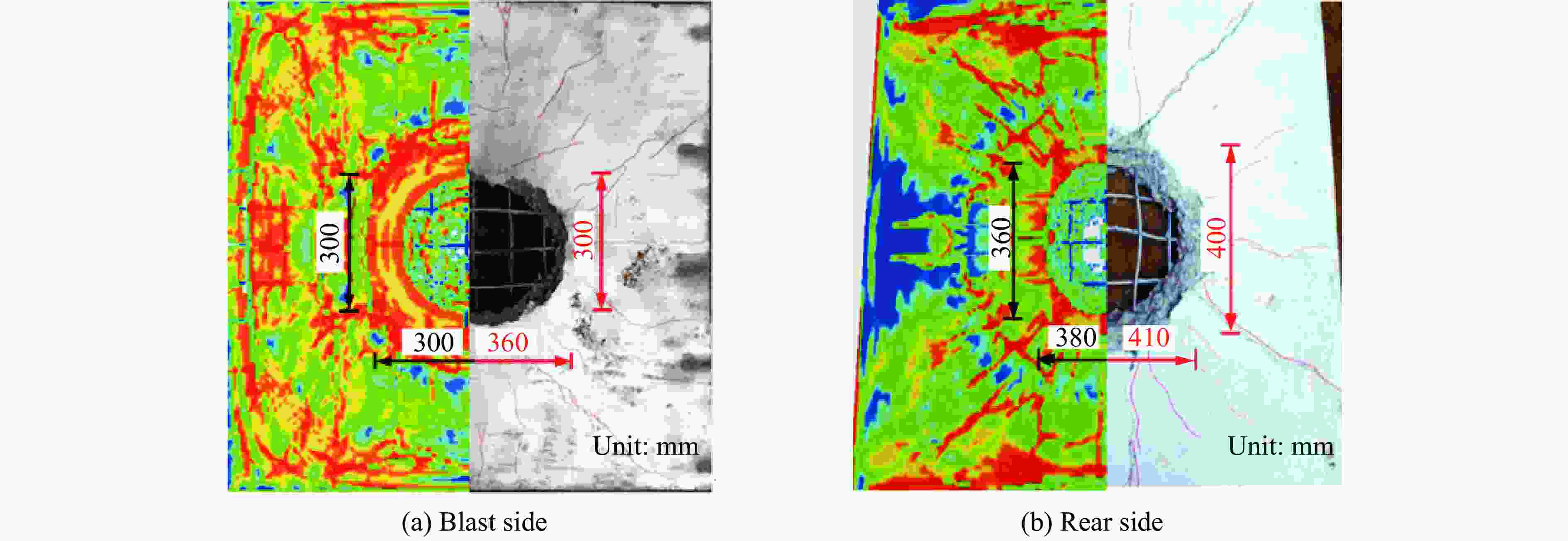
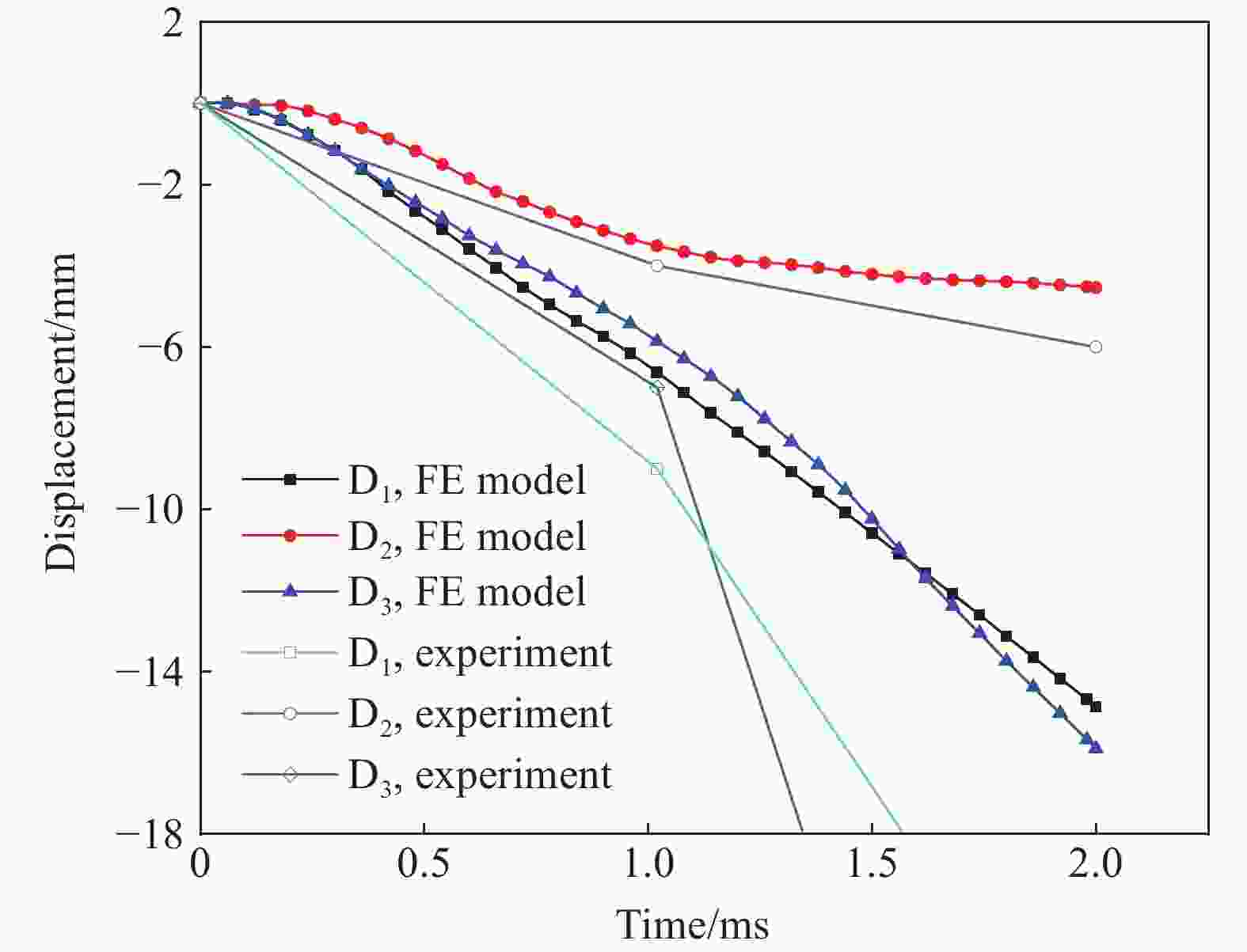
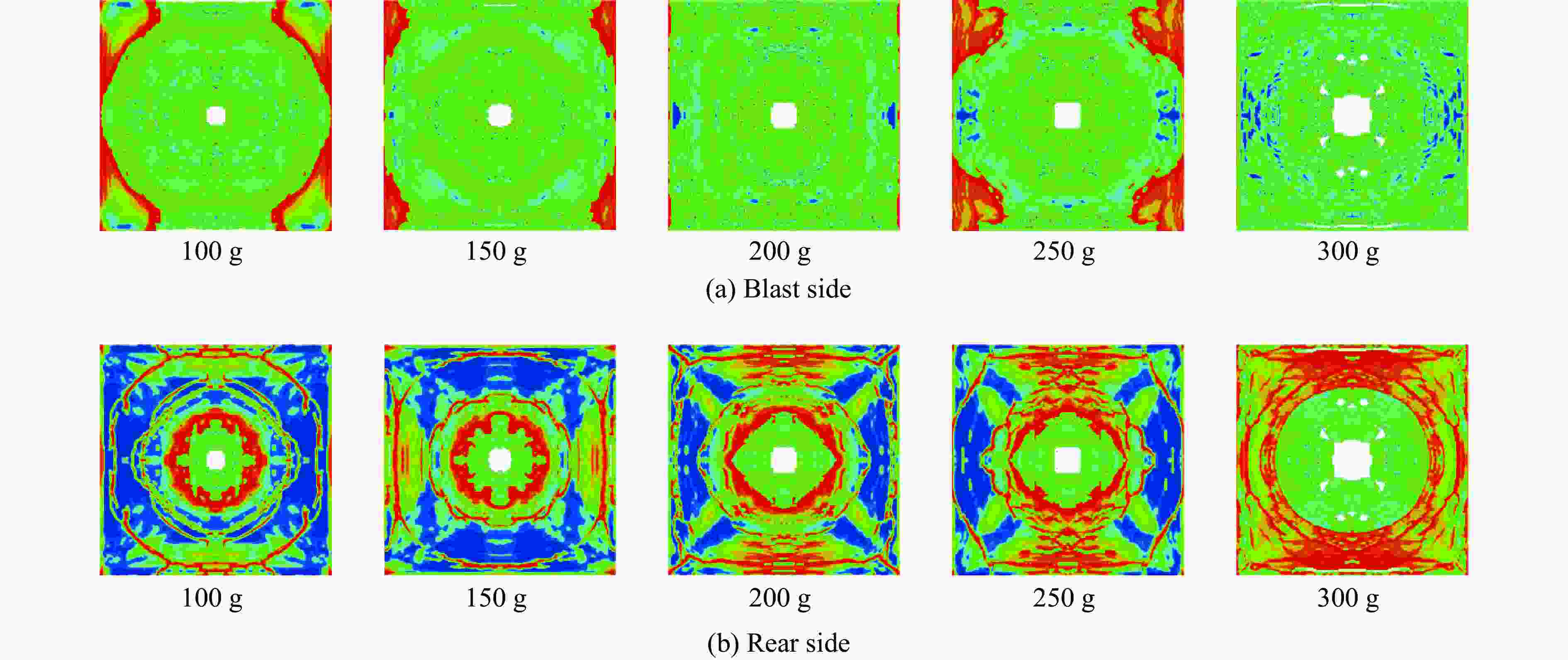
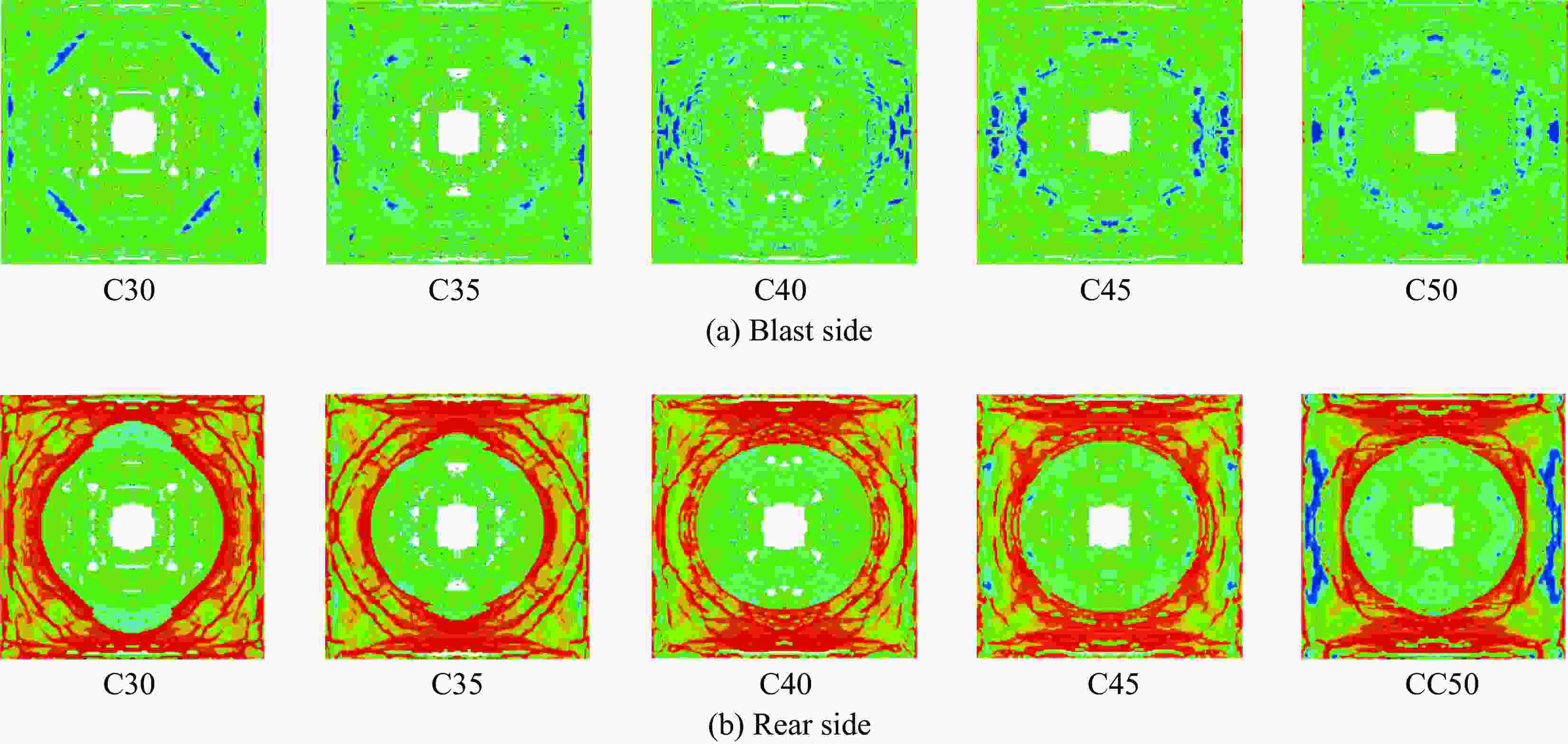
试件 迎爆面爆坑尺寸/mm 背爆面爆坑尺寸/mm 实验跨中挠度/mm 数值跨中挠度/mm 是否发生贯穿破坏 整体性 是否能继续承载 RCS 360×300 410×400 50 46.2 是 一般 否 SCS 280×180 35 27.4 否 好 是
下载: 导出CSV
表 3 混凝土-钢-混凝土组合板跨中挠度经验公式拟合结果
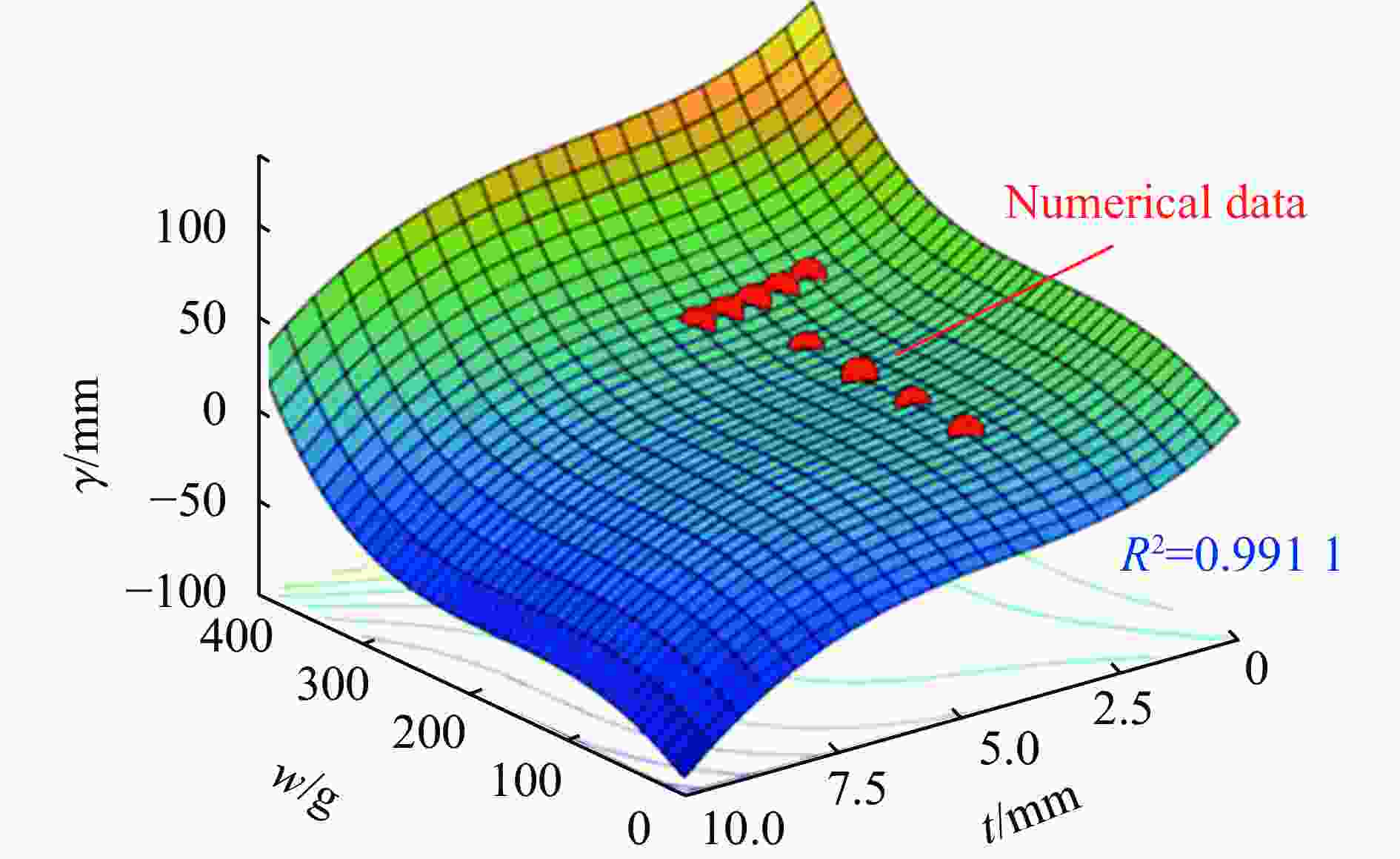
Table 3. Fitting results of empirical formula for mid-span deflection of SCS
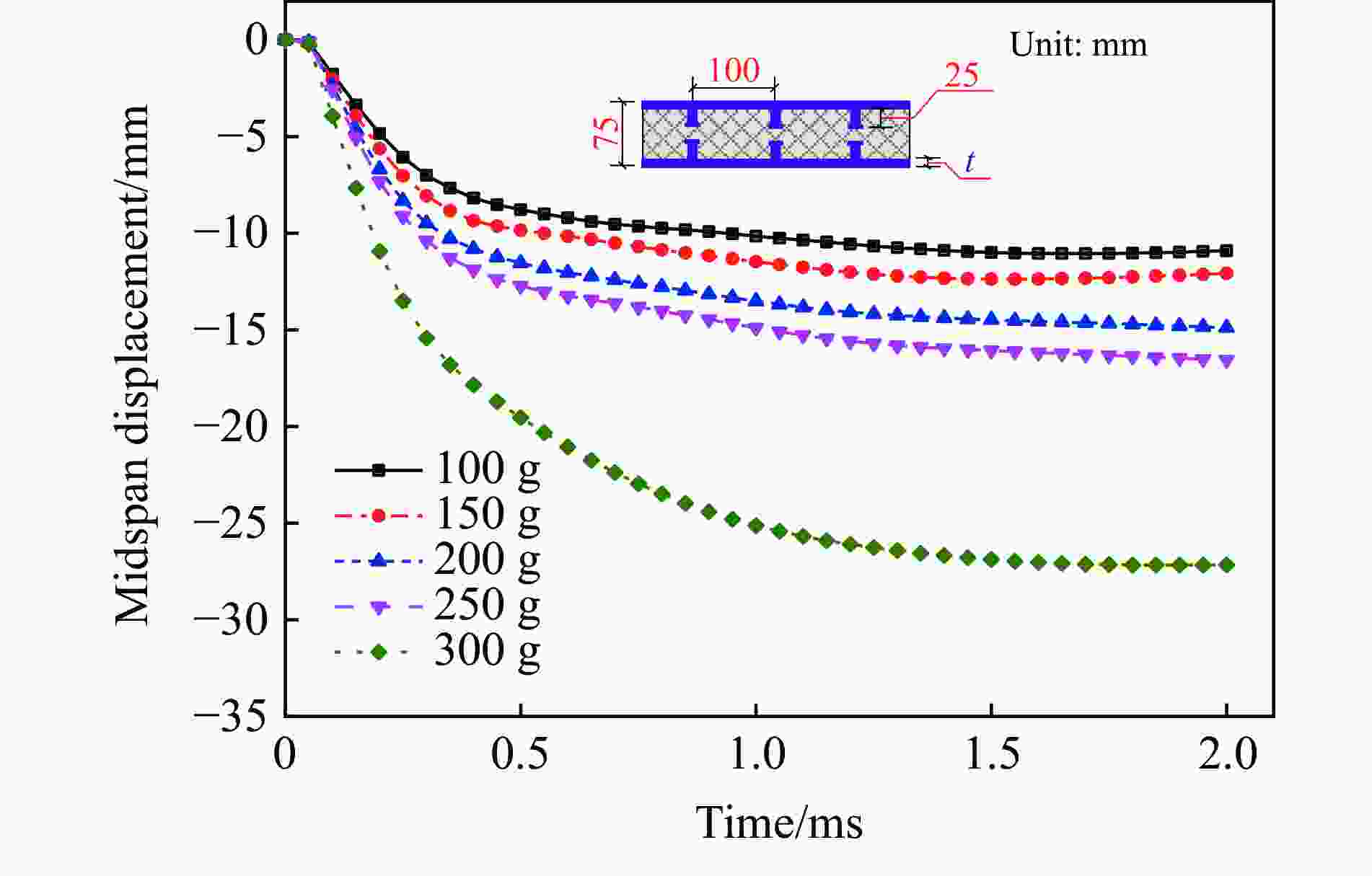
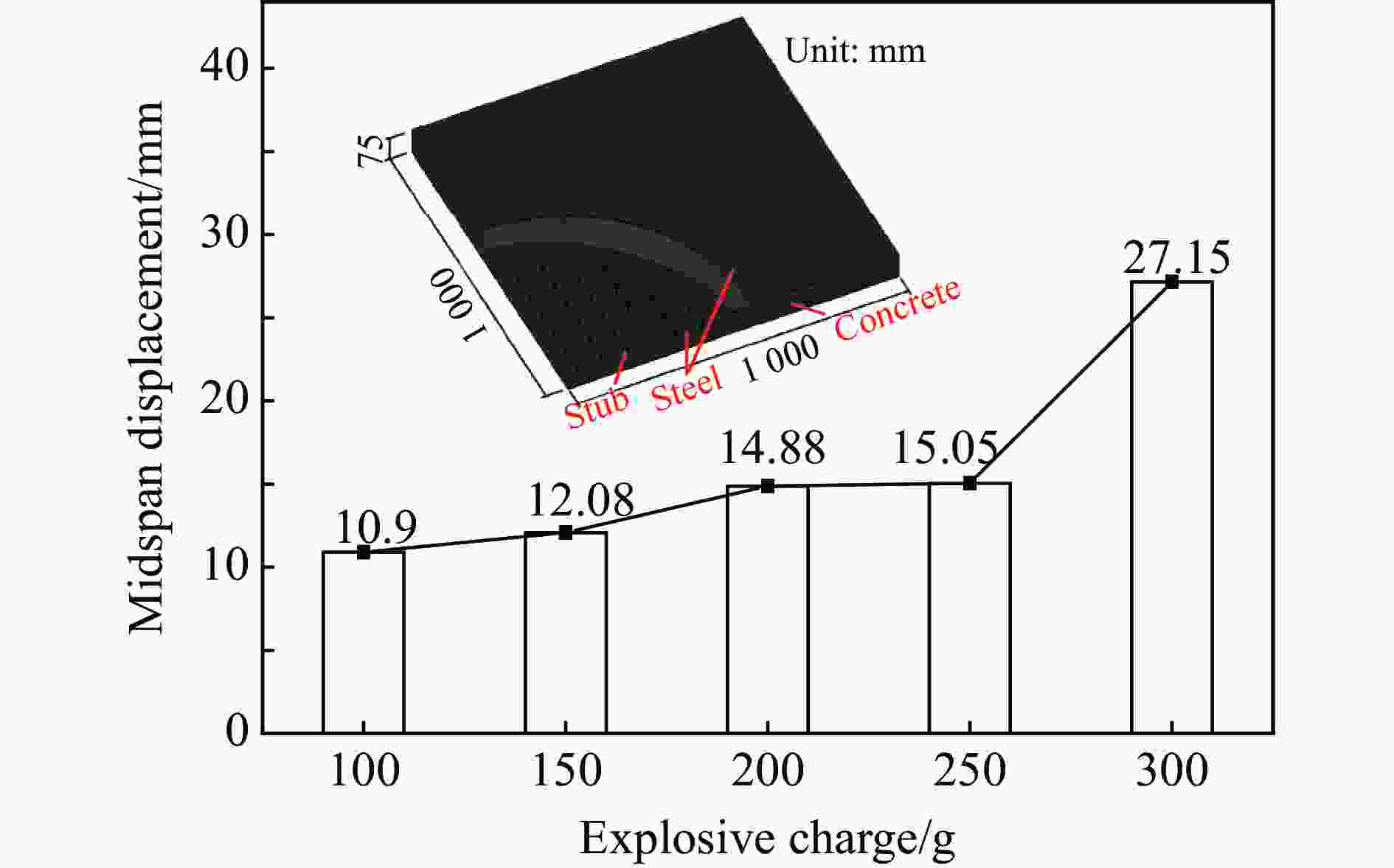
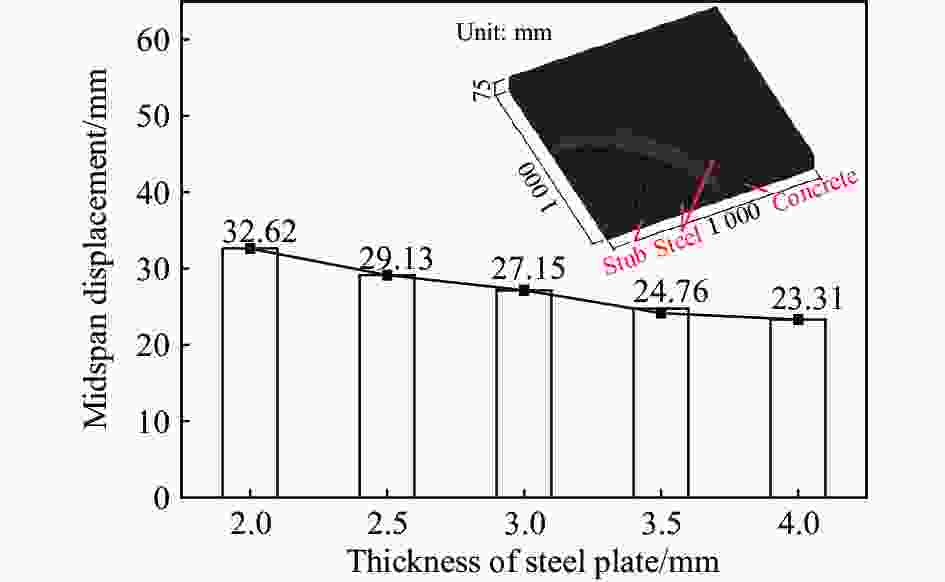
炸药量w/g 钢板厚度t/mm 实际挠度$ {\gamma }_{0} $/mm 预测挠度$ \gamma $/mm 误差/% 100 3.0 10.90 10.623 14 2.54 150 3.0 12.08 13.136 22 8.74 200 3.0 14.88 13.372 48 10.13 250 3.0 15.05 16.003 81 6.34 300 3.0 27.15 26.762 19 1.43 300 2.0 32.62 32.594 10 0.08 300 2.5 29.13 29.235 85 0.36 300 3.5 24.76 24.870 36 0.45 300 4.0 23.31 23.281 85 0.12
下载: 导出CSV
-
[1] 王威, 张龙旭, 苏三庆, 等. 波形钢板剪力墙抗震性能试验研究 [J]. 建筑结构学报, 2018, 39(5): 36–44. DOI: 10.14006/j.jzjgxb.2018.05.005.WANG W, ZHANG L X, SU S Q, et al. Experimental research on seismic behavior of corrugated steel plate shear wall [J]. Journal of Building Structures, 2018, 39(5): 36–44. DOI: 10.14006/j.jzjgxb.2018.05.005. [2] 聂建国, 樊健生, 黄远, 等. 钢板剪力墙的试验研究 [J]. 建筑结构学报, 2010, 31(9): 1–8. DOI: 10.14006/j.jzjgxb.2010.09.015.NIE J G, FAN J S, HUANG Y, et al. Experimental research on steel plate shear wall [J]. Journal of Building Structures, 2010, 31(9): 1–8. DOI: 10.14006/j.jzjgxb.2010.09.015. [3] ZHAO C F, LU X, WANG Q, et al. Experimental and numerical investigation of steel-concrete (SC) slabs under contact blast loading [J]. Engineering Structures, 2019, 196: 109337. DOI: 10.1016/j.engstruct.2019.109337. [4] ZHAO C F, WANG Q, LU X, et al. Blast resistance of small-scale RCS in experimental test and numerical analysis [J]. Engineering Structures, 2019, 199: 109610. DOI: 10.1016/j.engstruct.2019.109610. [5] SOHEL K M A, LIEW J Y R. Behavior of steel-concrete-steel sandwich slabs subject to impact load [J]. Journal of Constructional Steel Research, 2014, 100: 163–175. DOI: 10.1016/j.jcsr.2014.04.018. [6] LIEW J Y R, WANG T Y. Novel steel-concrete-steel sandwich composite plates subject to impact and blast load [J]. Advances in Structural Engineering, 2011, 14(4): 673–687. DOI: 10.1260/1369-4332.14.4.673. [7] ZHAO C F, CHEN J Y. Damage mechanism and mode of square reinforced concrete slab subjected to blast loading [J]. Theoretical and Applied Fracture Mechanics, 2013, 63: 54–62. DOI: 10.1016/j.tafmec.2013.03.006. [8] ZHAO C F, WANG Q, LU X, et al. Numerical study on dynamic behaviors of NRC slabs in containment dome subjected to close-in blast loading [J]. Thin-Walled Structures, 2019, 135: 269–284. DOI: 10.1016/j.tws.2018.11.013. [9] 赵春风, 王强, 王静峰, 等. 近场爆炸作用下核电厂安全壳穹顶钢筋混凝土板的抗爆性能 [J]. 高压物理学报, 2019, 33(2): 025101. DOI: 10.11858/gywlxb.20180598.ZHAO C F, WANG Q, WANG J F, et al. Blast resistance of containment dome reinforced concrete slab in NPP under close-in explosion [J]. Chinese Journal of High Pressure Physics, 2019, 33(2): 025101. DOI: 10.11858/gywlxb.20180598. [10] 赵春风, 卢欣, 何凯城, 等. 单钢板混凝土剪力墙抗爆性能研究 [J]. 爆炸与冲击, 2020, 40(12): 121403. DOI: 10.11883/bzycj-2020-0058.ZHAO C F, LU X, HE K C, et al. Blast resistance property of concrete shear wall with single-side steel plate [J]. Explosion and Shock Waves, 2020, 40(12): 121403. DOI: 10.11883/bzycj-2020-0058. [11] 汪维, 杨建超, 汪剑辉, 等. POZD涂层方形钢筋混凝土板抗接触爆炸试验研究 [J]. 爆炸与冲击, 2020, 40(12): 121402. DOI: 10.11883/bzycj-2020-0180.WANG W, YANG J C, WANG J H, et al. Experimental research on anti-contact explosion of POZD coated square reinforced concrete slab [J]. Explosion and Shock Waves, 2020, 40(12): 121402. DOI: 10.11883/bzycj-2020-0180. [12] YAN C, WANG Y H, ZHAI X M, et al. Low velocity impact performance of curved steel-concrete-steel sandwich shells with bolt connectors [J]. Thin-Walled Structures, 2020, 150: 106672. DOI: 10.1016/j.tws.2020.106672. [13] 中华人民共和国住房和城乡建设部. 钢板剪力墙技术规程: JGJ/T 380–2015 [S]. 北京: 中国建筑工业出版社, 2016. [14] HALLQUIST J O. LS-DYNA keyword user’s manual [Z]. Livermore: Livermore Software Technology Corporation, 2007. [15] MALVAR L J, CRAWFORD J E, MORILL K B. K&C concrete material model release Ⅲ: automated generation of material model input: Technical Report TR-99-24.3 [R]. Glendale: Karagozian and Case Structural Engineers, 2000. [16] BISCHOFF P H, PERRY S H. Compressive behaviour of concrete at high strain rates [J]. Materials and Structures, 1991, 24(6): 425–450. DOI: 10.1007/BF02472016. -
计量
- 文章访问数: 631
- HTML全文浏览量: 336
- PDF下载量: 119
- 被引次数: 0