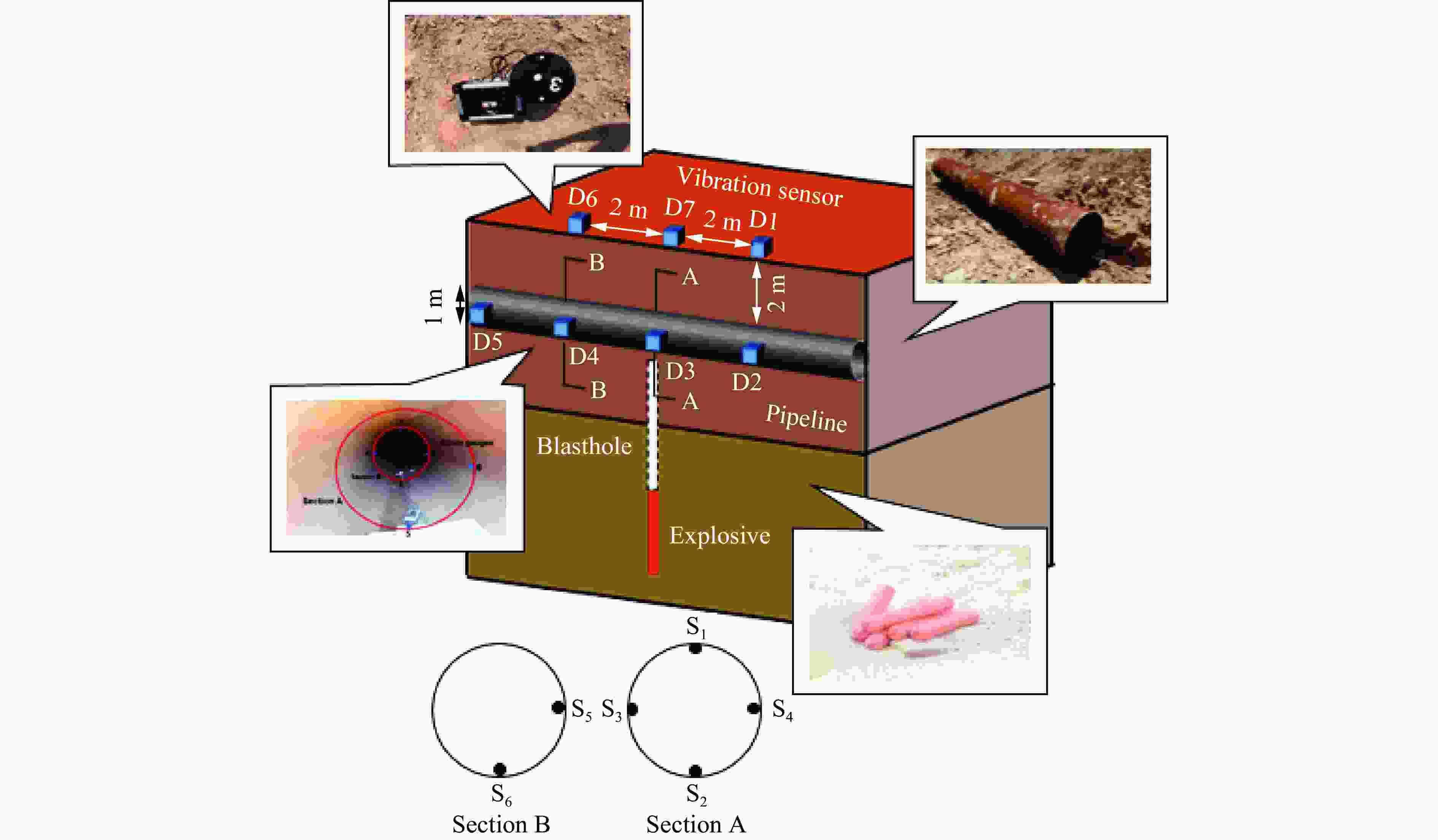
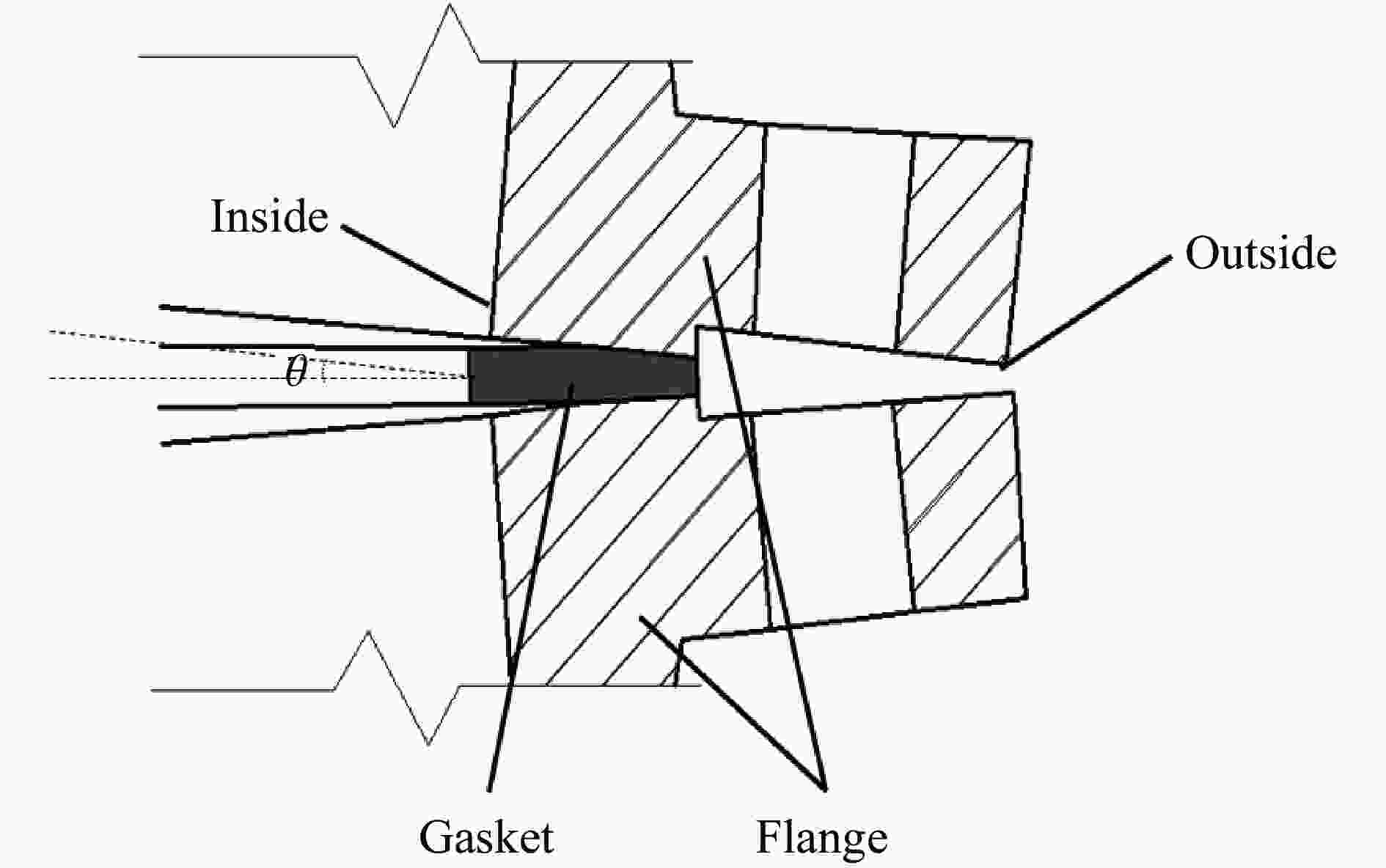
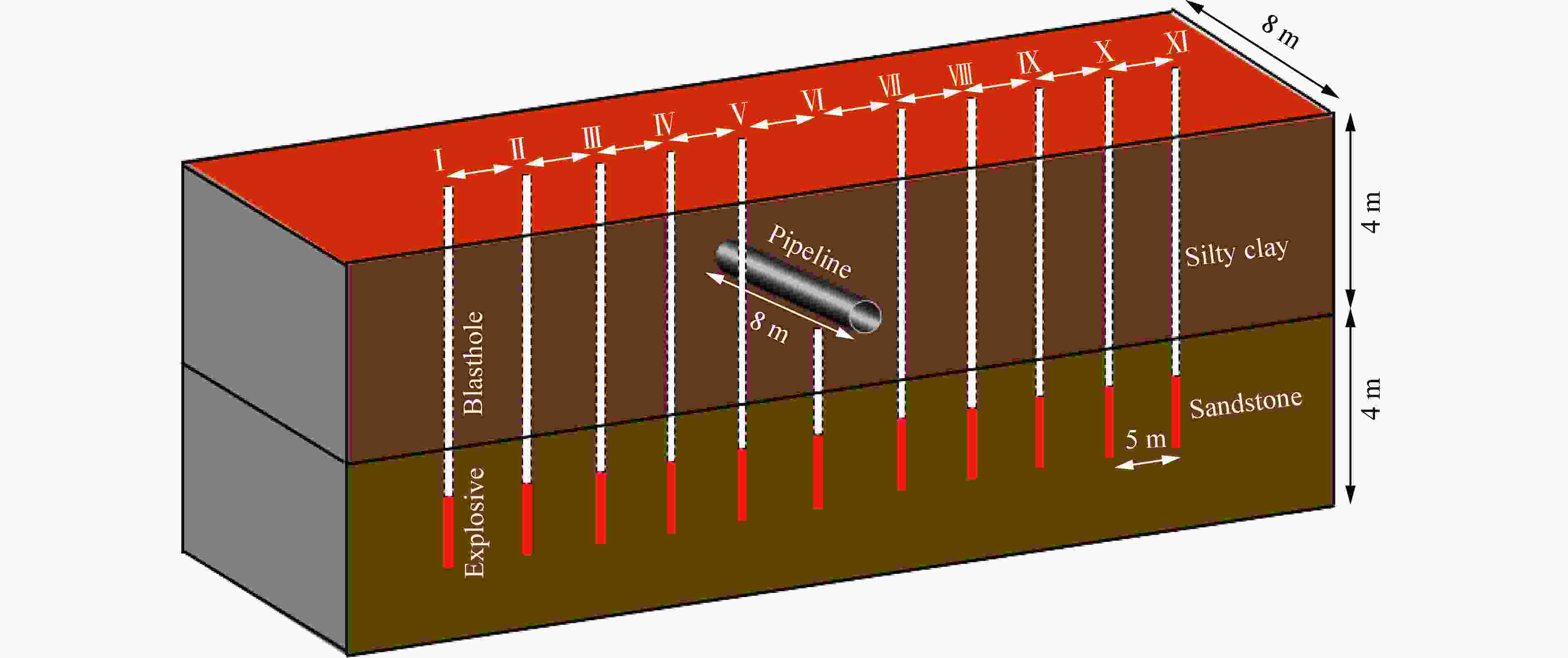
Dynamic failure mechanism of gas pipeline with flange joint under blasting seismic wave
-
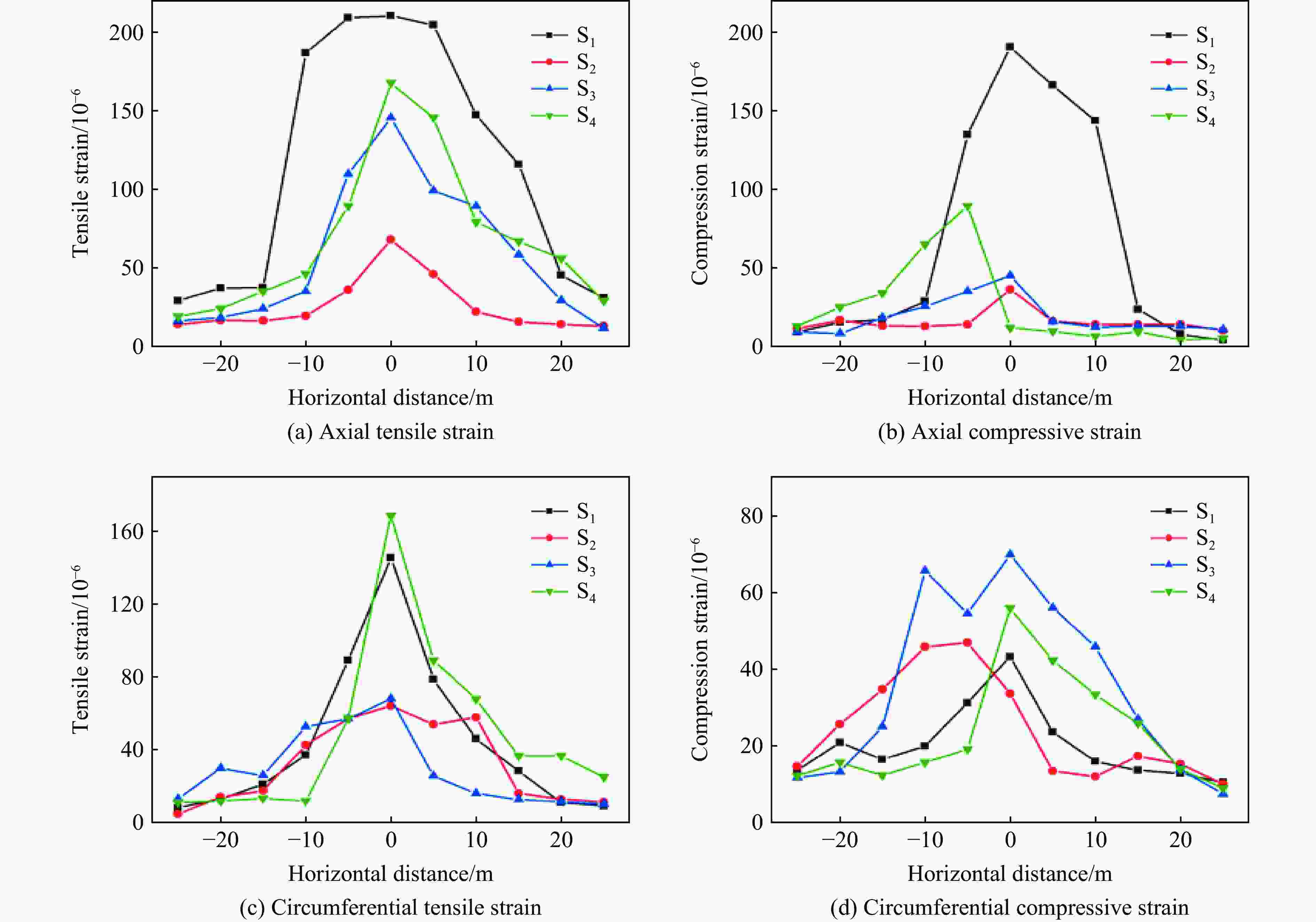
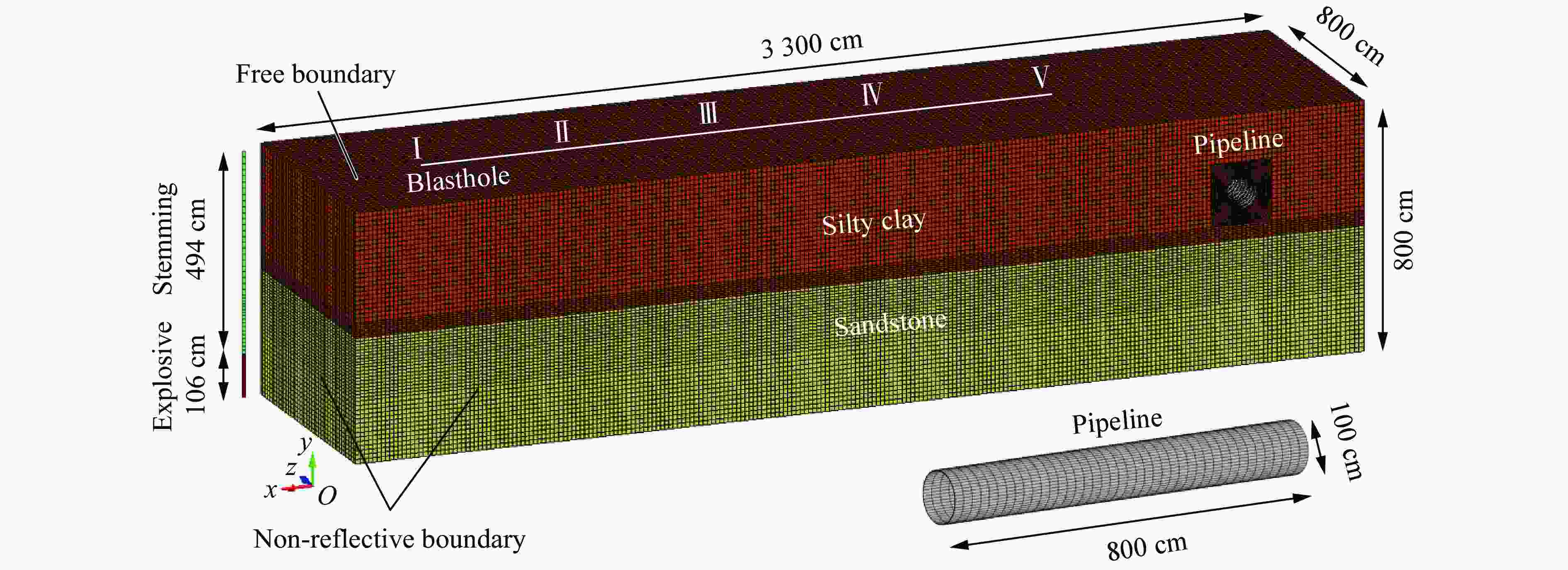
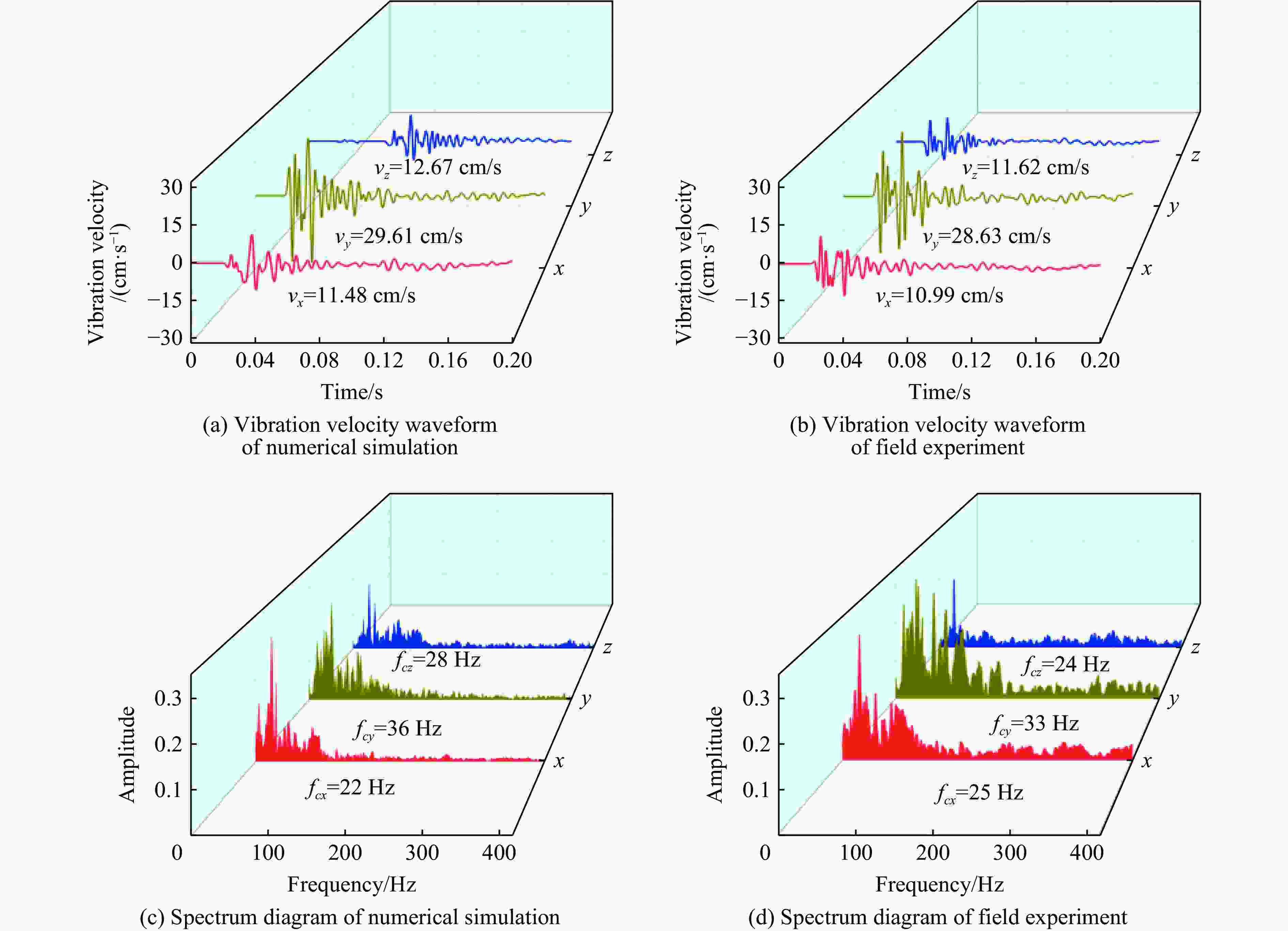
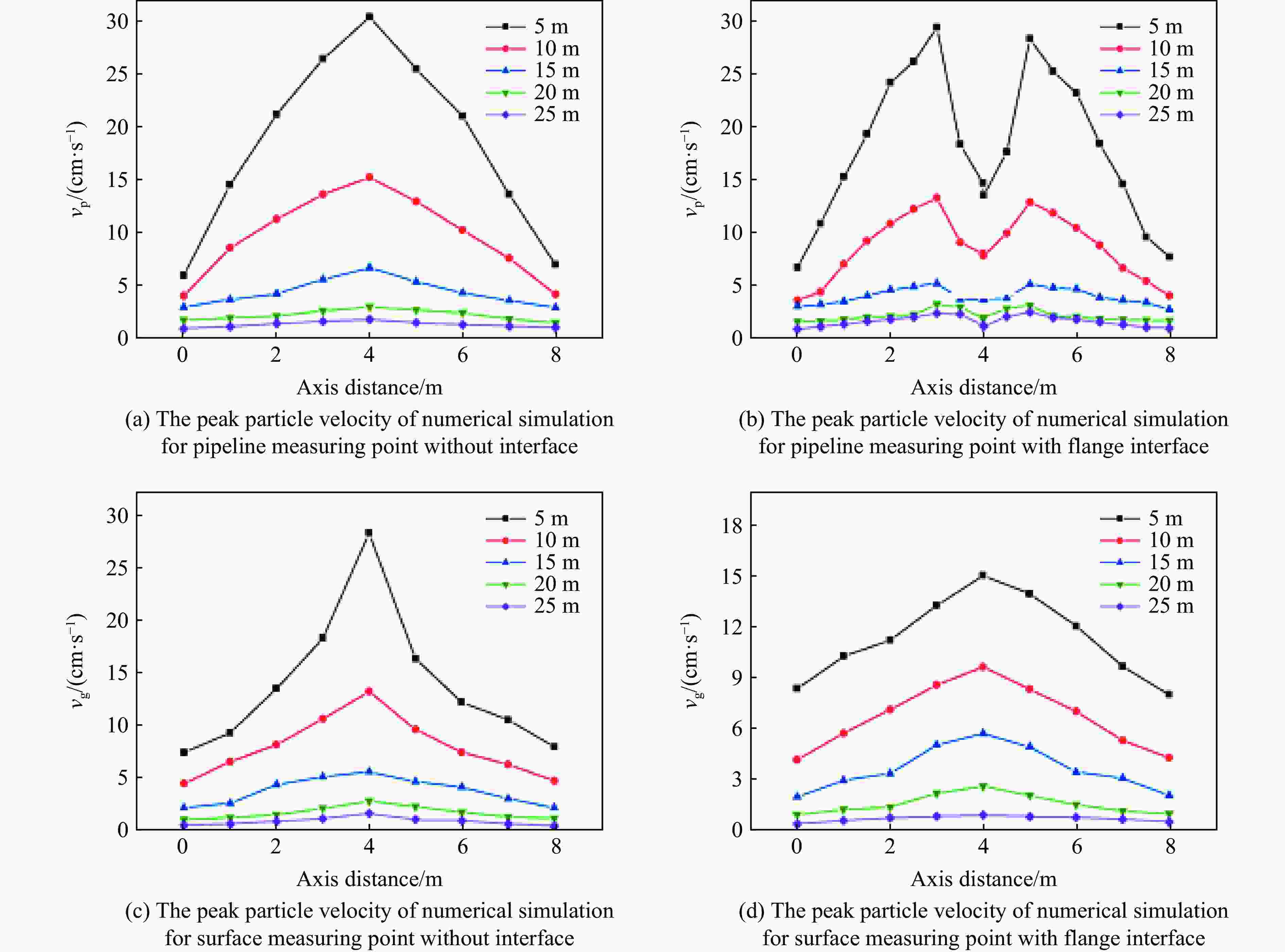
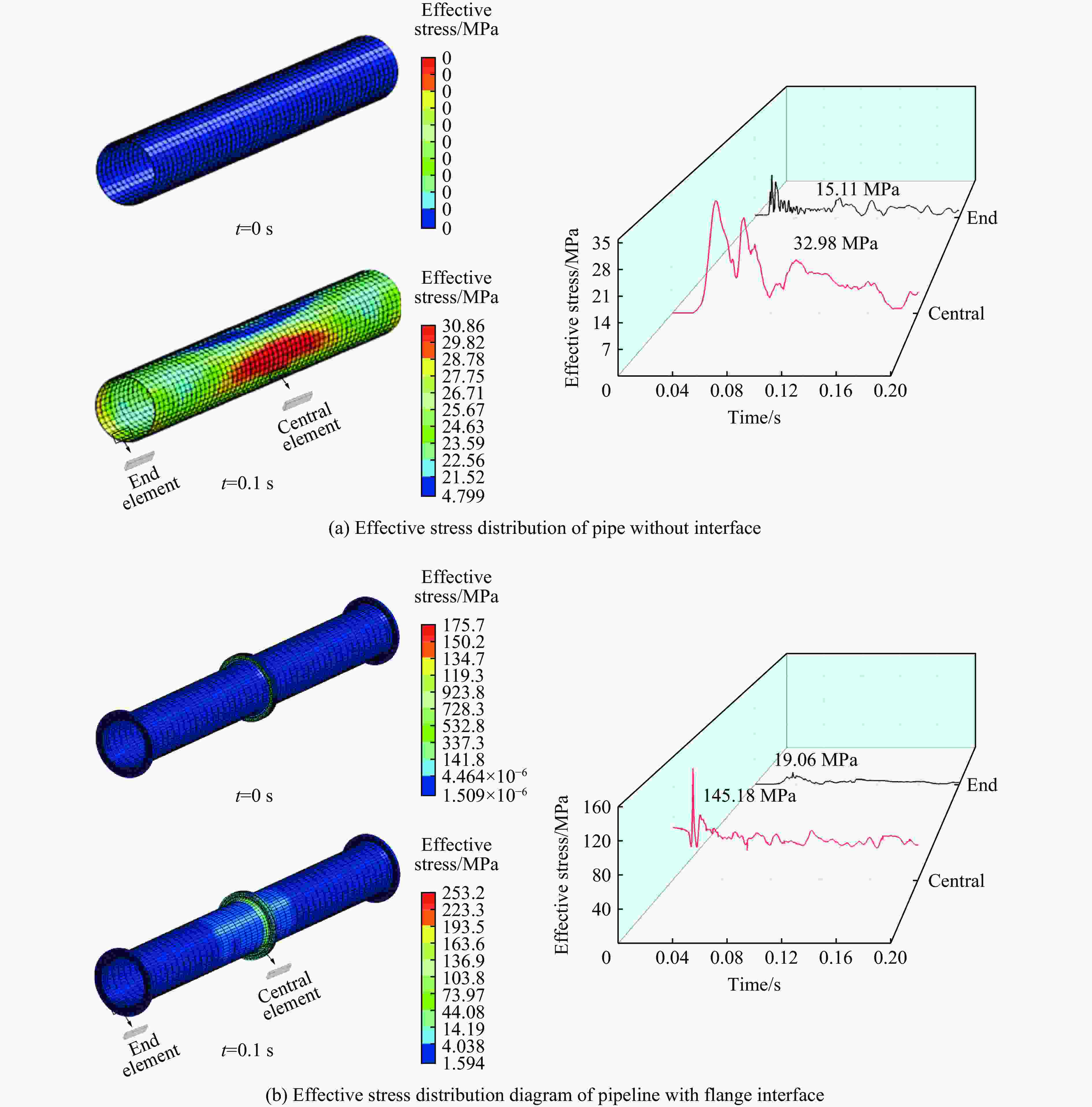
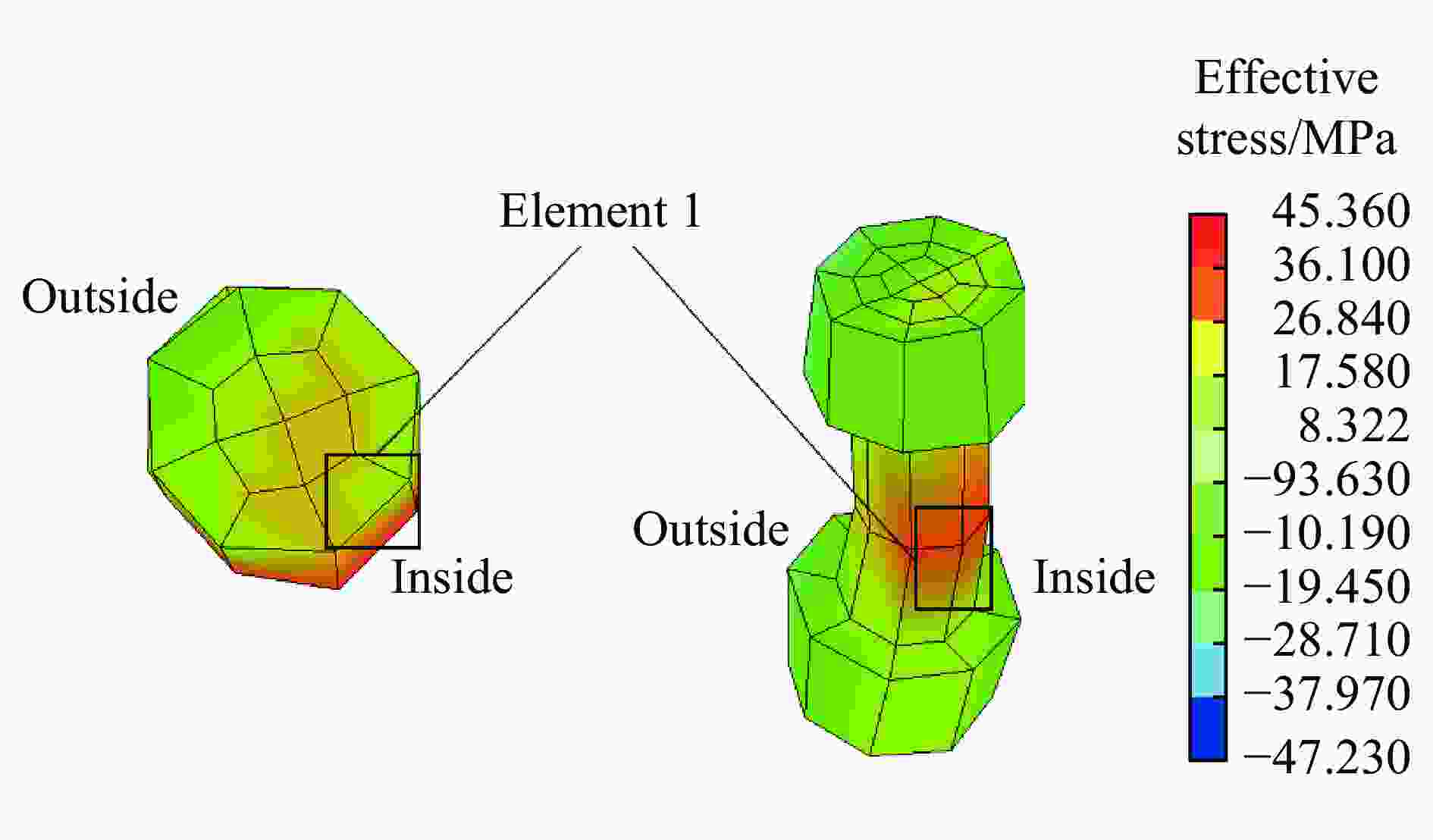
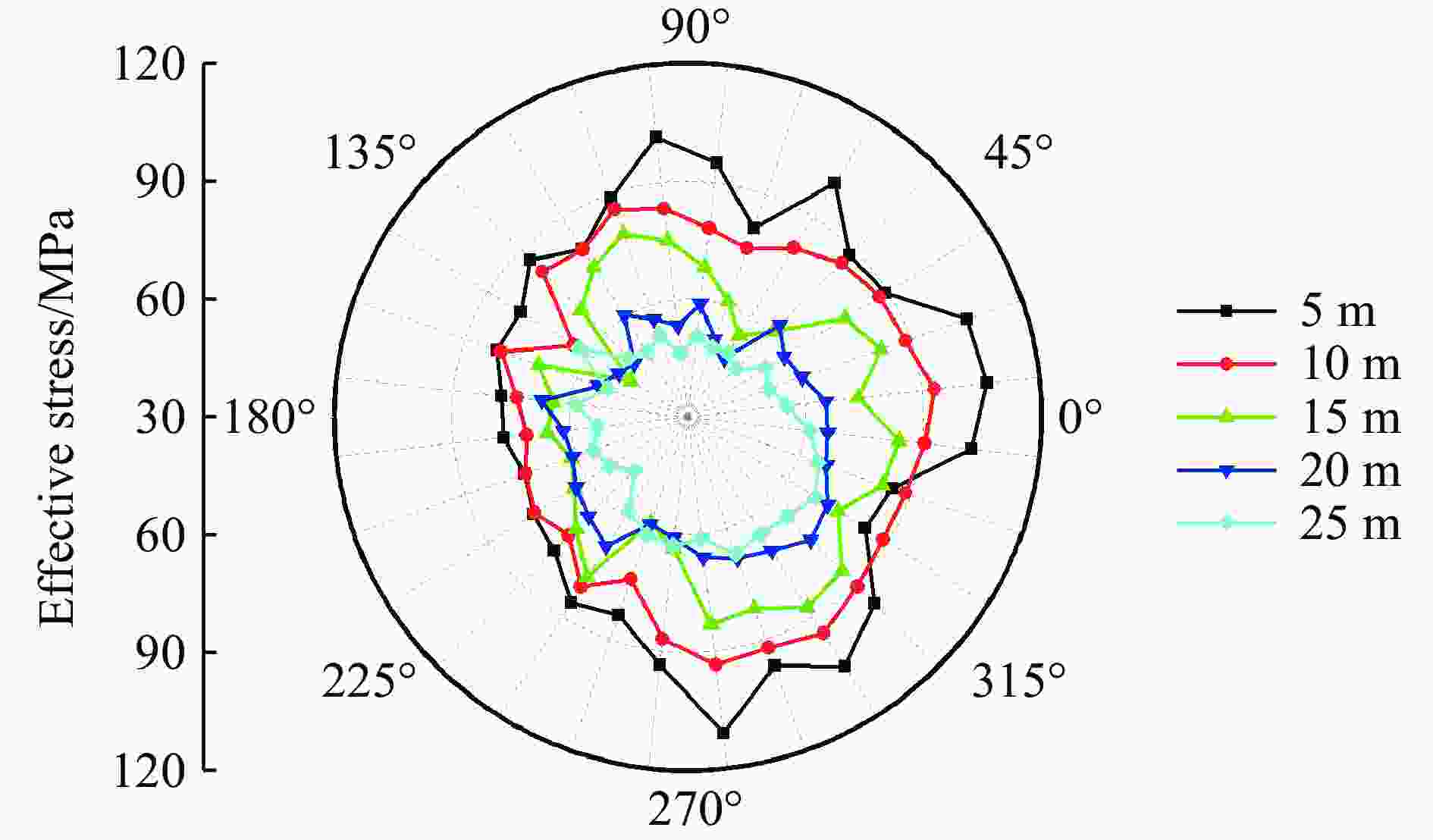
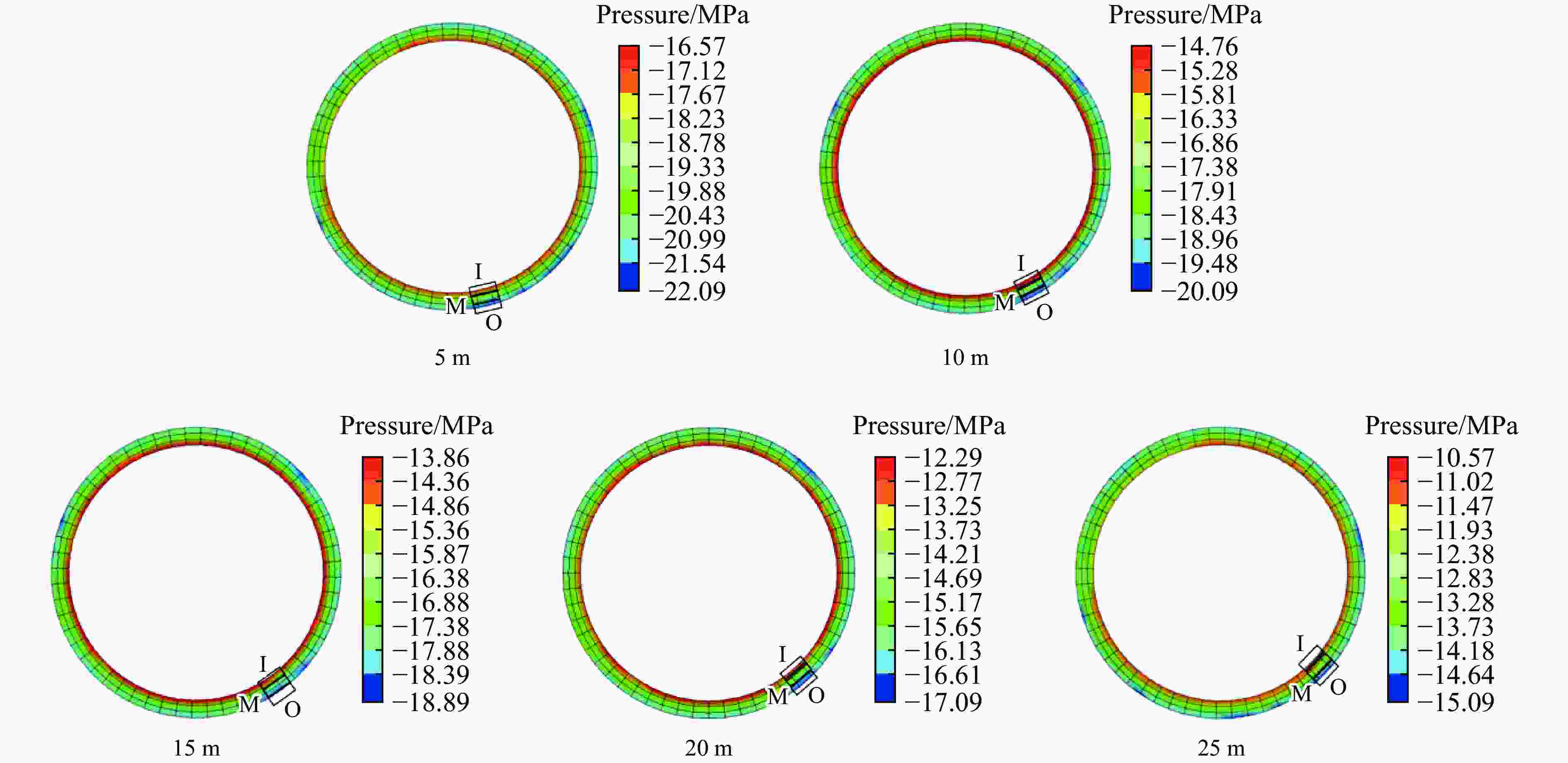
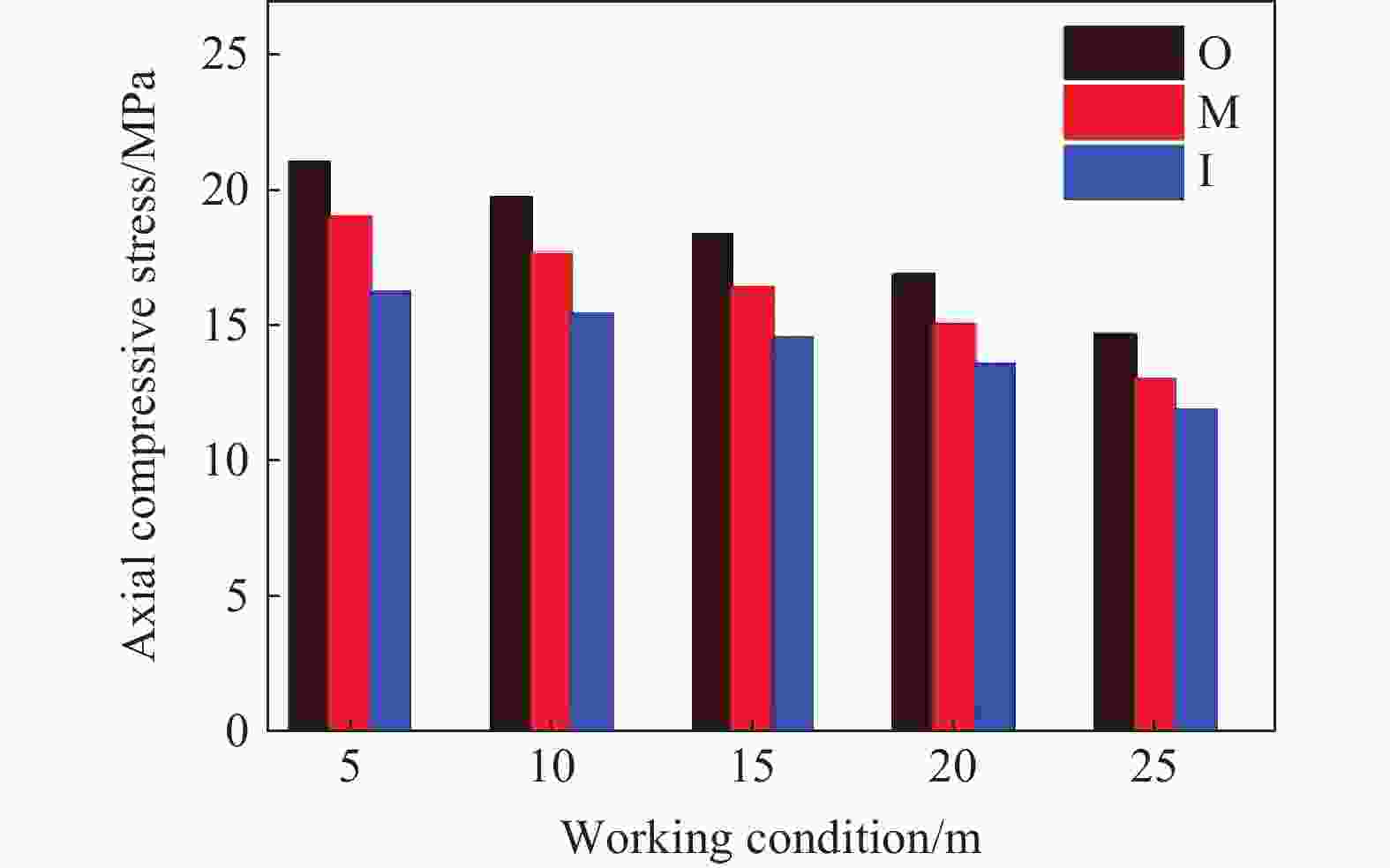
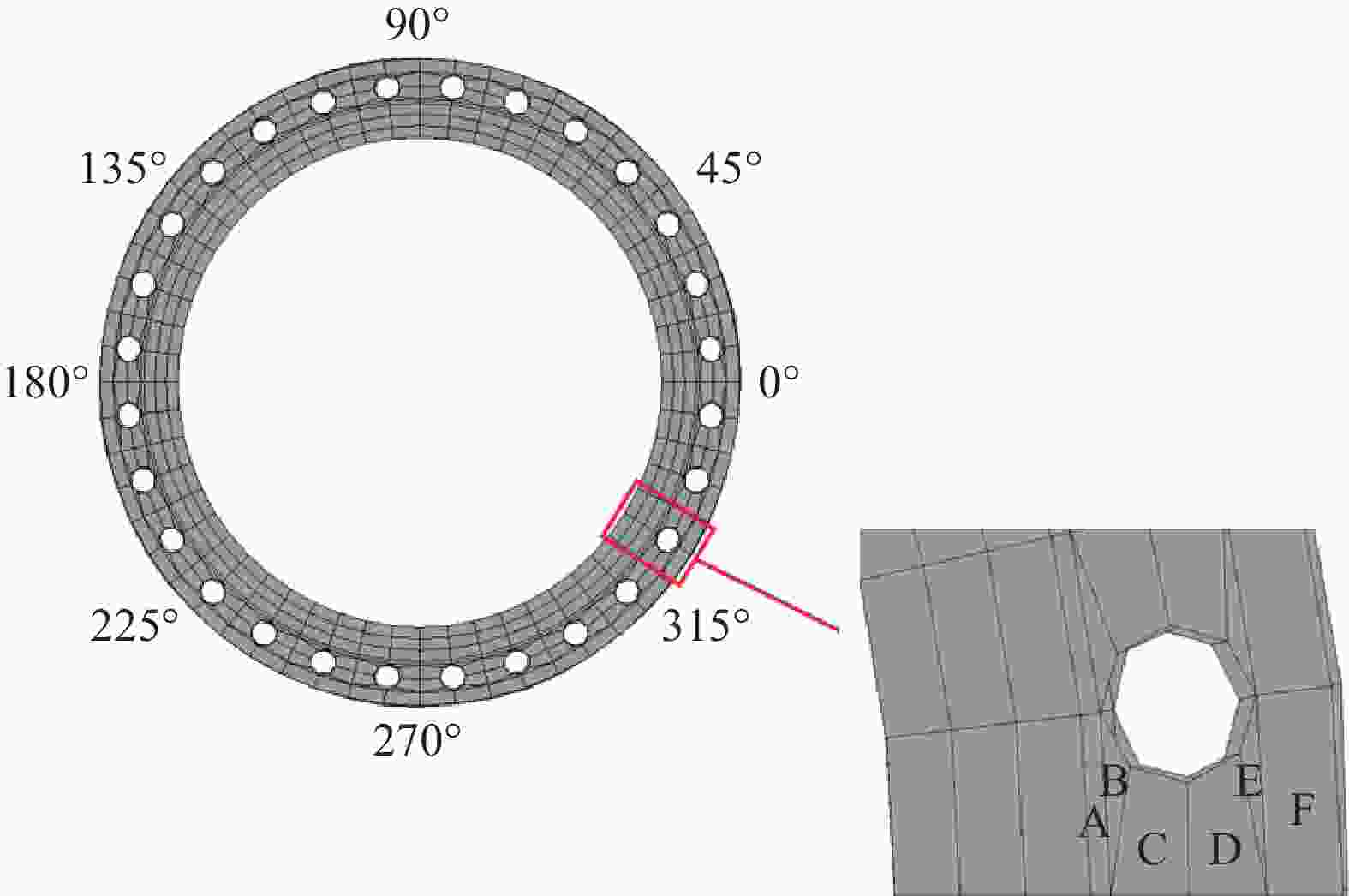
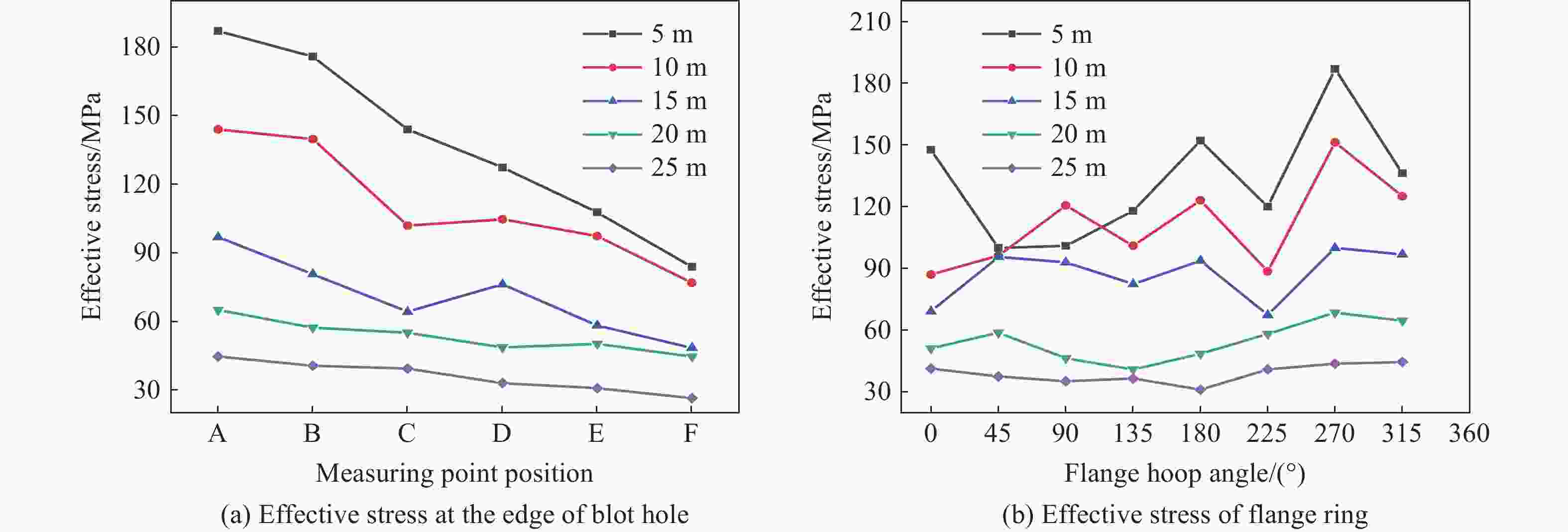
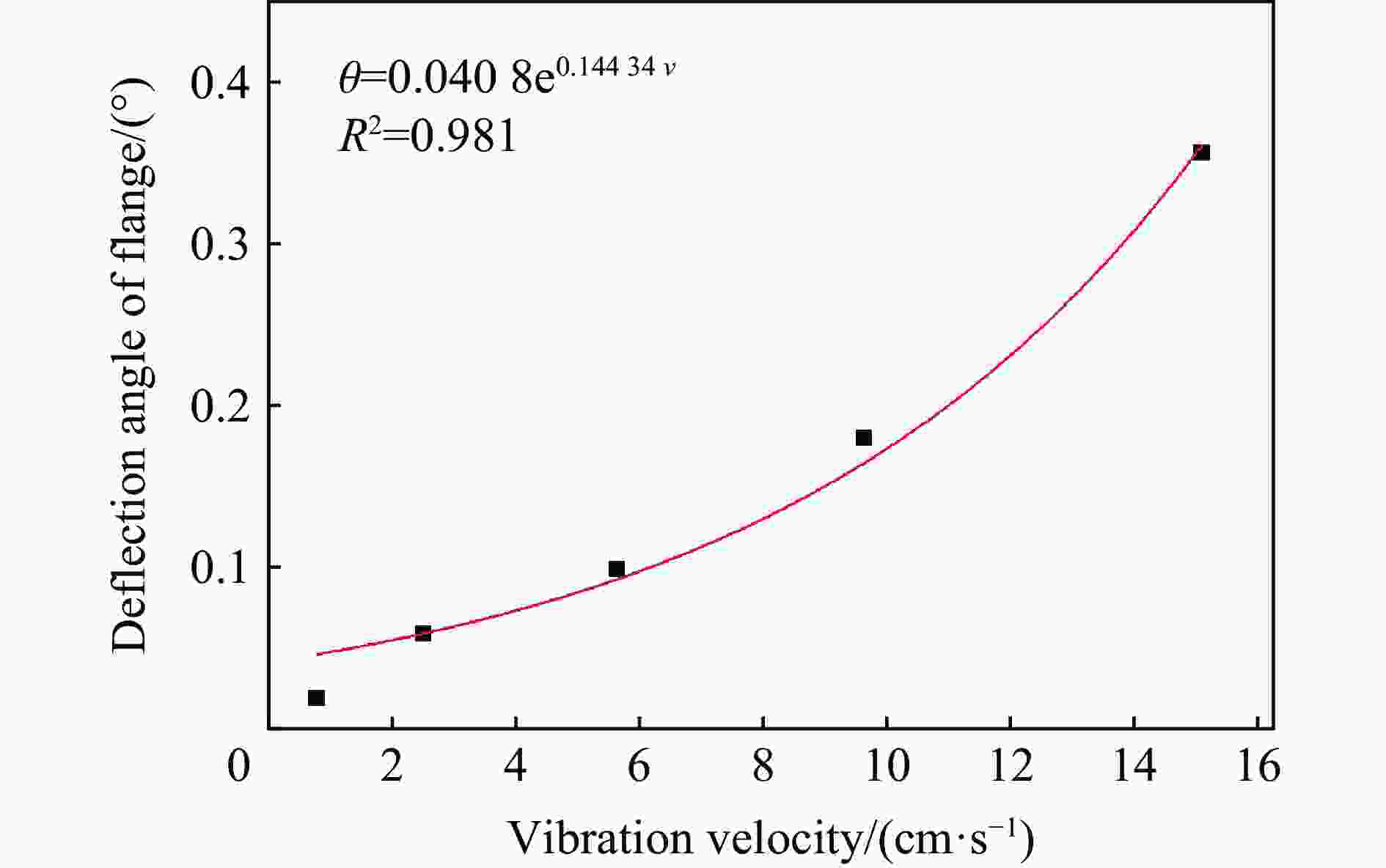
摘要: 基于典型城市燃气管道直埋地层特点，通过全尺寸直埋燃气管道爆破地震实验，并结合LS-DYNA动力有限元数值计算软件建立不同爆源距离的无接口和法兰接口的燃气管道模型，分析研究了爆破地震波作用下法兰接口燃气管道动力响应特征及其失效机制。研究结果表明：管道截面应变以轴向拉伸应变为主，环向应变为辅；不同爆破工况下，无接口管道和法兰接口管道及地表峰值振动速度随爆源距离减小而增大；沿管道轴线方向，无接口管道、地表峰值振动速度以管道中心截面为对称面沿两端不断减小，法兰接口管道峰值振速由两侧向中间逐渐增大，在法兰接口处突然减小；法兰接口处出现明显的应力集中现象；管道法兰接口处是爆破地震作用下研究的关键点，螺栓的峰值有效应力、垫片轴向压力、法兰峰值有效应力、法兰偏转角随爆源距离增大而减小；法兰管道偏转角与地表峰值振动速度具有对应关系，法兰接口燃气管道中心正上方地表的控制振速（13.82 cm/s）可作为邻近燃气管道爆破工程地表的安全控制值。Abstract: In the process of blasting and excavation of urban subways, controlling the impact of blasting vibration on adjacent pipelines is critical. Based on the characteristics of directly buried gas pipelines in Wuhan and the full-scale direct-buried gas pipeline blasting seismicexperiment, the dynamic finite element numerical calculation software LS-DYNA was used to establish gas pipeline without joints and flange gas pipeline models under different blasting source distances. The effects of blasting seismic wave’s dynamic response characteristics of flanged gas pipeline were analyzed. The research results show that the strain of pipeline section is mainly axial tensile strain, supplemented by circumferential strain. The peak particle velocity of pipeline without joints and flange pipes and the ground surface increase with the decrease of the distance from the blasting source under different blasting conditions. Along the pipeline axis, the peak vibration velocity of the pipeline without joints and the ground surface decreases along the two ends with the central section of the pipe as the symmetry plane. The peak particle velocity of the flange pipeline gradually increases from two sides to the middle but suddenly decreases at the flange joint. There is an obvious stress concentration at the flange interface. The flange joint is the key point of pipeline under blasting earthquake. The peak effective stress of the bolt, the axial pressure of the gasket, the peak effective stress of the flange, and the flange deflection angle decrease with the increase of the explosion source distance. The deflection angle of the flanged pipeline has a corresponding relationship with the peak vibration velocity of the ground surface. The control vibration speed of 13.82 cm/s on the surface directly above the center of the flanged gas pipeline is used as the safety control value of the adjacent gas pipeline under blasting engineering.
-
Key words:
- blasting vibration /
- dynamic response /
- vibration speed /
- flange interface /
- control vibration speed
-
岩石是隧道围岩开挖过程中最常见的一种介质材料，在寒区隧道开挖等工程问题方面，其不可避免会受到由于昼夜交替及季节变换引起的冻融循环作用。而隧道的开挖掘进过程中又经常会经过节理及断面等缺陷，并且伴随着冲击地压等动载荷作用，因此研究在冻融循环与动荷载共同作用下隧道内裂纹的断裂特性具有重要的意义。
目前，国内学者对于寒区隧道的研究已有不少成果。高焱等[1]统计分析了156座寒区隧道冻害调研资料，从两个方面对隧道寒区进行划分，并对寒区隧道保温排水的技术进行了分析。夏才初等[2, 3]采用有限元方法进行数值模拟，研究了冻融循环作用下隧道结构及围岩变形规律，并对控制隧底融沉变形的方法进行了分析。那通兴等[4]建立含相变的围岩温度场与渗流场耦合模型，对寒区隧道的围岩温度场进行数值分析，研究了渗透速率对围岩温度场的影响。
国内外关于冻融循环岩石相关性质的研究也较为深入。申艳军等[5-6]开展了不同倾角单裂隙砂岩的冻融循环试验，并对不同冻融次数的试件进行加卸载试验，研究了冻融与周期荷载联合作用下裂隙岩体的损伤特征及断裂演化规律。张慧梅等[7]研究了饱水红砂岩经过不同次数冻融循环后的变形破坏规律，通过单轴压缩试验分析了冻融循环岩石的强度、弹性模量及应力-应变曲线变化规律。闻磊等[8-9]对花岗斑岩和灰岩开展冻融循环试验，对比分析了不同冻融次数下两种岩石物理力学性质的变化规律。陈宇龙等[10]借助激光扫描显微镜对冻融页岩的表面裂纹的扩展过程进行细观研究，分析了冻融循环对裂纹深度、裂纹宽度和表面积比的影响。刘泉声等[11]基于力学和相变理论建立了考虑水分迁移下的冻胀力求解模型，对寒区岩体进行了数值模拟，分析了岩体裂隙的应力强度因子，验证了等效热膨胀系数法的可靠性。刘少赫等[12]采用霍普金森压杆对不同冻融循环次数的红砂岩进行冲击试验，分析了冻融红砂岩峰值应力、峰值应变和弹性模量，并利用电镜扫描对不同冻融次数的红砂岩进行了微观变化特征分析。Gholamreza等[13]选择了5种不同类型的砂岩进行不同次数的冻融循环试验，分析了随着冻融循环次数的增加，岩石的P波波速、孔隙率和单轴抗压强度的变化；并利用衰减函数模型对砂岩抗冻融的耐久性进行了分析，最后发现在冻融循环中，孔隙的大小和分布对岩石的的耐久性起主要作用。Ghobadi等[14]研究了9种砂岩在冻融循环作用下质量损失、P波波速损失的百分比和单轴抗压强度、点荷载等特性发生的变化。
含裂隙岩体在动荷载作用下的断裂特性也引起了众多学者的研究关注。周磊等[15-16]采用落锤冲击试验装置研究了在冲击荷载作用下隧道内裂纹的扩展规律，并利用有限元软件ABAQUS研究了裂纹的动态起裂韧度和动态扩展韧度。付安琪等[17]对中心直切槽半圆盘试样先后开展循环冲击损伤试验和静态三点弯曲断裂试验，研究了循环冲击损伤后大理岩的静态断裂力学特性。Wang等[18]、王蒙等[19]研究了侧开单裂纹半孔板在SHPB试验系统冲击下裂纹的动态扩展问题。Wang等[20]采用霍普金森压杆对单裂纹圆孔板试件进行冲击试验，测得其Ⅰ型裂纹动态断裂韧度。
近年来国内外学者对冻融岩体的力学性质研究主要针对静态力学性能，而关于冻融岩体的动态力学性能研究结果尚难于满足工程问题需要，尤其是针对西部严寒地区隧道内裂纹的动态扩展特性研究更是屈指可数。本文中采用四川青砂岩为原材料制作隧道模型试样，对其先后开展冻融循环试验和落锤冲击试验，并采用电镜对冻融循环后的试样进行扫描，研究试件内Ⅰ型裂纹的动态起裂特性及细观损伤机制，并通过ABAQUS有限元分析软件结合试验测试结果计算裂纹的动态起裂韧度。
1. 试验方案
1.1 试件模型及材料的选择
本文选择的砂岩模型试件尺寸为280 mm×350 mm×30 mm，隧道断面尺寸的宽度为50 mm，高度为60 mm，断面的上部分为圆弧拱顶，其半径为25 mm，裂纹位于圆弧拱顶位置，处于试件沿宽度方向的对称轴线上，裂纹长度为50 mm。为了使得裂纹尖端的应力集中现象更加明显，使用0.5 mm厚的钢锯条对裂纹尖端处进行锐化处理，试件模型及试件尺寸示意图如图1所示。
受条件所限，难以采用西部严寒地区的岩石试样，故采用四川青砂岩为原材料制作隧道模型试样。砂岩是由石英、长石等碎屑成分占50%以上的沉积碎屑岩，由碎屑和填隙物两部分构成，青砂岩强度适中，材质也比较均匀，适用于本试验研究。试验开始前对青砂岩材料的物理性质参数进行测试，测得参数如表1所示。
表 1 5组试件材料的力学参数Table 1. Mechanical parameters for five groups of specimen冻融次数 孔隙率/% 泊松比 弹性模量/GPa 纵波波速/（m·s−1） 横波波速/（m·s−1） 纵波波速降/% 横波波速降/% 0 12.52 0.262 12.56 2 562 1 455 0 0 10 12.96 0.270 10.50 2 378 1 334 7.2 8.3 20 13.35 0.276 9.14 2 254 1 253 12.0 13.9 30 13.87 0.283 8.10 2 153 1 185 16.0 18.5 40 14.51 0.286 7.31 2 085 1 141 18.6 21.6 1.2 冻融循环试验
为了研究冻融循环对岩石材料的影响，以循环的次数N为变量制作5组隧道模型试件，N分别为0、10、20、30和40。考虑到试验数据的有效性，且试验过程中的偶然误差会对试验结果造成影响，选择每组制作6个隧道模型试件，一共制作30个试件。另外，为了方便测试青砂岩在冻融循环后其物理力学性质参数的变化，以循环的次数N为变量制作5组
∅ 50 mm×100 mm的标准圆柱体试件，每组制作2个，一共10个试件。对所有试件进行饱水处理，然后进行冻融循环，进行冻融循环时，将试件放入高低温试验箱中冻结12 h，冻结温度为−20 ℃，然后放入常温的水中12 h进行融化，即为一次冻融循环。试验中采用的高低温试验箱可以达到的最低温度为−40 ℃，根据GB/T 50266—2013《工程岩体试验方法标准》[21]中对冻融试验的有关规定，在本文试验中设置为−20 ℃，高低温试验箱如图2所示。1.3 冲击试验
冲击试验采用落锤试验装置，如图3所示，由落锤、入射板及透射板组成。试验装置的入射板和透射板均由密度为2 850 kg/m3的LY12CZ铝合金制成，弹性模量为71.7 GPa，泊松比为0.33，入射板长度l1=3 000 mm，透射板长度l2=2 000 mm，两者的宽度均为300 mm，厚度均为30 mm，波速约为5 500 m/s。为了减少高频振荡并延长加载时间，在落锤与入射板撞击端粘贴黄铜片作为整形器；透射板底部与混凝土阻尼器相接触，将大部分应力波传入大地，以尽量消除反射波。落锤冲击速度由红外线测距仪测量落锤拉起高度与入射板之间的距离进行计算得到。试验开始前先将试件两端涂抹黄油，然后置于入射板与透射板之间，避免局部摩擦导致试件产生弯折等失稳破坏，并保持试件位置居中，保证受力均匀。在入射板和透射板上分别粘贴应变片，在裂纹尖端粘贴裂纹扩展计(crack propagation gauge, CPG)用于测量载荷以及裂纹起裂时间。当落锤自由落体冲击入射板后，超动态应变仪将采集应变片和CPG的电压信号，从而得到入射端和透射端载荷信息以及试件上裂纹的扩展时间。
1.4 裂纹扩展计及其工作原理
将CPG粘贴于隧道模型试件的裂纹尖端，如图4所示，其由玻璃丝布基底和敏感栅丝2个部分组成，敏感栅丝总长度l=44 mm，栅丝宽度b=10 mm。将裂纹扩展计沿着裂纹预计扩展路径粘贴并保证第一根栅丝和裂纹尖端重合，当裂纹扩展时，敏感栅丝发生断裂使得裂纹扩展计的电阻发生变化，导致CPG两端的电压信号发生突变形成台阶信号，即可测得预制裂纹的起裂时间。CPG的初始电阻为3.5 Ω，采用16 V的恒压电源提供电压，电压的调幅精度值可以达到1 mV。采用数字示波器采集CPG在裂纹扩展过程中因栅丝断裂引起的电压台阶信号，示波器的精度可以达到10 MHz，采集信号的时间步距为0.1 μs，所以通过裂纹扩展计采集到的数据误差较小，满足试验要求。
2. 试验结果分析
2.1 确定材料参数
标准圆柱体试件经过冻融循环后，随后测试其相关的动态力学参数。通过超声波波速测试仪得到试件的纵波波速和横波波速，如图4所示，每一个不同冻融循环次数的组有2个标准圆柱体试件，测试结果的平均值列于表1。随后分别计算出其泊松比μ和弹性模量Ed[22]：
μ=(cp/cs)2−22[(cp/cs)2−1)] (1) Ed=ρc2p(1+μ)(1−2μ)1−μ (2) 式中：μ为材料的泊松比，cp为材料的纵波波速，cs为材料的横波波速，Ed为材料的弹性模量，ρ为材料的密度。
岩石内部存在大量的裂纹、节理，在受到冻融循环后，水冰相变产生的体积膨胀使其内部众多微小的裂纹发生了扩展。随着冻融循环次数的增加，岩石内部损伤不断积累，裂隙越来越多，当波在通过含有裂隙的岩石时，由于发生折射、反射和能量损失，导致波速衰减，所以试件的波速随着冻融循环次数的增加而逐渐变小。从图5中可以看到，经过10次循环后，试件的纵波波速下降了7.2%，经过20、30与40次时，相比无冻融循环分别降低了12%、16%、18.6%；试件的弹性模量也在随着冻融次数的增加而逐渐下降，0次组试件的弹性模量平均值为12.56 GPa，经过40次冻融循环后下降到7.31 GPa，为0次组的58.2%，下降幅度明显，可见冻融循环对材料弹性模量的影响较为显著。
根据数据统计计算结果，每组试件物理力学性质参数的平均值如表1所示。由表1可以看出，随着冻融循环次数的增加，试件的纵波波速、横波波速和弹性模量在逐渐下降，而泊松比在逐渐增大，但增大的幅度较小。
2.2 冲击载荷计算
在对试件进行冲击试验的过程中，通过超动态应变仪采集入射端与透射端上粘贴的应变片的电压信号，存储在数字示波器中。选取一组落锤冲击试验典型试件作为处理对象，将测得的电压信号通过下式转化为应变信号：
ε=4U0nEK (3) 式中：ε为应变，U0为试验所测的电压信号，供桥电压E=2 V，灵敏度因数K=2.1，放大器的增益因数n=1 000。
根据一维弹性应力波假设，入射板作用在试件上端面的荷载为入射波和反射波的叠加，透射板作用在试件下端面的荷载可直接通过透射波得到，计算公式如下：
{pi(t)=AiEεi(t)pr(t)=AiEεr(t)pt(t)=AtEεt(t) (4) 式中：εi(t)为入射波应变时程曲线，εr(t)为反射波应变时程曲线，εt(t)为透射波应变时程曲线。
本次冲击试验主要考虑试件受到载荷以后的时间区间，所以将加载波到达试件上端边缘的时刻t0定义为零时刻。根据式(3)进行数据处理，由于在进行落锤冲击试验时不可避免会受到外界各种因素的干扰，会产生一些误差，所以需要通过一定的整形措施来寻找波头以尽量消除误差的影响，然后通过Origin软件进行降噪处理得到入射端与透射端的应变-时间曲线，如图6所示。根据式(4)进行计算，得到作用在试件上的载荷曲线，如图7所示。在随后进行的数值模拟中，会将其用作试件上的加载条件。
2.3 裂纹的动态起裂时刻
冲击试验中，预制裂纹的起裂时间是研究岩石起裂韧度的重要参数。预制裂纹起裂的同时CPG的第1根金属栅丝也被拉断，使CPG两端的电阻产生变化进而产生台阶电压信号，这时可以得到第1个台阶电压信号产生的时间t1，在2.2节中已知加载波到达试件的顶端的时刻为t0，则裂纹的起裂时间即为t=t1−t0，由此可得到每个试件的起裂时间。由于试验并非全部成功，所以本文将成功采集到的起裂时间数据列于表2中。
表 2 冲击试验结果Table 2. Impact test results试件 冲击速度/（m·s−1） 起裂时间/μs 动态起裂韧度/（MPa·m1/2） 动态加载率/（MPa·m1/2·s−1） 0-1 6.56 362 3.09 10 404 0-2 6.59 374 3.29 10 716 0-3 6.61 367 3.18 10 603 10-1 6.48 375 2.87 9 410 10-2 6.53 371 2.77 9 082 10-3 6.48 366 2.66 8 866 20-1 6.57 381 2.54 8 274 20-2 6.51 389 2.75 8 730 20-3 6.56 386 2.66 8 445 30-1 6.52 393 2.41 7 670 30-2 6.56 397 2.51 7 952 30-3 6.59 390 2.31 7 549 40-1 6.56 395 2.11 6 762 40-2 6.50 392 2.04 6 623 40-3 6.47 399 2.21 7 015 3. 动态起裂韧度的计算
动态断裂韧度是评价岩石材料抵抗裂纹起裂的重要参数，其被分为动态起裂韧度、动态扩展韧度和动态止裂韧度。本文将借助ABAQUS有限元软件采用试验-数值法计算动态起裂韧度，并比较在相同动载荷作用下，冻融循环的次数对青砂岩材料动态起裂韧度的影响。
3.1 试验-数值法
试验-数值法[23]在本文中的应用主要分为试验数据测试和数值分析两个部分。试验数据测试部分，通过落锤冲击试验得到应变时程曲线和动态载荷曲线，采用裂纹扩展计测得预制裂纹的起裂时刻。在数值分析部分，采用ABAQUS有限元分析软件将试验测得的动态载荷曲线施加到试件的数值模型上，通过计算即可得到受相同动态载荷作用下静止裂纹的应力强度因子。
3.2 动态起裂韧度计算
根据试件尺寸和表1中经过冻融循环后5组试件的力学性质参数，在ABAQUS中建立相应的二维数值模型，分别计算裂纹的动态应力强度因子曲线。裂纹尖端采用六节点三角形单元，其余部分采用八节点四边形单元，裂纹尖端采用1/4节点奇异单元以消除裂纹尖端应力的奇异性造成的非正常应力状态，数值模型的网格划分情况如图8所示。
将图7中的动态载荷曲线转化为应力边界条件作用在数值模型的上下两端，并且在数值模型中施加重力荷载以考虑重力的影响，进行计算可得到经过不同冻融循环次数后的5组试件在相同冲击载荷作用下的动态应力强度因子曲线，结合3.3节所测得的起裂时间，得到5组试件的动态起裂韧度可见表2。
图9为每组试件中N-1的起裂韧度计算结果，N表示冻融循环的次数，1表示每组的第一个试件，所以图中一共有5个试件的起裂韧度计算结果。对于冻融循环次数为0次的试件0-1，根据试验结果可知裂纹在362 μs时发生起裂现象，横坐标上362 μs时刻对应的纵坐标的值即为试件的动态起裂韧度为3.09 MPa·m1/2，为5个试件中的最大值，冻融次数为10、20、30的试件10-1、20-1、30-1的起裂韧度分别为2.87、2.54、2.41 MPa·m1/2，冻融循环次数为40次的试件40-1，其动态起裂韧度仅为2.11 MPa·m1/2，为5个试件N-1的最小值，相比试件0-1降低了31.7%，降低幅度较为明显。图10所示为冻融次数与起裂韧度的关系，图中散点分别代表不同冻融循环组的第1、2、3个试件的动态起裂韧度的值。从拟合曲线中可以得出：随着冻融循环次数的增加，试件的动态起裂韧度逐渐变小，前期下降较快，变化明显，后期下降幅度逐渐变小。
图 10 冻融次数与动态起裂韧度的关系曲线Figure 10. Relationship between freeze-thaw cycles and dynamic initiation toughness4. 破坏断裂面的细观分析
在岩石力学研究过程中，通过观测和分析岩石细观结构以解释岩石宏观力学性质是一种常用的方法[24-25]。本文采用扫描电镜对经过不同冻融循环次数的试件破坏后的断口形貌特征进行观测，结合5组试件孔隙率的变化对试样放大至50 μm尺度的图像进行分析，如图11所示。
图11(a)为冻融0次时的试样，孔隙率为12.52%，内部孔隙多为微孔隙，试样结构致密，表明较为平整，有少量岩渣散落在表面；图11(b)为冻融10次时的试样，观察可发现与图11(a)差别比较明显，这一组试件平均的孔隙率变为12.96%，孔隙中的水分子产生冻胀力，对岩石造成破坏，试样表面由于胶结物质脱落而不再平整，较为粗糙，有更多岩渣无规律的分布在试样表面；图11(c)为冻融20次时的试样，与图11(b)也有较大差别，试样表面的胶结物质流失变多导致结构更为松散，表面几乎没有平整的区域，非常的粗糙，在孔隙水冰相变的冻胀作用下孔隙发育速率增加，孔隙率变为13.35%；图11(d)为冻融30次时的试样，孔隙率变为13.87%，观察发现有较为明显的大孔隙出现，说明此时岩石内部胶结物质流失更多，颗粒间的联系被大大削弱，试样内部的孔隙经过扩展、汇合、贯通导致大孔隙出现；图11(e)为冻融40次时的试样，孔隙率为14.51%，其胶结物质流失严重，孪晶结构更加的松散，大孔隙也变得越来越多。
通过对比观察不同冻融循环次数下青砂岩试样放大至50 μm尺度的扫描电镜图片，可以得出以下结论：冻融循环会使青砂岩的胶结物质流失，使大量岩石矿物颗粒之间的黏结性变差，从而导致砂岩材料变得较为松散，孔隙率变大，并且有大孔隙出现，砂岩内部的微裂纹也随着冻融循环次数的增加而变多，这些细观的变化导致砂岩的宏观力学性能出现大幅度下降。
5. 结 论
本文对青砂岩模型试件先后进行冻融循环试验与动态冲击试验，得到青砂岩在经过不同次数冻融循环作用下的材料损伤参数，并根据试验-数值法采用ABAQUS有限元软件计算了动态起裂韧度，并对试件进行电镜扫描以研究冻融循环对砂岩材料动态断裂特性的影响，得到以下结论：
（1）岩石在经过冻融循环后受到了不同程度的损伤，导致其相关力学参数发生了改变。随着冻融循环次数的增加，青砂岩的波速逐渐下降，前期下降幅度较快，后期下降幅度逐渐减小，冻融循环40次后试件的波速下降了18.6%；青砂岩的弹性模量均随着冻融循环次数的增加逐渐减小，冻融循环40次后减小了41.8%；泊松比则随着冻融循环次数的增加逐渐增大，增大幅度并不明显，40次冻融循环后增大了9.16%。
（2）动态起裂韧度随着冻融循环次数的增加逐渐减小，且减小的幅度很大不同，试件在经过40次冻融循环后，起裂韧度降低了31.7%，说明冻融循环对材料的动态起裂韧度影响较大。
（3）由于冻融循环作用的影响，青砂岩内部的胶结物质流失使得晶体颗粒之间的黏结性下降，内部孔隙与细观裂缝增多，从而表征出材料的宏观力学性能下降。
-
图 5 实验和数值模拟的波形和频谱图
Figure 5. Waveform and spectrogram of experiment and numerical simulation
图 7 法兰接口管道数值模型示意图
Figure 7. Schematic diagram of numerical model of flange interface pipe
图 13 各个工况的螺栓的有效应力分布图
Figure 13. Effective stress distribution diagram of bolts in various working conditions
图 19 法兰偏转角与地表振速关系
Figure 19. Relationship between flange deflection angle and ground surface vibration velocity
表 1 模型材料参数
Table 1. Model material parameters
材料 密度/(g·cm−3) 弹性模量/GPa 剪切模量/GPa 泊松比 黏聚力/MPa 内摩擦角/（°） 抗拉强度/MPa 管道、法兰 7.85 205.000 1.2 0.33 420.000 螺栓 7.82 210.000 1.0 0.30 660.000 粉质黏土 1.98 0.012 4.3 0.28 0.035 15 0.028 砂岩 2.40 3.000 11.2 0.28 5.500 43 2.580 
下载: 导出CSV
表 2 爆轰产物状态方程参数
Table 2. Detonation product state equation parameters
ρ/（g·cm−3） A/GPa B/GPa R1 R2 ω E0/GPa V/cm3 1.25 214 18.2 4.2 0.9 0.1 4.19 1
下载: 导出CSV
表 3 数值模拟结果与实测数据对比分析
Table 3. Comparative analysis of numerical simulation results and measured data
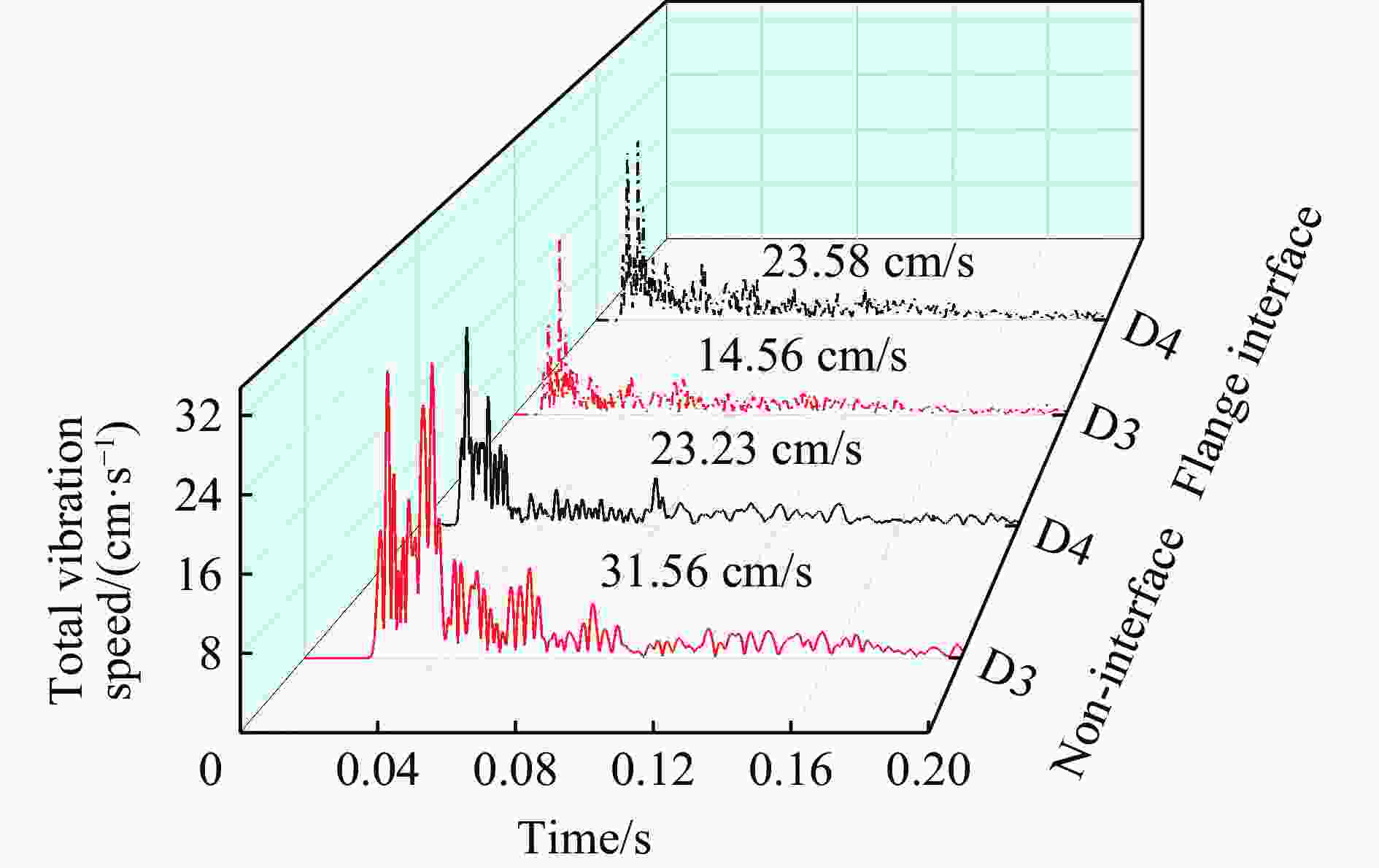
工况 监测点 合振动速度、应变 误差率/% 现场实验 数值模拟 Ⅰ D3 1.65 cm/s 1.72 cm/s 4.2 D4 1.17 cm/s 1.26 cm/s 7.6 D6 0.76 cm/s 0.72 cm/s 5.3 D7 1.45 cm/s 1.54 cm/s 6.2 S1 28.65×10−6 34.23×10−6 19.4 S2 13.54×10−6 8.56×10−6 3.7 Ⅱ D3 2.84 cm/s 2.76 cm/s 8.0 D4 1.99 cm/s 2.06 cm/s 3.5 D6 2.64 cm/s 2.73 cm/s 9.0 D7 1.32 cm/s 1.46 cm/s 10.6 S1 36.71×10−6 41.23×10−6 12.3 S2 16.12×10−6 13.15×10−6 18.4 Ⅲ D3 6.57 cm/s 6.98 cm/s 6.2 D4 4.18 cm/s 4.45 cm/s 6.4 D6 5.47 cm/s 5.78 cm/s 5.6 D7 3.98 cm/s 4.15 cm/s 4.3 S1 37.15×10−6 43.23×10−6 16.3 S2 15.96×10−6 18.56×10−6 16.2 Ⅳ D3 15.19 cm/s 15.32 cm/s 0.8 D4 11.21 cm/s 12.54 cm/s 1.3 D6 13.18 cm/s 14.25 cm/s 8.1 D7 7.34 cm/s 8.32 cm/s 13.4 S1 187.06×10−6 198.09×10−6 5.9 S2 19.23×10−6 22.63×10−6 17.7 Ⅴ D3 30.45 cm/s 31.56 cm/s 3.6 D4 21.19 cm/s 23.23 cm/s 9.6 D6 28.45 cm/s 29.56 cm/s 3.9 D7 12.15 cm/s 13.21 cm/s 8.7 S1 209.50×10−6 225.61×10−6 7.6 S2 35.62×10−6 42.66×10−6 19.8
下载: 导出CSV
表 4 垫片的各项参数
Table 4. The parameters of the gasket
密度/（g·cm−3） Ex/MPa Ey/MPa Ez/MPa μxy μyz μxz Gxy/MPa Gyz/MPa Gxz/MPa 7.85 232.17 434.51 19089.64 0.44 0.008 0.005 115.88 32770.11 103.59
下载: 导出CSV
-
[1] 管晓明, 张良, 王利民, 等. 隧道近距下穿管线的爆破振动特征及安全标准 [J]. 中南大学学报(自然科学版), 2019, 50(11): 2870–2885. DOI: 10.11817/j.issn.1672-7207.2019.11.026.GUAN X M, ZHANG L, WANG L M, et al. Blasting vibration characteristics and safety standard of pipeline passed down by tunnel in short distance [J]. Journal of Central South University (Science and Technology), 2019, 50(11): 2870–2885. DOI: 10.11817/j.issn.1672-7207.2019.11.026. [2] 夏宇磬, 蒋楠, 姚颖康, 等. 粉质黏土层预埋承插式混凝土管道对爆破振动的动力响应 [J]. 爆炸与冲击, 2020, 40(4): 043302. DOI: 10.11883/bzycj-2019-0207.XIA Y Q, JIANG N, YAO Y K, et al. Dynamic responses of a concrete pipeline with bell-and-spigot joints buried in a silty clay layer to blasting seismic waves [J]. Explosion and Shock Waves, 2020, 40(4): 043302. DOI: 10.11883/bzycj-2019-0207. [3] ASHFORD S A, JUIRNARONGRIT T. Response of single piles and pipelines in liquefaction–induced lateral spreads using controlled blasting [J]. Earthquake Engineering and Engineering Vibration, 2002, 1(2): 181–193. DOI: 10.1007/s11803-002-0064-3. [4] ABEDI A S, HATAF N, GHAHRAMANI A. Analytical solution of the dynamic response of buried pipelines under blast wave [J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 88: 301–306. DOI: 10.1016/j.ijrmms.2016.07.014. [5] KOURETZIS G P, BOUCKOVALAS G D, GANTES C J. Analytical calculation of blast-induced strains to buried pipelines [J]. International Journal of Impact Engineering, 2007, 34(10): 1683–1704. DOI: 10.1016/j.ijimpeng.2006.08.008. [6] LIU X B, ZHANG H, XIA M Y, et al. Mechanical response of buried polyethylene pipelines under excavation load during pavement construction [J]. Engineering Failure Analysis, 2018, 90: 355–370. DOI: 10.1016/j.engfailanal.2018.03.027. [7] 张震, 周传波, 路世伟, 等. 爆破振动作用下邻近埋地混凝土管道动力响应特性 [J]. 哈尔滨工业大学学报, 2017, 46(9): 79–84. DOI: 10.11918/j.issn.0367-6234.201611089.ZHANG Z, ZHOU C B, LU S W, et al. Dynamic response characteristic of adjacent buried concrete pipeline subjected to blasting vibration [J]. Journal of Harbin Institute of Technology, 2017, 46(9): 79–84. DOI: 10.11918/j.issn.0367-6234.201611089. [8] JIANG N, GAO T, ZHOU C B, et al. Effect of excavation blasting vibration on adjacent buried gas pipeline in a metro tunnel [J]. Tunnelling and Underground Space Technology, 2018, 81: 590–601. DOI: 10.1016/j.tust.2018.08.022. [9] 高坛, 周传波, 蒋楠, 等. 基坑开挖爆破下邻近管道振动速度安全阈值研究 [J]. 安全与环境学报, 2017, 17(6): 2191–2195. DOI: 10.13637/j.issn.1009-6094.2017.06.029.GAO T, ZHOU C B, JIANG N, et al. Study on the vibration velocity threshold of the adjacent pipeline under the blasting excavation of the foundation pit [J]. Journal of Safety and Environment, 2017, 17(6): 2191–2195. DOI: 10.13637/j.issn.1009-6094.2017.06.029. [10] 屈若枫, 徐光黎, 王金峰, 等. 武汉地区典型软土物理力学指标间的相关性研究 [J]. 岩土工程学报, 2014, 36(S2): 113–119. DOI: 10.11779/CJGE2014S2019.QU R F, XU G L, WANG J F, et al. Correlations of physical and mechanical properties of typical soft soils in Wuhan [J]. Chinese Journal of Geotechnical Engineering, 2014, 36(S2): 113–119. DOI: 10.11779/CJGE2014S2019. [11] 时党勇, 李裕春, 张胜民. 基于ANSYS/LS-DYNA 8.1进行显式动力分析[M]. 北京: 清华大学出版社, 2005: 156−158. [12] 王先军, 陈明祥, 常晓林, 等. Drucker-Prager系列屈服准则在稳定分析中的应用研究 [J]. 岩土力学, 2009, 30(12): 3733–3738. DOI: 10.3969/j.issn.1000-7598.2009.12.030.WANG X J, CHEN M X, CHANG X L, et al. Studies of application of Drucker-Prager yield criteria to stability analysis [J]. Rock and Soil Mechanics, 2009, 30(12): 3733–3738. DOI: 10.3969/j.issn.1000-7598.2009.12.030. [13] MOKHTARI M, NIA A A. A parametric study on the mechanical performance of buried X65 steel pipelines under subsurface detonation [J]. Archives of Civil and Mechanical Engineering, 2015, 15(3): 668–679. DOI: 10.1016/j.acme.2014.12.013. [14] 郑爽英, 杨立中. 隧道爆破地震下输气管道动力响应数值试验 [J]. 西南交通大学学报, 2017, 52(2): 264–271. DOI: 10.3969/j.issn.0258-2724.2017.02.008.ZHENG S Y, YANG L Z. Numerical experiments of dynamic response of buried gas pipeline under the action of seismic waves induced by tunnel blasting [J]. Journal of Southwest Jiaotong University, 2017, 52(2): 264–271. DOI: 10.3969/j.issn.0258-2724.2017.02.008. [15] 朱斌, 蒋楠, 贾永胜, 等. 下穿燃气管道爆破振动效应现场试验研究 [J]. 岩石力学与工程学报, 2019, 38(12): 2582–2592. DOI: 10.13722/j.cnki.jrme.2019.0183.ZHU B, JIANG N, JIA Y S, et al. Field experiment on blasting vibration effect of underpass gas pipeline [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(12): 2582–2592. DOI: 10.13722/j.cnki.jrme.2019.0183. [16] 中国机械工业联合会. 整体铸铁法兰: GB/T 17241.6-2008 [S]. 北京: 中国标准出版社, 2009. [17] 王志文, 蔡仁良. 化工容器设计[M]. 北京: 化学工业出版社, 2005: 42−45. [18] 中华人民共和国国家市场监督管理总局, 中国国家标准化管理委员会. 水及燃气用球墨铸铁管、管件和附件: GB/T 13295−2019 [S]. 北京: 中国标准出版社, 2019. [19] MATHAN G, PRASAD N S. Evaluation of effective material properties of spiral wound gasket through homogenization [J]. International Journal of Pressure Vessels and Piping, 2010, 87(12): 704–713. DOI: 10.1016/j.ijpvp.2010.10.003. [20] 蒋国庆, 马斌, 陈万华. 螺栓法兰连接结构有限元模型参数确定方法 [J]. 国防科技大学学报, 2020, 42(4): 51–56. DOI: 10.11887/j.cn.202004009.JIANG G Q, MA B, CHEN W H. Parameter determination method for bolted flange’s finite element model [J]. Journal of National University of Defense Technology, 2020, 42(4): 51–56. DOI: 10.11887/j.cn.202004009. [21] 蔡仁良, 顾伯勤, 宋鹏云. 过程装备密封技术[M]. 北京: 化学工业出版社, 2006: 51−52. [22] ASME锅炉及压力容器委员会压力容器分委员会. ASME锅炉及压力容器规范: 2010版. 第8卷. 第1册, 压力容器建造规则[M]. 北京: 中国石化出版社, 2011: 415. [23] 陆晓峰, 沈轶. 高温法兰密封接头的可靠性分析 [J]. 压力容器, 2007, 24(9): 20–24. DOI: 10.3969/j.issn.1001-4837.2007.09.005.LU X F, SHEN Y. Reliability analysis on bolted flanged joints at elevated temperature [J]. Pressure Vessel Technology, 2007, 24(9): 20–24. DOI: 10.3969/j.issn.1001-4837.2007.09.005. [24] 王和慧, 卢均臣, 关凯书, 等. 带接管组合法兰的强度和密封有限元分析 [J]. 压力容器, 2012, 29(2): 22–29. DOI: 10.3969/j.issn.1001-4837.2012.02.005.WANG H H, LU J C, GUAN K S, et al. Strength and seal FE analysis of combined flanges with a pipe [J]. Pressure Vessel Technology, 2012, 29(2): 22–29. DOI: 10.3969/j.issn.1001-4837.2012.02.005. -
下载:
计量
- 文章访问数: 494
- HTML全文浏览量: 317
- PDF下载量: 88
- 被引次数: 0