冻融循环对含纯Ⅰ型裂隙围岩的动态起裂特性影响规律

姜亚成; 周磊; 朱哲明; 李剑飞; 牛草原; 应鹏

doi:10.11883/bzycj-2020-0330

冻融循环对含纯Ⅰ型裂隙围岩的动态起裂特性影响规律

doi: 10.11883/bzycj-2020-0330

姜亚成^{1, 2,},
周磊^{1, 2, ,},
朱哲明^{1, 2},
李剑飞^{1, 2},
牛草原^{1, 2},
应鹏^{1, 2}

1.
四川大学建筑与环境学院，四川成都 610065
2.
四川大学深地科学与工程教育部重点实验室，四川成都 610065

基金项目: 国家自然科学基金（U19A2098，11672194，11702181）；深地科学与工程教育部重点实验室（四川大学）开放基金（DESE202005）

详细信息

作者简介:
姜亚成（1994－　），男，硕士研究生，jiangyc210@163.com

通讯作者:
周　磊（1990－　），男，博士，助理研究员，zhouleittkx@126.com

中图分类号: O389；TU45
计量
- 文章访问数: 444
- HTML全文浏览量: 235
- PDF下载量: 57
- 被引次数: 0
出版历程
- 收稿日期: 2020-09-21
- 修回日期: 2020-11-16
- 网络出版日期: 2021-04-14
- 刊出日期: 2021-04-14

Effects of freeze-thaw cycles on dynamic fracture initiation characteristics of surrounding rock with pure Ⅰ type fracture under impact loads

JIANG Yacheng^{1, 2
,},
ZHOU Lei^{1, 2
, ,},
ZHU Zheming^{1, 2},
LI Jianfei^{1, 2},
NIU Caoyuan^{1, 2},
YING Peng^{1, 2}

1.
College of Architecture and Environment, Sichuan University, Chengdu 610065, Sichuan, China
2.
MOE Key Laboratory of Deep Underground Science and Engineering, Sichuan University, Chengdu 610065, Sichuan, China

摘要

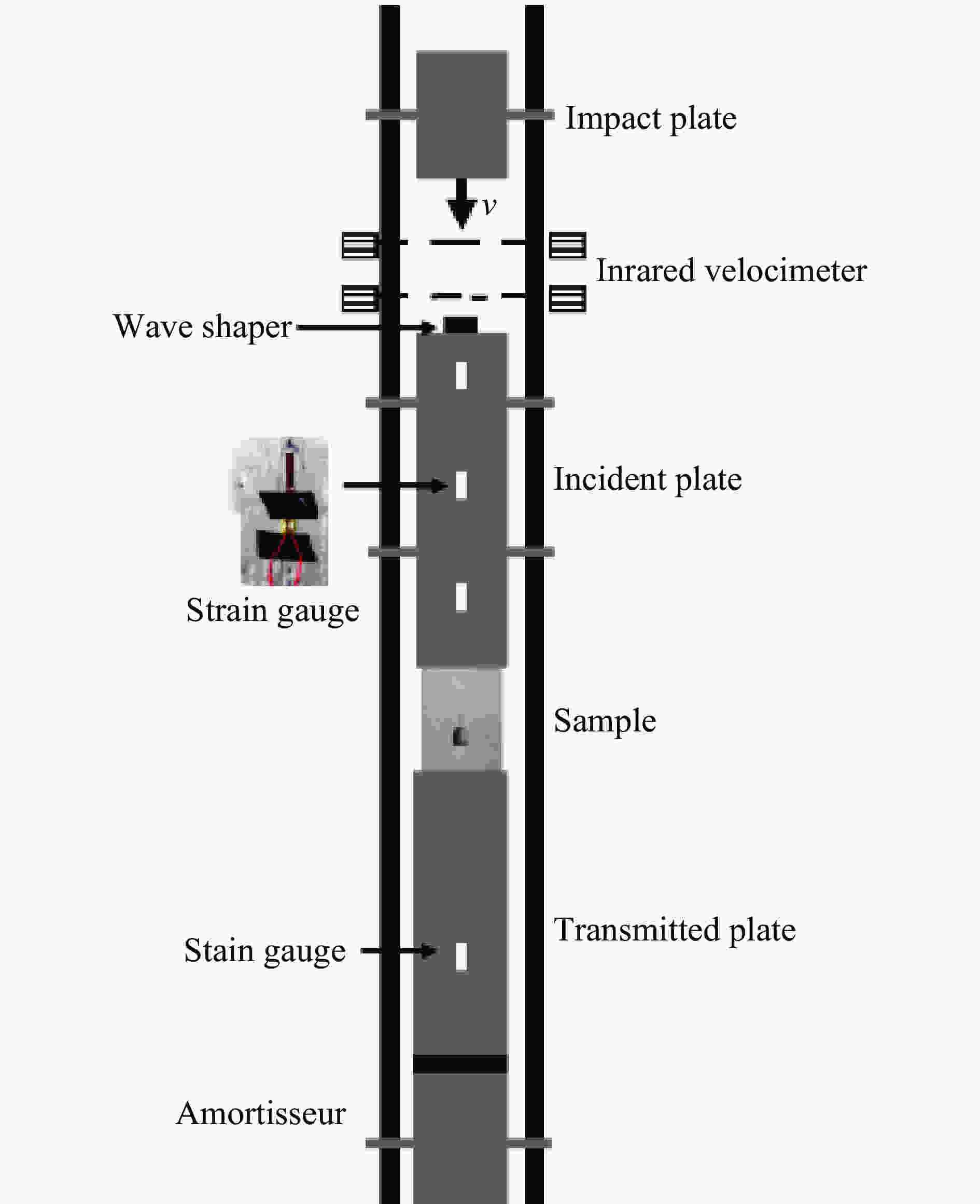
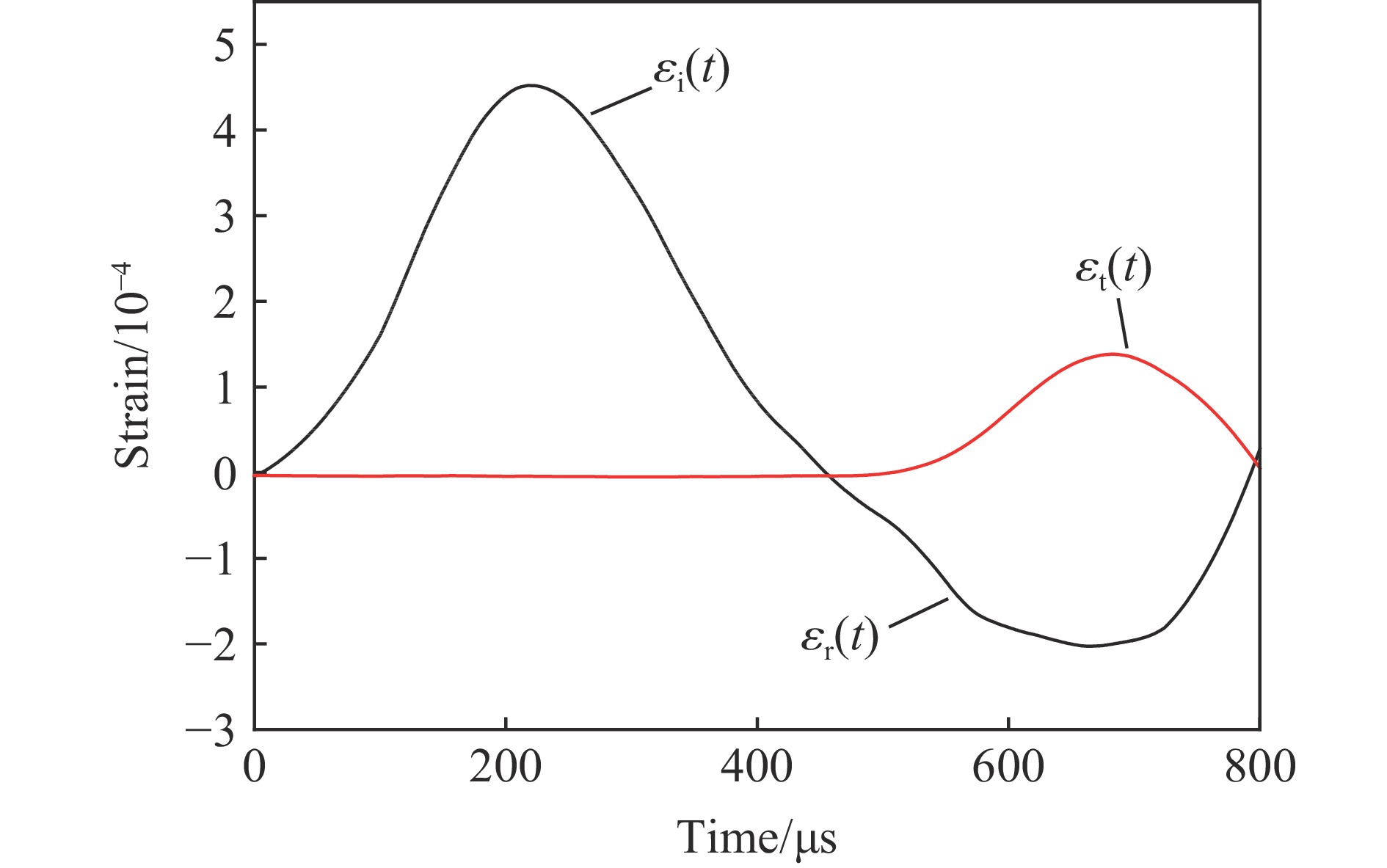
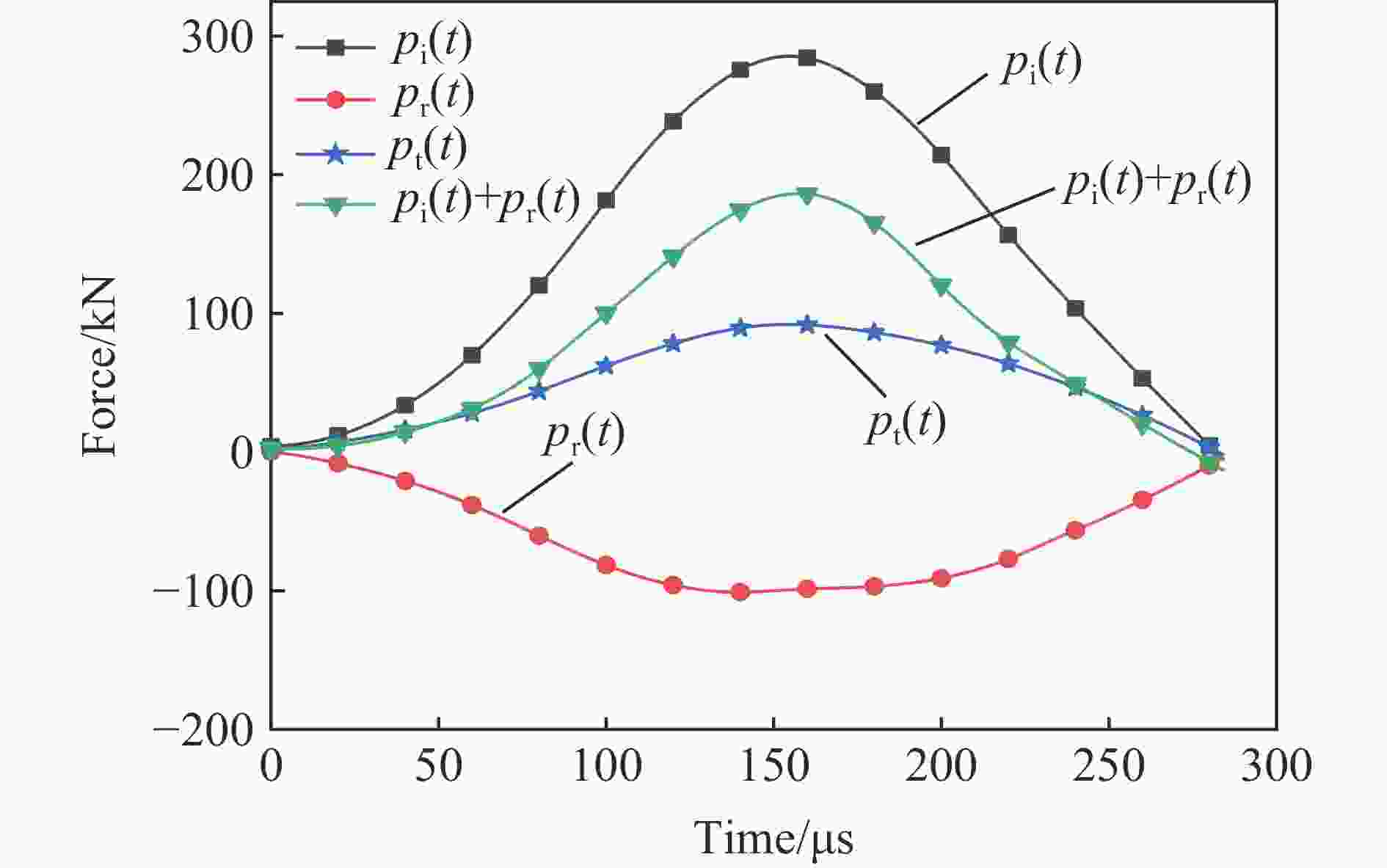
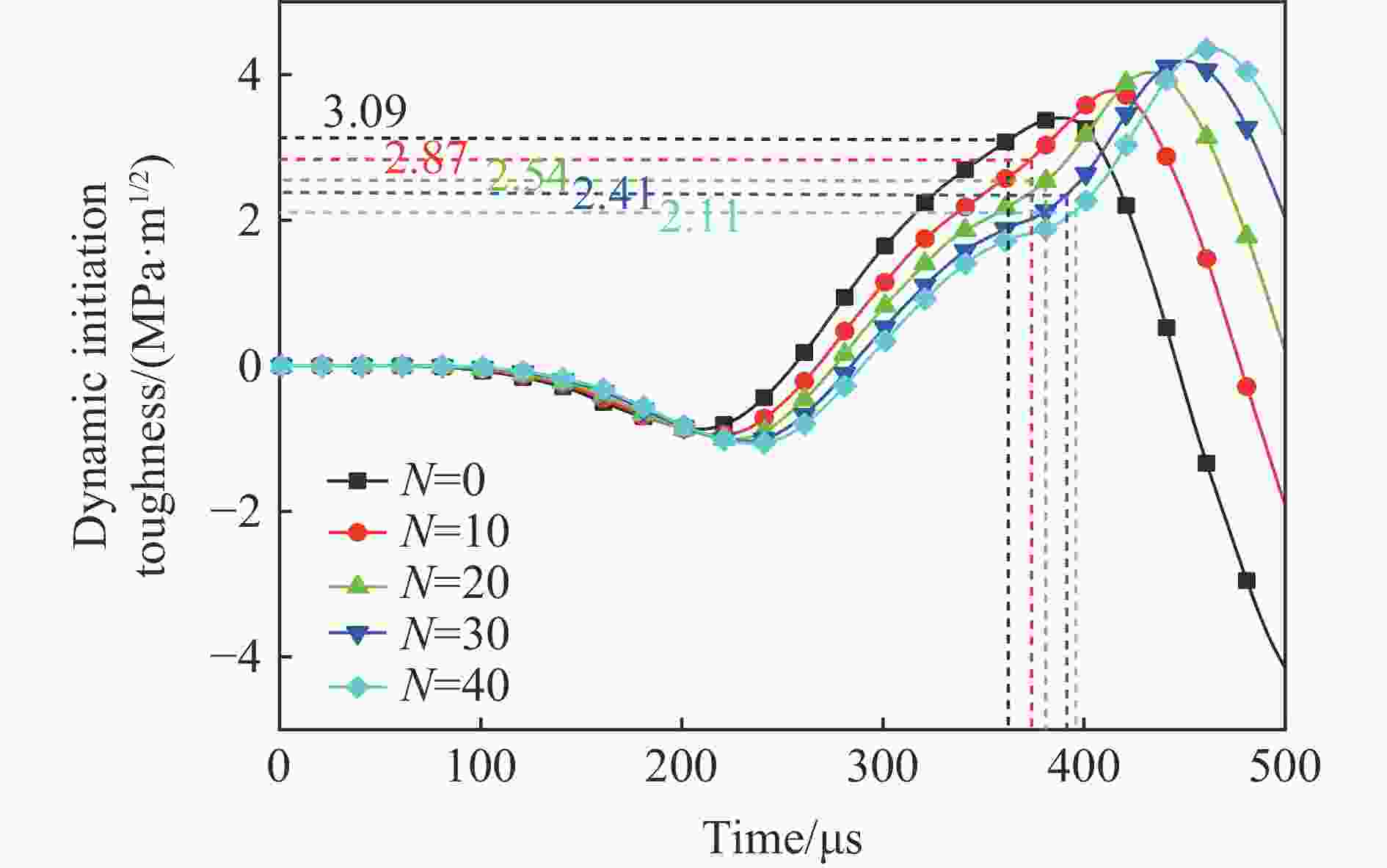
摘要: 以寒区隧道为工程背景研究在冻融循环作用下围岩内Ⅰ型裂纹的动态起裂特性演化规律，采用隧道模型试件作为研究对象，开展冻融循环试验与大尺度落锤冲击试验，得到岩石试件经历不同冻融循环次数后的相关力学参数，并在裂纹尖端粘贴裂纹扩展计(crack propagation gauge, CPG)测量预制裂纹的动态起裂时间。采用有限元软件建立相应的数值模型计算裂纹尖端的动态应力强度因子，采用试验-数值法计算动态起裂韧度，随后采用电镜对冻融循环后的试样进行扫描，研究冻融循环对岩石材料的细观损伤机制。研究结果表明：随着冻融循环次数的增加，岩石材料的纵波、横波波速与弹性模量逐渐减小，而泊松比逐渐增大；砂岩材料的动态起裂韧度随着冻融循环次数的增加逐渐减小，表征线性反比例的特性；材料内部的胶结物质会由于冻融循环的影响而流失，材料的孔隙和裂纹也随着冻融循环次数的增加而变多变大。
- 冻融循环 /
- 隧道模型 /
- 动态起裂韧度 /
- 细观损伤机制
Abstract: In order to investigate the dynamic initiation and evolution of mode Ⅰ crack in surrounding rock under the action of freeze-thaw cycle, taking a cold area tunnel as the engineering background, the freeze-thaw cycle test and large-scale drop weight test were carried out by using tunnel model specimens that were made of green sandstone in Sichuan province. The dynamic mechanical characteristics of specimens after different freeze-thaw cycles were measured and discussed. The elastic modulus and Poisson’s ratio of the specimens were calculated by longitudinal wave velocity, shear wave velocity. The dynamic strain gauges were glued at the incident plate and transmitted plate to collect voltage signals. The voltage signal was applied to calculate the curves of dynamic loading versus time recorded from the incident plate and transmission plate. Crack initiation time was determined by using a crack propagation gauge (CPG) measuring system. A traditional finite element method code was applied to establish some numerical models to calculate the curves of dynamic stress intensity factor under impact loads. The experimental-numerical method was used to determine dynamic fracture initiation toughness according to crack initiation time. A scanning electron microscope (SEM) was applied to analyze the micro-structure of sandstone material after different freeze-thaw cycles, and the mesoscopic damage mechanism of rock materials was obtained. The test results show that the longitudinal wave velocity, shear wave velocity and elastic modulus of sandstone gradually decrease with the number of freeze-thaw cycles, while Poisson’s ratio increases with the number of freeze-thaw cycles. The crack initiation time and dynamic initiation toughness of rock material decrease with the number of the freeze-thaw cycles. The cement material inside the rock will loss due to the effect of freeze-thaw cycles, and the pores and micro-cracks of the sandstone also increase with the number of freeze-thaw cycles.
- freeze-thaw cycles /
- tunnel model /
- dynamic initiation toughness /
- mesoscopic damage mechanism

HTML全文

内爆压力载荷包含准静态压力和冲击波超压，其中由炸药内爆产生的准静态压力虽然远小于冲击波的超压，但由于其加载时间长，能给结构以及内部设施造成持续的震荡与冲击，引起更大程度的毁伤。为了评估准静态压力对结构的毁伤效果，需要对准静态压力进行分析，其中炸药内爆的后燃烧效应在准静态压力计算中需要被重点关注。Kuhl等^[1-2]进行了冲击分散燃料（shock-dispersed-fuel，SDF）与铝、TNT的复合装药内爆试验，探讨了燃烧室容积和几何形状对后燃烧完全度的影响。静态压力表显示在空气中爆炸的压力和脉冲比在氮气中爆炸记录的要大得多，说明了后燃效应对准静态压力的显著影响。Feldgun等^[3]与Edri等^[4]进行TNT的全尺寸内爆试验，并将后燃分为完全与不完全两种情况，给出了准静态压力关于药量体积比的详细的预测模型；李旭东^[5]在此基础了简化了计算模型，并利用试验验证了TNT和RDX内爆在完全后燃烧下的准静态压力计算公式的准确性；王等旺等^[6]、王鑫等^[7]、张玉磊等^[8]进行了TNT在氧气不充足下的内爆试验，根据试验数据拟合了TNT内爆准静态压力计算公式；钟巍等^[9-11]以TNT为例系统地研究了后燃烧现象，提出了温度、准静态压力计算模型；徐维铮等^[12]在钟巍等^[9-11]的研究基础上，考虑了初始空气内能，建立了准静态压力与药量体积比的关系。上述研究主要以TNT等传统碳氢氧氮炸药为对象，研究了内爆后燃烧效应对准静态压力的影响，并通过试验拟合与理论推导给出了内爆准静态压力预测模型，为后续其他炸药的理论预测模型的建立奠定基础。

相比于TNT等传统碳氢氧氮炸药，含铝炸药能量密度高、爆热大，被广泛用于打击舰船舱室、建筑房间等具有密闭空间的目标。在含铝炸药理论研究中，李世伟等^[13]以RDX为对象研究了铝含量对含铝炸药爆热的影响，拟合了铝氧摩尔比与炸药爆热的方程；李媛媛等^[14]测量了不同铝粉粒径的含铝炸药在不同环境中的爆热；白玉^[15]通过试验和仿真给出了自由场中的含铝炸药爆炸场的温度分布模型。在试验研究上，张玉磊等^[16]进行了TNT炸药与某温压炸药内爆的对比试验，结果显示温压炸药的各威力参量对比同质量TNT都有较大提升；蒋欣利等^[17]利用LiF替代温压炸药中的铝粉进行内爆对照试验，研究了铝粉对温压炸药内爆的威力增强效果；李媛媛等^[18]开展不同铝含量含铝炸药的内爆试验，研究了炸药爆炸场的响应规律；段晓瑜^[19]、卢广照等^[20]分别进行了以RDX、CL-20为基的含铝炸药的内爆试验，获得了不同含铝量下的准静态压力数据。目前含铝炸药的研究领域，在试验上大多进行了含铝炸药与一般炸药的威力对比，定性地分析了铝粉对炸药的威力增强效果；在理论研究中存在一些通过试验与仿真数据拟合得到的温度分布模型与爆热模型，但缺少对内爆准静态压力的理论预测模型。

活性材料与炸药环状复合装药作为复合炸药，可以基于战斗部需求，选取组合不同模块装药，从而在提高炸药爆热的同时，提升装药的安定性。以含铝的活性材料为例：阳世清等^[21]测试了Al/PTFE的理化性能、热分解性能和力学性能；刘瑞华等^[22-23]分析了Al₂O₃/PTFE的热化学反应性能，阐述了多种铝基含氟铝热体系反应机理，并且借助热分析推断得出Al/PTFE的宏观反应过程。聚四氟乙烯（polytetrafluoroethylene, PTFE）作为一种新型的含能材料，它点火温度低、能量密度高，是一种重要的工业含能材料，具有较好的应用前景。上述对活性材料Al/PTFE理化性能与反应机理的研究为其在复合装药上的应用提供了理论支撑。

综上所述，目前含铝炸药、活性材料复合装药的反应机理复杂，缺少相关炸药的内爆准静态压力预测模型。本文针对上述问题，以具有代表性的活性材料Al/PTFE为对象，首先分析一般碳氢氧氮炸药后燃烧效应对内爆准静态压力的影响，归纳一般炸药的内爆准静态压力预测模型，构建一种活性材料与炸药环状复合装药内爆的准静态压力计算修正模型；开展活性材料与炸药环状复合装药、含铝炸药两种炸药的内爆试验，验证模型的精度，并且在对比分析两种炸药的试验结果后，推广模型至一般含铝炸药，并整合文献中的相关数据进行验证。

1. 内爆准静态压力计算模型优化

1.1 现有计算模型

密闭空间内炸药爆炸的能量释放包括爆轰阶段和后燃烧阶段：爆轰阶段炸药分子被外界能量活化后，分子运动速度增大，分子间碰撞增强，使得炸药分子破裂，释放出活性基团，他们之间相互发生剧烈化学反应，释放大量气体，同时产生大量热量导致气体产物温度上升并急剧绝热膨胀对外界做功；当爆轰产物膨胀后，由于爆轰产生的产物中包含多种易燃物，如一氧化碳、甲烷、碳等，这些易燃物与空气充分混合后，在高温高压的环境下，将会与空气中的氧气发生化学反应，燃烧放热，其化学能转换为系统的热能，最终表现为系统的准静态压力。具体的：

$E = {E_1} + {E_2} = mQ + \sum\limits_{i = 1}^n {{Q_i}}$

(1)

式中：E为炸药释放的能量，Q为炸药爆热，m为炸药质量， ${Q}_{i}$ 为后燃烧过程中每一化学反应的反应热，n为后燃烧发生的反应数目。

Edri等^[4]基于理想气体方程提出了一种考虑后燃烧情况下的准静态压力计算模型。在只由参与反应的物质组成的系统中，所有产生的热量都用于将产物加热到更高的温度，炸药释放的能量E完全转换为系统增加的能量 $\Delta Q$ ，则：

$\Delta Q = {n_{{\text{tot}}}}\int\limits_{{T_0}}^{{T_p}} {{C_p}{\text{d}}T}$

(2)

式中： ${n_{{\text{tot}}}}$ 为爆轰产物物质的量， ${C}_{p}$ 为爆轰产物定压摩尔热容， ${T_0}$ 为初始温度， ${T}_{p}$ 为恒定压力下的温度。

利用理想气体状态方程描述爆炸产物：

$pV = {n_{{\text{tot}}}}R{T_V} = {n_{{\text{tot}}}}R\gamma {T_p}$

(3)

式中：V为容器体积，R=8.314 J/(mol·K)， ${T}_{V}$ 为恒定体积下的温度， $\gamma$ 为爆轰产物绝热指数。最终，炸药释放的能量表现为准静态压力p：

$p = {T_p}\gamma R{n_{{\text{tot}}}}/V$

(4)

李旭东^[5]根据Edri等^[4]的研究简化了计算模型。首先利用工程上凝聚炸药爆轰产物的NMQ计算方法确定相关的化学反应式与化学反应热，从而得到各爆轰产物物质的量，取高温状态下混合气体的绝热指数为1.25，然后计算系统最终的准静态压力：

$p = \frac{{[E/({n_{{\text{tot}}}}{C_{p}}) + {T_0}]\gamma R{n_{{\text{tot}}}}}}{V} \qquad \quad {C_p} = \frac{1}{{{n_{{\text{tot}}}}}}\sum\limits_{i = 1}^n {{C_{pi}}{n_i}}$

(5)

式中： ${C}_{pi}$ 和 ${n}_{i}$ 分别为第i种爆轰产物的定压摩尔热容和物质的量。常见气体定压比热见表1^[11]。

表 1 常见气体定压比热容^[11]

Table 1. Common gas specific heat capacity at constant pressure^[11]

气体	温度/K	定压比热容/（J·mol⁻¹·K⁻¹）	气体	温度/K	定压比热容/（J·mol⁻¹·K⁻¹）
CO₂	300～2000	37.129	CO	298～2500	29.121
H₂O	298～2500	33.577	O₂	289～1500	29.359
N₂	298～2500	29.121	CH₄	291～1500	35.715

下载: 导出CSV

| 显示表格

1.2 分析与修正

目前对内爆准静态压力计算模型研究都局限于一般碳氢氧氮炸药，而将所得到的计算模型运用于Al/PTFE活性材料与炸药的环状复合装药时得到的结果偏差极大，需要对现有计算模型进行修正。而含铝炸药反应机理理论二次反应机理认为：铝粉在炸药爆轰时并未参与爆轰反应，反而稀释了炸药的浓度，降低了炸药释放的能量。因此，已有模型并不能满足对含铝炸药的计算精度要求。本文参考含铝炸药的二次反应机理，考虑Al/PTFE与炸药环状复合装药中铝含量对反应热的稀释，假设反应热的释放程度与炸药含量百分比 $\mu$ 存在线性关系，则实际释放的能量为

${E_0} = \mu {E_{\max }}$

(6)

式中： ${E}_{0}$ 为实际释放能量， ${E}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ 为最大反应热。

从而利用 $\mu$ 修正炸药释放的能量E，可以将式(5)改写为

$p = \frac{{[{E_0}/({n_{{\text{tot}}}}{C_p}) + {T_0}]\gamma R{n_{{\text{tot}}}}}}{V} = \frac{{[\mu {E_{\max }}/({n_{{\text{tot}}}}{C_p}) + {T_0}]\gamma R{n_{{\text{tot}}}}}}{V}$

(7)

在实际作战中，对于舰艇、建筑等目标的打击，一般使用半穿甲爆破型战斗部。首先利用战斗部动能击穿目标装甲结构，随后炸药在内部爆炸形成冲击波对结构造成毁伤。炸药的后燃烧反应的程度会影响炸药的总释放能量，因此为了较准确地计算内爆准静态压力，需要对后燃烧反应程度进行分析。受到炸药当量和空腔体积的影响，炸药会出现完全后燃烧与不完全后燃烧两种情况，所以药量和空腔体积之比存在一个临界值 $\varphi$ ，低于该临界值时炸药可以完全后燃，密闭空间内的氧气恰好全部消耗，此时反应方程式和临界值表达式分别为：

$a\mathrm{A}\mathrm{l}+{\mathrm{C}}_{b}{\mathrm{H}}_{c}{\mathrm{O}}_{d}{\mathrm{N}}_{e}+(1.5a+2b+0.5c-d){\mathrm{O}}_{2}\Rightarrow 0.5a\mathrm{A}{\mathrm{l}}_{2}{\mathrm{O}}_{3}+b\mathrm{C}{\mathrm{O}}_{2}+0.5c{\mathrm{H}}_{2}\mathrm{O}+0.5d{\mathrm{N}}_{2}$

(8)

$\varphi = \frac{{0.21M}}{{{V_{\rm m}}(1.5a + 2b + 0.5c - d)}}$

(9)

式中：M为炸药的摩尔质量， ${V}_{\rm m}$ 为空气的摩尔体积，a与炸药铝含量有关，b、c、d、e与炸药分子式相关，本文采用的黑索金（RDX）炸药化学式为 ${\mathrm{C}}_{3}{\mathrm{H}}_{6}{\mathrm{O}}_{6}{\mathrm{N}}_{6}$ 。

炸药的放热只与起始和终末状态有关，与变化途径无关。即只要确定爆轰过后的产物和原成分的生成焓，就可根据盖斯定律得出炸药的爆热，Al₂O₃、CO₂与气态H₂O的标准摩尔生成焓分别为1670、394和242 kJ/mol。在氧气足够时，碳元素、氢元素分别被氧化为二氧化碳和水，而铝元素可能的产物除了 $\mathrm{A}{\mathrm{l}}_{2}{\mathrm{O}}_{3}$ ，还包含 $\mathrm{A}\mathrm{l}\mathrm{N}$ ，然而 $\mathrm{A}\mathrm{l}\mathrm{N}$ 的制备不仅需要高温条件及长时间保温^[24]，同时由于氧气的过量，大部分 $\mathrm{A}\mathrm{l}\mathrm{N}$ 产物也会被氧化，所以实际爆轰后产生的 $\mathrm{A}\mathrm{l}\mathrm{N}$ 极少，对模型的准确性影响较小。

以Al/PTFE与RDX环状复合装药为例，在氧气足够时的反应方程式为：

${\mathrm{C}}_{3}{\mathrm{H}}_{6}{\mathrm{O}}_{6}{\mathrm{N}}_{6}\mathrm{A}{\mathrm{l}}_{a}+\left(0.75a+1.5\right){\mathrm{O}}_{2}\Rightarrow 0.5a\mathrm{A}{\mathrm{l}}_{2}{\mathrm{O}}_{3}+3\mathrm{C}{\mathrm{O}}_{2}+3{\mathrm{H}}_{2}\mathrm{O}+3{\mathrm{N}}_{2}\qquad {\Delta }H=(-1847-835a)\;{{\mathrm{kJ/mol}}}$

(10)

所以此时的实际释放能量为

${E}_{0}=\mu (1847+835a)\; {\mathrm{kJ/mol}}$

(11)

计算得到反应后各种物质的量，总物质的量以及平均定压比热容：

$\left\{ \begin{array}{l}{n}_{{\mathrm{H}}_{2}\mathrm{O}}=3{n}_{\mathrm{RDX}}\\ {n}_{{\mathrm{O}}_{2}}=0.21{n}_{\rm{air}}-(0.75a+1.5){n}_{\mathrm{RDX}}\\ {n}_{{\mathrm{N}}_{2}}=0.79{n}_{{\mathrm{air}}}+3{n}_{\mathrm{RDX}}\\ {n}_{\mathrm{CO}_{2}}=3{n}_{\mathrm{RDX}}\\ {n}_{\mathrm{tot}}=(7.5-0.75a){n}_{\mathrm{RDX}}+{n}_{\mathrm{air}}\\ {C}_{p}=\dfrac{29.1{n}_{\mathrm{air}}+{n}_{\mathrm{RDX}}\left(255.4-22.0a\right)}{{n}_{\mathrm{tot}}}\end{array}\right.$

(12)

式中： $\mu$ 、a都由复合炸药的组成决定。

将相关参数代入式(7)，同时令 $x={n}_{\mathrm{a}\mathrm{i}\mathrm{r}}$ , $y={n}_{\mathrm{R}\mathrm{D}\mathrm{X}}$ ，可以得到预测的准静态压力：

$p = \frac{{0.13\left( {x + 7.5y - 0.75ya} \right)\left( {x + 8.79y - 0.76ya + 213.72y\mu + 96.62ya\mu } \right)}}{{x\left( {x + 8.79y - 0.76ya} \right)}}$

(13)

2. 试　验

进行内爆试验，测试不同炸药在约束环境中爆炸后的准静态压力。现有研究表明准静态压力载荷峰值仅与炸药质量、舱室内体积有关，所以试验箱体尺寸参考舰船内部舱室结构使用缩比模型是可行的，试验所用箱体内部尺寸为1.5 m×1.5 m×1.5 m，容积为3.375 m³，爆炸箱整体的模型图1所示。压力测试点设计在爆炸箱体顶部。试验中使用的压力传感器灵敏度1 mV/psi (0.145 mV/kPa)，测量范围为0～5 kpsi (34.475 MPa)。

图 1 爆炸箱体模型

Figure 1. Model of the explosive enclosure

下载: 全尺寸图片幻灯片

装药结构置于爆炸箱中心，试验装药分为2种，一种是JHL-2含铝炸药，一种是由中心药柱JH-14和含铝外环Al/PTFE组合得到的复合装药，铝粉平均粒径为25 μm，PTFE粒径范围为20～70 μm。其中JHL-2炸药和铝粉的质量比为65∶30，JH-14药柱成分为：黑索今96.5%，氟橡胶3%，胶体石墨0.5%，圆环复合装药结构见图2。试验共4种工况，见表2：工况1和2各做两发试验，起爆方式为上端面中心雷管起爆，其中工况1第一发试验中内爆箱箱口朝上，装药结构由绳子从上方开口竖直吊至箱体中心，其余试验内爆箱箱口均朝向侧面，装药结构固定到木棍上伸至箱体中心。

图 2 环状复合装药结构与中心药柱

Figure 2. Circular composite charge structure and Central drug column

下载: 全尺寸图片幻灯片

表 2 试验工况

Table 2. Test conditions

工况	装药	质量/g	质量分数/%
工况	装药	质量/g	Al	RDX	其他
1	JH-14—Al/PTFE复合装药	150.03	14.0	42.5	33.5
1		150.03	14.0	42.5	33.5
2		152.56	22.7	41.7	35.6
2		152.56	22.7	41.7	35.6
3		353.00	29.5	66.3	4.2
4	JHL-2	360.00	30.0	65.0	5.0

下载: 导出CSV

| 显示表格

现场试验布局见图3。在试验后成功采集到了各工况的压力信号。复合装药爆炸后打开箱体，观察试验结果，开箱时有大量白烟散出，箱内未发现明显残余Al粉和PTFE，爆炸后铝粉扑在罐体内壁上，在螺栓连接处铝粉随爆轰产物气体外泄流出，留下印记，结果如图4所示。

图 3 试验现场布局

Figure 3. Layout of test site

下载: 全尺寸图片幻灯片

图 4 试验结果

Figure 4. Test results

下载: 全尺寸图片幻灯片

试验获得的典型超压曲线见图5。爆炸试验中准静态压力的获取主要是通过处理传感器测量到的压力波形得到，这种方式简单却可能因为不同的处理方法导致结果有出入，但这种差异通常很小，并不影响最终的结论。文献[25]中进行了不同气体环境下的TNT内爆试验，对空气中15 g药量的内爆试验准静态压力数据采用了加权平均算法、局部加权回归算法（窗口长度5 ms）与直接取压力平均值（10～20 ms）三种方法，进行了准静态压力的拟合，得到的结果分别为434.7、435.0、433.1 kPa，可见其结果差距很小。同时观察典型压力波形，由于存在箱体未完全密封的情况，压力曲线会逐渐衰减，于是取冲击波峰值到达5 ms后超压曲线上升段的平均值作为准静态超压。

图 5 试验测得的典型超压曲线

Figure 5. Test overpressure curve

下载: 全尺寸图片幻灯片

表3给出了利用式(5)和式(7)得到修正前后的Al/PTFE与炸药环状复合装药内爆的准静态压力理论计算结果及其与试验结果的对比。可以看出，计算值较试验值偏大，原因是：理论计算的前提条件是处于理想状态，而分析发现试验中铝粉分散等情况，这会消耗炸药的一部分内能；同时在试验中会出现容器结构受压变形、结构不完全封闭等情况，导致爆轰产物耗散等情况，故试验值偏小。对比采用本文方法进行修正前后的计算结果可以看出，修正后计算得到的结果偏差远小于修正前，平均误差为9.1%，最大误差为15.8%。

表 3 试验结果与计算结果比较

Table 3. Comparison between experimental and theoretical results

工况	装药质量/g	a	μ	试验压力/MPa	计算压力/MPa		误差/%
工况	装药质量/g	a	μ	试验压力/MPa	修正前	修正后	修正前	修正后
1	150.03	2.7	0.425	0.180	0.253	0.181	40.6	0.6
1	150.03	2.7	0.425	0.172	0.253	0.181	47.1	5.2
2	152.56	4.5	0.417	0.177	0.297	0.198	67.8	11.8
2	152.56	4.5	0.417	0.180	0.297	0.198	65.0	10.0
3	353.00	3.8	0.663	0.430	0.686	0.498	59.5	15.8
4	360.00	3.7	0.663	0.440	0.676	0.490	53.6	11.4

下载: 导出CSV

| 显示表格

对比工况3和4的试验结果，可以发现JHL-2含铝炸药与JH-14—Al/PTFE复合装药结构在含铝量与总装药量均接近时得到的准静态压力结果差距并不大，于是考虑将式(7)推广至一般含铝炸药的内爆准静态压力预测。而由于试验条件有限，因此利用文献中含铝炸药的内爆试验数据对式(7)进行验证。

段晓瑜^[19]在密闭空间开展了不同铝粉粒径、不同铝含量的RDX基含铝炸药内爆试验，获得了多组准静态压力试验数据。试验的爆炸箱容积为100 L，试验中氧气充足。表4给出了50 μm粒径铝粉条件下本文理论计算与段晓瑜^[19]试验数据的对比结果，得到各工况平均误差8.1%，最大误差为13.0%。

表 4 文献[19]试验结果与本文计算结果比较

Table 4. Comparison between test result in Ref.[19] and theoretical results in this paper

工况	药量/g	粒径/µm	a	μ	试验压力/MPa	计算压力/MPa	误差/%
19-1	100	50	1.6	80	0.69^[19]	0.78	13.0
19-2	100	50	2.9	70	0.79^[19]	0.80	1.3
19-3	100	50	3.8	65	0.88^[19]	0.81	8.0
19-4	100	50	4.8	60	0.90^[19]	0.80	11.1
19-5	100	50	7.3	50	0.82^[19]	0.76	7.3

下载: 导出CSV

| 显示表格

卢广照等^[20]进行了一系列CL-20基含铝炸药的内爆试验，爆炸罐容积为1.36 m³，试验工况见表5。根据试验工况，炸药处于完全后燃状态，反应方程式为：

表 5 文献[20]试验工况

Table 5. Test conditions in Ref.[20]

工况	药量/g	质量分数/%			工况	药量/g	质量分数/%
工况	药量/g	铝	CL-20	其他	工况	药量/g	铝	CL-20	其他
20-1	200	10	64.5	25.5	20-4	100	10	64.5	25.5
20-2	200	20	54.5	25.5	20-5	100	20	54.5	25.5
20-3	200	30	45.5	25.5	20-6	100	30	44.5	25.5

下载: 导出CSV

| 显示表格

${\mathrm{C}}_{6}{\mathrm{H}}_{6}{\mathrm{O}}_{12}{\mathrm{N}}_{12}\mathrm{A}{\mathrm{l}}_{a}+\left(0.25a+1.5\right){\mathrm{O}}_{2}\Rightarrow 0.5a\mathrm{A}{\mathrm{l}}_{2}{\mathrm{O}}_{3}+6\mathrm{C}{\mathrm{O}}_{2}+3{\mathrm{H}}_{2}\mathrm{O}+6{\mathrm{N}}_{2} \;\;\;\;\;\; \mathrm{\Delta }H=\left(-2605-835a\right)\text{kJ/mol}$

(14)

反应后各种物质的量、总物质的量以及平均定压比热容为：

$\left\{ \begin{array}{l}{n}_{{\text{H}}_{\text{2}}\text{O}}=3{n}_{\text{CL20}}\\ {n}_{{\text{O}}_{\text{2}}}=0.21{n}_{\text{air}}-(0.25a+1.5){n}_{\text{CL20}}\\ {n}_{{\text{N}}_{\text{2}}}=0.79{n}_{\text{air}}+6{n}_{\text{CL20}}\\ {n}_{{\text{CO}}_{\text{2}}}=6{n}_{\text{CL20}}\\ {n}_{\text{tot}}=(13.5-0.25a){n}_{\text{CL20}}+{n}_{\text{air}}\\ {C}_{pn}=\dfrac{29{n}_{\text{air}}+{n}_{\text{CL20}}\left(454-7a\right)}{{n}_{\text{tot}}}\end{array} \right.$

(15)

将相关参数代入式(7)，并令x=n_air, y=n_CL20，得到准静态压力p的表达式

$p=\frac{0.13\left(x+13.5y-0.25ya\right)\left(x+15.66y-0.24ya+301.43y\mu +96.62ya\mu \right)}{x\left(x+15.66y-0.24ya\right)}$

(16)

通过试验工况，可以计算不同工况下a的值，得到不同情况下的反应热，然后利用式(7)得到炸药内爆准静态理论计算结果，见表6。可以发现，计算得到结果的平均误差15.4%，最大误差为20.6%。

表 6 文献[20]试验结果与计算结果比较

Table 6. Comparison between experimental result in Ref.[20] and theoretical results in this paper

工况	药量/g	a	μ	试验压力/MPa	计算压力/MPa	误差/%
20-1	200	2.6	64.5	0.46^[20]	0.37	19.6
20-2	200	6.1	54.5	0.49^[20]	0.40	18.4
20-3	200	11.1	45.5	0.51^[20]	0.41	19.6
20-4	100	2.6	64.5	0.27^[20]	0.25	7.4
20-5	100	6.1	54.5	0.29^[20]	0.26	6.9
20-6	100	11.1	44.5	0.34^[20]	0.27	20.6

下载: 导出CSV

| 显示表格

分析表3、表4、表6的数据，发现文献[19]中以RDX为基含铝炸药的计算平均误差与最大误差都与本次计算误差接近，而文献[20]则误差较大，同时表3与表4中的计算结果几乎普遍偏大，而表6中的计算结果偏小。分析认为：原因是在固相的炸药环境中，不同炸药环境对铝粉的能量释放过程具有一定影响^[26]，为进一步减少产生的误差，需要进一步研究铝粉氧化燃烧的机制，深入认识固相炸药氧化环境对铝粉氧化燃烧的影响。

3. 结　论

在总结了一般炸药考虑后燃效应下的内爆准静态压力计算模型基础上，考虑Al/PTFE与炸药环状复合装药中铝含量对反应热的稀释，本文提出了一种约束条件下Al/PTFE与炸药环状复合装药的准静态压力计算模型，用以深入描述约束爆炸中的准静态压力变化。

考虑存在理论计算值会出现一定程度偏大的情况，Al/PTFE与炸药环状复合装药完全后燃下的准静态压力模型计算数据与试验数据吻合较好，平均误差为9.1%，最大误差为15.8%。

试验结果显示，Al/PTFE与炸药环状复合装药和含铝炸药的准静态压力相近。

对于其他文献中含铝炸药试验研究的内爆试验数据，本文方法预测准静态压力的平均误差为12.1%，最大误差为20.6%，说明本文计算模型同样适用于内爆下一般含铝炸药准静态压力的预测。

图 1 试件模型及尺寸示意图(单位：mm)

Figure 1. Sketch of specimen (unit: mm)

下载: 全尺寸图片幻灯片

图 2 高低温试验箱

Figure 2. High-low temperature test chamber

下载: 全尺寸图片幻灯片

图 3 试验装置示意图

Figure 3. Drop-weigh test system

下载: 全尺寸图片幻灯片

图 4 裂纹扩展计测试系统

Figure 4. CPG measuring system

下载: 全尺寸图片幻灯片

图 5 纵波波速与弹性模量变化曲线

Figure 5. Plots of P-wave velocity and elastic modulus

下载: 全尺寸图片幻灯片

图 6 入射端与透射端的脉冲信号曲线

Figure 6. Histories of the incident and transmitted plates

下载: 全尺寸图片幻灯片

图 7 动态载荷曲线

Figure 7. Histories of dynamic loads

下载: 全尺寸图片幻灯片

图 8 数值模型网格示意图

Figure 8. Sketch map of numerical model

下载: 全尺寸图片幻灯片

图 9 动态起裂韧度计算结果

Figure 9. Calculation results of dynamic initiation toughness

下载: 全尺寸图片幻灯片

图 10 冻融次数与动态起裂韧度的关系曲线

Figure 10. Relationship between freeze-thaw cycles and dynamic initiation toughness

下载: 全尺寸图片幻灯片

图 11 青砂岩的电镜扫描图

Figure 11. Scanning electron microscopes of sandstone

下载: 全尺寸图片幻灯片

表 1 5组试件材料的力学参数

Table 1. Mechanical parameters for five groups of specimen

冻融次数	孔隙率/%	泊松比	弹性模量/GPa	纵波波速/（m·s⁻¹）	横波波速/（m·s⁻¹）	纵波波速降/%	横波波速降/%
0	12.52	0.262	12.56	2 562	1 455	0	0
10	12.96	0.270	10.50	2 378	1 334	7.2	8.3
20	13.35	0.276	9.14	2 254	1 253	12.0	13.9
30	13.87	0.283	8.10	2 153	1 185	16.0	18.5
40	14.51	0.286	7.31	2 085	1 141	18.6	21.6

下载: 导出CSV

表 2 冲击试验结果

Table 2. Impact test results

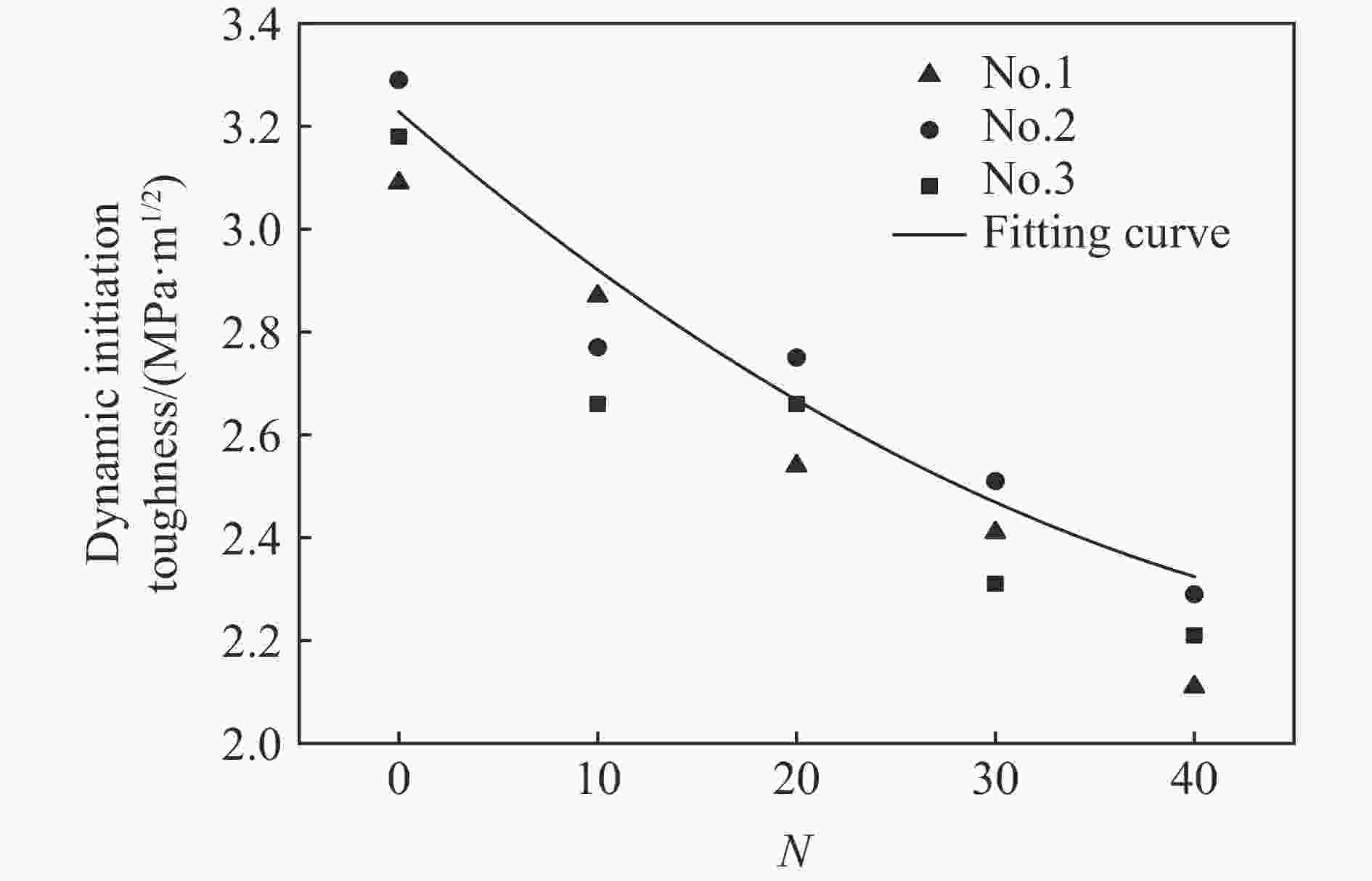
试件	冲击速度/（m·s⁻¹）	起裂时间/μs	动态起裂韧度/（MPa·m^1/2）	动态加载率/（MPa·m^1/2·s⁻¹）
0-1	6.56	362	3.09	10 404
0-2	6.59	374	3.29	10 716
0-3	6.61	367	3.18	10 603
10-1	6.48	375	2.87	9 410
10-2	6.53	371	2.77	9 082
10-3	6.48	366	2.66	8 866
20-1	6.57	381	2.54	8 274
20-2	6.51	389	2.75	8 730
20-3	6.56	386	2.66	8 445
30-1	6.52	393	2.41	7 670
30-2	6.56	397	2.51	7 952
30-3	6.59	390	2.31	7 549
40-1	6.56	395	2.11	6 762
40-2	6.50	392	2.04	6 623
40-3	6.47	399	2.21	7 015

下载: 导出CSV

参考文献(25)

[1]	高焱, 朱永全, 赵东平, 等. 隧道寒区划分建议及保温排水技术研究 [J]. 岩石力学与工程学报, 2018, 37(S2): 3489–3499. DOI: 10.13722/j.cnki.jrme.2016.1115. GAO Y, ZHU Y Q, ZHAO D P, et al. Study on classified suggestion of tunnel in cold region and thermal insulation-considered drainage technology [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(S2): 3489–3499. DOI: 10.13722/j.cnki.jrme.2016.1115.
[2]	夏才初, 白雪莹, 韩常领. 冻融作用下多年冻土隧道结构及围岩变形规律 [J]. 哈尔滨工程大学学报, 2020, 41(7): 1016–1021. DOI: 10.11990/jheu.201901077. XIA C C, BAI X Y, HAN C L. Deformation rules of surrounding rock and structure of permafrost tunnels under freezeing-thawing cycles [J]. Journal of Harbin Engineering University, 2020, 41(7): 1016–1021. DOI: 10.11990/jheu.201901077.
[3]	夏才初, 黄文丰, 韩常领. 冻融循环条件下寒区隧道衬砌的服役性能 [J]. 哈尔滨工程大学学报, 2020, 41(3): 347–356. DOI: 10.11990/jheu.201811029. XIA C C, HUANG W F, HAN C L. The study of service performance of tunnel lining in cold zone when suffered from freeze-thaw cycles [J]. Journal of Harbin Engineering University, 2020, 41(3): 347–356. DOI: 10.11990/jheu.201811029.
[4]	那通兴, 张国柱, 陈俊栋. 寒区隧道含相变围岩传热渗流耦合数值分析 [J]. 隧道建设, 2018, 38(2): 144–150. DOI: 10.3973/j.issn.2096-4498.2018.S2.020. NA T X, ZHANG G Z, CHEN J D. Coupling numerical analysis of heat transfer and seepage flow of surrounding rocks with phase transition in cold region tunnels [J]. Tunnel Construction, 2018, 38(2): 144–150. DOI: 10.3973/j.issn.2096-4498.2018.S2.020.
[5]	申艳军, 杨更社, 王铭, 等. 冻融-周期荷载下单裂隙类砂岩损伤及断裂演化试验分析 [J]. 岩石力学与工程学报, 2018, 37(3): 709–717. DOI: 10.13722/j.cnki.jrme.2017.1296. SHEN Y J, YANG G S, WANG Ming, et al. Experiments on the damage characteristic and fracture process of single-joint quasi-sandstone under the cyclic freezing-thawing and cyclic loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(3): 709–717. DOI: 10.13722/j.cnki.jrme.2017.1296.
[6]	申艳军, 杨更社, 荣腾龙, 等. 冻融循环作用下单裂隙类砂岩局部化损伤效应及端部断裂特性分析 [J]. 岩石力学与工程学报, 2017, 36(3): 562–570. DOI: 10.13722/j.cnki.jrme.2016.0122. SHEN Y J, YANG G S, RONG T L, et al. Localized damage effects of quasi-sandstone with single fracture and fracture behaviors of joint end under cyclic freezeing and thawing [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(3): 562–570. DOI: 10.13722/j.cnki.jrme.2016.0122.
[7]	张慧梅, 杨更社. 冻融环境下红砂岩力学特性试验及损伤分析 [J]. 力学与实践, 2013, 35(3): 57–61. DOI: 10.6052/1000-0879-12-379. ZHANG H M, YANG G S. Mechanical property experiment and damage analysis of red sandstone under freeze-thaw environment [J]. Mechanics in Engineering, 2013, 35(3): 57–61. DOI: 10.6052/1000-0879-12-379.
[8]	闻磊, 李夕兵, 尹彦波, 等. 冻融循环作用下花岗斑岩和灰岩物理力学性质对比分析及应用研究 [J]. 冰川冻土, 2014, 36(3): 632–639. DOI: 10.7522/j.issn.1000-0240.2014.0076. WEN L, LI X B, YIN Y B, et al. Study of physico-mechanical properties of granite porphyry and limestone in slopes of open-pit metal mine under freezing-thawing cycles and their application [J]. Journal of Glaciology and Geocryology, 2014, 36(3): 632–639. DOI: 10.7522/j.issn.1000-0240.2014.0076.
[9]	闻磊, 李夕兵, 唐海燕, 等. 变温度区间冻融作用下岩石物理力学性质研究及工程应用 [J]. 工程力学, 2017, 34(5): 247–256. DOI: 10.6052/j.issn.1000-4750.2015.11.0921. WEN L, LI X B, TANG H Y, et al. Study of physico-mechanical characteristics of rock under different frozen-thawed circle temperature range and its engineering application [J]. Engineering Mechanics, 2017, 34(5): 247–256. DOI: 10.6052/j.issn.1000-4750.2015.11.0921.
[10]	陈宇龙, 张科, 孙欢. 冻融循环作用下岩石表面裂纹扩展过程细观研究 [J]. 土木工程学报, 2019, 52(S1): 1–7. DOI: 10.15951/j.tmgcxb.2019.s1.001. CHEN Y L, ZHENG K, SUN H. Meso-research on the development of rock surface crack under freeze-thaw cycles [J]. China Civil Engineering Journal, 2019, 52(S1): 1–7. DOI: 10.15951/j.tmgcxb.2019.s1.001.
[11]	刘泉声, 黄诗冰, 康永水, 等. 低温冻结岩体单裂隙冻胀力与数值计算研究 [J]. 岩土工程学报, 2015, 37(9): 1572–1580. DOI: 10.11779/CJGE201509003. LIU Q S, HUANG S B, KANG Y S, et al. Numerical and theoretical studies on frost heaving pressure in a single fracture of frozen rock mass under low temperature [J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1572–1580. DOI: 10.11779/CJGE201509003.
[12]	刘少赫, 许金余, 王鹏, 等. 冻融红砂岩的SHPB试验研究及细观分析 [J]. 振动与冲击, 2017, 36(20): 203–209. DOI: 10.13465/j.cnki.jvs.2017.20.031. LIU S H, XU J Y, WANG P, et al. An SHPB experimental study and microscomic analysis of freeze-thaw red sandstone [J]. Journal of Vibration and Shock, 2017, 36(20): 203–209. DOI: 10.13465/j.cnki.jvs.2017.20.031.
[13]	GHOLAMREZA K, REZA Z S, YASIN A. The effect of freeze-thaw cycles on physical and mechanical properties of upper red formation sandstones, central part of Iran [J]. Arabian Journal of Geosciences, 2015, 8(8): 5991–6001. DOI: 10.1007/s12517-014-1653-y.
[14]	GHOBADI M H, BABAZADEH R. Experimental studies on the effects of cyclic freezing–thawing, salt crystallization, and thermal shock on the physical and mechanical characteristics of selected sandstones [J]. Rock Mechanics and Rock Engineering, 2015, 48: 1001–1016. DOI: 10.1007/s00603-014-0609-6.
[15]	周磊, 朱哲明, 董玉清, 等. 中低速冲击载荷下隧道内裂纹的动态响应 [J]. 岩石力学与工程学报, 2017, 36(6): 1363–1372. DOI: 10.13722/j.cnki.jrme.2016.1403. ZHOU L, ZHU Z M, DONG Y Q, et al. Dynamic response of cracks in tunnels under impact loading of medium-low speed [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(6): 1363–1372. DOI: 10.13722/j.cnki.jrme.2016.1403.
[16]	周磊, 朱哲明, 董玉清, 等. 冲击加载下隧道内裂纹的扩展特性及破坏行为 [J]. 爆炸与冲击, 2018, 38(4): 785–794. DOI: 10.11883/bzycj-2016-0383. ZHOU L, ZHU Z M, DONG Y Q, et al. The propagation characteristics and failure behavior of crack in tunnel under impact loads [J]. Explosion and Shock Waves, 2018, 38(4): 785–794. DOI: 10.11883/bzycj-2016-0383.
[17]	付安琪, 蔚立元, 苏海健, 等. 循环冲击损伤后大理岩静态断裂力学特性研究 [J]. 岩石力学与工程学报, 2019, 38(10): 2022–2020. DOI: 10.13722/j.cnki.jrme.2019.0323. FU A Q, WEI L Y, SU H J, et al. Experimental study on static fracturing mechanical characteristic of marble after cyclic impact loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(10): 2022–2020. DOI: 10.13722/j.cnki.jrme.2019.0323.
[18]	WANG M, ZHU Z, DONG Y, et al. Study of mixed-mode I/II fractures using single cleavage semicircle compression specimens under impacting loads [J]. Engineering Fracture Mechanics., 2017, 177: 33–44. DOI: 10.1016/j.engfracmech.2017.03.042.
[19]	王蒙, 朱哲明, 王雄. 冲击荷载作用下的Ⅰ/Ⅱ复合型裂纹扩展规律研究 [J]. 岩石力学与工程学报, 2016, 35(7): 1323–1332. DOI: 10.13722/j.cnki.jrme.2015.1260. WANG M, ZHU Z M, WANG X. The growth of mixed-mode Ⅰ/Ⅱ crack under impacting loads [J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(7): 1323–1332. DOI: 10.13722/j.cnki.jrme.2015.1260.
[20]	WANG Q Z, FENG F, NI M, et al. Measurement of mode Ⅰ and mode Ⅱ rock dynamic fracture toughness with cracked straight through flattened Brazilian disc impacted by split Hopkinson pressure bar [J]. Engineering Fracture Mechanics., 2011, 78(12): 2455–2469. DOI: 10.1016/j.engfracmech.2011.06.004.
[21]	住房与城乡建设部. 工程岩体试验方法标准: GB/T 50266—2013 [S]. 北京中国计划出版社, 2013: 17−18.
[22]	范天佑. 断裂动力学原理与应用 [M]. 北京: 北京理工大学出版社, 2006: 19−22.
[23]	GREGOIRE G, MAIGRE H, RETHORE J, et al. Dynamic crack propagation under mixed-mode loading-comparison between experiments and X-FEM simulations [J]. International Journal of Solids and Structures, 2007, 44: 6517–6534. DOI: 10.1016/j.ijsolstr.2007.02.044.
[24]	陶明, 汪军, 李占文, 等. 冲击荷载下花岗岩层裂断口-微观试验研究 [J]. 岩石力学与工程学报, 2019, 38(11): 2172–2181. DOI: 10.13722/j.cnki.jrme.2019.0185. TAO M, WANG J, LI Z W, et al. Meso and micro-experimental research on the fracture of granite spallation under impact loads [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(11): 2172–2181. DOI: 10.13722/j.cnki.jrme.2019.0185.
[25]	邓华锋, 支永艳, 段玲玲, 等. 水-岩作用下砂岩力学特性及微细观结构损伤演化 [J]. 岩土力学, 2019, 40(9): 3447–3456. DOI: 10.16285/j.rsm.2018.1002. DENG H F, ZHI Y Y, DUAN L L, et al. Mechanical properties of sandstone and damage evolution of microstructure under water-rock interaction [J]. Rock and Soil Mechanics, 2019, 40(9): 3447–3456. DOI: 10.16285/j.rsm.2018.1002.

施引文献

资源附件(0)

访问统计

图(11) / 表(2)

计量

文章访问数: 444
HTML全文浏览量: 235
PDF下载量: 57
被引次数: 0

1. 内爆准静态压力计算模型优化
1.1 现有计算模型
1.2 分析与修正
2. 试　验
3. 结　论

冻融循环对含纯Ⅰ型裂隙围岩的动态起裂特性影响规律

doi: 10.11883/bzycj-2020-0330

作者简介: 姜亚成（1994－ ），男，硕士研究生，jiangyc210@163.com

通讯作者: 周 磊（1990－ ），男，博士，助理研究员，zhouleittkx@126.com

计量

出版历程

Effects of freeze-thaw cycles on dynamic fracture initiation characteristics of surrounding rock with pure Ⅰ type fracture under impact loads

1. 内爆准静态压力计算模型优化

1.1 现有计算模型

1.2 分析与修正

2. 试 验

3. 结 论

计量

出版历程

目录

1. 内爆准静态压力计算模型优化

1.1 现有计算模型

1.2 分析与修正

2. 试 验

3. 结 论

作者简介:
姜亚成（1994－　），男，硕士研究生，jiangyc210@163.com

通讯作者:
周　磊（1990－　），男，博士，助理研究员，zhouleittkx@126.com

2. 试　验

3. 结　论

2. 试　验

3. 结　论