异型截面长杆弹侵彻半无限厚金属靶板实验研究

王晓东; 王江波; 徐立志; 杜忠华; 高光发

doi:10.11883/bzycj-2020-0335

异型截面长杆弹侵彻半无限厚金属靶板实验研究

doi: 10.11883/bzycj-2020-0335

南京理工大学机械工程学院，江苏南京 210094

基金项目: 国家自然科学基金(11772160，11472008)；爆炸科学与技术国家重点实验室开放课题(KFJJ18-01M)；江苏省研究生科研与实践创新计划(KYCX20_0319)

详细信息

作者简介:
王晓东（1993－　），男，博士研究生，18752006367@163.com

通讯作者:
高光发（1980－　），男，博士，教授，gfgao@ustc.edu.cn

中图分类号: O382; TJ413.2
计量
- 文章访问数: 603
- HTML全文浏览量: 408
- PDF下载量: 125
- 被引次数: 0
出版历程
- 收稿日期: 2020-09-21
- 修回日期: 2020-11-06
- 网络出版日期: 2021-03-05
- 刊出日期: 2021-03-10

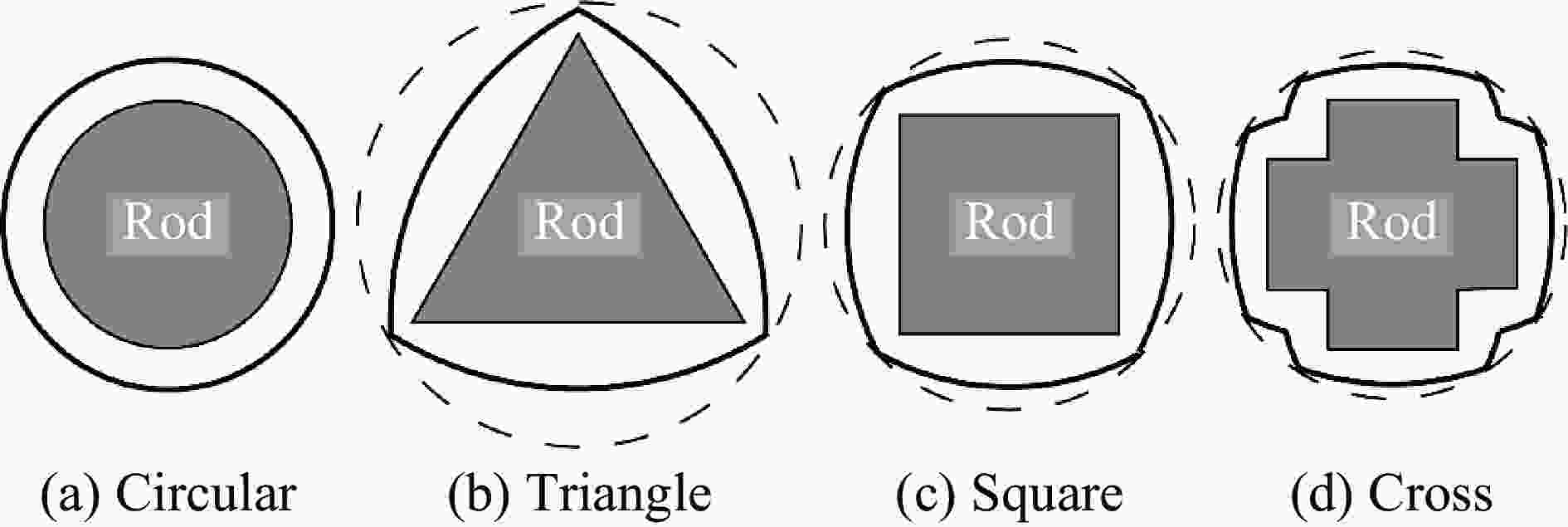
Experimental study on penetration of non-circular cross-section long-rod projectiles into semi-infinite metal target

School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China

摘要

摘要: 为了研究截面形状对长杆弹侵彻半无限金属靶板的最终侵彻深度的影响规律，开展了截面形状为圆形、三角形、正方形、十字形的等截面积的长杆弹侵彻半无限厚靶板的实验研究。实验分为两组，分别为长径比为8、弹芯材料为93钨合金的长杆弹侵彻装甲钢靶板实验以及长径比为15、弹芯材料为45钢的长杆弹垂直侵彻45钢靶板实验。实验后得到不同截面形状、不同长径比、不同弹靶材料的长杆弹在不同着靶速度下的侵彻深度。结果表明：三种异型截面长杆弹的侵彻能力均高于相同工况下的圆形截面长杆弹，且其中十字形截面长杆弹侵彻能力最优，正方形截面次之。通过对实验结果的宏观分析，得到三种异型截面长杆弹的截面形状对长杆弹侵彻半无限靶板侵彻威力的影响规律以及侵彻机理的宏观表现。
- 长杆弹 /
- 异型截面 /
- 影响规律 /
- 量纲分析
Abstract: To study the influences of the cross-sectional shapes on the final depths of penetration, a series of experiments were carried out on the penetration of long-rod projectiles with the same cross-sectional area different cross-sectional shapes into semi-infinite metal targets. The cross-sectional shapes were machined to be circular, square and cross, respectively. These experiments were divided into two groups. In one group of experiments, the long-rod projectiles with the aspect ratio of 8 and 93W alloy cores penetrated into armor-steel target plates. In another group of experiments, the long-rod projectiles with the aspect ratio of 15 and 45 steel cores penetrated into the 45 steel target plates. Depths of penetration under different impact velocities were experimentally obtained for different cross-sectional shapes, aspect ratios, and materials of projectiles and targets, respectively. Experimental results display that the penetration abilities of the three kinds of long-rod projectiles with non-circular cross-section are higher than that of the long-rod projectiles with circular cross-section under the same working conditions. And among the four kinds of long-rod projectiles, the penetration ability of the long-rod projectiles with cross section is the highest, followed by that of the long-rod projectiles with square section. With the increase of the impact velocity, the penetration gains of the cross and square cross-section long-rod projectiles to the circular cross-section ones increase. The cross-section shape of craters penetrated by the triangular cross-section long-rod projectiles takes on arc triangle, and the cross-section shape of craters penetrated by the long-rod projectiles with square and cross sections, respectively, takes on approximate circle. After penetration of the three kinds of non-circular cross-section long-rod projectiles, cracks at certain angles with the axial direction appear in the mushroomed heads of the projectile bodies, which leading to less resistance encountered by the projectiles in the process of penetration. The reason, why the penetration abilities of three kinds of non-circular cross-section long-rod projectiles are higher than that of the circular-section long-rod projectiles, is their structural self-sharpening in the process of penetration.
- long-rod projectiles /
- non-circular cross-section /
- influence law /
- dimensional analysis

HTML全文

图 1 四种不同的长杆弹截面形状

Figure 1. Cross-section shapes of different projectiles

下载: 全尺寸图片幻灯片

图 2 弹丸结构

Figure 2. Projectile structure

下载: 全尺寸图片幻灯片

图 3 实验布置

Figure 3. Experimental arrangement

下载: 全尺寸图片幻灯片

图 4 不同着靶速度下不同截面长杆弹侵彻威力

Figure 4. H/L of projectiles with different cross-sections at different velocities

下载: 全尺寸图片幻灯片

图 5 F和F′值变化

Figure 5. Value of F and F′

下载: 全尺寸图片幻灯片

图 6 弹坑截面形状

Figure 6. The cross-sections of craters

下载: 全尺寸图片幻灯片

图 7 弹底形态

Figure 7. Crater shapes

下载: 全尺寸图片幻灯片

图 8 弹坑截面示意图

Figure 8. The cavity cross-section

下载: 全尺寸图片幻灯片

图 9 弹体裂纹

Figure 9. Fracture characteristics of cores

下载: 全尺寸图片幻灯片

表 1 各物理量的量纲

Table 1. Dimension of each physical quantity

物理量	M	L	T
${\ \rho _{\rm{p} } }$	1	−3	0
L	0	1	0
v	0	1	−1
${\sigma _{\rm{p}}}$	1	−1	−2
${\sigma _{\rm{t}}}$	1	−1	−2
${E_{\rm{p}}}$	1	−1	−2
${E_{\rm{t}}}$	1	−1	−2
$\ {\rho _{\rm{t} } }$	1	−3	0

下载: 导出CSV

表 2 各物理量量纲（变换后）

Table 2. Dimension of each physical quantity (after change)

物理量	ρ_p	L	V
${\ \rho _{\rm{p} } }$	1	0	0
L	0	1	0
v	0	0	1
${\sigma _{\rm{p}}}$	1	0	2
${\sigma _{\rm{t}}}$	1	0	2
${E_{\rm{p}}}$	1	0	2
${E_{\rm{t}}}$	1	0	2
${\ \rho _{\rm{t} } }$	1	0	0

下载: 导出CSV

表 3 弹芯尺寸

Table 3. Projectile dimensions

序号	截面形状	材料	L/mm	D^*/mm	T/mm	U/mm
1	圆形	93钨合金	64	8	−	−
2	三角形	93钨合金	64	8	10.77	−
3	正方形	93钨合金	64	8	7.09	−
4	十字形	93钨合金	64	8	8.08	4.2
5	圆形	45钢	90	6	−	−
6	三角形	45钢	90	6	8.08	−
7	正方形	45钢	90	6	5.32	−
8	十字形1	45钢	90	6	3.16	6.06
9	十字形2	45钢	90	6	6.67	4.27
注：D为等效圆直径，表达式为$D^{}=\sqrt {4S/{\text{π } } }$；S为弹芯截面积。

下载: 导出CSV

表 4 实验结果

Table 4. Experimental results

序号	弹芯材料	靶板材料	截面形状	着靶速度/(m·s⁻¹)	侵彻深度/mm	序号	弹芯材料	靶板材料	截面形状	着靶速度/(m·s⁻¹)	侵彻深度/mm
1	93W	603钢	圆形	1615	68.0	25	45钢	45钢	圆形	1538	42.5
2	93W	603钢	三角形	1429	53.0	26	45钢	45钢	圆形	1719	55.0
3	93W	603钢	三角形	1462	54.5	27	45钢	45钢	圆形	1747	53.8
4	93W	603钢	三角形	1596	69.3	28	45钢	45钢	三角形	1288	27.5
5	93W	603钢	三角形	1601	64.9	29	45钢	45钢	三角形	1298	25.5
6	93W	603钢	正方形	1371	54.7	30	45钢	45钢	三角形	1371	25.5
7	93W	603钢	正方形	1374	54.7	31	45钢	45钢	三角形	1548	44.0
8	93W	603钢	正方形	1467	54.5	32	45钢	45钢	三角形	1558	41.5
9	93W	603钢	正方形	1489	60.0	33	45钢	45钢	三角形	1695	53.5
10	93W	603钢	正方形	1625	76.0	34	45钢	45钢	正方形	1376	36.0
11	93W	603钢	正方形	1639	72.0	35	45钢	45钢	正方形	1388	35.5
12	93W	603钢	正方形	1642	75.5	36	45钢	45钢	正方形	1401	32.0
13	93W	603钢	十字形	1388	52.0	37	45钢	45钢	正方形	1412	34.0
14	93W	603钢	十字形	1415	54.2	38	45钢	45钢	正方形	1582	46.0
15	93W	603钢	十字形	1452	60.0	39	45钢	45钢	正方形	1589	50.0
16	93W	603钢	十字形	1473	60.7	40	45钢	45钢	正方形	1702	63.0
17	93W	603钢	十字形	1495	63.5	41	45钢	45钢	十字形1	1358	15.5
18	93W	603钢	十字形	1571	67.0	42	45钢	45钢	十字形1	1464	15.5
19	93W	603钢	十字形	1593	75.8	43	45钢	45钢	十字形1	1472	15.0
20	45钢	45钢	圆形	1317	26.5	44	45钢	45钢	十字形1	1502	51.0
21	45钢	45钢	圆形	1335	24.5	45	45钢	45钢	十字形1	1718	66.0
22	45钢	45钢	圆形	1423	32.5	46	45钢	45钢	十字形2	1469	17.0
23	45钢	45钢	圆形	1478	35.0	47	45钢	45钢	十字形2	1445	16.5
24	45钢	45钢	圆形	1516	37.0	48	45钢	45钢	十字形2	1445	15.5

下载: 导出CSV

参考文献(17)

[1]	王猛. 细晶钨合金穿甲弹芯侵彻机理分析及试验研究[D]. 南京: 南京理工大学, 2013: 79−105.
[2]	杜忠华, 杜成鑫, 朱正旺, 等. 钨丝/锆基非晶复合材料长杆体弹芯穿甲实验研究 [J]. 稀有金属材料与工程, 2016, 45(5): 1308–1313. DU Z H, DU C X, ZHU Z W, et al. An experimental study on perforation behavior of pole penetrator prepared from Wf/Zr-based bulk metallic glass matrix composite [J]. Rare Metal Materials and Engineering, 2016, 45(5): 1308–1313.
[3]	CHEN X W, WEI L M, LI J C. Experimental research on the long rod penetration of tungsten-fiber/Zr-based metallic glass matrix composite into Q235 steel target [J]. International Journal of Impact Engineering, 2015, 79: 102–116. DOI: 10.1016/j.ijimpeng.2014.11.007.
[4]	CHOI-YIM H, CONNER R D, SZUECS F, et al. Quasistatic and dynamic deformation of tungsten reinforced Zr₅₇Nb₅Al₁₀Cu_15.4Ni_12.6 bulk metallic glass matrix composites [J]. Scripta Materialia, 2001, 45(9): 1039–1045. DOI: 10.1016/S1359-6462(01)01134-4.
[5]	庞春旭, 何勇, 沈晓军, 等. 刻槽弹体旋转侵彻混凝土效应试验研究 [J]. 兵工学报, 2015, 36(1): 46–52. DOI: 10.3969/j.issn.1000-1093.2015.01.007. PANG C X, HE Y, SHEN X J, et al. Experimental investigation on penetration of grooved projectiles into concrete targets [J]. Acta Armamentarii, 2015, 36(1): 46–52. DOI: 10.3969/j.issn.1000-1093.2015.01.007.
[6]	邓佳杰, 张先锋, 刘闯, 等. 头部对称刻槽弹体侵彻半无限厚铝合金靶实验与理论模型 [J]. 爆炸与冲击, 2018, 38(6): 1231–1240. DOI: 10.11883/bzycj-2017-0413. DENG J J, ZHANG X F, LIU C, et al. Experimental and theoretical study of symmetrical grooved-nose projectile penetrating into semi-infinite aluminum target [J]. Explosion and Shock Waves, 2018, 38(6): 1231–1240. DOI: 10.11883/bzycj-2017-0413.
[7]	ZHANG S, WU H J, ZHANG X X, et al. High-velocity penetration of concrete targets with three types of projectiles: experiments and analysis [J]. Latin American Journal of Solids and Structures, 2017, 14(9): 1614–1628. DOI: 10.1590/1679-78253753.
[8]	梁斌, 陈小伟, 姬永强, 等. 先进钻地弹概念弹的次口径高速深侵彻实验研究 [J]. 爆炸与冲击, 2008, 28(1): 1–9. DOI: 10.11883/1001-1455(2008)01-0001-09. LIANG B, CHEN X W, JI Y Q, et al. Experimental study on deep penetration of reduced-scale advanced earth penetrating weapon [J]. Explosion and Shock Waves, 2008, 28(1): 1–9. DOI: 10.11883/1001-1455(2008)01-0001-09.
[9]	张奎华, 沈培辉, 杜忠华. 变截面长杆对半无限靶的侵彻特性分析 [J]. 弹箭与制导学报, 2006, 26(4): 135–136, 139. DOI: 10.3969/j.issn.1673-9728.2006.04.042. ZHANG K H, SHEN P H, DU Z H. Analysis of variational section long-rods into semi-infinite targets [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(4): 135–136, 139. DOI: 10.3969/j.issn.1673-9728.2006.04.042.
[10]	董玉财. 管-杆伸出式侵彻体侵彻机理及相关问题研究[D]. 南京: 南京理工大学, 2014: 14−77.
[11]	GARON K, FAMINU O. Aeroballistic range tests of missiles with non-circular cross sections[C]// 41st Aerospace Sciences Meeting and Exhibit. Reno: American Institute of Aeronautics and Astronautics, 2003: 1-10. DOI: 10.2514/6.2003-1243.
[12]	易文俊, 王中原, 杨凯, 等. 三角形截面弹丸的飞行性能研究 [J]. 弹道学报, 2007, 19(2): 5–7, 20. DOI: 10.3969/j.issn.1004-499X.2007.02.002. YI W J, WANG Z Y, YANG K, et al. Research of flight characteristics of projectile with triangular cross-section [J]. Journal of Ballistics, 2007, 19(2): 5–7, 20. DOI: 10.3969/j.issn.1004-499X.2007.02.002.
[13]	BLESS S J, LITTLEFIELD D L, ANDERSON JR C E, et al. The penetration of non-circular cross-section penetrators [C] // 15th International Symposium on Ballistics. Jerusalem: IBS, 1995: 43−50.
[14]	曾国强. 异型弹芯侵彻性能的研究[D]. 南京: 南京理工大学, 2006: 21−27.
[15]	杜忠华, 曾国强, 余春祥, 等. 异型侵彻体垂直侵彻半无限靶板试验研究 [J]. 弹道学报, 2008, 20(1): 19–21. DU Z H, ZENG G Q, YU C X, et al. Experimental research of novel penetrator vertically penetrating semi-infinite target [J]. Journal of Ballistics, 2008, 20(1): 19–21.
[16]	荣光, 孙瑞胜, 薛晓中, 等. 两种非圆截面弹芯的侵彻性能研究 [J]. 兵工学报, 2009, 30(4): 385–388. DOI: 10.3321/j.issn:1000-1093.2009.04.001. RONG G, SUN R S, XUE X Z, et al. Penetration performance study on two kinds of non-circular cross-sectional projectiles [J]. Acta Armamentarii, 2009, 30(4): 385–388. DOI: 10.3321/j.issn:1000-1093.2009.04.001.
[17]	ROSENBERG Z, DEKEL E. A computational study of the relations between material properties of long-rod penetrators and their ballistic performance [J]. International Journal of Impact Engineering, 1998, 21(4): 283–296. DOI: 10.1016/S0734-743X(97)00068-7.