高速冲击表面处理对金属材料力学性能和组织结构的影响

高玉魁; 陶雪菲

doi:10.11883/bzycj-2020-0342

高速冲击表面处理对金属材料力学性能和组织结构的影响

doi: 10.11883/bzycj-2020-0342

高玉魁^{1, 2,},
陶雪菲³

1.
同济大学材料科学与工程学院，上海 201804
2.
上海市金属功能材料开发应用重点实验室，上海 201804
3.
同济大学航空航天与力学学院，上海 200092

详细信息

作者简介:
高玉魁（1973－　），男，博士，教授，ykgao12088@126.com

中图分类号: O347.3; TB31
计量
- 文章访问数: 1218
- HTML全文浏览量: 858
- PDF下载量: 64
- 被引次数: 0
出版历程
- 收稿日期: 2020-09-22
- 修回日期: 2020-11-21
- 网络出版日期: 2021-03-18
- 刊出日期: 2021-04-14

A review on the influences of high speed impact surface treatments on mechanical properties and microstructures of metallic materials

GAO Yukui^{1, 2
,},
TAO Xuefei³

1.
School of Materials Science and Engineering, Tongji University, Shanghai 201804, China
2.
Shanghai Key Laboratory od R&D for Metallic Function Materials, Shanghai 201804, China
3.
School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China

摘要

摘要: 高速冲击表面处理过程中的应变率对金属材料的宏观力学性能和微观组织结构都具有重要影响。根据当前应变率效应的研究成果，从宏观与微观相结合的角度出发，综述了高速冲击表面处理过程中应变率对金属材料强度和塑性的影响规律，并重点阐述了不同应变率下金属材料内部微观组织结构的演变规律，主要包括晶粒结构、绝热剪切带、相变、位错组态和析出相以及变形孪晶等。此外，还分析了组织结构随应变率的演化和微观变形机制的转变对材料力学性能的强化和弱化机理。最后，对高速冲击表面处理梯度组织的变形特点进行了总结。提出了不同组织结构对材料性能影响的综合效应模型，以期为应变率效应的深入研究奠定基础。
- 高速冲击表面处理 /
- 金属材料 /
- 应变率效应 /
- 力学性能 /
- 微观组织结构
Abstract: The strain rate during the process of high speed impact surface treatments has a significant effect on the mechanical properties as well as the microstructures of metallic materials. In this paper, the effects of strain rate during the process of high speed impact surface treatments on the variation of both strength and ductility of metallic materials are reviewed from macroscopic and microscopic prospective based on the current research achievements. The emphases are concentrated on the microstructural evolution under various strain rates, including grain structures, adiabatic shear bands, phases, dislocation structures, precipitates and deformation twins. At relatively low strain rates, grains tend to be elongated with respect to the loading direction, and they may be refined when the strain increases to a certain extent. In comparison, with the increment of strain rates, the free path of dislocation motion is remarkably reduced so that grains can be further refined to consume the impact energy and dislocations are multiplied significantly. However, the relatively high strain rates may also bring about adiabatic temperature rise and frictional heat, which may give rise to dynamic recovery and recrystallization in some materials so that the dislocation density would in turn be reduced. Moreover, precipitates can be formed and they may interact with dislocations owing to the combined effects of high strain rates and temperature rise. When the strain rates increase to the extremely high level, the movement of dislocations may be inhibited and deformation twins can be triggered to coordinate the deformation. As a result, the strain rate effects are complicated phenomena which comprehensively affect the microstructural strengthening and softening effects. Based on these, the influences of both microstructural evolution and the transition of microscopic deformation mechanisms with strain rates on the enhancement and deterioration of mechanical properties are analyzed. Finally, the characteristics of deformation mechanisms of the gradient microstructures derived from high velocity impact surface treatments are concluded. Furthermore, a comprehensive model embodying the influences of different microstructures is proposed, which can provide a foundation for the further researches of strain rate effects.
- high speed impact surface treatment /
- metallic materials /
- strain rate effects /
- mechanical properties /
- microstructures

HTML全文

图 1 材料性能的影响因素示意图^[3]

Figure 1. Schematic diagram of the influencing factors of mechanical properties^[3]

下载: 全尺寸图片幻灯片

图 2 根据应变率的加载模式分类^[7]

Figure 2. Classifications of loads with reference to strain rate^[7]

下载: 全尺寸图片幻灯片

图 3 不同材料高速冲击表面处理前后力学性能变化^{[21, 23]}

Figure 3. Mechanical properties of different materials processed by various high velocity impact surface treatments^{[21, 23]}

FSW: Friction stir welding; LW: laser-welded; HAZ: heat affected zone; FZ: fusion zone

下载: 全尺寸图片幻灯片

图 4 不同材料经高速冲击表面处理后的塑性变化^[24-26]

Figure 4. The plastic changes of different materials processed by high velocity impact surface treatments^[24-26]

下载: 全尺寸图片幻灯片

图 5 不同材料经高速冲击表面处理后的拉伸断口^[27-28]

Figure 5. Tensile fracture morphologies of different materials after high speed impact surface treatment^[27-28]

下载: 全尺寸图片幻灯片

图 6 不同梯度材料的应力应变曲线^[30-31]

Figure 6. The stress-strain curves of different gradient materials^[30-31]

下载: 全尺寸图片幻灯片

图 7 低应变率表面处理后的晶粒形貌^[34-35]

Figure 7. Grain structure of materials processed by low-strain-rate surface treatments^[34-35]

下载: 全尺寸图片幻灯片

图 8 表面形变处理横截面梯度形貌^[37-39]

Figure 8. The cross section morphologies of the specimen processed by surface mechanical treatment^[37-39]

下载: 全尺寸图片幻灯片

图 9 AA2060铝锂合金喷丸过程中的动态回复再结晶^[46]

Figure 9. Dynamic recovery and recrystallization of AA2060 Al-Li alloy induced by shot peening^[46]

下载: 全尺寸图片幻灯片

图 10 AA2060铝锂合金喷丸前后晶粒取向图^[46]

Figure 10. Grain orientation map of AA2060 Al-Li alloy before and after shot peening^[46]

下载: 全尺寸图片幻灯片

图 11 304奥氏体不锈钢的冲击相变^[57]

Figure 11. Phase transformation of 304 austenite stainless steel by impact deformation^[57]

下载: 全尺寸图片幻灯片

图 12 不同材料在不同高速冲击表面处理下的形变诱发相变^[60-62]

Figure 12. Deformation induced phase transformation of different materials under different high velocity impact surface treatments^[60-62]

下载: 全尺寸图片幻灯片

图 13 位错组态随应变量和应变率的演变规律示意图^[66-67]

Figure 13. Proposed diagram of dislocation evolution with the increment of plastic strain and strain rates^[66-67]

(LGs: large grains; DLs: dislocation lines; DWs: dislocation walls; DTs: dislocation tangles; UFGs: ultrafine-grains; NGs: nano-grains)

下载: 全尺寸图片幻灯片

图 14 高速冲击表面处理后不同深度处的位错组态^[68-70]

Figure 14. Dislocations at different depths after high velocity impact surface treatments^[68-70]

下载: 全尺寸图片幻灯片

图 15 不同材料在不同高速冲击表面处理变形时析出相变化^[72-74]

Figure 15. The variation of precipitates of different materials deformed under different high velocity impact surface treatments^[72-74]

下载: 全尺寸图片幻灯片

图 16 位错运动通过强化相方式^[77]

Figure 16. The ways of dislocation moving through strengthening phases^[77]

下载: 全尺寸图片幻灯片

图 17 应变率对位错与析出相之间相互作用的影响^[77]

Figure 17. Effects of strain rate on the interaction of dislocations and precipitates^[77]

下载: 全尺寸图片幻灯片

图 18 位错到变形孪晶的演变规律示意图^[68]

Figure 18. Schematic diagram of the transformation from dislocations to deformation twins with the increment of plastic strain and strain rates^[68]

下载: 全尺寸图片幻灯片

图 19 高应变率下变形孪晶^[85-86]

Figure 19. Deformation twins occurred under high strain rates^[85-86]

下载: 全尺寸图片幻灯片

图 20 纳米晶铝TEM图像^[41]

Figure 20. TEM micrographs of nanocrystalline aluminum deformed by manually grinding^[41]

下载: 全尺寸图片幻灯片

图 21 Thompson双四面体与纳米孪晶片层的相对位向关系^[89]

Figure 21. A schematics showing the relative orientation between a double Thompson tetrahedra and twin lamellae^[89]

下载: 全尺寸图片幻灯片

图 22 试样变形示意图

Figure 22. Schematic diagram of sample deformation

下载: 全尺寸图片幻灯片

参考文献(100)

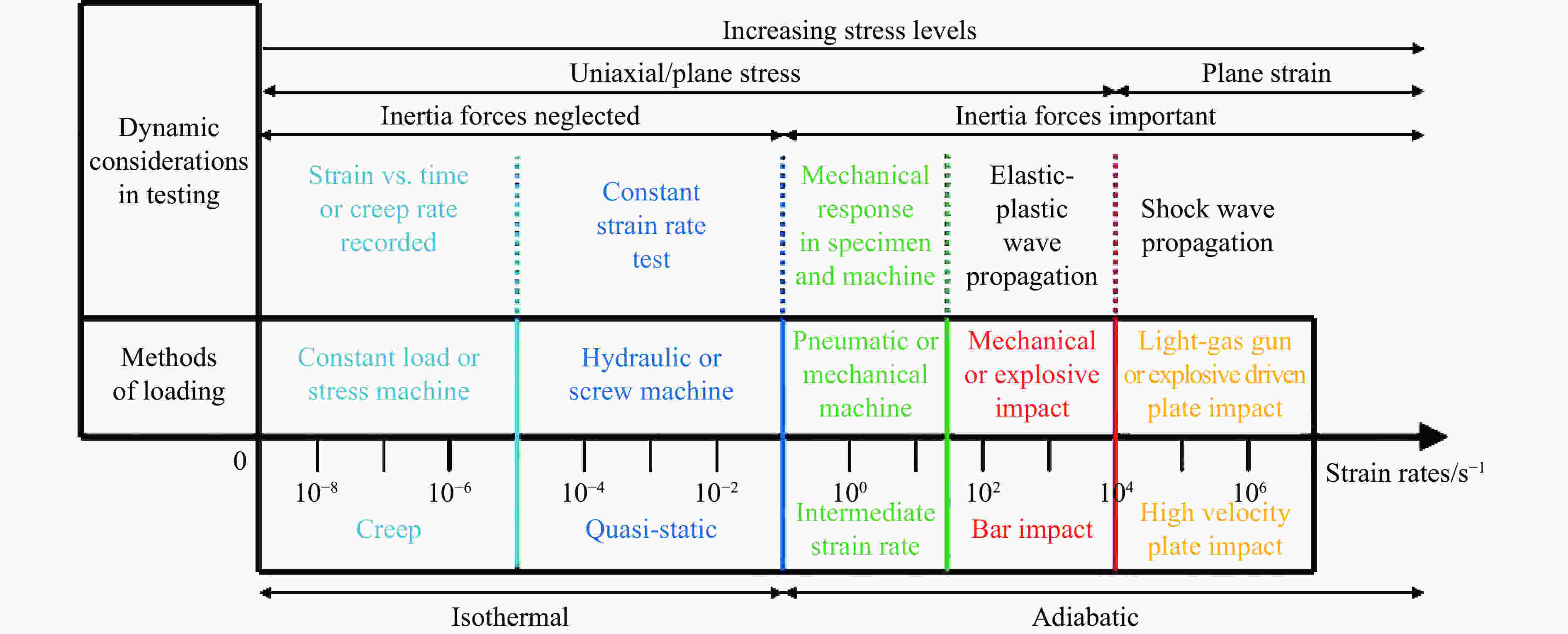
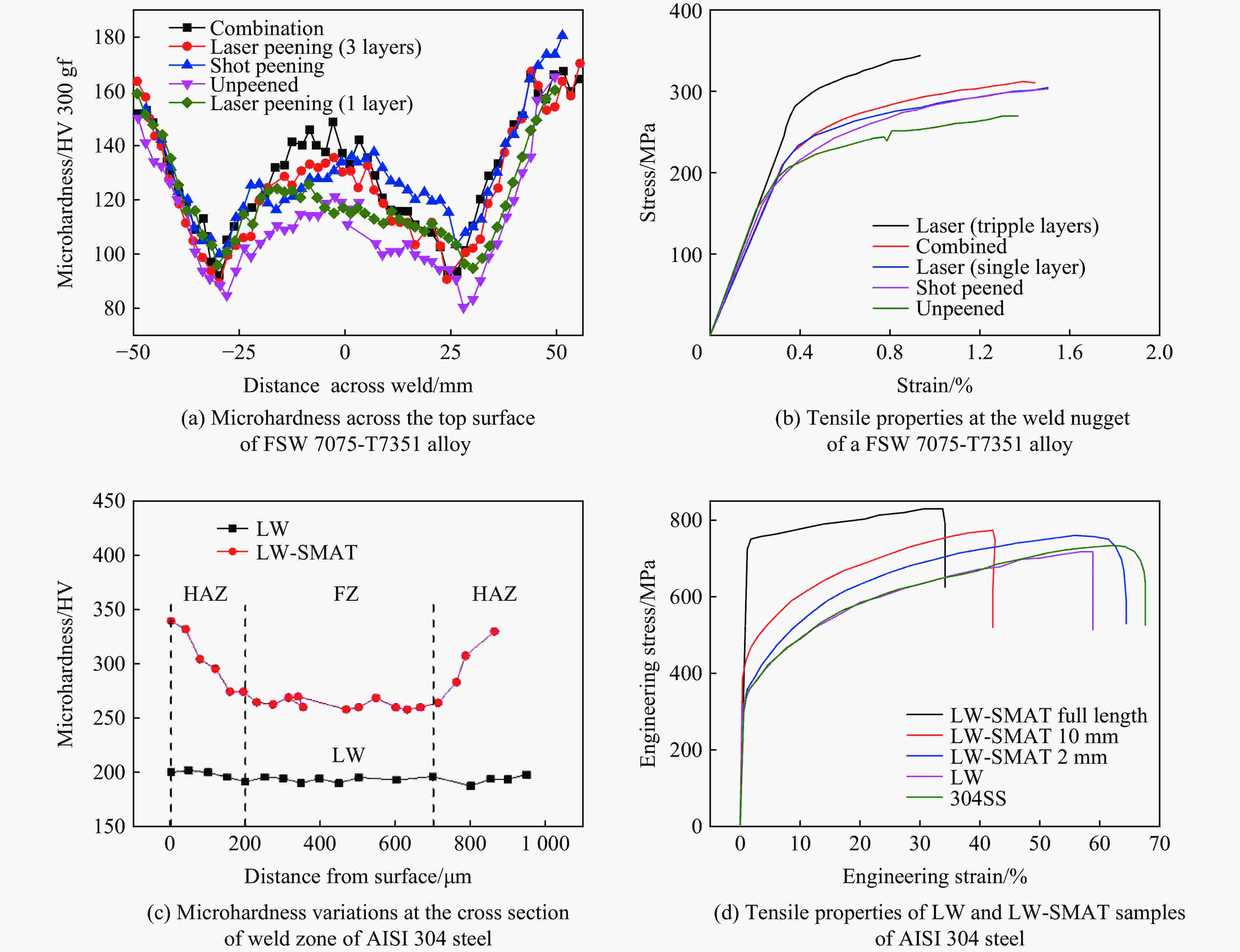
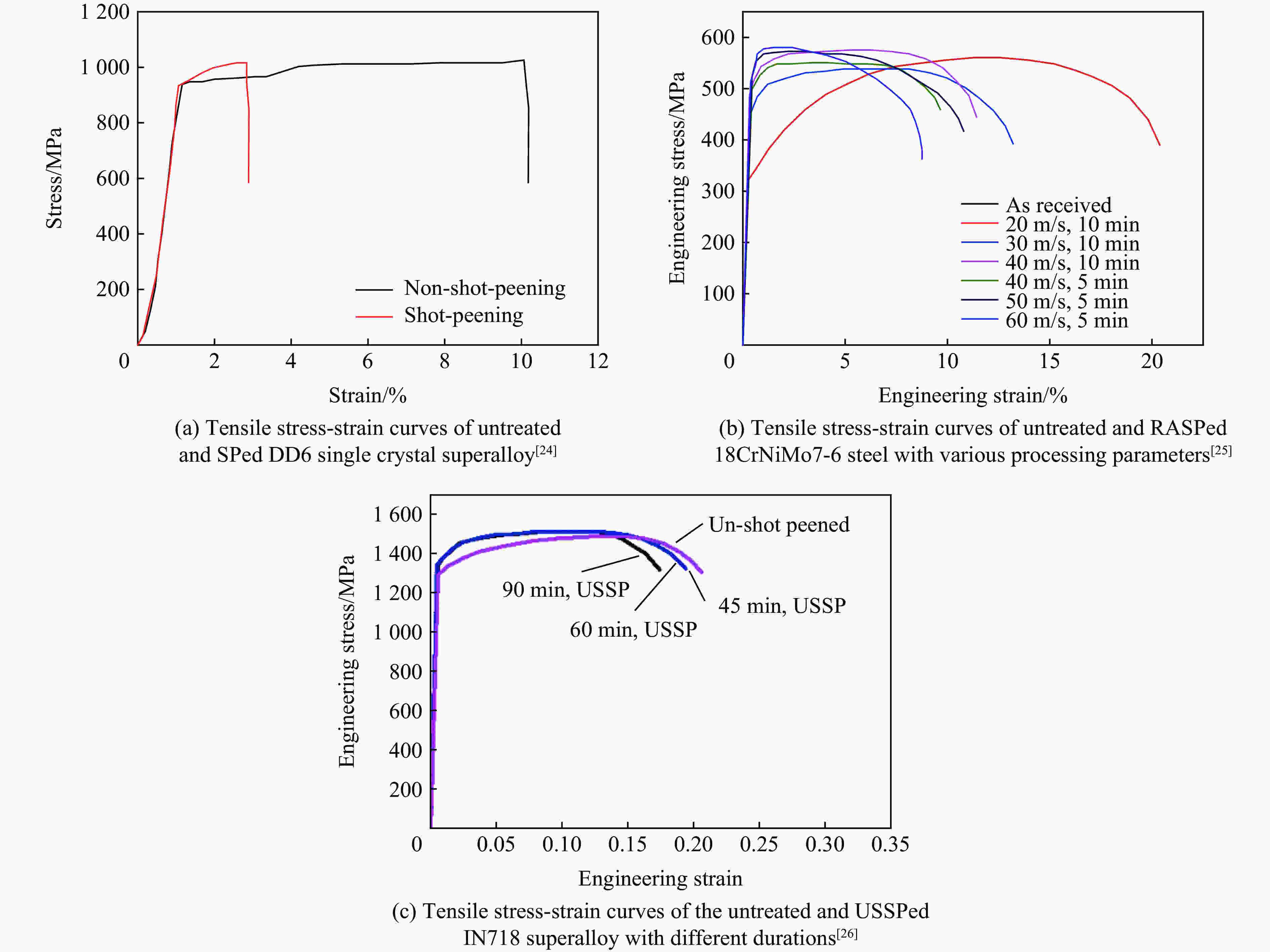
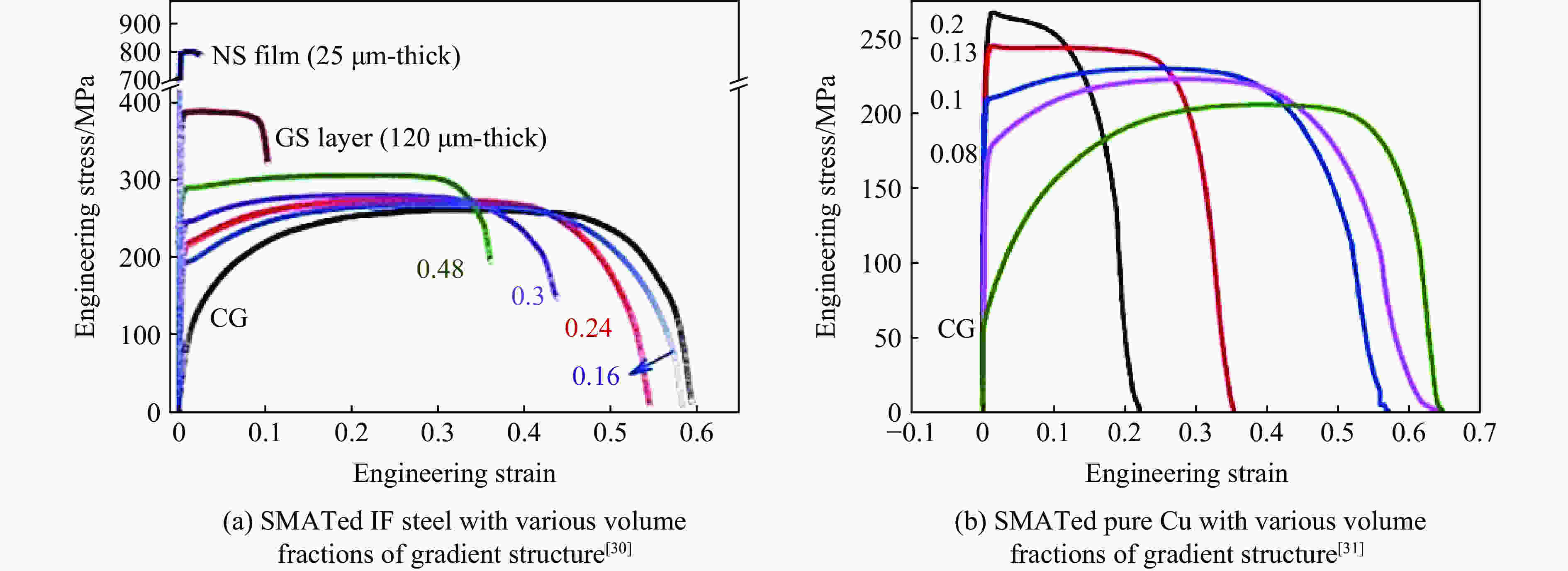
[1]	BOBBILI R, RAMAKRISHNA B, MADHU V, et al. Prediction of flow stress of 7017 aluminium alloy under high strain rate compression at elevated temperatures [J]. Defence Technology, 2015, 11(1): 93–98. DOI: 10.1016/j.dt.2014.08.004.
[2]	PRAKASH G, SINGH N K, GUPTA N K. Deformation behaviours of Al2014-T6 at different strain rates and temperatures [J]. Structures, 2020, 26: 193–203. DOI: 10.1016/j.istruc.2020.03.068.
[3]	GRACIO J J, BARLAT F, RAUCH E, et al. A review of the relationship between microstructural features and the stress-strain behavior of metals [J]. Materialwissenschaft und Werkstofftechnik, 2005, 36(10): 572–577. DOI: 10.1002/mawe.200500916.
[4]	MIKHAYLOVSKAYA A, YAKOVTSEVA O, SITKINA M, et al. Grain-boundary and intragranular deformation in ultrafine-grained aluminum-based alloy at high strain rate [J]. Materials Letters, 2020, 276: 128242. DOI: 10.1016/j.matlet.2020.128242.
[5]	惠旭龙, 白春玉, 刘小川, 等. 宽应变率范围下2A16-T4铝合金动态力学性能 [J]. 爆炸与冲击, 2017, 37(5): 871–878. DOI: 10.11883/1001-1455(2017)05-0871-08. HUI X L, BAI C Y, LIU X C, et al. Dynamic mechanical properties of 2A16-T4 aluminum alloy at wide-ranging strain rates [J]. Explosion and Shock Waves, 2017, 37(5): 871–878. DOI: 10.11883/1001-1455(2017)05-0871-08.
[6]	惠旭龙, 白春玉, 葛宇静, 等. 2A16铝合金中应变率力学性能研究 [J]. 振动与冲击, 2017, 36(19): 66–70. DOI: 10.13465/j.cnki.jvs.2017.19.010. HUI X L, BAI C Y, GE Y J, et al. Dynamic properties of 2A16 aluminum alloy under intermediate strain rate [J]. Journal of Vibration and Shock, 2017, 36(19): 66–70. DOI: 10.13465/j.cnki.jvs.2017.19.010.
[7]	EL-ATY A A, XU Y, ZHANG S H, et al. Impact of high strain rate deformation on the mechanical behavior, fracture mechanisms and anisotropic response of 2060 Al-Cu-Li alloy [J]. Journal of Advanced Research, 2019, 18: 19–37. DOI: 10.1016/j.jare.2019.01.012.
[8]	ANDRADE U R, MEYERS M A, CHOKSHI A H. Constitutive description of work- and shock-hardened copper [J]. Scripta Metallurgica et Materialia, 1994, 30(7): 933–938. DOI: 10.1016/0956-716X(94)90418-9.
[9]	JOHNSON G R, HOLMQUIST T J. Evaluation of cylinder-impact test data for constitutive model constants [J]. Journal of Applied Physics, 1988, 64(8): 3901–3910. DOI: 10.1063/1.341344.
[10]	RULE W K, JONES S E. A revised form for the Johnson−Cook strength model [J]. International Journal of Impact Engineering, 1998, 21(8): 609–624. DOI: 10.1016/S0734-743X(97)00081-X.
[11]	高宁, 朱志武. 铝合金应变率效应综述及其机理研究 [J]. 应用数学和力学, 2014, 35(S1): 208–212. GAO N, ZHU Z W. Study on the strain rate effects and mechanisms for aluminum alloys [J]. Applied Mathematics and Mechanics, 2014, 35(S1): 208–212.
[12]	ZERILLI F J, ARMSTRONG R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations [J]. Journal of Applied Physics, 1987, 61(5): 1816–1825. DOI: 10.1063/1.338024.
[13]	JIAO M Y, MA L F, JIA W T, et al. A new phenomenological model describing the compressive thermal deformation flow stress of cast-rolled AZ31B Mg alloy [J]. Materials Research Express, 2019, 6(9): 096597. DOI: 10.1088/2053-1591/ab30ae.
[14]	ZERILLI F J, ARMSTRONG R W. Description of tantalum deformation behavior by dislocation mechanics based constitutive relations [J]. Journal of Applied Physics, 1990, 68(4): 1580–1591. DOI: 10.1063/1.346636.
[15]	ZERILLI F J, ARMSTRONG R W. The effect of dislocation drag on the stress-strain behavior of FCC metals [J]. Acta Metallurgica et Materialia, 1992, 40(8): 1803–1808. DOI: 10.1016/0956-7151(92)90166-C.
[16]	马鸣图, 李洁, 赵岩, 等. 汽车用金属材料在高应变速率下响应特性的研究进展 [J]. 机械工程材料, 2017, 41(9): 1–13, 24. DOI: 10.11973/jxgccl201709001. MA M T, LI J, ZHAO Y, et al. Research progress of response characteristics of metallic materials for automotive under high strain rates [J]. Materials for Mechanical Engineering, 2017, 41(9): 1–13, 24. DOI: 10.11973/jxgccl201709001.
[17]	朱建士, 胡晓棉, 王裴, 等. 爆炸与冲击动力学若干问题研究进展 [J]. 力学进展, 2010, 40(4): 400–423. DOI: 10.6052/1000-0992-2010-4-j2009-144. ZHU J S, HU X M, WANG P, et al. A review on research progress in explosion mechanics and impact dynamics [J]. Advances in Mechanics, 2010, 40(4): 400–423. DOI: 10.6052/1000-0992-2010-4-j2009-144.
[18]	卢泓昱, 刘志奇, 宋建丽, 等. 花键冷敲成形本构关系研究 [J]. 太原科技大学学报, 2015, 36(3): 184–189. DOI: 10.3969/j.issn.1673-2057.2015.03.005. LU H Y, LIU Z Q, SONG J L, et al. Study of constitutive relation in cold rolling spline [J]. Journal of Taiyuan University of Science and Technology, 2015, 36(3): 184–189. DOI: 10.3969/j.issn.1673-2057.2015.03.005.
[19]	KIM J B, SHIN H. Comparison of plasticity models for tantalum and a modification of the PTW model for wide ranges of strain, strain rate, and temperature [J]. International Journal of Impact Engineering, 2009, 36(5): 746–753. DOI: 10.1016/j.ijimpeng.2008.11.003.
[20]	刘旭红, 黄西成, 陈裕泽, 等. 强动载荷下金属材料塑性变形本构模型评述 [J]. 力学进展, 2007, 37(3): 361–374. DOI: 10.6052/1000-0992-2007-3-J2006-184. LIU X H, HUANG X C, CHEN Y Z, et al. A review on constitutive models for plastic deformation of metal materials under dynamic loading [J]. Advances in Mechanics, 2007, 37(3): 361–374. DOI: 10.6052/1000-0992-2007-3-J2006-184.
[21]	HATAMLEH O. The effects of laser peening and shot peening on mechanical properties in friction stir welded 7075-T7351 aluminum [J]. Journal of Materials Engineering and Performance, 2008, 17(5): 688–694. DOI: 10.1007/s11665-007-9163-7.
[22]	KHUN N W, TRUNG P Q, BUTLER D L. Mechanical and tribological properties of shot-peened SAE 1070 steel [J]. Tribology Transactions, 2016, 59(5): 932–943. DOI: 10.1080/10402004.2015.1121313.
[23]	CHEN A Y, JIA Y Q, PAN D, et al. Reinforcement of laser-welded stainless steels by surface mechanical attrition treatment [J]. Materials Science and Engineering: A, 2013, 571: 161–166. DOI: 10.1016/j.msea.2013.02.018.
[24]	韩梅, 喻健, 李嘉荣, 等. 喷丸对DD6单晶高温合金拉伸性能的影响 [J]. 材料工程, 2019, 47(8): 169–175. DOI: 10.11868/j.issn.1001-4381.2019.000191. HAN M, YU J, LI J R, et al. Influence of shot peening on tensile properties of DD6 single crystal superalloy [J]. Journal of Materials Engineering, 2019, 47(8): 169–175. DOI: 10.11868/j.issn.1001-4381.2019.000191.
[25]	朱敏, 吴桂林, 李玉胜, 等. 旋转加速喷丸处理18CrNiMo7-6钢的微观结构与力学性能 [J]. 材料导报, 2018, 32(10): 1645–1649, 1662. DOI: 10.11896/j.issn.1005-023X.2018.10.014. ZHU M, WU G L, LI Y S, et al. Microstructure and mechanical properties of 18CrNiMo7-6 steel processed by rotationally accelerated shot peening [J]. Materials Reports, 2018, 32(10): 1645–1649, 1662. DOI: 10.11896/j.issn.1005-023X.2018.10.014.
[26]	KUMAR S, RAO G S, CHATTOPADHYAY K, et al. Effect of surface nanostructure on tensile behavior of superalloy IN718 [J]. Materials & Design, 2014, 62: 76–82. DOI: 10.1016/j.matdes.2014.04.084.
[27]	YANG C, LIU Y G, SHI Y H, et al. Microstructure characterization and tensile properties of processed TC17 via high energy shot peening [J]. Materials Science and Engineering: A, 2020, 784: 139298. DOI: 10.1016/j.msea.2020.139298.
[28]	ZHOU W F, REN X D, YANG Y, et al. Tensile behavior of nickel with gradient microstructure produced by laser shock peening [J]. Materials Science and Engineering: A, 2020, 771: 138603. DOI: 10.1016/j.msea.2019.138603.
[29]	LU K. Making strong nanomaterials ductile with gradients [J]. Science, 2014, 345(6203): 1455–1456. DOI: 10.1126/science.1255940.
[30]	WU X L, JIANG P, CHEN L, et al. Synergetic strengthening by gradient structure [J]. Materials Research Letters, 2014, 2(4): 185–191. DOI: 10.1080/21663831.2014.935821.
[31]	YANG X C, MA X L, MOERING J, et al. Influence of gradient structure volume fraction on the mechanical properties of pure copper [J]. Materials Science and Engineering: A, 2015, 645: 280–285. DOI: 10.1016/j.msea.2015.08.037.
[32]	高玉魁. 表面完整性理论与应用[M]. 北京: 化学工业出版社, 2014: 4−9.
[33]	FENG X, SUN Y P, ZHOU S P, et al. Influence of strain rate on microstructures and mechanical properties of 2524Al alloy fabricated by a novel large strain rolling [J]. Materials Research Express, 2020, 7(2): 026519. DOI: 10.1088/2053-1591/ab70e0.
[34]	ZHANG S W, ZHANG D W, WANG Y F, et al. The planetary rolling process of forming the internal thread [J]. The International Journal of Advanced Manufacturing Technology, 2020, 107(7-8): 3543–3551. DOI: 10.1007/s00170-020-05289-8.
[35]	高玉魁, 柳鸿飞. 低塑性抛光技术对材料表面完整性影响的研究进展 [J]. 航空制造技术, 2019, 62(18): 14–22. DOI: 10.16080/j.issn1671-833x.2019.18.014. GAO Y K, LIU H F. Research progress of low plasticity burnishing on surface integrity of materials [J]. Aeronautical Manufacturing Technology, 2019, 62(18): 14–22. DOI: 10.16080/j.issn1671-833x.2019.18.014.
[36]	孟丽君. 应变速率对强塑性变形晶粒细化的影响[D]. 太原: 太原理工大学, 2006: 27−43.
[37]	LI Y S, LI L Z, NIE J F, et al. Microstructural evolution and mechanical properties of a 5052 Al alloy with gradient structures [J]. Journal of Materials Research, 2017, 32(23): 4443–4451. DOI: 10.1557/jmr.2017.310.
[38]	LIU W B, JIN X, ZHANG B, et al. A coupled EBSD/TEM analysis of the microstructure evolution of a gradient nanostructured ferritic/martensitic steel subjected to surface mechanical attrition treatment [J]. Materials, 2019, 12(1): 140. DOI: 10.3390/ma12010140.
[39]	YANG Y, ZHANG H, QIAO H C. Microstructure characteristics and formation mechanism of TC17 titanium alloy induced by laser shock processing [J]. Journal of Alloys and Compounds, 2017, 722: 509–516. DOI: 10.1016/j.jallcom.2017.06.127.
[40]	ZHANG X D, HANSEN N, GAO Y K, et al. Hall-Petch and dislocation strengthening in graded nanostructured steel [J]. Acta Materialia, 2012, 60(16): 5933–5943. DOI: 10.1016/j.actamat.2012.07.037.
[41]	CHEN M W, MA E, HEMKER K J, et al. Deformation twinning in nanocrystalline aluminum [J]. Science, 2003, 300(5623): 1275–1277. DOI: 10.1126/science.1083727.
[42]	XIAO X D, SUN Y, YANG Z C, et al. Dynamic response of target with different peening media [J]. Surface Engineering, 2020, 36(4): 386–396. DOI: 10.1080/02670844.2019.1624302.
[43]	GURAO N P, KAPOOR R, SUWAS S. Texture evolution in high strain rate deformed Cu-10Zn alloy [J]. Materials Science and Engineering: A, 2012, 558: 761–765. DOI: 10.1016/j.msea.2012.07.112.
[44]	PANDEY A, KHAN A S, KIM E Y, et al. Experimental and numerical investigations of yield surface, texture, and deformation mechanisms in AA5754 over low to high temperatures and strain rates [J]. International Journal of Plasticity, 2013, 41: 165–188. DOI: 10.1016/j.ijplas.2012.09.006.
[45]	CANOVA G R, FRESSENGEAS C, MOLINARI A, et al. Effect of rate sensitivity on slip system activity and lattice rotation [J]. Acta Metallurgica, 1988, 36(8): 1961–1970. DOI: 10.1016/0001-6160(88)90298-2.
[46]	TAO X F, GAO Y K, KANG J M, et al. Softening effects induced by shot peening for an aluminum-lithium alloy [J]. Metallurgical and Materials Transactions A, 2020, 51(1): 410–418. DOI: 10.1007/s11661-019-05506-4.
[47]	邹途祥. 纯铝的晶粒细化机制及动态力学性能的研究[D]. 太原: 太原理工大学, 2008: 63.
[48]	HEMKER K J. Understanding how nanocrystalline metals deform [J]. Science, 2004, 304(5668): 221–223. DOI: 10.1126/science.1097058.
[49]	SCHIØTZ J, JACOBSEN K W. A maximum in the strength of nanocrystalline copper [J]. Science, 2003, 301(5638): 1357–1359. DOI: 10.1126/science.1086636.
[50]	YANG C F, PAN J H, LEE T H. Work-softening and anneal-hardening behaviors in fine-grained Zn-Al alloys [J]. Journal of Alloys and Compounds, 2009, 468(1–2): 230–236. DOI: 10.1016/j.jallcom.2008.01.067.
[51]	ZHANG W L, HE L J, LU Z G, et al. Microstructural characteristics and formation mechanism of adiabatic shear bands in Al-Zn-Mg-Cu alloy under dynamic shear loading [J]. Materials Science and Engineering: A, 2020, 791: 139430. DOI: 10.1016/j.msea.2020.139430.
[52]	KHAN M A, WANG Y W, YASIN G, et al. Adiabatic shear band localization in an Al-Zn-Mg-Cu alloy under high strain rate compression [J]. Journal of Materials Research and Technology, 2020, 9(3): 3977–3983. DOI: 10.1016/j.jmrt.2020.02.024.
[53]	NIE Y, CLAUS B, GAO J, et al. In situ observation of adiabatic shear band formation in aluminum alloys [J]. Experimental Mechanics, 2020, 60(2): 153–163. DOI: 10.1007/s11340-019-00544-w.
[54]	OWOLABI G M, ODESHI A G, SINGH M N K, et al. Dynamic shear band formation in aluminum 6061-T6 and aluminum 6061-T6/Al₂O₃ composites [J]. Materials Science and Engineering: A, 2007, 457(1-2): 114–119. DOI: 10.1016/j.msea.2006.12.034.
[55]	XIONG Y Y, LI N, JIANG H W, et al. Microstructural Evolutions of AA7055 aluminum alloy under dynamic and quasi-static compressions [J]. Acta Metallurgica Sinica (English Letters), 2014, 27(2): 272–278. DOI: 10.1007/s40195-014-0041-7.
[56]	王礼立. 冲击载荷下的材料动态失稳和动态屈服 [J]. 力学学报, 1989, 21(S1): 142–147. DOI: 10.6052/0459-1879-1989-s1-1989-249. WANG L L. The dynamic instability and dynamic yield of materials under impact loading [J]. Acta Mechanica Sinica, 1989, 21(S1): 142–147. DOI: 10.6052/0459-1879-1989-s1-1989-249.
[57]	高玉魁. 冲击强化对304奥氏体不锈钢拉伸性能的影响 [J]. 材料工程, 2014(8): 36–40. DOI: 10.11868/j.issn.1001-4381.2014.08.007. GAO Y K. Influence of impact enhancements on tensile property of 304 austenite steel [J]. Journal of Materials Engineering, 2014(8): 36–40. DOI: 10.11868/j.issn.1001-4381.2014.08.007.
[58]	STARMAN B, HALLBERG H, WALLIN M, et al. Differences in phase transformation in laser peened and shot peened 304 austenitic steel [J]. International Journal of Mechanical Sciences, 2020, 176: 105535. DOI: 10.1016/j.ijmecsci.2020.105535.
[59]	LUO K Y, LU J Z, ZHANG Y K, et al. Effects of laser shock processing on mechanical properties and micro-structure of ANSI 304 austenitic stainless steel [J]. Materials Science and Engineering: A, 2011, 528(13–14): 4783–4788. DOI: 10.1016/j.msea.2011.03.041.
[60]	MIN N, LI W, JIN X J. α to γ transformation in the nanostructured surface layer of pearlitic steels near room temperature [J]. Scripta Materialia, 2008, 59(8): 806–809. DOI: 10.1016/j.scriptamat.2008.05.038.
[61]	CHEN S, MU J, WANG Y D, et al. Formation of omega phase induced by laser shock peening in Ti-17 alloy [J]. Materials Characterization, 2020, 159: 110017. DOI: 10.1016/j.matchar.2019.110017.
[62]	LU Y, ZHAO J B, QIAO H C, et al. A study on the surface morphology evolution of the GH4619 using warm laser shock peening [J]. AIP Advances, 2019, 9(8): 085030. DOI: 10.1063/1.5082755.
[63]	HSU H C, LIN Y C, WANG S H, et al. Corrigendum to “Inducement of bainite and carbide transformation from retained austenite based on a high strain rate” [Scr. Mater. 62 (2010) 372–375] [J]. Scripta Materialia, 2010, 62(9): 726. DOI: 10.1016/j.scriptamat.2010.01.029.
[64]	郎玉婧, 崔华, 蔡元华, 等. 应变诱导析出对7050合金连续热变形组织的影响 [J]. 中国有色金属学报, 2012, 22(10): 2726–2733. DOI: 10.19476/j.ysxb.1004.0609.2012.10.004. LANG Y J, CUI H, CAI Y H, et al. Effect of strain-induced precipitation on subsequent hot deformed microstructure of 7050 alloy [J]. The Chinese Journal of Nonferrous Metals, 2012, 22(10): 2726–2733. DOI: 10.19476/j.ysxb.1004.0609.2012.10.004.
[65]	WANG Y, LIN D L, LAW C C. A correlation between tensile flow stress and Zener-Hollomon factor in TiAl alloys at high temperatures [J]. Journal of Materials Science Letters, 2000, 19(13): 1185–1188. DOI: 10.1023/A:1006723629430.
[66]	POUR-ALI S, KIANI-RASHID A R, BABAKHANI A, et al. Correlation between the surface coverage of severe shot peening and surface microstructural evolutions in AISI 321: a TEM, FE-SEM and GI-XRD study [J]. Surface and Coatings Technology, 2018, 334: 461–470. DOI: 10.1016/j.surfcoat.2017.11.062.
[67]	HUANG F, TAO N R. Effects of strain rate and deformation temperature on microstructures and hardness in plastically deformed pure aluminum [J]. Journal of Materials Science & Technology, 2011, 27(1): 1–7. DOI: 10.1016/S1005-0302(11)60017-0.
[68]	POUR-ALI S, KIANI-RASHID A R, BABAKHANI A. Surface nanocrystallization and gradient microstructural evolutions in the surface layers of 321 stainless steel alloy treated via severe shot peening [J]. Vacuum, 2017, 144: 152–159. DOI: 10.1016/j.vacuum.2017.07.016.
[69]	TAO N R, WANG Z B, TONG W P, et al. An investigation of surface nanocrystallization mechanism in Fe induced by surface mechanical attrition treatment [J]. Acta Materialia, 2002, 50(18): 4603–4616. DOI: 10.1016/S1359-6454(02)00310-5.
[70]	YANG Y, ZHOU K, ZHANG H, et al. Thermal stability of microstructures induced by laser shock peening in TC17 titanium alloy [J]. Journal of Alloys and Compounds, 2018, 767: 253–258. DOI: 10.1016/j.jallcom.2018.06.030.
[71]	LEE W S, CHEN T H. Rate-dependent deformation and dislocation substructure of Al-Sc alloy [J]. Scripta Materialia, 2006, 54(8): 1463–1468. DOI: 10.1016/j.scriptamat.2005.12.054.
[72]	蔡大勇. GH169及GH696高温合金热加工工艺基础研究[D]. 秦皇岛: 燕山大学, 2003: 66−74.
[73]	YE C, SUSLOV S, KIM B J, et al. Fatigue performance improvement in AISI 4140 steel by dynamic strain aging and dynamic precipitation during warm laser shock peening [J]. Acta Materialia, 2011, 59(3): 1014–1025. DOI: 10.1016/j.actamat.2010.10.032.
[74]	LIAO Y L, YE C, GAO H, et al. Dislocation pinning effects induced by nano-precipitates during warm laser shock peening: dislocation dynamic simulation and experiments [J]. Journal of Applied Physics, 2011, 110(2): 023518. DOI: 10.1063/1.3609072.
[75]	BASAVAKUMAR K G, MUKUNDA P G, CHAKRABORTY M. Influence of grain refinement and modification on microstructure and mechanical properties of Al-7Si and Al-7Si-2.5Cu cast alloys [J]. Materials Characterization, 2008, 59(3): 283–289. DOI: 10.1016/j.matchar.2007.01.011.
[76]	MYHR O R, HOPPERSTAD O S, BØRVIK T. A combined precipitation, yield stress, and work hardening model for Al-Mg-Si alloys incorporating the effects of strain rate and temperature [J]. Metallurgical and Materials Transactions A, 2018, 49(8): 3592–3609. DOI: 10.1007/s11661-018-4675-3.
[77]	冯飞. 应变速率对GH4169合金拉伸变形行为的影响[D]. 沈阳: 东北大学, 2013: 55−57.
[78]	ZHANG P, WANG Y Q, XIE Y N, et al. A study on the dynamic shock performance of 7055-T6I4 aluminum alloy based on experimental and simulation [J]. Vacuum, 2018, 157: 306–311. DOI: 10.1016/j.vacuum.2018.08.042.
[79]	YANG Y, WANG H M, ZHOU K, et al. Effect of laser shock peening and annealing temperatures on stability of AA2195 alloy near-surface microstructure [J]. Optics & Laser Technology, 2019, 119: 105569. DOI: 10.1016/j.optlastec.2019.105569.
[80]	张孜昭, 许晓嫦, 刘志义, 等. 应变速率对强变形Al-Cu合金中析出相低温回溶速度的影响 [J]. 热处理, 2010, 25(2): 15–18. DOI: 10.3969/j.issn.1008-1690.2010.02.003. ZHANG Z Z, XU X C, LIU Z Y, et al. Effect of strain rate on redissolution rate of precipitated phase at low temperature in severely plastically deformed Al-Cu alloy [J]. Heat Treatment, 2010, 25(2): 15–18. DOI: 10.3969/j.issn.1008-1690.2010.02.003.
[81]	AN X H, WU S D, WANG Z G, et al. Significance of stacking fault energy in bulk nanostructured materials: insights from Cu and its binary alloys as model systems [J]. Progress in Materials Science, 2019, 101: 1–45. DOI: 10.1016/j.pmatsci.2018.11.001.
[82]	ZENER C, HOLLOMON J H. Effect of strain rate upon plastic flow of steel [J]. Journal of Applied Physics, 1944, 15(1): 22–32. DOI: 10.1063/1.1707363.
[83]	LI Y S, ZHANG Y, TAO N R, et al. Effect of the Zener-Hollomon parameter on the microstructures and mechanical properties of Cu subjected to plastic deformation [J]. Acta Materialia, 2009, 57(3): 761–772. DOI: 10.1016/j.actamat.2008.10.021.
[84]	CHEN A Y, RUAN H H, WANG J, et al. The influence of strain rate on the microstructure transition of 304 stainless steel [J]. Acta Materialia, 2011, 59(9): 3697–3709. DOI: 10.1016/j.actamat.2011.03.005.
[85]	ZHANG H W, HEI Z K, LIU G, et al. Formation of nanostructured surface layer on AISI 304 stainless steel by means of surface mechanical attrition treatment [J]. Acta Materialia, 2003, 51(7): 1871–1881. DOI: 10.1016/S1359-6454(02)00594-3.
[86]	LAINÉ S J, KNOWLES K M, DOORBAR P J, et al. Microstructural characterisation of metallic shot peened and laser shock peened Ti-6Al-4V [J]. Acta Materialia, 2017, 123: 350–361. DOI: 10.1016/j.actamat.2016.10.044.
[87]	YMAKOV V, WOLF D, PHILLPOT S R, et al. Dislocation processes in the deformation of nanocrystalline aluminium by molecular-dynamics simulation [J]. Nature Materials, 2002, 1(1): 45–49. DOI: 10.1038/nmat700.
[88]	LIAO X Z, ZHOU F, LAVERNIA E J, et al. Deformation twins in nanocrystalline Al [J]. Applied Physics Letters, 2003, 83(24): 5062–5064. DOI: 10.1063/1.1633975.
[89]	卢磊, 尤泽升. 纳米孪晶金属塑性变形机制 [J]. 金属学报, 2014, 50(2): 129–136. DOI: 10.3724/sp.j.1037.2013.00697. LU L, YOU Z S. Plastic deformation mechanisms in nanotwinned metals [J]. Acta Metallurgica Sinica, 2014, 50(2): 129–136. DOI: 10.3724/sp.j.1037.2013.00697.
[90]	LU K, LU L, SURESH S. Strengthening materials by engineering coherent internal boundaries at the nanoscale [J]. Science, 2009, 324(5925): 349–352. DOI: 10.1126/science.1159610.
[91]	马晓光. 层错能对面心立方金属冷拔微观组织及织构演化的影响[D]. 西安: 西北工业大学, 2018: 1−18.
[92]	LI X Y, WEI Y J, LU L, et al. Dislocation nucleation governed softening and maximum strength in nano-twinned metals [J]. Nature, 2010, 464(7290): 877–880. DOI: 10.1038/nature08929.
[93]	CHEN H, LI F G, LI J H, et al. Hardening and softening analysis of pure titanium based on the dislocation density during torsion deformation [J]. Materials Science and Engineering: A, 2016, 671: 17–31. DOI: 10.1016/j.msea.2016.06.046.
[94]	WANG X, LI Y S, ZHANG Q, et al. Gradient structured copper by rotationally accelerated shot peening [J]. Journal of Materials Science & Technology, 2017, 33(7): 758–761. DOI: 10.1016/j.jmst.2016.11.006.
[95]	HASSANI-GANGARAJ S M, CHO K S, VOIGT H J L, et al. Experimental assessment and simulation of surface nanocrystallization by severe shot peening [J]. Acta Materialia, 2015, 97: 105–115. DOI: 10.1016/j.actamat.2015.06.054.
[96]	FANG T H, LI W L, TAO N R, et al. Revealing extraordinary intrinsic tensile plasticity in gradient nano-grained copper [J]. Science, 2011, 331(6024): 1587–1590. DOI: 10.1126/science.1200177.
[97]	LIU X C, ZHANG H W, LU K. Strain-induced ultrahard and ultrastable nanolaminated structure in nickel [J]. Science, 2013, 342(6156): 337–340. DOI: 10.1126/science.1242578.
[98]	WANG C, WANG L, WANG C L, et al. Dislocation density-based study of grain refinement induced by laser shock peening [J]. Optics & Laser Technology, 2020, 121: 105827. DOI: 10.1016/j.optlastec.2019.105827.
[99]	ZHOU W F, REN X D, REN Y P, et al. Initial dislocation density effect on strain hardening in FCC aluminium alloy under laser shock peening [J]. Philosophical Magazine, 2017, 97(12): 917–929. DOI: 10.1080/14786435.2017.1285073.
[100]	WU X L, YANG M X, YUAN F P, et al. Heterogeneous lamella structure unites ultrafine-grain strength with coarse-grain ductility [J]. Proceedings of the National Academy of Sciences of the United States of America, 2015, 112(47): 14501–14505. DOI: 10.1073/pnas.1517193112.