NEPE推进剂低高应变率下改进的黏-超弹本构模型

孙政伟; 许进升; 周长省; 陈雄; 杜红英

doi:10.11883/bzycj-2020-0343

NEPE推进剂低高应变率下改进的黏-超弹本构模型

doi: 10.11883/bzycj-2020-0343

1.
南京理工大学机械工程学院，江苏南京 210094
2.
晋西工业集团有限责任公司技术中心，山西太原 030027

详细信息

作者简介:
孙政伟（1994－　），男，博士研究生，1250197845@qq.com

通讯作者:
许进升（1985－　），男，博士，副教授，xujinsheng@njust.edu.cn

中图分类号: O347
计量
- 文章访问数: 794
- HTML全文浏览量: 240
- PDF下载量: 99
- 被引次数: 0
出版历程
- 收稿日期: 2020-09-22
- 修回日期: 2020-12-18
- 网络出版日期: 2021-03-05
- 刊出日期: 2021-03-10

An improved visco-hyperelastic constitutive behaviour of NEPE propellant at low and high strain rates

1.
School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China
2.
Technology Center, Jinxi Industries Group Corporation Ltd., Taiyuan 030027, Shanxi, China

摘要

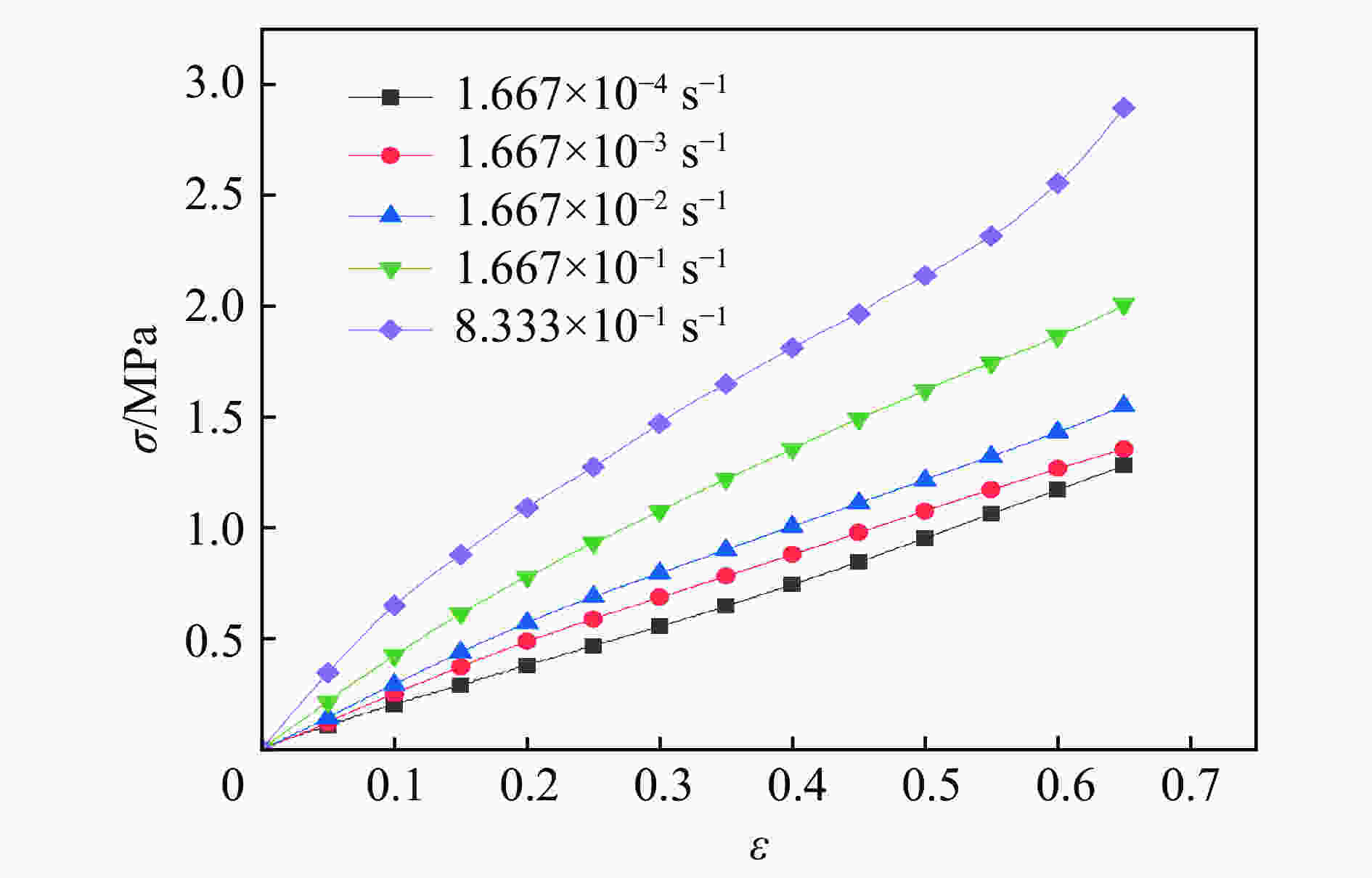
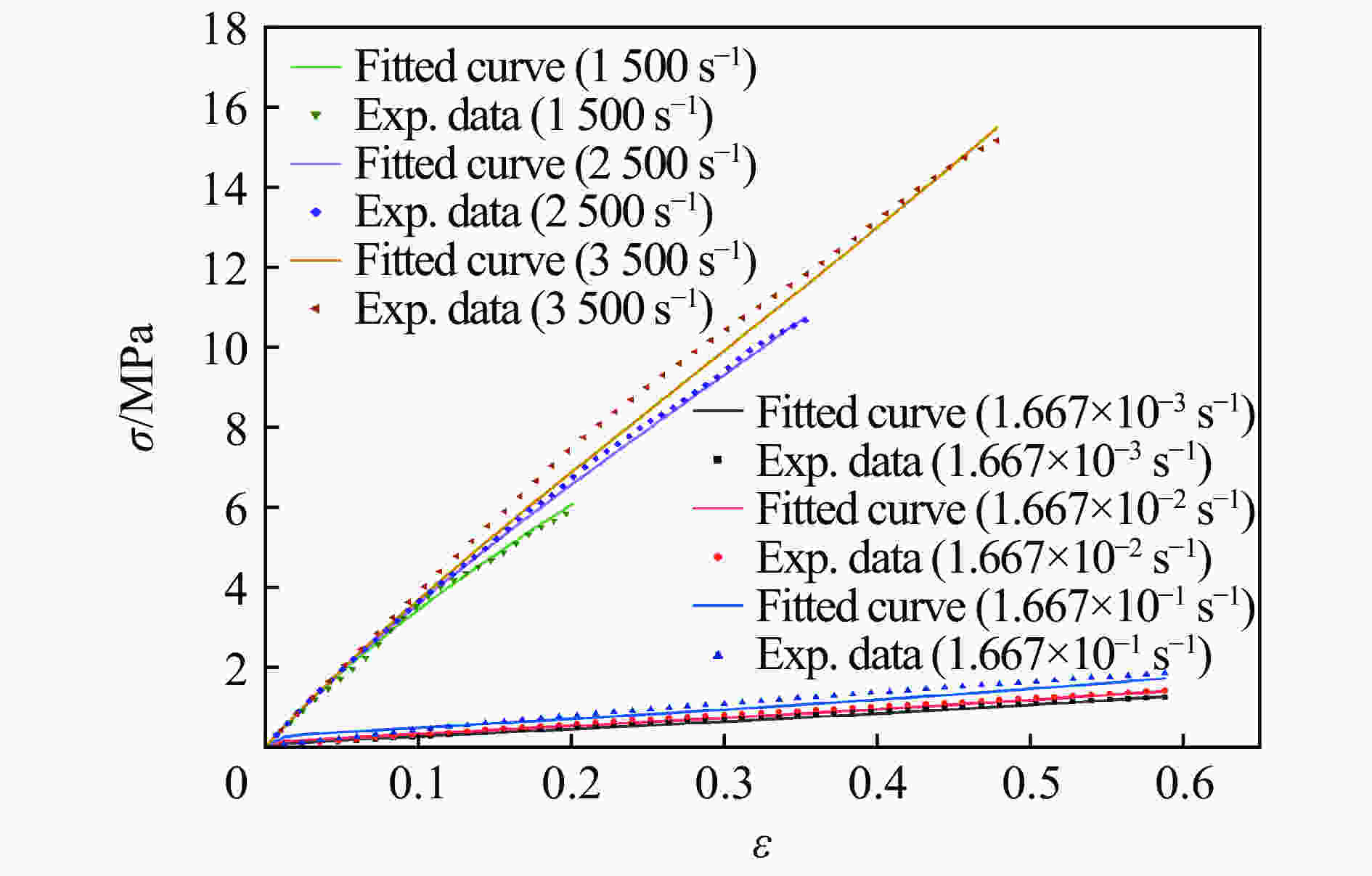
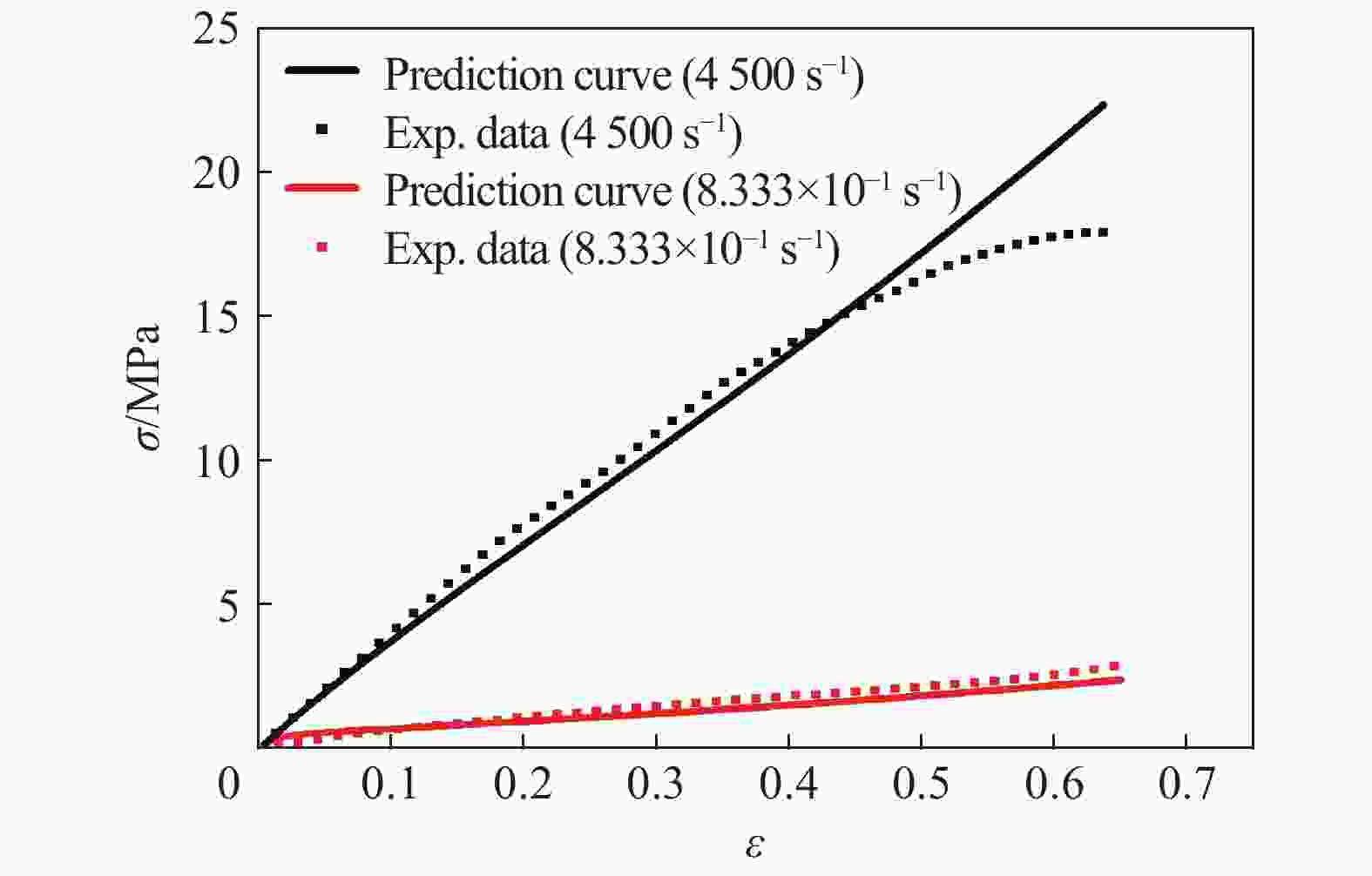
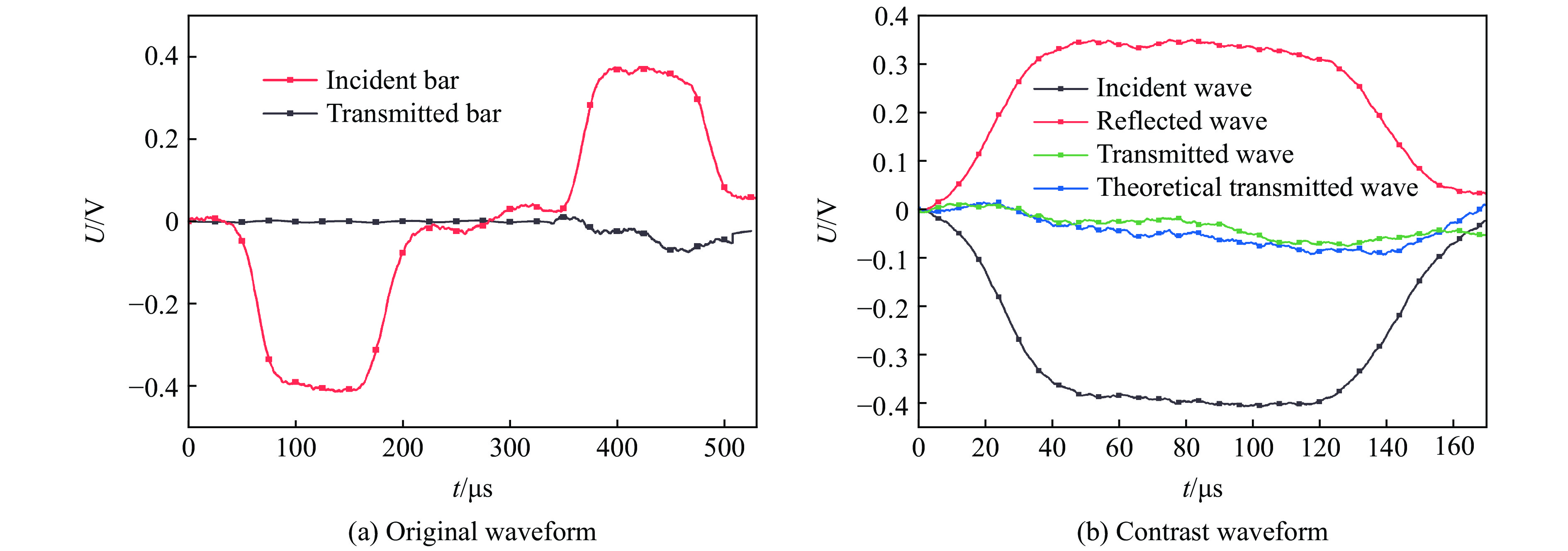
摘要: 为研究低高应变率条件下NEPE推进剂的力学特性，通过电子万能试验机和分离式霍普金森杆装置，对NEPE推进剂进行了准静态和冲击实验，得到了不同应变率下（1.667×10⁻⁴～4 500 s⁻¹）的应力-应变曲线。实验结果表明NEPE推进剂具有明显的非线性弹性和应变率敏感性，随着应变率的增加，材料的强度、屈服应力和弹性模量显著增加，与低应变率相比，高应变率条件下材料的应变率敏感性更高。在高速冲击下材料内部瞬间产生大量热量无法及时散发出去，使得材料内部温度升高，导致材料出现软化效应，力学性能降低。本文建立了一个非线性黏超弹本构模型，其中采用Rivlin应变能函数来描述稳态超弹响应部分，采用积分型本构模型来描述材料的动态黏弹性响应部分，考虑到松弛时间具有应变率相关性，本文采用了一个率相关松弛函数来替代传统的Prony级数形式。使用极慢速压缩实验数据对本构模型中的超弹部分进行拟合获得超弹参数，然后用准静态和动态实验数据对本构模型进行拟合得出其他参数。不同应变率下的预测曲线与实验曲线具有较好的重合度，证明了该模型可以很好地描述低高应变率下NEPE推进剂的力学特性。
- NEPE推进剂 /
- 低高应变率 /
- 本构模型 /
- 松弛函数 /
- 非线性
Abstract: In order to study the mechanical properties of NEPE propellant at low and high strain rates, the quasi-static and impact eperiments of NEPE propellant were carried out by the electronic universal testing machine and split Hopkinson bar, and the stress-strain curves of NEPE propellant under different strain rates (1.667×10⁻⁴−4 500 s⁻¹) were obtained by processing the experiment data. By analyzing the stress-strain curve of low and high strain rates experiment, it can be found that NEPE propellant has obvious nonlinear elasticity and strain rate sensitivity. With the increase of strain rate, the strength, yield stress and elastic modulus of the material increase significantly. Compared with low strain rate, the strain rate sensitivity of the material at high strain rate is higher. Under the high speed impact, a large amount of heat is generated inside the material and cannot be released in time, which makes the internal temperature of the material rise, leading to softening effect of the material and reduction of mechanical properties. In this paper, a nonlinear visco-hyperelastic constitutive model is established to describe the mechanical properties of NEPE propellant at low and high strain rates, in which the Rivlin strain energy function is used to describe the static hyperelastic behaviour, and an integral constitutive model is used to characterize the dynamic response of the material. Considering that the relaxation time has strain rate correlation, a rate-dependent relaxation function is adopted in this paper to replace the traditional Prony series. The hyperelastic parameters were obtained by fitting the hyperelastic part of the constitutive model with extremely slow compression experiment data, and then the other parameters were obtained by fitting the constitutive model with quasi-static and dynamic experiment data. It was proved that the model could well describe the mechanical properties of NEPE propellant at low and high strain rates by the good coincidence degree between the prediction curve and the experiment curve under different strain rates.
- NEPE propellant /
- low and high strain rates /
- constitutive model /
- relaxation function /
- nonlinear

HTML全文

图 1 SHPB实验波形图

Figure 1. Wave profiles by SHPB experiment

下载: 全尺寸图片幻灯片

图 2 低应变率下的应力应变曲线

Figure 2. Stress-strain curves at low strain rates

下载: 全尺寸图片幻灯片

图 3 高应变率下的应力应变曲线

Figure 3. Stress-strain curves at high strain rates

下载: 全尺寸图片幻灯片

图 4 准静态实验后获得的恢复试件（应变为70%）

Figure 4. Recovered specimens after quasi-static compression at the strain of 70%

下载: 全尺寸图片幻灯片

图 5 准静态实验后获得的恢复试件（95%应变）

Figure 5. Recovered specimens after quasi-static compression at the strain of 95%

下载: 全尺寸图片幻灯片

图 6 动态试件

Figure 6. Specimens after dynamic compression

下载: 全尺寸图片幻灯片

图 7 Rivlin超弹模型准静态实验拟合曲线

Figure 7. Rivlin model fit to quasi-static experimental data

下载: 全尺寸图片幻灯片

图 8 低高应变率下实验曲线与拟合曲线

Figure 8. Comparison between fitted results and experiment data at low and high rates

下载: 全尺寸图片幻灯片

图 9 低/高应变率下实验曲线与预测曲线

Figure 9. Comparison between prediction curves and experiment data at low and high rates

下载: 全尺寸图片幻灯片

表 1 Rivlin超弹模型参数

Table 1. Rivlin fitted parameters

A₁₀ A₀₁ A₁₁ R

0.814 −0.442 0.079 0.999

下载: 导出CSV

表 2 黏弹参数

Table 2. Viscoelastic parameters

M₁ M₁ φ_ref η R

25.9 0.1 0.021 0.648 0.997

下载: 导出CSV

参考文献(22)

[1]	LIU X, AO W, LIU H, et al. Aluminum agglomeration on burning surface of NEPE propellants at 3−5 MPa [J]. Propellants, Explosives, Pyrotechnics, 2017, 42(3): 260–268. DOI: 10.1002/prep.201600131.
[2]	MOONEY M. A theory of large elastic deformation [J]. Journal of Applied Physics, 1940, 11(9): 582–592. DOI: 10.1063/1.1712836.
[3]	RIVLIN R S. Large elastic deformations of isotropic materials: II: some uniqueness theorems for pure, homogeneous deformation [J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1948, 240(822): 491–508. DOI: 10.1098/rsta.1948.0003.
[4]	OGDEN R W. Large deformation isotropic elasticity: on the correlation of theory and experiment for incompressible rubberlike solids [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1972, 326(1567): 565–584. DOI: 10.1098/rspa.1972.0026.
[5]	YEOH O H. Some forms of the strain energy function for rubber [J]. Rubber Chemistry and Technology, 1993, 66(5): 754–771. DOI: 10.5254/1.3538343.
[6]	DUNCAN E J S, MARGETSON J. A nonlinear viscoelastic theory for solid rocket propellants based on a cumulative damage approach [J]. Propellants, Explosives, Pyrotechnics, 1998, 23(2): 94–104. DOI: 10.1002/(SICI)1521-4087(199804)23:2<94::AID-PREP94>3.0.CO;2-C.
[7]	HINTERHOELZL R M, SCHAPERY R A. FEM implementation of a three-dimensional viscoelastic constitutive model for particulate composites with damage growth [J]. Mechanics of Time-Dependent Materials, 2004, 8(1): 65–94. DOI: 10.1023/B:MTDM.0000027683.06097.76.
[8]	朱兆祥, 徐大本, 王礼立. 环氧树脂在高应变率下的热粘弹性本构方程和时温等效性 [J]. 宁波大学学报, 1988(1): 58–67. ZHU Z X, XU D B, WANG L L. Thermoviscoelastic constitutive equation and time-temperature equivalence of epoxy resin at high strain rates [J]. Journal of Ningbo University, 1988(1): 58–67.
[9]	常新龙, 赖建伟, 张晓军, 等. HTPB推进剂高应变率粘弹性本构模型研究 [J]. 推进技术, 2014, 35(1): 123–127. DOI: 10.13675/j.cnki.tjjs.2014.01.001. CHANG X L, LAI J W, ZHANG X J, et al. High strain-rate viscoelastic constitutive model for HTPB propellant [J]. Journal of Propulsion Technology, 2014, 35(1): 123–127. DOI: 10.13675/j.cnki.tjjs.2014.01.001.
[10]	杨龙, 谢侃, 裴江峰, 等. HTPB推进剂拉伸力学行为的应变速率相关超弹本构模型 [J]. 推进技术, 2017, 38(3): 687–694. DOI: 10.13675/j.cnki.tjjs.2017.03.027. YANG L, XIE K, PEI J F, et al. A strain-rate-dependent hyperelastic constitutive model for tensile mechanical behaviour of HTPB propellant [J]. Journal of Propulsion Technology, 2017, 38(3): 687–694. DOI: 10.13675/j.cnki.tjjs.2017.03.027.
[11]	WANG Z J, QIANG H F, WANG T J, et al. A thermovisco-hyperelastic constitutive model of HTPB propellant with damage at intermediate strain rates [J]. Mechanics of Time-Dependent Materials, 2018, 22(3): 291–314. DOI: 10.1007/s11043-017-9357-9.
[12]	GUO H, GUO W G, AMIRKHIZI A V. Constitutive modeling of the tensile and compressive deformation behavior of polyurea over a wide range of strain rates [J]. Construction and Building Materials, 2017, 150: 851–859. DOI: 10.1016/j.conbuildmat.2017.06.055.
[13]	韩龙, 许进升, 封涛, 等. 考虑细观脱湿损伤的NEPE推进剂粘弹性本构模型研究 [J]. 推进技术, 2017, 38(8): 1885–1892. DOI: 10.13675/j.cnki.tjjs.2017.08.027. HAN L, XU J S, FENG T, et al. Research on viscoelastic constitutive model for NEPE composite propellant with meso-mechanics damage due to particle dewetting [J]. Journal of Propulsion Technology, 2017, 38(8): 1885–1892. DOI: 10.13675/j.cnki.tjjs.2017.08.027.
[14]	DAVIES R M. A critical study of the Hopkinson pressure bar [J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1948, 240(821): 375–457. DOI: 10.1098/rsta.1948.0001.
[15]	KOLSKY H. An investigation of the mechanical properties of materials at very high rates of loading [J]. Proceedings of the Physical Society. Section B, 1949, 62(11): 676. DOI: 10.1088/0370-1301/62/11/302.
[16]	YANG L M, SHIM V P W, LIM C T. A visco-hyperelastic approach to modelling the constitutive behaviour of rubber [J]. International Journal of Impact Engineering, 2000, 24(6−7): 545–560. DOI: 10.1016/S0734-743X(99)00044-5.
[17]	Van SLIGTENHORST C, CRONIN D S, BRODLAND G W. High strain rate compressive properties of bovine muscle tissue determined using a split Hopkinson bar apparatus [J]. Journal of Biomechanics, 2006, 39(10): 1852–1858. DOI: 10.1016/j.jbiomech.2005.05.015.
[18]	RIVLIN R S. Some topics in finite elasticity [C] // Proceedings of the First Symposium on Naval Structural Mechanics, 1960: 169–198. DOI: 10.1007/978-1-4612-2416-7_25.
[19]	TRUESDELL C, NOLL W. The non-linear field theories of mechanics [M]. Berlin: Springer, 1992. DOI: 10.1007/978-3-662-13183-1.
[20]	KHAJEHSAEID H, ARGHAVANI J, NAGHDABADI R, et al. A visco-hyperelastic constitutive model for rubber-like materials: a rate-dependent relaxation time scheme [J]. International Journal of Engineering Science, 2014, 79: 44–58. DOI: 10.1016/j.ijengsci.2014.03.001.
[21]	FORRESTAL M J, WRIGHT T W, CHEN W. The effect of radial inertia on brittle samples during the split Hopkinson pressure bar test [J]. International Journal of Impact Engineering, 2007, 34(3): 405–411. DOI: 10.1016/j.ijimpeng.2005.12.001.
[22]	DAVIES E D H, HUNTER S C. The dynamic compression testing of solids by the method of the split Hopkinson pressure bar [J]. Journal of the Mechanics and Physics of Solids, 1963, 11(3): 155–179. DOI: 10.1016/0022-5096(63)90050-4.