Key physical problems in the expanding fracture of explosively driven metallic shells
-
摘要: 爆炸加载下金属壳体膨胀断裂过程是武器研制领域关注的重要课题，该过程包含着丰富的力学与材料学基础科学问题，吸引着众多学者的长期关注。本文中通过分析爆炸加载下金属壳体膨胀断裂过程，明确了其中蕴含的3个关键物理问题：材料动态拉伸本构、壳体膨胀断裂机理和破片尺寸控制机理，综合分析了这3个关键物理问题的研究现状与趋势。Abstract: The expansion fracture process of metallic shells under explosive loading is an important topic in fields of weapon design. This process contains a wealth of basic science problems in materials science and mechanics, which has attracted the long-term attention of many scholars. Based on the analysis of the expansion fracture behavior of metal shells under explosive loading, three key physical problems were clarified: dynamic tensile constitutive law of metals, expansion fracture mechanism of shells and mechanism of fragment size. The current status and research trends of the three physical problems were comprehensively analyzed. For the aspect of dynamic tensile constitutive law of metals, it is need to develop some new experimental methods to stretch the material at higher strain rates, to develop the experimental techniques of expanding cylindrical and spherical shells for studying the dynamic tensile constitutive relationship of materials under three dimentional stress state, and to develop the transient acceleration measurement technique and the interpretation method of expansion ring experimental data. For the expansion fracture mechanism, the main development trends are to develop the in-situ or freezing diagnostic techniques to capture key parameters in the fracture process of shells, to use the statistical method to study the fracture behavior, to reveal the essential mechanism of the fracture mode transition and the Ivanov plastic peak phenomena, and to study the mechanism of expanding fracture shells at the micro level. For the mechanism of fragment size, it is need to study the relationship between the fragment size and all the potential control variables with the experimental and modeling method, to analyze the relationship between the micro heterogeneity of the material and the statistical distribution of the fragment size by taking the probability distribution of fracture strain as a bridge, and to analyze the influence of two-dimensional or three-dimensional effects on fragment size distribution and develop new models.
-
轴对称旋转壳体是战斗部常用典型结构的代表，其在内部炸药爆轰驱动下的膨胀断裂问题一直是武器研究的热点之一。一些武器战斗部利用炸药加载下壳体断裂形成的破片实现杀伤，战斗部的杀伤范围和杀伤程度与壳体破片的飞散速度、飞散角度、破片尺寸、破片形貌等密切相关[1-3]。
金属壳体在膨胀断裂过程中，经历了复杂的加/卸载路径、大变形过程，存在多种断裂模式（层裂、剪切、拉伸）的竞争与耦合，尤其是柱壳/球壳作为一种轴对称结构，其破坏位置存在一定的随机性，并非由加载条件或样品构型事先决定，这种自发破坏行为（spontaneous fracture）能够更深层次地反映材料自身对不同破坏机制的敏感性以及断裂的概率特性。因此，金属壳体膨胀断裂行为研究也将推动力学与材料学、概率统计学等学科的交叉融合，提升对材料损伤断裂机理的认识。
基于该问题强烈的军事需求背景及其对材料损伤断裂学科的巨大推动作用，多年来美国[4-6]、俄罗斯[7]、法国[8]、和中国[9-12]等各大国的众多研究机构和人员，都持续开展了此项研究工作。美国利弗莫尔国家实验室（LLNL）对该问题高度重视，于2002年将柱壳膨胀断裂过程图像作为LLNL6～7月刊的封面图片刊出（见图1），吸引全球研究者关注这一重要问题。
图 1 美国利弗莫尔国家实验室2002年6～7月刊的封面图片Figure 1. Cover picture of Livermore National Laboratory, June—July 20021. 关键物理问题分析
爆炸加载下金属壳体膨胀断裂问题的研究始于20世纪40年代[13]，经过众多学者数十年的理论、实验与数值模拟研究，取得了一些基本认识。以JOB9003炸药柱爆轰加载45钢柱壳膨胀断裂过程为典型代表对其力学过程描述如下：
（1）内部高能炸药爆轰后在金属柱壳内表瞬间施加数十吉帕高压，柱壳内形成由内表面向外表面传播的高强度冲击波，冲击波到达柱壳外表面后向内反射形成拉伸波（见图2～3），在特定的炸药/柱壳厚度比下，反射拉伸波会与炸药爆轰的后续稀疏波在柱壳内部相遇，形成吉帕量级的拉应力，此时柱壳极有可能发生层裂或形成拉伸损伤，对于较薄的柱壳，发生层裂的概率较低（见图3～4）。
图 4 理论分析柱壳可能的断裂模式Figure 4. Possible fracture modes of cylindrical shellsbased on the theoretical analysis（2）爆轰产物持续驱动柱壳加速运动，柱壳内表面附近将经历数微秒的三维压应力状态，加之爆轰产物的高温环境，使内表面附近极易形成绝热剪切带，而外表面附近基本处于环向拉应力状态，径向裂纹容易在外表面附近起始（见图4），壳体中部由于应力波的传播导致其应力状态在拉伸与压缩之间不断切换，加卸载过程较为复杂（见图2～3）。
（3）由于黏性效应，冲击波传播一段时间后强度趋于零（见图2～3），柱壳整体将处于环向拉伸状态，当变形超过一定阈值后（此时柱壳中部应力状态有可能仍处于拉伸与压缩不断切换的阶段），壳体发生径向贯穿断裂，由于材料的不均匀性和加工等因素带来的壳体结构非对称性，造成壳体发生断裂的位置和时间具有随机性，率先发生断裂的位置会抑制其周围一定范围内断裂的发生或已有裂纹的进一步扩展，裂纹之间的复杂影响机制最终导致破片尺寸在空间呈现一定的规律性（见图5）。
（4）当裂纹贯穿壳体后，壳体内部的高压爆轰产物迅速向外泄漏，爆轰产物对壳体的驱动能力急剧下降（见图2、5）。
从上述动作过程的分析可以看出，金属壳体膨胀断裂过程研究涉及到的主要物理问题包括：
（1）材料动态拉伸本构。内部爆炸加载下金属壳体膨胀运动过程中，壳体大部分区域长时间均处于静水拉应力状态，壳体的运动速度、断裂的起始与演化过程均与壳体材料的动态拉伸应力应变关系密切相关，而且韧性金属材料在断裂前均发生大塑性变形，因此金属材料的大变形动态拉伸本构关系是爆炸加载下金属壳体膨胀断裂过程研究的重要问题。
（2）壳体膨胀断裂机理。金属壳体在内部炸药爆轰加载下存在层裂、绝热剪切、拉伸等多种断裂模式的耦合与竞争，断裂过程和机理极为复杂。深入认识并掌握壳体膨胀断裂机理是科学预测壳体膨胀断裂行为、指导实际工程应用的前提，因此壳体膨胀断裂机理研究是爆炸加载下金属壳体膨胀断裂过程研究的核心问题，同时也极具挑战性。
（3）破片尺寸控制机理。金属壳体在内部炸药爆轰加载下会形成多个破片，破片尺寸与壳体材料自身的微细观不均匀性、宏观本构关系和外部的加载条件等多个因素相关，而且呈现一定的概率分布特性。破片尺寸研究在实际工程中具有重要应用价值，是爆炸加载下金属壳体膨胀断裂过程研究关心的重要问题。
下面将从这3个方面对爆炸加载下金属壳体膨胀断裂问题的研究现状与趋势进行分析阐述。
2. 研究现状及趋势分析
2.1 材料动态拉伸本构
动态加载下金属材料的力学行为与静态加载时有显著差异[14]，而且金属材料的高应变率本构关系存在一定的拉压不对称性[15-17]，所以在静态压缩条件下得到的本构关系不能用于表征金属材料的动态拉伸力学行为。目前用于材料动态拉伸本构关系研究的实验技术主要有Hopkinson拉杆（SHTB）[18-19]和膨胀环实验技术[20-25]。
SHTB实验技术于1960年由Harding等[18]最先提出，SHTB实验技术的优点是实验数据处理方法较为规范成熟，缺点是试件内存在应力应变分布不均匀问题，而且其拉伸应变率最高[19]只能达到5×103 s−1，而爆炸加载下金属壳体膨胀运动的典型应变率范围为103～105 s−1，SHTB实验技术不能覆盖该应变率范围。
膨胀环实验技术主要包括爆炸膨胀环和电磁膨胀环两类。爆炸膨胀环实验技术最早由Johnson等[20]于1963年提出，其原理如图6所示。两个雷管同时起爆中心柱形装药的两端，驱动器在爆轰产物的作用下向外膨胀运动，由于驱动器比样品环材料阻抗高，因此当反射拉伸波从试样环外表面传至驱动器与试样环的接触面时，试样环将脱离驱动器自由飞行。汤铁钢等[21]使用中心爆炸丝线起爆技术替代了雷管的两端起爆，如图7所示，该技术产生了较好的柱面爆轰波，大幅提高了膨胀环运动的稳定性。
电磁膨胀环技术最早由Niordson[22]于1965年提出，桂毓林等[23]、陈红等[24]也相继建立了电磁膨胀环实验装置，桂毓林等[23]增加了电流截断技术，实现了膨胀环在运动后期不受外力的自由飞行。电磁膨胀环实验原理如图8所示，金属试样环套在一个螺线管外侧，闭合开关K1接通电容器C的两端，高强度电流通过螺线管，在螺线管周围产生强大的磁场。磁场的巨大变化在金属试样环内激发高强度的感应电流，该感应电流同时又处在螺线圈所产生的磁场内，试样环受到安培力的作用向外膨胀运动。
无论是爆炸膨胀环还是电磁膨胀环，均有一段不受外力作用的自由飞行阶段[25]，在该阶段膨胀环仅在环向应力的作用下做减速运动。由于膨胀环的环向尺寸远大于径向和轴向尺寸，因此可假定膨胀环在自由飞行阶段径向和轴向应力为零，处于一维应力状态。膨胀环在该阶段的控制方程为：
σθ=−ρ0r¨r (1) 式中：σθ为环向应力，ρ0为膨胀环的初始密度，r为膨胀环的实时外径，
¨r 为膨胀环的实时加速度。利用实验中获得的膨胀环运动速度可求得其变形信息[25]，根据公式（1）可获得膨胀环中的应力，这就是利用膨胀环实验技术研究材料动态拉伸本构的原理。
相比于SHTB，膨胀环实验是对一个轴对称的环形样品进行加载，其优点是没有边界效应，加载应变率可高达104 s−1量级，缺点是膨胀环数据处理方法还不完善，公式（1）中的加速度需要对速度进行微分运算获取，导致环向应力的不确定度较大。此外，电磁加载的热效应和爆炸加载的强冲击过程也会对材料的屈服应力产生显著影响，这种影响需要在数据处理过程中进行评估。
除了电磁膨胀环和爆炸膨胀环之外，Liang等[26]、郑宇轩等[27]改变了膨胀环的驱动方式，相继发展了基于气炮和霍普金森压杆（SHPB）的膨胀环实验技术，由于气炮与SHPB实验技术的普及率较高，因此这两类技术更有利于膨胀环实验技术的推广。
在研究材料动态拉伸本构关系方面，近期的研究趋势及重点关注点如下：
（1）提高动态拉伸加载应变率范围。目前SHTB实验技术中，材料的拉伸应变率只能达到103 s−1量级，膨胀环实验技术可以提升到104 s−1量级，但还不能覆盖爆炸加载下金属壳体膨胀运动的应变率范围（103～105 s−1），还需要发展更高应变率下材料动态拉伸实验技术，如使用电磁套筒驱动柱壳膨胀实验技术[28]等。
（2）完善膨胀环实验数据测试与处理方法。利用膨胀环实验技术来研究材料动态拉伸本构关系时，数据处理需要的直接物理量是膨胀环的加速度，但目前的实验技术只能测量膨胀环的表面速度，微分计算会导致较大的不确定度，因此需要发展高精度的瞬态加速度测量技术；另一方面，膨胀环在运动过程中，其应力、应变、应变率、温度等物理量均处于变化状态，如何充分利用这些数据得到材料的本构关系仍值得深入研究。
（3）明确本构关系在复杂应力状态下的适用性。目前无论是SHTB还是膨胀环实验技术，得到的都是材料在一维/准一维应力条件下的动态拉伸本构关系，然而爆炸加载下金属壳体处于复杂应力状态，此时一维应力条件下得到的本构关系是否仍然适用尚不清楚，因此，发展研究材料在复杂应力状态下动态拉伸本构关系的膨胀柱壳、膨胀球壳实验技术将是一个趋势。
2.2 壳体膨胀断裂机理
断裂机理是壳体膨胀断裂研究中最核心的内容，也最为复杂，其主要关注点为断口模式、裂纹的起始与传播过程、断裂判据等。
早期，以Taylor(1963年)为代表的研究者[29]认为，壳体的断裂受环向拉应力控制，裂纹首先在壳体外表面产生，并沿径向向内传播，当内表面的环向应力由压缩变为拉伸状态时，裂纹贯穿壳体。随着研究的不断深入，许多研究者[30-36]认识到，Taylor假定的拉伸断裂模式只是在较低爆轰压力下的典型表现，在高爆轰压力加载下，柱壳的断口与径向成45°夹角，为剪切断裂模式。其中最具代表性的工作是胡八一等[30-32]于1992～1993年开展的系列实验研究。他们对回收破片进行了细致分析，发现45钢柱壳在低爆轰压力加载下，断口以拉伸断裂为主，裂纹沿柱壳径向，呈现解理和准解理特征；在高爆轰压力加载下，断口以剪切断裂为主，裂纹与柱壳径向呈45°夹角，呈现密排韧窝特征；随着装药爆轰能量的逐步升高，破片中的剪切断裂面比例逐渐增大，如图9所示。
在裂纹的起始位置与演化过程研究方面，人们分别针对拉伸断裂和剪切断裂开展了研究，并根据各自观察到的实验结果和理论分析，给出了相应的解释。对于低爆轰压力下的典型拉伸断裂，Taylor[29]认为裂纹起始于外表面，向内传播；Beetle等[33]（1971年）和胡八一等[30-32]的实验结果显示拉伸断口可能起始于柱壳中部或外表面附近，然后沿径向分别向内外表面扩展；李永池等[37]（1999年）和张世文等[38]（2008年）利用数值模拟分析指出，柱壳的等效应变始终是内表面最大，拉伸裂纹应该在内表面起始。对于较高爆轰压力下的典型剪切断裂，Hoggott等[39]（1968年）认为，首先在柱壳内壁生成了大量绝热剪切带并扩展至外壁面，而后在环向拉应力的作用下，裂纹从外壁面起始并沿剪切失稳面向内壁扩展，并最终导致柱壳贯穿断裂；Beetle等[33]（1971年）通过分析破片断裂面的细观结构和特征，发现剪切裂纹成核于邻近柱壳内表面附近，并沿最大剪应力方向分别向内、外壁扩展；胡八一等[30]认为剪切裂纹可同时产生于柱壳内外表面，内表面的剪切滑移和环向拉应力作用下的剪切起裂同时发生，共同完成了绝热剪切断裂。总的来看，不同的研究者对裂纹的起始位置与演化过程观点迥异，实验、理论与数值模拟结果存在较大分歧。
Ivanov[40]最先（1976年）分析了断裂应变与加载应变率的关系，发现随着应变率的升高，断裂应变先增加后减小，即著名的“Ivanov塑性峰”现象，如图10所示；Olive等[41]以实验为基础，对金属柱壳的断裂应变进行了研究，提出了半经验的断裂判据，也发现了塑性峰现象；随后，陈大年等[42-43]、李永池等[37]也在实验中观察到了类似的现象。Ivanov[40]从能量的观点对此现象给出了解释，但其分析所采取的一些假定却与事实存在较大偏差，如Ivanov假定认为柱壳一开始运动裂纹便起始并开始传播；Feng等[44]（1993年）从微孔洞损伤演化的角度出发，提出了柱壳断裂应变的损伤度判据，并尝试解释Ivanov塑性峰现象。Ivanov和封加波等给出的理论能够解释部分实验结果，但其分析均未考虑柱壳的具体断裂模式，其理论适用性有限。汤铁钢等[45-46]开展了不同应变率下45钢的膨胀断裂实验，其结果进一步证实了Ivanov塑性峰现象存在的客观性，并在实验中发现，随着应变率升高同时出现了塑性峰现象和断裂模式转换现象。
材料与结构的断裂行为除了是材料与外界载荷相互作用的结果以外，还与材料本身的初始细观结构息息有关。在不大幅度改变材料化学成分的前提下，仅通过对材料初始细观结构的调控，实现柱壳膨胀断裂性能的改善具有非常重要的实用价值。
金山等[47]（2006年）研究了不同热处理条件下45钢柱壳的膨胀断裂性能，研究发现：随着回火温度的升高，45钢的晶粒尺寸越小，静态延展性越好，柱壳的断裂应变越大。而针对铍青铜柱壳的实验研究[48]（2006年）发现，经过固溶处理后的铍青铜柱壳晶粒结构明显不同，其膨胀断裂性能也发生显著变化。Goto等[4]（2008年）研究发现柱壳材料的细观相结构也会对其断裂过程产生重要影响：对于高强度马氏体的AerMet100合金，破片中观察到了大量绝热剪切带（见图11）；而对于包含铁素体和珠光体的低强度AISI1018钢，破坏过程由孔洞联合主导（见图12）。汤铁钢对45钢[45-46]柱壳的膨胀断裂过程的研究也证实了Goto等[4]的结论，实验结果显示：45钢膨胀断裂过程图像中可以清晰地看到大量断裂面的产生与滑移过程，而20钢图像中几乎看不到断裂面，二者呈现完全不同的断裂过程。
除了基体细观结构，柱壳内外表面的细观结构也会对其膨胀断裂行为产生重要影响。胡八一等[32]在TC4柱壳膨胀断裂破片中，发现了一种剪切“单旋性”现象，即剪切带在顺时针与逆时针两个扩展方向上，有一个方向明显占优。胡海波等[49]（2004年）发现这种现象广泛存在于LY12铝、钛合金、HR2钢和45钢等多种金属中。与此同时，Xue等[50]，Yang等[51]和Lovinger等[52-53]在304不锈钢、7075Al、纯Ti和TC4柱壳的向内爆轰压缩过程中也发现了类似的单旋剪切模式，Liu等[54]结合数值模拟指出这种现象可能与材料的微观结构相关，但进一步的实验与理论分析并未跟进。
对于爆炸加载下金属壳体膨胀断裂机理研究，近期的研究趋势如下。
（1）发展断裂过程关键参量的实验诊断技术。近些年来对爆炸加载下金属壳体膨胀断裂机理研究相关工作的推动相对缓慢，物理认知提升有限，这主要是由于目前极度缺乏柱壳膨胀断裂过程中关键参量的原位诊断或冻结诊断技术。因此，要获得突破性的进展，发展应用新的实验测试技术、诊断方法是关键。目前有较大前景的诊断技术有多点密排激光干涉测速[55]、全回收技术[56]、冻结回收技术、X光照相技术以及基于同步辐射光源的破片微介观表征技术等。
（2）应用概率统计方法研究断裂过程。壳体的膨胀断裂过程是多处成核的，且断裂是一个概率性问题，壳体的断裂应变并不是一个固定的值，而是一个概率分布区间，这种概率性的结果与材料微介观的不均匀性密切相关。因此寻找描述材料微介观不均匀性的方法，将概率统计方法应用于研究壳体的断裂过程将是一个重要的研究趋势。
（3）揭示拉剪断裂模式转换及“Ivanov”塑性峰的本质机理。实验上观察到随着爆轰加载压力的升高，金属壳体的膨胀断裂模式发生了由拉伸向剪切的转变，与此同时断裂应变出现了先增加后减小的“Ivanov”塑性峰现象。断裂模式转换的内在机制和“Ivanov”塑性峰现象的产生机制是壳体膨胀断裂研究中非常重要的两个科学问题，需要深入研究。
（4）将断裂机理研究深入到材料微介观。对于爆炸加载下壳体的膨胀断裂机理研究，一方面需要深入认识断裂过程中材料微细观结构的演化，另一方面需要揭示材料初始微细观结构与壳体膨胀断裂的关联。近年来金属材料的表面改性技术迅速发展，使得通过调控柱壳表面细观结构来控制柱壳膨胀断裂性能成为可能，是极具潜力的研究方向。
2.3 破片尺寸控制机理
1947年，Mott[57]最早开始研究破片尺寸，并提出了著名的Mott波理论。Mott一方面认为材料断裂应变存在随机性，另一方面忽略断裂过程，断裂发生后从裂口处向周围发出Mott卸载波。需要注意的是，Mott波的波速小于材料的弹性波速，Mott卸载波经过的区域失去了生成新裂纹的可能，如图13所示。该理论认为Mott波传播距离和断裂应变的随机性是破片尺寸的主控机制，并通过理论推导建立了破片尺寸的统计分布与断裂应变统计分布的定量表达式。
Grady等[58]推广了Mott波传播距离控制碎片尺度的思想，他们认为，材料的分离（断裂）是一个内聚断裂（cohesive fracture）过程，与材料的内在断裂能有关。基于该观点，Grady等推导得到了一个用断裂能来表征的破片尺度公式：
S=(12Gcρ˙ε2)1/3 (2) 式中：S为破片尺寸，Gc为材料内在断裂能，ρ为密度，
˙ε 为应变率。Lambert[59]等和Hopson等[60-61]以Mott波理论为指导，提出连续损伤模型，并在数值模拟程序中利用该模型研究了破片尺寸的统计规律。其研究结果很好地预测了低强度钢（AmrMet100）柱壳的破片尺寸，但将其应用于高强度钢（Eglin Steel 1）和钨合金（Aero224）时，计算获得的破片尺寸相比实验结果明显偏大。
Zhou[62]等（2006年）把金属环、金属柱壳的破坏过程作为一个失稳问题处理，采用摄动法进行研究，即先求得方程的均匀解，然后在均匀解基础上加入小扰动，建立小扰动增长的控制方程，他们认为增长最快扰动的波长即对应于破片尺寸。通过理论分析，Zhou等给出了断口自组织特征间距的表达式，并发现一维韧性金属杆拉伸断裂的破片尺寸通常为自组织特征间距的整数倍。在此基础上，陈磊等[63]采用有限元方法数值模拟研究了金属环断裂碎片数目随初始膨胀速度的变化规律。郑宇轩等[64-65]）深入关注了一维拉伸杆中的动态破碎，通过统计学模拟表明：碎片的尺寸分布具有一定的阶梯分布特性（量子化），而且自组织间距越小，碎片尺寸的“量子化”特性越明显。
总的来说，目前认识到的控制破片尺寸的物理机制主要有4种：材料的非均匀性或结构的非对称性、断裂耗散能、自组织特征间距和Mott卸载波。Mott[57]、Grady[58]、周风华[62]等分别基于各自的思想，通过理论分析得到了预测破片尺寸的理论模型，Zhang等[66-68]将其应用于实际断裂问题时，理论预测与实际的破片尺寸差异较大。
对于爆炸加载下金属壳体膨胀断裂破片尺寸，未来的研究趋势如下。
（1）开展单变量调控的实验与数值模拟研究。目前对于破片尺寸已有较多的理论研究工作，提出了众多破片尺寸的控制机理，但最终得到的模型预测能力有限。目前亟需开展单变量调控的实验与数值模拟工作，检验理论模型中破片尺寸与各个物理量的依赖关系是否正确。
（2）揭示破片尺寸统计分布的控制机理。Mott之后，很少有学者对破片尺寸统计分布的机理进行过深入的理论分析，Mott认为破片的尺寸分布与材料断裂应变的统计分布相关，而断裂应变的统计分布与材料和结构的微介观不均匀性密切相关，但目前很少有学者对这三者之间的关联直接开展实验工作进行研究分析。
（3）发展破片尺寸的二维或三维理论模型。目前发展的破片尺寸理论模型基本都是基于一维的，但断裂问题实际是三维的，因此亟需从理论上分析二维/三维效应对破片尺寸分布带来的影响，发展相应的二维/三维理论模型，提升理论预测能力。
3. 总 结
爆轰加载下金属壳体膨胀断裂问题由于其强烈的军事需求及其对材料损伤断裂学科的巨大推动作用，从20世纪40年代开始，已从不同视角对其进行了广泛研究，该过程中包含的主要物理问题为材料动态拉伸本构、壳体膨胀断裂机理和破片尺寸控制机理。
针对材料动态拉伸本构研究，近期主要发展趋势为：发展更高应变率下材料拉伸加载实验技术，发展用于研究材料在复杂应力状态下动态拉伸本构关系的膨胀柱壳和膨胀球壳实验技术，发展瞬态加速度测量技术和膨胀环实验数据解读方法。
针对壳体膨胀断裂机理研究，近期的主要发展趋势为：发展壳体膨胀断裂过程中关键参量的原位诊断或冻结诊断技术，充分利用概率统计学的方法对断裂过程进行研究，揭示断裂模式转换及Ivanov塑性峰的本质机理，深入到微介观层次认识壳体膨胀的深层次机制。
针对破片尺寸控制机理研究，近期主要发展趋势为：开展系统精密的单变量调控实验或数值模拟，以材料断裂应变的概率分布为桥梁分析材料微介观不均匀性与破片尺寸统计分布的关联，理论分析二维或三维效应对破片尺寸分布带来的影响并发展相应的模型。
-
图 1 美国利弗莫尔国家实验室2002年6～7月刊的封面图片
Figure 1. Cover picture of Livermore National Laboratory, June—July 2002
图 4 理论分析柱壳可能的断裂模式
Figure 4. Possible fracture modes of cylindrical shellsbased on the theoretical analysis
-
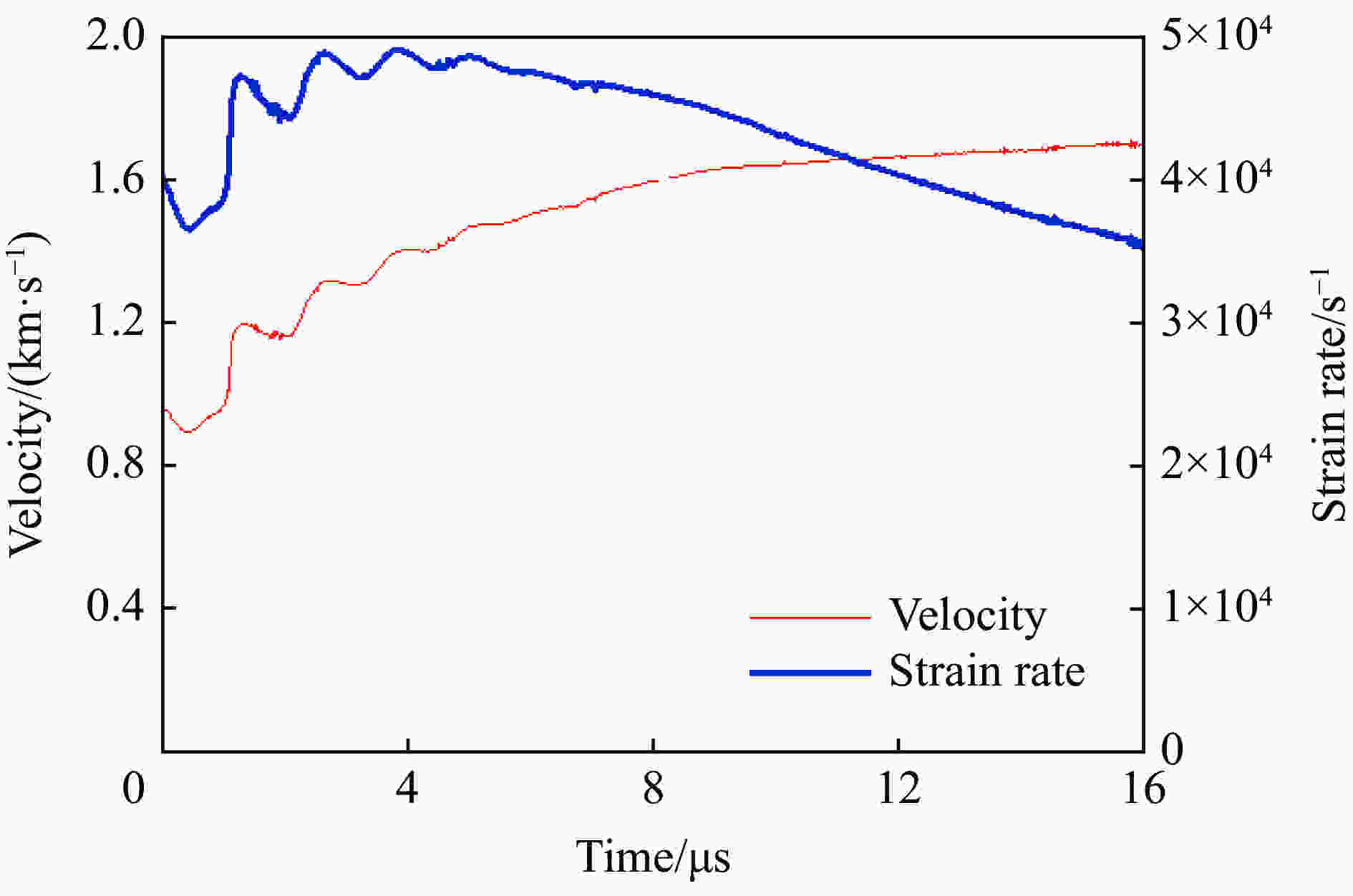
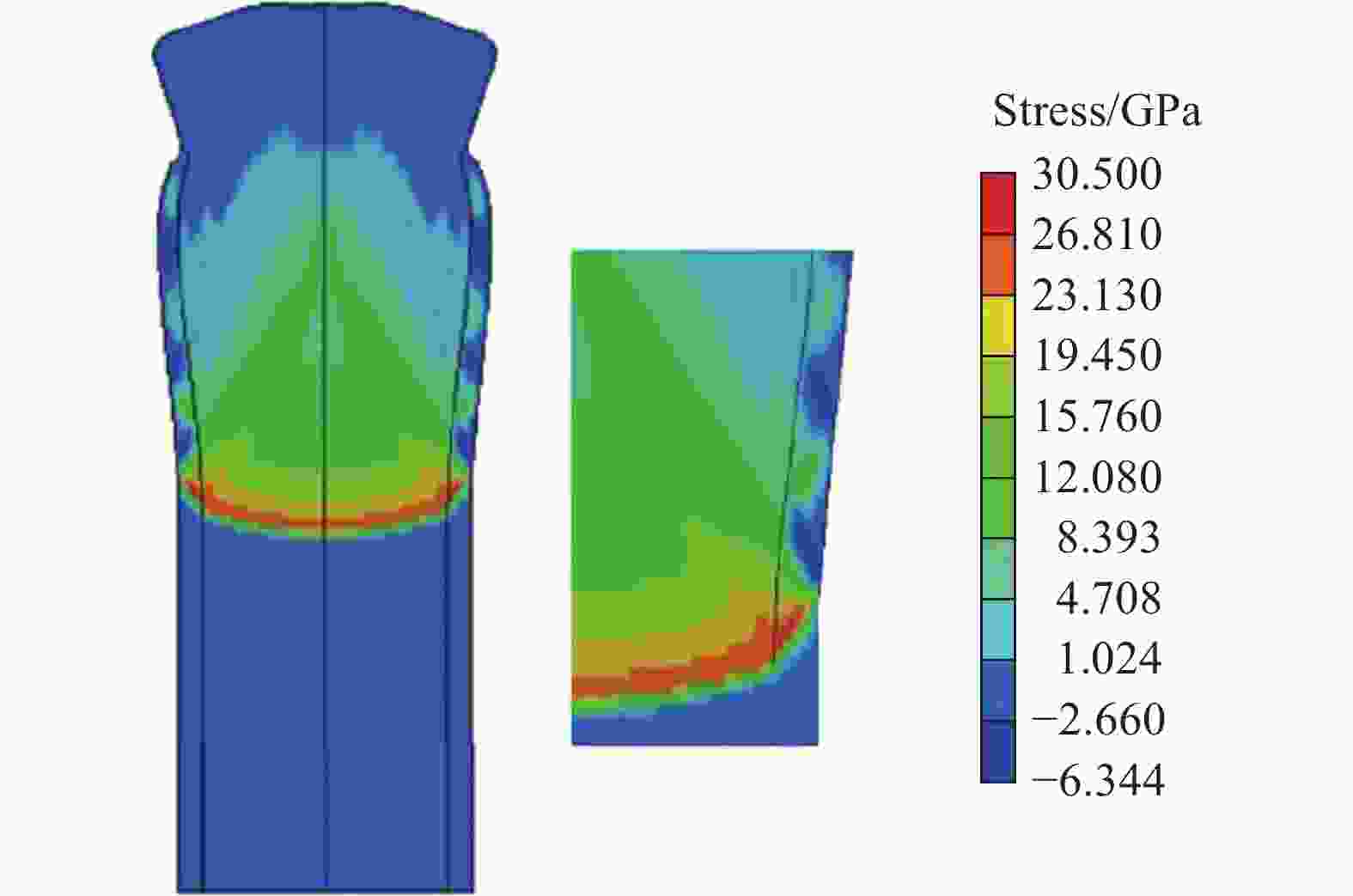
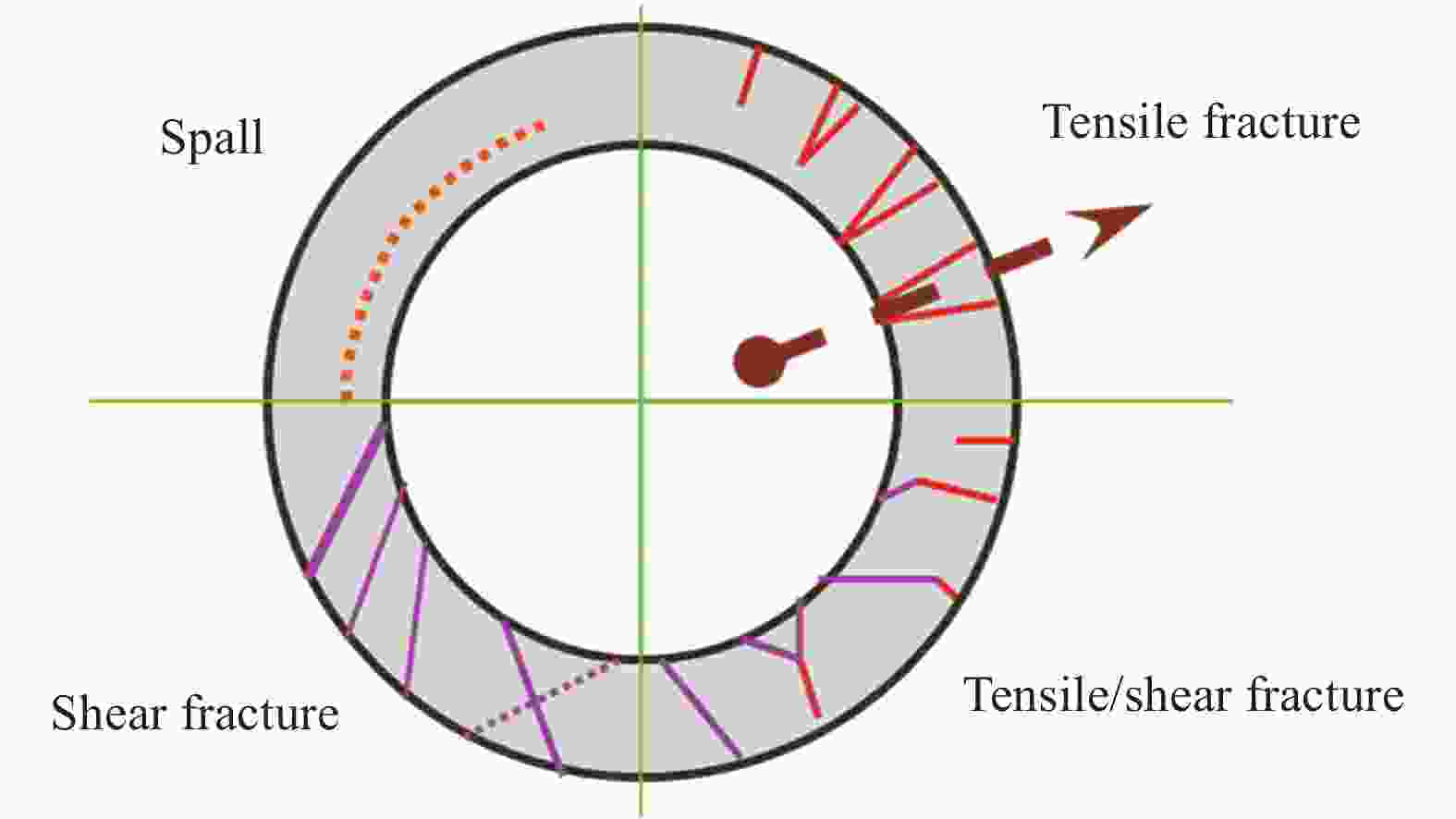
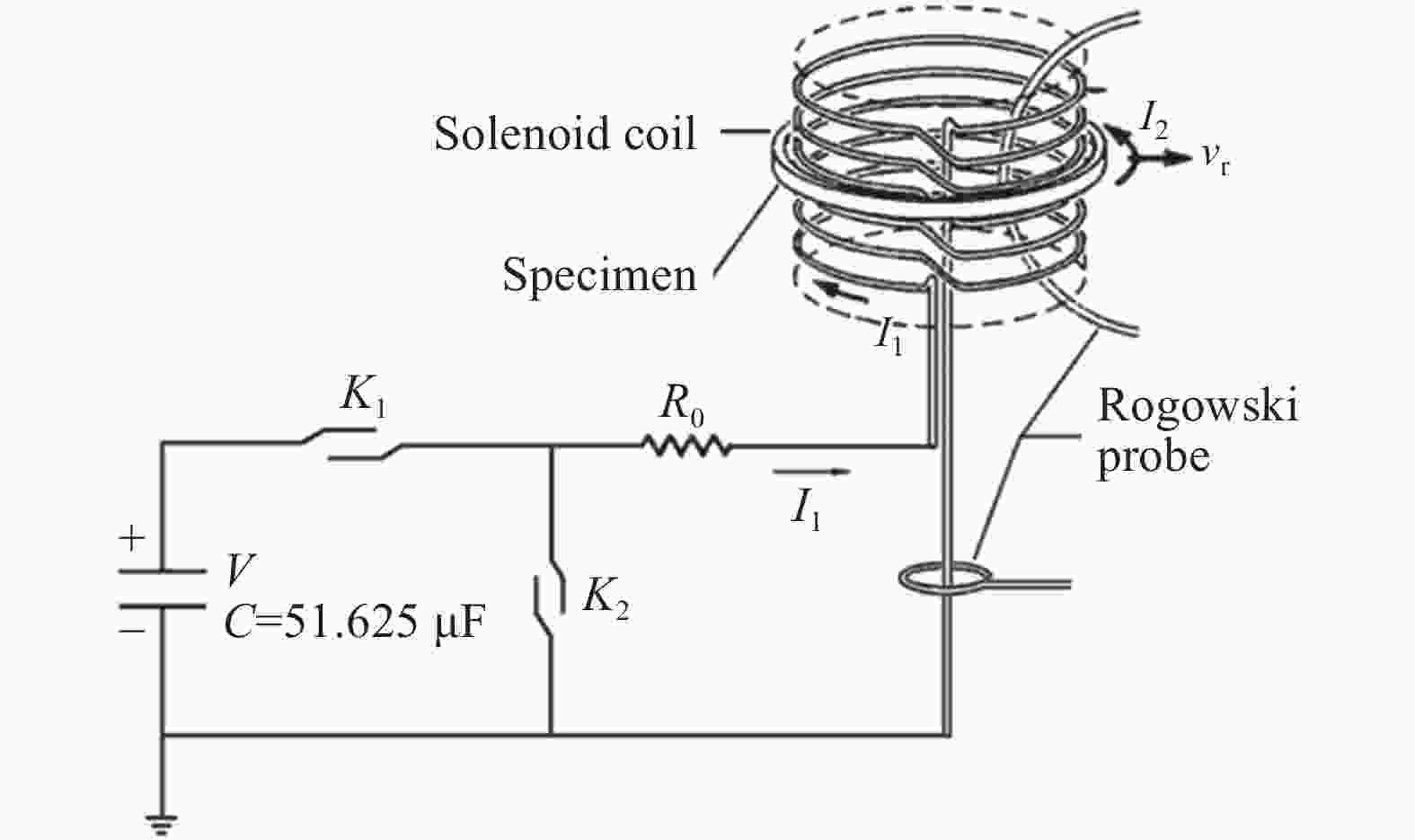
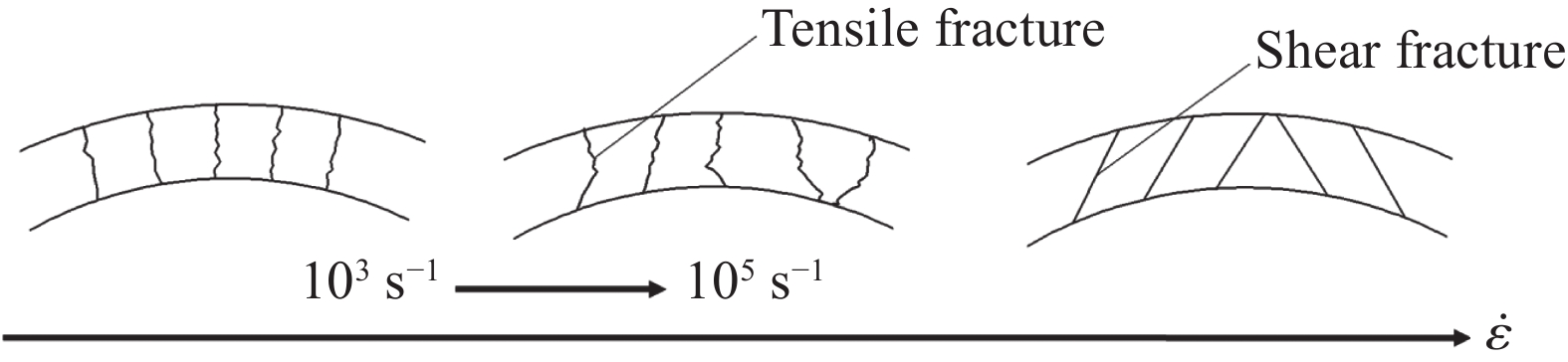
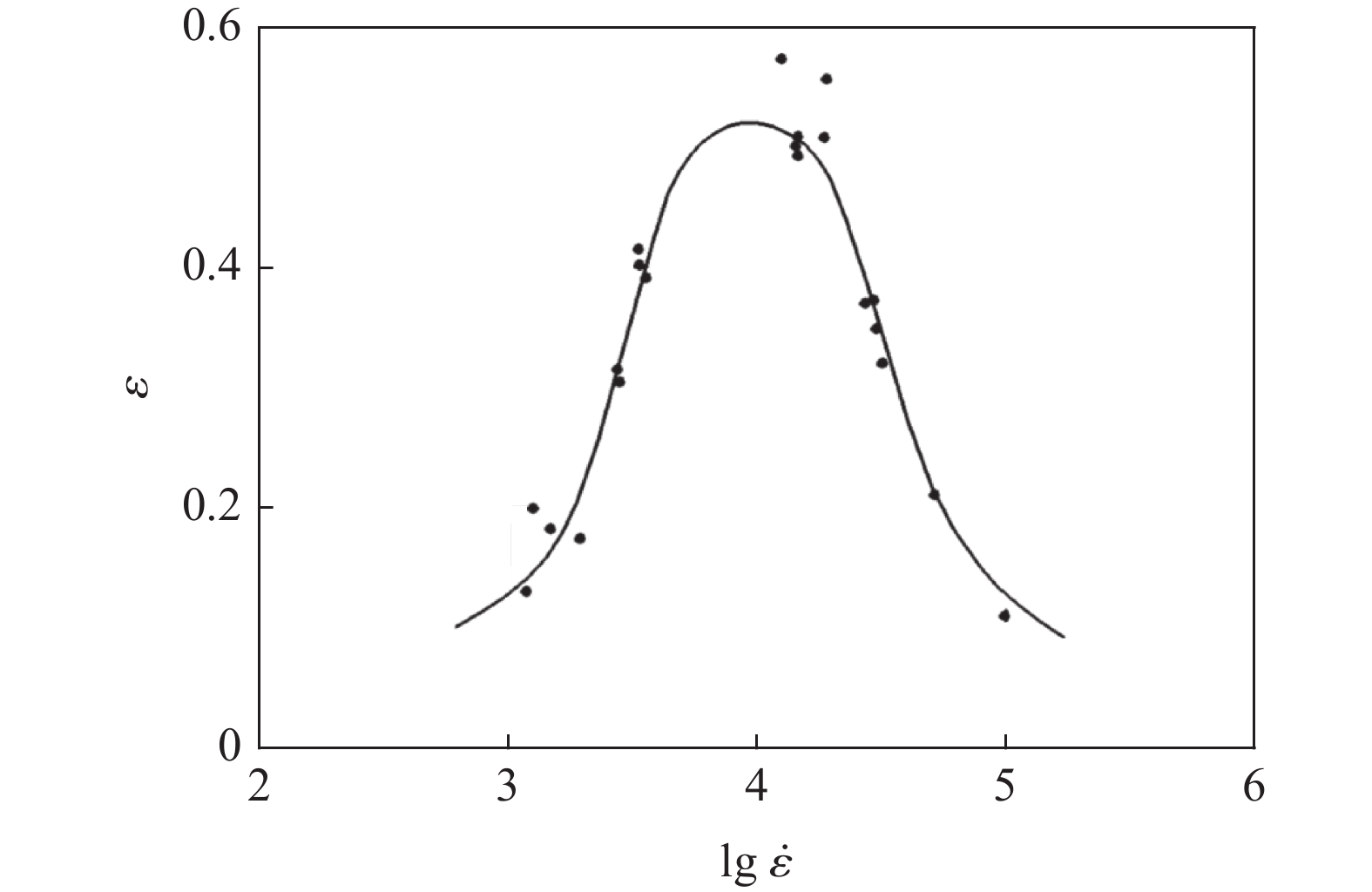
[1] ZHANG Z B, HUANG F L, CAO Y, et al. A fragments mass distribution scaling relations for fragmenting shells with variable thickness subjected to internal explosive loading [J]. International Journal of Impact Engineering, 2018, 120: 79–94. DOI: 10.1016/j.ijimpeng.2018.05.013. [2] 孙学清, 张国伟, 杨陕平. 定向战斗部破片飞散方向控制技术研究 [J]. 弹箭与制导学报, 2008, 28(1): 102–104. DOI: 10.3969/j.issn.1673-9728.2008.01.030.SUN X Q, ZHANG G W, YANG S P. Study on fragments dispersing direction control of directional warhead [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(1): 102–104. DOI: 10.3969/j.issn.1673-9728.2008.01.030. [3] 徐文灿, 张连玉. 导弹预制破片战斗部杀伤威力的工程计算 [J]. 兵工学报, 1992, 13(2): 24–30.XU W C, ZHANG L Y. Lethality calculation for preformed fragment warheads [J]. Acta Armamentarii, 1992, 13(2): 24–30. [4] GOTO D M, BECKER R, ORZECHOWSKI T J, et al. Investigation of the fracture and fragmentation of explosively driven rings and cylinders [J]. International Journal of Impact Engineering, 2008, 35(12): 1547–1556. DOI: 10.1016/j.ijimpeng.2008.07.081. [5] HOPSON M V, SCOTT C M. Applicability of statistical descriptions of AerMet100 steel subjected to different triaxial stress states for fracture calculations [J]. Procedia Engineering, 2013, 58: 684–691. DOI: 10.1016/j.proeng.2013.05.079. [6] HOPSON M V, SCOTT C M, LAMBERT D. Applicability of statistical flaw distributions of eglin steel for fracture calculations [J]. Procedia Engineering, 2015, 103: 213–220. DOI: 10.1016/j.proeng.2015.04.029. [7] GOLOVESHKIN V A, MYAGKOV N N. Fragmentation model for expanding cylinder [J]. International Journal of Fracture, 2014, 187(2): 239–243. DOI: 10.1007/s10704-014-9936-6. [8] BOLIS C, COUNILH D, LAGRANGE J M, et al. Fragmentation of a titanium alloy shell in expansion: from experiment to simulation [J]. Procedia Engineering, 2013, 58: 672–677. DOI: 10.1016/j.proeng.2013.05.077. [9] LIU M T, REN G W, FAN C, et al. Experimental and Numerical studies on the expanding fracture behavior of an explosively driven 1045 steel cylinder [J]. International Journal of Impact Engineering, 2017, 109: 240–252. DOI: 10.1016/j.ijimpeng.2017.07.008. [10] NING J G, DUAN Y, XU X Z, et al. Velocity characteristics of fragments from prismatic casing under internal explosive loading [J]. International Journal of Impact Engineering, 2017, 109: 29–38. DOI: 10.1016/j.ijimpeng.2017.05.018. [11] DONG X L, YU X L, PAN S J, et al. Analysis of fracture behaviour of exploded metal cylinders with varied charge [J]. EPJ Web of Conferences, 2018, 183: 01036. DOI: 10.1051/epjconf/201818301036. [12] 刘龙飞, 周强. 表面粗糙度对6061铝合金薄壁管冲击膨胀断裂性能的影响 [J]. 爆炸与冲击, 2018, 38(4): 749–758. DOI: 10.11883/bzycj-2016-0389.LIU L F, ZHOU Q. Effect of surface roughness on impact expansion fracture of 6061 aluminum alloy thin-walled cylindrical tube [J]. Explosion and Shock Waves, 2018, 38(4): 749–758. DOI: 10.11883/bzycj-2016-0389. [13] GURNEY R W. The initial velocities of fragments from bombs, shell and grenades[R]. BRL Report No. 405, Aberdeen: Ballistic Research Laboratory, 1943. [14] MEYERS M A. Dynamic behavior of materials [M]. New York: John Wiley & Sons, Inc., 1994. [15] NEERAJ T, SAVAGE M F, TATALOVICH J, et al. Observation of tension-compression asymmetry in α and α/β titanium alloys [J]. Philosophical Magazine, 2005, 85(2/3): 279–295. DOI: 10.1080/14786430412331315707. [16] ZHOU P, BEEH E, FRIEDRICH H E. Influence of tension-compression asymmetry on the mechanical behavior of AZ31B magnesium alloy sheets in bending [J]. Journal of Materials Engineering and Performance, 2016, 25(3): 853–865. DOI: 10.1007/s11665-016-1961-3. [17] MAEDA T, NOMA N, KUWABARA T, et al. Experimental verification of the tension-compression asymmetry of the flow stresses of a high strength steel sheet [J]. Procedia Engineering, 2017, 207: 1976–1981. DOI: 10.1016/j.proeng.2017.10.1099. [18] HARDING J, WOOD E O, CAMPBELL J D. Tensile testing of materials at impact rates of strain [J]. Journal of Mechanical Engineering Science, 1960, 2(2): 88–96. DOI: 10.1243/JMES_JOUR_1960_002_016_02. [19] CHEN W W, SONG B. Split Hopkinson (Kolsky) bar-design, testing and applications [M]. New York: Springer, 2011. DOI: 10.1007/978-1-4419-7982-7. [20] JOHNSON P C, STEIN B A, DAVIS R S. Measurement of dynamic plastic flow properties under uniform stress [C] // Symposium on Dynamic Behavior of Materials. West Conshohocken: ASTM International, 1963: 195−197. DOI: 10.1520/STP42030S. [21] TANG T G, REN G W, GUO Z L, et al. An improved technique of expanding metal ring experiment under high explosive loading [J]. Review of Scientific Instruments, 2013, 84(4): 043908. DOI: 10.1063/1.4802255. [22] NIORDSON F I. A unit for testing materials at high strain rates [J]. Experimental Mechanics, 1965, 5(1): 29–32. DOI: 10.1007/BF02320901. [23] 桂毓林, 孙承纬, 李强, 等. 实现金属环动态拉伸的电磁加载技术研究 [J]. 爆炸与冲击, 2006, 26(6): 481–485. DOI: 10.11883/1001-1455(2006)06-0481-05.GUI Y L, SUN C W, LI Q, et al. Experimental studies on dynamic tension of metal ring by electromagnetic loading [J]. Explosion and Shock Waves, 2006, 26(6): 481–485. DOI: 10.11883/1001-1455(2006)06-0481-05. [24] 陈红. 电磁驱动金属膨胀环动态拉伸实验技术[D]. 宁波: 宁波大学, 2012.CHEN H. Dynamic tension experimental technique of electromagneticall driven expanding metal ring[D]. Ningbo: Ningbo University, 2012. [25] 刘明涛, 汤铁钢, 郭昭亮, 等. 膨胀环实验平台及其在材料动力学行为研究中的应用 [J]. 实验力学, 2016, 31(1): 47–56. DOI: 10.7520/1001-4888-15-022.LIU M T, TANG T G, GUO Z L, et al. Expanding ring experimental platform and its application in material dynamic mechanical behavior investigation [J]. Journal of Experimental Mechanics, 2016, 31(1): 47–56. DOI: 10.7520/1001-4888-15-022. [26] LIANG M Z, LI X Y, QIN J G, et al. Improved expanding ring technique for determining dynamic material properties [J]. Review of Scientific Instruments, 2013, 84(6): 065114. DOI: 10.1063/1.4811658. [27] 郑宇轩, 周风华, 胡时胜. 一种基于SHPB的冲击膨胀环实验技术 [J]. 爆炸与冲击, 2014, 34(4): 483–488. DOI: 10.11883/1001-1455(2014)04-0483-06.ZHENG Y X, ZHOU F H, HU S S. An SHPB-based experimental technique for dynamic fragmentations of expanding rings [J]. Explosion and Shock Waves, 2014, 34(4): 483–488. DOI: 10.11883/1001-1455(2014)04-0483-06. [28] AVRIEL E, LOVINGER Z, NEMIROVSKY R, et al. Investigating the strength of materials at very high strain rates using electro-magnetically driven expanding cylinders [J]. Mechanics of Materials, 2018, 117: 165–180. DOI: 10.1016/j.mechmat.2017.11.009. [29] TAYLOR G I. The fragmentation of tubular bombs [J]. Scientific Papers of GI Taylor, 1963, 3(44): 387–390. [30] 胡八一, 董庆东, 韩长生, 等. 爆炸金属管的绝热剪切断裂宏观研究 [J]. 爆炸与冲击, 1992, 12(4): 319–325.HU B Y, DONG Q D, HAN C S, et al. The macroscopic study of adiabatic shear fracture of metal tubes under explosive loading [J]. Explosion and Shock Waves, 1992, 12(4): 319–325. [31] 胡八一, 董庆东, 韩长生, 等. 爆炸金属管绝热剪切断裂的细观研究 [J]. 爆炸与冲击, 1993, 13(4): 305–312.HU B Y, DONG Q D, HAN C S, et al. Mesoscopic study of adiabatic shear fracture of the metal tubes under internal explosive loading [J]. Explosion and Shock Waves, 1993, 13(4): 305–312. [32] 胡八一, 董庆东, 韩长生, 等. 内部爆轰加载下的钢管膨胀断裂研究 [J]. 爆炸与冲击, 1993, 13(1): 49–54.HU B Y, DONG Q D, HAN C S, et al. Studies of expansion and fracture of explosive-filled steel cylinders [J]. Explosion and Shock Waves, 1993, 13(1): 49–54. [33] BEETLE J C, RINNOVATORE J V, CORRIE J D. Fracture morphology of explosively loaded steel cylinders [C] // Proceedings of the Scanning Electron Microscope Symposium. Chicago, 1971: 137−144. [34] MARTINEAU R L. A viscoplastic model of expanding cylindrical shells subjected to internal explosive detonations [R]. New Mexico: Los Alamos National Lab., 1998. DOI: 10.2172/663184. [35] MARTINEAU R L, PRIME M B, ANDERSON C A, et al. An explicit model of expanding cylindrical shells subjected to high explosive detonations[R]. New Mexico: Los Alamos National Lab., 1999. DOI: 10.2172/334315. [36] MARTINEAU R L, ANDERSON C A, SMITH F W. Expansion of cylindrical shells subjected to internal explosive detonations [J]. Experimental Mechanics, 2000, 40(2): 219–225. DOI: 10.1007/BF02325049. [37] 李永池, 李大红, 魏志刚, 等. 内爆炸载荷下圆管变形、损伤和破坏规律的研究 [J]. 力学学报, 1999, 31(4): 442–449. DOI: 10.3321/j.issn:0459-1879.1999.04.008.LI Y C, LI D H, WEI Z G, et al. Research on the deformation, damage and fracture rules of circular tubes under inside-explosive loading [J]. Acta Mechanica Sinica, 1999, 31(4): 442–449. DOI: 10.3321/j.issn:0459-1879.1999.04.008. [38] 张世文, 刘仓理, 于锦泉. 微缺陷对圆管膨胀断裂的影响 [J]. 爆炸与冲击, 2008, 28(4): 316–323. DOI: 10.11883/1001-1455(2008)04-0316-08.ZHANG S W, LIU C L, YU J Q. Influences of microdefects on expanding fracture of a metal cylinder [J]. Explosion and Shock Waves, 2008, 28(4): 316–323. DOI: 10.11883/1001-1455(2008)04-0316-08. [39] HOGGATT C R, RECHT R F. Fracture behavior of tubular bombs [J]. Journal of Applied Physics, 1968, 39(3): 1856–1862. DOI: 10.1063/1.1656442. [40] IVANOV A G. Explosive deformation and destruction of tubes [J]. Strength of Materials, 1976, 8(11): 1303–1306. DOI: 10.1007/BF01528752. [41] OLIVE F, NICAUD A, MARILLEAU J, et al. Rupture behavior of metals in explosive expansion [J]. Institute of Physics Conference Series, 1979(17): 242–252. [42] 陈大年, 王德生, 马松合, 等. 两类动态断裂 [J]. 爆炸与冲击, 1987, 7(1): 27–33.CHEN D N, WANG D S, MA S H, et al. Two kinds of dynamic fracture [J]. Explosion and Shock Waves, 1987, 7(1): 27–33. [43] 陈大年, 尹志华. 对膨胀壳体材料失稳的一种简化处理 [J]. 爆炸与冲击, 1999, 19(3): 193–198.CHEN D N, YIN Z H. A simplified approach to material instability of expanding shells [J]. Explosion and Shock Waves, 1999, 19(3): 193–198. [44] FENG J P, JING F Q, ZHANG G R. Dynamic ductile fragmentation and the damage function model [J]. Journal of Applied Physics, 1997, 81(6): 2575–2578. DOI: 10.1063/1.363921. [45] 汤铁钢, 李庆忠, 孙学林, 等. 45钢柱壳膨胀断裂的应变率效应 [J]. 爆炸与冲击, 2006, 26(2): 129–133. DOI: 10.11883/1001-1455(2006)02-0129-05.TANG T G, LI Q Z, SUN X L, et al. Strain-rate effects of expanding fracture of 45 steel cylinder shells driven by detonation [J]. Explosion and Shock Waves, 2006, 26(2): 129–133. DOI: 10.11883/1001-1455(2006)02-0129-05. [46] 汤铁钢, 谷岩, 李庆忠, 等. 爆轰加载下金属柱壳膨胀破裂过程研究 [J]. 爆炸与冲击, 2003, 23(6): 529–533.TANG T G, GU Y, LI Q Z, et al. Expanding fracture of steel cylinder shell by detonation driving [J]. Explosion and Shock Waves, 2003, 23(6): 529–533. [47] 金山, 汤铁钢, 孙学林, 等. 不同热处理条件下45钢柱壳的动态性能 [J]. 爆炸与冲击, 2006, 26(5): 423–428. DOI: 10.11883/1001-1455(2006)05-0423-06.JIN S, TANG T G, SUN X L, et al. Dynamic characteristics of 45 steel cylinder shell by different heat treatment conditions [J]. Explosion and Shock Waves, 2006, 26(5): 423–428. DOI: 10.11883/1001-1455(2006)05-0423-06. [48] 金山, 汤铁钢, 李庆忠, 等. 铍青铜柱壳膨胀断裂研究 [J]. 高压物理学报, 2006, 20(4): 434–438. DOI: 10.11858/gywlxb.2006.04.016.JIN S, TANG T G, LI Q Z, et al. Expanding fracture of beryllium bronze cylinder shell [J]. Chinese Journal of High Pressure Physics, 2006, 20(4): 434–438. DOI: 10.11858/gywlxb.2006.04.016. [49] 胡海波, 汤铁钢, 胡八一, 等. 金属柱壳在爆炸加载断裂中的单旋现象 [J]. 爆炸与冲击, 2004, 24(2): 97–107.HU H B, TANG T G, HU B Y, et al. An study of uniform shear bands orientation selection tendency on explosively loaded cylindrical shells [J]. Explosion and Shock Waves, 2004, 24(2): 97–107. [50] XUE Q, NESTERENKO V F, MEYERS M A. Evaluation of the collapsing thick-walled cylinder technique for shear-band spacing [J]. International Journal of Impact Engineering, 2003, 28(3): 257–280. DOI: 10.1016/S0734-743X(02)00103-3. [51] YANG Y, ZENG Y, GAO Z W. Numerical and experimental studies of self-organization of shear bands in 7075 aluminium alloy [J]. Materials Science and Engineering: A, 2008, 496(1/2): 291–302. DOI: 10.1016/j.msea.2008.07.043. [52] LOVINGER Z, RIKANATI A, ROSENBERG Z, et al. Electro-magnetic collapse of thick-walled cylinders to investigate spontaneous shear localization [J]. International Journal of Impact Engineering, 2011, 38(11): 918–929. DOI: 10.1016/j.ijimpeng.2011.06.006. [53] LOVINGER Z, RITTEL D, ROSENBERG Z. An experimental study on spontaneous adiabatic shear band formation in electro-magnetically collapsing cylinders [J]. Journal of the Mechanics and Physics of Solids, 2015, 79: 134–156. DOI: 10.1016/j.jmps.2015.04.007. [54] LIU M T, GUO Z L, FAN C, et al. Modeling spontaneous shear bands evolution in thick-walled cylinders subjected to external High-strain-rate loading [J]. International Journal of Solids and Structures, 2016, 97/98: 336–354. DOI: 10.1016/j.ijsolstr.2016.07.014. [55] REN G W, GUO Z L, FAN C, et al. Dynamic shear fracture of an explosively-driven metal cylindrical shell [J]. International Journal of Impact Engineering, 2016, 95: 35–39. DOI: 10.1016/j.ijimpeng.2016.04.012. [56] HIROE T, FUJIWARA K, HATA H, et al. Deformation and fragmentation behaviour of exploded metal cylinders and the effects of wall materials, configuration, explosive energy and initiated locations [J]. International Journal of Impact Engineering, 2008, 35(12): 1578–1586. DOI: 10.1016/j.ijimpeng.2008.07.002. [57] MOTT N F. Fragmentation of shell cases [J]. Proceedings of the Royal Society of London: Series A: Mathematical and Physical Sciences, 1947, 189(1018): 300–308. DOI: 10.1098/rspa.1947.0042. [58] GRADY D E, OLSEN M L. A statistics and energy based theory of dynamic fragmentation [J]. International Journal of Impact Engineering, 2003, 29(1/2/3/4/5/6/7/8/9/10): 293–306. DOI: 10.1016/j.ijimpeng.2003.09.026. [59] LAMBER D E, OSBORN J, HOPSON M V. Explosively driven fragmentation experiments for continuum damage modeling [J]. Journal of Pressure Vessel Technology, 2012, 134(3): 031209. DOI: 10.1115/1.4006119. [60] HOPSON M V, SCOTT C M, PATEL R. Computational comparisons of homogeneous and statistical descriptions of AerMet100 steel subjected to high strain rate loading [J]. International Journal of Impact Engineering, 2011, 38(6): 451–455. DOI: 10.1016/j.ijimpeng.2010.10.016. [61] HOPSON M V, LAMBERT D E, WEIDERHOLD J. Computational comparisons of homogeneous and statistical descriptions of steel subjected to explosive loading [C] // Proceedings of the ASME 2010 pressure Vessels and Piping Division/K-PVP Conference. Washington: ASME, 2010: 257−262. DOI: 10.1115/PVP2010-25330. [62] ZHOU F, MOLINARI J F, RAMESH K T. An elastic–visco-plastic analysis of ductile expanding ring [J]. International Journal of Impact Engineering, 2006, 33(1/2/3/4/5/6/7/8/9/10/11/12): 880–891. DOI: 10.1016/j.ijimpeng.2006.09.070. [63] 陈磊, 周风华, 汤铁钢. 韧性金属圆环高速膨胀碎裂过程的有限元模拟 [J]. 力学学报, 2011, 43(5): 861–870. DOI: 10.6052/0459-1879-2011-5-lxxb2010-675.CHEN L, ZHOU F H, TANG T G. Finite element simulations of the high velocity expansion and fragmentation of ductile metallic rings [J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(5): 861–870. DOI: 10.6052/0459-1879-2011-5-lxxb2010-675. [64] 郑宇轩, 陈磊, 胡时胜, 等. 韧性材料冲击拉伸碎裂中的碎片尺寸分布规律 [J]. 力学学报, 2013, 45(4): 580–587. DOI: 10.6052/0459-1879-12-338.ZHENG Y X, CHEN L, HU S S, et al. Characteristics of fragment size distribution of ductile materials fragmentized under high strainrate tension [J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(4): 580–587. DOI: 10.6052/0459-1879-12-338. [65] 郑宇轩, 周风华, 胡时胜, 等. 固体的冲击拉伸碎裂 [J]. 力学进展, 2016, 46(1): 201612. DOI: 10.6052/1000-0992-16-004.ZHENG Y X, ZHOU F H, HU S S, et al. Fragmentations of solids under impact tension [J]. Advances in Mechanics, 2016, 46(1): 201612. DOI: 10.6052/1000-0992-16-004. [66] ZHANG H, RAVI-CHANDAR K. On the dynamics of necking and fragmentation–I. Real-time and post-mortem observations in Al 6061-O [J]. International Journal of Fracture, 2006, 142(3/4): 183–217. DOI: 10.1007/s10704-006-9024-7. [67] ZHANG H, RAVI-CHANDAR K. On the dynamics of necking and fragmentation-Ⅱ. Effect of material properties, geometrical constraints and absolute size [J]. International Journal of Fracture, 2008, 150: 3–36. DOI: 10.1007/s10704-008-9233-3. [68] ZHANG H, RAVI-CHANDAR K. On the dynamics of localization and fragmentation-Ⅳ. Expansion of Al 6061-O tubes [J]. International Journal of Fracture, 2010, 163(1): 41–65. DOI: 10.1007/s10704-009-9441-5. 期刊类型引用(6)
1. 贾琦，杜东兴，孔金星，刘思来，彭照波，杨全威. 超声滚压工艺参数对45钢表面完整性与冲击性能的影响. 机械工程材料. 2024(10): 28-34 . 
百度学术2. 李满江，赵志豪，董新龙，付应乾，俞鑫炉，周刚毅. 内部爆炸作用下20钢柱壳的变形及相变. 爆炸与冲击. 2023(01): 109-120 . 
本站查看3. 张世文，陈艳，但加坤，李英雷，刘明涛，汤铁钢. 爆轰驱动下45钢半球壳膨胀断裂破片回收研究. 高压物理学报. 2023(02): 159-168 . 百度学术4. Zhi-yong Yin，Xiao-wei Chen. Numerical study on the dynamic fracture of explosively driven cylindrical shells. Defence Technology. 2023(09): 154-168 . 必应学术5. 邓宇轩，张先锋，冯可华，刘闯，杜宁，刘均伟，李鹏程. 椭圆截面战斗部爆炸驱动破片作用过程的数值模拟. 高压物理学报. 2022(02): 155-165 . 百度学术6. 杨智程，刘龙飞，刘炼煌，殷鹏志，吴志强. 外部爆炸载荷下表面粗糙度对45钢柱壳剪切带行为的影响. 高压物理学报. 2022(04): 114-126 . 百度学术其他类型引用(2)
-
下载:
下载:
百度学术
计量
- 文章访问数: 1268
- HTML全文浏览量: 444
- PDF下载量: 213
- 被引次数: 8