On the overload phenomenon in dynamic Brazilian disk experiments of rocks
-
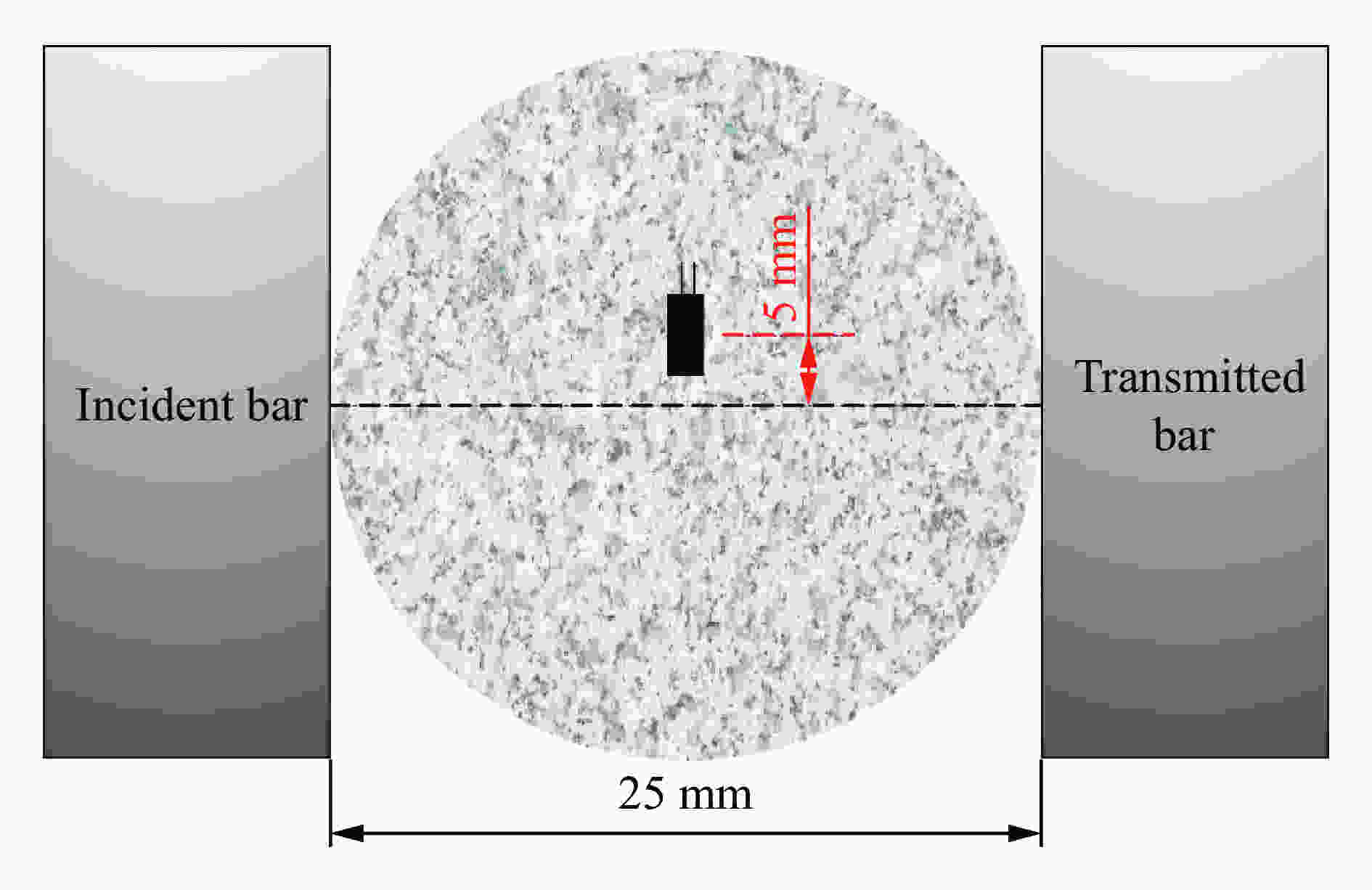
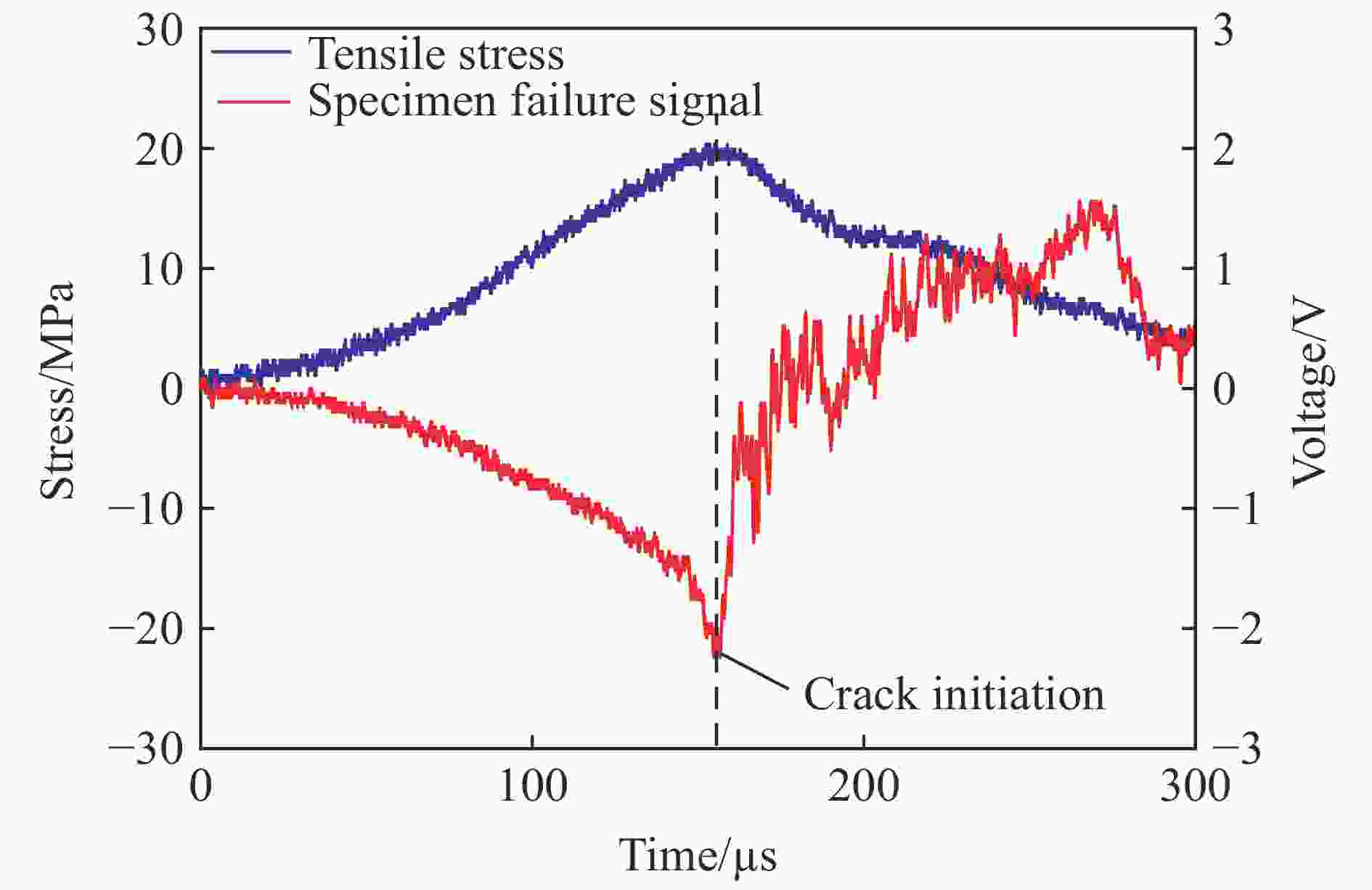
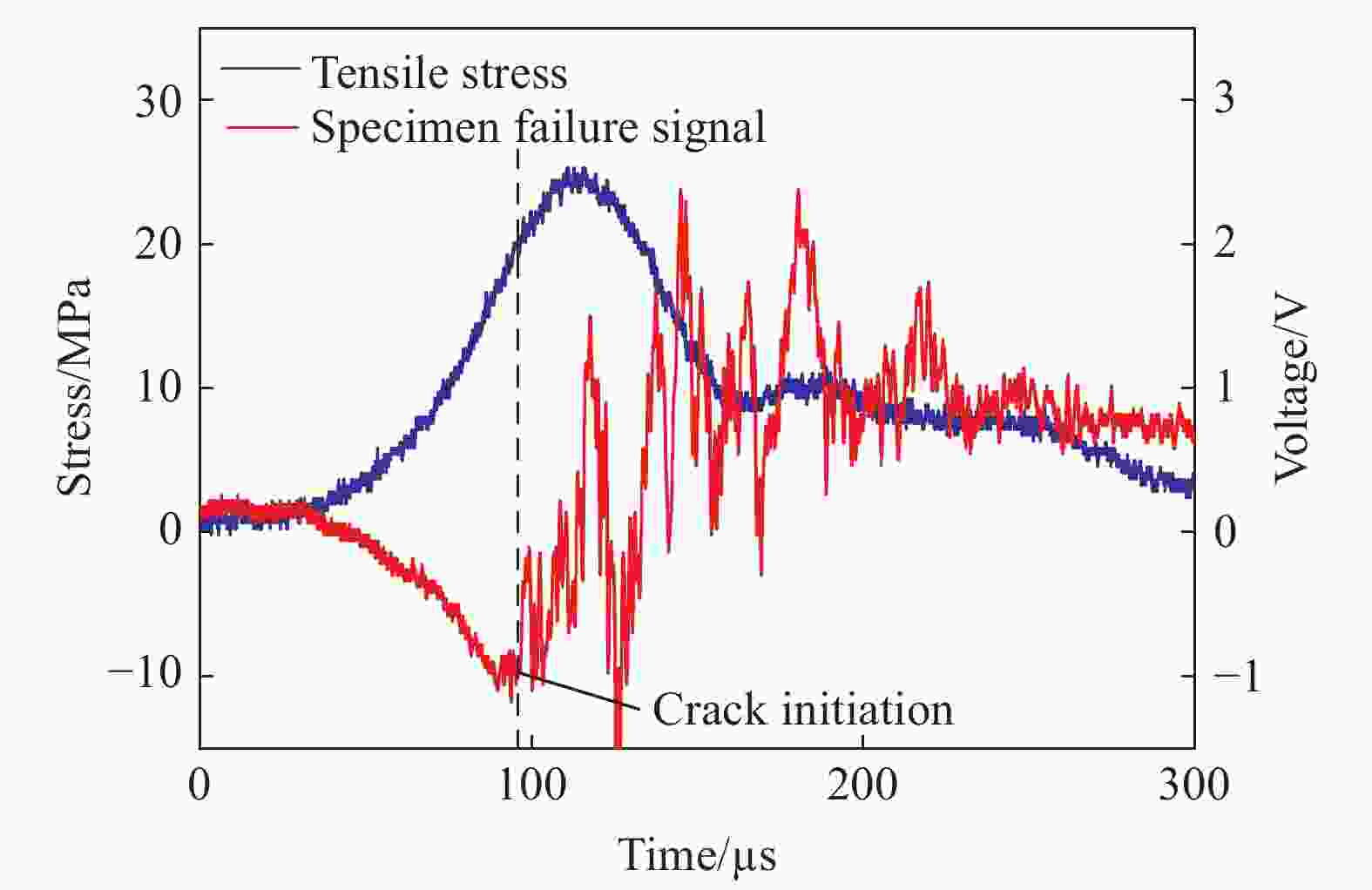
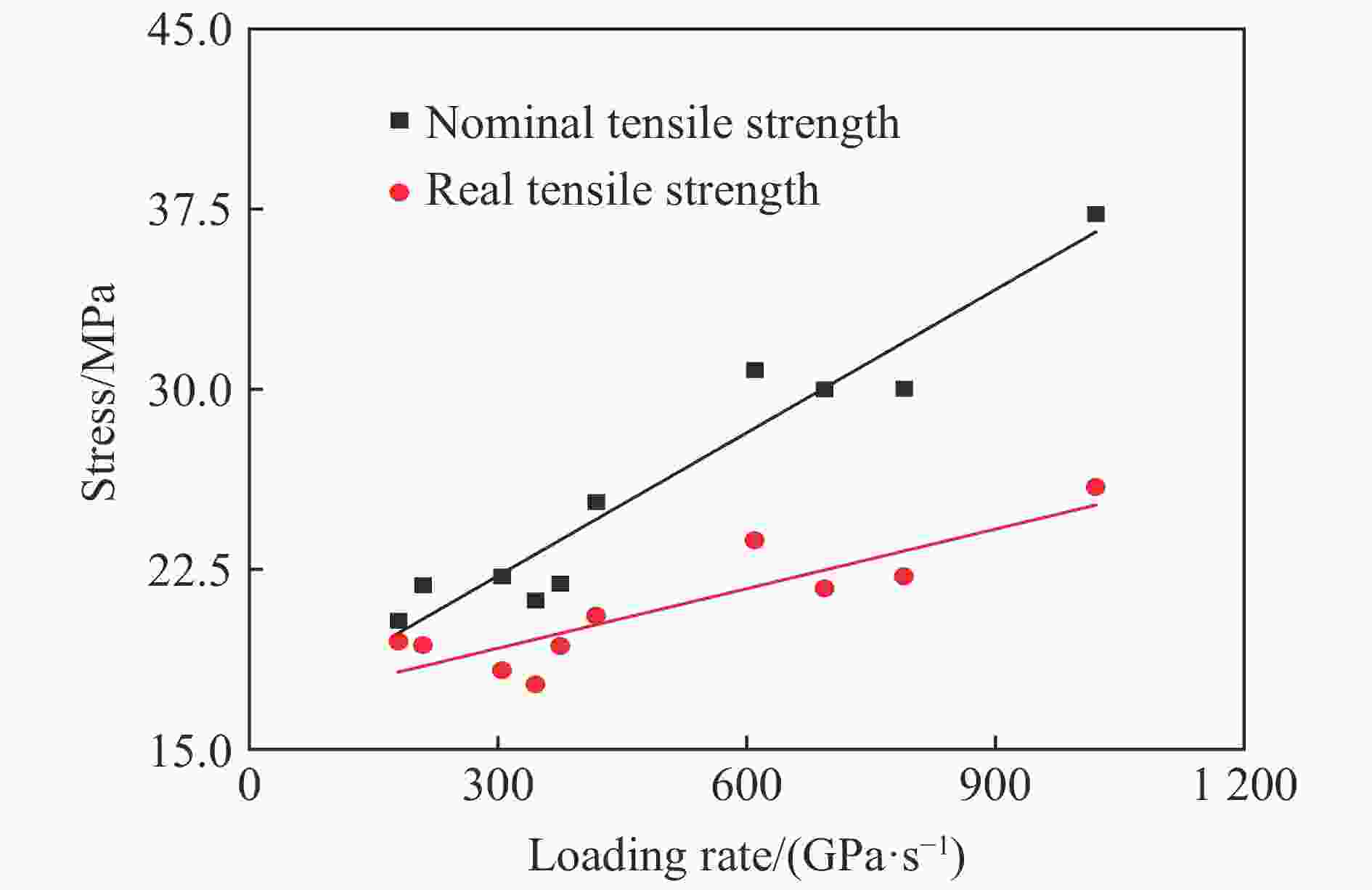
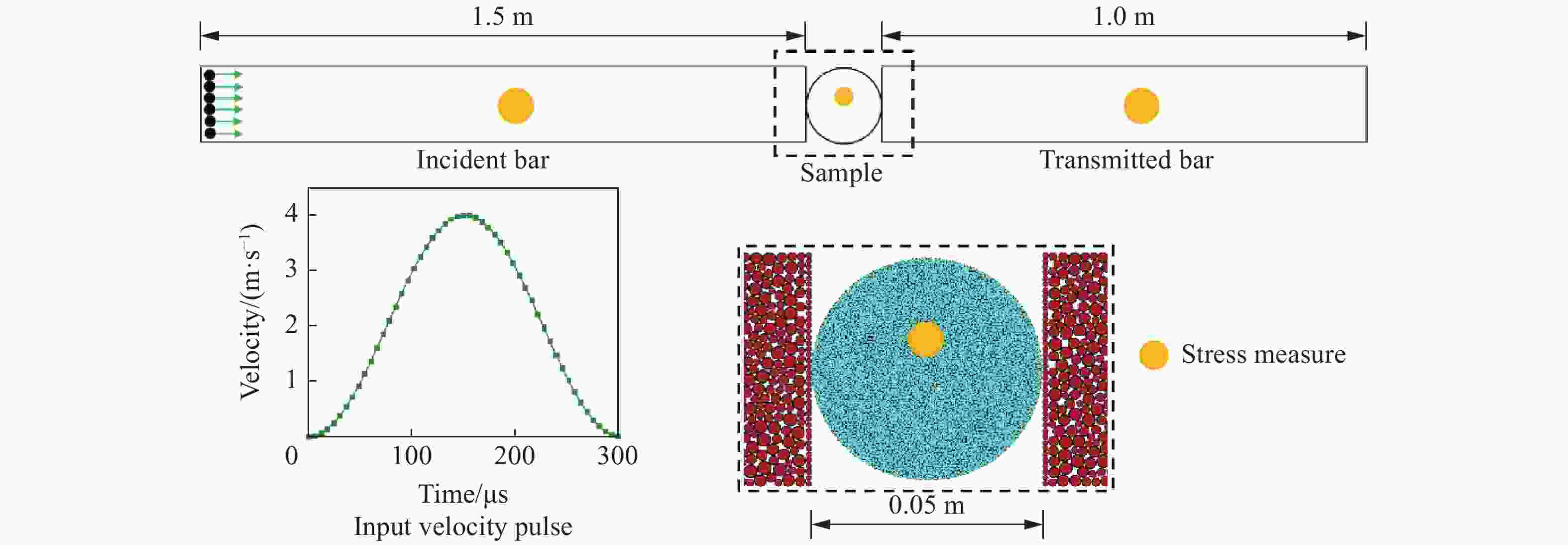
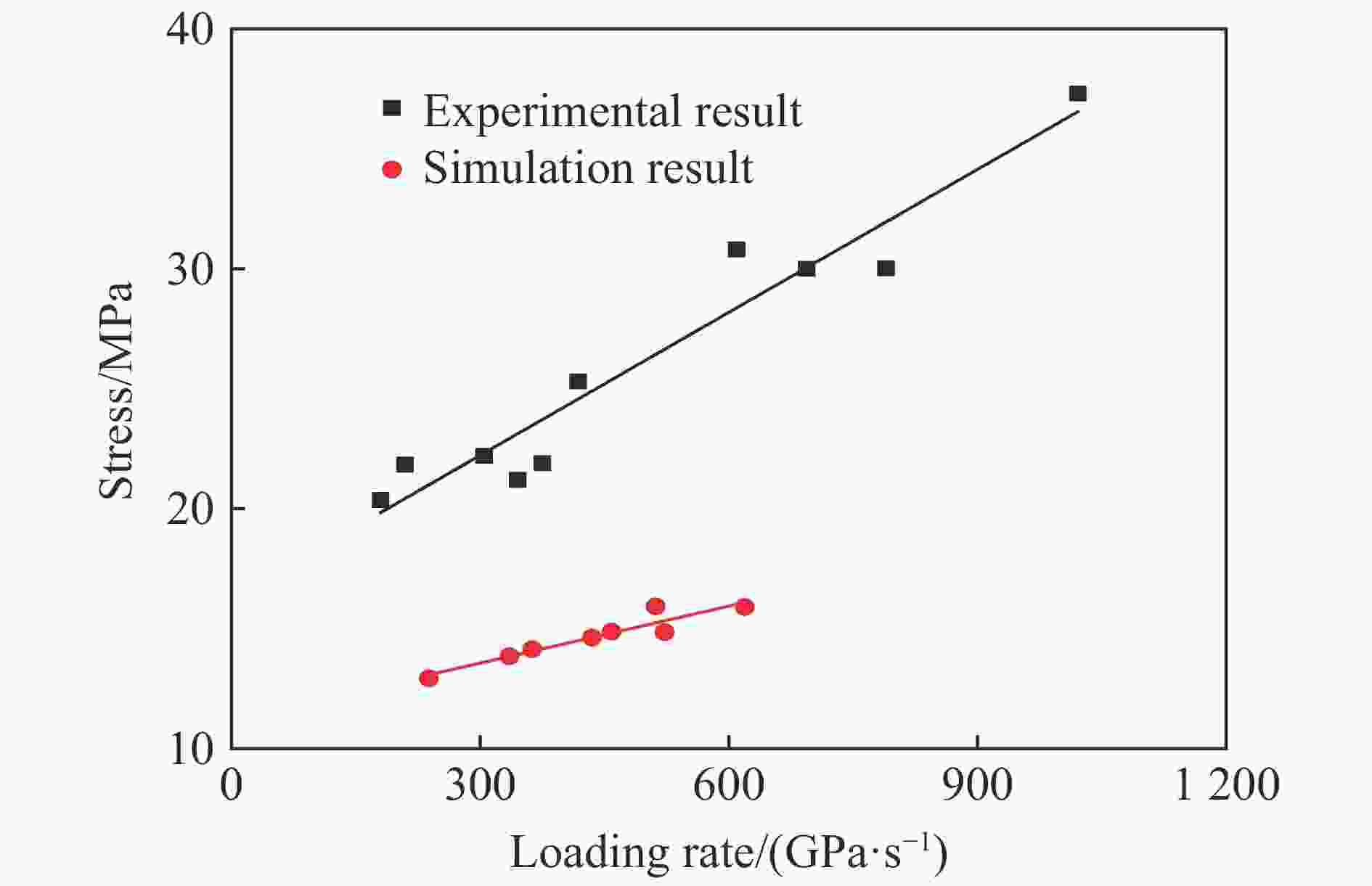
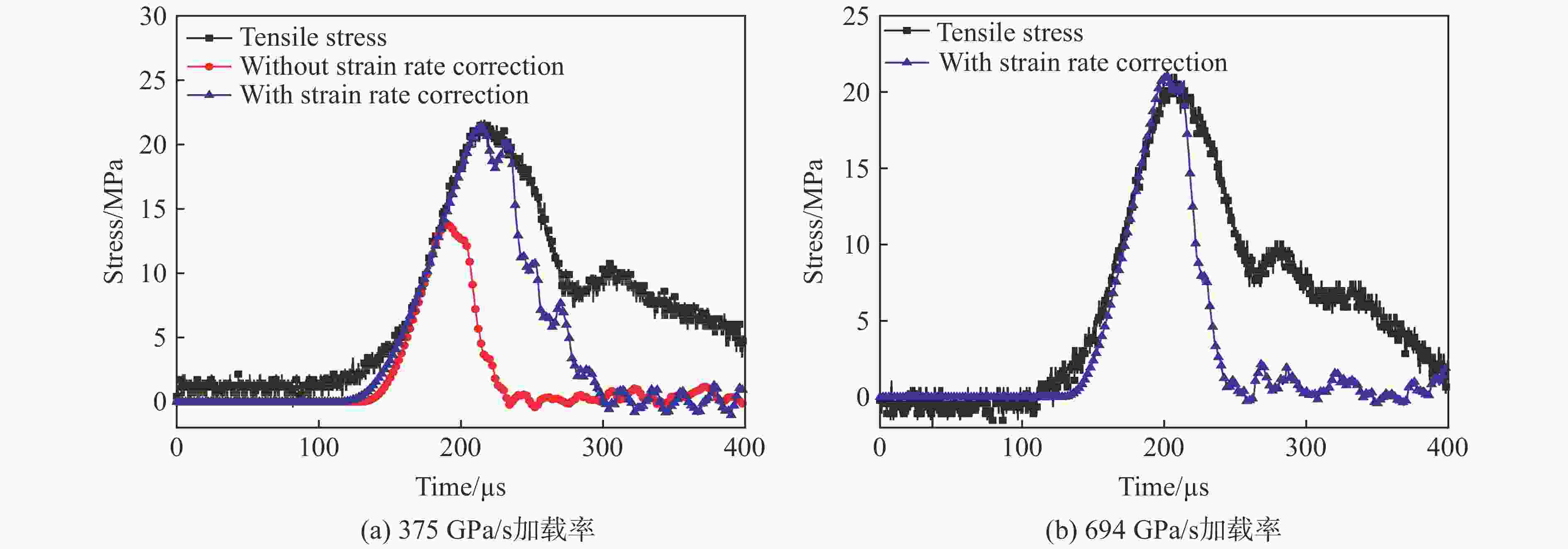
摘要: 巴西圆盘实验是国际岩石力学与工程学会（ISRM）推荐的测量岩石静态拉伸强度的方法之一，也是该学会推荐的唯一测量岩石动态拉伸强度的方法。但是巴西圆盘实验得到的静态或者动态拉伸强度往往较真实值偏大，其中一个原因是所谓的过载现象，而且其相应的过载效应在动态巴西圆盘测试中尤为明显。为探究岩石材料动态劈裂拉伸强度的过载效应机理及其率相关性，利用SHPB实验装置开展了不同加载率条件下的动态巴西圆盘实验，对岩石材料劈裂拉伸强度的过载特性进行了定量分析；结合颗粒流程序进行了相关实验的数值模拟，得到了圆盘破裂的微观过程。结果表明：（1）动态巴西圆盘实验得到的岩石拉伸强度存在明显的过载现象，圆盘试样拉伸强度的过载比随加载率增加呈对数形式增加；（2）依据动态拉伸强度实验结果对模型参数引入率相关性后，模拟观察到的过载效应更加贴近实验观测。这些结果表明巴西圆盘实验中拉伸强度的过载现象是客观存在的，其机理与试样的圆盘构型以及测试方法有关。结合实验和数值结果，解释了巴西圆盘实验的过载机理，证明了动态巴西圆盘实验修正的必要性并给出了相应的方案，以获取岩石材料的真实动态拉伸强度。Abstract: The Brazilian disk (BD) test is one of the testing methods suggested by the International Society for Rock Mechanics and Rock Engineering (ISRM) for determining the static tensile strength of rocks. Meanwhile, it is also the only method suggested by ISRM to determine the dynamic tensile strength of rock materials. However, it is worth noting that both static and dynamic tensile strengths of rocks tend to be overestimated using the BD specimen. This can be partially attributed to the overload phenomenon, which is particularly pronounced in dynamic BD tests. In this manuscript, the physical interpretation of the load used in BD test is revised based on the Griffith criterion. To systemically investigate the mechanism and the loading rate dependence of the overload phenomenon for rock materials, the dynamic BD tests under different loading rates were conducted using split Hopkinson pressure bar (SHPB) system. A strain gauge was attached 5 mm off the disk center to detect the failure onset. Then the transmitted wave signal was recorded and processed according to the distance of wave propagation on the transmitted bar and the specimen. The so-called nominal tensile strength and the real tensile strength were obtained through analyzing. The overload phenomenon was then quantitatively evaluated using the pre-defined overload ratio. Additionally, numerical simulations were carried out through the particle flow code (PFC) to observe the failure processes of the disk specimens in microscale. The loading rate dependency was introduced to revise the micro parameters to get a better simulation result. The overload phenomenon and the overload ratio were observed and calculated. The results show that: (1) the overload phenomenon of tensile strength can be obviously observed in the dynamic BD tests, and the overload ratio of the tensile strength logarithmically increases with the loading rate. (2) The overload phenomenon inspected by numerical simulation agrees well with the experimental observation. These results have demonstrated that the overload phenomenon does exist in dynamic BD tests. Its intrinsic mechanism is related to the geometry of specimen and the principle of the testing method based on the experimental and numerical tests. The overload ratio can reach 40% under a high loading rate. It is thus necessary to correct the result from the dynamic BD test to determine the real dynamic tensile strength using the method proposed in this work.
-
激波与液滴的相互作用问题，是一个与Richtmyer-Meshkov(RM)不稳定性有关的、典型的可压缩性气液两相流问题[1]，对该问题的深入研究在超音速雨滴侵蚀、燃气轮机燃烧室的设计、激波抛洒以及爆轰发动机中燃料燃烧的稳定性等方面均有着重要应用。
W.Lane[2]最早在激波管中对液滴在稳态和瞬态气流中的破碎进行了实验研究，并提出液滴的变形破碎是一个边界层不断脱落的过程。W.E.Krauss[3]随后也研究了边界层分离与液滴破碎雾化之间的关系。O.Engel[4]着重研究了激波对液滴的雾化作用，他认为高速气流在液滴表面生成不稳定波在液滴破碎过程中起重要作用。A.Ranger等[5]在水平激波管中进行了激波马赫数1.3~3.5的实验，揭示了液滴在激波作用下出现压缩变形到破碎雾化的过程。发现入射激波马赫数较高时，液滴的压缩变形和破碎雾化几乎同时发生，液滴迅速形成薄雾状结构。C.Kauffman等[6]研究了燃料液滴在氧气环境中与激波相互作用的过程：在入射激波马赫数3~5的情况下，液滴的燃烧先发生在从原始液滴脱落的雾状燃料上，在激波扫过一段时间后，整个燃料的燃烧过程才会发生。A.Wierzba等[7]利用全息干涉技术研究了液滴在激波作用下的变形破碎过程，并把液滴脱落破碎分成4个阶段：压缩变形，横向直径增大至最大值，破碎雾化和横向直径减小至零。L.P.Hisang等[8-9]给出了在液滴破碎模式与We(Weber数)的关系：随着We从零开始增加，液滴会依次出现无变形、无振荡变形、振荡变形、袋式破碎、混合破碎和剪切破碎模式，并当We继续增加时会出现突发破碎(catastrophic breakup)情况。
陆守香等[10]研究了激波冲击后液滴变形和破碎的近似理论模型。耿继辉等[11]实验观测了液滴在激波作用下的加速、变形及破碎过程。蔡斌等[12]通过应用VOF方法和湍流模型对液滴在气流中的破碎过程进行了数值模拟，并分析了We、Oh(Ohnesorge数)以及气液密度比对液滴破碎过程的影响。姚雯等[13]通过求解二维Euler方程，并将表面张力转换为体积力，考察了激波流场中液滴变形与破碎过程。楼建峰等[14]将VOF方法和标准k-ε湍流模型组合，进行了液滴在气流中变形破碎过程的数值模拟，并分析了几个关键参数(Weber数、Ohnesorge数、气液密度比)对液滴破碎过程的影响。其结果表明，We对液滴变形破碎起促进作用，而Oh和液气密度比起阻碍抑制作用。
本文中，首先在水平激波管中进行激波与液滴作用的实验研究，然后利用数值模拟技术计算该实验条件下液滴破碎过程。再通过对比分析，详细描述液滴在激波作用下的变形破碎过程。
1. 实验方法
水平激波装置示意图如图 1所示。包括真空箱的激波管整体总长为12 m。激波发生系统由高压气瓶、圆形高压段、圆形低压段及方形低压段组成，实验段通过法兰与方形低压段及真空箱连接，两个压力传感器安装在方形低压段，用于测量激波马赫数。高速摄影仪放置在实验段的侧面，在实验段的前后侧板上装有透明的有机玻璃板，上、下板开有液滴下落入口和排液孔。实验段内截面尺寸为120 mm×120 mm，长为500 mm。在实验段上方的液滴下落入口插入不同直径的尖针，以便形成一个在实验段自由下落的直径可控的液滴。控制破膜时间，使入射激波刚好扫过下降的液滴，用高速摄影仪拍摄整个液滴的变形破碎过程。
2. 数学模型与计算方法
针对液滴在激波作用下的变形破碎，为了方便地模拟两相界面的变形情况，数值模拟中选用基于VOF模型的RANS方程，湍流模型使用标准k-ε双方程模型。其二维控制方程组为如下通用形式：
∂(ρϕ)∂t+∂(ρuϕ)∂x+∂(ρvϕ)∂y=∂∂x(Γϕ∂ϕ∂x)+∂∂y(Γϕ∂ϕ∂y)+Sϕ (1) 式中：ρ为两相平均密度，ρ=α1ρ1 + (1-α1)ρ2，其中α1、ρ1和ρ2分别表示气相质量分数、气相密度和液相密度；Φ为通用因变量，其取值为1、u(x方向速度)、v(y方向速度)、E(总能)、k(湍流动能)和ε(湍流耗散)时方程分别对应连续方程、动量方程、能量方程、湍流动能输运方程和湍流耗散方程；ΓΦ 为输运系数，包括黏性输运(根据气相质量分数加权计算[15])和湍流输运；SΦ为源项，主要为重力项、压力作用项、湍流作用项和相间相互作用项等组成。方程中各项具体表达式及参数取值可参见文献[15-16]。
根据液滴在气流中破碎的结构特点，选取了如图 2所示的计算区域。其中计算区域尺寸为2 cm×8 cm，液滴直径根据实验数据分别为1.64、2.16、2.46 mm。计算使用ANSYS Fluent软件中的Coupled求解器，数值离散使用二阶MUSCL格式，计算区域网格数目为42万。波后区域参数根据运动正激波解求得，也以此作为左边界入口边界参数，其他3个边界选自由出口边界。设定激波初始位置位于液滴前缘上游2 mm处。在与实验结果对比时，第1张图片的时刻均为激波通过后的0.125 ms。
3. 结果分析
实验采用We(Weber数)与Oh(Ohnesorge数)来分析液滴破碎变形，其具体计算公式分别为：We=ρau2d0/σw和O h=\mu_{\mathit{\boldsymbol{w}}} / \sqrt{\rho_{\mathit{\boldsymbol{w}}} d_{0} \sigma_{\mathit{\boldsymbol{w}}}}，We表示惯性了力和表面张力之比，Oh表示黏性力和表面张力之比。其中，ρa为空气密度，u为波后气流速度；ρw、σw和μw分别为液滴的密度、表面张力和动力黏度；d0为液滴的初始直径。实验和计算中各参数的具体数值，如表 1所示，表中Ma为入射激波马赫数。
表 1 实验参数Table 1. Experimental parameters实验 液滴 Ma d0/mm We Oh 1 水 1.10 1.64 94.48 0.002 9 2 水 1.10 2.16 124.44 0.002 6 3 水 1.10 2.46 141.72 0.002 4 4 水 1.25 1.68 518.75 0.002 9 5 甘油 1.10 2.46 167.23 3.450 0 实验1的实验与数值模拟结果如图 3(a)所示。左列为数值模拟结果，图示的是密度云图，右列为实验照片，上下两幅图时间间隔为0.25 ms。从图中可以看到，实验与计算的液滴变化趋势是相近的，从开始的压缩变形为一个薄圆盘状结构，其后液滴的横向直径增大，轴向直径降低；紧接着，薄圆盘状结构逐渐扩展，更细小的液滴从上下两端不断脱落，原始的球形液滴演化成了云团状，并继续沿横向和轴向扩张。由前4幅对比可以看出，激波作用后刚开始数值模拟中液滴的横向变形没有实验中的剧烈，仍显得比较“胖”，第4幅左图数值模拟结果也就没能出现类似右图中的细棍状结构。最后两张对比图片中，虽然大致上两者的雾化扩张类似，但是，数值模拟中液滴中间已经只剩下一个点状水粒，而实验照片显示液滴中间是被打散的极小液滴密集而成的云团结构。最后一张对比图中，可以明显看到实验中液滴已经雾化成云团，而数值模拟结果仍然显示液滴有未破碎的内核存在，这是因为VOF模型中没有加入液滴的破碎机制。
图 3 实验1~3的数值模拟结果(左)与实验照片(右)(Δt=0.25 ms)Figure 3. Numerical simulation (left) and experimental (right) results of experiments 1-3图 3(b)给出了实验2的数值模拟结果和实验结果。由图可以明显看出，数值模拟的液滴变形演变速度比实验的慢。与图 3(a)不同，在图 3(b)的最后一幅图中，两相界面上出现了尖钉和气泡，这是RM不稳定性作用的结果。因为当初始液滴的直径增大时，由于液滴的体积和质量更大，其破碎变形肯定比小直径的液滴慢，所以在图 3(a)中液滴还没来得及出现RM不稳定的结构就破碎了。
图 3(c)给出了实验3的数值结果和实验结果。在前5幅图中，液滴的变化和实验照片一致。在第6幅图中，计算与实验结果都出现了RM不稳定性引起的尖钉和气泡结构，计算结果中向左侧突起的尖钉结构比较明显，而实验结果的右侧包裹有明显的气泡结构，可是计算与实验中液滴的横向直径增加趋势仍然是一致的。实验结果的前4幅图中，液滴中偏左位置的白色圆孔不是气泡结构，而是由于液滴反光造成的拍摄干扰。
图 4给出了液滴横向直径与初始直径之比d/d0随时间的变化关系。在激波作用后液滴变形的初始线性增长阶段和中期非线性发展阶段，数值结果与实验结果符合很好，而在后期的破碎发展阶段，数值结果与实验结果偏离。尤其是实验1中最后一组数据，实验观测到液滴核心的横向直径已经因液滴周围突发破碎而减小，而数值结果则相反，原因是数值计算中没有加入突发破碎模型。
图 4 实验1~3液滴横向直径与初始直径之比Figure 4. Ratio of transverse diameter andinitial diameter of experiments 1-3图 5给出了实验4的数值计算和实验结果对比图。实验4与实验1具有相同的Oh，而两者的We差别较大。从实验中可以看出，在激波扫过后，液滴几乎没有出现明显的压缩变形就发生突然破碎，这说明随着We增大到一定程度，液滴的破碎模式发生了根本性改变：We较小时液滴经历由变形到破碎的剪切破碎模式，而当We增大到一定值时，为突发破碎模式。一般而言，破碎模式的临界We在500左右，本文中实验也验证了这一点。图 5中的计算结果没有出现液滴突发破碎模式，说明在数值模拟中应该加入突发破碎的机制，而其他研究者还没有指出这一点。
图 5 实验4的数值模拟结果(左)与实验照片(右)(Δt=0.25 ms)Figure 5. Numerical simulation (left) andexperimental (right) results of experiment 4综合上面的讨论可知，当Oh相同时，We越大，破碎速度越快。实验1的液滴经过1.5 ms后，横向直径才达到最大而开始裂解破碎。而实验4的液滴经过0.25 ms，就完成了横向扩张，开始裂解破碎。这表明We在液滴破碎过程中加强了液滴的不稳定，为不稳定因素。
为了得到相同We条件下，不同Oh对液滴变形和破碎的影响，对实验5进行了模拟计算，其We与实验3相近，而Oh则相差较大，结果如图 6所示。甘油液滴从初始变形上就不同于水滴，甘油液滴在波后气流的作用下，先是迎风面开始扁平化，背风面仍然保持原先的半圆状结构，同时两侧也在伸长，但后部的弧形结构明显很完整。相对而言，水滴受到波后气流作用下，其右侧半圆结构很快向内凹陷，形成开口状结构。这两个明显的差异，应该是由于甘油的黏性系数远大于水的黏性系数而造成。相同初始直径的水滴，在实验3的模拟结果中，刚到第4张图就可以观察到，水滴的微滴剥离非常明显，并且在后续图片中，已经出现了表示RM不稳定性的尖钉状结构。而在图 6中，随着甘油液滴横向扩张结束，两翼开始向后弯曲变形，但整体结构仍然保持完整，没有出现大规模的微滴剥离。并且在数值模拟结果中，整体液滴的变形演化速度慢于水滴。由此可见，Oh的减小使破碎速度显著加快，说明Oh对破碎起抑制作用。
图 7为实验3(水滴)与实验5(甘油液滴)的数值计算结果的涡量云图对比图。由图可以看出，甘油液滴算例中的涡量从开始就处于不对称的状态，之后出现了类似于卡门涡街的现象，不断有涡旋一上一下地从液滴后方脱落，向下游传播，一直持续到液滴大规模破碎为止。水滴的算例中则没有这个现象。这是因为甘油的黏性远大于水滴的黏性，其破碎速度比水滴的慢很多。
4. 结论
实验观测和数值计算结果表明：(1)液滴在激波的作用下，要经历从压缩变形、RM不稳定性变形、细小液雾剥离到雾化破碎等过程。不同参数下的结果显示，液滴变形破碎的发展趋势一致，但发展速度明显不同。数值模拟结果与实验结果基本吻合。(2)实验数据与数值模拟结果显示，在液滴破碎过程中We的增加促进液滴的破碎，为不稳定因素。当We增加到一定值后，液滴破碎模式由剪切破碎转变为突发破碎。Oh的增加对液滴的破碎起抑制作用，黏性同样会抑制液滴的破碎。
对比分析指出，在液滴变形的初期及中期，数值计算与实验结果吻合较好。在液滴变形的后期，需要在数值计算中考虑雾化模型；而随着激波马赫数的提高，还要考虑突发破碎机制，其中包括激波冲击气/液界面引起的扰动。根据计算的速度云图[17]，可知液滴的上下承受着高剪应力(由速度梯度造成)，所以液滴的变形破碎不仅与RM不稳定性有关，还与Kelvin-Helmholtz(KH)不稳定性有关。图 6~7所示的对甘油液滴的计算结果，对于寻找RM不稳定性的实验方法有重要参考价值，即如果使用黏弹性流体(如果冻)，那就应该考虑增加激波强度，以保证其本构方程与Navier-Stokes方程相似。
-
图 1
\varnothing 50 mm分离式霍普金森压杆试验系统Figure 1.
\varnothing 50 mm split Hopkinson pressure bar system
图 2 典型动态巴西圆盘实验动态应力平衡验证
Figure 2. Verification of dynamic stress balance in typical Dynamic BD test
图 3 试样起裂监测应变片粘贴位置
Figure 3. Schematics of a strain gauge cemented on the specimen for detecting failure onset
图 4 180 GPa/s加载率工况圆盘应力过载修正
Figure 4. The overload correction for specimen’s tensile stress under 180 GPa/s loading rate
图 5 418 GPa/s加载率工况圆盘应力过载修正
Figure 5. The overload correction for specimen’s tensile stress under 418 GPa/s loading rate
图 8
\varnothing 50 mm的SHPB数值实验系统Figure 8.
\varnothing 50 mm split Hopkinson pressure bar numerical system
图 9 实验与模拟入射波波形对照
Figure 9. Incident wave comparison between lab experiment and numerical simulation
图 10 实验与模拟名义拉伸强度的率效应
Figure 10. The rate dependency for experimental and numerical nominal tensile stress
图 11 不同加载率下实验与模拟圆盘的拉伸应力
Figure 11. Experimental and numerical tensile stress under different loading rates
图 12 典型数值模拟动态应力平衡验证
Figure 12. Verification of dynamic stress balance in typical numerical dynamic BD test
图 14 375 GPa/s加载率实验与模拟破坏模式
Figure 14. Experimental and numerical disk failure pattern under 375 GPa/s loading rate
图 15 1021 GPa/s加载率实验与模拟破坏模式
Figure 15. Experimental and numerical disk failure pattern under 1021 GPa/s loading rate
图 16 345.3 GPa/s加载率工况模拟结果过载修正
Figure 16. The overload correction for numerical tensile stress under 345.3 GPa/s loading rate
图 17 实验与数值模拟动态巴西劈裂实验过载比
Figure 17. Experimental and numerical overload ratio for dynamic BD tests
图 18 609.6 GPa/s加载工况数值模拟中的过载现象以及圆盘破坏过程
Figure 18. The overload phenomenon and the failure process of numerical specimen under 609.6 GPa/s loading rate
表 1 动态巴西圆盘实验结果
Table 1. Dynamic BD experimental results
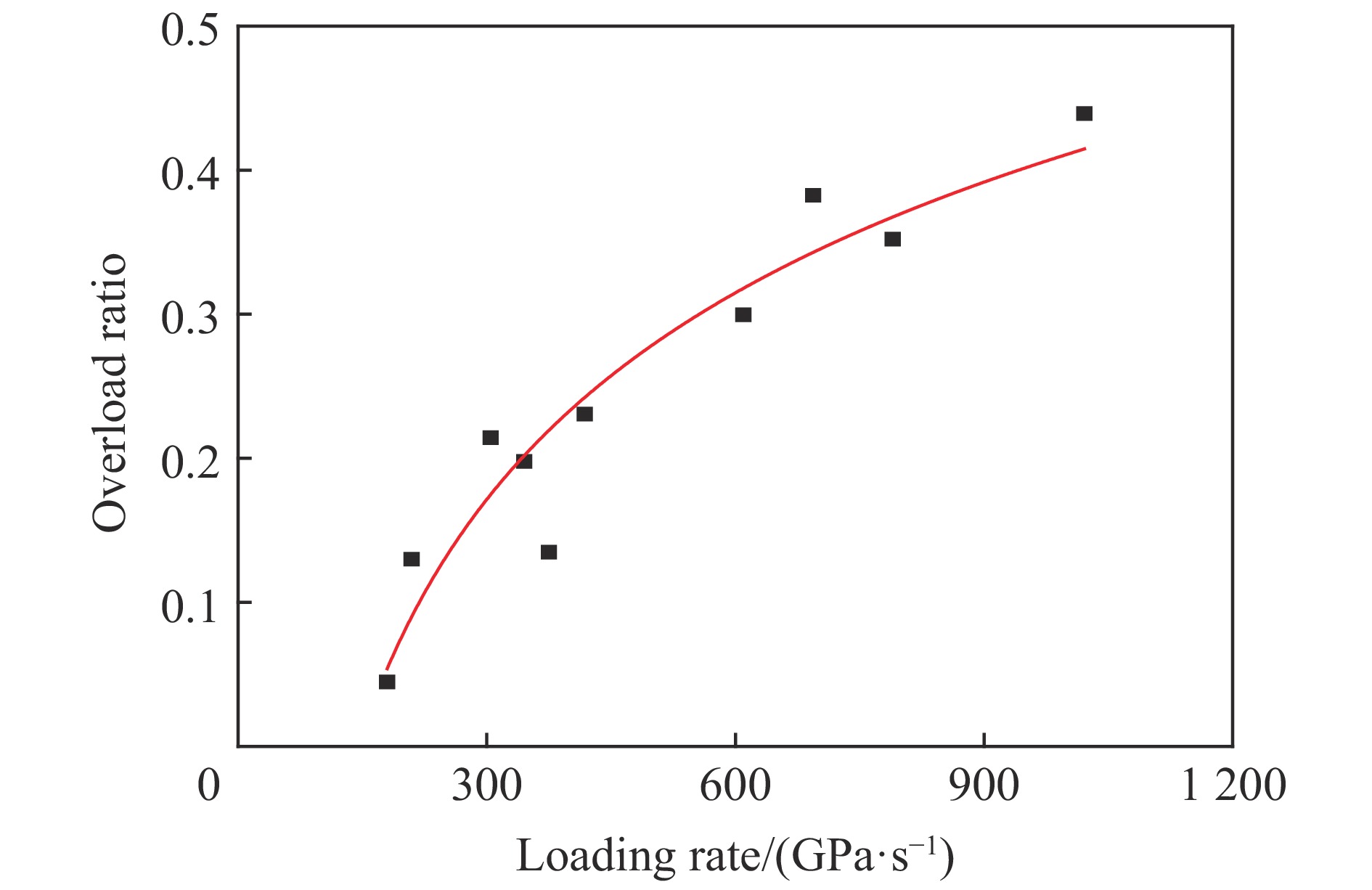
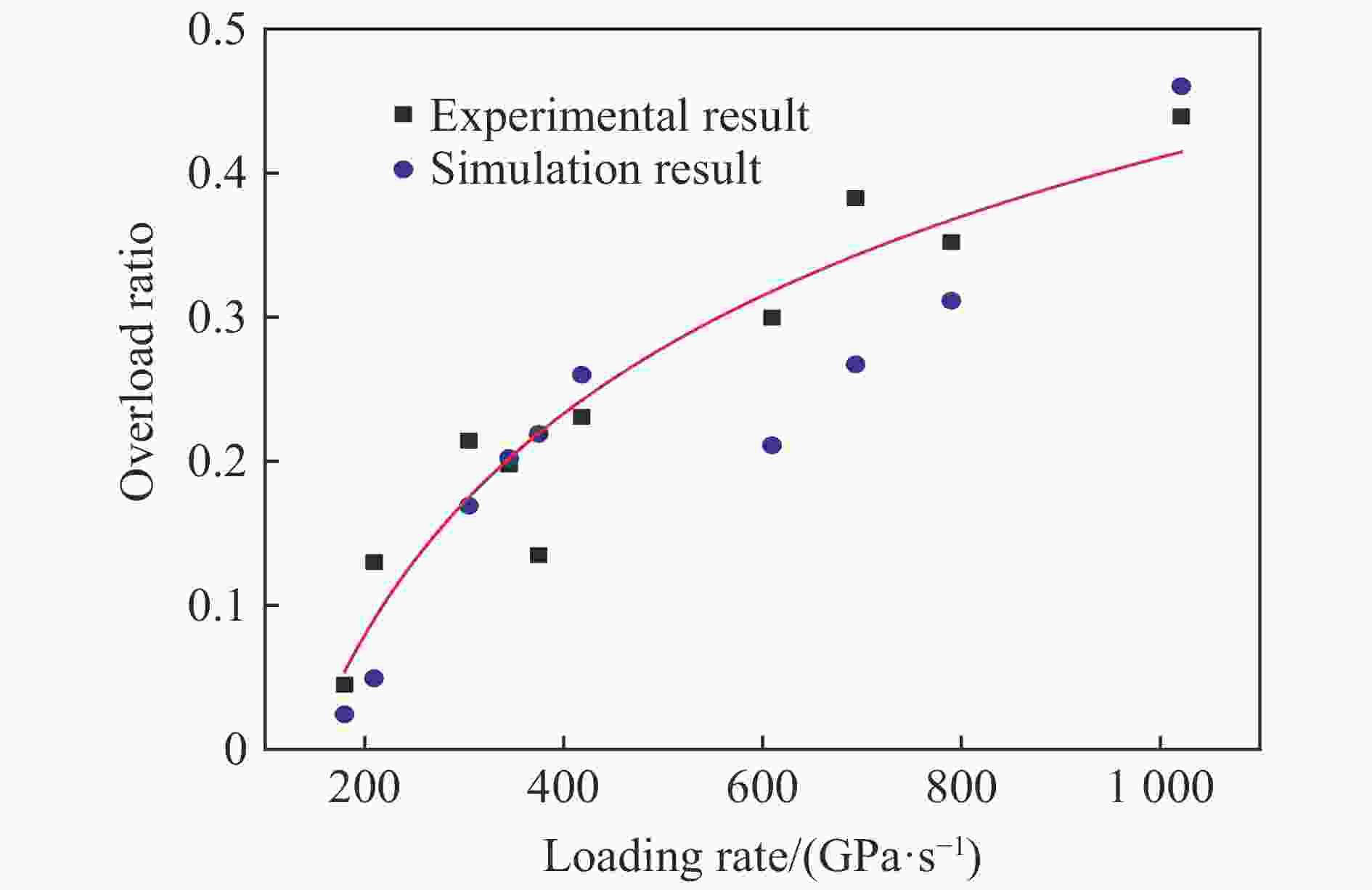
加载率/（GPa·s−1） 名义拉伸强度/MPa 真实拉伸强度/MPa 过载时间/μs 过载比 179.9 20.36 19.49 4.72 0.045 209.5 21.84 19.33 10.96 0.130 304.8 22.20 18.28 16.50 0.213 345.3 21.20 17.70 15.28 0.198 375.0 21.90 19.30 10.64 0.135 418.4 25.30 20.56 13.76 0.231 609.6 30.80 23.70 12.72 0.300 693.8 30.00 21.70 13.28 0.383 790.0 30.02 22.20 10.08 0.352 1 021.2 37.30 25.92 16.80 0.439 
下载: 导出CSV
表 2 试样主要模型微观参数
Table 2. Parameters of the numerical specimen
密度/
（kg·m−3）颗粒刚
度比黏结刚
度比颗粒变形
模量/GPa黏结变形
模量/GPa拉伸黏结
强度/MPa内聚力/
MPa摩擦角/
（°）2 800 1.403 1.403 19.70 19.70 23 23 45
下载: 导出CSV
表 3 杆件主要模型微观参数
Table 3. Parameters of the numerical bar
密度/
（kg·m−3）颗粒刚
度比黏结刚
度比颗粒变形
模量/GPa黏结变形
模量/GPa拉伸黏结
强度/MPa剪切黏结
强度/MPa7 800 1 1 200 200 10100 10100
下载: 导出CSV
表 4 模型宏观参数与材料宏观参数对比
Table 4. Macroscopic parameters of the numerical model and real rock
模型/材料 泊松比 弹性模量/GPa 名义拉伸强度/MPa 数值模型 0.19 41.45 11.24 真实材料 0.124～0.218 38.774～46.593 9.788～12.268
下载: 导出CSV
-
[1] 章奇锋, 周春宏, 周辉, 等. 锦屏Ⅱ水电站辅助洞岩爆灾害评价及对策研究 [J]. 岩土力学, 2009, 30(S2): 422–426, 445. DOI: 10.16285/j.rsm.2009.s2.045.ZHANG Q F, ZHOU C H, ZHOU H, et al. Research on rock burst estimation and control measures for auxiliary tunnels in Jinping Ⅱ hydropower station [J]. Rock and Soil Mechanics, 2009, 30(S2): 422–426, 445. DOI: 10.16285/j.rsm.2009.s2.045. [2] ZHOU Y X, XIA K, LI X B, et al. Suggested methods for determining the dynamic strength parameters and Mode-I fracture toughness of rock materials [M]// ULUSAY R. The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007-2014. Cham: Springer International Publishing, 2015: 35−44. DOI: 10.1007/978-3-319-07713-0_3. [3] ZHANG Q B, ZHAO J. A review of dynamic experimental techniques and mechanical behaviour of rock materials [J]. Rock Mechanics and Rock Engineering, 2014, 47(4): 1411–1478. DOI: 10.1007/s00603-013-0463-y. [4] ULUSAY R, AND HUDSON J A. Suggested methods for determining tensile strength of rock materials [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1978, 15(3): 99–103. DOI: 10.1016/0148-9062(78)90003-7. [5] HUDSON J A. Tensile strength and the ring test [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1969, 6(1): 91–97. DOI: 10.1016/0148-9062(69)90029-1. [6] ZHAO J, LI H B. Experimental determination of dynamic tensile properties of a granite [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(5): 861–866. DOI: 10.1016/S1365-1609(00)00015-0. [7] LUONG M P. Tensile and shear strengths of concrete and rock [J]. Engineering Fracture Mechanics, 1990, 35(1−3): 127–135. DOI: 10.1016/0013-7944(90)90190-R. [8] HONDROS G. The evaluation of Poisson’s ratio and the modules of materials of a low tensile resistance by the Brazilian (indirect tensile) test with particular reference to concrete [J]. Australian Journal of Applied Science, 1959, 10: 243–268. [9] ROSS C A, THOMPSON P Y, TEDESCO J W. Split-hopkinson pressure-bar tests on concrete and mortar in tension and compression [J]. Materials Journal, 1989, 86(5): 475–481. DOI: 10.14359/2065. [10] 陈登平, 王永刚, 贺红亮, 等. 强角闪石化橄榄二辉岩的动态拉伸强度实验研究 [J]. 爆炸与冲击, 2005, 25(6): 559–563. DOI: 10.11883/1001-1455(2005)06-0559-05.CHEN D P, WANG Y G, HE H L, et al. Dynamic tensile strength of amphibolized olivine websterite (AOW) rock [J]. Explosion and Shock Waves, 2005, 25(6): 559–563. DOI: 10.11883/1001-1455(2005)06-0559-05. [11] XIA K W, YAO W, WU B B. Dynamic rock tensile strengths of Laurentian granite: experimental observation and micromechanical model [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2017, 9(1): 116–124. DOI: 10.1016/j.jrmge.2016.08.007. [12] WU B B, CHEN R, XIA K W. Dynamic tensile failure of rocks under static pre-tension [J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 80: 12–18. DOI: 10.1016/j.ijrmms.2015.09.003. [13] MELLOR M, HAWKES I. Measurement of tensile strength by diametral compression of discs and annuli [J]. Engineering Geology, 1971, 5(3): 173–225. DOI: 10.1016/0013-7952(71)90001-9. [14] FREW D J, FORRESTAL M J, CHEN W. Pulse shaping techniques for testing elastic-plastic materials with a split Hopkinson pressure bar [J]. Experimental Mechanics, 2005, 45(2): 186. DOI: 10.1007/BF02428192. [15] 李夕兵, 古德生, 赖海辉. 冲击载荷下岩石动态应力-应变全图测试中的合理加载波形 [J]. 爆炸与冲击, 1993, 13(2): 125–130.LI X B, GU D S, LAI H H. On the reasonable loading stress waveforms determined by dynamic stress-strain curves of rocks by SHPB [J]. Explosion and Shock Waves, 1993, 13(2): 125–130. [16] DAI F, HUANG S, XIA K W, et al. Some fundamental issues in dynamic compression and tension tests of rocks using split hopkinson pressure bar [J]. Rock Mechanics and Rock Engineering, 2010, 43(6): 657–666. DOI: 10.1007/s00603-010-0091-8. [17] JIANG F C, LIU R T, ZHANG X X, et al. Evaluation of dynamic fracture toughness KId by Hopkinson pressure bar loaded instrumented Charpy impact test [J]. Engineering Fracture Mechanics, 2004, 71(3): 279–287. DOI: 10.1016/S0013-7944(03)00139-5. [18] SHI C, YANG W K, YANG J X, et al. Calibration of micro-scaled mechanical parameters of granite based on a bonded-particle model with 2D particle flow code [J]. Granular Matter, 2019, 21(2): 38. DOI: 10.1007/s10035-019-0889-3. [19] YANG J X, SHI C, YANG W K, et al. Numerical simulation of column charge explosive in rock masses with particle flow code [J]. Granular Matter, 2019, 21(4): 96. DOI: 10.1007/s10035-019-0950-2. [20] ZHOU Z L, LI X B, ZOU Y, et al. Dynamic brazilian tests of granite under coupled static and dynamic loads [J]. Rock Mechanics and Rock Engineering, 2014, 47(2): 495–505. DOI: 10.1007/s00603-013-0441-4. -
下载:
计量
- 文章访问数: 960
- HTML全文浏览量: 368
- PDF下载量: 144
- 被引次数: 0