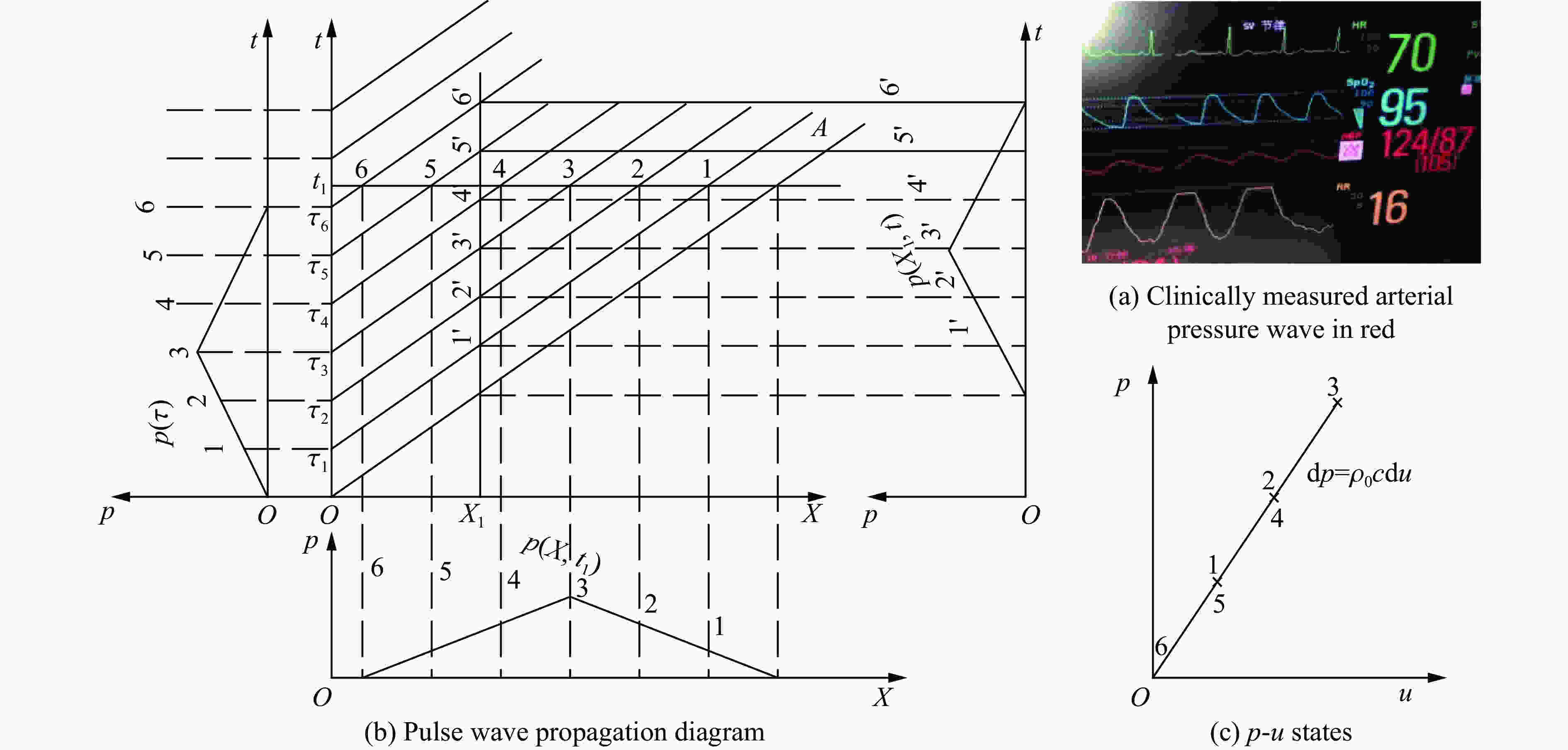
| [1] |
孙庆伟, 王春梅, 高艳华, 等. 医用生理学[M]. 北京: 中国医药科技出版社, 2000.
|
| [2] |
朱思明. 医用生理学[M]. 北京: 北京科学出版社, 2002.
|
| [3] |
HALL J E. Guyton and Hall textbook of medical physiology [M]. Philadelphia: Elsevier, 2016.
|
| [4] |
BARRETT K E, BARMAN S M, BROOKS H L, et al. Ganong’s review of medical physiology [M]. 26th ed. New York: McGraw-Hill Education, 2019.
|
| [5] |
SALVI P. Pulse waves: how vascular hemodynamics affects blood pressure [M]. 2nd ed. Cham: Springer, 2017.
|
| [6] |
EULER L. Principia pro motu sanguinis per arterias determinando [M]. Opera Postuma, 1862: 814−823.
|
| [7] |
SKALAK R, KELLER S R, SECOMB T W. Mechanics of blood flow [J]. Journal of Biomechanical Engineering, 1981, 103(2): 102–115. DOI: 10.1115/1.3138253.
|
| [8] |
孙广仁. 中医基础理论[M]. 北京: 中国中医药出版社, 2002.
|
| [9] |
WANG L L, WANG H. Mechanics modeling and inverse analyses of pulse wave system from the view-point of traditional Chinese medicine [C] // Proceedings of the ASME 2016, 35th International Conference on Ocean, Offshore and Arctic Engineering. Busan, South Korea: ASME, 2016. DOI: 10.1115/OMAE2016-55106.
|
| [10] |
王礼立, 王晖. 脉搏波系统的力学模型及反演兼对若干中医学问题的讨论 [J]. 力学学报, 2016, 48(6): 1416–1424. DOI: 10.6052/0459-1879-15-322.WANG L L, WANG H. Mechanics modeling and inverse analyses of pulse waves system with discussions on some concepts in the traditional Chinese medicine [J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(6): 1416–1424. DOI: 10.6052/0459-1879-15-322.
|
| [11] |
王礼立, 王晖, 杨黎明, 等. 论脉搏波客观化和定量化研究的症结所在 [J]. 中华中医药杂志, 2017, 32(11): 4855–4863. DOI: CNKI:SUN:BXYY.0.2017-11-020.WANG L L, WANG H, YANG L M, et al. Crux of objectification and quantification of pulse waves [J]. China Journal of Traditional Chinese Medicine and Pharmacy, 2017, 32(11): 4855–4863. DOI: CNKI:SUN:BXYY.0.2017-11-020.
|
| [12] |
王唯工. 气血的弦律[M]. 台北: 大塊文化, 2010.
|
| [13] |
王礼立. 应力波基础[M]. 2版. 北京: 国防工业出版社, 2005.WANG L L. Foundation of stress waves [M]. 2nd ed. Beijing: National Defense Industry Press, 2005.
|
| [14] |
COTTER G, WILLIAMS S G, VERED Z, et al. Role of cardiac power in heart failure [J]. Current Opinion in Cardiology, 2003, 18(3): 215–222. DOI: 10.1097/00001573-200305000-00007.
|
| [15] |
ASKARI A T, MESSERLI A W. Cardiovascular hemodynamics: an introductory guide [M]. New York: Humana Press, 2019.
|
| [16] |
FUSTER R, O’ROURKE R, WALSH R, et al. Hurst’s the heart [M]. 12th ed. New York: The McGraw-Hill Companies, Inc, 2008.
|
| [17] |
NOSÉ Y, YOSHIKAWA M, MURABAYASHI S, et al. Development of rotary blood pump technology: past, present, and future [J]. Artificial Organs, 2000, 24(6): 412–420. DOI: 10.1046/j.1525-1594.2000.06634.x.
|
| [18] |
NOSÉ Y, MOTOMURA T. Is it a mistake to develop a totally implantable blood pump for destination therapy? [J]. Artificial Organs, 2005, 29(2): 93–94. DOI: 10.1111/j.1525-1594.2005.29031.x.
|
| [19] |
BEHBAHANI M, BEHR M, HORMES M, et al. A review of computational fluid dynamics analysis of blood pumps [J]. European Journal of Applied Mathematics, 2009, 20(4): 363–397. DOI: 10.1017/S0956792509007839.
|
| [20] |
NICHOLS W W, O'ROURKE M, VLACHOPOULOS C. McDonald’s blood flow in arteries: theoretical, experimental and clinical principles [M]. 6th ed. London: CRC Press, 2011.
|
| [21] |
缪馥星, 王晖, 王礼立, 等. 血液-血管耦合特性与脉搏波传播特性的关系 [J]. 爆炸与冲击, 2020, 40(4): 031101. DOI: 10.11883/bzycj-2020-0082.MIAO Fuxing, WANG Hui, WANG Lili, et al. Relationship between the blood-vessel coupling characteristics and the propagation of pulse waves [J]. Explosion and Shock Waves, 2020, 40(4): 031101. DOI: 10.11883/bzycj-2020-0082.
|
| [22] |
WANG LIN Y Y, WANG W K. A hemodynamics model to study the collective behavior of the ventricular-arterial system [J]. Journal of Applied Physics, 2013, 113(2): 024702. DOI: 10.1063/1.4775754.
|
| [23] |
WEBSTER J G. Design of pulse oximeters [M]. London: CRC Press, 1997.
|






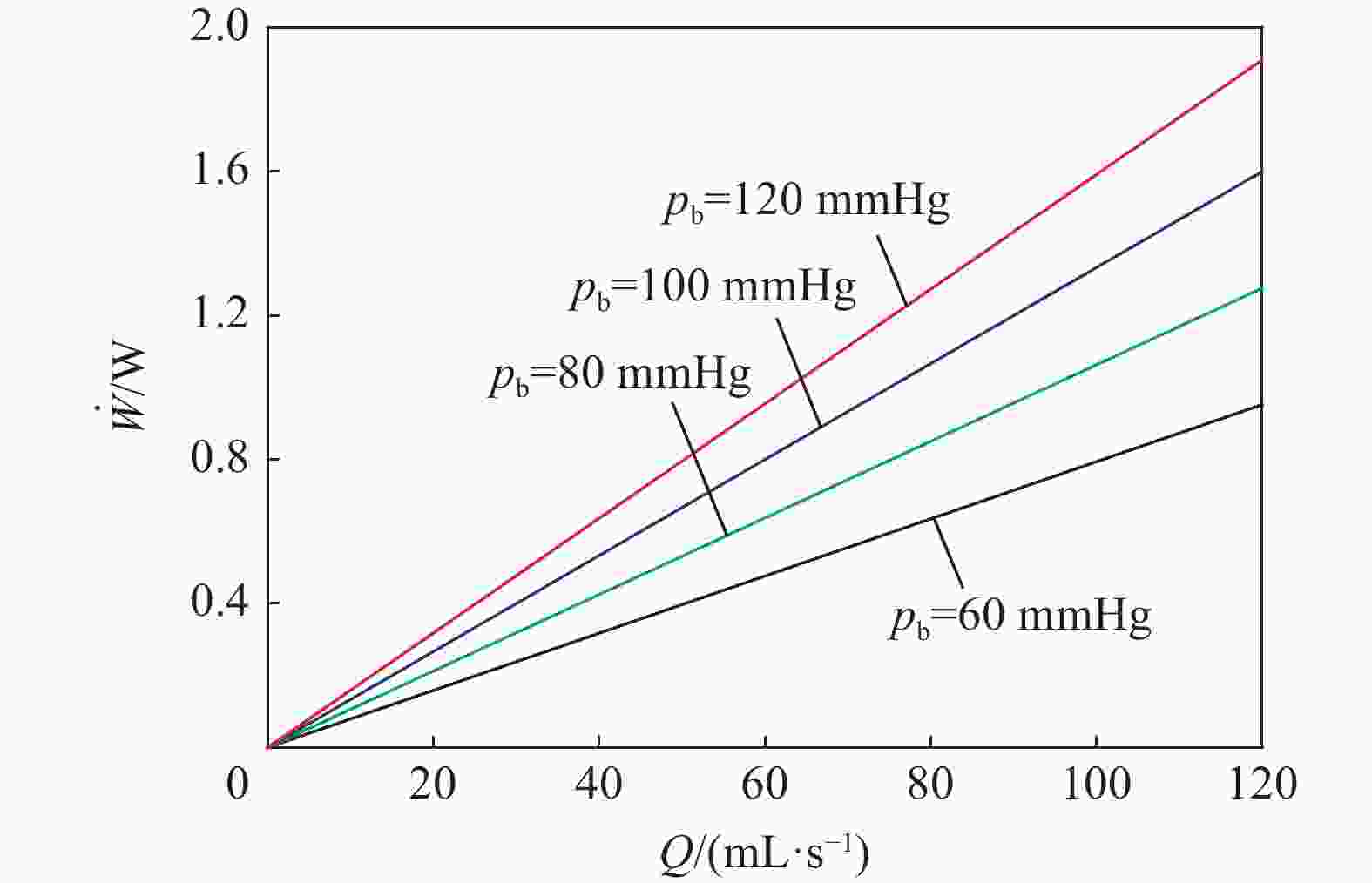
 下载:
下载: