空腔膨胀理论靶体阻力模型及其应用研究进展

刘均伟; 张先锋; 刘闯; 陈海华; 熊玮; 谈梦婷

doi:10.11883/bzycj-2021-0010

空腔膨胀理论靶体阻力模型及其应用研究进展

doi: 10.11883/bzycj-2021-0010

南京理工大学机械工程学院，江苏南京 210094

基金项目: 国家自然科学基金面上项目(11772159)；国家自然科学基金(11790292)

详细信息

作者简介:
刘均伟（1996－　），男，博士研究生，liujunwei@njust.edu.cn

通讯作者:
张先锋（1978－　），男，博士，教授，博士生导师，lynx@njust.edu.cn

中图分类号: O382；TJ410
计量
- 文章访问数: 1257
- HTML全文浏览量: 888
- PDF下载量: 302
- 被引次数: 0
出版历程
- 收稿日期: 2021-01-06
- 修回日期: 2021-04-12
- 网络出版日期: 2021-09-06
- 刊出日期: 2021-10-13

Research progress of target resistance model of cavity expansion theory and its application

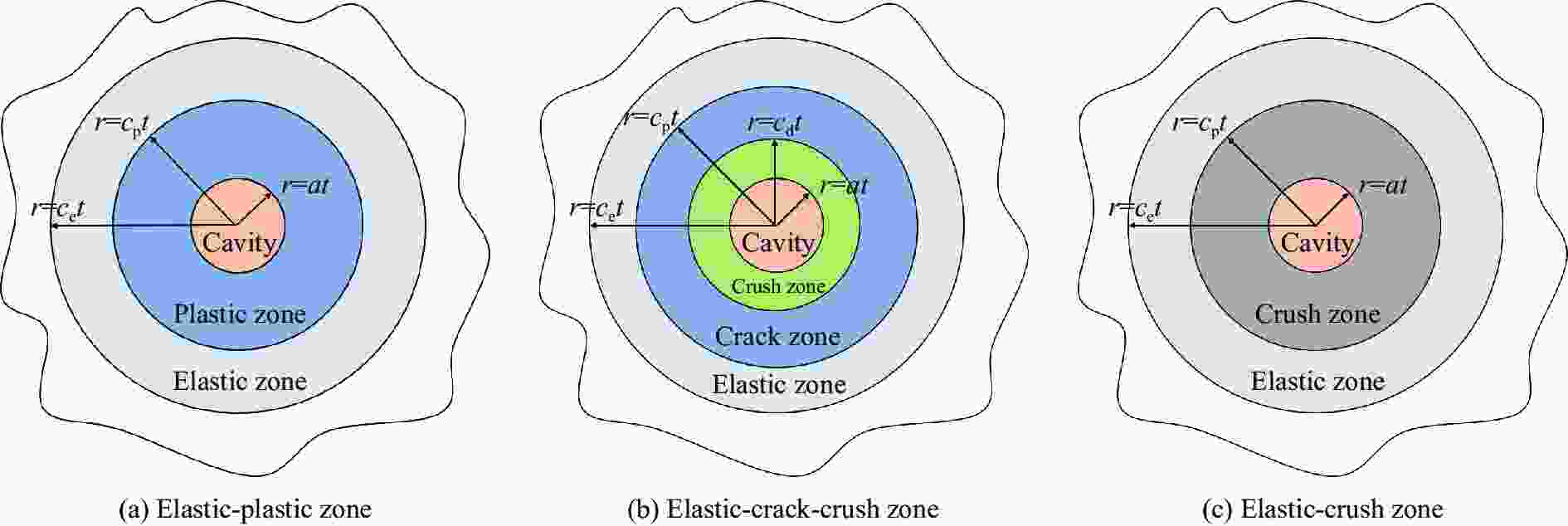
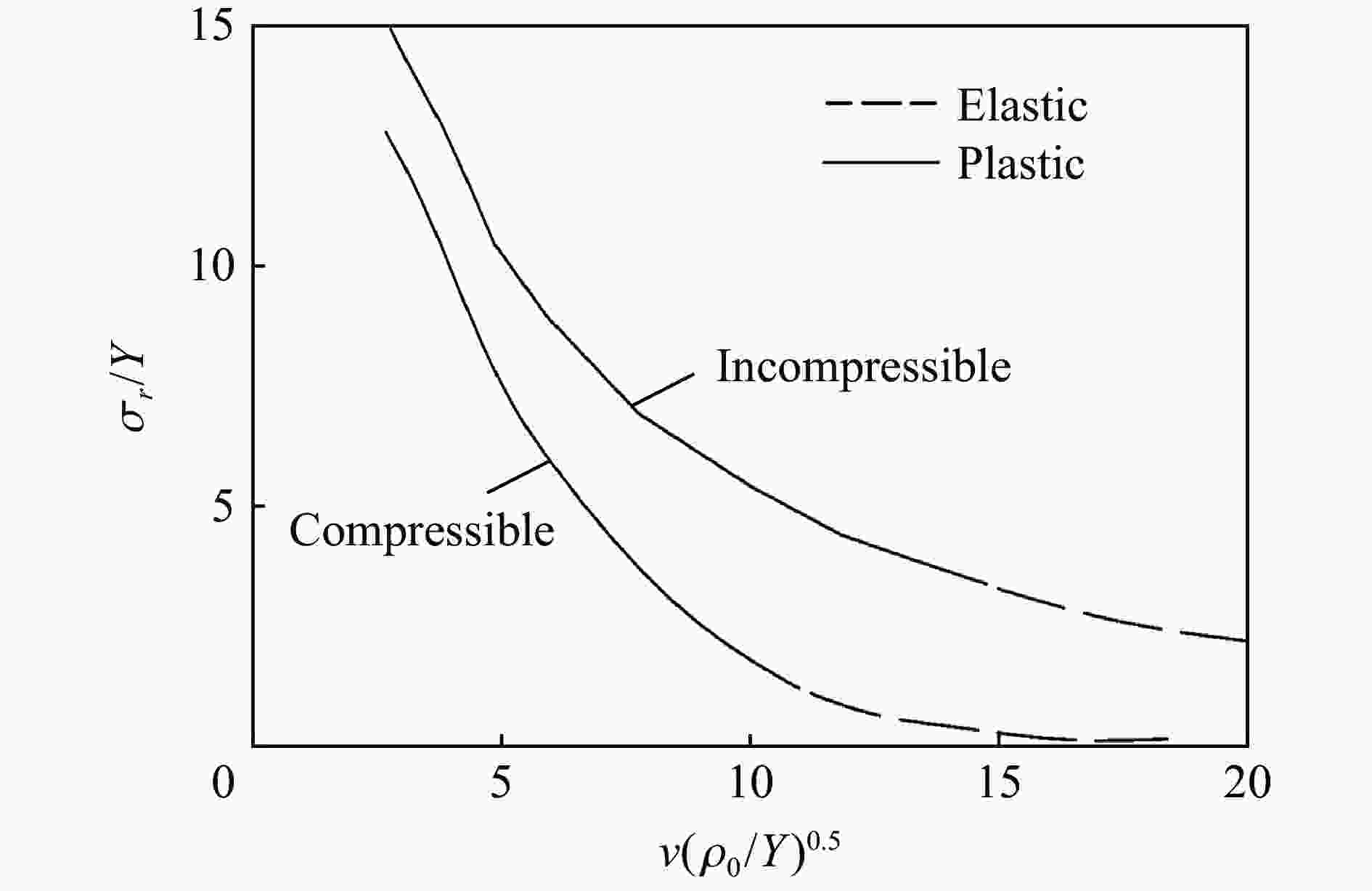
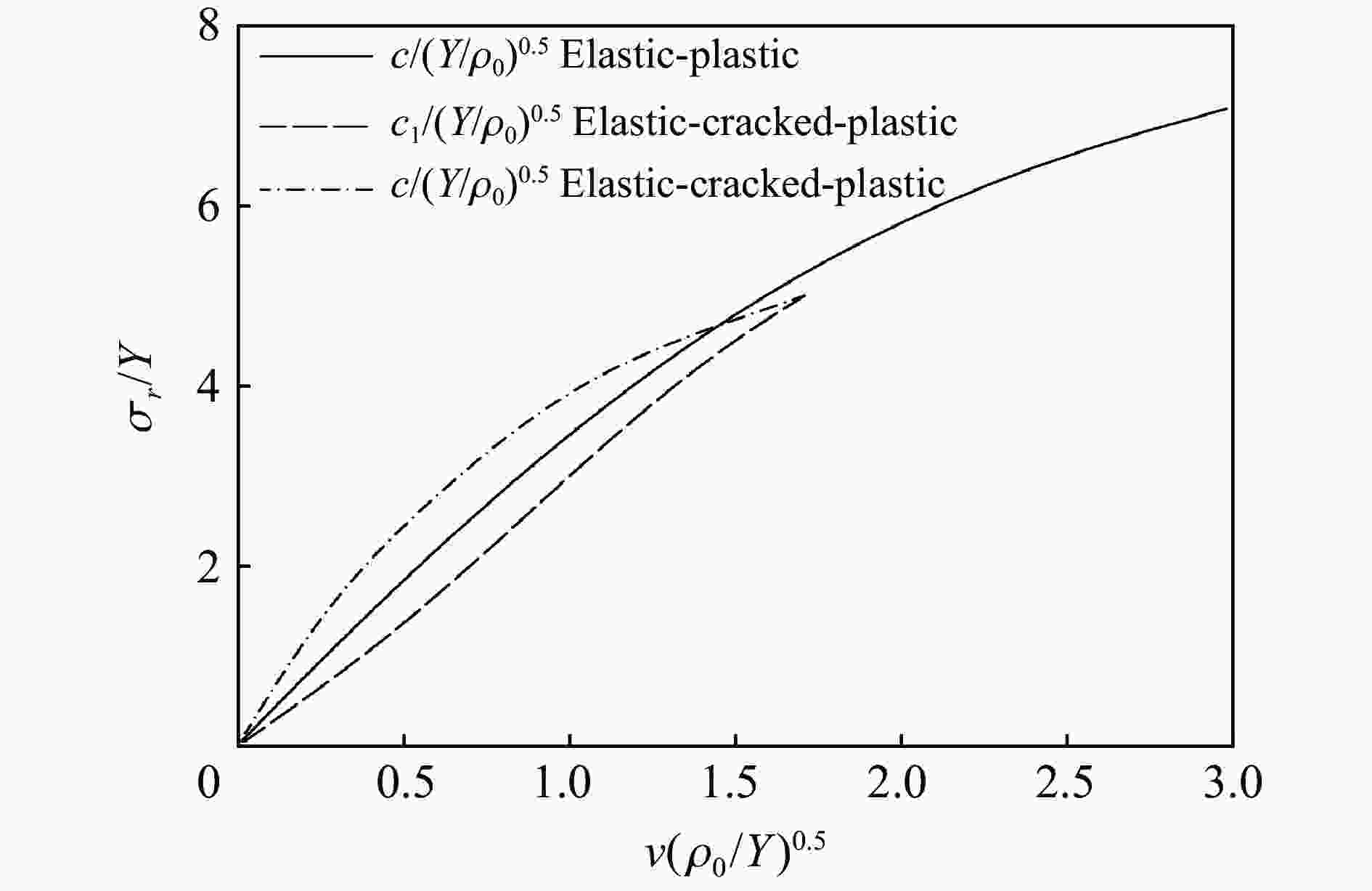
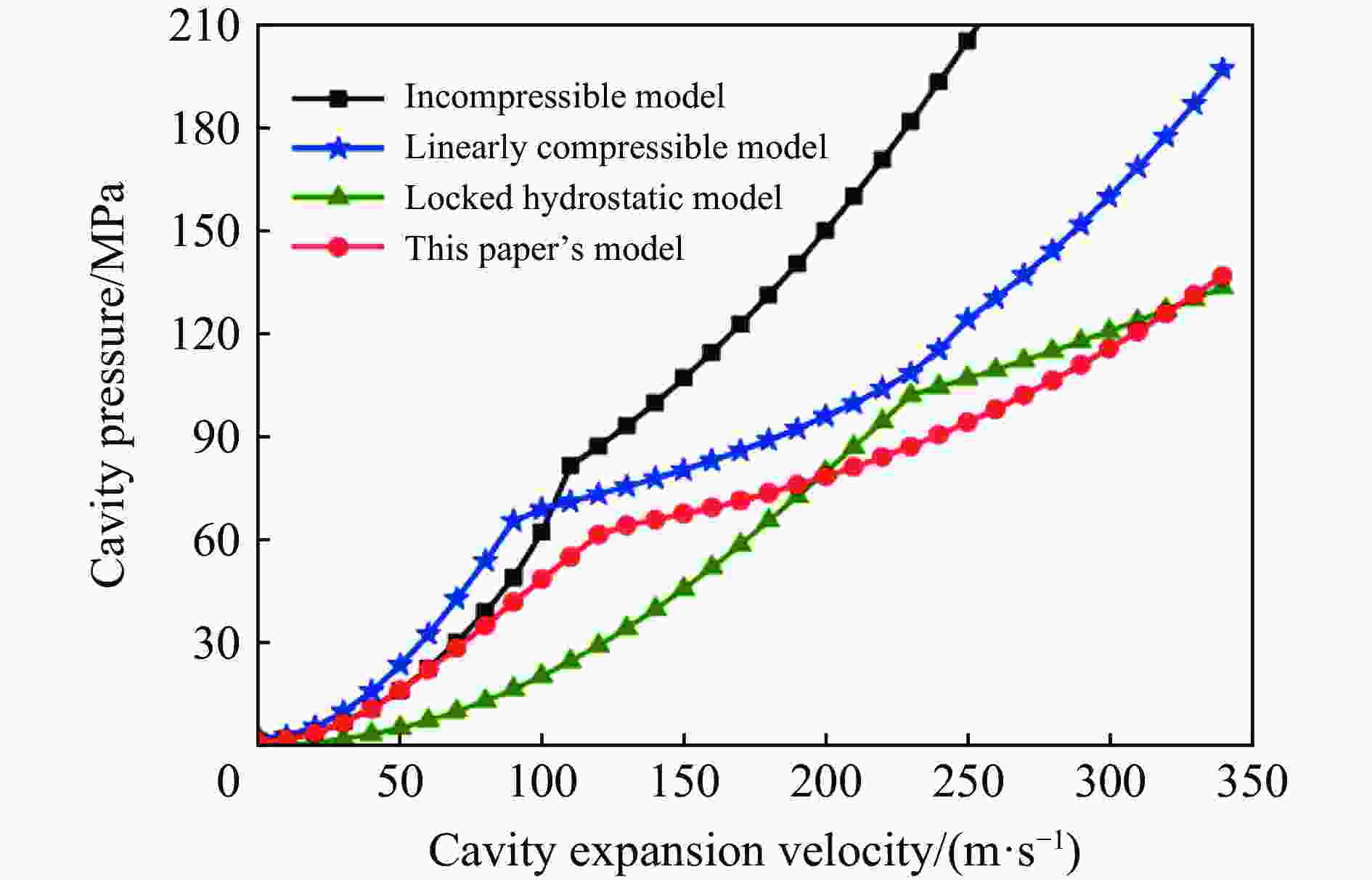
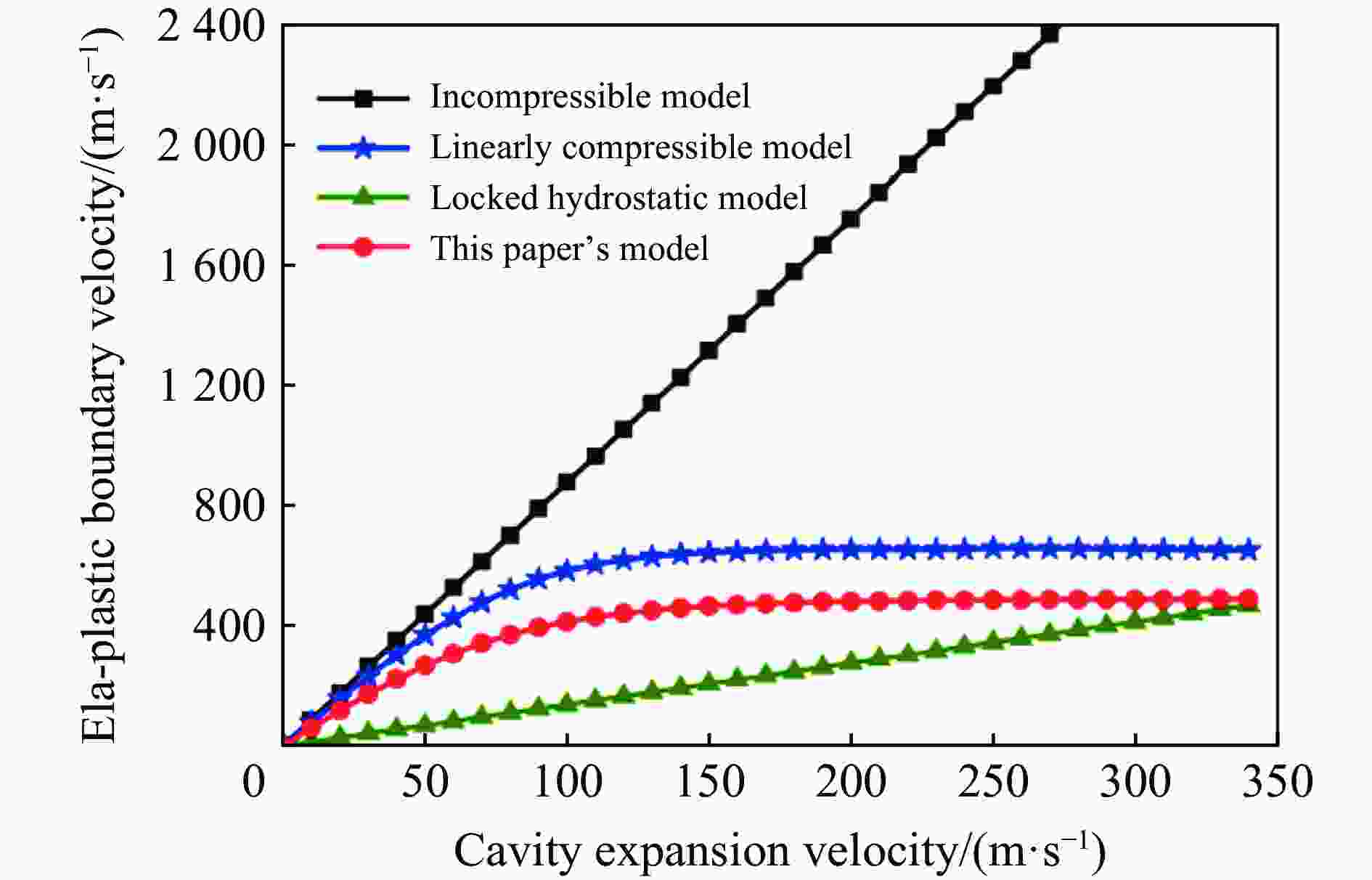
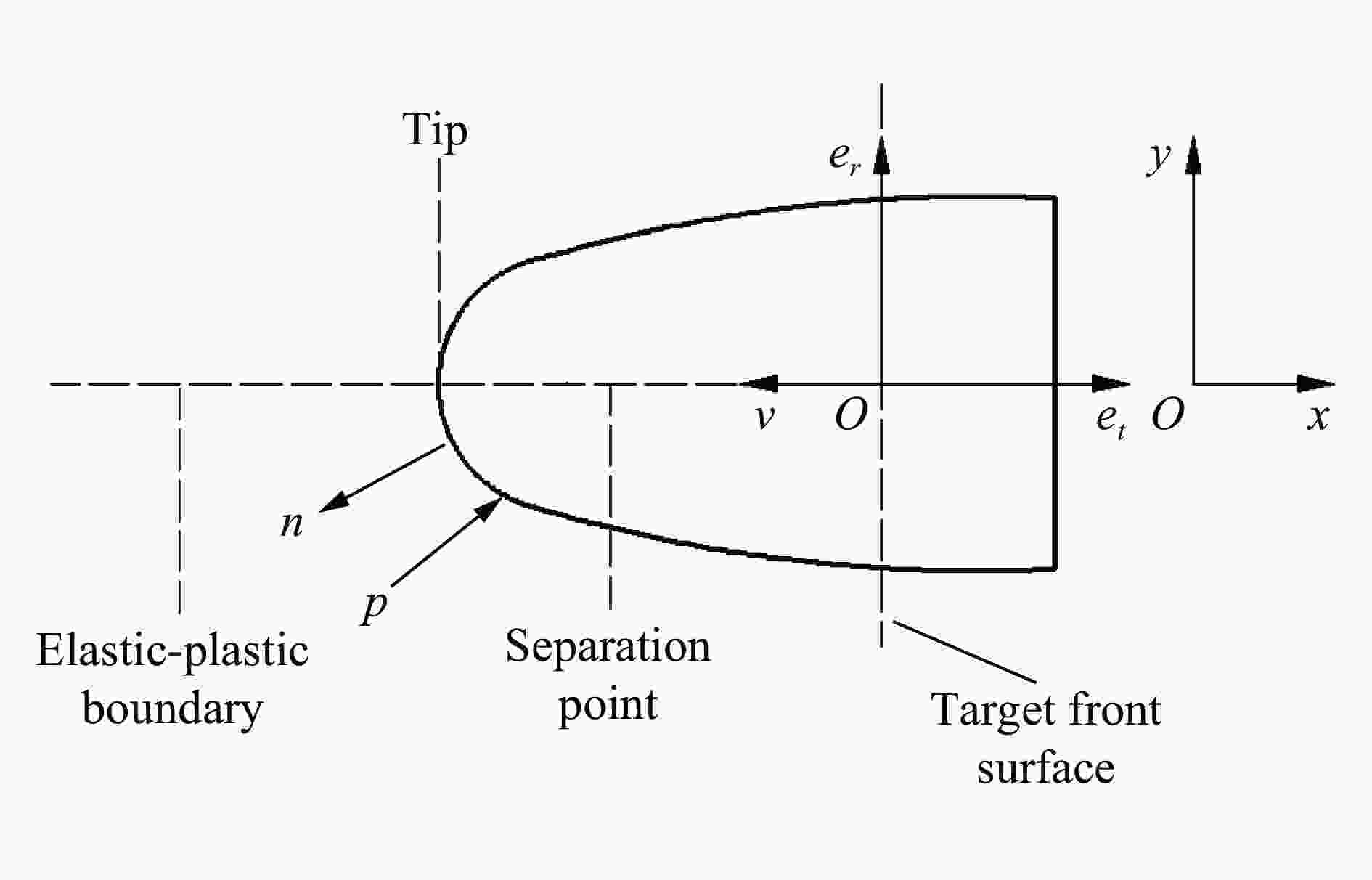
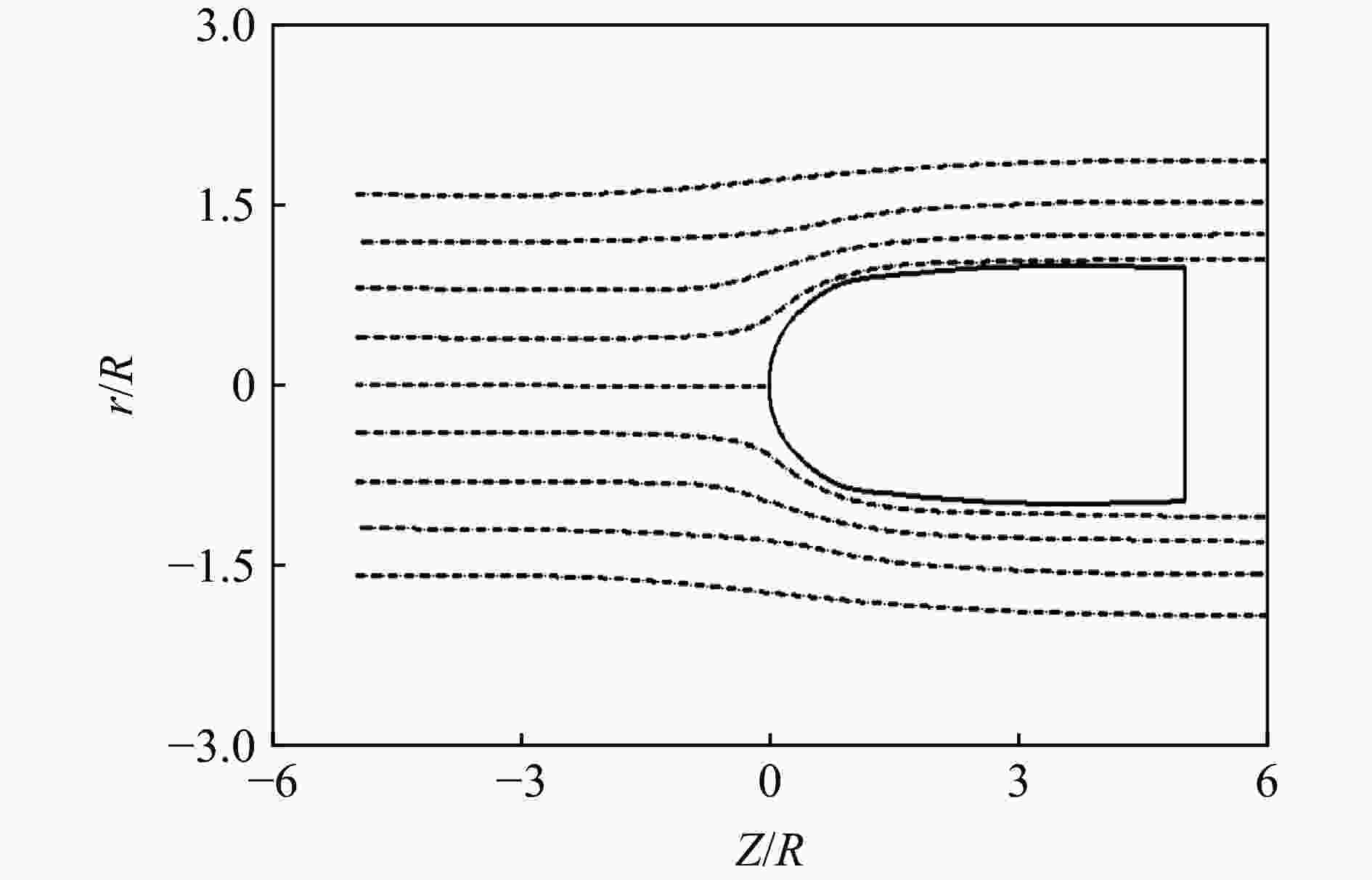
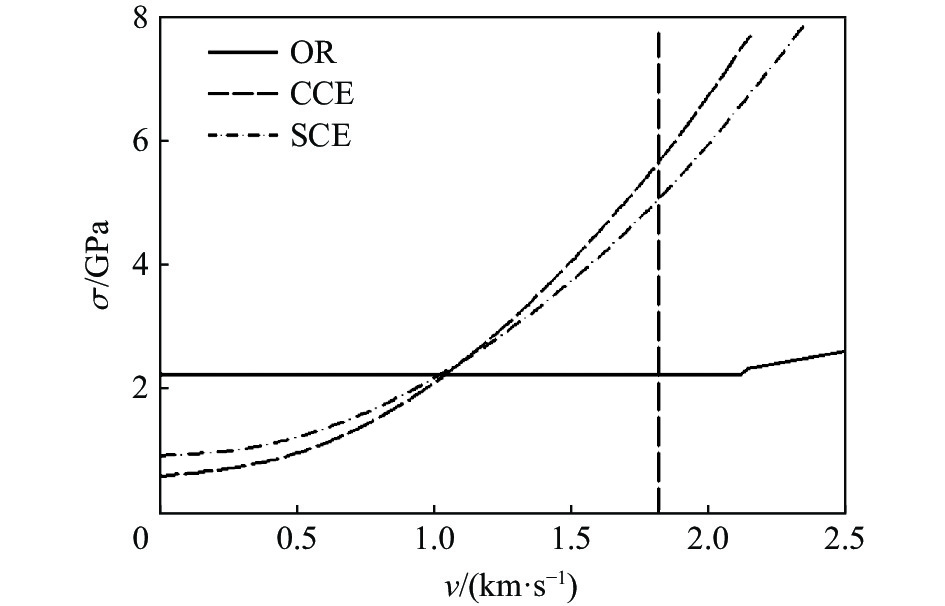
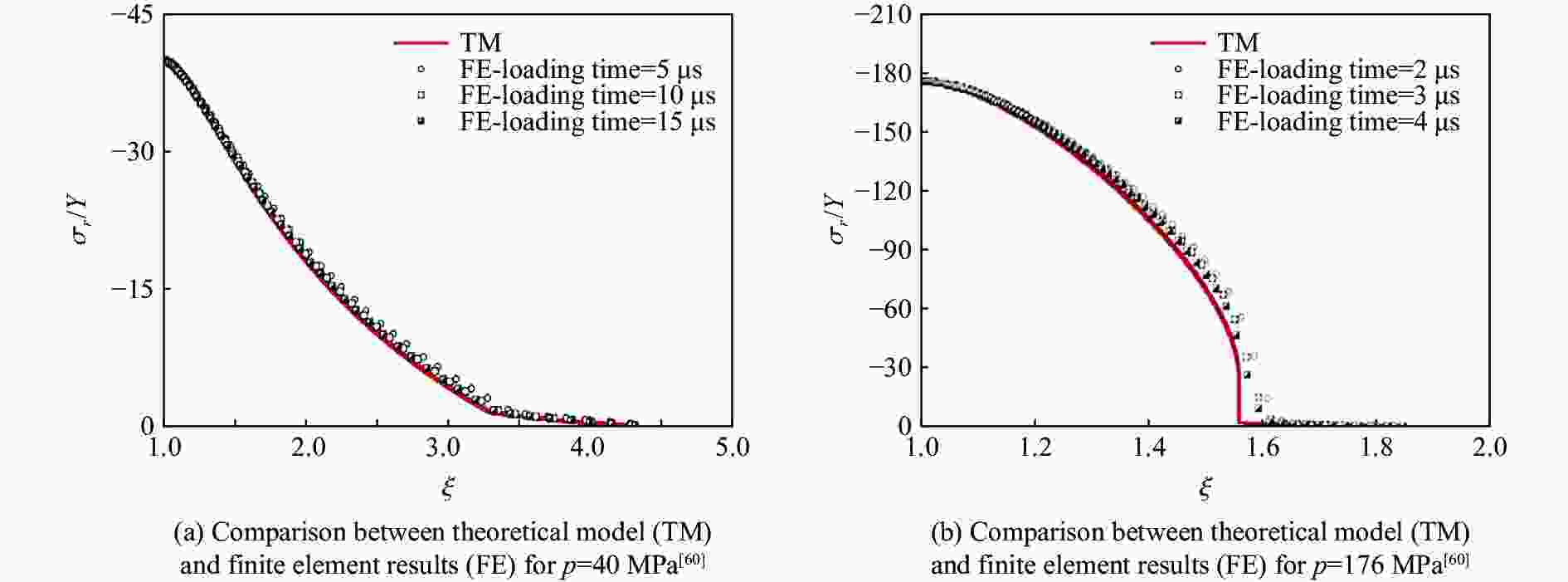
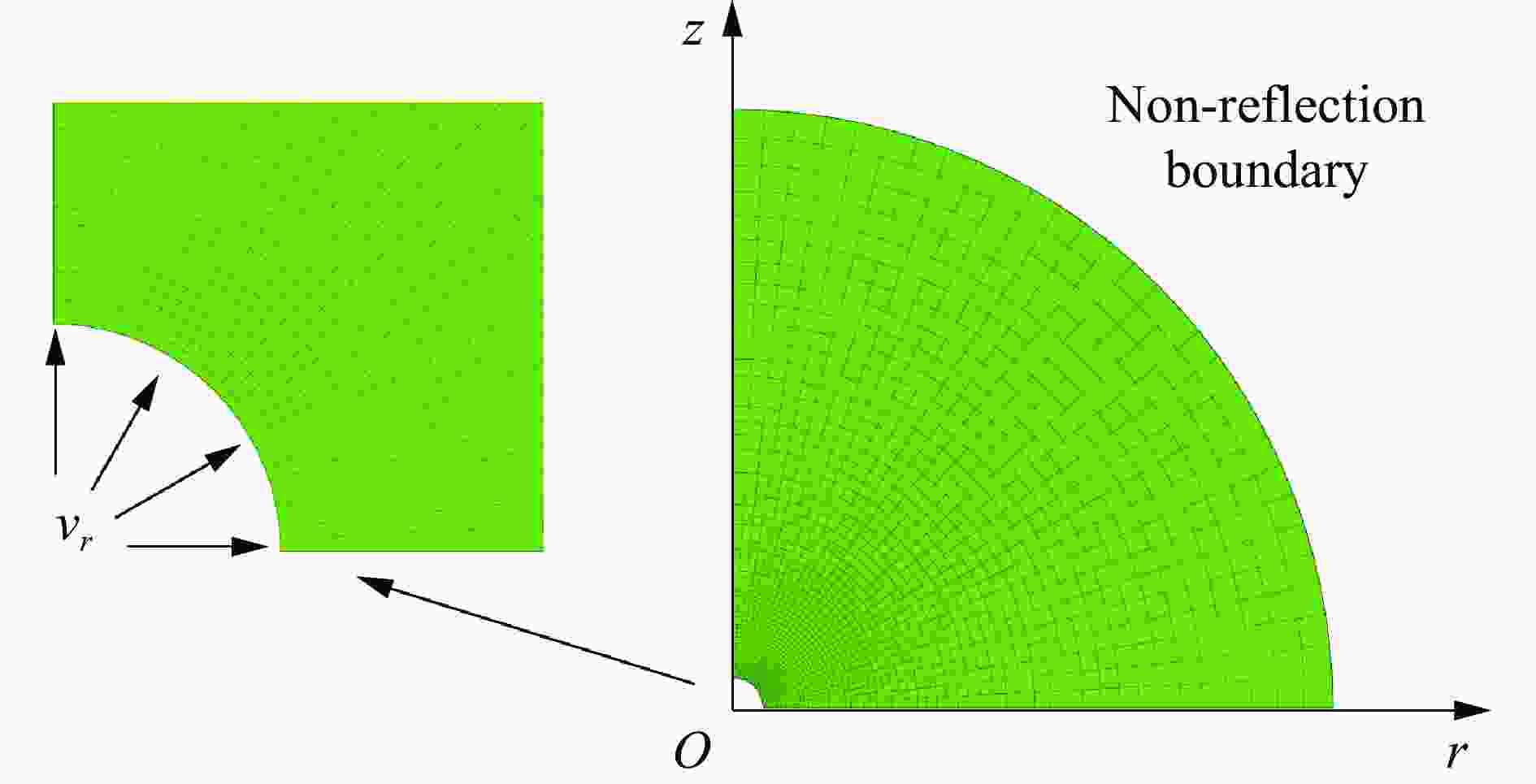
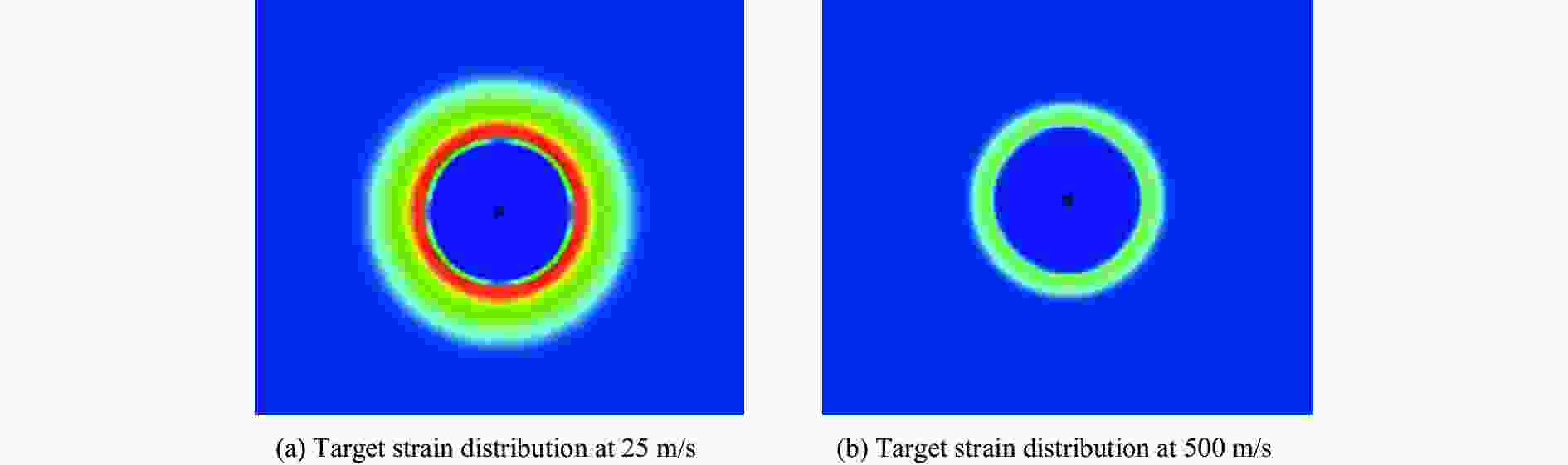
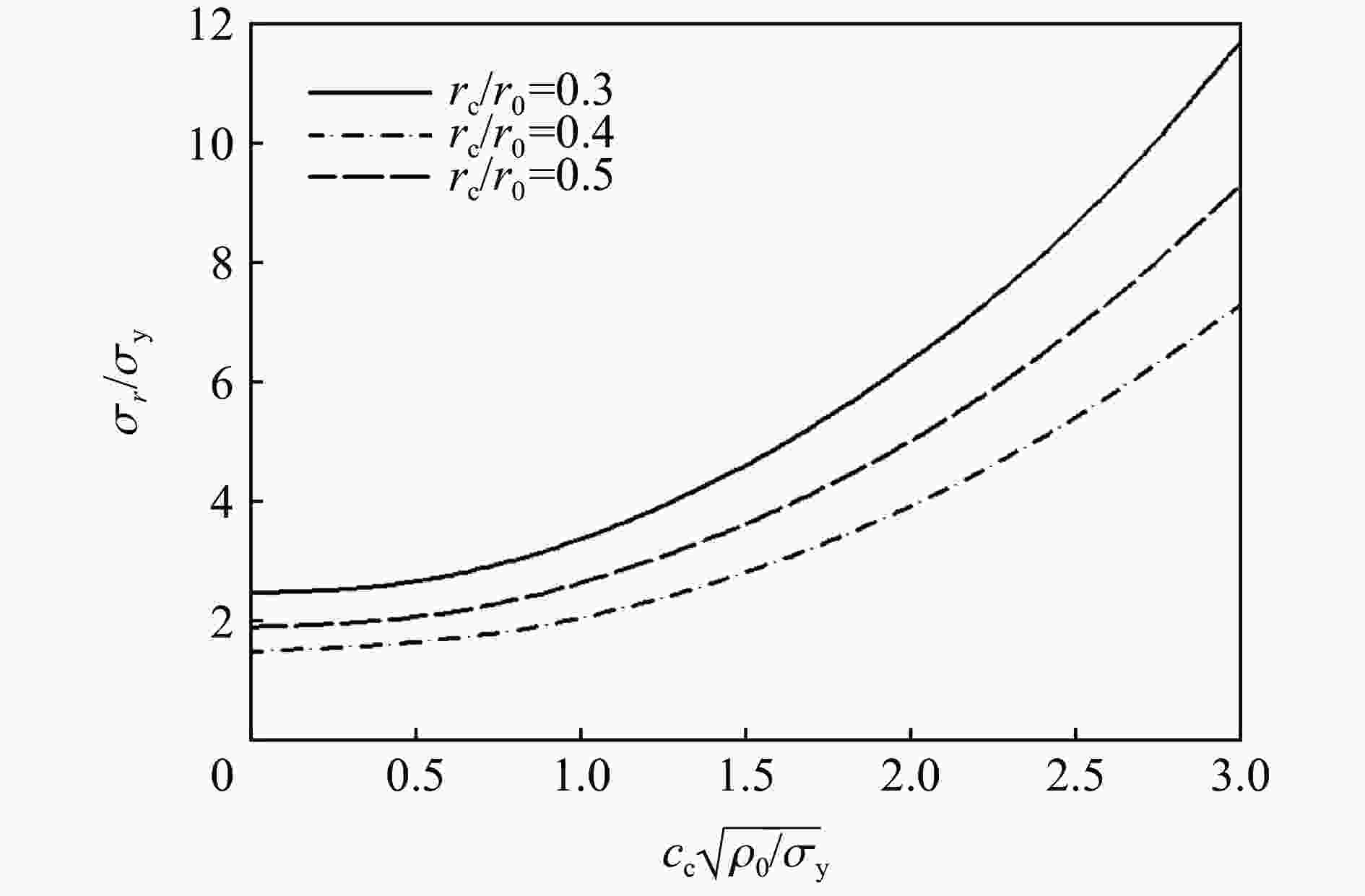
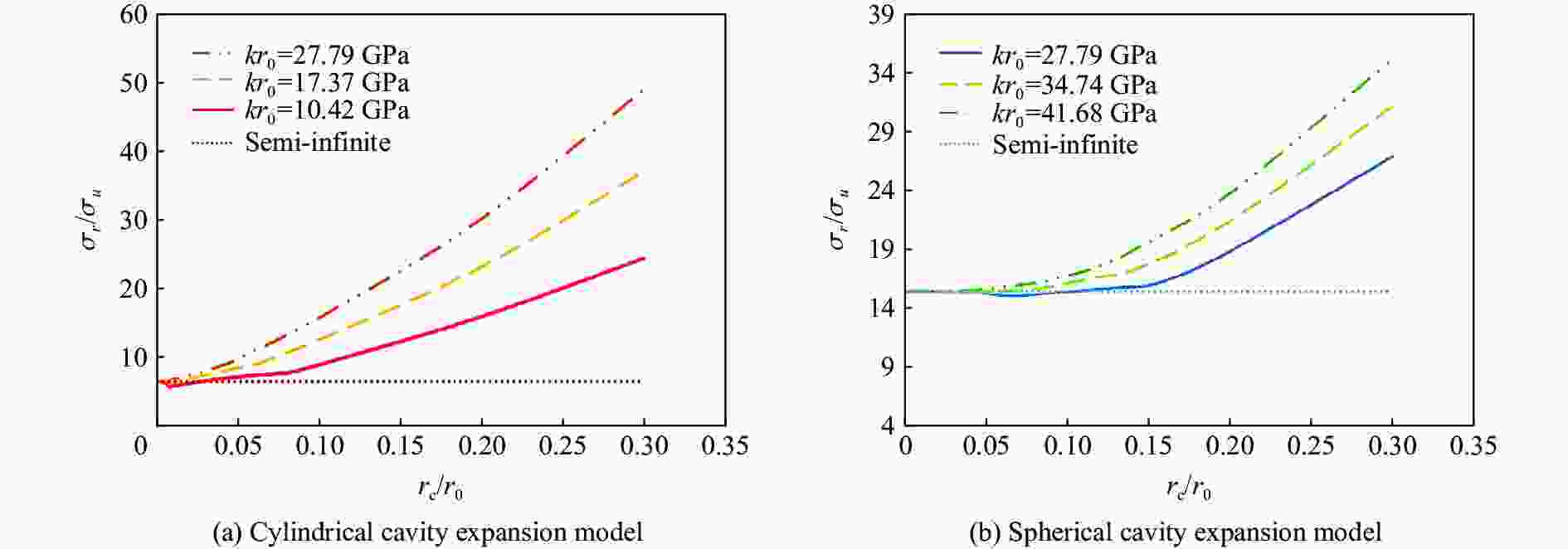
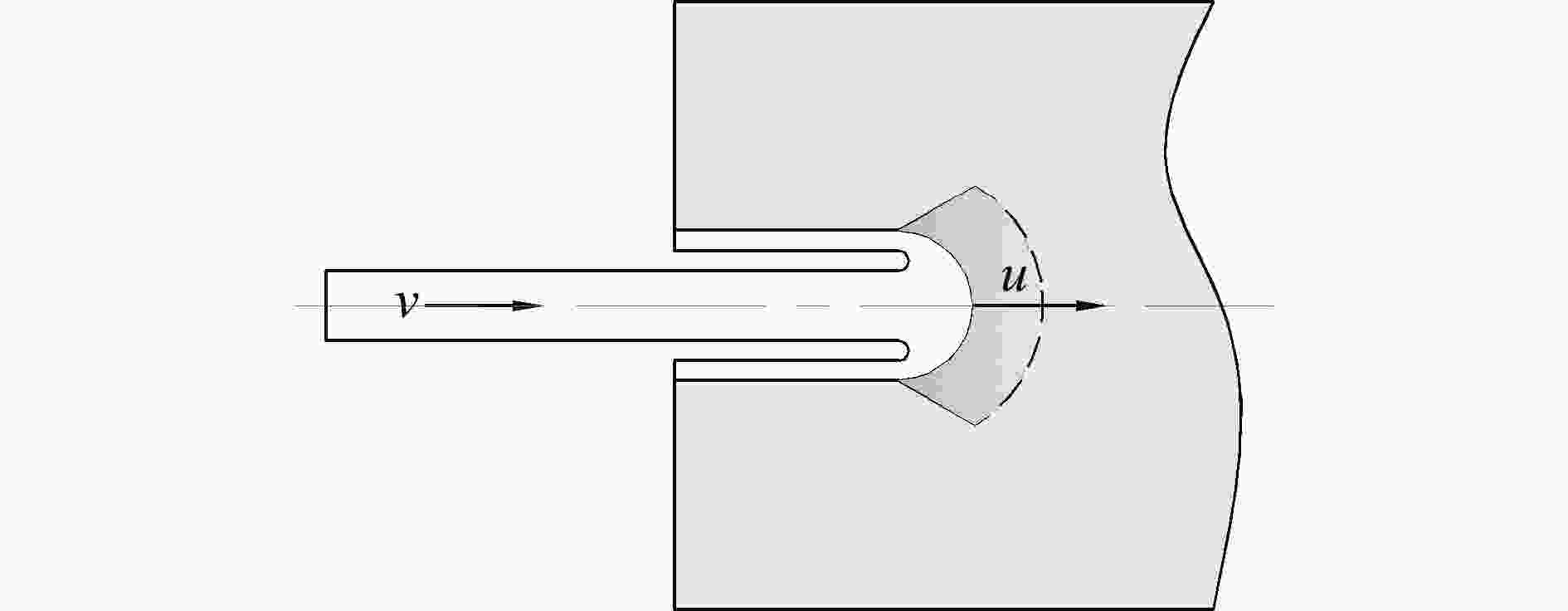
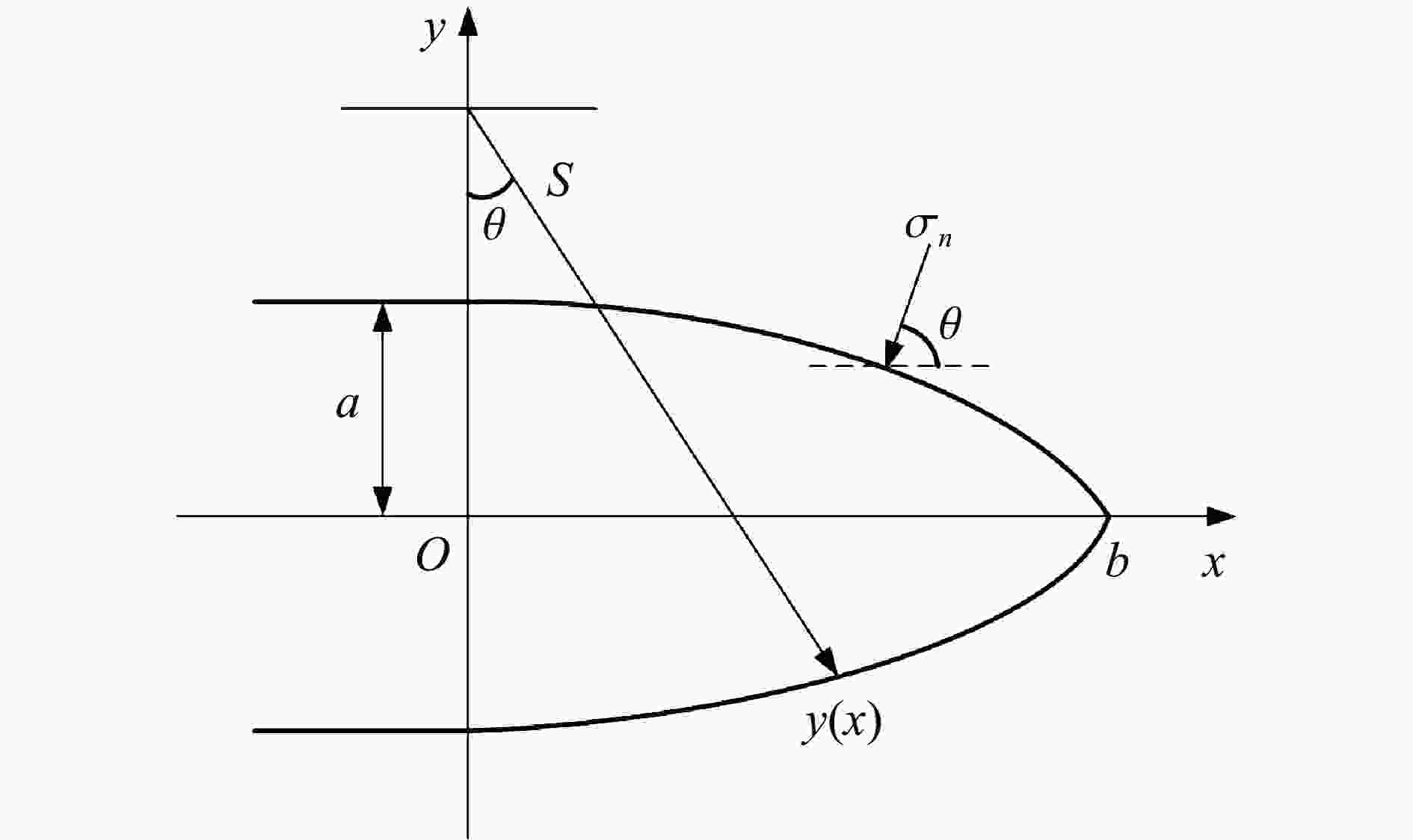
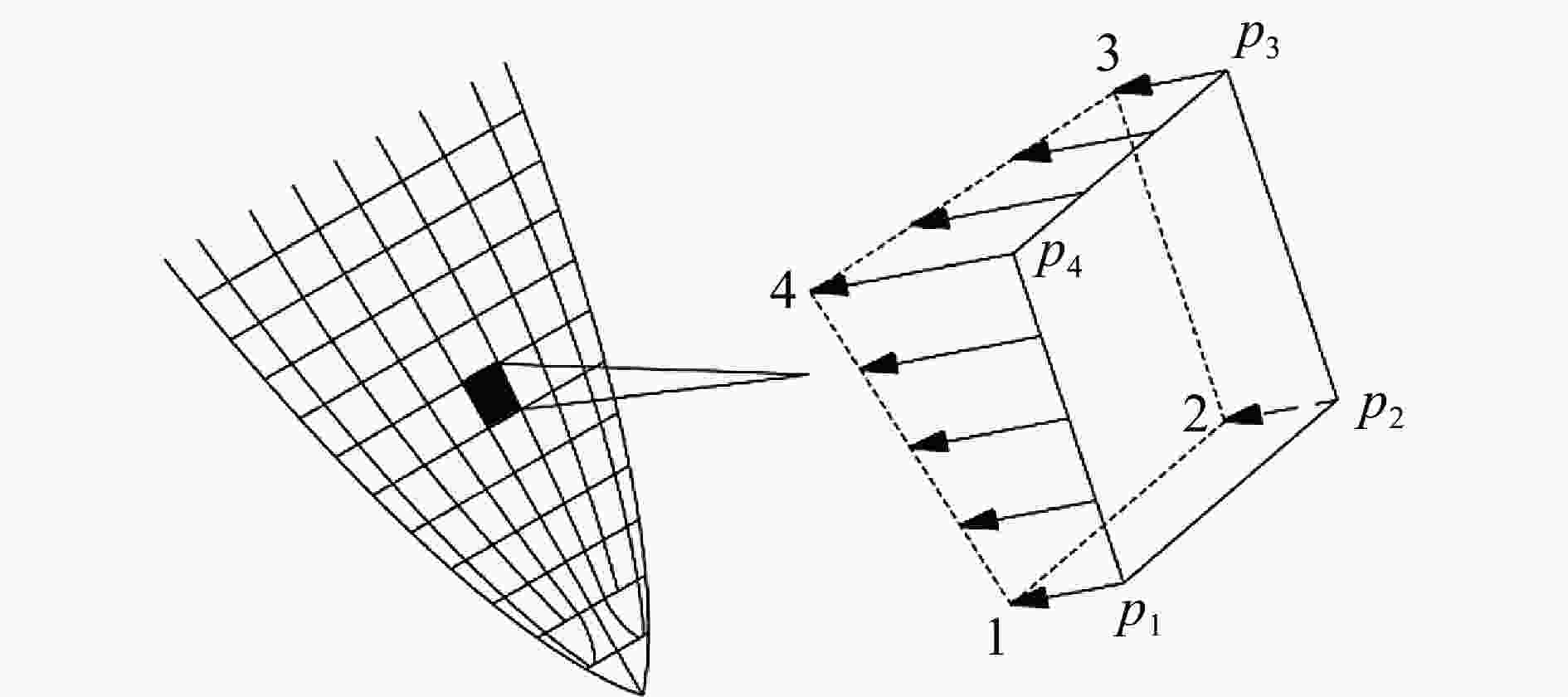
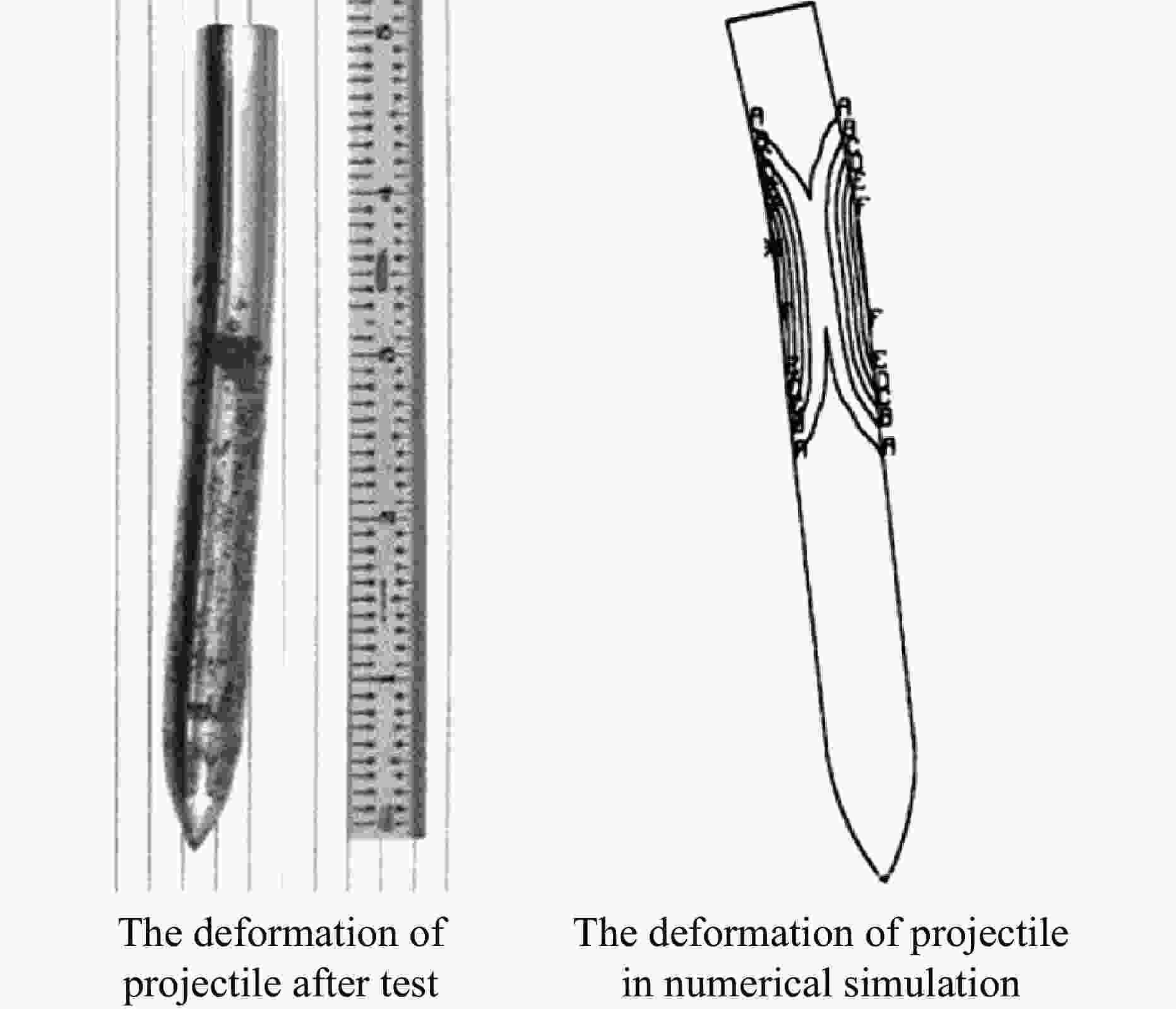
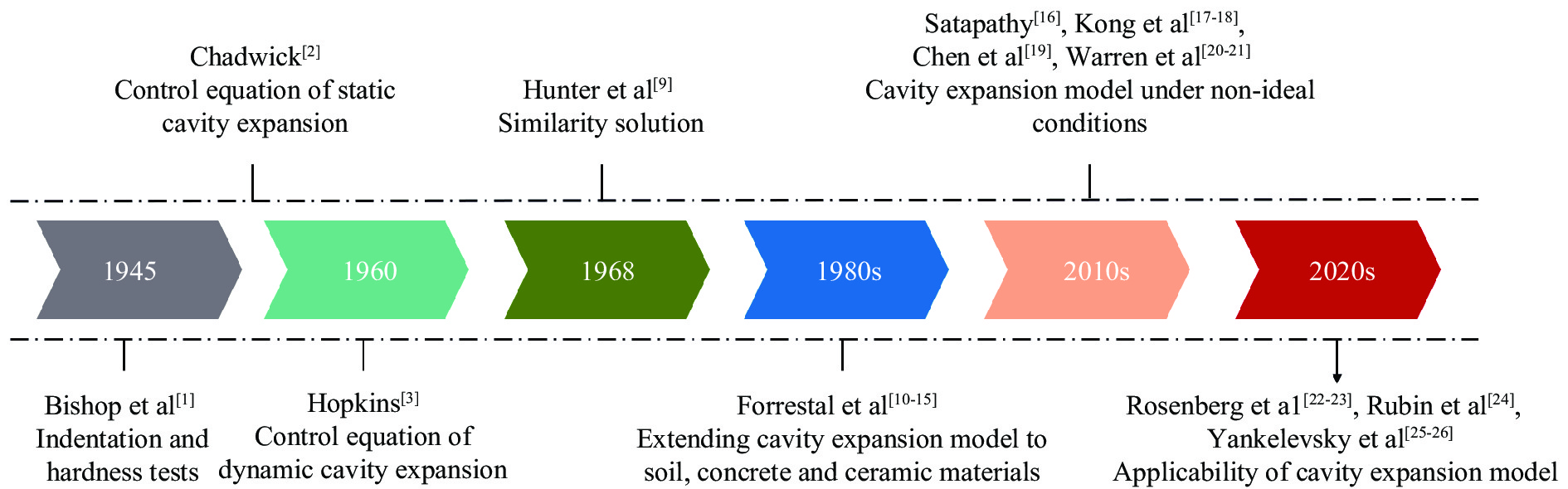
Department of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China

摘要

摘要: 从静/动态空腔膨胀模型的理论体系出发，介绍了空腔膨胀模型在不同方向上取得的成果，主要涉及理想侵彻条件的空腔膨胀压力计算模型及数值模拟方法和空腔膨胀模型在典型侵彻问题及复杂弹靶条件下的应用。在理想侵彻条件下的空腔膨胀压力计算模型中，主要讨论了靶体材料、屈服准则和状态方程对空腔边界应力的影响规律及空腔膨胀模型的适用性问题；根据数值模拟中初始条件的不同，介绍了空腔表面恒定速度/恒定压力两种数值模拟方法，证明了数值模拟方法的可靠性；整理了空腔膨胀模型的基本假设、适用范围、工程应用特点，列举了其在典型侵彻问题及多层复合靶板、约束靶体、弹体刻槽和异形截面形状弹体等复杂弹靶条件下的应用。针对空腔膨胀模型的研究现状，总结了目前空腔膨胀模型在冲击动力学领域的应用方向，归纳了空腔膨胀模型应用中尚存在的问题，展望了空腔膨胀模型下一步的重点发展方向。
- 侵彻 /
- 空腔膨胀 /
- 阻力模型
Abstract: The cavity expansion theory is one of the main basic theories for the theoretical analysis of penetration problems. It is mainly used to analyze the failure response characteristics of typical target materials under impact load, and then to determine the penetration resistance of the target. It is widely used in the analysis of high-speed impact penetration and failure problems. Domestic and foreign scholars have made abundant research achievements on plastic and (quasi) brittle materials based on the theory of cylindrical and spherical cavity expansion. Starting from the theoretical system of the static/dynamic cavity expansion model, the results of the cavity expansion model in different directions are introduced, mainly involving the cavity expansion pressure theoretical calculation model and numerical simulation method under ideal penetration conditions, and the application of cavity expansion model to typical penetration problems and complex missile target conditions. The theoretical calculation model under ideal penetration conditions based on cavity expansion theory mainly discusses the influence aspects of target material, yield criterion and equation of state on target resistance and the applicability of the cavity expansion model. According to the different initial conditions in the numerical simulation, two numerical simulation methods of cavity surface constant velocity/constant pressure are introduced, and the reliability of the numerical simulation method is proved. The basic assumptions, application scope and engineering application characteristics of the cavity expansion model are summarized, and its applications in typical penetration problems and complex missile targets such as multilayer composite target plate, constrained target, projectile grooves and projectile body with special cross-section are listed. Based on the current status of the cavity expansion model, we summarized the current cavity expansion model application direction in the field of impact dynamics, and the problems existing in the application of the cavity expansion model, as well as the key development direction in the cavity expansion model.
- penetration /
- cavity expansion theory /
- resistance model

HTML全文

图 1 空腔膨胀模型发展路线图^{[1-3, 9-26]}

Figure 1. The development circuit diagram of cavity expansion model^{[1-3, 9-26]}

下载: 全尺寸图片幻灯片

图 2 塑性材料破坏情况^[29]

Figure 2. Failure of plastic material^[29]

下载: 全尺寸图片幻灯片

图 3 脆性材料破坏情况^[27]

Figure 3. Failure of brittle material^[27]

下载: 全尺寸图片幻灯片

图 4 响应区示意图

Figure 4. Schematic diagram of response area

下载: 全尺寸图片幻灯片

图 5 不同速度下的空腔径向应力分布^[11-12]

Figure 5. Radial stress distribution of cavity atdifferentvelocity^[11-12]

下载: 全尺寸图片幻灯片

图 6 不同分区下界面移动速度^[30]

Figure 6. Interface moving speed under different partitions^[30]

下载: 全尺寸图片幻灯片

图 7 剪切强度-压力数据和屈服准则^[44]

Figure 7. Shear strength-pressure data and yield criteria^[44]

下载: 全尺寸图片幻灯片

图 8 压力体积应变测试数据和状态方程^[44]

Figure 8. Pressure-volumetric strain tests data and EOS^[44]

下载: 全尺寸图片幻灯片

图 9 粉碎和破碎区域的速度^[10]

Figure 9. Speeds of the comminuted and cracked zones^[10]

下载: 全尺寸图片幻灯片

图 10 不同屈服准则下径向应力与速度的关系^[10]

Figure 10. The relationship between radial stress and velocity under different yield criteria^[10]

下载: 全尺寸图片幻灯片

图 11 空腔径向应力与空腔速度的关系^[38]

Figure 11. The relation between cavity radial pressure and cavity velocity^[38]

下载: 全尺寸图片幻灯片

图 12 空腔速度与弹塑性界面移动速度的关系^[38]

Figure 12. The relation between the velocity of the cavity and elastoplastic interface^[38]

下载: 全尺寸图片幻灯片

图 13 刚体侵彻不可压缩理想弹塑性目标的头部区域示意图^[52]

Figure 13. Sketch of the nose region of a rigid projectile penetrating an incompressible elastic-perfectly plastic target^[52]

下载: 全尺寸图片幻灯片

图 14 Rankine形弹体的稳态流场^[53]

Figure 14. Steady-state flow field for an ovoid of Rankine shaped projectile^[53]

下载: 全尺寸图片幻灯片

图 15 OR、CCE和SCE模型预测的侵彻速度平均轴向阻力应力^[52]

Figure 15. Average axial resistance stress as a function of the penetration velocity predicted by the OR, CCE and SCE models^[52]

下载: 全尺寸图片幻灯片

图 16 不同压力时数值模拟与理论值对比^[60]

Figure 16. Comparison between numerical simulation and theoretical values at different pressures^[60]

下载: 全尺寸图片幻灯片

图 17 球形空腔膨胀计算的有限元模型

Figure 17. Finite element model for spherical cavity expansion calculation

下载: 全尺寸图片幻灯片

图 18 不同膨胀速度下靶体应变分布^[63]

Figure 18. Target strain distribution at different expansion velocities^[63]

下载: 全尺寸图片幻灯片

图 19 球形空腔分别以400 m/s和600 m/s的速度膨胀时得到的空腔表面径向应力随时间变化曲线^[5]

Figure 19. Radial stress at the spherical cavity surface versus time for cavity expansion velocities of 400 m/s and 600 m/s^[5]

下载: 全尺寸图片幻灯片

图 20 空腔表面径向应力随空腔膨胀速度的变化曲线^[5]

Figure 20. Radius stress at cavity surface versus cavity expansion velocity^[5]

下载: 全尺寸图片幻灯片

图 21 长杆弹侵彻坑附近和1/2面积受内压的膨胀空腔附近的速度场^[59]

Figure 21. Velocity field near long rod projectile penetrating crater and 1/2 area expansion cavity under internal pressure^[59]

下载: 全尺寸图片幻灯片

图 22 混凝土响应分区形成过程^[65]

Figure 22. Formation process of concrete target response regions^[65]

下载: 全尺寸图片幻灯片

图 23 不同侵彻速度下的混凝土等效应变云图^[65]

Figure 23. The equivalent strain diagrams of concrete under different penetration velocities^[65]

下载: 全尺寸图片幻灯片

图 24 3种强度混凝土在不同膨胀压力下的空腔边界速度时间历程数值模拟结果^[66]

Figure 24. Simulation results of cavity wall velocities for three strengths concrete with different expansion pressures^[66]

下载: 全尺寸图片幻灯片

图 25 抗压强度分别为20、30、40、48、60、80 MPa混凝土的膨胀压力阈值^[66]

Figure 25. Threshold values of expansion pressures for concrete strength of 20, 30, 40, 48, 60, and 80 MPa^[66]

下载: 全尺寸图片幻灯片

图 26 4种可能的情况下的腔轮廓原理图^[71]

Figure 26. Schematic of cavity profiles for four-different possible scenarios, in ceramic targets backed by semi-infinite metal^[71]

下载: 全尺寸图片幻灯片

图 27 椭圆长短轴比对侵彻阻力、深度的影响规律^[72]

Figure 27. Influence of ellipse axial ratio on penetration resistance and depth^[72]

下载: 全尺寸图片幻灯片

图 28 椭圆孔受力状态示意图^[73]

Figure 28. Diagram of stress state of elliptical hole^[73]

下载: 全尺寸图片幻灯片

图 29 椭圆空腔边界受力状态^[73]

Figure 29. The state of force at the boundary of an elliptic cavity^[73]

下载: 全尺寸图片幻灯片

图 30 压剪联合作用下的空腔分区^[4]

Figure 30. Cavity partition under combined action of compression and shear^[4]

下载: 全尺寸图片幻灯片

图 31 弹体侵彻深度理论与实验对比^[4]

Figure 31. Comparison of predicted and experimental DOP data^[4]

下载: 全尺寸图片幻灯片

图 32 球形空腔压力-空腔膨胀速度^[76]

Figure 32. Spherical cavity pressure-cavity expansion velocity diagram^[76]

下载: 全尺寸图片幻灯片

图 33 有限球形空腔压力-空腔膨胀速度^[75-76]

Figure 33. Pressure-cavity expansion velocity diagram of a finite spherical cavity^[75-76]

下载: 全尺寸图片幻灯片

图 34 柱形/球形空腔膨胀模型下约束强度对空腔边界压力的影响规律^[80]

Figure 34. Effect of confinement strength on boundary pressure of cylindrical/spherical cavity expansion model^[80]

下载: 全尺寸图片幻灯片

图 35 不同约束程度下径向应力与空腔速度的关系^[68]

Figure 35. The transmutation discipline of radial stress at cavity wall^[68]

下载: 全尺寸图片幻灯片

图 36 流体侵彻示意图

Figure 36. Schematic diagram of fluid penetration

下载: 全尺寸图片幻灯片

图 37 弹体结构示意图

Figure 37. Schematic diagram of missile body structure

下载: 全尺寸图片幻灯片

图 38 弹体表面单元受力定义

Figure 38. Definition of force on surface element of projectile body

下载: 全尺寸图片幻灯片

图 39 尖卵形弹体以459 m/s的速度侵彻石灰石的实验结果与数值模拟结果对比^[91]

Figure 39. Comparison between the experimental and numerical simulation results of projectile penetrating limestone at the speed of 459 m/s^[91]

下载: 全尺寸图片幻灯片

图 40 弹体以45°碰撞角斜侵彻金属铝靶的仿真与试验结果对比图^[102]

Figure 40. Comparison of simulation and test results of oblique penetration of projectile into metal aluminum target at 45° impact angle^[102]

下载: 全尺寸图片幻灯片

图 41 自由面模型、弹靶分离模型对侵彻弹道的影响^[104]

Figure 41. Influence of free surface model and projectile separation model on penetration trajectory^[104]

下载: 全尺寸图片幻灯片

表 1 常见的几种屈服准则与状态方程

Table 1. Several common yield criteria and equations of state

屈服准则/状态方程	函数表达式	备注
Mohr-Coulomb	$\left\| {{\sigma _r} - {\sigma _\theta }} \right\| = Y$	$ {\sigma }_{r} $和$ {\sigma }_{\theta } $分别为径向应力与环向应力，Y为屈服强度
Tresca	$\left\| {{\sigma _r} - {\sigma _\theta }} \right\| = \lambda p + {\tau _0}$	$ {\tau }_{0}=\dfrac{3-\lambda }{3}Y $
Griffith	${\left( {{\sigma _r} - {\sigma _\theta }} \right)^2} = Y\left( {{\sigma _r}{\text{ + }}{\sigma _\theta }} \right)$	$ {\sigma }_{r} $和$ {\sigma }_{\theta } $分别为径向应力与环向应力，Y为屈服强度
Drucker-Prager	$ \left\{ \begin{array}{*{20}{l}} {\sigma _r} - {\sigma _\theta } = \lambda p + {\tau _0}& p \text{＜} {p_{\text{m}}} \\ {\sigma _r} - {\sigma _\theta }{\text{ = }}\left( {{\tau _0}{\text{ + }}\lambda {p_{\text{m}}}} \right)\dfrac{{{p_1} - p}}{{{p_1} - {p_{\text{m}}}}}& {p_{\text{m}}} \text{≤} p \text{≤} {p_1} \\ {\sigma _r} - {\sigma _\theta }{\text{ = }}0 & p \text{＞}{p_1} \end{array} \right. $	$ {\sigma }_{r} $和$ {\sigma }_{\theta } $分别为径向应力与环向应力， Y为屈服强度，p₁、p_m为临界压力
Hoek-Brown	${\left( {{\sigma _r} - {\sigma _\theta }} \right)^2} = Y\left( {{m_0}{\sigma _r}{\text{ + }}{\sigma _\theta }} \right)$	无量纲数m₀与材料强度及脆性程度有关
统一强度理论	$\dfrac{1}{{1{\text{ + }}b}}\left( {{\sigma _1} + b{\sigma _2}} \right) - \gamma {\sigma _3} = {\sigma _{\text{t}}}$	$ \gamma ={\sigma }_{\mathrm{t}}/{\sigma }_{\mathrm{c}} $为靶体材料拉压比，$ {\sigma }_{\mathrm{t}} $和$ {\sigma }_{\mathrm{c}} $分别为靶体材料的抗拉和抗压强度，b为中间主应力的效应参数
Voce应变硬化	$\sigma {\text{ = }}\left\{ \begin{array}{*{20}{l}} E\varepsilon & \sigma \text{≤} Y \\ Y + \displaystyle\sum\limits_{i = 1}^2 {{Q_i}} \left( {1 - \exp \left( {{C_i}\varepsilon } \right)} \right) & \sigma \text{＞}Y \end{array} \right.$	Q_i和C_i为硬化参数
线性压力-体积应变	${p_{\text{m}}} = K\varepsilon $	$ \varepsilon $为应变
三段式线性状态方程	${p_{\text{m}}} = \left\{ \begin{array}{*{20}{l}} K\varepsilon & p \text{≤} {p_{\text{c}}} \\ {p_{\text{c}}} + {K_{\text{c}}}\left( {\mu - {\mu _{\text{c}}}} \right)& {p_{\text{c}}} \text{＜}p \text{≤} {p_1} \\ {p_1} + {K_1}\left( {\mu - {\mu _{\text{p}}}} \right)& p \text{＞}{p_1} \end{array} \right.$	K、K_c、K₁为弹性区、孔隙压实区和密实区的体积模量，p_c、p₁为临界压力

下载: 导出CSV

表 2 不同$R_{\rm t} $的表达式

Table 2. Different values of R_t

来源	R_t表达式	备注
Bishop^[1]	${R_{\text{t}}} = \dfrac{{{\sigma _{\text{y}}}}}{{\sqrt 3 }}\left\{ {1 + \ln \left[ {\dfrac{{\sqrt 3 E}}{{\left( {5 - 4v} \right){\sigma _{\text{y}}}}}} \right]} \right\}$	$ {\sigma }_{\mathrm{y}} $为靶体屈服强度
Rubin^[89]	${R_{\text{t}}} = \ln \left( {4{\varsigma ^2}} \right){Y_{\text{p}}} - {f_{\text{t}}} - \left( {2/3 + \ln 4} \right){\sigma _{\text{y}}}$	Y_p为弹体屈服强度，$ {\sigma }_{\mathrm{y}} $为靶体屈服强度， f_t为与靶体材料相关的常数
Godwin^[85]	${R_{\text{t}}} = \left( {{\text{2 + }}2\sqrt {1{\text{ - }}{Y_{\text{p}}}/{Y_{\text{t}}}} } \right){\sigma _{\text{y}}}$	Y_p为弹体屈服强度，$ {\sigma }_{\mathrm{y}} $为靶体屈服强度
A-W模型^[84]	$ {R_{\text{t}}} = \dfrac{7}{3}\ln \left( {{\alpha _{\text{k}}}} \right){\sigma _{\text{t}}} $	$ {\alpha }_{k} $为与靶体材料相关的常数
S-W-Z-S模型^[90]	$ {R_{\text{t}}} = \dfrac{2}{3}{\sigma _{\text{y}}}\left( {1 + \ln \dfrac{{2E}}{{3{\sigma _{\text{y}}}}}} \right) + \dfrac{2}{{27}}{{\rm{\pi }}^2}E $	$ {\sigma }_{\mathrm{y}} $为靶体屈服强度，E为弹性模量
L-W模型^[88]	$ \begin{aligned} {R_{\text{t}}} =\,& S + C{\rho _{\text{t}}}{\left( {{U_{{\text{F0}}}}\exp \left( { - {{\left( {\dfrac{{u - {U_{{\text{F0}}}}}}{{n{U_{{\text{F0}}}}}}} \right)}^2}} \right)} \right)^2} -\\ & \dfrac{1}{2}{\rho _{\text{t}}}{\left( {u - {U_{{\text{F0}}}}\exp \left( { - {{\left( {\dfrac{{u - {U_{{\text{F0}}}}}}{{n{U_{{\text{F0}}}}}}} \right)}^2}} \right)} \right)^2} \end{aligned} $	$ {U_{{\text{F0}}}} = \sqrt {{Y_{\text{H}}}/{\rho _{\text{t}}}} $，S为靶体静态阻力，Y_H为材料动态屈服强度

下载: 导出CSV

表 3 侵彻深度理论预测公式

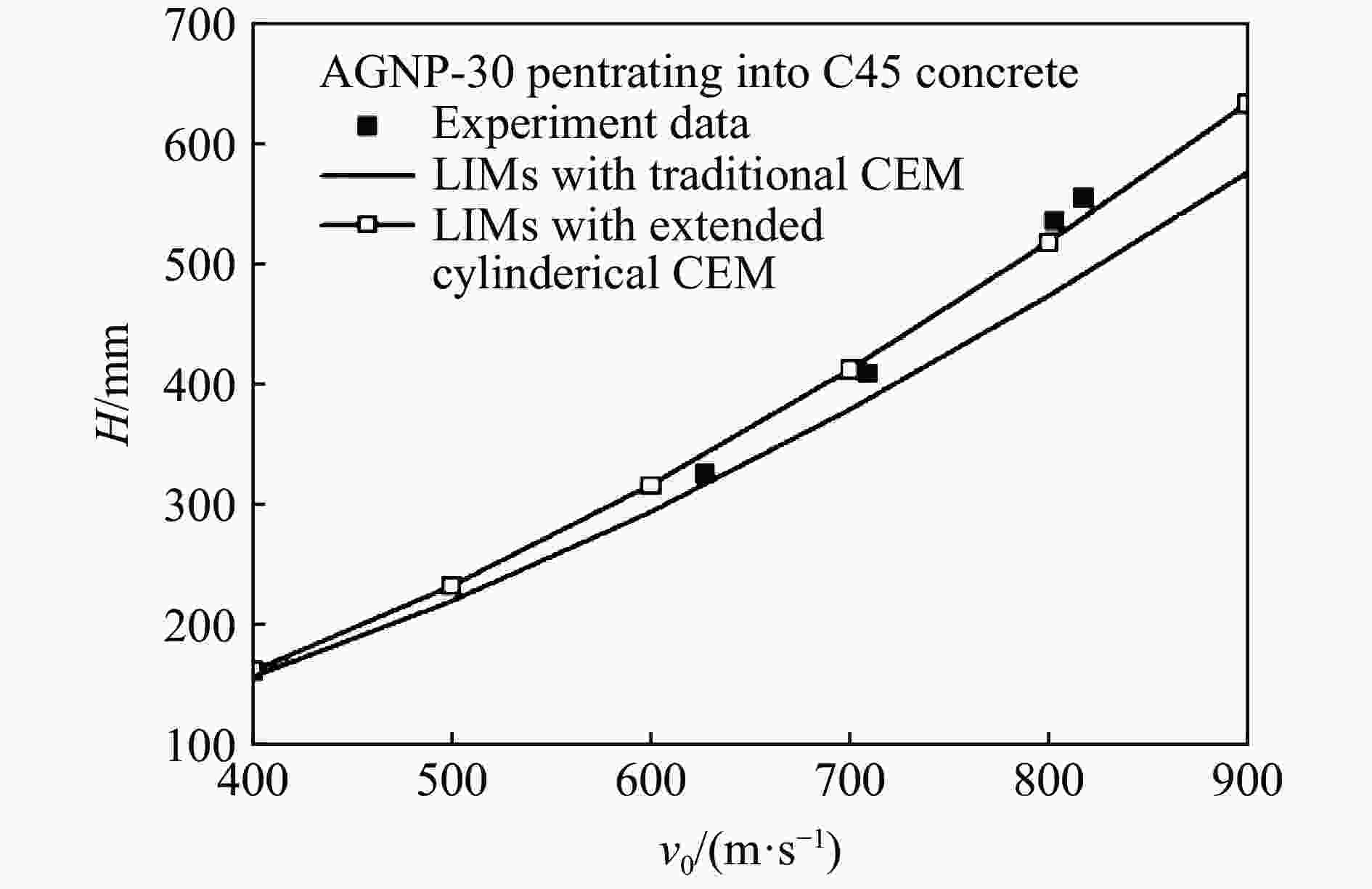
Table 3. Theory prediction formula of penetration depth

来源	侵彻深度预测公式
Frew等^[101]	$ \begin{aligned} \dfrac{P}{{\left( {L + {{2a} / 3}} \right)}} =\,& \dfrac{1}{C}\left( {\dfrac{{{\rho _{\text{p}}}}}{{{\rho _0}}}} \right)\left\{ {\ln \left[ {1 + \dfrac{{2B}}{{3A}}\left( {\sqrt {\dfrac{{{\rho _0}}}{Y}v} } \right) + \dfrac{C}{{2A}}{{\left( {\sqrt {\dfrac{{{\rho _0}}}{Y}v} } \right)}^2}} \right]} \right.+ \\ &\left. { \dfrac{{4B}}{{\sqrt {18AC - 4{B^2}} }}\left[ {{\rm{arctan}}\dfrac{{2B}}{{\sqrt {18AC - 4{B^2}} }} - {\rm{arctan}}\left[ {\dfrac{{3C\sqrt {{{{\rho _0}} / Y}} v + 2B}}{{\sqrt {18AC - 4{B^2}} }}} \right]} \right]} \right\} \end{aligned} $
Warren^[91]	$ P = \dfrac{m}{{2{\text{π }}{a^2}{\rho _0}N}}\ln \left( {1 + \dfrac{{N{\rho _0}{v^2}}}{R}} \right) + 4a $
Wen^[92]	$P = \left\{ \begin{array}{*{20}{l}} \left( {\sqrt {4\psi - 1} - 2\psi \cos \psi } \right)a & P \text{≤} {L_{\text{N}}} \\ \dfrac{P}{{L + 8{\psi ^3}\eta a}} = \left( {\dfrac{{{\rho _{\text{p}}}}}{{{\rho _{\text{t}}}}}} \right)\dfrac{{{\rho _{\text{t}}}{v^2}}}{{{\sigma _{\text{e}}}}}\dfrac{1}{{2\left[ {1 + \beta \sqrt {\dfrac{{{\rho _{\text{t}}}}}{{{\sigma _{\text{e}}}}}} v} \right]}} + \dfrac{{\left( {\sqrt {4\psi - 1} - 8{\psi ^3}\eta } \right)a}}{{L + 8{\psi ^3}\eta a}}& P\text{＞} {L_{\text{N}}} \end{array} \right. $
Teland等^[96]	$ P = \dfrac{2}{{\text{π }}}\dfrac{M}{N}\ln \left[ {\dfrac{{\left[ {1 - \dfrac{{\text{π }}}{4}\dfrac{{{R^2}}}{M}{X_1}} \right]\dfrac{{v_0^2}}{S} + \dfrac{M}{N} - \dfrac{{\text{π }}}{4}\dfrac{{{R^2}}}{M}{X_1}}}{{\dfrac{M}{N} + \dfrac{{\text{π }}}{4}{X_1}}}} \right]{\text{ + }}{X_1} $
Kong等^[17]	$ \begin{aligned} \dfrac{P}{{{l_{{\text{eff}}}}}} =\,& \dfrac{{{\rho _{\text{p}}}}}{{2{N_2}C{\rho _0}}}\ln \left( {\dfrac{{A{f_{\text{c}}}{N_0} + {N_1}B\sqrt {{\rho _0}{f_{\text{c}}}} v + {N_2}C{\rho _0}{v^2}}}{{A{f_c}{N_0}}}} \right) + \dfrac{{{\rho _{\text{p}}}{N_1}B\sqrt {{\rho _0}{f_{\text{c}}}} }}{{{N_2}C{\rho _0}\sqrt {{\rho _0}{f_{\text{c}}}\left( {4AC{N_0}{N_2} - N_1^2{B^2}} \right)} }}\times \\ &\left[ {\arctan \left( {\dfrac{{{N_1}B\sqrt {{\rho _0}{f_{\text{c}}}} }}{{\sqrt {{\rho _0}{f_{\text{c}}}\left( {4AC{N_0}{N_2} - N_1^2{B^2}} \right)} }}} \right) - \arctan \left( {\dfrac{{{N_1}B\sqrt {{\rho _0}{f_{\text{c}}}} + 2{N_2}C{\rho _0}v}}{{\sqrt {{\rho _0}{f_{\text{c}}}\left( {4AC{N_0}{N_2} - N_1^2{B^2}} \right)} }}} \right)} \right] + \dfrac{{kd}}{{{l_{{\text{eff}}}}}} \end{aligned} $
注：表中参数与上文一致，A、B、C、N₁、N₂、k、d、M、l_eff等为与材料或弹体结构相关的常数。

下载: 导出CSV

参考文献(107)

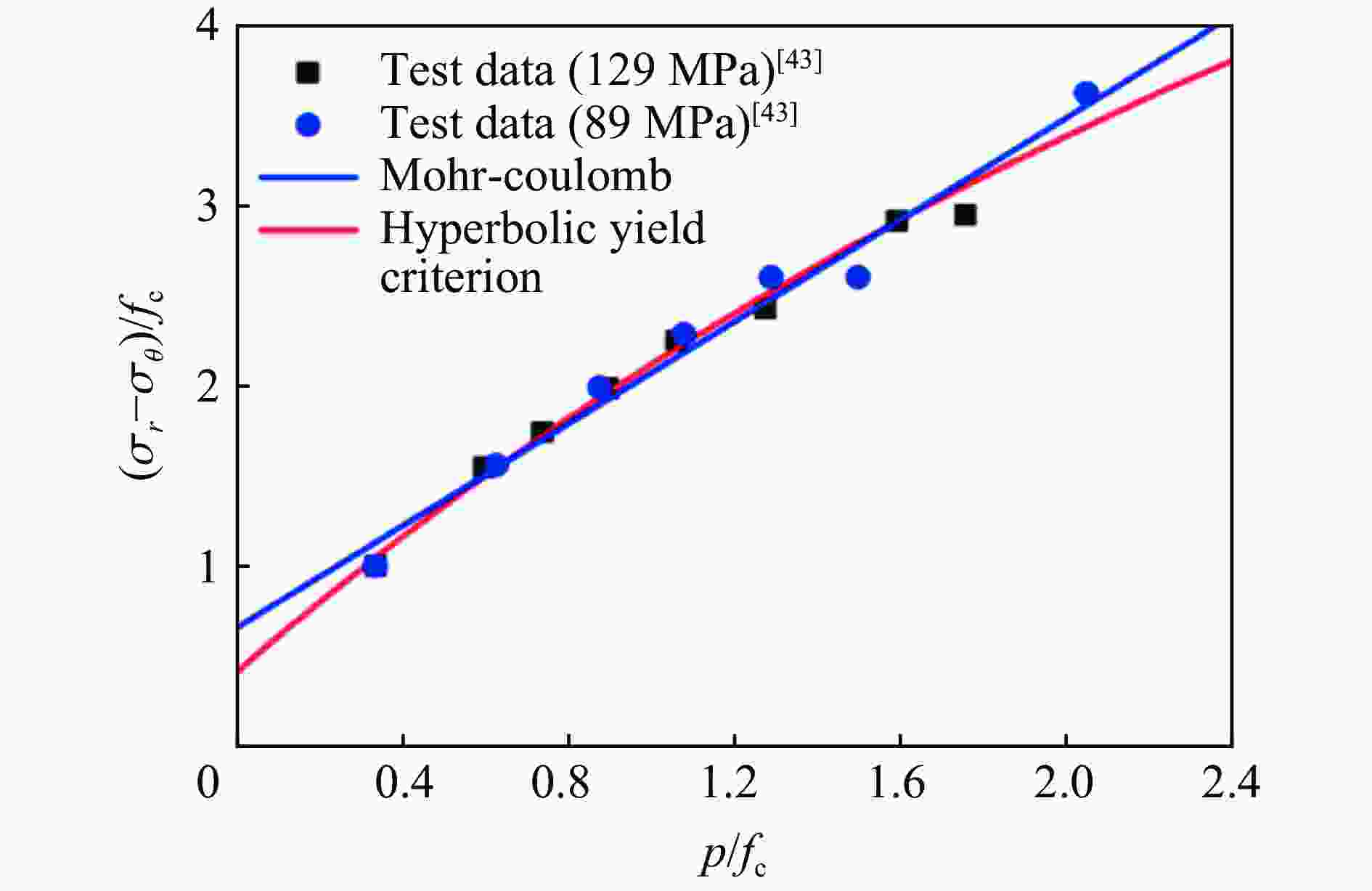
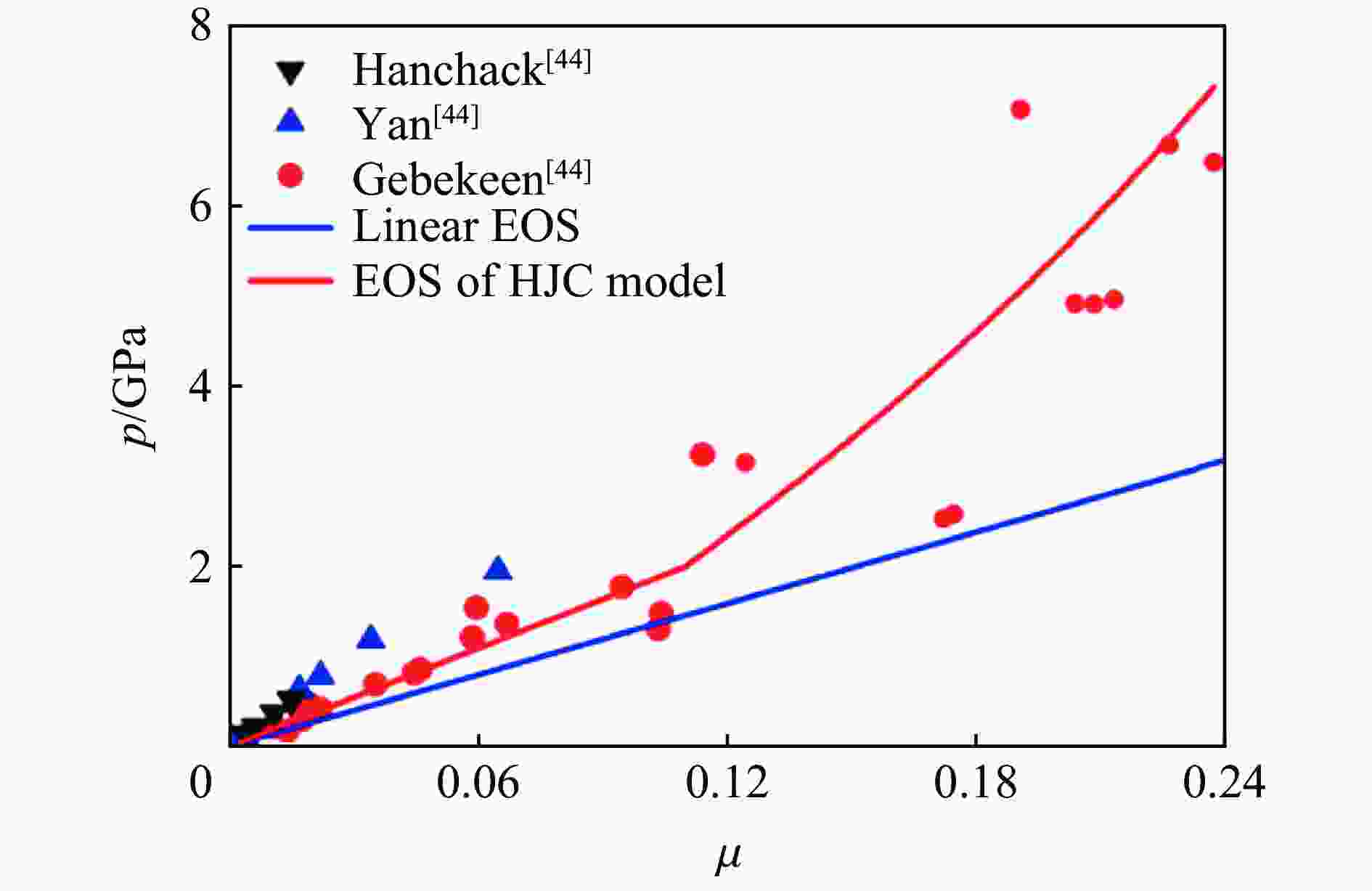
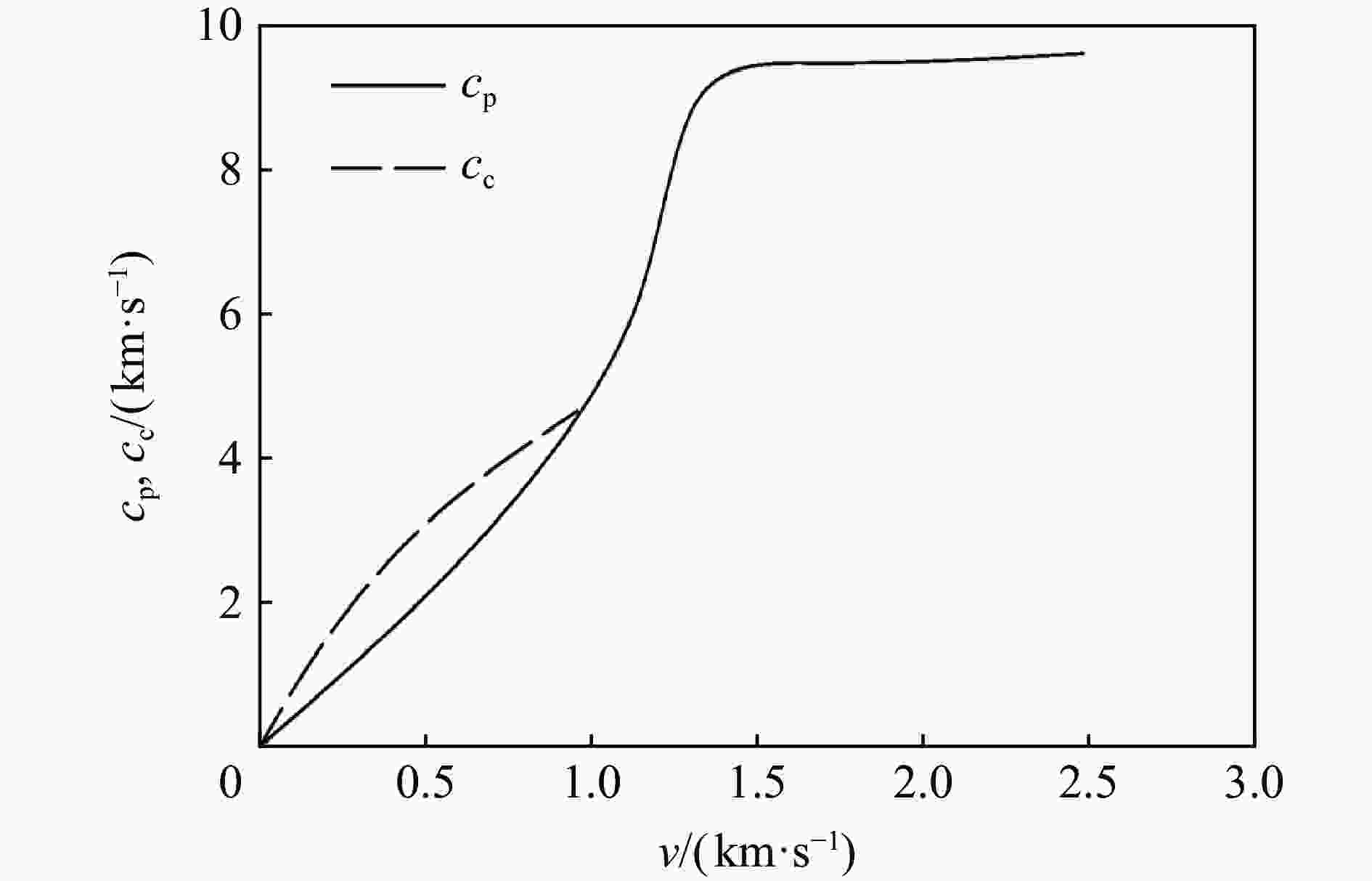
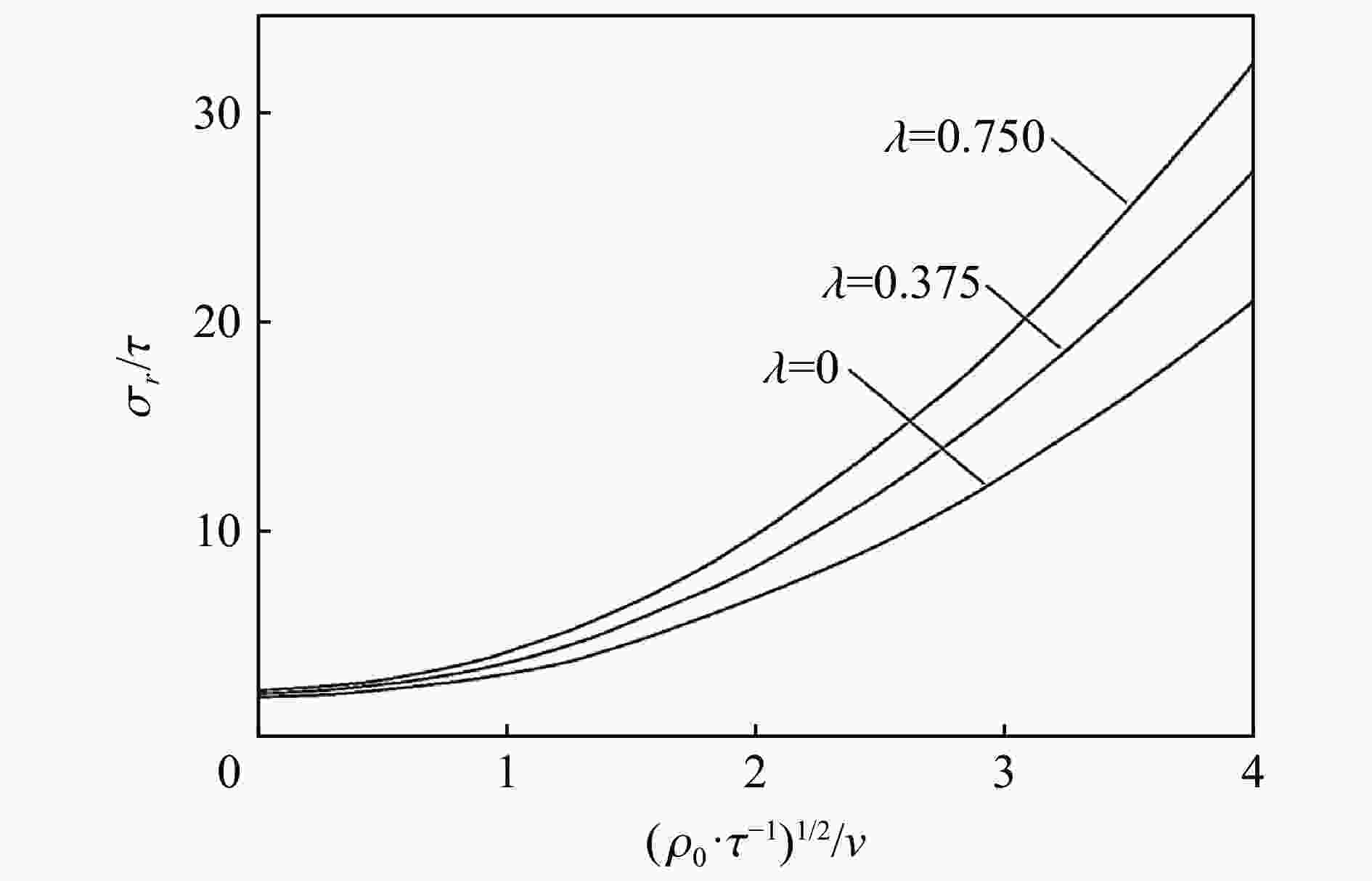
[1]	BISHOP R F, HILL R, MOTT N F. The theory of indentation and hardness tests [J]. Proceedings of the Physical Society (1926−1948), 1945, 57(3): 147–159. DOI: 10.1088/0959-5309/57/3/301.
[2]	CHADWICK P. The quasi-static expansion of a spherical cavity in metals and ideal soils [J]. Quarterly Journal of Mechanics and Applied Mathematics, 1959, 12(1): 52–71. DOI: 10.1093/qjmam/12.1.52.
[3]	HOPKINS H G. Dynamic expansion of spherical cavities in metals [J]. Progress in Solid Mechanics, 1960, 1(3): 83–164.
[4]	邓佳杰, 张先锋, 刘闯, 等. 头部非对称刻槽弹体侵彻混凝土目标性能研究 [J]. 兵工学报, 2018, 39(7): 1249–1258. DOI: 10.3969/j.issn.1000-1093.2018.07.001. DENG J J, ZHANG X F, LIU C, et al. Research on penetration of asymmetrically grooved nose projectile into concrete target [J]. Acta Armamentarii, 2018, 39(7): 1249–1258. DOI: 10.3969/j.issn.1000-1093.2018.07.001.
[5]	何涛, 文鹤鸣. 靶体响应力函数的确定方法及其在侵彻力学中的应用 [J]. 中国科学技术大学学报, 2007, 37(10): 1249–1261. DOI: 10.3969/j.issn.0253-2778.2007.10.017. HE T, WEN H M. Determination of the analytical forcing function of target responseand its applications in penetration mechanics [J]. Journal of University of Science and Technology of China, 2007, 37(10): 1249–1261. DOI: 10.3969/j.issn.0253-2778.2007.10.017.
[6]	TATE A. Further results in the theory of long rod penetration [J]. Journal of the Mechanics and Physics of Solids, 1969, 17(3): 141–150. DOI: 10.1016/0022-5096(69)90028-3.
[7]	YANKELEVSKY D Z, ADIN M A. A simplified analytical method for soil penetration analysis [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1980, 4(3): 233–254. DOI: 10.1002/nag.1610040304.
[8]	FELDGUN V R, YANKELEVSKY D Z, KARINSKI Y S. A new simplified analytical model for soil penetration analysis of rigid projectiles using the Riemann problem solution [J]. International Journal of Impact Engineering, 2017, 101: 49–65. DOI: 10.1016/j.ijimpeng.2016.10.015.
[9]	HUNTER S C, CROZIER R J M. Similarity solution for the rapid uniform expansion of a spherical cavity in a compressible elastic-plastic solid [J]. The Quarterly Journal of Mechanics & Applied Mathematics, 1968, 21(4): 467–486. DOI: 10.1093/qjmam/21.4.467.
[10]	FORRESTAL M J, LUK V K. Penetration into soil targets [J]. International Journal of Impact Engineering, 1992, 12(3): 427–444. DOI: 10.1016/0734-743X(92)90167-R.
[11]	FORRESTAL M J, LUK V K. Dynamic spherical cavity-expansion in a compressible elastic-plastic solid [J]. Journal of Applied Mechanics, 1988, 55(2): 275–279. DOI: 10.1115/1.3173672.
[12]	FORRESTAL M J, OKAJIMA K, LUK V K. Penetration of 6061-T651 aluminum targets with rigid long rods [J]. Journal of Applied Mechanics, 1988, 55(4): 755–760. DOI: 10.1115/1.3173718.
[13]	LUK V K, FORRESTAL M J. Penetration into semi-infinite reinforced-concrete targets with spherical and ogival nose projectiles [J]. International Journal of Impact Engineering, 1987, 6(4): 291–301. DOI: 10.1016/0734-743X(87)90096-0.
[14]	FORRESTAL M J, LONGCOPE D B, NORWOOD F R. A model to estimate forces on conical penetrators into dry porous rock [J]. Journal of Applied Mechanics, 1981, 48(1): 25–29. DOI: 10.1115/1.3157587.
[15]	FORRESTAL M J. Penetration into dry porous rock [J]. International Journal of Solids and Structures, 1986, 22(12): 1485–1500. DOI: 10.1016/0020-7683(86)90057-0.
[16]	SATAPATHY S. Dynamic spherical cavity expansion in brittle ceramics [J]. International Journal of Solids and Structures, 2001, 38(32–33): 5833–5845. DOI: 10.1016/S0020-7683(00)00388-7.
[17]	KONG X Z, WU H, FANG Q, et al. Rigid and eroding projectile penetration into concrete targets based on an extended dynamic cavity expansion model [J]. International Journal of Impact Engineering, 2017, 100: 13–22. DOI: 10.1016/j.ijimpeng.2016.10.005.
[18]	KONG X Z, WU H, FANG Q, et al. Projectile penetration into mortar targets with a broad range of striking velocities: test and analyses [J]. International Journal of Impact Engineering, 2017, 106: 18–29. DOI: 10.1016/j.ijimpeng.2017.02.022.
[19]	陈小伟, 李小笠, 陈裕泽, 等. 刚性弹侵彻动力学中的第三无量纲数 [J]. 力学学报, 2007, 39(1): 77–84. DOI: 10.3321/j.issn:0459-1879.2007.01.010. CHEN X W, LI X L, CHEN Y Z, et al. The third dimensionless parameter in the penetration dynamics of rigid projectiles [J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(1): 77–84. DOI: 10.3321/j.issn:0459-1879.2007.01.010.
[20]	WARREN T L, TABBARA M R. Simulations of the penetration of 6061-T6511 aluminum targets by spherical-nosed VAR 4340 steel projectiles [J]. International Journal of Solids and Structures, 2000, 37(32): 4419–4435. DOI: 10.1016/S0020-7683(99)00148-1.
[21]	Warren T L, Forrestal M J. Effects of strain hardening and strain-rate sensitivity on the penetration of aluminum targets with spherical-nosed rods [J]. International Journal of Solids and Structures, 1998, 35(35): 3737–3753. DOI: 10.1016/S0020-7683(97)00211-4.
[22]	ROSENBERG Z, DEKEL E. The penetration of rigid long rods-revisited [J]. International Journal of Impact Engineering, 2009, 36(4): 551–564. DOI: 10.1016/j.ijimpeng.2008.06.001.
[23]	ROSENBERG Z, KOSITSKI R, DEKEL E. Comment on: "Rigid and eroding projectile penetration into concrete targets based on an extended cavity expansion model" by Kong et al. Int. J. Impact Eng. (2017) [J]. International Journal of Impact Engineering, 2017, 104: A1–A3. DOI: 10.1016/j.ijimpeng.2017.03.004.
[24]	RUBIN M B. Analytical formulas for penetration of a long rigid projectile including the effect of cavitation [J]. International Journal of Impact Engineering, 2012, 40−41: 1–9. DOI: 10.1016/j.ijimpeng.2011.09.008.
[25]	YANKELEVSKY D Z, FELDGUN V R. Issues in modelling the penetration of thick targets by rigid long rods [J]. International Journal of Impact Engineering, 2020, 137: 103474. DOI: 10.1016/j.ijimpeng.2019.103474.
[26]	YANKELEVSKY D, FELDGUN V. The embedment of a high velocity rigid ogive nose projectile into a concrete target [J]. International Journal of Impact Engineering, 2020, 144: 103631. DOI: 10.1016/j.ijimpeng.2020.103631.
[27]	COLLOMBET F, TRANCHET J Y. Damage behaviour of alumina submitted to a divergent spherical wave [J]. Journal de Physique IV, 1994, 4(C8): 641–646. DOI: 10.1051/jp4:1994897.
[28]	CURRAN D R, SEAMAN L, COOPER T, et al. Micromechanical model for comminution and granular flow of brittle material under high strain rate application to penetration of ceramic targets [J]. International Journal of Impact Engineering, 1993, 13(1): 53–83. DOI: 10.1016/0734-743X(93)90108-J.
[29]	WEI H Y, ZHANG X F, LIU C, et al. Oblique penetration of ogive-nosed projectile into aluminum alloy targets [J]. International Journal of Impact Engineering, 2021, 148: 103745. DOI: 10.1016/j.ijimpeng.2020.103745.
[30]	FORRESTAL M J, TZOU D Y. A spherical cavity-expansion penetration model for concrete targets [J]. International Journal of Solids and Structures, 1997, 34(31/32): 4127–4146. DOI: 10.1016/S0020-7683(97)00017-6.
[31]	李志康, 黄风雷. 混凝土材料的动态空腔膨胀理论 [J]. 爆炸与冲击, 2009, 29(1): 95–100. DOI: 10.11883/1001-1455(2009)01-0095-06. LI Z K, HUANG F L. A dynamic spherical cavity-expansion theory for concrete materials [J]. Explosion and Shock Waves, 2009, 29(1): 95–100. DOI: 10.11883/1001-1455(2009)01-0095-06.
[32]	张先锋, 李向东, 沈培辉, 等. 终点效应学[M]. 北京: 北京理工大学出版社, 2017: 33−39. ZHANG X F, LI X D, SHEN P H, et al. Terminal effects[M]. Beijing: Beijing Institute of Technology Press, 2017: 33−39.
[33]	DAVIS R O, SCOTT R F, MULLENGER G. Rapid expansion of a cylindrical cavity in a rate-type soil [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1984, 21(4): 126.
[34]	HILL R. A theory of earth movement near a deep underground explosion [Z]. Armament Research Establishment, Memo, 1948: 21−48.
[35]	HUANG Y, HUTCHINSON J W, TVERGAARD V. Cavitation instabilities in elastic-plastic solids [J]. Journal of the Mechanics and Physics of Solids, 1991, 39(2): 223–241. DOI: 10.1016/0022-5096(91)90004-8.
[36]	HE T, WEN H M, GUO X J. A spherical cavity expansion model for penetration of ogival-nosed projectiles into concrete targets with shear-dilatancy [J]. Acta MechanicaSinica, 2011, 27(6): 1001–1012. DOI: 10.1007/s10409-011-0505-1.
[37]	FENG J, LI W B, WANG X M, et al. Dynamic spherical cavity expansion analysis of rate-dependent concrete material with scale effect [J]. International Journal of Impact Engineering, 2015, 84: 24–37. DOI: 10.1016/j.ijimpeng.2015.05.005.
[38]	SHI C C, WANG M Y, LI J, et al. A model of depth calculation for projectile penetration into dry sand and comparison with experiments [J]. International Journal of Impact Engineering, 2014, 73: 112–122. DOI: 10.1016/j.ijimpeng.2014.06.010.
[39]	SHAO R Z, WU C Q, LIU Z X, et al. Penetration resistance of ultra-high-strength concrete protected with layers of high-toughness and lightweight energy absorption materials [J]. Composite Structures, 2018, 185: 807–820. DOI: 10.1016/j.compstruct.2017.11.038.
[40]	WU H, REN G M, FANG Q, et al. Response of ultra-high performance cementitious composites filled steel tube (UHPCC-FST) subjected to low-velocity impact [J]. Thin-Walled Structures, 2019, 144: 106341. DOI: 10.1016/j.tws.2019.106341.
[41]	CAO Y Y Y, TAN Q H, JIANG Z G, et al. A nonlinear rate-dependent model for predicting the depth of penetration in ultra-high performance fiber reinforced concrete (UHPFRC) [J]. Cement and Concrete Composites, 2020, 106: 103451. DOI: 10.1016/j.cemconcomp.2019.103451.
[42]	LIU J, WU C Q, SU Y, et al. Experimental and numerical studies of ultra-high performance concrete targets against high-velocity projectile impacts [J]. Engineering Structures, 2018, 173: 166–179. DOI: 10.1016/j.engstruct.2018.06.098.
[43]	LIU J, WU C Q, CHEN X W. Numerical study of ultra-high performance concrete under non-deformable projectile penetration [J]. Construction and Building Materials, 2017, 135: 447–458. DOI: 10.1016/j.conbuildmat.2016.12.216.
[44]	KONG X Z, WU H, FANG Q, et al. Analyses of rigid projectile penetration into UHPCC target based on an improved dynamic cavity expansion model [J]. Construction and Building Materials, 2016, 126: 759–767. DOI: 10.1016/j.conbuildmat.2016.09.093.
[45]	PENG Y, WU H, FANG Q, et al. Modified spherical cavity-expansion model for projectile penetration into concrete targets [J]. Acta MechanicaSinica, 2019, 35(3): 518–534. DOI: 10.1007/s10409-018-0815-7.
[46]	张欣欣, 武海军, 黄风雷. 考虑剪胀效应的混凝土动态柱形空腔膨胀理论 [J]. 北京理工大学学报, 2016, 36(10): 1006–1010. DOI: 10.15918/j.tbit1001-0645.2016.10.004. ZHANG X X, WU H J, HUANG F L. Theory of dynamic cylindrical cavity expansion of concrete with shear-dilatancy [J]. Transactions of Beijing Institute of Technology, 2016, 36(10): 1006–1010. DOI: 10.15918/j.tbit1001-0645.2016.10.004.
[47]	HANAGUD S, ROSS B. Large deformation, deep penetration theory for a compressible strain-hardening target material [J]. AIAA Journal, 1971, 9(5): 905–911. DOI: 10.2514/3.6294.
[48]	NORWOOD F R. Cylindrical cavity expansion in a locking soil: SLA-74-0201 [R]. Albuquerque: Sandia Labs, 1974.
[49]	SATAPATHY S, BLESS S. Calculation of penetration resistance of brittle materials using spherical cavity expansion analysis [J]. Mechanics of Materials, 1996, 23(4): 323–330. DOI: 10.1016/0167-6636(96)00022-1.
[50]	SUBRAMANIAN R, BLESS S J. Penetration of semi-infinite AD995 alumina targets by tungsten long rod penetrators from 1.5 to 3.5 km/s [J]. International Journal of Impact Engineering, 1995, 17(4−6): 807–816. DOI: 10.1016/0734-743X(95)99901-3.
[51]	GOODIER J N. On the mechanics of indentation and cratering in solid targets of strain-hardening metal by impact of hard and soft spheres [C]// Proceedings of the 7th Symposium on Hypervelocity Impact. New York: AIAA, 1965: 215−259.
[52]	RUBIN M B. The fundamental assumptions of cavity expansion models for penetration-revisited [J]. International Journal of Impact Engineering, 2020, 146: 103723. DOI: 10.1016/j.ijimpeng.2020.103723.
[53]	RAPOPORT L, RUBIN M B. Separation and velocity dependence of the drag force applied to a rigid ovoid of Rankine nosed projectile penetrating an elastic-perfectly-plastic target [J]. International Journal of Impact Engineering, 2009, 36(8): 1012–1018. DOI: 10.1016/j.ijimpeng.2008.11.005.
[54]	KAWATA K, SHIOIRI J. High velocity deformation of solids \|\| an experimental study on the penetration of rigid projectiles into epoxy resin targets [M]. New York: Springer-Verlag, 1978: 345−350.
[55]	KONG X Z, WU H, FANG Q, et al. Response to: comment on“rigid and eroding projectile penetration into concrete targets based on an extended cavity expansion model”by Kong et al. Int. J. Impact Eng. 2017 by Z. Rosenberg et al. [J]. International Journal of Impact Engineering, 2017, 104: 150–153. DOI: 10.1016/j.ijimpeng.2017.03.003.
[56]	FELDGUN V R, YANKELEVSKY D Z, KARINSKI Y S. Cavitation phenomenon in penetration of rigid projectiles into elastic-plastic targets [J]. International Journal of Impact Engineering, 2021, 151: 103837. DOI: 10.1016/j.ijimpeng.2021.103837.
[57]	COHEN T, MASRI R, DURBAN D. Shock waves in dynamic cavity expansion [J]. Journal of Applied Mechanics, 2010, 77(4): 041009. DOI: 10.1115/1.4000914.
[58]	DENG Y J, CHEN X W, YAO Y. Study on the cavity expansion response of the concrete target under penetration [J]. Scientia Sinica Physica, Mechanica & Astronomica, 2020, 50(2): 024606. DOI: 10.1360/sspma-2019-0184.
[59]	ROSENBERG Z, DEKEL E. A numerical study of the cavity expansion process and its application to long-rod penetration mechanics [J]. International Journal of Impact Engineering, 2008, 35(3): 147–154. DOI: 10.1016/j.ijimpeng.2007.01.005.
[60]	RODRÍGUEZ-MARTÍNEZ M, COHEN T, ZAERA R. Approaching steady cavitation: the time scale in hypervelocity cavity expansion in work hardening and transformation hardening solids [J]. International Journal of Impact Engineering, 2014, 73: 43–55. DOI: 10.1016/j.ijimpeng.2014.06.005.
[61]	MASRI R, DURBAN D. Deep penetration analysis with dynamic cylindrical cavitation fields [J]. International Journal of Impact Engineering, 2009, 36(6): 830–841. DOI: 10.1016/j.ijimpeng.2008.12.006.
[62]	ANDERSON C E. Analytical models for penetration mechanics: a review [J]. International Journal of Impact Engineering, 2017, 108: 3–26. DOI: 10.1016/j.ijimpeng.2017.03.018.
[63]	WARREN T L, FOSSUM A F, FREW D J. Penetration into low-strength (23 MPa) concrete: target characterization and simulations [J]. International Journal of Impact Engineering, 2004, 30(5): 477–503. DOI: 10.1016/S0734-743X(03)00092-7.
[64]	ROSENBERG Z, DEKEL E. Analytical solution of the spherical cavity expansion process [J]. International Journal of Impact Engineering, 2009, 36(2): 193–198. DOI: 10.1016/j.ijimpeng.2007.12.014.
[65]	牛振坤, 陈小伟, 邓勇军, 等. 混凝土靶侵彻过程中空腔膨胀响应分区 [J]. 爆炸与冲击, 2019, 39(2): 023301. DOI: 10.11883/bzycj-2017-0368. NIU Z K, CHEN X W, DENG Y J, et al. Cavity expansion response of concrete targets under penetration [J]. Explosion and Shock Waves, 2019, 39(2): 023301. DOI: 10.11883/bzycj-2017-0368.
[66]	王一楠, 黄风雷. 混凝土材料动态球形空腔膨胀的数值模拟 [J]. 北京理工大学学报, 2010, 30(1): 5–9. DOI: 10.15918/j.tbit1001-0645.2010.01.010. WANG Y N, HUANG F L. Numerical simulation of dynamic spherical cavity expansion for concrete materials [J]. Transactions of Beijing Institute of Technology, 2010, 30(1): 5–9. DOI: 10.15918/j.tbit1001-0645.2010.01.010.
[67]	晋小超, 杨华伟, 王志华, 等. 混凝土材料球形空腔膨胀的数值研究 [J]. 太原理工大学学报, 2016, 47(3): 405–410. DOI: 10.16355/j.cnki.issn1007-9432tyut.2016.03.024. JIN X C, YANG H W, WANG Z H, et al. Numerical study on the dynamic spherical cavity expansion of concrete materials [J]. Journal of Taiyuan University of Technology, 2016, 47(3): 405–410. DOI: 10.16355/j.cnki.issn1007-9432tyut.2016.03.024.
[68]	MENG C M, TAN Q H, JIANG Z G, et al. Approximate solutions of finite dynamic spherical cavity-expansion models for penetration into elastically confined concrete targets [J]. International Journal of Impact Engineering, 2018, 114: 182–193. DOI: 10.1016/j.ijimpeng.2018.01.001.
[69]	WOOLSEY P. Ceramic materials screening by residual penetration ballistic testing [C]// Proceedings of13th International Symposium of Ballistics. Stockholm, 1992: 109−116.
[70]	BEN-DOR G, DUBINSKY A, ELPERIN T. New results on ballistic performance of multi-layered metal shields: review [J]. Theoretical and Applied Fracture Mechanics, 2017, 88: 1–8. DOI: 10.1016/j.tafmec.2016.11.002.
[71]	SATAPATHY S S. Application of cavity expansion analysis to penetration problems [D]. Austin: The University of Texas at Austin, 1997: 82−100.
[72]	WOO H J. Cavity expansion analysis of non-circular cross-sectional penetration problems [D]. Austin: The University of Texas at Austin, 1997.
[73]	王文杰, 张先锋, 邓佳杰, 等. 椭圆截面弹体侵彻砂浆靶规律分析 [J]. 爆炸与冲击, 2018, 38(1): 164–173. DOI: 10.11883/bzycj-2017-0020. WANG W J, ZAHNG X F, DENG J J, et al. Analysis of projectile penetrating into mortar target with elliptical cross-section [J]. Explosion and Shock Waves, 2018, 38(1): 164–173. DOI: 10.11883/bzycj-2017-0020.
[74]	LITTLEFIELD D L, ANDERSON C E, PARTOM Y, et al. The penetration of steel targets finite in radial extent [J]. International Journal of Impact Engineering, 1997, 19(1): 49–62. DOI: 10.1016/S0734-743X(96)00001-2.
[75]	ZHEN M, JIANG Z G, SONG D Y. A dynamic cylindrical cavity expansion model for the penetration of confined concrete targets [J]. Applied Mechanics and Materials, 2013, 341–342: 467–471. DOI: 10.4028/www.scientific.net/AMM.341-342.467.
[76]	ZHEN M, JIANG Z G, SONG D Y, et al. Analytical solutions for finite cylindrical dynamic cavity expansion in compressible elastic-plastic materials [J]. Applied Mathematics and Mechanics, 2014, 35(8): 1039–1050. DOI: 10.1007/s10483-014-1842-7.
[77]	FANG Q, KONG X Z, HONG J, et al. Prediction of projectile penetration and perforation by finite cavity expansion method with the free-surface effect [J]. Acta MechanicaSolidaSinica, 2014, 27(6): 597–611. DOI: 10.1016/s0894-9166(15)60005-2.
[78]	KONG X Z, FANG Q, WU H J, et al. Finite spherical cavity expansion method for layering effect [J]. Acta Mechanica SolidaSinica, 2016, 29(6): 642–654. DOI: 10.1016/s0894-9166(16)30334-2.
[79]	CHENG Y, YANG H W, SUN D A. Cavity expansion in unsaturated soils of finite radial extent [J]. Computers and Geotechnics, 2018, 102: 216–228. DOI: 10.1016/j.compgeo.2018.06.013.
[80]	曹扬悦也. 约束混凝土抗侵彻机理与工程模型研究[D]. 长沙: 国防科学技术大学, 2015: 45−65. CAO Y Y Y. Investigation on the mechanisms and engineering modeling of confined concrete against penetration [D]. Changsha: National University of Defense Technology, 2015: 45−65.
[81]	TATE A. Long rod penetration models—Part I. A flow field model for high speed long rod penetration [J]. International Journal of Mechanical Sciences, 1986, 28(8): 535–548. DOI: 10.1016/0020-7403(86)90051-2.
[82]	TATE A. Long rod penetration models—Part II. Extensions to the hydrodynamic theory of penetration [J]. International Journal of Mechanical Sciences, 1986, 28(9): 599–612. DOI: 10.1016/0020-7403(86)90075-5.
[83]	FORRESTAL M J, LONGCOPE D B. Target strength of ceramic materials for high‐velocity penetration [J]. Journalof Applied Physics, 1990, 67(8): 3669–3672. DOI: 10.1063/1.345322.
[84]	ANDERSON C E Jr, WALKER J D. An examination of long-rod penetration [J]. International Journal of Impact Engineering, 1991, 11(4): 481–501. DOI: 10.1016/0734-743X(91)90015-8.
[85]	GODWIN R P, CHAPYAK E J. Apparent target strength in long-rod penetration [J]. International Journal of Impact Engineering, 1998, 21(1–2): 77–88. DOI: 10.1016/S0734-743X(97)00029-8.
[86]	GALANOV B A, IVANOV S M, KARTUZOV V V. Investigation of penetration resistance using a new modification of the Alekseevskii-Tate model [J]. International Journal of Impact Engineering, 2003, 29(1–10): 263–272. DOI: 10.1016/j.ijimpeng.2003.09.021.
[87]	GALANOV B A, IVANOV S M, KARTUZOV V V. On one new modification of Alekseevskii-Tate model for nonstationary penetration of long rods into targets [J]. International Journal of Impact Engineering, 2001, 26(1–10): 201–210. DOI: 10.1016/S0734-743X(01)00084-7.
[88]	LAN B, WEN H M. Alekseevskii-Tate revisited: an extension to the modified hydrodynamic theory of long rod penetration [J]. Science China Technological Sciences, 2010, 53(5): 1364–1373. DOI: 10.1007/s11431-010-0011-x.
[89]	RUBIN M B, YARIN A L. A generalized formula for the penetration depth of a deformable projectile [J]. International Journal of Impact Engineering, 2002, 27(4): 387–398. DOI: 10.1016/S0734-743X(01)00061-6.
[90]	孙庚辰, 吴锦云, 赵国志, 等. 长杆弹垂直侵彻半无限厚靶板的简化模型 [J]. 兵工学报, 1981(4): 1–8. SUN G C, WU J Y, ZHAO G Z, et al. A simplified model of the penetration of the long-rod penetrator against the plates with semi-infinite thickness at normal angle [J]. Acta Armamentarii, 1981(4): 1–8.
[91]	WARREN T L. Simulations of the penetration of limestone targets by ogive-nose 4340 steel projectiles [J]. International Journal of Impact Engineering, 2002, 27(5): 475–496. DOI: 10.1016/S0734-743X(01)00154-3.
[92]	WEN H M. Predicting the penetration and perforation of FRP laminates struck normally by projectiles with different nose shapes [J]. Composite Structures, 2000, 49(3): 321–329. DOI: 10.1016/S0263-8223(00)00064-7.
[93]	WEN H M. Penetration and perforation of thick FRP laminates [J]. Composites Science and Technology, 2001, 61(8): 1163–1172. DOI: 10.1016/S0266-3538(01)00020-3.
[94]	WEN H M. Predicting the penetration and perforation of targets struck by projectiles at normal incidence [J]. Mechanics of Structures and Machines, 2002, 30(4): 543–577. DOI: 10.1081/SME-120015076.
[95]	LI Q M, REID S R, WEN H M, et al. Local impact effects of hard missiles on concrete targets [J]. International Journal of Impact Engineering, 2005, 32(1–4): 224–284. DOI: 10.1016/j.ijimpeng.2005.04.005.
[96]	TELAND J A, SJØL H. Penetration into concrete by truncated projectiles [J]. International Journal of Impact Engineering, 2004, 30(4): 447–464. DOI: 10.1016/S0734-743X(03)00073-3.
[97]	LI Q M, CHEN X W. Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile [J]. International Journal of Impact Engineering, 2003, 28(1): 93–116. DOI: 10.1016/S0734-743X(02)00037-4.
[98]	CHEN X W, FAN S C, LI Q M. Oblique and normal perforation of concrete targets by a rigid projectile [J]. International Journal of Impact Engineering, 2004, 30(6): 617–637. DOI: 10.1016/j.ijimpeng.2003.08.003.
[99]	BEN-DOR G, DUBINSKY A, ELPERIN T. Estimation of perforation thickness for concrete shield against high-speed impact [J]. Nuclear Engineering and Design, 2010, 240(5): 1022–1027. DOI: 10.1016/j.nucengdes.2009.12.029.
[100]	BEN-DOR G, DUBINSKY A, ELPERIN T. Shape optimization of impactor penetrating into concrete or limestone targets [J]. International Journal of Solids and Structures, 2003, 40(17): 4487–4500. DOI: 10.1016/s0020-7683(03)00212-9.
[101]	FREW D J, FORRESTAL M J, HANCHAK S J. Penetration experiments with limestone targets and ogive-nose steel projectiles [J]. Journal of Applied Mechanics, 2000, 67(4): 841–845. DOI: 10.1115/1.1331283.
[102]	王松川. 弹体斜侵彻弹道快速预测方法研究[D]. 长沙: 国防科学技术大学, 2011: 28−34. WANG S C. Quick prediction method of oblique penetration trajectory [D]. Changsha: National University of Defense Technology, 2011: 28−34.
[103]	康海峰, 代廷静, 沈培辉, 等. 弹体形状对侵彻弹道的影响分析 [J]. 弹箭与制导学报, 2012, 32(2): 73–76. DOI: 10.3969/j.issn.1673-9728.2012.02.020. KANG H F, DAI T J, SHEN P H, et al. The analysis of the influence of projectile’s shape on penetration trajectory [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(2): 73–76. DOI: 10.3969/j.issn.1673-9728.2012.02.020.
[104]	闪雨, 黄风雷, 武海军, 等. 动能弹非正侵彻弹道稳定性研究[C]// 第六届全国强动载效应及防护学术会议暨2014年复杂介质/结构的动态力学行为创新研究群体学术研讨会论文集. 北京: 中国力学学会, 2014: 10.
[105]	王浩, 武海军, 闫雷, 等. 椭圆横截面弹体斜贯穿双层间隔薄钢板研究 [J/OL]. 兵工学报, 2020: 1−12[2021-01-06]. https://kns.cnki.net/kns/brief/default_result.aspx. DOI: 10.3969/j.issn.1000-1093.2020.S2.001. WANG H, WU H J, YAN L, et al. Research on oblique perforation of truncated ogive-nosed projectiles with elliptic cross-section into double-layered thin steel plate with gap space [J/OL]. Acta Armamentarii, 2020: 1−12[2021-01-06]. https://kns.cnki.net/kns/brief/default_result.aspx. DOI: 10.3969/j.issn.1000-1093.2020.S2.001.
[106]	周航, 孔纲强, 曹兆虎, 等. 椭圆形孔扩张弹性分析 [J]. 固体力学学报, 2015, 36(1): 85–91. DOI: 10.19636/j.cnki.cjsm42-1250/o3.2015.01.011. ZHOU H, KONG G Q, CAO Z H, et al. Elastic analysis of elliptical cavity expansion [J]. Chinese Journal of Solid Mechanics, 2015, 36(1): 85–91. DOI: 10.19636/j.cnki.cjsm42-1250/o3.2015.01.011.
[107]	周航, 孔纲强, 刘汉龙. 饱和土体中椭圆孔扩张弹塑性解 [J]. 岩土工程学报, 2014, 36(5): 983–988. DOI: 10.11779/CJGE201405025. ZHOU H, KONG G Q, LIU H L. Elasto-plastic solution for elliptical cavity expansion in saturated soils [J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 983–988. DOI: 10.11779/CJGE201405025.