深部硐室长期稳定性的两个力学问题

王明洋; 徐天涵; 邓树新; 陈昊祥

doi:10.11883/bzycj-2021-0023

深部硐室长期稳定性的两个力学问题

doi: 10.11883/bzycj-2021-0023

1.
中国人民解放军陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏南京 210007
2.
南京理工大学机械工程学院，江苏南京 210094
3.
北京建筑大学北京交通基础设施建设国际合作基地，北京 100044

基金项目: 国家自然科学基金重大科研仪器研制项目（51527810）；国家自然科学基金青年科学基金（51909120）

详细信息

作者简介:
王明洋（1966－　），男，博士，教授，博士生导师，wmyrf@163.com

通讯作者:
徐天涵（1995－　），男，博士研究生，martinxu41@126.com

中图分类号: O389; TD322
计量
- 文章访问数: 693
- HTML全文浏览量: 446
- PDF下载量: 129
- 被引次数: 26
出版历程
- 收稿日期: 2021-01-18
- 修回日期: 2021-04-27
- 网络出版日期: 2021-06-17
- 刊出日期: 2021-07-05

Mechanical problems for the long-term stability of rocks surrounding deep level underground tunnels

1.
State Key Laboratory of Disaster Prevention and Mitigation of Explosion and Impact, Army Engineering University of PLA, Nanjing 210007, Jiangsu, China
2.
School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China
3.
Beijing International Cooperation Base for Municipal Transportation Infrastructures, Beijing University of Civil Engineering and Architecture, Beijing 100044, China

摘要

摘要: 在陈宗基院士关于地下硐室长期稳定性力学问题研究的基础上，采用Sadovsky院士关于复杂地质岩体的等级构造学说，围绕深部岩体非均匀构造与封闭应力固有的统计力学属性，研究了岩体非均匀变形与封闭应力特性，以及深部硐室围岩的长期稳定性等两个力学问题。给出了岩体非均匀构造与封闭应力的数学表征；根据质量守恒定律得到了计算深部硐室围岩长期变形的一般公式；得到了围岩变形中劈裂扩容变形占主要部分的结论，并且阐明了深部围岩卸荷时更易出现劈裂破坏的原因。给出了劈裂破坏形态的演进序列与扩容位移的计算方法。将围岩松动圈范围、破裂区位置和边壁位移的计算结果与锦屏一级电站厂房现有监测数据进行了对比，两者相当吻合。
- 地应力 /
- 非均匀块系构造 /
- 非相容变形 /
- 剪切强度 /
- 围岩分区破裂化现象
Abstract: Based on the research of Academician Tan Tjong-Kie on the long-term stability mechanics of underground tunnel and considering Academician Sadovsky’s structural hierarchy theories on complex geological rock masses, the inherent statistical mechanical properties of inhomogeneous structure and closed stress in deep rock masses were investigated. Two mechanical problems were mainly studied, i.e. characteristics of inherent non-uniform deformation and closed stress of rock masses, and long-term stability of deep tunnels. The quantitative mathematical characterization of inherent non-uniform deformation and closed stress of rock masses were given using the method of statistical mechanics. Based on the law of mass conservation, a general calculation method of long-term stability and deformation of rock masses surrounding deep level tunnels was proposed. The Maxwell model was used to calculate the threshold of splitting. A post-peak failure model of rock was established to estimate the in-situ stress at which rock undergoes post-peak failure. With the help of the theory of the hirerachical structure of rock masses, the maximum value of rock displacement due to splitting dilatation was obtained. A dimensionless energy factor was introduced to define the extent of zonal disintegration of surrounding rock masses. It was concluded that the splitting and dilatancy deformation is the main part of the deformation of surrounding rocks. The reasons why unloading splitting failure is more likely to take place in rock masses surrounding deep level tunnels were explained. The split evolution pattern of rock masses surrounding deep level tunnels and the calculation method of dilatancy displacement were obtained. The calculation results of the range of loosening zone, the location of the rupture zone in rock masses surrounding deep level tunnels, and the displacement of the sidewall were compared with the existing monitoring data in the underground powerhouse of the Jinping Ⅰ Hydropower Station, and the agreement is good.
- geo-stress /
- heterogeneous blocky structure /
- non-compatible deformation /
- shear strength /
- zonal disintegration of surrounding rock masses

HTML全文

如何控制爆破振动，减少爆破施工对周围环境和人员的危害，一直是爆破工程安全技术人员研究的重要课题^[1-2]。目前，爆破领域衡量爆破振动强度的物理量主要是速度和加速度^[3]。虽然理论上已经有许多测试爆破振动速度和加速度的仪器与设备，但从实施难易程度看，爆破振动速度传感器的测量容易受到环境或传感器安装条件的限制，有时无法直接测量。和爆破振动速度传感器相比，爆破振动加速度传感器的安装要容易，这是因为爆破振动加速度传感器具有体积小、重量轻、安装方便、灵敏度高等优点。因此，在实际工程中爆破振动加速度测试得到了广泛的应用^[4-5]。

理论上，对监测到的实测爆破振动加速度信号进行一次数值积分即可得到爆破振动速度信号。对实测爆破振动加速度信号进行数值积分的算法，按数据处理过程可以分为频域积分法和时域积分法两种。频域积分法主要是利用傅里叶正、反变换，积分在频域内以傅里叶系数来表示，这就不可避免地存在由于频率截断误差而引起的能量泄漏^[6]。时域积分法通常采用梯形公式，受零点漂移或灵敏度漂移影响较大，需要对爆破振动信号进行剔除趋势项或滤波处理，具有代表性的算法主要有差分法、低通滤波法、最小二乘法、小波变换法或固有模态分解法等^[7-9]。然而，采用上述方法仍不能将爆破振动信号中的时域积分趋势项予以去除，残余的微小误差在时域积分过程中也会积累而逐渐放大，甚至会使爆破振动信号发生非线性失真，而时域积分算法本身也会产生趋势项，从而严重降低爆破振动信号频谱分析的精度。

为了更精确地提取爆破振动信号中振动峰值和各频率区间内能量等重要特征，必须对爆破振动加速度信号时域积分中的趋势项予以去除。本文中以此为切入点，在模式自适应小波原理的基础上^[10]，通过对实测爆破振动加速度信号进行梯形数值积分，构建将时域积分后的爆破振动速度信号作为小波基函数的方法，用构造模式自适应爆破振动小波基函数的方法来剔除时域积分后爆破振动速度信号中的趋势项，从而提高爆破振动信号时域和频域分辨率。

1. 模式自适应小波理论

1.1 连续小波变换

设函数ψ(t)∈L²(R)，其连续傅里叶变换为 $\hat{\psi }(\omega )$ ^[11]。当 $\hat{\psi }(\omega )$ 满足下列容许性条件：

${{C}_{\psi }}=\int_{\bf{R}}{\frac{{{\left| \hat{\psi }(\omega ) \right|}^{2}}}{\left| \omega \right|}\text{d}\omega }<\infty$

时，则称函数ψ(t)为一个基本小波。若将该基本小波ψ(t)通过伸缩与平移等运算处理后，就可得到一组连续小波序列，称之为连续小波基函数，即：

${{\psi }_{a, b}}\left( t \right)=\frac{1}{\sqrt{\left| a \right|}}\psi \left( \frac{t-b}{a} \right)$

(1)

式中：a为尺度因子(a≠0)，b为平移因子。

对于任意平方可积的函数或信号f(t)，即f(t)∈L²(R)，其关于小波基函数ψ_{a, b}(t)的连续小波变换为：

${{W}_{f}}\left( a, b \right)=<f\left( t \right), {{\psi }_{a, b}}\left( t \right)>=\frac{1}{\sqrt{\left| a \right|}}\int_{\bf{R}}{f\left( t \right)\overline{\psi \left( \frac{t-b}{a} \right)}\text{d}t}$

(2)

式中：＜f(t), ψ_{a, b}(t)＞为函数或信号f(t)与小波基函数ψ_{a, b}(t)的内积， $\overline{\psi \left( \frac{t-b}{a} \right)}$ 为 $\psi \left( \frac{t-b}{a} \right)$ 的共轭函数。

由式(2)可以看出，连续小波变换的实质是将函数或信号f(t)以小波基函数序列ψ_{a, b}(t)为基底进行展开，由此可以求得函数或信号f(t)在小波基函数序列ψ_{a, b}(t)上的投影，即采用不同时间、不同尺度的小波基函数序列对被分析函数或信号f(t)进行相似性分析。若要使被分析函数或信号f(t)的时频特征在小波变换系数上更好地呈现，则需要将被分析函数或信号f(t)在小波基函数序列ψ_{a, b}(t)上的投影系数尽可能大。换一句话说，小波基函数序列ψ_{a, b}(t)的时域波形应与被分析函数或信号f(t)的特征波形具有良好的局部形状相似性。

1.2 模式自适应连续小波

模式自适应连续小波是利用最佳平方逼近方法来设计一个与给定函数(或信号波形)的局部特征相似度高的小波^[12]。具体的实现方法有多项式逼近法和常数正交函数空间投影法2种。若给定的函数(或信号波形)比较简单，则可以选择多项式逼近法；若给定的函数(或信号波形)比较复杂，则可以选择常数正交函数空间投影法。参数规则度定义了模式自适应连续小波在紧支撑区间上的边界约束，可以是“无”或“连续”或“可微”。若对给定函数(或信号波形)进行多项式逼近，参数规则度选择连续约束条件时，多项式拟合阶次应大于等于3；参数规则度选择可微约束条件时，多项式拟合阶次应大于等于5。

基于上述构造模式自适应连续小波的思想^[13-14]，其过程大致可以分为3个步骤：

(1) 根据给定函数(或信号波形)的检测模式x(t)，设置逼近方法和边界条件，构建模式自适应连续小波ψ_x(t)，不失一般性，设模式自适应连续小波的紧支撑区间为[0, 1]，则有 $\int_{0}^{1}{{{\psi }_{x}}(t)\text{d}t=0}$ 以及 ${{\left\| {{\psi }_{x}}(t) \right\|}_{2}}=1$ ；

(2) 检测给定函数(或信号波形)上所有的虚警，对任意b和a>0的情况，搜索函数(或信号波形)的局部极大值点；

(3) 检测和丢弃给定函数(或信号波形)上所有错误的虚警，这一规则必须应用于确定每个虚警是否错误。

2. 爆破振动信号趋势项的去除

2.1 爆破振动加速度信号的测试

爆破振动加速度信号测试时，除了考虑选择性能优良的仪器、设备与测试系统外，还需要根据爆破振动加速度信号测试的目的来标定测振系统与设置测振仪量程、采样频率、触发与延迟时间等参数^[15]。

通过对某个矿床进行大量的爆破振动加速度测试，从中抽取1个测点所监测到的爆破振动加速度信号进行分析，实测爆破振动加速度信号a时程曲线及其相应的傅里叶功率谱密度P见图 1。

图 1 爆破振动加速度信号及功率谱密度

Figure 1. Time history and power spectrum density of blast vibration acceleration signal

下载: 全尺寸图片幻灯片

2.2 爆破振动加速度信号的积分变换

将爆破振动加速度信号转化为速度信号时，常采用梯形求积的数值积分法。设实测爆破振动加速度信号为{x(k)} (k=0, 1, 2, …N; N为爆破振动速度信号序列中包含离散采样点的个数)，则可以根据梯形求积公式，求得爆破振动速度信号为

$y\left( k \right)=\Delta t\sum\limits_{i=1}^{k}{\frac{x\left( i-1 \right)+x\left( i \right)}{2}}\ \ \ \ \ k=1, 2, 3, \cdots , N$

(3)

根据式(3)，采用MATLAB编程语言对实测爆破振动加速度信号进行梯形数值积分，结果如图 2(a)所示。图 2(b)为时域积分后爆破振动速度信号的傅里叶功率谱密度。从图 2可以看出，爆破振动速度信号时程曲线存在明显的零点漂移现象；爆破振动速度信号功率谱密度中的优势频率主要集中在0~100 Hz频率范围内，再对功率谱密度低频部分进行局部放大，可以清楚地观察到0~5 Hz频率范围内具有较大幅值的低频直流分量。因此，爆破振动速度信号中趋势项的存在严重影响了爆破振动速度信号时程曲线波动特征的准确性和功率谱分析的分辨率，必须予以去除。

图 2 时域积分后的爆破振动速度信号及功率谱密度

Figure 2. Time history and power spectrum density of blast vibration velocity signal after time integration

下载: 全尺寸图片幻灯片

2.3 去均值化

爆破振动速度信号的均值是爆破振动速度信号离散值{y(k)} (k=0, 1, 2, …N)在整个时间坐标轴上的积分平均，其物理含义为该爆破振动速度信号变化的中心趋势，或称为零点漂移。由测振仪或传感器的低频直流分量引起，因此，可以通过去均值公式来实现：

$y'\left( k \right)=y\left( k \right)-{{\mu }_{y}}=y\left( k \right)-\sum\limits_{k=1}^{N}{y\left( k \right)/N}$

(4)

式中：y′(k)为去均值后的爆破振动速度信号；y(k)为爆破振动速度信号；μ_y为爆破振动速度信号的算术平均值。

2.4 模式自适应连续小波法去除爆破振动信号趋势项

利用MATLAB软件平台上的小波工具箱(Wavelet Toolbox)，对图 2(a)所示的爆破振动速度信号进行去均值化处理，然后对其进行模式自适应波形匹配，构造出满足小波容许性条件的模式自适应小波基，用构造模式自适应小波基的方法剔除去均值化后爆破振动速度信号中的趋势项。图 3(a)和3(b)分别为去除趋势项后爆破振动速度信号时程曲线及其相应的傅里叶功率谱密度。从图 3(a)可以看出，去除趋势项后爆破振动速度信号第一个记录点和最后一个记录点的速度值均为零，与图 2(a)中的时程曲线进行比较，模式自适应连续小波法已成功去除了去均值化后爆破振动速度信号中趋势项的影响。对比分析图 3(b)与图 2(b)可以看出，模式自适应连续小波法已成功去除了低频直流分量的干扰，同时可知去除趋势项后的爆破振动速度信号功率谱(见图 3(b))与实测爆破振动加速度信号功率谱(见图 1(b))的优势频率均为92 Hz，且两者的相关系数高达0.953 8，由此可以表明用模式自适应连续小波法去除爆破振动信号中的趋势项是完全可行的。

图 3 去除趋势项后的爆破振动速度信号及功率谱密度

Figure 3. Time history and power spectrum density of blast vibration velocity signal after removal trend

下载: 全尺寸图片幻灯片

3. 爆破振动信号各频率区间的能量分布

3.1 爆破振动信号各频率区间的划分

采用小波包分析技术对爆破振动信号进行各频率区间分解，分解的有效深度实际上应根据爆破振动信号分析的目的以及所采用爆破振动记录仪的最小工作频率而定。本次现场实验所选用的采样频率为1 024 Hz，由Shannon采样定理可知，则其Nyquist频率为512 Hz。由于爆破振动记录仪的最小工作频率为5 Hz，根据小波包分解原理以及试验分析的需要，可以将各测点爆破振动信号分解到第7层，则爆破地震波按照从低到高划分为如下128个频率区间：0~4，4~8，8~12，…，508~512 Hz。

3.2 各频率区间信号的能量表征

选取爆破振动信号的全频带[0 Hz, 512 Hz]作为频率区间，对爆破振动信号进行小波包分解，然后由小波包重构公式求取爆破振动信号各频率区间内的重构子信号，则原始爆破振动信号完全可以由这些重构子信号来表示^[16]，即：

$f\left( t \right)=\sum\limits_{j=0}^{{{2}^{7}}-1}{{{S}_{7, j}}\left( t \right)={{S}_{7, 0}}\left( t \right)+{{S}_{7, 1}}\left( t \right)+\cdots +{{S}_{7, {{2}^{7}}-1}}\left( t \right)}$

(5)

式中：S_{7, j}(t) (j=0, 1, 2, …, 2⁷-1)为原始爆破振动信号f(t)第j个节点上的重构子信号。

爆破振动信号各频率区间内的重构子信号能量可以表示为：

${{E}_{7, j}}=\int {{\left| {{S}_{7, j}}\left( t \right) \right|}^{2}}\text{d}t=\sum\limits_{k=1}^{m}{{{\left| {{x}_{j, k}}\left( t \right) \right|}^{2}}}$

(6)

式中：x_{j, k}(t) (j=0, 1, 2, …, 2⁷-1;k=1, 2, …, m)为重构子信号S_{7, j}(t)离散采样点的幅值；m为爆破振动信号离散采样点的个数。

由式(6)可知，设原始爆破振动信号的总能量为E₀，则有：

${{E}_{0}}=\sum\limits_{j=0}^{{{2}^{7}}-1}{{{E}_{7, j}}}$

(7)

爆破振动信号各频率区间内的重构子信号能量占被分析信号总能量的比例为

${{\eta }_{j}}=\frac{{{E}_{7, j}}}{{{E}_{0}}}\times 100\%\$

(8)

3.3 各频率区间信号的能量分布规律

根据式(6)~(8)，用MATLAB语言编写程序，然后分别对图 1(a)所示的爆破振动加速度信号和图 3(a)所示的去除趋势项后的爆破振动速度信号进行小波包分解，得到各频率区间内信号能量分布的计算结果，图 4(a)和4(b)分别为爆破振动加速度信号和去除趋势项后爆破振动速度信号在不同频率范围内的能量分布。通过分别对照图 4(a)与图 1(b)以及图 4(b)与图 3(b)可以看出，与建立在传统Fourier变换基础上的频谱分析相比，基于小波变换的能量分析具有更精细的频率分辨率。从图 4可以看出，爆破振动信号绝大部分能量都集中在40~140 Hz频率范围内，分别占爆破振动信号总能量的89.08%和92.89%，但两者的相关系数仅为0.546 6；实测爆破振动加速度信号与爆破振动速度信号在不同频率范围内能量分布的方差分别为7.214 7和5.955 2，由此表明爆破振动速度信号比实测爆破振动加速度信号在不同频率范围内能量分布更均匀。若将爆破振动信号各频率区间范围划分得稍宽一点，即划分成如下8个频率区间：0~20、20~40、40~60、60~80、80~100、100~120、120~140和140~512 Hz，则爆破振动信号各频率区间内能量占被分析信号总能量的百分比见表 1。由表 1可以计算出，实测爆破振动加速度信号与爆破振动速度信号各频率区间内能量分布的相关系数高达0.968 1。由此表明，各频率区间范围划分越宽，实测爆破振动加速度信号与爆破振动速度信号各频率区间内能量分布的相关程度越高。

图 4 爆破振动信号的能量分布

Figure 4. Energy distribution of blast vibration signal in different frequency ranges

下载: 全尺寸图片幻灯片

表 1 爆破振动信号各频率区间内能量分数

Table 1. Percentage of energy of blast vibration signals in different frequency ranges

加速度信号		速度信号
f/Hz	能量分数/%	f/Hz	能量分数/%
0~20	0.32	0~20	0.65
20~40	1.28	20~40	1.41
40~60	8.95	40~60	7.18
60~80	4.76	60~80	8.66
80~100	25.49	80~100	25.06
100~120	34.92	100~120	41.38
120~140	14.96	120~140	10.61
140~512	9.32	140~512	5.05

下载: 导出CSV

| 显示表格

3. 结论

(1) 在模式自适应小波原理的基础上，提出了将实测爆破振动加速度信号梯形数值积分后的爆破振动速度信号作为一个模式自适应小波基的方法，采用该方法可成功去除时域积分后爆破振动速度信号中趋势项的干扰，并通过实测爆破振动加速度信号功率谱与爆破振动速度信号功率谱的比较，验证了该方法是切实可行的；

(2) 通过对去除趋势项后的爆破振动速度信号进行能量特征分析，并将此法与爆破振动速度信号傅里叶谱分析作了比较：基于小波变换的能量分析比傅里叶谱分析具有更精细的频率分辨率，更适合于对频率分辨率要求更高的爆破振动信号进行分析；

(3) 将实测爆破振动加速度信号与去除趋势项后爆破振动速度信号的各频率区间内能量特征作了比较，得到频率区间范围划分越宽，实测爆破振动加速度信号与爆破振动速度信号在不同频率范围内能量分布的相关程度越高；反之，相关程度越低。

图 1 岩体的构造等级示意图

Figure 1. Sketch of hierarchical structure of rock blocks

下载: 全尺寸图片幻灯片

图 2 第n级非均匀构造单元的变形阶段

Figure 2. The deformation stages of the nth non-uniform structure

下载: 全尺寸图片幻灯片

图 3 硐室开挖前后侧墙围岩应力状态的变化^[1]

Figure 3. The change of stress state of surrounding rocks before and after the tunneling^[1]

下载: 全尺寸图片幻灯片

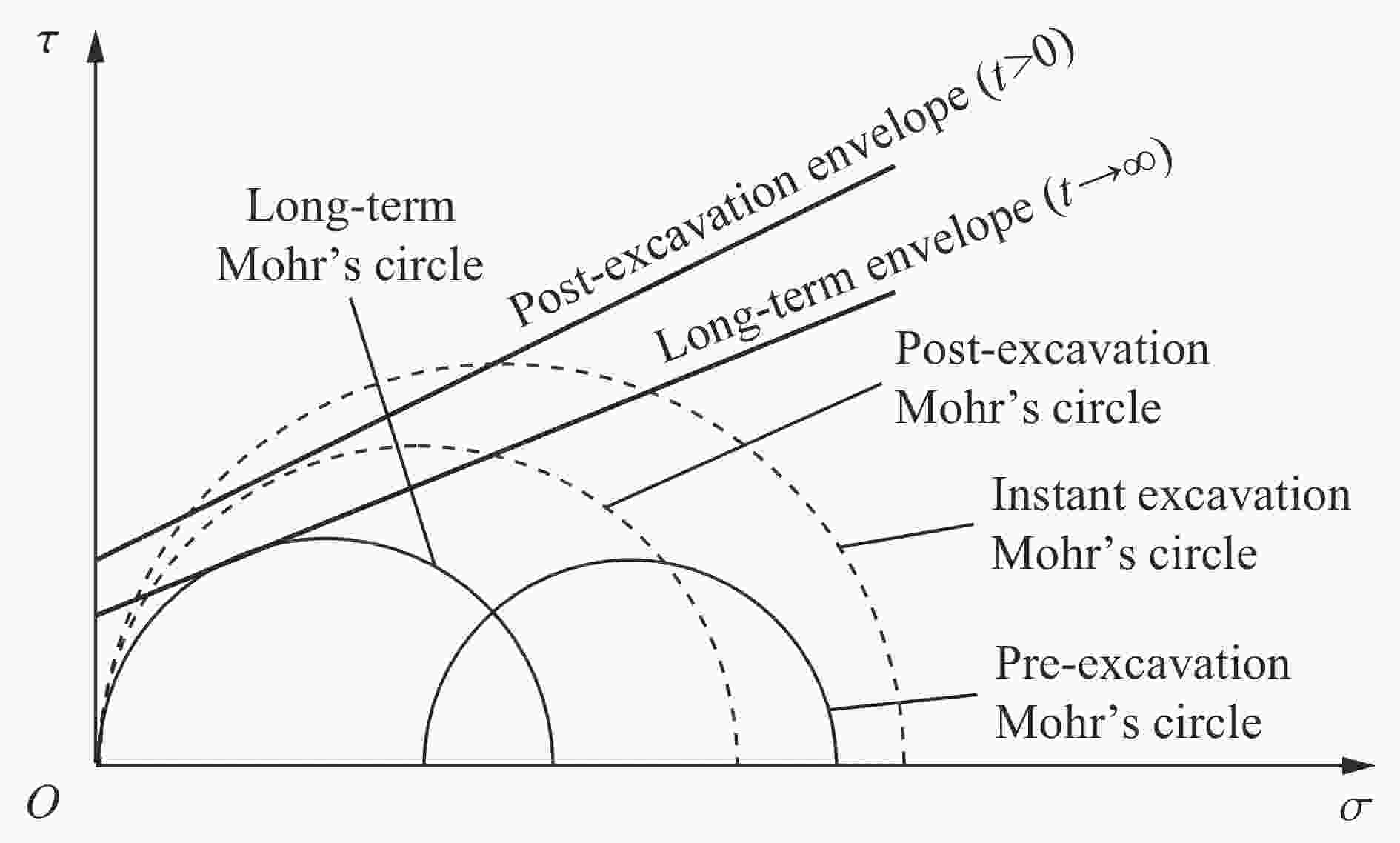
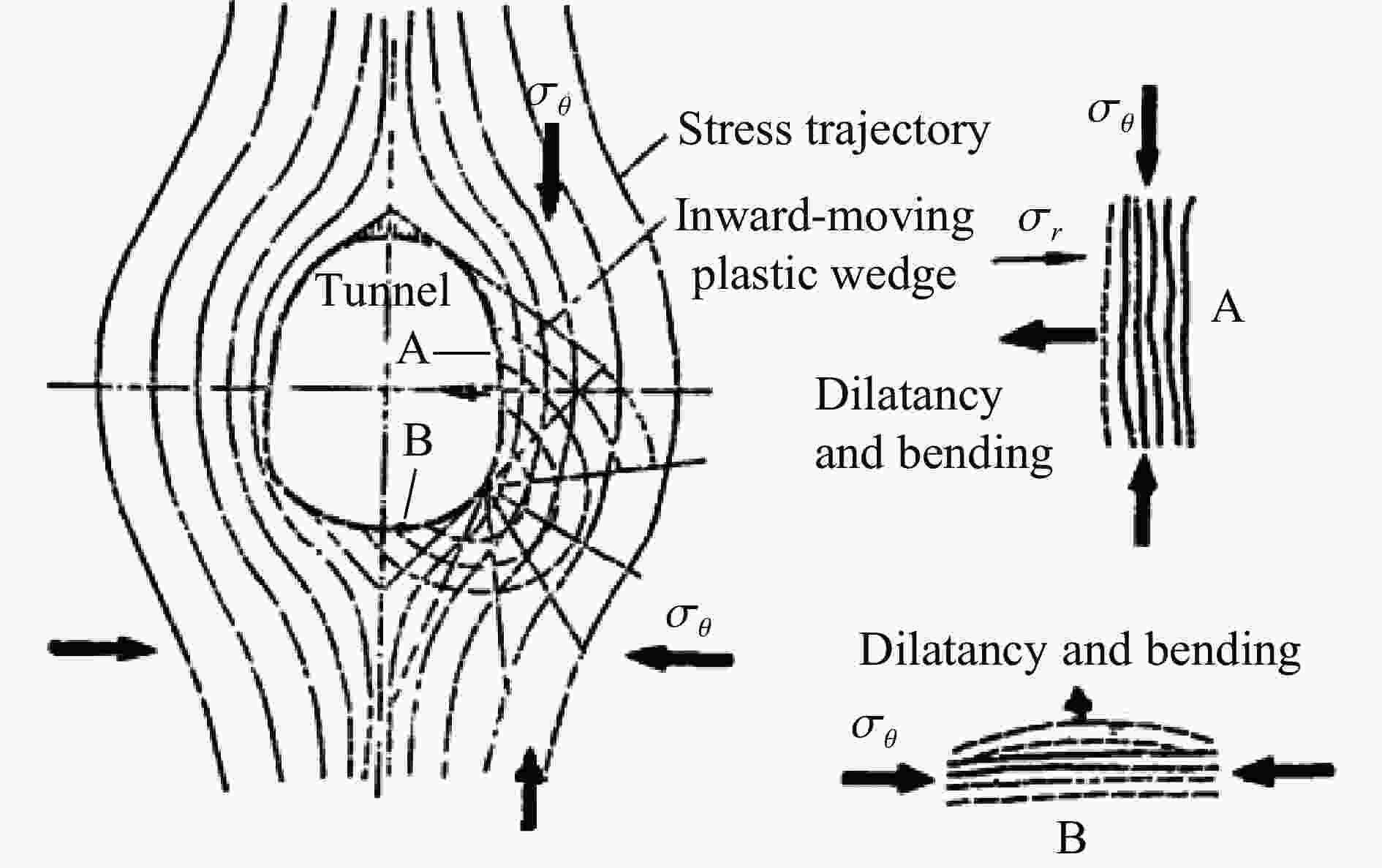
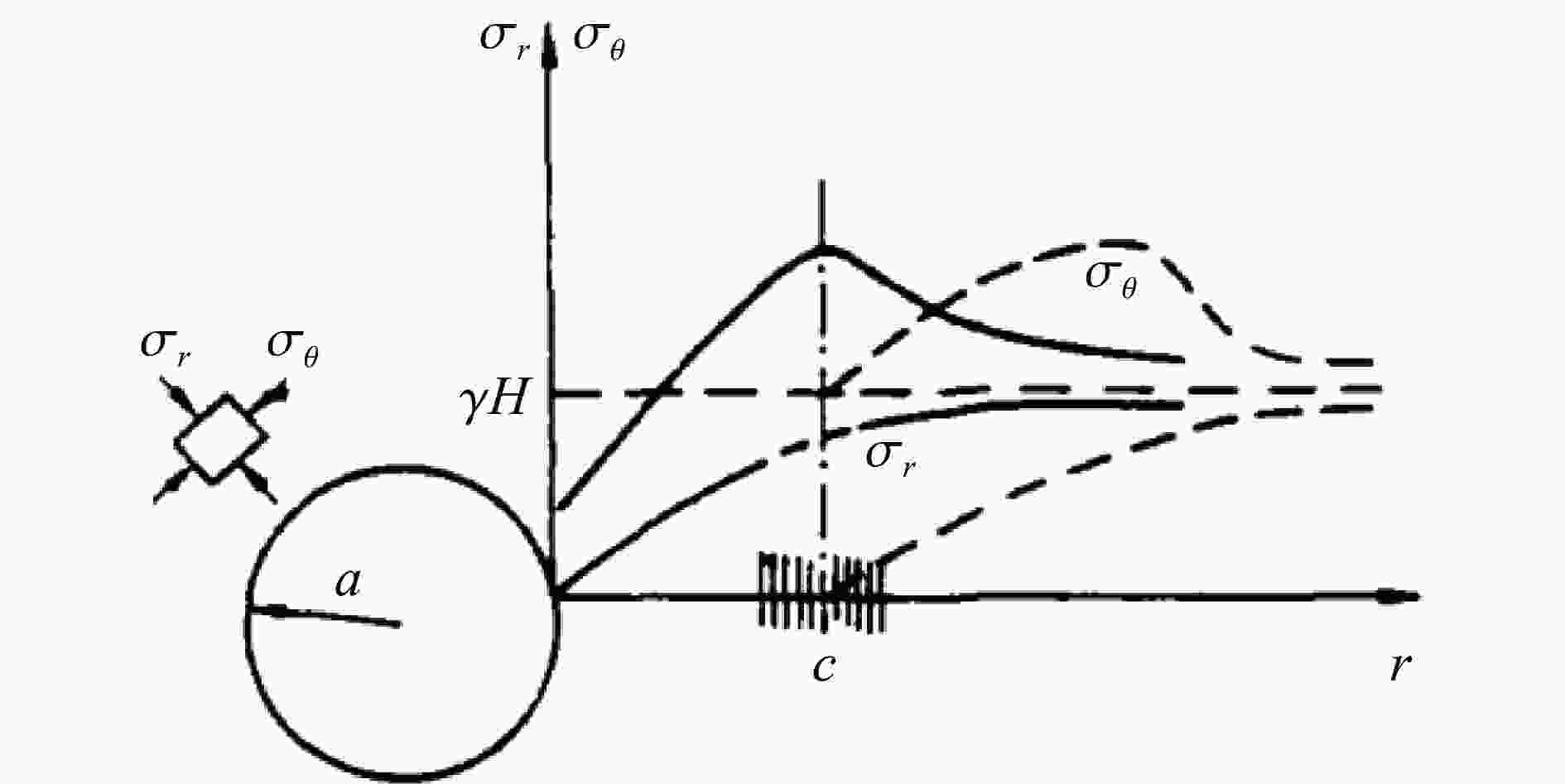
图 4 硐室开挖前后侧墙围岩应力圆^[1]

Figure 4. The stress circles of surround rocks before and after the tunneling

下载: 全尺寸图片幻灯片

图 5 三向应力状态时的强度准则

Figure 5. Strength criterion at triaxial stress state

下载: 全尺寸图片幻灯片

图 6 锦屏大理岩真三轴实验结果

Figure 6. The true triaxial test results of the marble in Jinping.

下载: 全尺寸图片幻灯片

图 7 体积变形与剪切变形的关系

Figure 7. The relationship between bulk and shear deformations

下载: 全尺寸图片幻灯片

图 8 塑性区围岩位移示意图

Figure 8. The deformation of surrounding rocks in the plastic zone

下载: 全尺寸图片幻灯片

图 9 地下硐室围岩劈裂示意图^[1]

Figure 9. The schematic diagram of spalling of rocks surrounding deep level tunnels^[1]

下载: 全尺寸图片幻灯片

图 10 深部围岩劈裂示意图

Figure 10. The splitting of deep surrounding rocks

下载: 全尺寸图片幻灯片

图 11 深部围岩分区破裂示意图

Figure 11. Diagram of zonal disintegration of deep surrounding rocks

下载: 全尺寸图片幻灯片

图 12 分区破裂半径计算与监测结果对比^[25]

Figure 12. A comparison between the in-situ and theoretical radii of zonal disintegration^[25]

下载: 全尺寸图片幻灯片

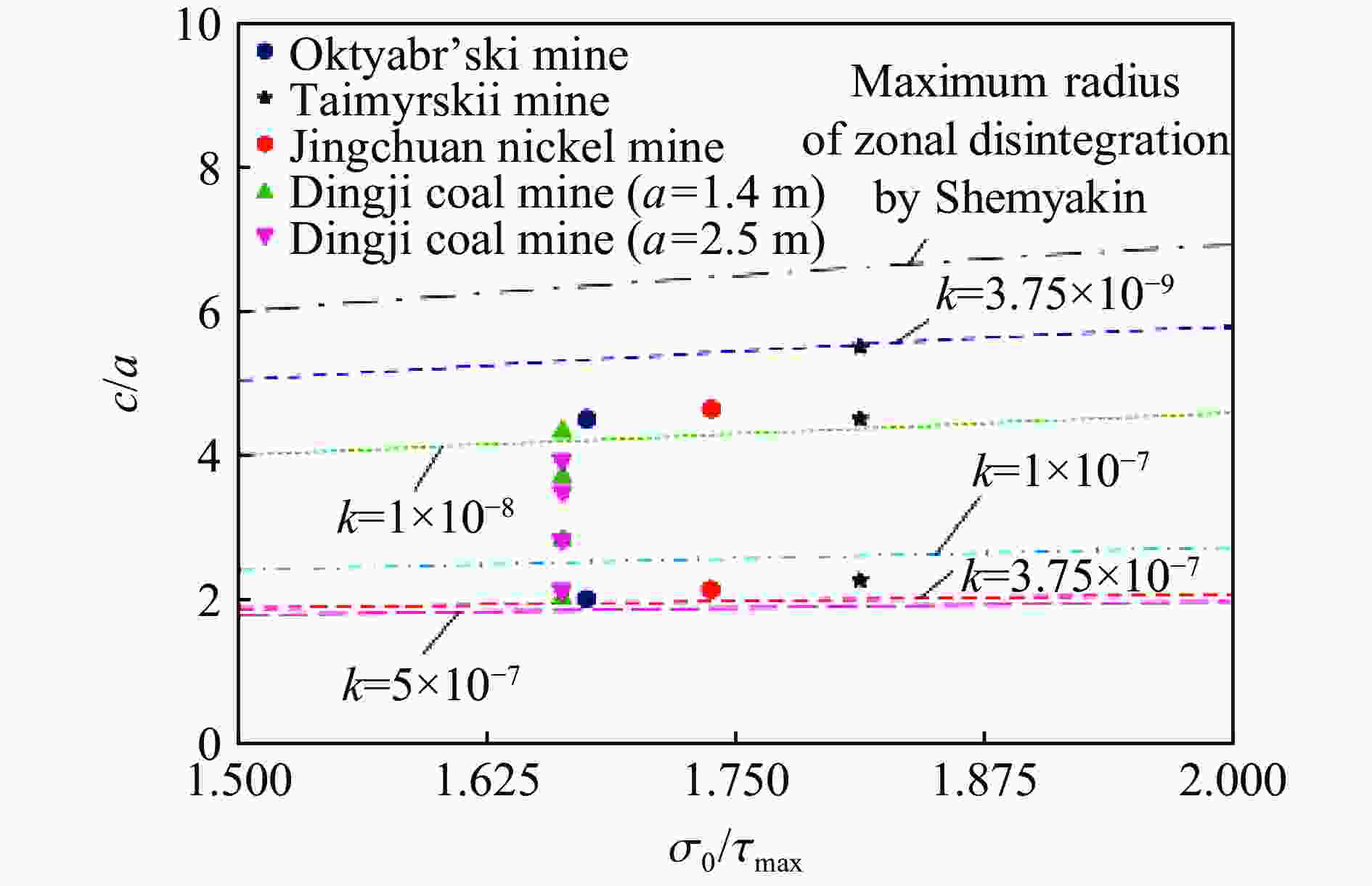
表 1 分区破裂区半径c_i/a与能量因子k之间的关系^[25]

Table 1. The relationship between the radii of zonal disintegration c_i/a and the energy factor k^[25]

c_i/a	k
exp(1/2)	1.4×10⁻⁶
exp(1)	1.0×10⁻⁷
exp(3/2)	1.0×10⁻⁸
exp(2)	1.4×10⁻⁹

下载: 导出CSV

表 2 围岩变形理论与现场实测结果对比

Table 2. Comparison of the theoretical and in-situ results

硐室	等效半径/m	ψ_Δ	理论扩容变形/mm	理论剪切变形/mm	理论总变形/mm	实测变形/mm
主变室^[18]	14.17	0.5×10⁻²	60.9	37.0	97.9	233.4
		1.0×10⁻²	121.7		158.7
		1.5×10⁻²	182.6		219.6^*
		2.0×10⁻²	243.5		280.5
主厂房^[17]	23.82	0.5×10⁻²	102.3	62.2	164.5	上游220.0 下游247.0
		1.0×10⁻²	204.6		266.8^*
		1.5×10⁻²	307.0		369.2
		2.0×10⁻²	409.3		471.5
尾调室^[17]	17.50	0.5×10⁻²	75.2	45.7	120.9^*	125.0
		1.0×10⁻²	150.3		196.0
		1.5×10⁻²	225.5		271.2
		2.0×10⁻²	300.7		346.4
注：表中数据加*号的阶段为与实际最接近的变形阶段。

下载: 导出CSV

参考文献(43)

[1]	陈宗基. 地下巷道长期稳定性的力学问题 [J]. 岩石力学与工程学报, 1982, 1(1): 1–20. CHEN Z J. The mechanical problems for the long-term stability of ground galleries [J]. Chinese Journal of Rock Mechanics and Engineering, 1982, 1(1): 1–20.
[2]	陈宗基, 吴海青. 我国在复杂岩层中的巷道掘进——兼论构造应力与时间效应的重要性 [J]. 岩石力学与工程学报, 1988, 7(1): 1–14. DOI: 10.3321/j.issn:1000-324X.1999.03.022. CHEN Z J, WU H Q. Tunnelling in complex rock formations in China—importance of geotectonic stress and time effects [J]. Chinese Journal of Rock Mechanics and Engineering, 1988, 7(1): 1–14. DOI: 10.3321/j.issn:1000-324X.1999.03.022.
[3]	陈宗基, 康文法. 岩石的封闭应力、蠕变和扩容及本构方程 [J]. 岩石力学与工程学报, 1991, 10(4): 299–312. CHEN Z J, KANG W F. On the locked in stress, creep and dilatation of rocks, and the constitutive equations [J]. Chinese Journal of Rock Mechanics and Engineering, 1991, 10(4): 299–312.
[4]	陈宗基. 根据流变学与地球动力学观点研究新奥法 [J]. 岩石力学与工程学报, 1988, 7(2): 97–106. CHEN Z J. The NATM studied from the viewpoint of rheology and geodynamics [J]. Chinese Journal of Rock Mechanics and Engineering, 1988, 7(2): 97–106.
[5]	陈宗基, 石泽全, 于智海, 等. 用8000 kN多功能三轴仪测量脆性岩石的扩容、蠕变及松弛 [J]. 岩石力学与工程学报, 1989, 8(2): 97–118. CHEN Z J, SHI Z Q, YU Z H, et al. Dilatancy creep and relaxation of brittle rocks measured with the 8000 kN multipurpose triaxial apparatus [J]. Chinese Journal of Rock Mechanics and Engineering, 1989, 8(2): 97–118.
[6]	ADUSHKIN V V, SPIVAK A A. Geomechanics of large-scale explosions [M]. Moscow: Nedra, 1993.
[7]	SADOVSKY M A. Nature of lumpiness of rock [J]. Doklady Akademii Nauk SSSR, 1979, 247(4): 829–831.
[8]	KURLENYA M V, ADUSHKIN V V, OPARIN V N. Alternating reaction of rocks to dynamic action [J]. Doklady Akademii Nauk SSSR, 1992, 2: 323.
[9]	KURLENYA M V, OPARIN V N. Problems of nonlinear geomechanics. PartⅠ [J]. Journal of Mining Science, 1999, 35(3): 216–230. DOI: 10.1007/BF02550237.
[10]	KURLENYA M V, OPARIN V N. Problems of nonlinear geomechanics. PartⅡ [J]. Journal of Mining Science, 2000, 36(4): 305–326. DOI: 10.1023/A:1026673105750.
[11]	钱七虎. 战略防护工程面临的核钻地弹威胁及连续介质力学模型的不适用性 [M]//钱七虎. 钱七虎院士论文选集. 北京: 科学出版社, 2007.
[12]	KOCHARYAN G G, SPIVAK A A. BUDKOV A M Movement of rock blocks during large-scale underground explosion. Part Ⅱ: estimates by analytical models, numerical calculations, and comparative analysis of theoretical and experimental data [J]. Journal of Mining Science, 2001, 37(2): 149–168. DOI: 10.1023/A:1012327627277.
[13]	KOCHARYAN G G, SPIVAK A A. Movement of rock blocks during large-scale underground explosions. PartⅠ: experimental data [J]. Journal of Mining Science, 2001, 37(1): 64–76. DOI: 10.1023/A:1016736919590.
[14]	陈宗基. 岩爆的工程实录、理论与控制 [J]. 岩石力学与工程学报, 1987, 6(1): 1–18. CHEN Z J. Rockbursts, case records, theory and control [J]. Chinese Journal of Rock Mechanics and Engineering, 1987, 6(1): 1–18.
[15]	ADUSHKIN V V, OPARIN V N. From the alternating-sign explosion response of rocks to the pendulum waves in stressed geomedia. PartⅠ [J]. Journal of Mining Science, 2012, 48(2): 203–222. DOI: 10.1134/S1062739148020013.
[16]	ADUSHKIN V V, SPIVAK A A. Chapter 8: the influence of faults, joints, and fractures, on mechanical effects of underground nuclear explosions [M]// ANASTASIA S, PAUL R, trans. Underground Explosions. 2015: 431−479.
[17]	黄书岭, 王继敏, 丁秀丽, 等. 基于层状岩体卸荷演化的锦屏Ⅰ级地下厂房洞室群稳定性与调控 [J]. 岩石力学与工程学报, 2011, 30(11): 2203–2216. HUANG S L, WANG J M, DING X L, et al. Stability and control for underground caverns of JinpingⅠ hydropower station based on unloading evolution of layered rockmass [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(11): 2203–2216.
[18]	QIAN Q H, ZHOU X P. Failure behaviors and rock deformation during excavation of underground cavern group for Jinping I hydropower station [J]. Rock Mechanics and Rock Engineering, 2018, 51(8): 2639–2651. DOI: 10.1007/s00603-018-1518-x.
[19]	FENG X T, PEI S F, JIANG Q, et al. Deep fracturing of the hard rock surrounding a large underground cavern subjected to high geostress: in situ observation and mechanism analysis [J]. Rock Mechanics and Rock Engineering, 2017, 50(8): 2155–2175. DOI: 10.1007/s00603-017-1220-4.
[20]	ZHAO J, FENG X T, ZHANG X W, et al. Brittle-ductile transition and failure mechanism of Jinping marble under true triaxial compression [J]. Engineering Geology, 2018, 232: 160–170. DOI: 10.1016/j.enggeo.2017.11.008.
[21]	李帅军, 冯夏庭, 徐鼎平, 等. 白鹤滩水电站主厂房第Ⅰ层开挖期围岩变形规律与机制研究 [J]. 岩石力学与工程学报, 2016, 35(S2): 3947–3959. DOI: 10.13722/j.cnki.jrme.2016.0799. LI S J, FENG X T, XU D P, et al. Study of the characteristics and mechanism of surrounding rock deformation during the first layer excavation in Baihetan hydorpower station underground main powerhouses [J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(S2): 3947–3959. DOI: 10.13722/j.cnki.jrme.2016.0799.
[22]	REVUZHENKO A P. Mechanics of elastoplastic media and nonstandard analysis [M]. Novosbirsk: Izd, NGU, 2000.
[23]	WANG M Y, LI J, MA L J, et al. Study on the characteristic energy factor of the deep rock mass under weak disturbance [J]. Rock Mechanics and Rock Engineering, 2016, 49(8): 3165–3173. DOI: 10.1007/s00603-016-0968-2.
[24]	王明洋, 李杰. 爆炸与冲击中的非线性岩石力学问题Ⅲ: 地下核爆炸诱发工程性地震效应的计算原理及应用 [J]. 岩石力学与工程学报, 2019, 38(4): 695–707. DOI: 10.13722/j.cnki.jrme.2018.1078. WANG M Y, LI J. Nonlinear mechanics problems in rock explosion and shock. Part Ⅲ: the calculation principle of engineering seismic effects induced by underground nuclear explosion and its application [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(4): 695–707. DOI: 10.13722/j.cnki.jrme.2018.1078.
[25]	王明洋, 陈昊祥, 李杰, 等. 深部巷道分区破裂化计算理论与实测对比研究 [J]. 岩石力学与工程学报, 2018, 37(10): 2209–2218. DOI: 10.13722/j.cnki.jrme.2018.0458. WANG M Y, CHEN H X, LI J, et al. Theoretical research on zonal disintegration of rock masses around deep tunnels and comparisons with in-situ observations [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(10): 2209–2218. DOI: 10.13722/j.cnki.jrme.2018.0458.
[26]	李杰, 陈伟, 施存程, 等. 基于块系构造的大规模地下爆炸不可逆位移计算方法 [J]. 爆炸与冲击, 2018, 38(6): 1271–1277. DOI: 10.11883/bzycj-2017-0201. LI J, CHEN W, SHI C C, et al. Calculation method of irreversible displacement region radius based on block hierarchical structure under large-scale underground explosion [J]. Explosion and Shock Waves, 2018, 38(6): 1271–1277. DOI: 10.11883/bzycj-2017-0201.
[27]	ADUSHKIN V V, SPIVAK A A. Underground explosions, section 7.2: description of block deformations [M]. ANASTASIA S, PAUL R, trans, 2015: 424−428.
[28]	王明洋, 范鹏贤, 李文培. 岩石的劈裂和卸载破坏机制 [J]. 岩石力学与工程学报, 2009, 29(2): 234–241. WANG M Y, FAN P X, LI W P. Mechanism of splitting and unloading failure of rock [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 29(2): 234–241.
[29]	LI J, FAN P X, WANG M Y. The stress conditions of rock core disking based on an energy analysis [J]. Rock Mechanics and Rock Engineering, 2019, 52(2): 465–470. DOI: 10.1007/s00603-018-1634-7.
[30]	DENG S X, LI J, JIANG H M, et al. Experimental and theoretical study of the fault slip events of rock masses around underground tunnels induced by external disturbances [J]. Engineering Geology, 2018, 233: 191–199. DOI: 10.1016/j.enggeo.2017.12.007.
[31]	李杰, 蒋海明, 王明洋, 等. 爆炸与冲击中的非线性岩石力学问题(Ⅰ): 一维块系岩体波动特性的试验研究 [J]. 岩石力学与工程学报, 2018, 37(1): 38–50. DOI: 10.13722/j.cnki.jrme.2017.0490. LI J, JIANG H M, WANG M Y, et al. Nonlinear mechanical problems in rock explosion and shock. Part Ⅰ: experimental research on properties of one-dimensional wave propagation in block rock masses [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1): 38–50. DOI: 10.13722/j.cnki.jrme.2017.0490.
[32]	李杰, 蒋海明, 王明洋, 等. 爆炸与冲击中的非线性岩石力学问题(Ⅱ): 冲击扰动诱发岩块滑移的物理模拟试验 [J]. 岩石力学与工程学报, 2018, 37(2): 291–301. DOI: 10.13722/j.cnki.jrme.2017.0684. LI J, JIANG H M, WANG M Y, et al. Nonlinear mechanical problems in rock explosion and shock. Part Ⅱ: physical model test on sliding of rock blocks triggered by external disturbance [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(2): 291–301. DOI: 10.13722/j.cnki.jrme.2017.0684.
[33]	BRADY H G, BROWN E T. 地下采矿岩石力学 [M]. 3版. 佘诗刚, 朱万成, 赵文, 等译. 北京: 科学出版社, 2011: 264−269. BRADY H G, BROWN E T. Rock mechanics for underground mining [M]. 3rd ed. SHE Shigang, ZHU Wangcheng, ZHAO Wen, et al, trans. Beijing: Science Press, 2001: 264−269.
[34]	KUZNETSOV G N. Contemporary Problems in Rock Mechanics [M]. Moscow: Nauka, 1972.
[35]	BALLIVY G, DAYRE M. The mechanical properties of rocks [J]. Bulletin of the International Association of Engineering Geology, 1984, 29: 339–342. DOI: 10.1007/BF02594432.
[36]	SHEMYAKIN E I. Two problems in rock mechanics arising out of the working of deep ore or coal deposits [J]. Soviet Mining, 1975, 11(6): 632–646. DOI: 10.1007/BF02507493.
[37]	SHEMYAKIN E I. On invariants of the stress-strain state in mathematical models for mechanics of continua [J]. Doklady Physics, 2000, 45(8): 419–421. DOI: 10.1134/1.1310737.
[38]	WILSON A H. The stability of underground workings in the soft rocks of the Coal Measures [J]. International Journal of Mining Engineering, 1983, 1(2): 91–187. DOI: 10.1007/BF00880785.
[39]	NIKOLAEVSKIY V N. Geomechanics and fluidodynamics: with applications to reservoir engineering [M]. Dordrecht: Springer, 1996.
[40]	NIKITIN L V, ODINTSEV V N. A dilatancy model of tensile macrocracks in compressed rock [J]. Fatigue & Fracyure of Engineering Materials & Structures, 1999, 22(11): 1003–1009.
[41]	SHEMYAKIN E I, FISENKO G L, KURLENYA M V, et al. Zonal disintegration of rocks around underground mines, part Ⅲ: theoretical concepts [J]. Soviet Mining, 1987, 23(1): 1–6. DOI: 10.1046/j.1460-2695.1999.00232.x.
[42]	SHEMYAKIN E I, KURLENYA M V, OPARIN V N, et al. Zonal disintegration of rocks around underground workings. IV. practical applications [J]. Soviet Mining, 1989, 25(4): 297–302. DOI: 10.1007/BF02528546.
[43]	周钟, 巩满福, 侯东奇, 等. 四川省雅砻江锦屏Ⅰ级水电站地下厂房洞室群施工期围岩稳定与支护设计报告(4) [R]. 成都: 中国水电工程顾问集团成都勘测设计研究院, 2008. ZHOU Z, GONG M F, HOU D Q, et al. Report on surrounding rock mass stability and support design for underground powerhouse caverns group construction of Jinping Ⅰ hydropower project located on Yalong River (4) [R]. Chengdu: HydroChina Chengdu Engineering Corporation, 2008.

施引文献

期刊类型引用(17)

1.	范国轩，吴海燕，林伟国，张磊，陈晓磊. 基于正负区间统计分析的信号趋势项自适应消除方法. 北京化工大学学报(自然科学版). 2024(05): 77-85 . 百度学术
2.	徐振洋，莫宏毅，包松，赵建宇，王雪松，刘鑫，陈占扬. 基于VMD-Teager的露天边坡爆破振动信号能量特征研究. 振动与冲击. 2023(07): 77-88+105 . 百度学术
3.	莫宏毅，徐振洋，刘鑫，张久洋，姜厦航. 基于SSA-VMD的爆破振动信号趋势项去除方法. 振动与冲击. 2023(11): 304-312+330 . 百度学术
4.	付晓强，俞缙，刘纪峰，杨仁树，戴良玉. 隧道爆破振动信号畸变校正与混沌多重分形特征研究. 振动与冲击. 2022(06): 76-85 . 百度学术
5.	鲁超，吴贤振，刘建伟，程杰. 基于小波与EMD的井下深孔爆破振动信号对比分析. 中国矿业. 2021(02): 84-90 . 百度学术
6.	贾贝，凌天龙，侯仕军，刘殿书. 基于变分模态分解的延时识别法在短延时微差爆破中的应用. 北京理工大学学报. 2021(04): 341-348 . 百度学术
7.	李晨，梁书锋，刘传鹏，程健，刘殿书. 基于改进的集合经验模态分解的爆破振动信号趋势项消除方法. 北京理工大学学报. 2021(06): 636-641 . 百度学术
8.	付晓强，张仁巍，雷振，刘纪峰，崔秀琴，刘幸. 煤矿立井爆破信号趋势项和噪声消除方法. 兰州工业学院学报. 2020(01): 57-62 . 百度学术
9.	付晓强，杨仁树，崔秀琴，刘幸，刘纪峰，雷振. 冻结立井爆破振动信号多重分形去趋势波动分析. 振动与冲击. 2020(06): 51-58 . 百度学术
10.	贾贝，凌天龙，侯仕军，刘殿书，王潇. 变分模态分解在爆破信号趋势项去除中的应用. 爆炸与冲击. 2020(04): 123-131 . 本站查看
11.	付晓强，杨仁树，刘纪峰，张会芝，张仁巍. 冻结立井爆破近区井壁振动信号基线漂移校正和消噪方法. 爆炸与冲击. 2020(09): 100-112 . 本站查看
12.	付晓强，刘纪峰，黄凌君，蔡雪霁，王军芳，刘静. 城市地铁区间隧道爆破振动信号趋势项和噪声消除方法. 铁道科学与工程学报. 2020(09): 2328-2337 . 百度学术
13.	付晓强，崔秀琴，杨立云，雷振，蔡雪霁，李阳. 变分模态分解算法在煤矿井筒爆破信号趋势项消除中的应用. 煤矿安全. 2020(10): 248-252 . 百度学术
14.	钱如峰，徐洋，盛晓伟，程福荣. 基于小波变换的簇绒地毯织机噪声源识别. 东华大学学报(自然科学版). 2019(04): 571-575+582 . 百度学术
15.	王勇胜. 深大调压井开挖爆破振动效应分析及安全评价. 中国水能及电气化. 2019(10): 61-65 . 百度学术
16.	焦伟，顾克秋，赵跃跃. 基于小波能谱和熵谱的炮架结构冲击响应分析. 兵器装备工程学报. 2018(01): 102-105 . 百度学术
17.	张军，牛宝良，黄含军，黄海莹，王军评，岳晓红. 爆炸分离冲击数据的零漂校正. 装备环境工程. 2018(05): 6-9 . 百度学术