Effect of loading rate on the modeⅡ dynamic fracture characteristics of 40Cr steel
-
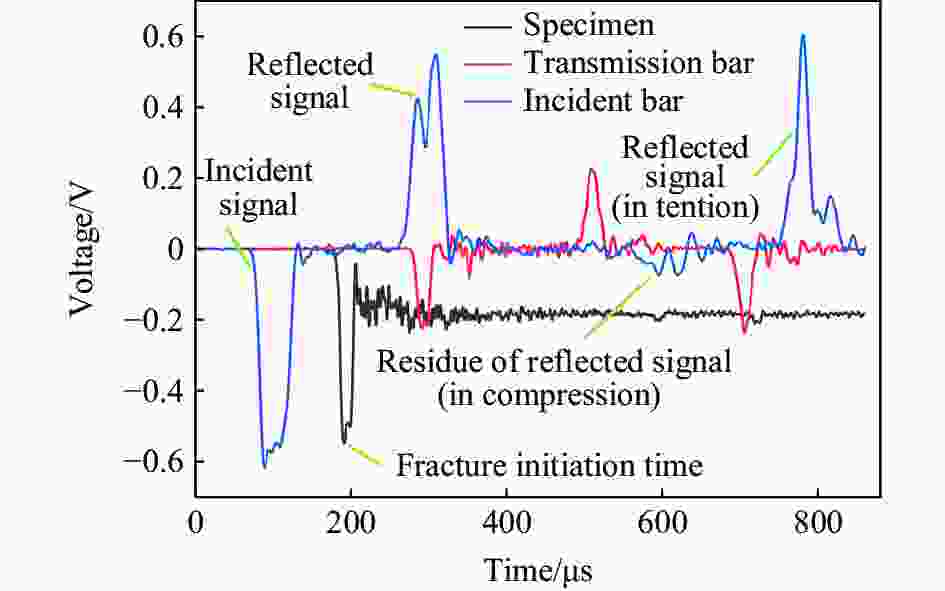
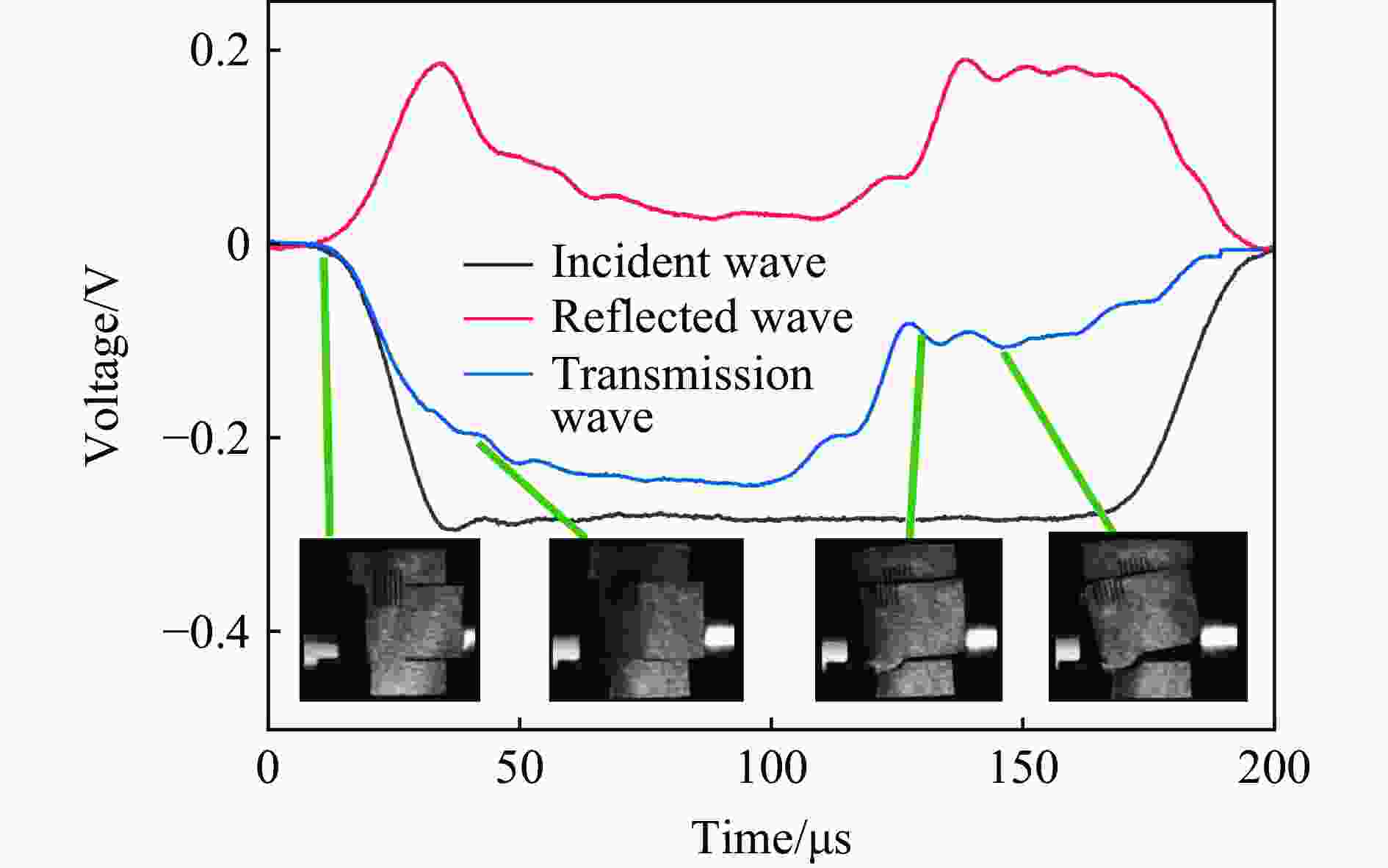
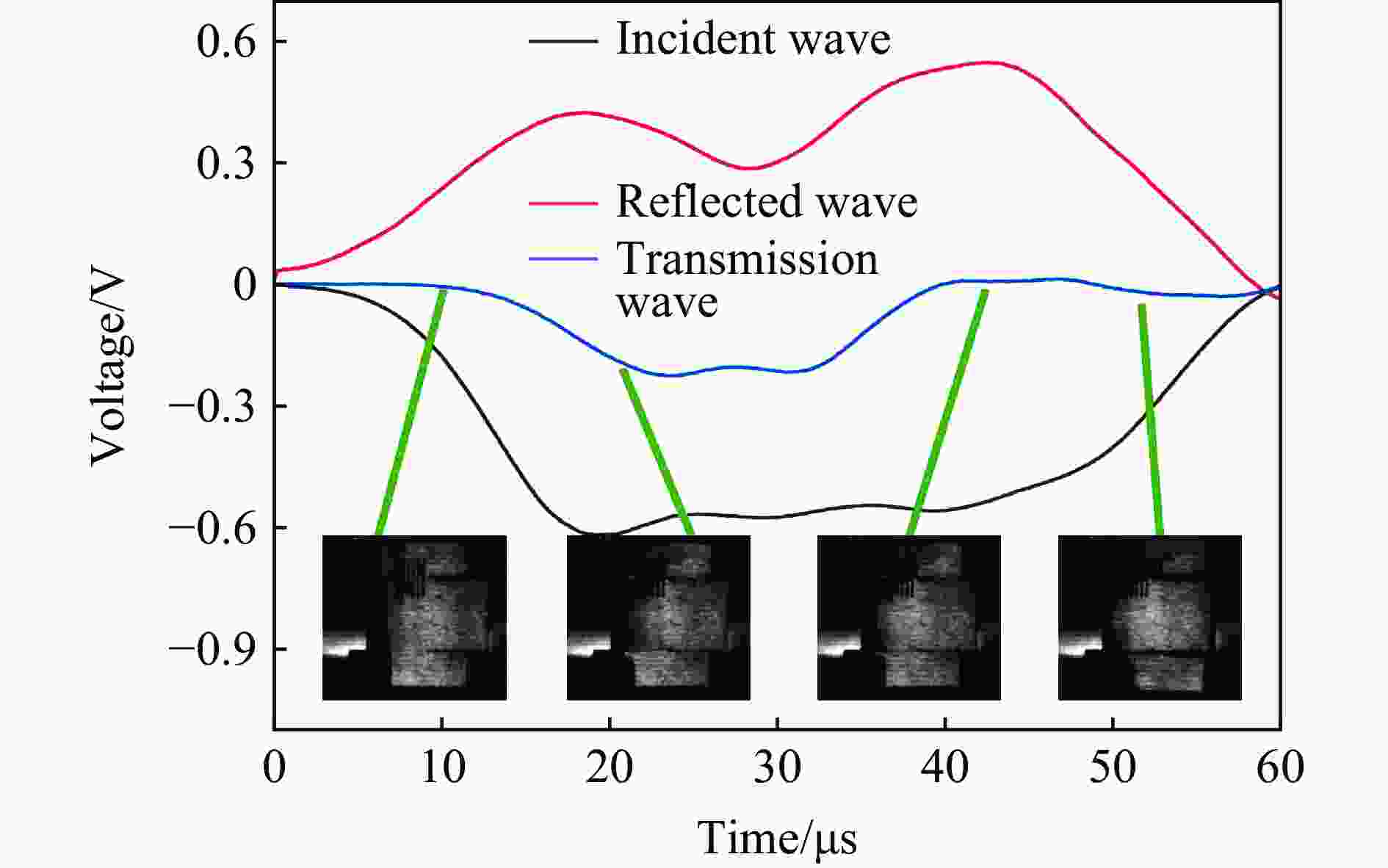
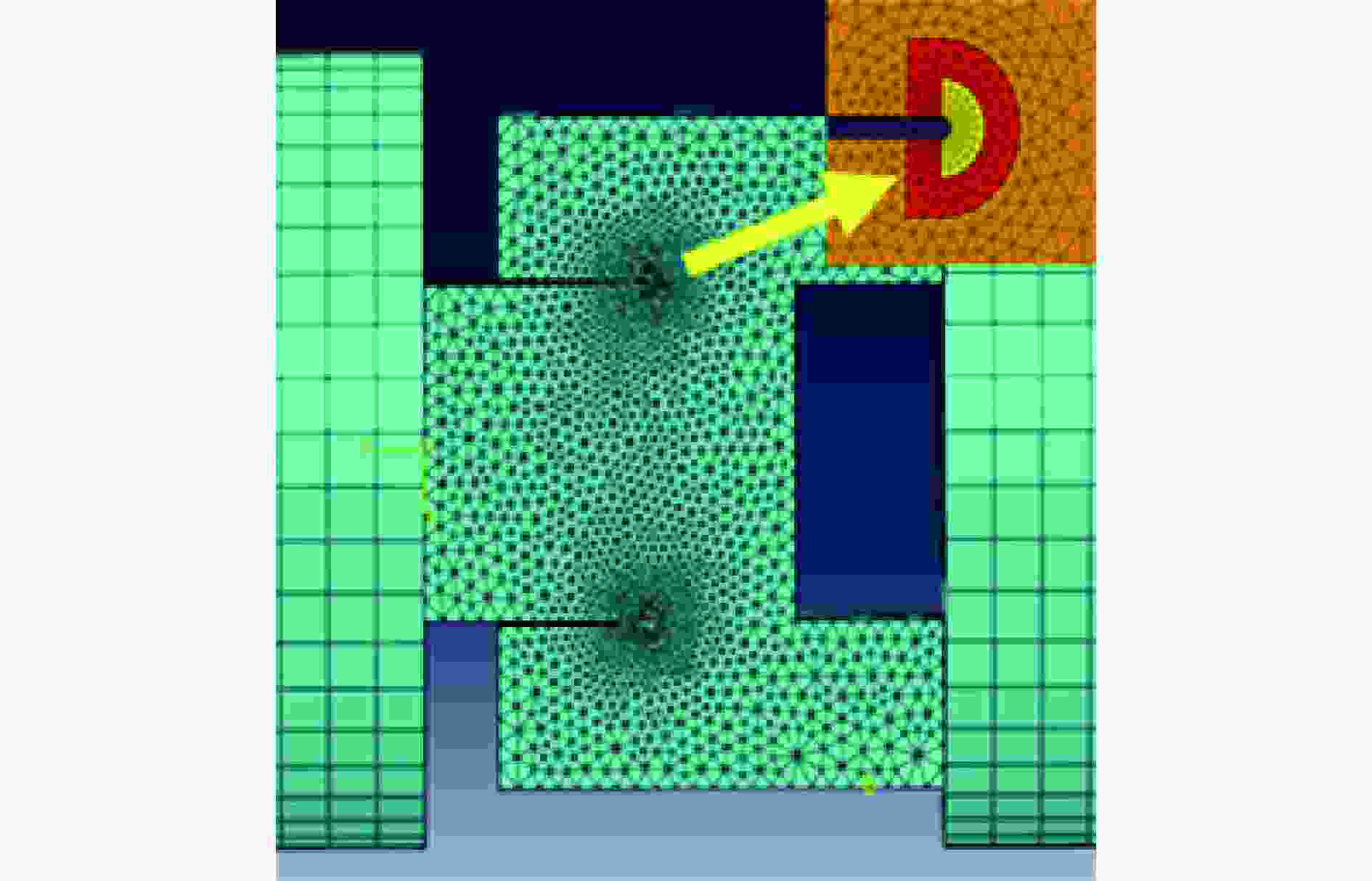
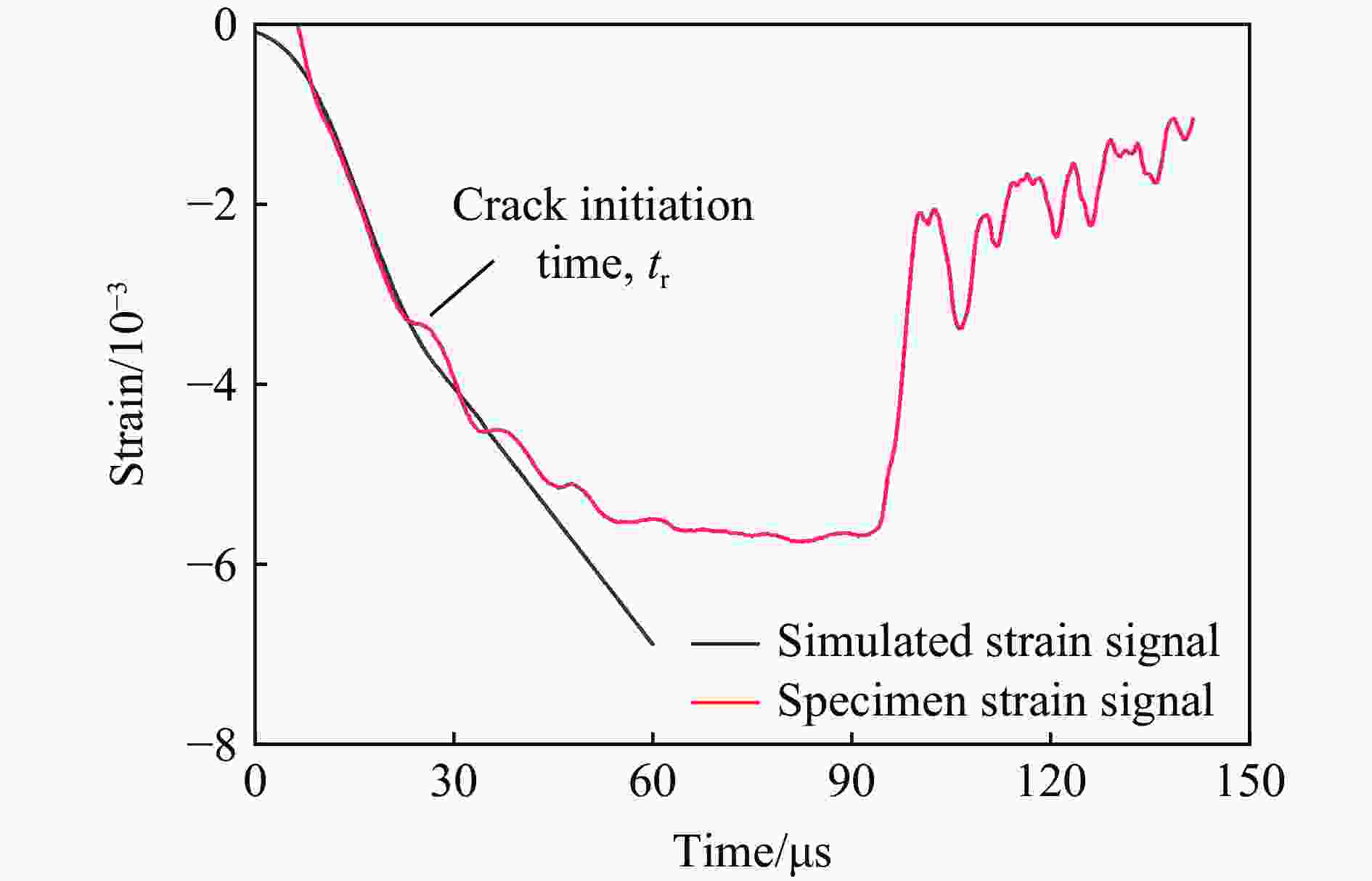
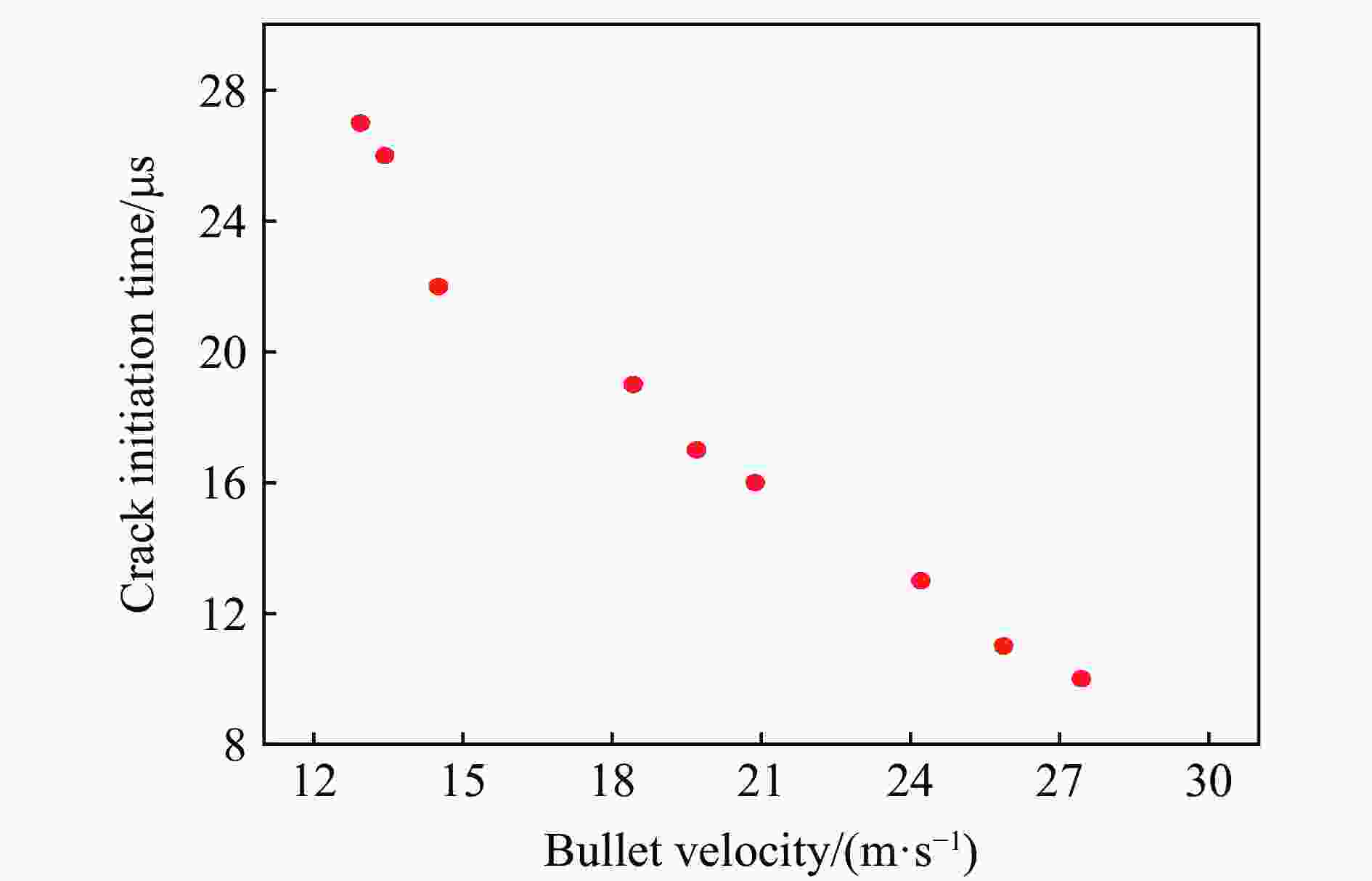
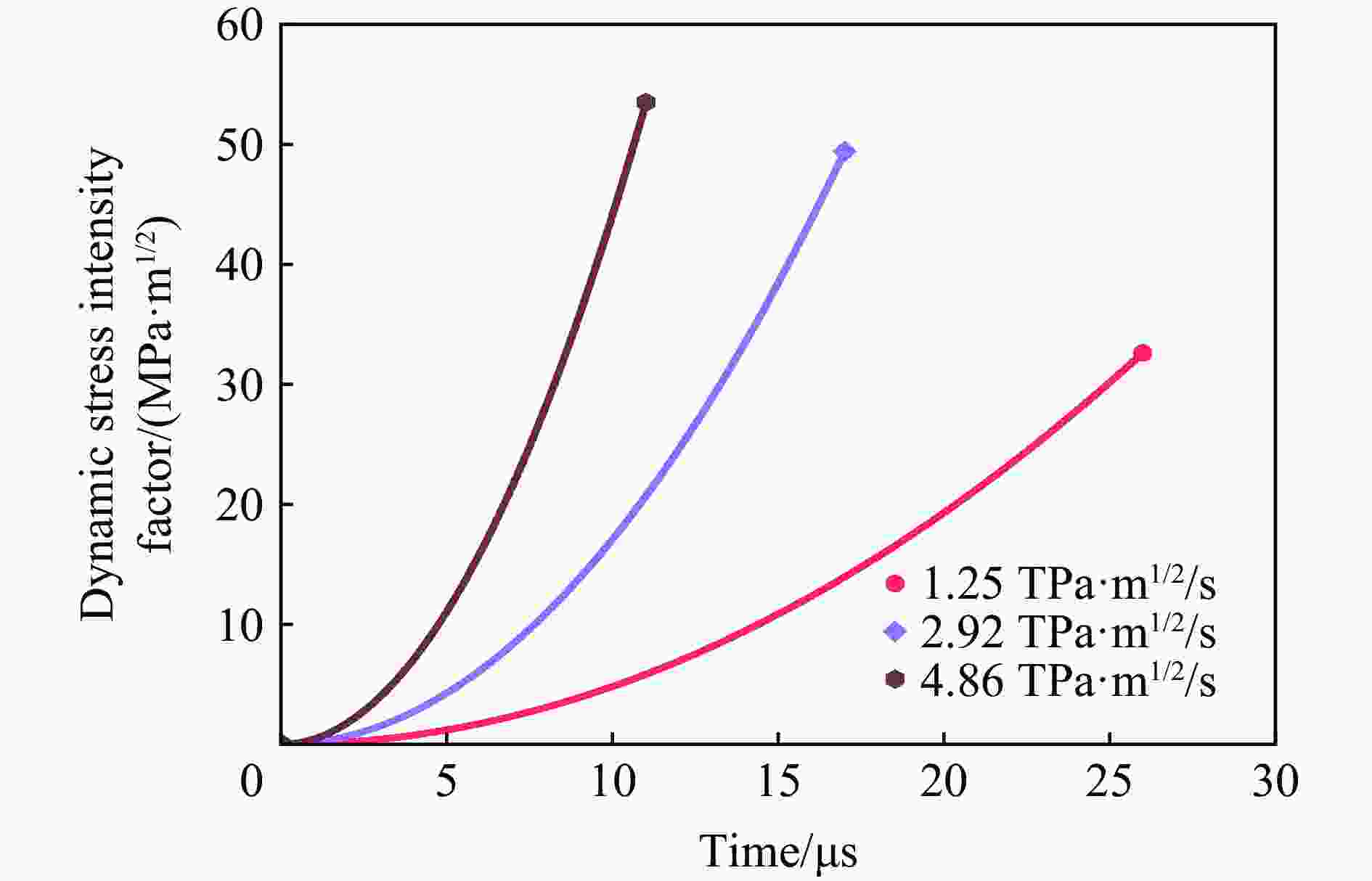
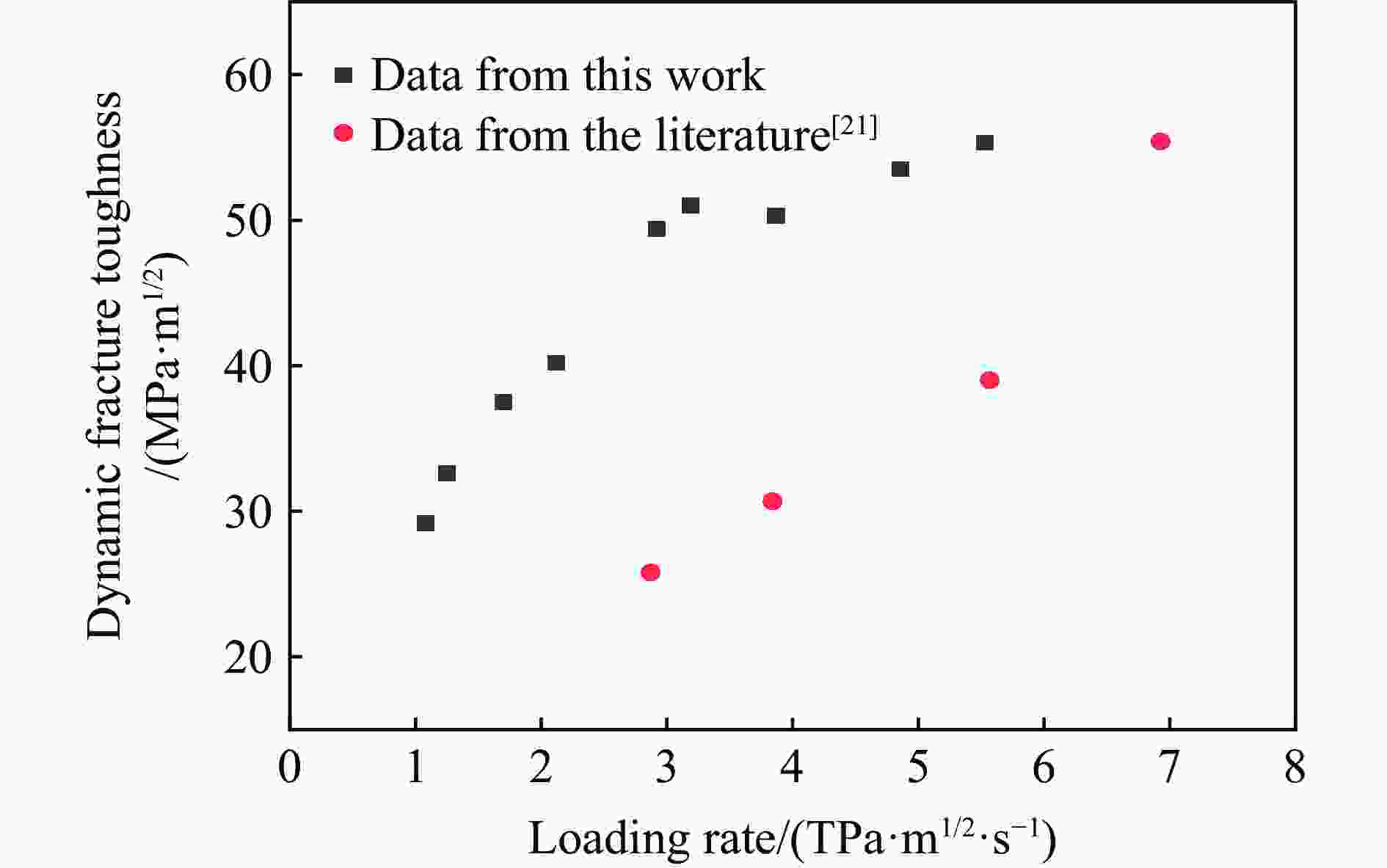
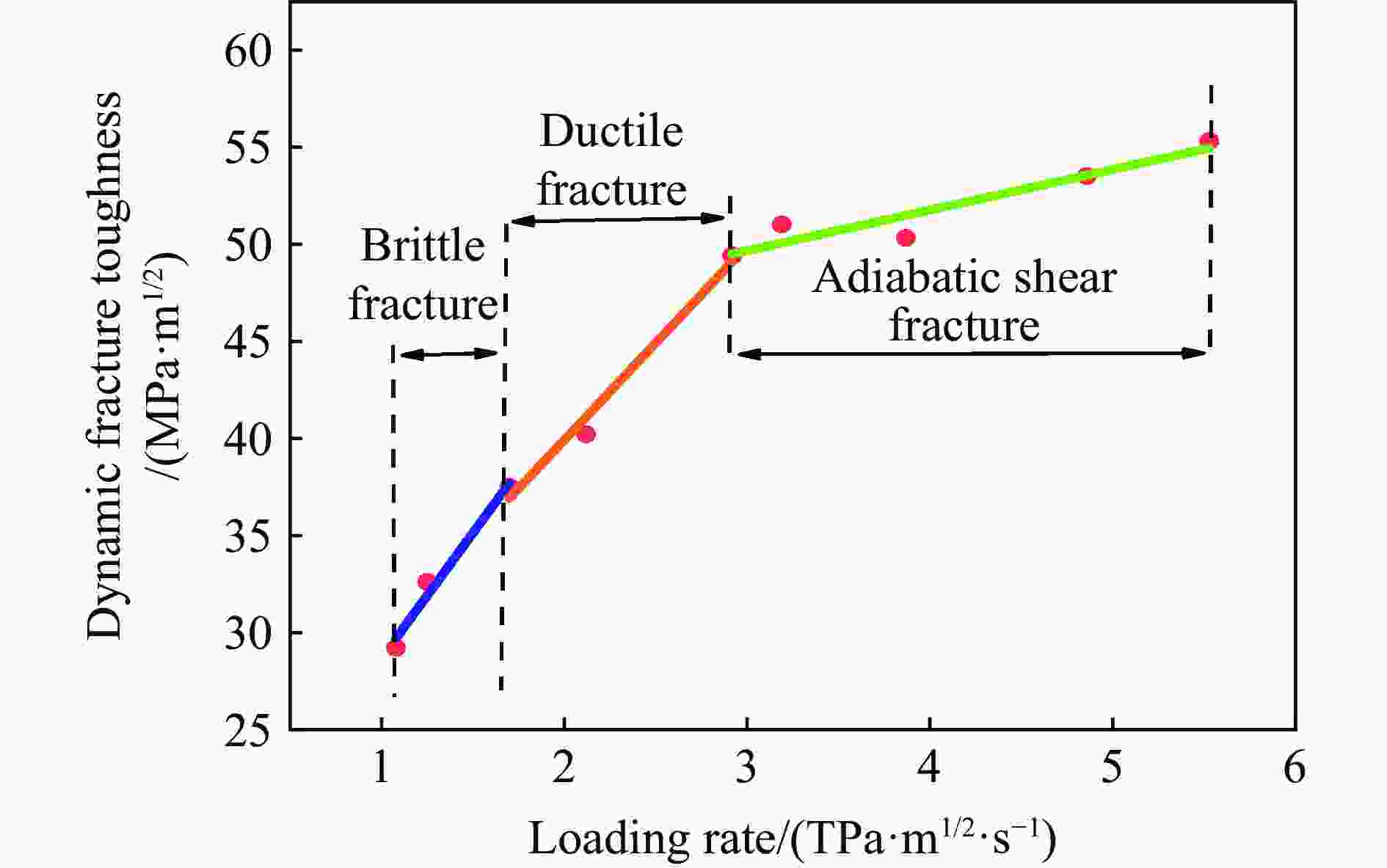
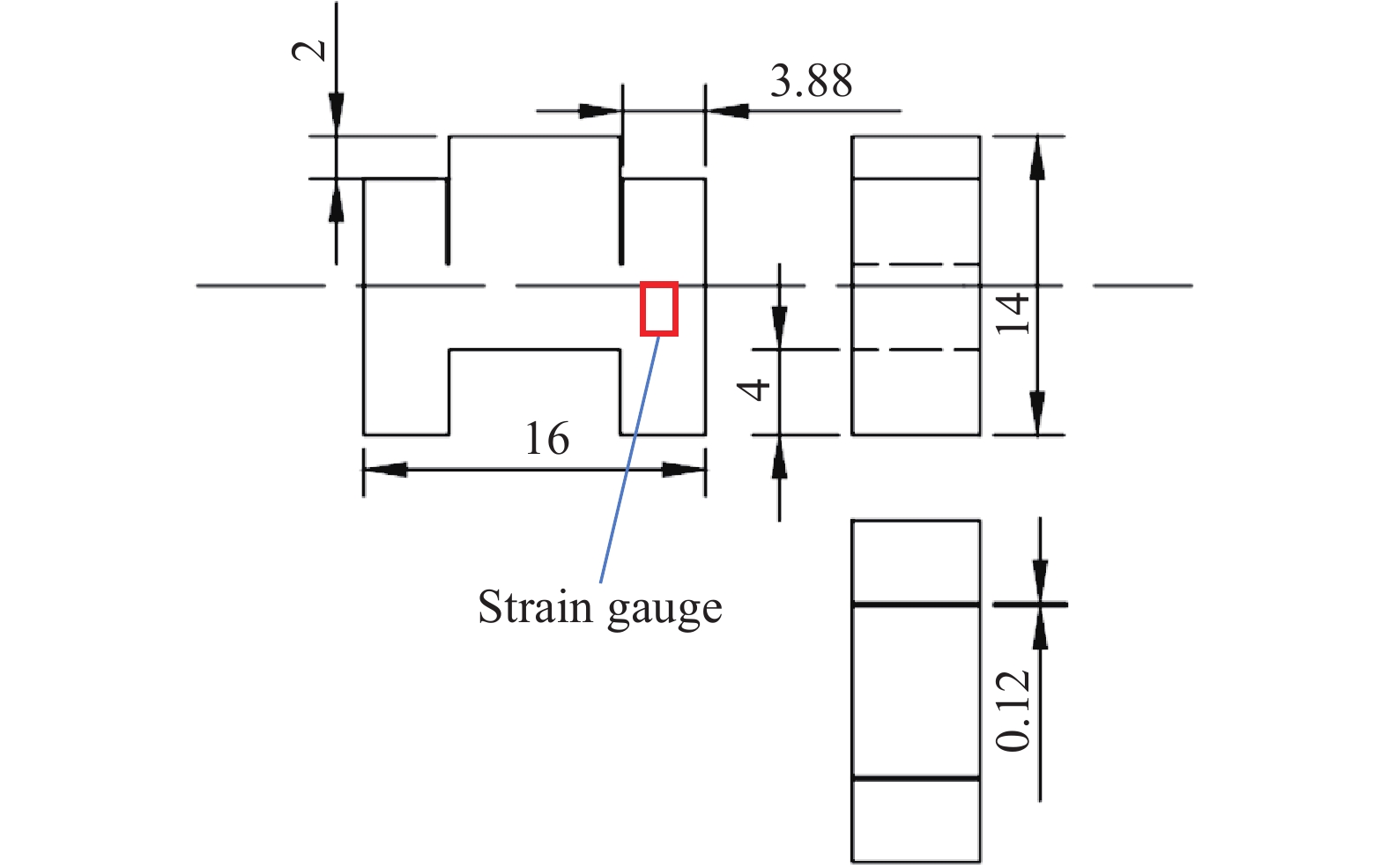
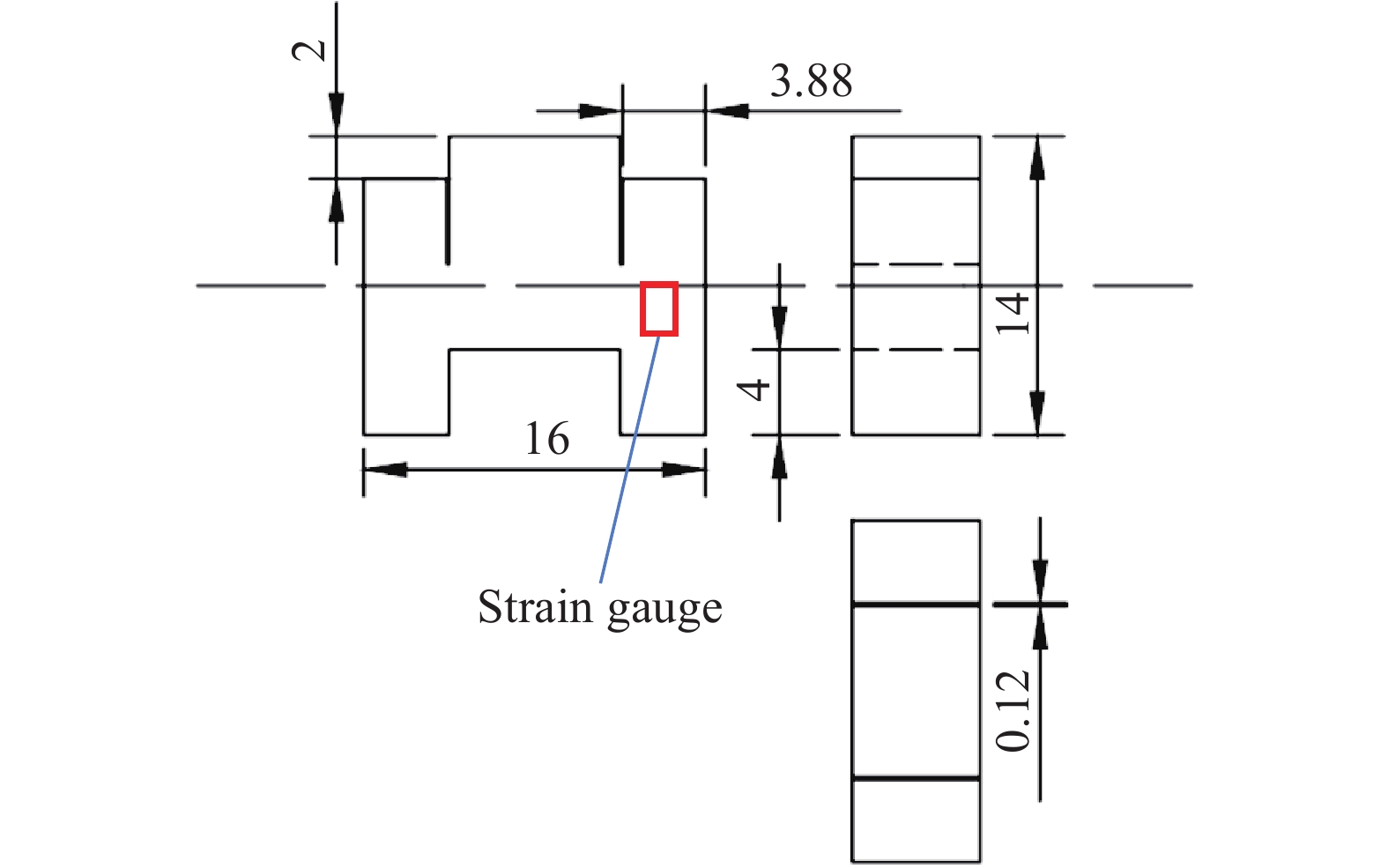
摘要: 采用新型Ⅱ型动态断裂测试技术,对高强钢40Cr在高加载速率下的Ⅱ型动态断裂特性进行了测试研究。基于新设计的Ⅱ型动态断裂试样和分离式霍普金森压杆(split Hopkinson pressure bar, SHPB)技术,通过实验-数值方法确定了裂尖在加载过程中的应力强度因子曲线。采用应变片法确定了试样的起裂时间,最终得到40Cr的Ⅱ型动态断裂韧性值,并对其加载速率相关性和材料的失效机理进行了研究。结果表明,在1.08~5.53 TPa·m1/2/s的加载速率范围内,40Cr的Ⅱ型动态断裂韧性基本表现为与加载速率成正相关的变化趋势。通过对试样断口形貌的分析,确定了材料的失效模式及机理,发现随着加载速率的增加,存在拉伸型失效向绝热剪切型失效模式转变的现象。Abstract: 40Cr high strength steel is often used in aerospace and national defense fields due to its excellent mechanical properties. Therefore, the research on the mode Ⅱ dynamic fracture characteristics and failure mechanism of 40Cr high strength steel under high-speed impact has important scientific significance and engineering value. Experiments and numerical simulations were carried out to study the mode Ⅱ dynamic fracture properties of 40Cr material under high loading rates. Based on the newly designed specimen and the novel test technique for mode Ⅱ dynamic fracture, the experimental-numerical method was used to determine the dynamic stress intensity factor curve of the crack tip during the loading process. The crack initiation time of the specimen was obtained by the strain gauge pasted on the specimen, and the mode Ⅱ dynamic fracture toughness of 40Cr was finally determined. The effect of loading rate and the failure mechanism of the material were also studied. The results show that within the present loading rate range of this work (1.08−5.53 TPa·m1/2/s), the mode Ⅱ dynamic fracture toughness of 40Cr presents a positive correlation with the loading rate. Through the analysis of the fracture morphology of the recovered specimen, it is found that there exists a transition from tensile failure mode to adiabatic shear failure mode with the increase of loading rate, and the critical loading rate is about 2.92 TPa·m1/2/s. When KⅡd≤1.70 TPa·m1/2/s, the 40Cr steel mainly exhibits brittle fracture; when KⅡd is in the range of 2.12−2.92 TPa·m1/2/s, the fracture mainly presents the morphological characteristics of ductile fracture; when KⅡd ≥ 3.19 TPa·m1/2/s, the material failure is mainly caused by adiabatic shear bands. Brittle fracture is dominated by strain rate hardening mechanism, ductile fracture is dominated by strain/strain rate hardening and thermal softening mechanisms, and adiabatic shear fracture is dominated by thermal softening mechanism.
-
表 1 高强钢40Cr的元素成分及质量分数
Table 1. Composition and mass fraction of high-strength steel 40Cr
w(C)/% w(Mn)/% w(Si)/% w(Cr)/% w(Ni)/% 0.37~0.45 0.50~0.80 0.20~0.40 0.80~1.10 − 表 2 高强钢40Cr的力学性能参数
Table 2. Mechanical properties of high strength steel 40Cr
材料 ρ/(kg·m−3) E/GPa $\ \mu $ $ {\sigma }_{\mathrm{b}} $/MPa 40Cr 7820 199 0.3 1987 表 3 入射杆、透射杆的力学性能参数
Table 3. Mechanical properties of the incident and transmission bars
材料 ρ/(kg·m−3) E/GPa $\ \mu $ 18Ni 8000 190 0.3 表 4 高强钢40Cr的动态断裂韧性值
Table 4. Dynamic fracture toughness values of high strength steel 40Cr
L/m p/MPa tf/µs KⅡd/(MPa·m1/2) ${\dot{K} }_{\text{Ⅱ}\mathrm{d} }$/(TPa·m1/2/s) 0.380 0.18 27 29.2 1.08 0.380 0.19 26 32.6 1.25 0.380 0.22 22 37.5 1.70 0.203 0.18 19 40.2 2.12 0.203 0.20 17 49.4 2.92 0.203 0.22 16 51.0 3.19 0.100 0.14 13 50.3 3.87 0.100 0.16 11 53.5 4.86 0.100 0.18 10 55.3 5.53 注: L为子弹长度,p为气压,tf为起裂时间,KⅡd为Ⅱ型断裂韧性,$ {\dot{K}}_{\text{Ⅱ}\mathrm{d}} $为加载速率 表 5 不同断口形貌下DFT与加载速率的线性拟合参数
Table 5. Linear fitting parameters of DFT and the loading rates under different fracture morphology
材料 断口类型 A b 40Cr 脆性 12.88 15.80 韧性 9.98 19.94 绝热剪切型 2.09 43.39 -
[1] 黄浩. 40Cr表面激光熔覆硬质涂层及其应用研究[D]. 河北秦皇岛: 燕山大学, 2016. [2] KALTHOFF J F. Shadow optical analysis of dynamic shear fracture [J]. Optical Engineering, 1988, 27(10): 271035. DOI: 10.1117/12.7976772. [3] KALTHOFF J F. Transition in the failure behavior of dynamically shear loaded cracks [J]. Applied Mechanics Reviews, 1990, 43(S5): 47–50. DOI: 10.1115/1.3120818. [4] KALTHOFF J F. Modes of dynamic shear failure in solids [J]. International Journal of Fracture, 2000, 101(1): 1–31. DOI: 10.1023/A: 1007647800529. [5] KALTHOFF J F, BÜRGEL A. Influence of loading rate on shear fracture toughness for failure mode transition [J]. International Journal of Impact Engineering, 2004, 30(8): 957–971. DOI: 10.1016/j.ijimpeng.2004.05.004. [6] ZHOU M, ROSAKIS A J, RAVICHANDRAN G. Dynamically propagating shear bands in impact-loaded prenotched plates—Ⅰ. experimental investigations of temperature signatures and propagation speed [J]. Journal of the Mechanics and Physics of Solids, 1996, 44(6): 981–1006. DOI: 10.1016/0022-5096(96)00003-8. [7] ZHOU M, RAVICHANDRAN G, ROSAKIS A J. Dynamically propagating shear bands in impact-loaded prenotched plates—Ⅱ. numerical simulations [J]. Journal of the Mechanics and Physics of Solids, 1996, 44(6): 1007–1021, 1023-1032. DOI: 10.1016/0022-5096(96)00004-X. [8] ZHOU M, ROSAKIS A J, RAVICHANDRAN G. On the growth of shear bands and failure-mode transition in prenotched plates: a comparison of singly and doubly notched specimens [J]. International Journal of Plasticity, 1998, 14(4): 435–451. DOI: 10.1016/S0749-6419(98)00003-5. [9] RAVI-CHANDAR K. On the failure mode transitions in polycarbonate under dynamic mixed-mode loading [J]. International Journal of Solids and Structures, 1995, 32(6): 925–938. DOI: 10.1016/0020-7683(94)00169-W. [10] RAVI-CHANDAR K, LU J, YANG B, et al. Failure mode transitions in polymers under high strain rate loading [J]. International Journal of Fracture, 2000, 101(1): 33–72. DOI: 10.1023/A: 1007581101315. [11] MASON J J, ROSAKIS A J, RAVICHANDRAN G. On the strain and strain rate dependence of the fraction of plastic work converted to heat: an experimental study using high speed infrared detectors and the Kolsky bar [J]. Mechanics of Materials, 1994, 17(2): 135–145. DOI: 10.1016/0167-6636(94)90054-X. [12] CHU D Y, LI X, LIU Z L, et al. A unified phase field damage model for modeling the brittle-ductile dynamic failure mode transition in metals [J]. Engineering Fracture Mechanics, 2019, 212: 197–209. DOI: 10.1016/j.engfracmech.2019.03.031. [13] CHIANG F. Moiré and speckle methods applied to elastic-plastic fracture studies[C]//Experimental Techniques in Fracture Mechanics. New York: VCH, 1993: 291-325. [14] SANFORD R J. Determining fracture parameters with full-field optical methods [J]. Experimental Mechanics, 1989, 29(3): 241–247. DOI: 10.1007/BF02321401. [15] PATTERSON E A, OLDEN E J. Optical analysis of crack tip stress fields: a comparative study [J]. Fatigue & Fracture of Engineering Materials & Structures, 2004, 27(7): 623–635. DOI: 10.1111/j.1460-2695.2004.00774.X. [16] MA L, KOBAYASHI A S, ATLURI S N, et al. Crack linkup: an experimental analysis [J]. Experimental Mechanics, 2002, 42(2): 147–152. DOI: 10.1007/BF02410876. [17] GOECKE K E, MOSHIER M A. A technique to measure fatigue crack growth threshold [J]. Experimental Mechanics, 2002, 42(2): 182–185. DOI: 10.1007/BF02410881. [18] 王洪山. 几种实用的断裂试验方法 [J]. 理化检验-物理分册, 2001, 37(7): 292–294. DOI: 10.3969/j.issn.1001-4012.2001.07.005.WANG H S. Some kinds of practical fracture test methods [J]. Physical Testing and Chemical Analysis Part A: Physical Testing, 2001, 37(7): 292–294. DOI: 10.3969/j.issn.1001-4012.2001.07.005. [19] 姜风春, 刘瑞堂. 动态断裂韧性测试方法的有效性分析 [J]. 哈尔滨工程大学学报, 1999, 20(3): 97–101. DOI: 10.3969/j.issn.1006-7043.1999.03.017.JIANG F C, LIU R T. Analysis of validity of dynamic fracture toughness measurement [J]. Journal of Harbin Engineering University, 1999, 20(3): 97–101. DOI: 10.3969/j.issn.1006-7043.1999.03.017. [20] 郑坚, 王泽平, 段祝平. 动态断裂的加载和测试技术 [J]. 力学进展, 1994, 24(4): 459–475. DOI: 10.6052/1000-0992-1994-4-j1994-042.ZHENG J, WANG Z P, DUAN Z P. Loading and measuring techniques indynamic fracture testing [J]. Advances in Mechanics, 1994, 24(4): 459–475. DOI: 10.6052/1000-0992-1994-4-j1994-042. [21] 许泽建, 李玉龙, 刘元镛, 等. 两种高强钢在高加载速率下的Ⅱ型动态断裂韧性 [J]. 金属学报, 2006, 42(6): 635–640. DOI: 10.3321/j.issn: 0412-1961.2006.06.013.XU Z J, LI Y L, LIU Y Y, et al. Mode Ⅱ dynamic fracture toughness of two high strength steels under high loading rate [J]. Acta Metallurgica Sinica, 2006, 42(6): 635–640. DOI: 10.3321/j.issn: 0412-1961.2006.06.013. [22] 许泽建, 黄风雷, 何晓东. 一种用于纯Ⅱ型动态断裂的试验件: CN201820669843.4 [P]. 2018-12-11. [23] XU Z J, HE X D, HAN Y, et al. A different viewpoint on mechanism of fracture to shear-banding failure mode transition [J]. Journal of the Mechanics and Physics of Solids, 2020, 145: 104165. DOI: 10.1016/j.jmps.2020.104165. [24] XU Z J, HAN Y, FAN C Z, et al. Dynamic shear fracture toughness and failure characteristics of Ti-6Al-4V alloy under high loading rates [J]. Mechanics of Materials, 2021, 154: 103718. DOI: 10.1016/j.mechmat.2020.103718. [25] JIANG F C, VECCHIO K S. Hopkinson bar loaded fracture experimental technique: a critical review of dynamic fracture toughness tests [J]. Applied Mechanics Reviews, 2009, 62(6): 060802. DOI: 10.1115/1.3124647. [26] BAI Y L, DODD B. Adiabatic shear localization: occurrence, theories, and applications [M]. Oxford: Pergamon Press, 1992: 73−75. [27] NEMAT-NASSER S, ISAACS J B, STARRETT J E. Hopkinson techniques for dynamic recovery experiments [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1991, 435(1894): 371–379. DOI: 10.1098/rspa.1991.0150. -






 下载:
下载: