Numerical simulations of response and failure of carbon nanotube/carbon fibre reinforced plastic laminates under impact loading
-
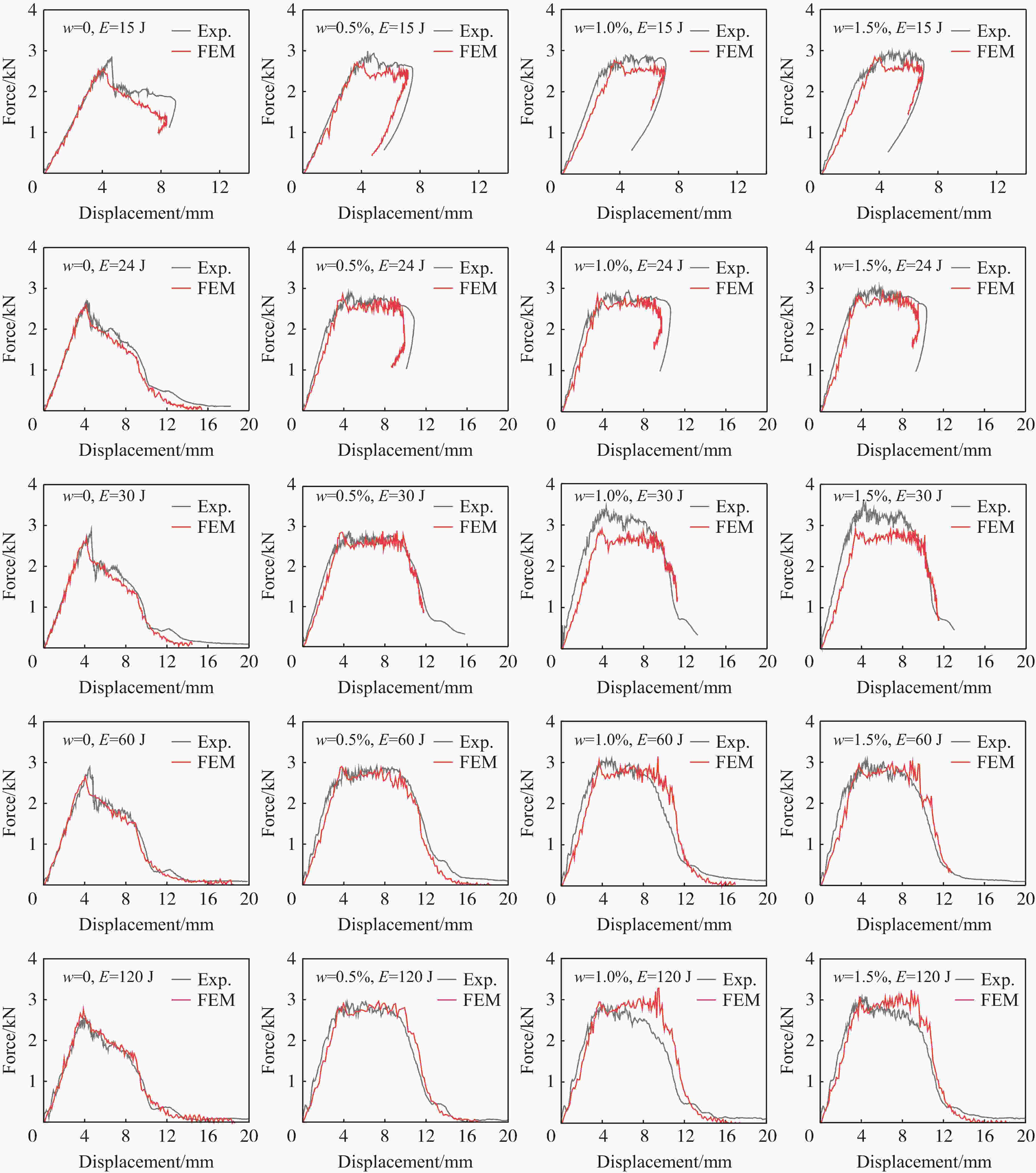
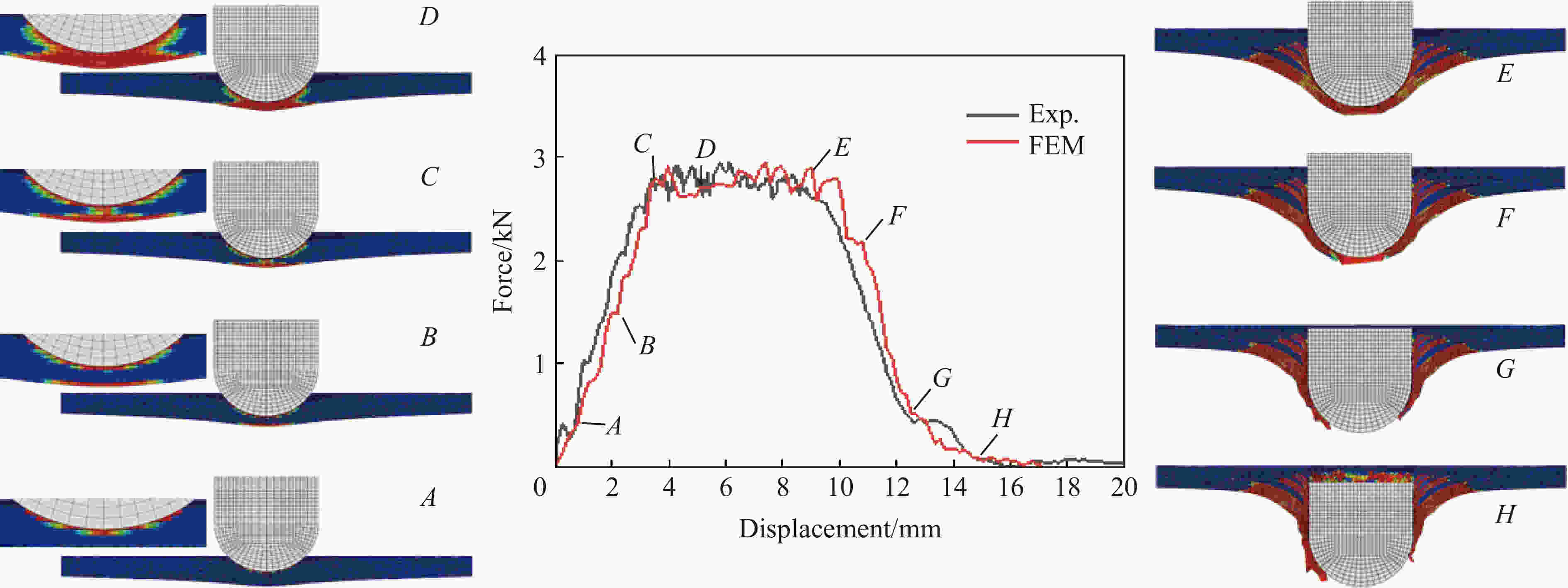
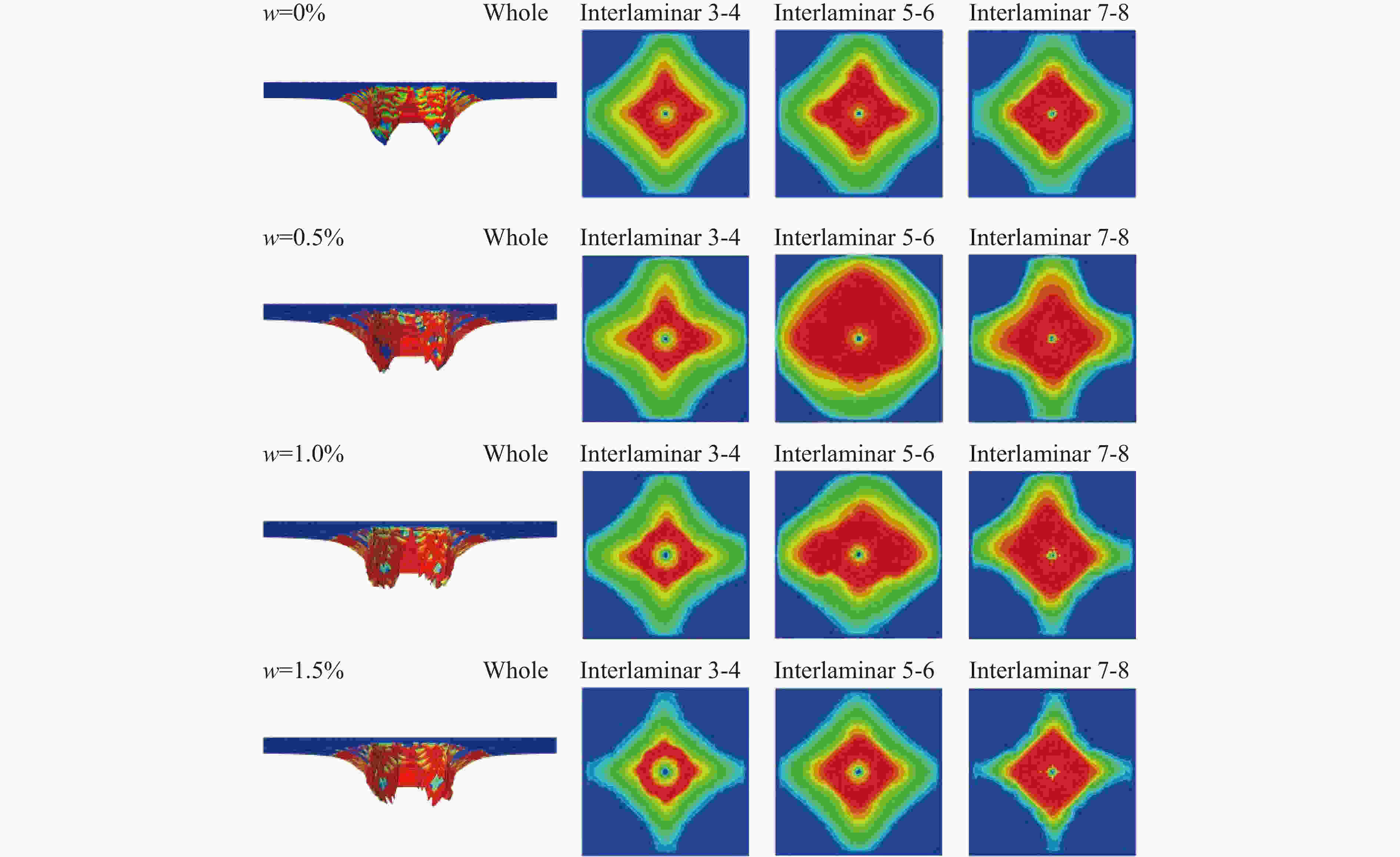
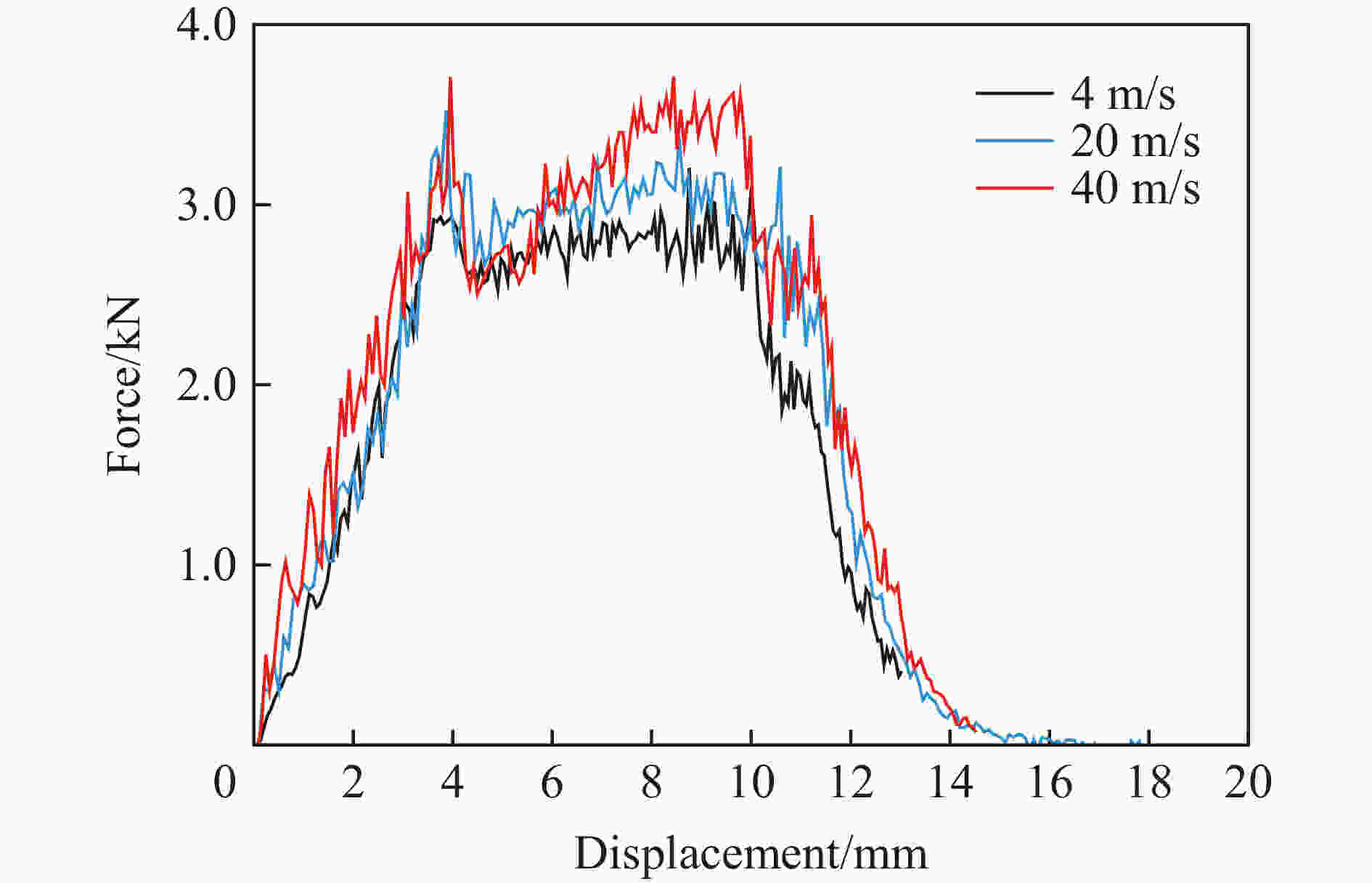
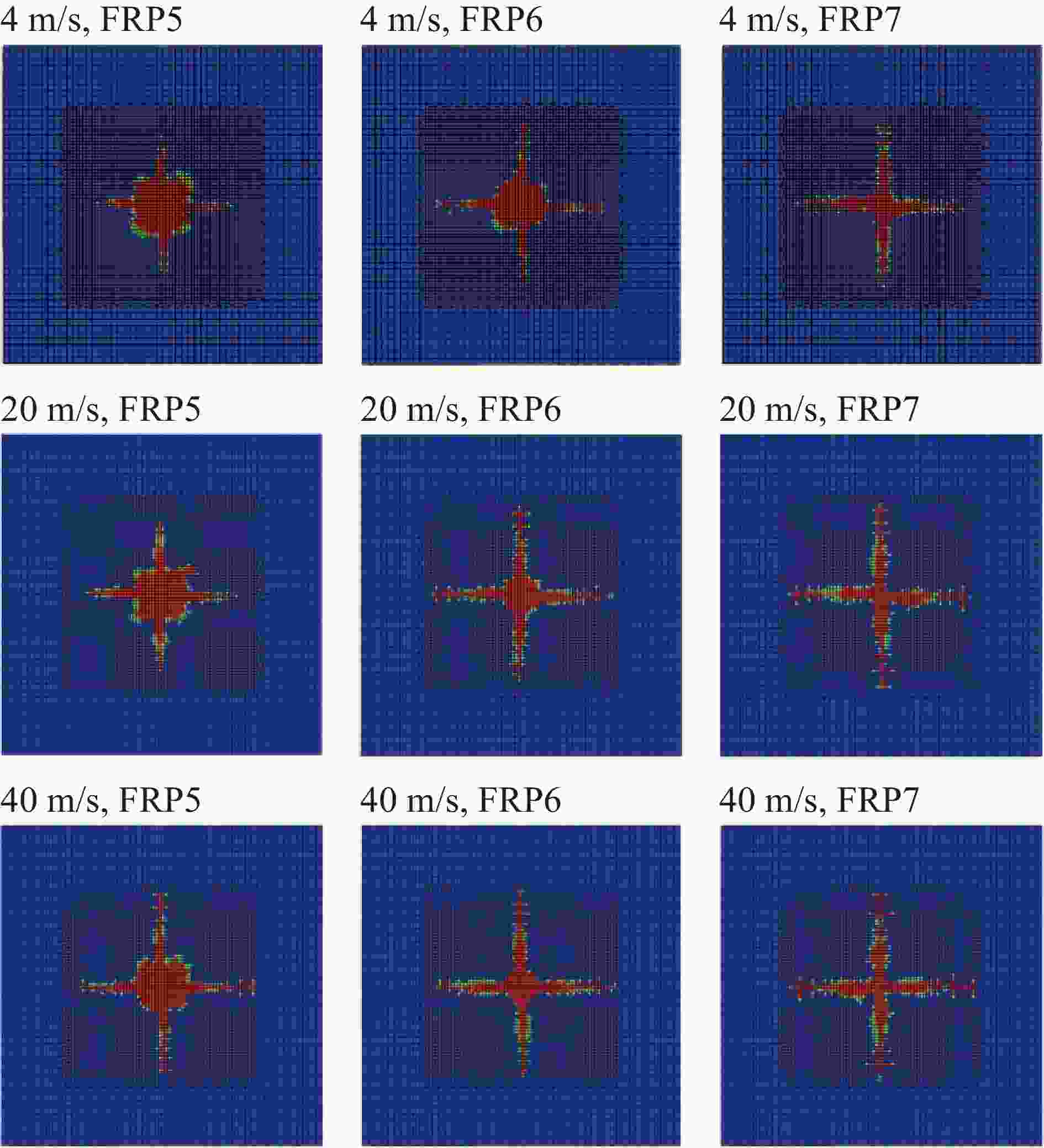
摘要: 碳纳米管/碳纤维增强复合材料（carbon nanotube/carbon fibre reinforced plastic，CNT/CFRP）是一种多尺度复合材料，比传统CFRP有更好的综合性能和更广阔的应用前景。对CNT/CFRP在低速冲击下的响应和破坏进行了数值模拟研究。首先，基于先前的研究通过引入基体增韧因子、残余强度因子并改进损伤耦合方程，建立了新的FRP动态渐进损伤模型；然后，利用新建立的本构模型并结合黏结层损伤模型，对4种碳纳米管含量的增韧碳纤维增强树脂基复合材料层合板在5个能量下的冲击实验进行了数值模拟；最后，将模拟结果与文献中的相关实验结果进行了比较，并讨论了冲击速度的影响。结果表明：新建立的FRP本构模型能够预测CNT/CFRP层合板在低速冲击载荷作用下的响应、破坏过程和分层形貌，模拟得到的载荷-位移曲线和破坏形貌与实验吻合较好；冲击速度会影响CNT/CFRP层合板拉伸和压缩破坏的比例，相同的冲击能量下，更大的冲击速度会造成更多的拉伸破坏。Abstract: Fibre reinforced plastic (FRP) laminates have been widely used in various engineerings due to their excellent mechanical properties. However, FRP laminates may be subjected to impact loading and delamination is one of the major concerns which is caused by the poor performance of matrix and the poor bonding between fibre and matrix. To improve the bonding strength, some toughening technologies have been developed including the modification of matrix by adding nano fillers such as carbon nanotubes. In this paper, numerical simulations of the response and failure of carbon nanotube/carbon fibre reinforced plastic (CNT/CFRP) under low velocity impact loading were performed. Firstly, on the basis of the previous work, a new dynamic progressive damage model for FRP laminates was developed by introducing a matrix toughening factor and a residual strength factor into the damage criterion and damage evolution equation respectively, together with an improved damage coupling equation which was changed from the original sum form to product form. The new dynamic progressive damage model was used to describe the intralaminar damage, and a cohesive element model to describe the interlaminar damage of the CNT/CFRP laminates. Both models were incorporated into the ABAQUS/Explicit finite element program by the user-defined material subroutine VUMAT. Then, numerical simulation was conducted for the response and failure of CNT/CFRP composites subjected to low velocity impact loading. Finally, the numerical results were compared with some available experimental data and the influence of impact velocity was discussed. It transpires that the results predicted from the present model are found to be in good agreement with the test data for CNT/CFRP laminates in terms of load-displacement curve and failure pattern, and the delamination damage at the interlaminar interface decreases gradually with increasing CNT content. It also transpires that the impact velocity affects the ratio of compression and tensile failure of FRP laminates, and under the same impact energy, a larger impact velocity will cause more tensile failure.
-
纤维增强树脂基（fibre reinforced plastics, FRP）复合材料具有比强度高、比模量高、可设计性强、耐高温、耐疲劳等特性，已被广泛应用于航空、航天、武器、船舶、交通、建筑等领域。FRP层合板是主要的结构形式，应用范围也最广泛，然而传统的FRP层合板各向异性严重，垂直于纤维方向的力学性能较低，抗分层能力弱，限制了其优势性能的充分发挥。
随着纳米材料的发展，一些基于纳米填料改性的复合材料增韧技术受到了关注。碳纳米管（carbon nanotube, CNT）是最典型的纳米填料，它可作为基质富集区域的增强材料而分散在基体中。当裂纹扩展至碳纳米管附近时，碳纳米管横亘在裂纹前端，通过桥联作用抑制裂纹扩展（裂纹桥接），裂纹继续扩展将涉及路径偏转或碳纳米管的脱黏、拔出、断裂，引起开裂能的耗散，从而提高FRP复合材料的断裂韧性。同时，碳纳米管的加入还增强了纤维和基体间的界面强度，改善了FRP层合板中的应力分布。以碳纳米管（纳米级）、纤维（微米级）、聚合物基体制备的多尺度复合材料，不仅具有抗冲击损伤、抗分层等优异的力学性能，而且还具有吸波、隐身、防雷击等优点，这进一步扩大了FRP复合材料的应用潜力。
关于CNT基体改性对CFRP力学性能影响的研究发现，CNT/CFRP复合材料的强度[1]、模量[2]、断裂韧性[2]、界面剪切强度[3]和层间剪切强度[2,4-5]等都有不同程度的提高。Tarfaoui等[6]利用ABAQUS软件的基于Hashin准则的FRP本构模型，对CNT/CFRP层合板的开孔拉伸实验进行了数值模拟，考虑不同含量CNT对CFRP的力学性能（模量和强度）的影响，模拟结果与实验载荷-位移曲线吻合较好。而CNT/CFRP层合板在冲击载荷作用下响应和破坏的数值模拟，目前尚未见相关报道。
本文中，拟对CNT/CFRP层合板的冲击响应和破坏进行数值模拟。首先，基于文献[7-9]的研究，引入基体增韧因子、残余强度因子，改进损伤耦合方程，建立新的FRP动态渐进损伤模型，以描述碳纳米管基体改性为FRP带来的增韧效果；然后，利用所建立的模型并结合黏结层损伤模型，对CNT/CFRP层合板在低速冲击作用下的响应和破坏进行数值模拟，并与实验数据进行比较；最后，利用建立的模型，进一步研究冲击速度对FRP层合板冲击响应的影响。
1. FRP动态渐进损伤模型
由于纳米填料（如碳纳米管）的尺度是纳米级、纤维的尺度是微米级，将这两种增强相建立为一个模型是不现实的。另外，传统的FRP渐进损伤本构模型描述的复合材料行为偏弹脆性，没有考虑CNT改性带来的增韧效果。因此，仍将纳米填料改性的纤维增强树脂基复合材料视为宏观上的正交各向异性材料，引入基体增韧因子S、残余强度因子frs，改进损伤耦合方程，建立可描述复合材料韧性行为的新FRP动态渐进损伤模型。
1.1 损伤准则
纤维增强树脂基复合材料的失效模式原则上可以分为纤维失效和基体失效两种，每种失效又因不同的加载方式而存在不同的模式。基于Yen[9]的损伤准则思路，针对编织纤维增强树脂基复合材料，考虑3类纤维损伤（面内的纤维拉/剪损伤、面内的纤维压缩损伤、厚度方向的纤维压溃）和2类基体损伤（面内的基体剪切损伤、厚度方向的基体拉/剪损伤）。这里，给出相关变量和材料常数：损伤因子fi，当fi ≥ 1时相应模式的损伤开始发生；拉伸强度St,x、St,y、St,z；压缩强度Sc,x、Sc,y、Sc,z；纤维剪切强度Sfs,x、Sfs,y；基体剪切强度Sxy、Sxz、Syz。其中，下标x、y、z分别代表3个材料主方向。
（1）面内的纤维拉/剪损伤
纤维方向的拉伸载荷以及横向冲击作用下厚度方向的剪切载荷会使纤维拉直、基体损伤，进而造成纤维断裂。与基体材料相比，纤维的刚度和强度更大，纤维方向上的应力主要通过纤维传递，基体的损伤几乎不会削弱纤维中拉伸应力的传递。因此，面内的拉剪损伤起始由纤维决定，经纱纤维和纬纱纤维的损伤因子分别为：
f21=(Ex⟨εx⟩St,x)2+(GxzγxzSfs,x)2 (1) f22=(Ey⟨εy⟩St,y)2+(GyzγyzSfs,y)2 (2) （2）面内的纤维压缩损伤：
f23=(Ex⟨ε′x⟩Sc,x)2,ε′x=−εx−⟨−εz⟩EzEx (3) f24=(Ey⟨ε′y⟩Sc,y)2,ε′y=−εy−⟨−εz⟩EzEy (4) （3）厚度方向的纤维压溃：
f25=(Ez⟨−εz⟩Sc,z)2 (5) （4）面内的基体剪切损伤：
f26=S2(GxyγxySxy)2 (6) （5）厚度方向的基体拉/剪损伤：
f27=S2((Ez⟨εz⟩St,z)2+(GxzγxzSxz+Ssr)2+(GyzγyzSyz+Ssr)2) (7) Ssr=Eztanφ⟨−εz⟩ (8) 式中：φ为库伦摩擦角。厚度方向剪切作用下的基体损伤和厚度方向的压缩应变ɛz相关，遵循Coulomb-Mohr理论。
需要指出，式(6)～(7)中的S与文献[9]中的S有不同的意义。在文献[9]中，S作为分层修正系数，仅在描述厚度方向基体拉/剪破坏的损伤准则中添加，用于描述FRP层间弱界面影响，通常大于1。而在本文中，将引入黏结层损伤模型来讨论层间分层情况，S只作为基体增韧因子，添加至描述基体损伤的项（模式6~7），用于描述CNT基体改性对FRP的增韧效果，S通常小于1。
1.2 损伤软化及损伤耦合
纤维增强树脂基复合材料层合板达到上述损伤准则的阈值后，材料的应力和刚度并不迅速下降为零，而有一个逐渐累积退化的过程。通常假设，FRP层合板的损伤演化由模量的逐渐退化导致失效。在有限元计算中，仅用模量退化描述的损伤演化行为，会产生应变集中从而导致计算结果强烈的网格依赖性。Xin等[8]引入单元特征尺寸Lc（δeq=Lcɛeq），采用应力-位移关系取代通常情况下的应力-应变关系来描述材料的损伤演化过程，该方法能在一定程度上解决单元敏感性问题。本文中，损伤演化过程也采用应力-位移关系。
纤维和基体损伤是根据方向区分的，实际上只是某一方向的损伤由纤维或基体主导。例如，纤维方向的拉伸失效，虽由纤维断裂不断累积造成，但基体同样也发生破坏。通常，树脂基体的失效应变比增强纤维的失效应变高很多，因此，在纤维断裂后，载荷会从纤维转移至纤维基体界面，断裂的纤维从基体中拔出也将吸收一部分能量。纳米填料加入FRP的树脂基体中，为纤维基体界面提供了更有效的载荷传递，界面剪切强度提高，最终，纤维拔出阶段载荷强度提高。本文中，在Xin等[7-8]的线性损伤软化的基础上，引入残余强度因子frs描述断裂纤维从基体中拔出过程的吸能。对纤维的损伤演化采用图1(a)所示的双线性软化形式，其中AB段为损伤开始前的弹性阶段，BC段为纤维逐渐断裂的过程，CD段则为断裂纤维从基体中拔出的过程。另外，由于基体损伤主导方向的强度较低，这部分损伤通常开始早、发展快，为避免基体损伤发展过快而主导最终的破坏，对基体的损伤演化采用如图1(b)所示的演化形式，相当于frs=1。如frs=0，则退化为原线性软化形式。
最终，损伤演化方程为：
ϕj={min(δfeq,j(δeq,j−δ0eq,j)δeq,j(δfeq,j−δ0eq,j),1−frs,jfj)j=1∼51−1fjj=6∼7 (9) 式中：状态变量ϕj描述单一模式损伤的程度，其定义域为[0,1]。
损伤起始等效位移和损伤起始等效应力的计算方法为：
δ0eq,j=δeq,jfj,σ0eq,j=σeq,jfj (10) 不同损伤模式的等效位移和等效应力的计算方法见表1。
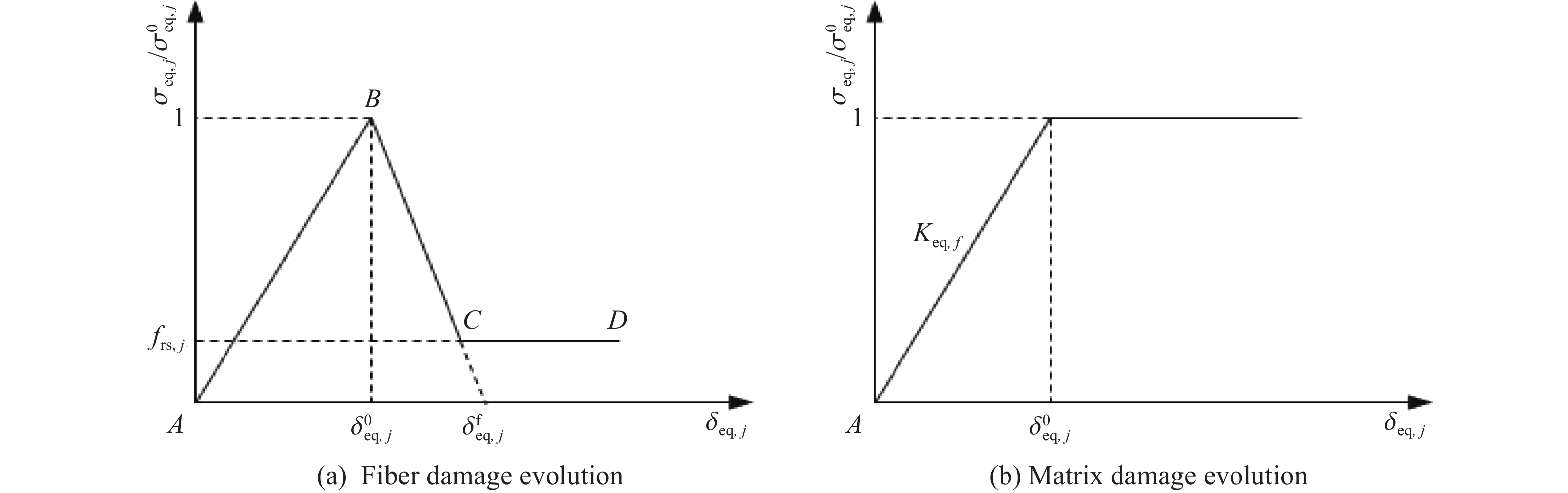
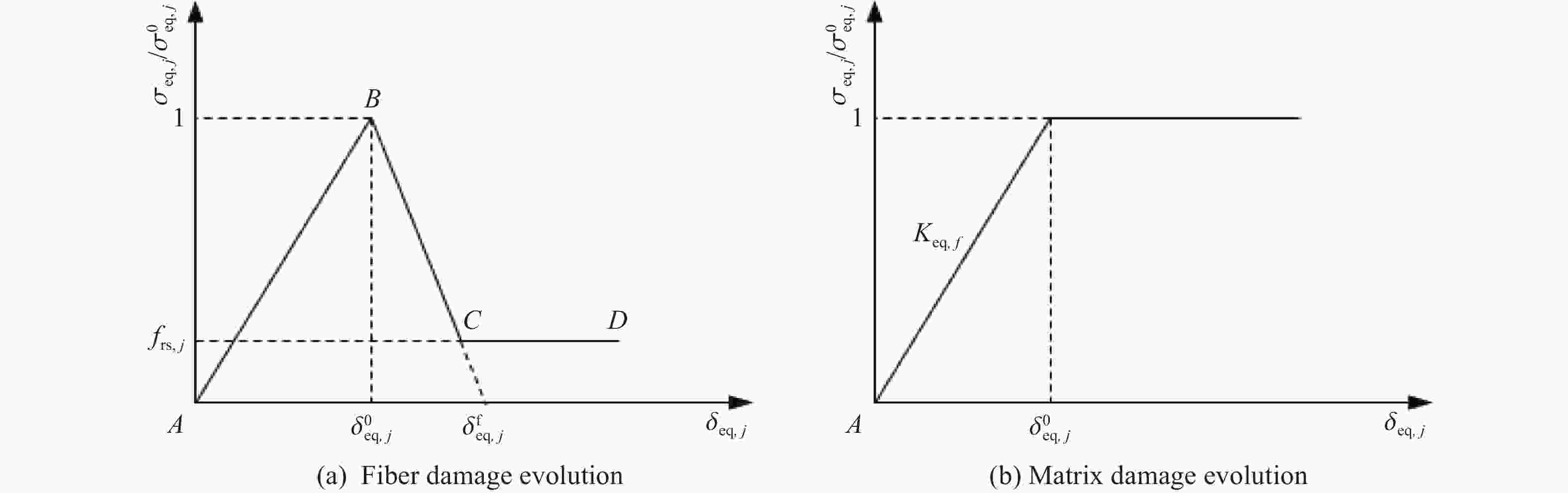
表 1 等效位移和等效应力Table 1. Equivalent displacement and equivalent stressj 损伤模式 δeq,j σeq,j 1 x方向的纤维拉/剪损伤 Lc√⟨εx⟩2+γ2xz Lc(Ex⟨εx⟩2+Gxzγ2xz)/δeq,1 2 y方向的纤维拉/剪损伤 Lc√⟨εy⟩2+γ2yz Lc(Ey⟨εy⟩2+Gyzγ2yz)/δeq,2 3 x方向的纤维压缩损伤 Lc⟨ε′x⟩ Ex⟨ε′x⟩ 4 y方向的纤维压缩损伤 Lc⟨ε′y⟩ Ey⟨ε′y⟩ 5 厚度方向的纤维压溃 Lc⟨−εz⟩ Ez⟨−εz⟩ 6 面内的基体剪切损伤 Lc√γ2xy Gxy√γ2xy 7 厚度方向的基体拉剪损伤 Lc√⟨εz⟩2+γ2xz+γ2yz Lc(Ez⟨εz⟩2+Gxzγ2xz+Gyzγ2yz)/δeq,7 FRP复合材料不同模式的损伤演化不是完全独立的，他们存在相互作用，因此引入损伤变量ωi，表示受到不同破坏模式ϕj协同作用后模量的缩减程度。在MAT162、FRP本构模型[8]中，不同模式下的损伤以加和的形式耦合（ωi=qijϕj,max），这样损伤耦合形式预测的损伤量偏高，基体损伤主导了最后的破坏，这是不够准确的。因此，本文中提出了乘积式耦合：
1−ωi=7∏j=16∏i=1(1−qijϕj,max) (11) qij = [101010001011000000101111111001011011010101] (12) 其实，原加和形式的损伤耦合就相当于提取了式（11）的一阶近似，在损伤为小量时，两者是等价的，而对于损伤很容易达到1情况（如冲击、侵彻等），采用乘积形式的损伤耦合形式更合理。
由损伤变量
ωi 表征的柔度矩阵为：Sij=[1(1−ω1)Ex−νxyEy−νxzEz000−νyxEx1(1−ω2)Ey−νyzEz000−νzxEx−νzyEy1(1−ω3)Ez0000001(1−ω4)Gxy0000001(1−ω5)Gy{\textit{z}}0000001(1−ω6)Gxz] (13) 刚度矩阵Cij为柔度矩阵Sij的逆矩阵，即：
Cij=S−1ij (14) 用更新的刚度矩阵和更新的应变便可以得到更新的应力，即：
σ=Cijε (15) 1.3 失效准则
考虑FRP单层板的各向异性，与MAT162类似，以下3种失效准则用于有限元模拟中的单元删除：（1）基于最大应变准则的纤维拉伸失效，当ɛx≥ɛx,limit或ɛy≥ɛy,limit时，单元删除；（2）基于体应变的拉伸和压缩失效，当ɛV≥ɛexpn或ɛV≤ɛcrsh时，单元删除；（3）基于等效应变的畸变单元删除，当ɛe≥ɛdistor时，单元删除。
1.4 应变率效应
Xin等[7-8]引入动态增强因子，描述了FRP的应变率效应。本文中，采用相同形式的动态增强因子：
fdi=C+12(((C(C+1)/2−1)tanh(B(log˙ε˙ε0−A)))+1) (16) 于是，考虑应变率效应后的强度和模量可以表示为：
Srt=fdiS0,Ert =fdiE0 (17) 另需指出的是，本文中模型适用于一般的FRP层合板，为了本构模型的完整性，考虑了应变率效应。但对下面数值模拟验证所采用的CFRP层合板，由文献[7]得知CFRP应变率效应不敏感，因此在数值模拟中，取动态增强因子fdi=1，即经验参数C=1。
2. 黏结层损伤模型
蒋振等[10]提出了考虑应变率效应的黏结层损伤模型，该模型基于B-K失效准则，引入与FRP本构模型中相同形式的动态增强因子，考虑牵引力-位移关系中刚度与强度的应变率效应，混合模式下的分层损伤通过损伤变量D描述。黏结层损伤模型的具体介绍见文献[10]。
3. 有限元模型与材料参数
Soliman等[11]对4种MWCNTs（multi walled carbon nanotubes）含量的碳纳米管改性编织碳纤维增强树脂基复合材料进行了5种能量下的落锤冲击实验。本文中，根据实验中的描述，建立了有限元模型，如图2所示。落锤系统简化为直径12.7 mm、质量14.93 kg的球头弹；靶板尺寸为50 mm×50 mm×2.7 mm，单层板厚度为0.27 mm，共10层，层与层之间通过偏置方法插入了零厚度的Cohesive单元，FRP单元与Cohesive单元是共节点的。在满足求解精度的条件下，为了提高计算效率，对靶板进行如下形式的网格划分：冲击影响区域（约2倍弹径）30 mm×30 mm范围内单元较密（面内尺寸为0.5 mm×0.5 mm）、外围较疏（面内尺寸为1 mm×1 mm），中间采用蝴蝶型网格过渡。弹体和FRP单层板用C3D8R单元创建，黏结层用COH3D8单元创建。靶板四周施加固定约束，弹体设置为刚体，弹体与靶板间采用通用接触，摩擦因数设为0.2。对弹体施加的速度分别为1.42、1.8、2.0、2.85和4.0 m/s，用以模拟能量分别为15、24、30、60和120 J的落锤冲击实验。
图 2 冲击载荷下 CFRP 层合板的有限元模型Figure 2. Finite element model for CFRP laminates under impact loading本文中新的FRP本构模型及文献[10]中的黏结层损伤模型，通过用户材料子程序（VUMAT）编程实现并嵌入到有限元软件ABAQUS中，用于碳纳米管改性碳纤维增强复合材料冲击实验的模拟。下面简单介绍模型中相关材料参数的确定。
表2为CFRP单层板的材料参数，这些参数来源于文献[12-14]，暂未考虑碳纳米管改性对CFRP层内强度和模量的影响，因而在算例中，这部分参数是相同的。表3为反映碳纳米管改性对CFRP影响的材料参数，包括基体增韧因子S、残余强度因子frs,j、失效参数ɛx,limit、ɛy,limit、ɛexpn、ɛcrsh、ɛdistor，这些参数通过试算确定，不考虑经纱和纬纱纤维的不同，认为ɛx,limit和ɛy,limit相等。
表 2 CFRP单层板的材料参数Table 2. Parameters for CFRP laminate表 3 CNT/CFRP材料参数Table 3. Parameters for CNT/CFRP laminatesw/% S frs,j ɛx,limit, ɛy,limit ɛexpn ɛcrsh ɛdistor j=1~2 j=3~5 0 1.0 0.08 0.1 2.1 3.3 0.001 2.0 0.5 0.5 0.15 0.1 2.4 5.2 0.001 5.0 1.0 0.5 0.15 0.1 2.4 5.2 0.001 5.0 1.5 0.5 0.15 0.1 2.4 5.2 0.001 5.0 在分析大量实验数据的基础上，给出了CNT/FRP层间剪切强度随CNT含量变化的规律，如图3所示。可以看出，当CNT含量不超过2.0%时，CNT/FRP的层间剪切强度Ssil与CNT的质量分数w成近似线性关系，可以用经验公式表达：
图 3 CNT含量对CNT/FRP层间剪切强度的影响Figure 3. Effect of CNT content on the intelaminar shear strengthSsil=(1+0.25w)Ssil,0 (18) 式中：Ssil,0为没有添加CNT时FRP的层间剪切强度。
图4为不同CNT含量下的牵引力-位移关系。假设3种分层模式下的牵引力强度（
t0n ，t0s ，t0t ）、失效位移（δfn ，δfs ，δft ）随CNT含量的变化满足与层间剪切强度相同的线性关系，则断裂韧性增比将是层间剪切强度增比的平方。模拟所需的黏结层单元参数见表4，其中无MWCNTs的黏结层单元参数来源于文献[22]，其余参数则按上述经验公式和假设预测。
图 4 不同CNT含量黏结层模型的牵引力-位移关系Figure 4. The traction-separation law in the cohesive element model with different CNT contents表 4 黏结层单元参数Table 4. Parameters for cohesive elements4. 结果与讨论
图5为数值模拟得到的载荷-位移曲线与实验[11]的比较，图中红线为数值模拟结果，黑线为实验曲线。实验结果显示： MWCNTs含量0.5%、1.0%和1.5%的CFRP层合板在能量15、24、60和120 J冲击下的峰值载荷是相近的，均约为2.8 kN，只有能量30 J冲击下MWCNTs含量1.0%和1.5%的CFRP层合板峰值载荷有所差别（3.5 kN），Soliman等[11]未给出合理解释。由图可以看出，数值模拟预测的峰值载荷、平台长度都与实验结果吻合较好。总体来看，新建立的FRP本构模型能够较准确地描述碳纳米管基体改性对CFRP的增韧效果，这种增韧效果主要体现为冲击响应过程中载荷在达到峰值后维持一段时间不变即在载荷-位移曲线中呈现一段平台，本文中提出的模型能较好地描述这个现象。另外，本文中还未考虑碳纳米管改性对CFRP层内强度和模量的影响，若考虑则会得到与实验更吻合的模拟结果。
图6为数值模拟的破坏形貌的正面图和侧面图与实验结果[11]的比较。由图可以看出，模拟结果与实验相同，靶板形成鼓包，背面呈现十字形破坏。
图7为数值模拟的MWCNTs含量0.5%的CFRP层合板在能量120 J冲击下的破坏历程。由图可以看出，破坏的各阶段与载荷-位移曲线的特征相对应。在冲击过程中，先是冲击面的压缩损伤（见图7(a)），接着是冲击背面开始的自下而上发展的拉伸损伤（见图7(b)），拉伸损伤集中在各层的十字形区域；在压缩损伤与拉伸损伤在中间层汇集前，接触力不断增大，当两种损伤在中间层汇集时，接触力达到峰值（见图7(c)），对应载荷-位移曲线平台起点；而后损伤继续在面内扩展，此过程接触力维持几乎恒定（见图7(d)），对应载荷-位移曲线的平台段；当冲击背面开始拉伸破坏（见图7(e)）删除单元时，对应载荷-位移曲线平台终点；随着自下而上的拉伸破坏，单元相继被删除，接触力逐渐减小，直至完全穿透（见图7(f)～(h)）。
图8～9分别为数值模拟的能量15和120 J冲击下不同含量MWCNTs增韧CFRP层合板的层间损伤云图。由图8可以看出，当冲击能量较低不足以穿透CFRP层合板时，随着MWCNTs含量的增加，层间界面的分层损伤面积逐渐减小。而当冲击能量较高CFRP层合板被穿透时，分层将承担一部分吸能。由图9可以看出：相较于CFRP层合板，MWCNTs/CFRP层合板分层面积增大，因此吸能增多；但是，随着MWCNTs含量增加，分层面积逐渐减小，最大分层面积出现在中性层及其附近的层间界面5-6（CFRP层合板总共有10层，界面5-6刚好就对应中性截面）。经分析，当弹体穿透到中性层时，中性层以下FRP因面内拉伸损伤而难以承受面外压缩载荷，弹体继续前进将造成中性层附近的层间界面撕裂，直到层合板的未打穿部分因为面内拉伸破坏，最终被穿透。
图 8 冲击能量为15 J时不同MWCNTs含量CFRP层合板的分层形貌Figure 8. Delaminations of CFRP laminatses with different MWCNTs content under the impact energy of 15 J
图 9 冲击能量为120 J时不同MWCNTs含量CFRP层合板的分层形貌Figure 9. Delaminations of CFRP laminates with different MWCNTs content under the impact energy of 120 J为进一步探讨冲击速度对CNT/CFRP冲击响应的影响，在CNT含量0.5%、冲击能量120 J的算例中，保持其他参数不变，只改变弹体密度和冲击速度，实现相同冲击能量下不同冲击速度的加载。图10为相同冲击能量不同冲击速度下的载荷-位移曲线，可以看出，随着冲击速度的提高，载荷-位移曲线的首次峰值载荷提高，平台后端上翘。图11为不同冲击速度下FRP层合板中间三层的最终层内损伤云图，为辨别拉伸和压缩破坏，不显示变形。中心圆形的损伤由压缩造成，十字形损伤则由拉伸引起。可以看出，随着冲击速度的增大，CFRP6中心压缩损伤区域逐渐减小，穿透该层涉及更多的拉伸撕裂。因此，冲击速度会影响FRP层合板压缩和拉伸破坏的比例，相同冲击能量下，更大的冲击速度会造成更多的拉伸破坏。
图 10 冲击能量为120 J时不同冲击速度对CNT/CFRP冲击载荷-位移曲线的影响Figure 10. Effect of impact velocity on the impact load-displacement curve for CNT/CFRP under the impact energy of 120 J
图 11 冲击能量为120 J时下不同冲击速度对CNT/CFRP损伤的影响Figure 11. Effect of impact velocity on the damage of CNT/CFRP under the impact energy of 120 J5. 结 论
对碳纳米管/碳纤维增强复合材料（CNT/CFRP）层合板低速冲击下的响应和破坏进行了数值模拟。基于先前的研究工作，引入基体增韧因子、残余强度因子并改进损伤耦合方程，建立了新的FRP动态渐进损伤模型，该模型能够描述纳米填料掺入纤维增强复合材料基体后的增韧效果。将模拟结果与文献[11]中的相关实验结果进行了比较，并讨论了冲击速度的影响。结果表明：新建立的FRP本构模型能够预测CNT/CFRP层合板在低速冲击载荷作用下的响应、破坏过程和分层形貌，模拟得到的载荷-位移曲线和破坏形貌与实验较好吻合；冲击速度会影响CNT/CFRP层合板拉伸和压缩破坏的比例，相同的冲击能量下，更大的冲击速度会造成更多的拉伸破坏。
-
图 2 冲击载荷下 CFRP 层合板的有限元模型
Figure 2. Finite element model for CFRP laminates under impact loading
图 3 CNT含量对CNT/FRP层间剪切强度的影响
Figure 3. Effect of CNT content on the intelaminar shear strength
图 4 不同CNT含量黏结层模型的牵引力-位移关系
Figure 4. The traction-separation law in the cohesive element model with different CNT contents
图 8 冲击能量为15 J时不同MWCNTs含量CFRP层合板的分层形貌
Figure 8. Delaminations of CFRP laminatses with different MWCNTs content under the impact energy of 15 J
图 9 冲击能量为120 J时不同MWCNTs含量CFRP层合板的分层形貌
Figure 9. Delaminations of CFRP laminates with different MWCNTs content under the impact energy of 120 J
图 10 冲击能量为120 J时不同冲击速度对CNT/CFRP冲击载荷-位移曲线的影响
Figure 10. Effect of impact velocity on the impact load-displacement curve for CNT/CFRP under the impact energy of 120 J
图 11 冲击能量为120 J时下不同冲击速度对CNT/CFRP损伤的影响
Figure 11. Effect of impact velocity on the damage of CNT/CFRP under the impact energy of 120 J
表 1 等效位移和等效应力
Table 1. Equivalent displacement and equivalent stress
j 损伤模式 δeq,j σeq,j 1 x方向的纤维拉/剪损伤 Lc√⟨εx⟩2+γ2xz Lc(Ex⟨εx⟩2+Gxzγ2xz)/δeq,1 2 y方向的纤维拉/剪损伤 Lc√⟨εy⟩2+γ2yz Lc(Ey⟨εy⟩2+Gyzγ2yz)/δeq,2 3 x方向的纤维压缩损伤 Lc⟨ε′x⟩ Ex⟨ε′x⟩ 4 y方向的纤维压缩损伤 Lc⟨ε′y⟩ Ey⟨ε′y⟩ 5 厚度方向的纤维压溃 Lc⟨−εz⟩ Ez⟨−εz⟩ 6 面内的基体剪切损伤 Lc√γ2xy Gxy√γ2xy 7 厚度方向的基体拉剪损伤 Lc√⟨εz⟩2+γ2xz+γ2yz Lc(Ez⟨εz⟩2+Gxzγ2xz+Gyzγ2yz)/δeq,7 
下载: 导出CSV
表 3 CNT/CFRP材料参数
Table 3. Parameters for CNT/CFRP laminates
w/% S frs,j ɛx,limit, ɛy,limit ɛexpn ɛcrsh ɛdistor j=1~2 j=3~5 0 1.0 0.08 0.1 2.1 3.3 0.001 2.0 0.5 0.5 0.15 0.1 2.4 5.2 0.001 5.0 1.0 0.5 0.15 0.1 2.4 5.2 0.001 5.0 1.5 0.5 0.15 0.1 2.4 5.2 0.001 5.0
下载: 导出CSV
-
[1] TARFAOUI M, LAFDI K, EL MOUMEN A. Mechanical properties of carbon nanotubes based polymer composites [J]. Composites Part B:Engineering, 2016, 103: 113–121. DOI: 10.1016/j.compositesb.2016.08.016. [2] BISHT A, DASGUPTA K, LAHIRI D. Investigating the role of 3D network of carbon nanofillers in improving the mechanical properties of carbon fiber epoxy laminated composite [J]. Composites Part A:Applied Science and Manufacturing, 2019, 126: 105601. DOI: 10.1016/j.compositesa.2019.105601. [3] SAGER R J, KLEIN P J, LAGOUDAS D C, et al. Effect of carbon nanotubes on the interfacial shear strength of T650 carbon fiber in an epoxy matrix [J]. Composites Science and Technology, 2009, 69(7/8): 898−904. DOI: 10.1016/j.compscitech.2008.12.021. [4] CHA J, KIM J, RYU S, et al. Strengthening effect of melamine functionalized low-dimension carbon at fiber reinforced polymer composites and their interlaminar shear behavior [J]. Composites Part B: Engineering, 2019, 173: 106976. DOI: 10.1016/j.compositesb.2019.106976. [5] ZHANG Q J, WU J Q, GAO L, et al. Dispersion stability of functionalized MWCNT in the epoxy-amine system and its effects on mechanical and interfacial properties of carbon fiber composites [J]. Materials and Design, 2016, 94: 392–402. DOI: 10.1016/j.matdes.2016.01.062. [6] TARFAOUI M, EL MOUMEN A, LAFDI K. Progressive damage modeling in carbon fibers / carbon nanotubes reinforced polymer composites [J]. Composites Part B: Engineering, 2017, 112: 185–195. DOI: 10.1016/j.compositesb.2016.12.056. [7] XIN S H, WEN H M. Numerical study on the perforation of fiber reinforced plastic laminates struck by high velocity projectiles [J]. The Journal of Strain Analysis for Engineering Design, 2012, 47(7): 513–523. DOI: 10.1177/0309324712454650. [8] XIN S H, WEN H M. A progressive damage model for fiber reinforced plastic composites subjected to impact loading [J]. International Journal of Impact Engineering, 2015, 75: 40–52. DOI: 10.1016/j.ijimpeng.2014.07.014. [9] YEN C F. A ballistic material model for continuous-fiber reinforced composites [J]. International Journal of Impact Engineering, 2012, 46: 11–22. DOI: 10.1016/j.ijimpeng.2011.12.007. [10] 蒋振, 文鹤鸣. 粘结单元在模拟FRP层合板低速冲击响应中的应用 [J]. 爆炸与冲击, 2019, 39(4): 043202. DOI: 10.11883/bzycj-2017-0245.JIANG Z, WEN H M. Application of cohesive elements in modeling the low-velocity impact response and failure of fiber reinforced plastic laminates [J]. Explosion and Shock Waves, 2019, 39(4): 043202. DOI: 10.11883/bzycj-2017-0245. [11] SOLIMAN E M, SHEYKA M P, TAHA M R. Low-velocity impact of thin woven carbon fabric composites incorporating multi-walled carbon nanotubes [J]. International Journal of Impact Engineering, 2012, 47: 39–47. DOI: 10.1016/j.ijimpeng.2012.03.002. [12] VARAS D, ARTERO-GUERRERO J A, PERNAS-SÁNCHEZ J, et al. Analysis of high velocity impacts of steel cylinders on thin carbon/epoxy woven laminates [J]. Composite Structures, 2013, 95: 623–629. DOI: 10.1016/j.compstruct.2012.08.015. [13] NAIK N K, SEKHER Y C, MEDURI S. Damage in woven-fabric composites subjected to low-velocity impact [J]. Composites Science and Technology, 2000, 60(5): 731–744. DOI: 10.1016/S0266-3538(99)00183-9. [14] GÓMEZ-DEL RÍO T, ZAERA R, BARBERO E, et al. Damage in CFRPs due to low velocity impact at low temperature [J]. Composites Part B: Engineering, 2005, 36(1): 41–50. DOI: 10.1016/j.compositesb.2004.04.003. [15] BEHERA R P, RAWAT P, SINGH K K, et al. Fracture analysis and mechanical properties of three phased glass / epoxy laminates reinforced with multiwalled carbon nanotubes [J]. Journal of Science: Advanced Materials and Devices, 2019, 4(2): 299–309. DOI: 10.1016/j.jsamd.2019.03.003. [16] GAURAV A, SINGH K K. ILSS improvement of quasi-isotropic glass fiber reinforced epoxy laminate enhanced with arc discharged multi-walled carbon nanotubes [J]. Materials Today: Proceedings, 2018, 5(2): 8638–8644. DOI: 10.1016/j.matpr.2017.11.563. [17] RATHORE D K, PRUSTY R K, KUMAR D S, et al. Mechanical performance of CNT-filled glass fiber / epoxy composite in in-situ elevated temperature environments emphasizing the role of CNT content [J]. Composites Part A: Applied Science and Manufacturing, 2016, 84: 364–376. DOI: 10.1016/j.compositesa.2016.02.020. [18] BÖGER L, WICHMANN M H G, MEYER L O, et al. Load and health monitoring in glass fibre reinforced composites with an electrically conductive nanocomposite epoxy matrix [J]. Composites Science and Technology, 2008, 68(7/8): 1886−1894. DOI: 10.1016/j.compscitech.2008.01.001. [19] ZAHID S, NASIR M A, NAUMAN S, et al. Experimental analysis of ILSS of glass fibre reinforced thermoplastic and thermoset textile composites enhanced with multiwalled carbon nanotubes [J]. Journal of Mechanical Science and Technology, 2019, 33(1): 197–204. DOI: 10.1007/s12206-018-1219-0. [20] ZHANG T, CHEN J L, WANG K, et al. Improved interlaminar crack resistance of glass fiber / poly (phenylene sulfide) thermoplastic composites modified with multiwalled carbon nanotubes [J]. Polymer Composites, 2019, 40(11): 4186–4195. DOI: 10.1002/pc.25279. [21] KHURRAM A A, HUSSAIN R, AFZAL H, et al. Carbon nanotubes for enhanced interface of fiber metal laminate [J]. International Journal of Adhesion and Adhesives, 2018, 86: 29–34. DOI: 10.1016/j.ijadhadh.2018.08.008. [22] LIU Y J, JIANG Z, WEN H M. Predicting impact induced delamination of FRP laminates [J]. International Journal of Impact Engineering, 2020, 137: 103436. DOI: 10.1016/j.ijimpeng.2019.103436. 期刊类型引用(6)
1. 杨可谞，何成龙，霍子怡，毛翔. UHMWPE背板厚度对铝复合板抗侵彻增强效应分析. 爆炸与冲击. 2024(02): 72-87 . 
本站查看2. 姚昱，方海，祝露，朱俊羽. 纤维增强复合材料缠绕管桩弯曲冲击吸能试验与模拟. 振动与冲击. 2024(13): 299-305 . 
百度学术3. 李峰，陈姝予，张荣荣，周思齐. 碳纳米纤维增强模拟月壤地聚合物抗冲击性能研究. 华中科技大学学报(自然科学版). 2024(08): 76-83 . 百度学术4. 崔旭，王祖昊. CFRP层合板力学性能数值模拟的研究进展. 航空制造技术. 2023(15): 60-70 . 百度学术5. 王金贵，胡超，罗飞云，张苏. 泄爆面积对甲烷-空气预混泄爆容器结构响应影响的实验研究. 爆炸与冲击. 2022(04): 139-150 . 本站查看6. 薛程，李彦斌，杭晓晨，郑浩，王天怡，费庆国. 复合材料机翼热气弹剪裁研究及分析系统研发. 东南大学学报(自然科学版). 2022(05): 899-906 . 百度学术其他类型引用(5)
-
下载:
百度学术
计量
- 文章访问数: 655
- HTML全文浏览量: 291
- PDF下载量: 122
- 被引次数: 11