超细晶D6A钢动态拉伸力学特性实验研究

杨泽洲; 申勇峰; 冯晓伟; 薛文颖; 谢若泽; 胡艳辉

doi:10.11883/bzycj-2021-0051

超细晶D6A钢动态拉伸力学特性实验研究

doi: 10.11883/bzycj-2021-0051

1.
中国工程物理研究院总体工程研究所，四川绵阳 621999
2.
东北大学材料各向异性与织构教育部重点实验室，辽宁沈阳 110819
3.
东北大学轧制技术与连轧自动化国家重点实验室，辽宁沈阳 110819

详细信息

作者简介:
杨泽洲（1996－　），男，硕士研究生，yangzezhou19@gscaep.ac.cn

通讯作者:
冯晓伟（1984－　），男，博士，副研究员，414fengxw@caep.cn

中图分类号: O347.3
计量
- 文章访问数: 329
- HTML全文浏览量: 108
- PDF下载量: 46
- 被引次数: 0
出版历程
- 收稿日期: 2021-02-02
- 修回日期: 2021-05-11
- 网络出版日期: 2022-03-30
- 刊出日期: 2022-05-09

Investigation on dynamic tensile properties of an ultrafine grained D6A steel

1.
Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999, Sichuan, China
2.
Key Laboratory for Anisotropy and Texture of Materials, Northeastern University, Shenyang 110819, Liaoning, China
3.
State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110819, Liaoning, China

摘要

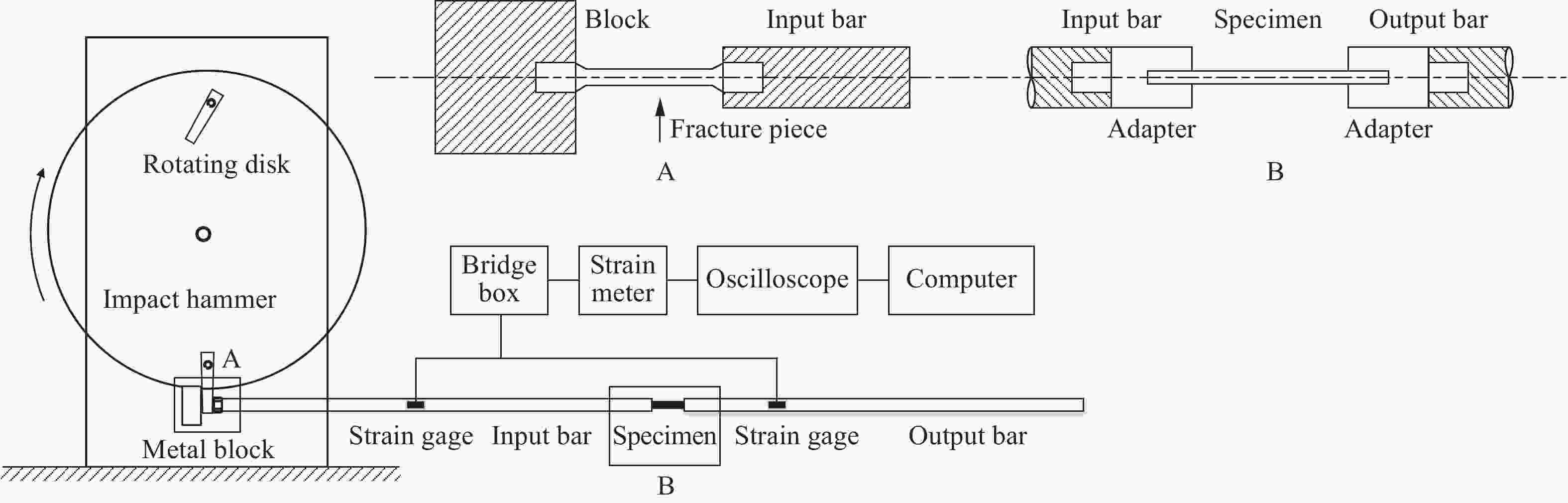
摘要: 为了推进超细晶D6A钢在半穿甲战斗部壳体上的应用，研究了动态加载下其宏观力学行为和细观变形机理。运用旋转盘式Hopkinson拉杆技术，开展了超细晶D6A低合金钢（平均晶粒尺寸为510 nm）的动态拉伸实验，获得了不同应变率（500～1000 s⁻¹）下超细晶钢的应力-应变曲线。运用TEM观测微观形貌，从细观层次研究了高应变率拉伸作用下超细晶钢的动态力学特性。结果表明，超细晶D6A钢具有较高的动态拉伸强度和良好的延展性。并且，晶粒细化和纳米析出相（渗碳体）是超细晶钢同时拥有高强度和较好韧性的重要因素；在动态拉伸过程中析出的大量纳米级渗碳体，与高密度晶界共同作用限制了位错运动，从而产生额外的塑性变形抗力，有效提升了超细晶钢的强度；在塑性变形阶段超细晶钢出现的明显应力下降现象，是可动位错密度增高的结果。
- 超细晶D6A钢 /
- 动态拉伸实验 /
- 动态强韧化 /
- 应力下降
Abstract: In order to promote the application process of an ultrafine grained (UFG) D6A low-alloy medium-carbon steel in semi-armor-piercing warhead shells, mechanical behaviors and microscopic deformation mechanism of the UFG D6A steel under dynamic loading were studied. The UFG D6A steel (d = 510 nm) was prepared by using inter-critical rolling and low temperature annealing process, whose microstructure features show that nanoscale spherical cementite grains are uniformly distributed in the equiaxed ferrite matrix. Dynamic tensile experiments were performed with a rotating Hopkinson bar apparatus at strain rates ranging from 500 s⁻¹ to 1000 s⁻¹. Micromorphology of specimens before and after tensile loading was observed by transmission electron microscopy. Combined with these observations, the dynamic mechanical properties of the UFG steel under high strain rates were extensively studied. The results reveal that the UFG D6A steel achieves both excellent strength and well toughness simultaneously with a dynamic tensile strength of 2 200 MPa and an average dynamic fracture elongation of 13%. The dynamic tensile strength is obviously higher than the quasi-static tensile strength (approximately 2 times), while the toughness is lower than that under quasi-static conditions. It is observed that the cementite content increases dramatically during the dynamic tensile experiment process, which can effectively restrict the movement of dislocations to produce additional plastic deformation resistance. Consequently, grain refinement and the precipitation of nanosized carbides are considered to play key roles for strengthening the steel. The severe plastic deformation reduces the average grain size and increases the density of grain boundaries within the material, which is considered to eventually lead to the decrease of dynamic fracture elongation of the UFG D6A steel. The drops of yield stress were observed apparently during dynamic tensile process, which is mainly due to the increase of the mobile dislocation density. These research results may give deeper insights into the relationship between material microstructure and mechanical behavior of UFG steels, and provide a significantly experimental and theoretical basis for the application of UFG D6A steels in the military equipment field.
- ultrafine grained D6A steel /
- dynamic tensile experiment /
- dynamic strengthening and toughening /
- yield drop

HTML全文

图 1 钢退火组织的SEM形貌

Figure 1. The SEM morphologies of annealing structures of the steels

下载: 全尺寸图片幻灯片

图 2 钢的晶粒尺寸分布

Figure 2. Grain size distributions of the steels

下载: 全尺寸图片幻灯片

图 3 超细晶D6A钢组合试件照片

Figure 3. Photographs of the ultrafine grained D6A steel combined specimens

下载: 全尺寸图片幻灯片

图 4 霍普金森拉杆系统

Figure 4. The Hopkinson tension bar system

下载: 全尺寸图片幻灯片

图 5 不同应变速率下超细晶D6A钢的工程应力-应变曲线和真实应力-应变曲线^[11]

Figure 5. Engineering and true stress-strain curves of the ultrafine grained D6A steels at different strain rates^[11]

下载: 全尺寸图片幻灯片

图 6 超细晶D6A钢的高应变率应力-应变曲线

Figure 6. Stress-strain curves of the ultrafine grained D6A steel at high strain rates

下载: 全尺寸图片幻灯片

图 7 超细晶D6A钢在不同应变率下的强度和延伸率

Figure 7. Strengths and elongations of the ultrafine grained D6A steel at different strain rates

下载: 全尺寸图片幻灯片

图 8 超细晶D6A钢加载前后的TEM形貌

Figure 8. The SEM morphologies of the ultrafine grained D6A steel before and after loading

下载: 全尺寸图片幻灯片

图 9 超细晶D6A钢拉伸断口形貌

Figure 9. The tensile fracture morphology of the ultrafine grained D6A steel

下载: 全尺寸图片幻灯片

表 1 超细晶D6A钢化学成分的质量分数

Table 1. Mass fractions of chemical compositions in the ultrafine grained D6A steel

w(C)/%	w(Si)/%	w(Mn)/%	w(Cr)/%	w(Mo)/%	w(Al)/%	w(Ni)/%	w(V)/%	w(Fe)/%
0.43	0.17	0.73	1.05	1.01	0.02	0.61	0.09	95.89

下载: 导出CSV

表 2 室温下超细晶D6A钢的准静态拉伸力学参数^[11]

Table 2. Quasi-static tensile mechanical parameters of the ultrafine grained D6A steels at room temperature^[11]

温度/℃	应变率/s⁻¹	屈服强度/MPa		拉伸强度/MPa		工程伸长率/%
温度/℃	应变率/s⁻¹	工程	真实	工程	真实	工程伸长率/%
25	1.7×10⁻¹	1110	1120	1120	1250	25
25	1.7×10⁻²	1100	1115	1115	1245	25
25	1.7×10⁻³	1095	1110	1110	1240	25

下载: 导出CSV

表 3 室温下超细晶D6A钢的动态拉伸力学参数

Table 3. Dynamic tensile mechanical parameters of the ultrafine grained D6A steel at room temperature

温度/℃	应变率/s⁻¹	强度/MPa	伸长率/%
25	560	1960	12.72
25	580	1950	13.42
25	620	1980	13.48
25	910	2210	12.43
25	920	1980	13.53
25	1030	2240	12.37

下载: 导出CSV

参考文献(27)

[1]	JIA D, RAMESH K T, MA E. Effects of nanocrystalline and ultrafine grain sizes on constitutive behavior and shear bands in iron [J]. Acta Materialia, 2003, 51(12): 3495–3509. DOI: 10.1016/s1359-6454(03)00169-1.
[2]	OKITSU Y, TAKATA N, TSUJI N. Mechanical properties of ultrafine grained ferritic steel sheets fabricated by rolling and annealing of duplex microstructure [J]. Journal of Materials Science, 2008, 43(23/24): 7391–7396. DOI: 10.1007/s10853-008-2971-9.
[3]	OKITSU Y, TAKATA N, TSUJI N. Dynamic deformation behavior of ultrafine-grained iron produced by ultrahigh strain deformation and annealing [J]. Scripta Materialia, 2011, 64(9): 896–899. DOI: 10.1016/j.scriptamat.2011.01.026.
[4]	HU Y S, YU Z Y, FAN G L, et al. Simultaneous enhancement of strength and ductility with nano dispersoids in nano and ultrafine grain metals: a brief review [J]. Reviews on Advanced Materials Science, 2020, 59(1): 352–360. DOI: 10.1515/rams-2020-0028.
[5]	王鹏杰, 申勇峰, 冯晓伟, 等. 轧制-退火工艺制备超细晶D6A钢的微观组织与织构 [J]. 钢铁研究学报, 2016, 28(9): 54–59. DOI: 10.13228/j.boyuan.issn1001-0963.20160042. WANG P J, SHEN Y F, FENG X W, et al. Microstructures and textures of ultrafine grained D6A steel by using rolling and annealing [J]. Journal of Iron and Steel Research, 2016, 28(9): 54–59. DOI: 10.13228/j.boyuan.issn1001-0963.20160042.
[6]	JIA N, SHEN Y F, LIANG J W, et al. Nanoscale spheroidized cementite induced ultrahigh strength-ductility combination in innovatively processed ultrafine-grained low alloy medium-carbon steel [J]. Scientific Reports, 2017, 7(1): 2679. DOI: 10.1038/s41598-017-02920-9.
[7]	LIANG J W, SHEN Y F, ZHANG C S, et al. In situ neutron diffraction in quantifying deformation behaviors of nano-sized carbide strengthened UFG ferritic steel [J]. Materials Science and Engineering: A, 2018, 726: 298–308. DOI: 10.1016/j.msea.2018.04.094.
[8]	WEI Q, SCHUSTER B E, MATHAUDHU S N, et al. Dynamic behaviors of body-centered cubic metals with ultrafine grained and nanocrystalline microstructures [J]. Materials Science and Engineering: A, 2007, 493(1/2): 58–64. DOI: 10.1016/j.msea.2007.05.126.
[9]	张世雄. 超细晶/纳米晶纯钛的制备及动态力学性能研究 [D]. 北京: 北京理工大学, 2016: 43–50.
[10]	刘晓燕, 张琪, 杨西荣, 等. 超细晶工业纯钛的变形、应变速率敏感性和激活体积 [J]. 稀有金属材料与工程, 2020, 49(6): 1867–1872. LIU X Y, ZHANG Q, YANG X R, et al. Deformation, strain rate sensitivity and activation volume of ultrafine-grained commercially pure Ti [J]. Rare Metal Materials and Engineering, 2020, 49(6): 1867–1872.
[11]	LIANG J W, SHEN Y F, MISRA R D K, et al. High strength-superplasticity combination of ultrafine-grained ferritic steel: the significant role of nanoscale carbides [J]. Journal of Materials Science and Technology, 2021, 83: 131–144. DOI: 10.1016/j.jmst.2020.11.078.
[12]	TSUJI N, ITO Y, SAITO Y, et al. Strength and ductility of ultrafine grained aluminum and iron produced by ARB andannealing [J]. Scripta Materialia, 2002, 47(12): 893–899. DOI: 10.1016/S1359-6462(02)00282-8.
[13]	ZAISER M. Scale invariance in plastic flow of crystalline solids [J]. Advances in Physics, 2006, 55(1/2): 185–245. DOI: 10.1080/00018730600583514.
[14]	ZHANG T W, JIAO Z M, WANG Z H, et al. Dynamic deformation behaviors and constitutive relations of an AlCoCr_1.5Fe_1.5NiTi_0.5 high-entropy alloy [J]. Scripta Materialia, 2017, 136: 15–19. DOI: 10.1016/j.scriptamat.2017.03.039.
[15]	ZHANG T W, MA S G, ZHAO D, et al. Simultaneous enhancement of strength and ductility in a NiCoCrFe high-entropy alloy upon dynamic tension: micromechanism and constitutive modeling [J]. International Journal of Plasticity, 2020, 124: 226–246. DOI: 10.1016/j.ijplas.2019.08.013.
[16]	MEYERS M A. Dynamic behavior of materials [M]. New Jersey: John Wiley and Sons, 1994: 345-349. DOI: 10.1002/9780470172278.
[17]	DE HOSSON J T M, ROOS A, HOSSON E D. Temperature rise due to fast-moving dislocations [J]. Philosophical Magazine A, 2001, 81(5): 1099–1120. DOI: 10.1080/01418610108214431.
[18]	QIN K, YANG L M, HU S S. Mechanism of strain rate effect based on dislocation theory [J]. Chinese Physics Letters, 2009, 26(3): 036103. DOI: 10.1088/0256-307X/26/3/036103.
[19]	GLADMAN T. Second phase particle distribution and secondary recrystallisation [J]. Scripta Metallurgica et Materialia, 1992, 27(11): 1569–1573. DOI: 10.1016/0956-716X(92)90146-6.
[20]	ZHOU B C, YANG T, ZHOU G, et al. Mechanisms for suppressing discontinuous precipitation and improving mechanical properties of NiAl-strengthened steels through nanoscale Cu partitioning [J]. Acta Materialia, 2021, 205: 116561. DOI: 10.1016/J.ACTAMAT.2020.116561.
[21]	ZENER C, HOLLOMON J H. Plastic flow and rupture of metals [J]. Transactions of the America Society of Mechanical, 1944, 33: 163–235.
[22]	徐永波, 白以龙. 动态载荷下剪切变形局部化、微结构演化与剪切断裂研究进展 [J]. 力学进展, 2007, 37(4): 496–516. DOI: 10.3321/j.issn:1000-0992.2007.04.002. XU Y B, BAI Y L. Shear localization, microstructure evolution and fracture under high-strain rate [J]. Advances in Mechanics, 2007, 37(4): 496–516. DOI: 10.3321/j.issn:1000-0992.2007.04.002.
[23]	SWADENER J G, MISRA A, HOAGLAND R G, et al. A mechanistic description of combined hardening and size effects [J]. Scripta Materialia, 2002, 47(5): 343–348. DOI: 10.1016/S1359-6462(02)00156-2.
[24]	GRAÇA S, COLAÇO R, VILAR R. Indentation size effect in nickel and cobalt laser clad coatings [J]. Surface and Coatings Technology, 2007, 202(3): 538–548. DOI: 10.1016/j.surfcoat.2007.06.031.
[25]	REZAEE M, ZAREI-HANZAKI A, MOHAMADIZADEH A, et al. High-temperature flow characterization and microstructural evolution of Ti6242 alloy: yield drop phenomenon [J]. Materials Science and Engineering: A, 2016, 673: 346–354. DOI: 10.1016/j.msea.2016.07.043.
[26]	BARMOUZ M, ABRINIA K, KHOSRAVI J. Using hardness measurement for dislocation densities determination in FSPed metal in order to evaluation of strain rate effect on the tensile behavior [J]. Materials Science and Engineering: A, 2013, 559: 917–919. DOI: 10.1016/j.msea.2012.08.086.
[27]	FAN J K, KOU H C, LAI M J, et al. High temperature discontinuous yielding in a new near β titanium alloy Ti-7333 [J]. Rare Metal Materials and Engineering, 2014, 43(4): 808–812. DOI: 10.1016/S1875-5372(14)60089-8.