Combustion characteristics of rotating detonation based on liquid hydrocarbon fuel
-
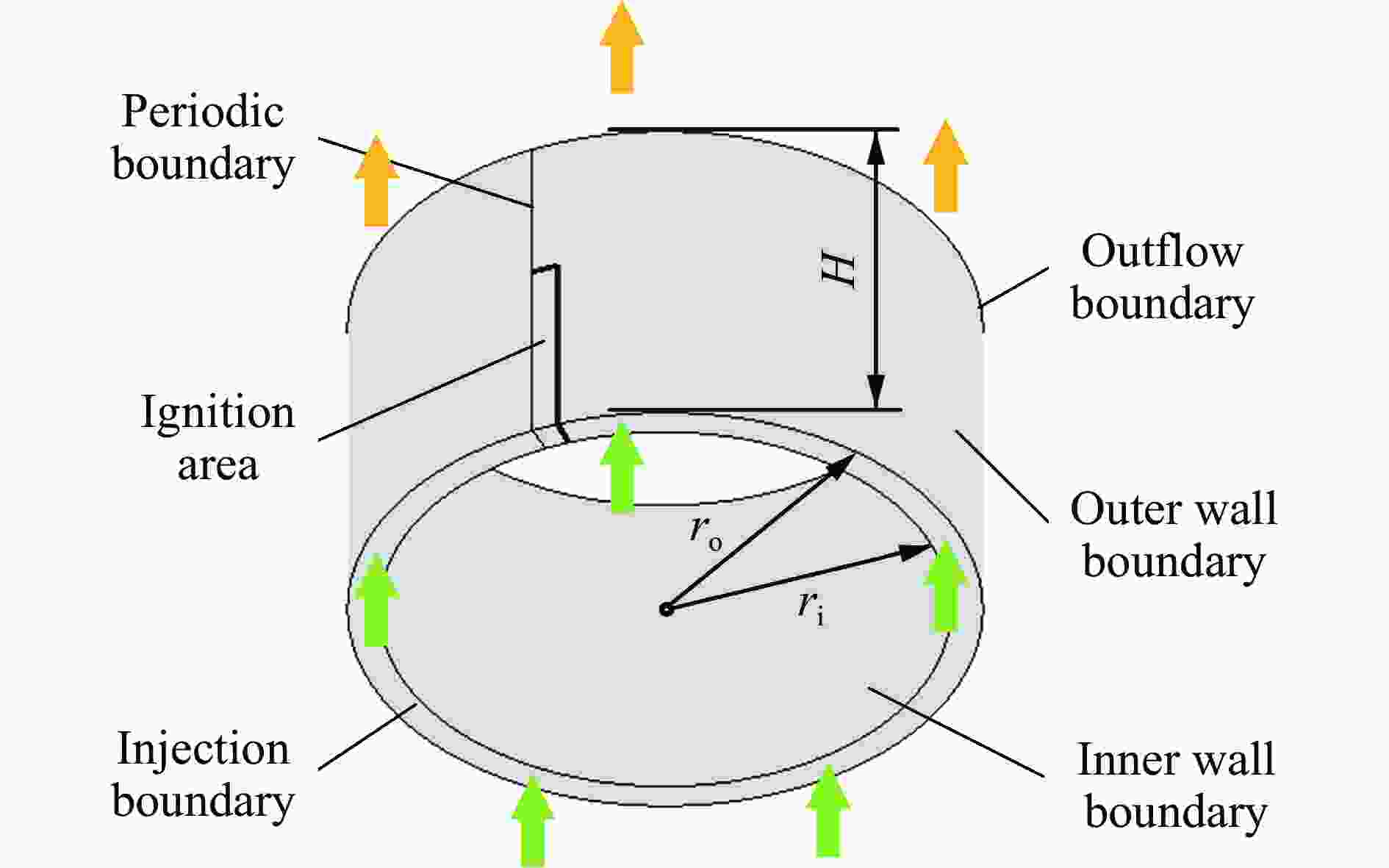
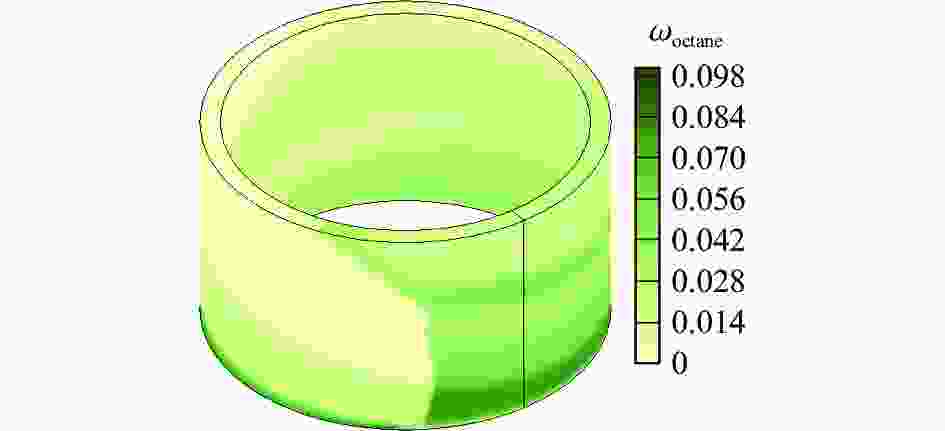
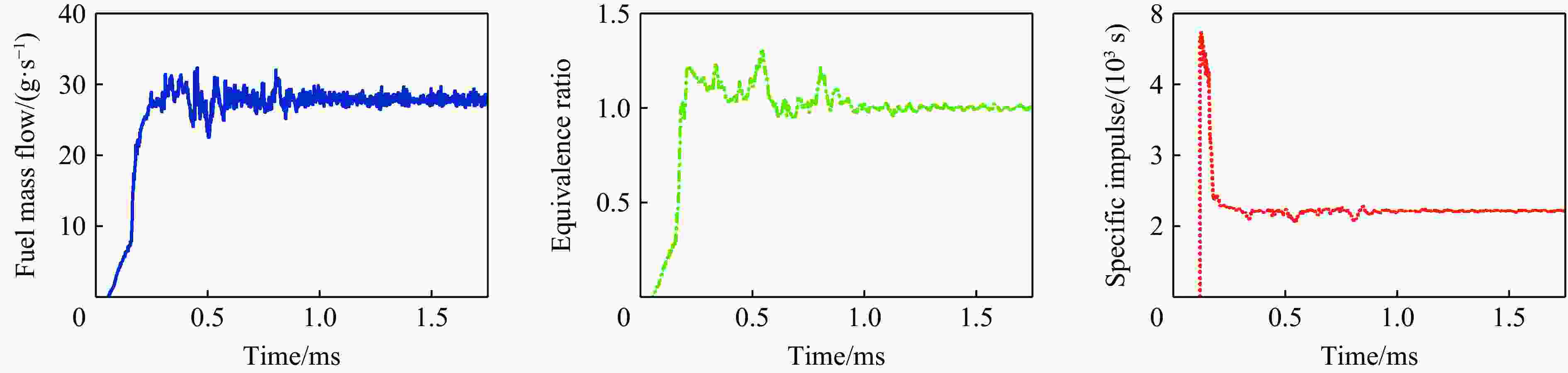
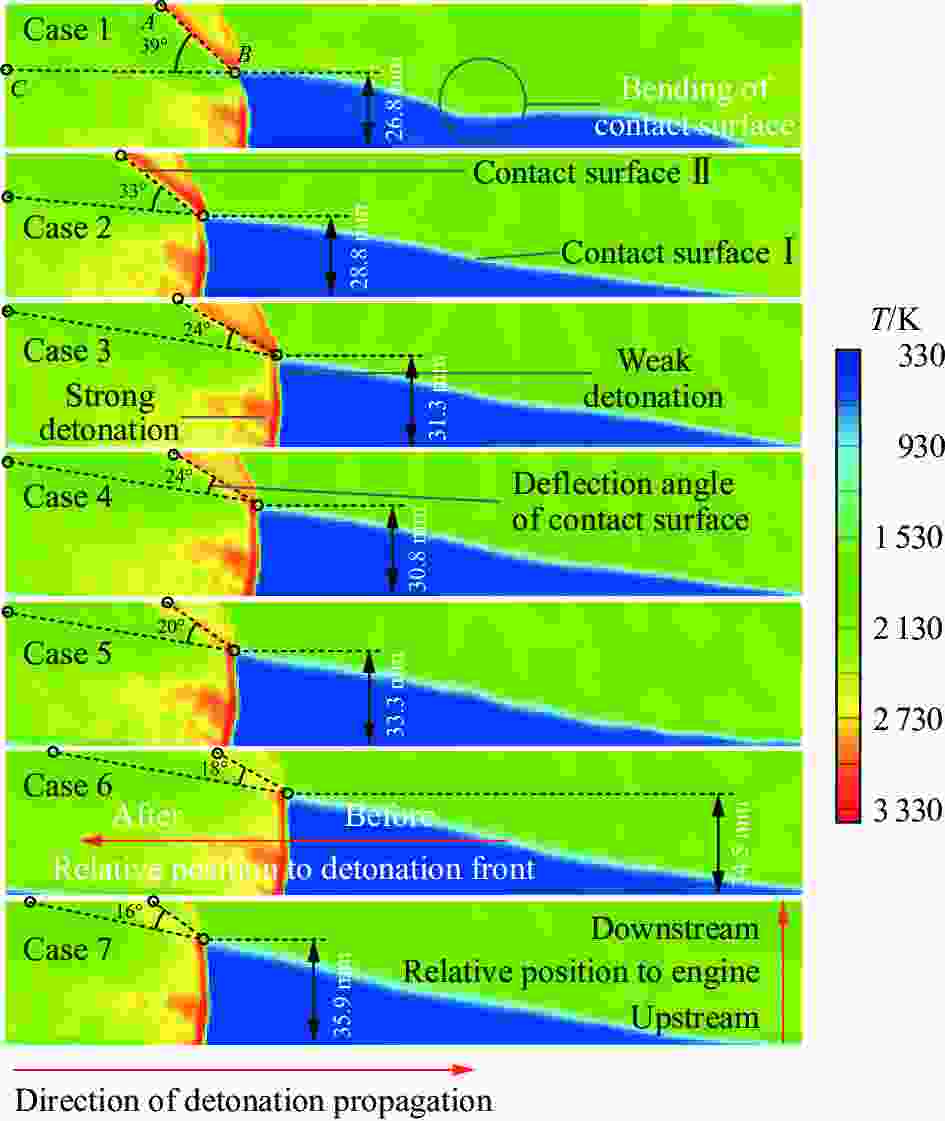
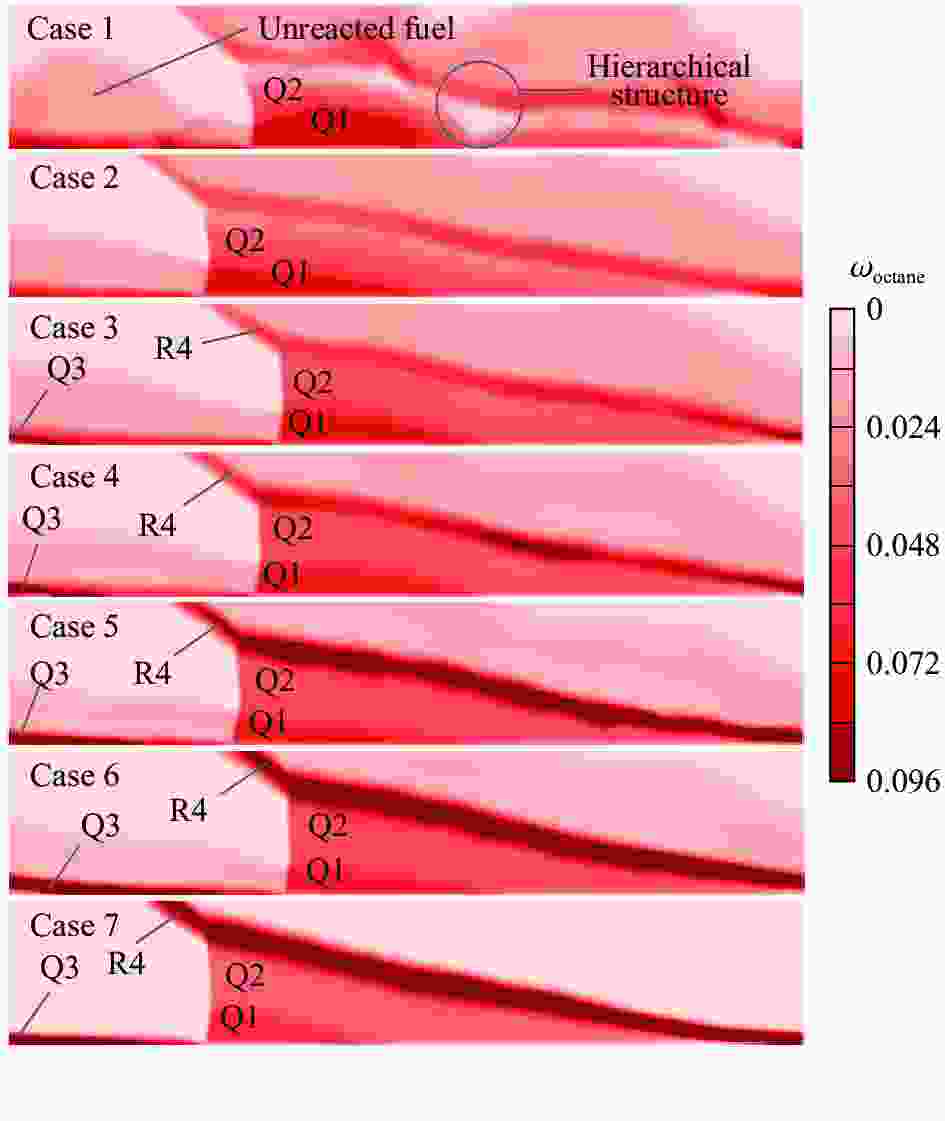
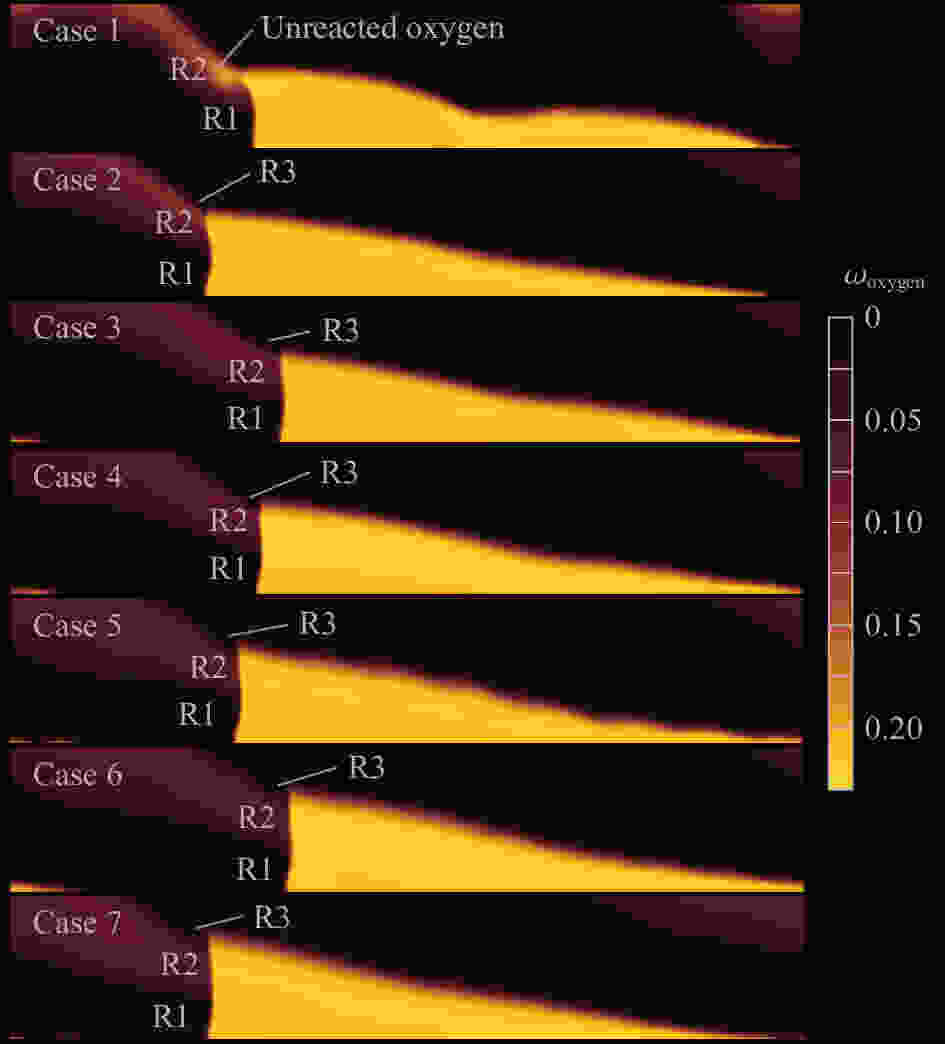
摘要: 为了探索液体碳氢燃料参与旋转爆轰所产生的不完全燃烧现象,采用守恒元与求解元方法,开展柱坐标系下的汽油/空气两相旋转爆轰燃烧室三维数值模拟研究,针对燃料喷注压力和反应物当量比对旋转爆轰流场结构及燃烧室性能的影响进行分析。分析结果表明:保持总当量比为1.00,随着燃料喷注压力的上升,燃烧室内燃料不均匀分布增强,产生局部富燃区,燃料在燃烧室未能完全反应,导致燃烧室燃料比冲下降;保持喷注压力不变,减小当量比,在贫燃工况下依然存在局部富燃区,导致燃烧室内出现不完全燃烧现象,降低燃烧室比冲性能。由此可知,反应物喷注方案对气液两相旋转爆轰的不完全燃烧有显著影响。Abstract: The liquid hydrocarbon fuel droplets need to be broken up and vaporized before further participating in detonation combustion, resulting in a more complex phenomenon in liquid-hydrocarbon fueled rotating detonation combustors (RDCs). To explore the incomplete combustion phenomena in liquid hydrocarbon-fueled rotating detonation, the conservation element and solution element method (CE/SE method) was used to simulate a two-phase three-dimensional RDC fueled with a liquid gasoline/air mixture. The Euler-Euler model was used to establish the three-dimensional gas-liquid two-phase governing equations in the cylindrical coordinate system. The source terms were solved by the fourth-order Runge-Kutta method. The phase transition was described by the droplet stripping and evaporation model. Furthermore, the energy and momentum exchange between the two phases was considered. The internal energy of the components was calculated from the enthalpy values of the polynomial fitting and the temperature was solved by Newton iteration. The injection conditions of the gas and liquid phases were assigned by different back pressures. The reactant equivalence ratio can be obtained by the area ratio of the droplets and the gas flow. The effects of the injection pressure and the equivalence ratio on the structure and performance of the rotating detonation flow field were analyzed. When the total equivalent ratio is fixed to 1.00, the inhomogeneous distribution of the fuel in the combustor is enhanced with the increase of the fuel injection pressure, resulting in some local fuel-rich areas. The fuel fails to completely combust in the combustor, leading to a decrease of the specific impulse. With a constant injection pressure and a reduced equivalent ratio, there are still local fuel-rich areas, resulting in incomplete combustion and reduced specific impulse performance. The results show that the reactant injection scheme has a significant effect on the incomplete combustion of the gas-liquid two-phase rotating detonations.
-
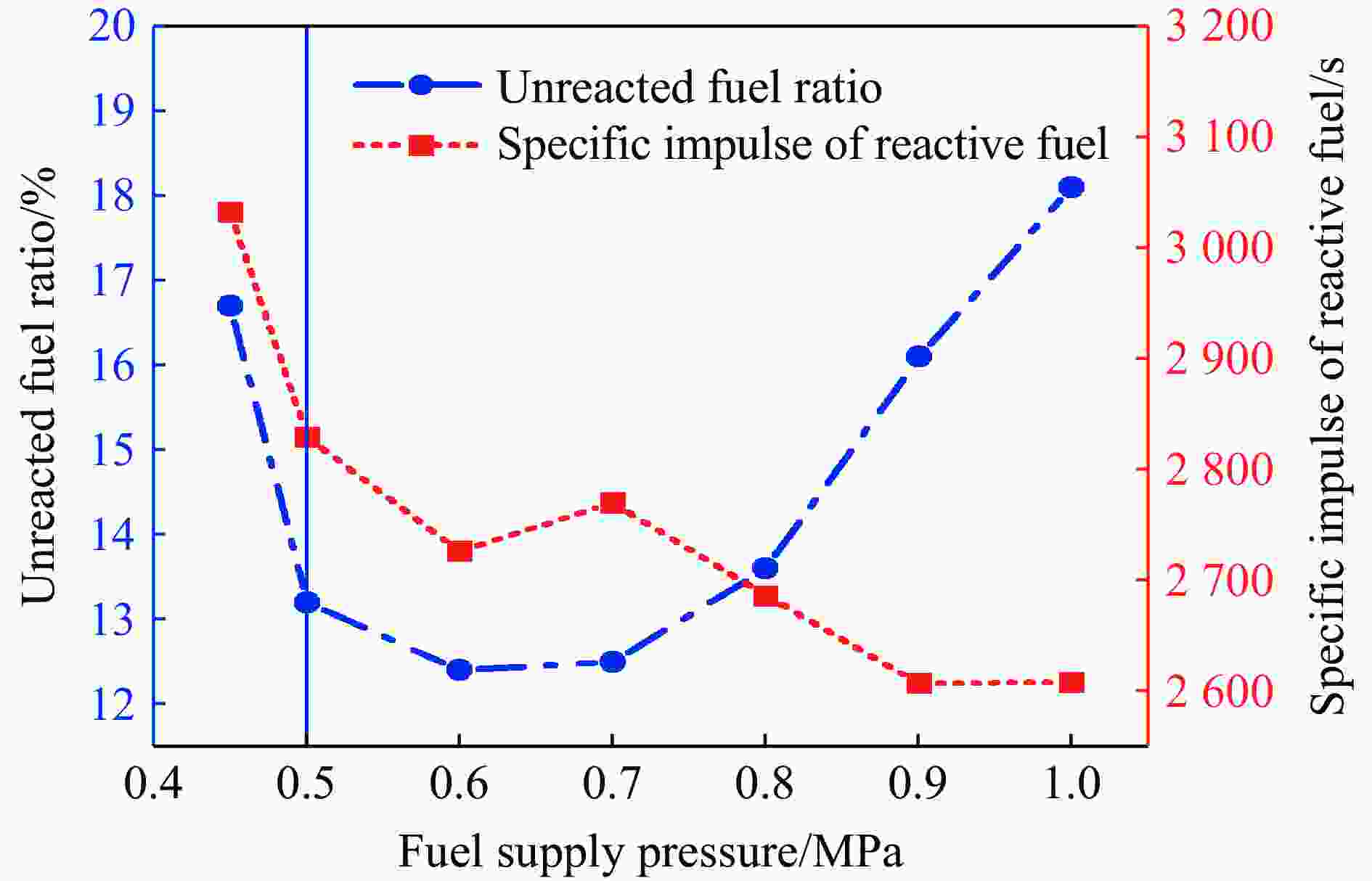
表 1 燃烧室在不同燃料喷注压力下的表现(当量比约为1.00)
Table 1. Performance of RDC at different fuel supply pressures (equivalence ratio of about 1.00)
算例 燃料喷注压力/
MPa空气流量/
(g∙s−1)当量比 未燃燃料比例/% 平均推力/N 燃料比冲 /s 基于反应燃料的燃料比冲/s 爆轰波传播速度/
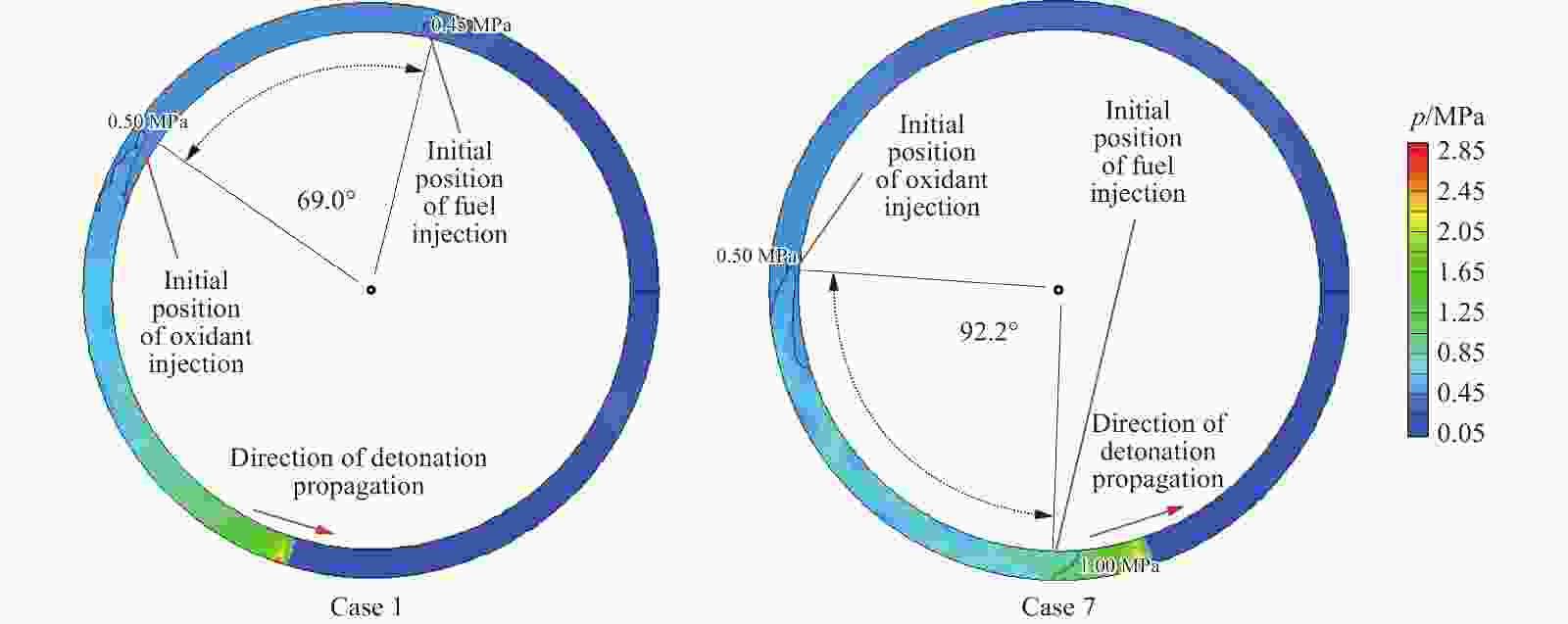
(m∙s−1)1 0.45 423.0 1.00 16.7 685.6 2 525.6 3 032.3 1 771 2 0.50 430.9 1.00 13.2 676.4 2 456.2 2 829.0 1 798 3 0.60 432.2 1.00 12.4 670.0 2 424.4 2 767.3 1 799 4 0.70 432.2 0.99 12.5 664.9 2 423.1 2 770.1 1 798 5 0.80 430.0 1.02 13.6 655.1 2 321.1 2 686.1 1 792 6 0.90 430.0 1.04 16.1 634.4 2 187.0 2 607.3 1 785 7 1.00 432.2 1.04 18.1 619.6 2 136.0 2 608.1 1 778 表 2 燃烧室在不同当量比下的表现
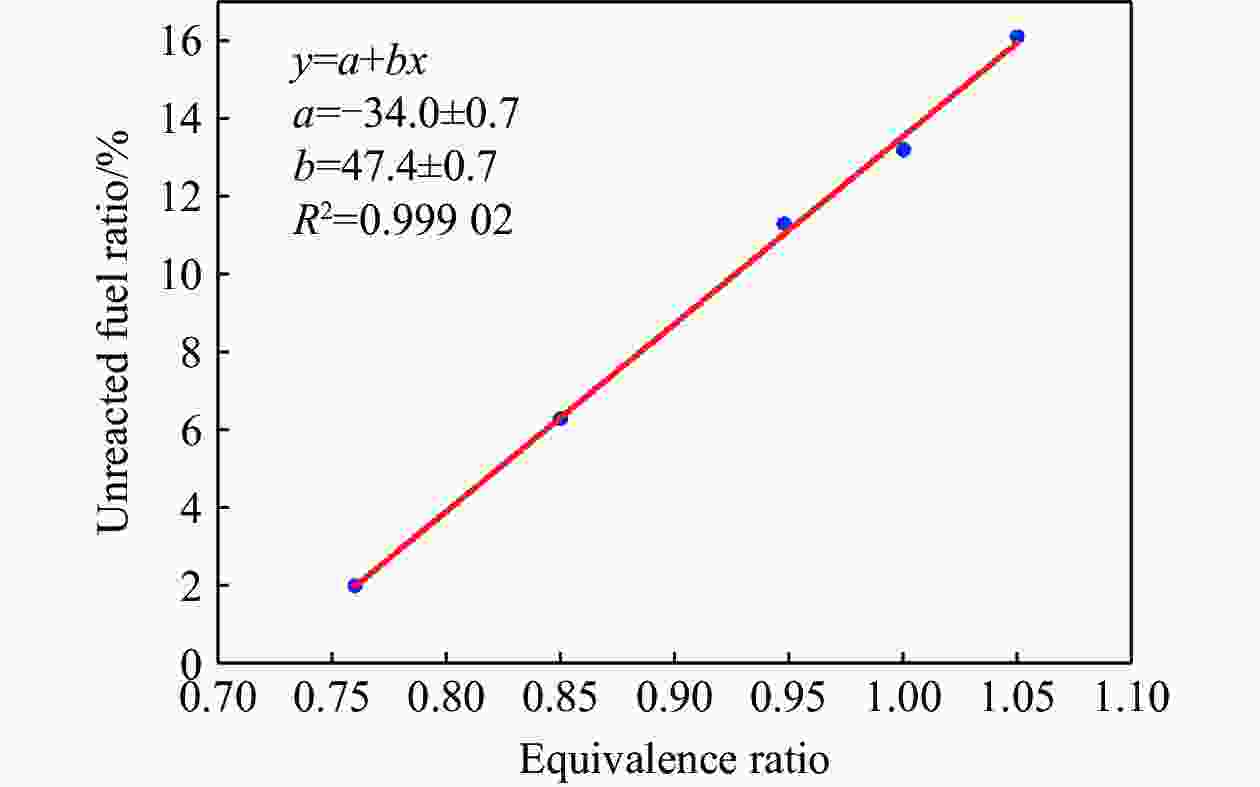
Table 2. Performance of RDC at different equivalence ratios
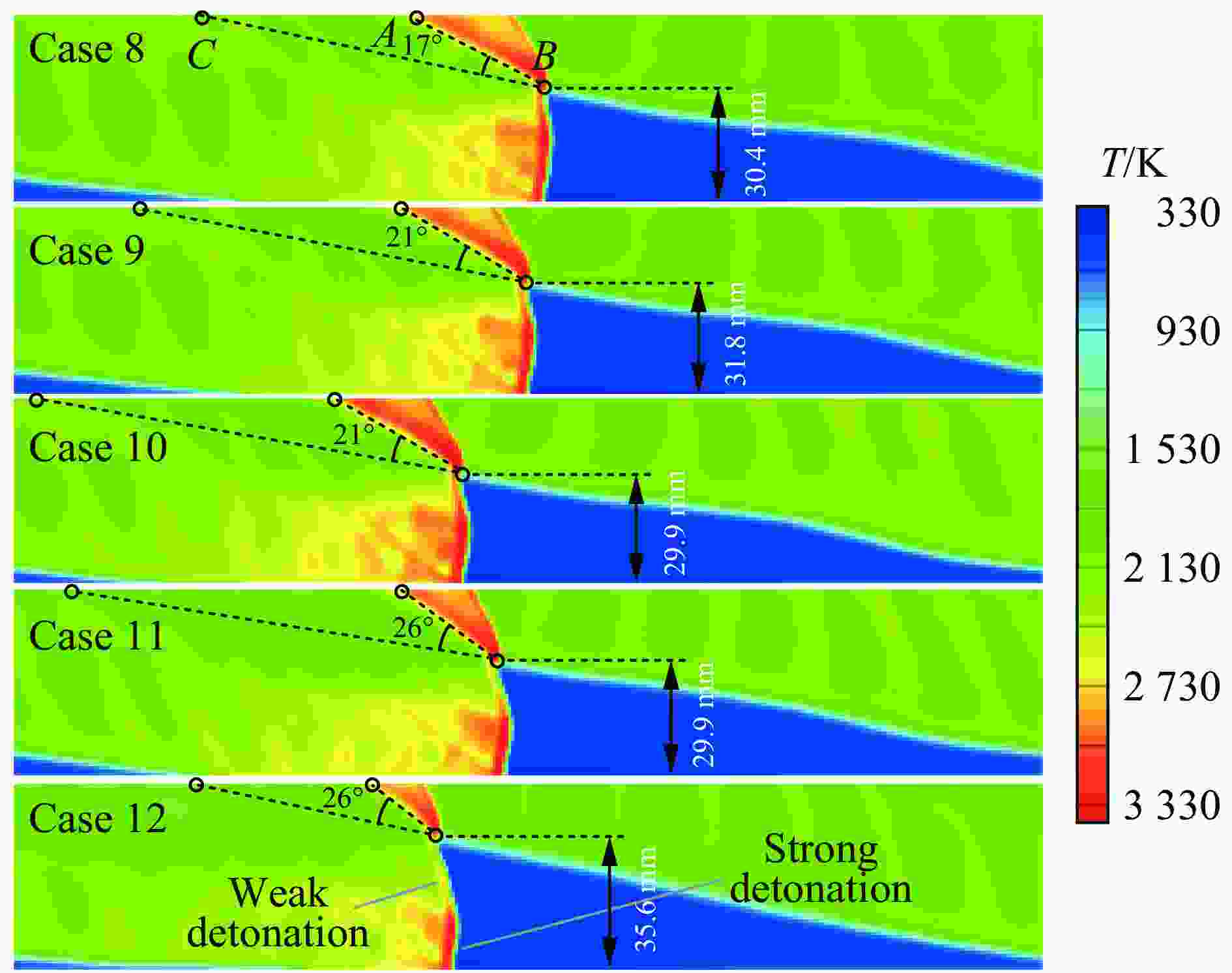
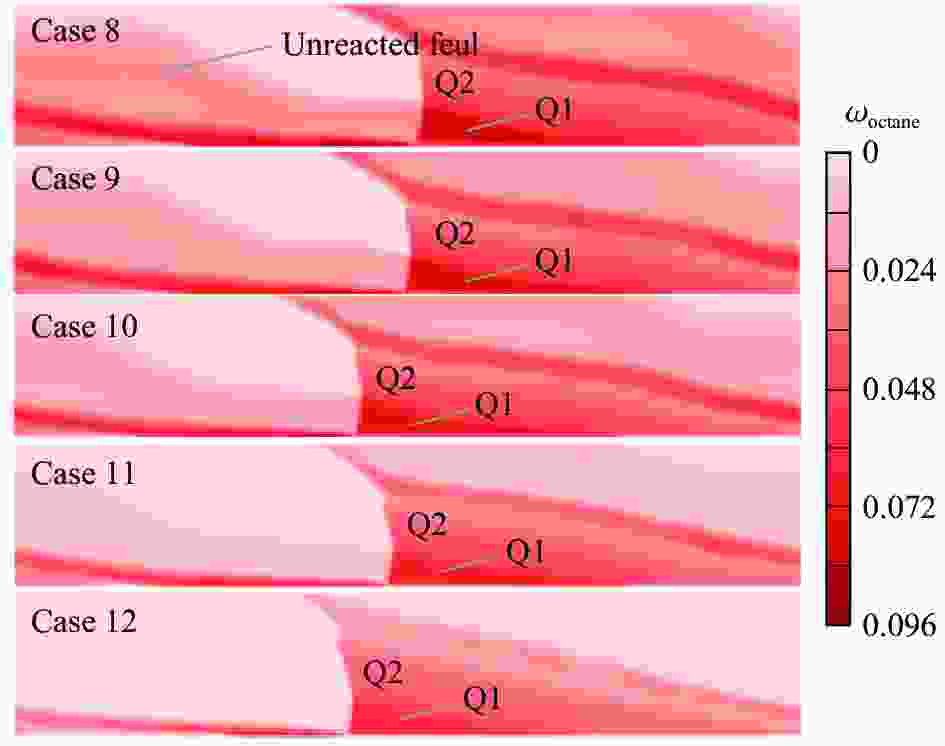
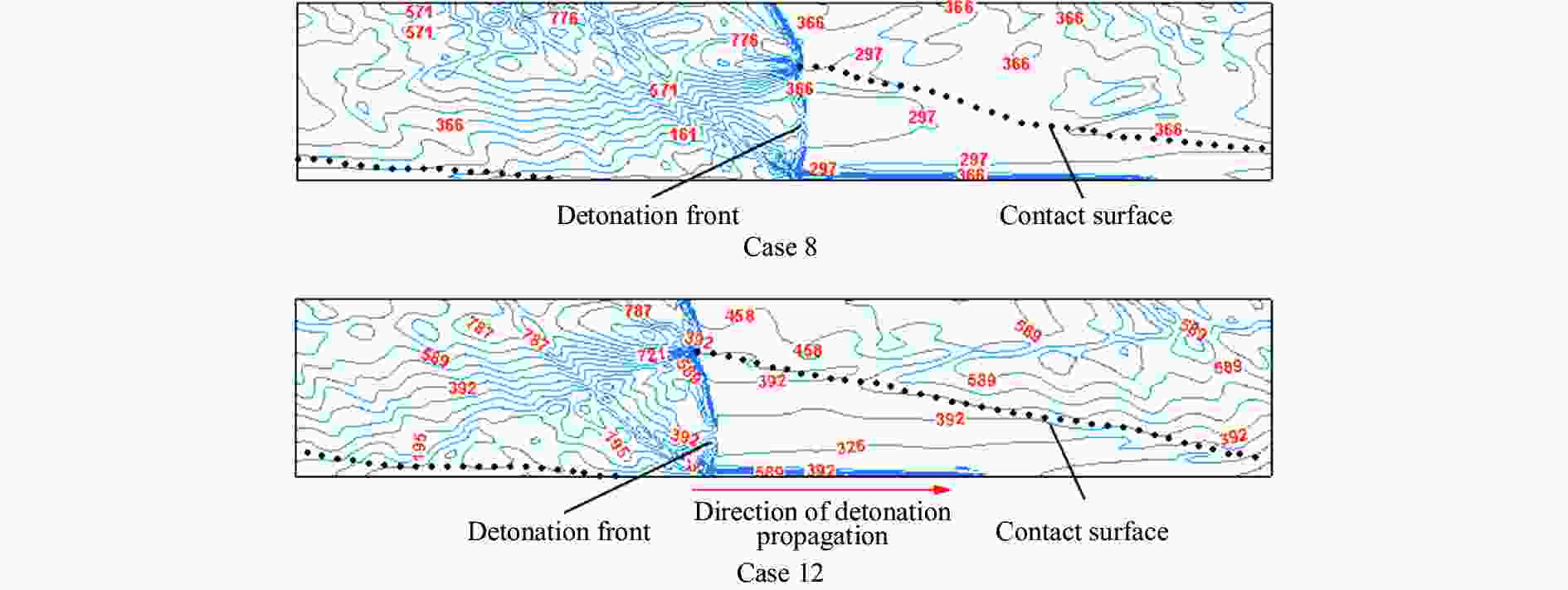
算例 当量比 空气流量/(g∙s−1) 燃料流量/(g∙s−1) 未燃燃料比例/% 平均推力/N 燃料比冲 /s 基于反应燃料的燃料比冲/s 爆轰波传播速度/(m∙s−1) 8 1.05 431.7 29.8 16.1 684.9 2 345.2 2 795.3 1 798 9 1.00 430.9 28.1 13.2 676.4 2 456.2 2 829.0 1 798 10 0.95 429.1 26.7 11.3 658.9 2 518.3 2 841.9 1 797 11 0.85 427.0 23.9 6.3 636.2 2 716.3 2 899.7 1 789 12 0.76 425.7 21.2 2.0 591.7 2 848.0 2 907.0 1 771 表 3 燃烧室在不同燃料喷注压力下的表现(当量比为0.90)
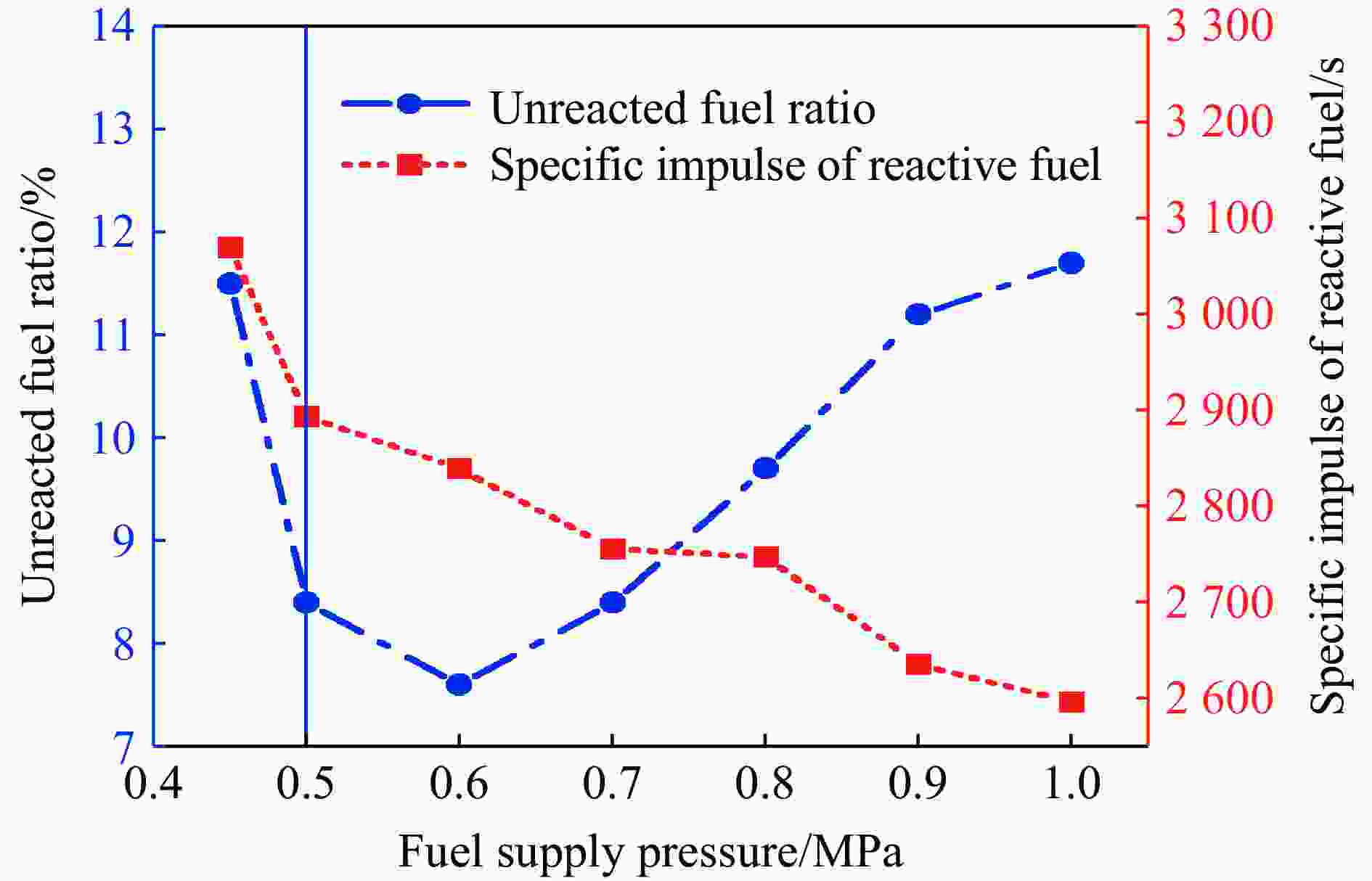
Table 3. Performance of RDC at different fuel supply pressures (equivalence ratio of 0.90)
算例 燃料喷注压力/MPa 空气流量/(g·s−1) 当量比 未燃燃料比例/% 平均推力/N 燃料比冲 /s 基于反应燃料的燃料比冲/s 爆轰波传播速度/(m·s−1) 13 0.45 427.5 0.89 11.5 662.3 2 715.2 3 069.7 1 783 14 0.50 430.9 0.88 8.4 648.0 2 655.5 2 893.8 1 788 15 0.60 429.3 0.88 7.6 645.8 2 623.3 2 839.3 1 792 16 0.70 431.0 0.90 8.4 628.7 2 523.8 2 755.7 1 787 17 0.80 430.8 0.91 9.7 622.6 2 482.4 2 747.7 1 790 18 0.90 431.6 0.92 11.2 596.7 2 339.1 2 635.1 1 790 19 1.00 431.3 0.90 11.7 573.0 2 292.0 2 595.7 1 789 -
[1] HEISER W H, PRATT D T. Thermodynamic cycle analysis of pulse detonation engines [J]. Journal of Propulsion and Power, 2002, 18(1): 68–76. DOI: 10.2514/2.5899. [2] 王健平, 周蕊, 武丹. 连续旋转爆轰发动机的研究进展 [J]. 实验流体力学, 2015, 29(4): 12–25. DOI: 10.11729/syltlx20150048.WANG J P, ZHOU R, WU D. Progress of continuously rotating detonation engine research [J]. Journal of Experiments in Fluid Mechanics, 2015, 29(4): 12–25. DOI: 10.11729/syltlx20150048. [3] BYKOVSKII F A, ZHDAN S A, VEDERNIKOV E F. Continuous spin detonations [J]. Journal of Propulsion and Power, 2006, 22(6): 1204–1216. DOI: 10.2514/1.17656. [4] FROLOV S M, SHAMSHIN I O, AKSENOV V S, et al. Rocket engine with continuously rotating liquid-film detonation [J]. Combustion Science and Technology, 2020, 192(1): 144–165. DOI: 10.1080/00102202.2018.1557643. [5] KINDRACKI J. Experimental research on rotating detonation in liquid fuel-gaseous air mixtures [J]. Aerospace Science and Technology, 2015, 43: 445–453. DOI: 10.1016/j.ast.2015.04.006. [6] LI J M, CHANG P H, LI L, et al. Investigation of injection strategy for liquid-fuel rotating detonation engine [C]//2018 AIAA Aerospace Sciences Meeting. Kissimmee: AIAA, 2018. DOI: 10.2514/6.2018-0403. [7] YI T H, LOU J, TURANGAN C, et al. Propulsive performance of a continuously rotating detonation engine [J]. Journal of Propulsion and Power, 2011, 27(1): 171–181. DOI: 10.2514/1.46686. [8] 徐雪阳, 卓长飞, 武晓松, 等. 非预混喷注对旋转爆震发动机影响的数值研究 [J]. 航空学报, 2016, 37(4): 1184–1195. DOI: 10.7527/S1000-6893.2015.0195.XU X Y, ZHUO C F, WU X S, et al. Numerical simulation of injection schemes with separate supply of fuel and oxidizer effects on rotating detonation engine [J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(4): 1184–1195. DOI: 10.7527/S1000-6893.2015.0195. [9] 李宝星, 翁春生. 气体与液体两相连续旋转爆轰发动机爆轰波传播特性三维数值模拟研究 [J]. 兵工学报, 2017, 38(7): 1358–1367. DOI: 10.3969/j.issn.1000-1093.2017.07.014.LI B X, WENG C S. Three-dimensional numerical simulation on the propagation characteristics of detonation wave in gas-liquid two-phase continuous rotating detonation engine [J]. Acta Armamentarii, 2017, 38(7): 1358–1367. DOI: 10.3969/j.issn.1000-1093.2017.07.014. [10] SUN B, MA H. Two-dimensional numerical study of two-phase rotating detonation wave with different injections [J]. AIP Advances, 2019, 9(11): 115307. DOI: 10.1063/1.5113881. [11] WANG F, WENG C S, WU Y W, et al. Numerical research on kerosene/air rotating detonation engines under different injection total temperatures [J]. Aerospace Science and Technology, 2020, 103: 105899. DOI: 10.1016/j.ast.2020.105899. [12] HAYASHI A K, TSUBOI N, DZIEMINSKA E. Numerical study on JP-10/air detonation and rotating detonation engine [J]. AIAA Journal, 2020, 58(12): 5078–5094. DOI: 10.2514/1.J058167. [13] 徐高, 翁春生, 武郁文, 等. 气相与液相两相连续旋转爆轰发动机二维数值模拟 [J]. 兵工学报, 2020, 41(S1): 21−29. DOI: 10.3969/j.issn.1000-1093.2020.S1.004.XU G, WENG C S, WU Y W, et al. Two-dimensional numerical simulation of gas-liquid two-phase continuous rotating detonation engine [J]. Acta Armamentarii, 41(S1): 21−29. DOI: 10.3969/j.issn.1000-1093.2020.S1.004. [14] SCHWER D A, KAILASANATH K. Numerical study of the effects of engine size on rotating detonation engines [C]//49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando: AIAA, 2011. DOI: 10.2514/6.2011-581. [15] 武丹, 王健平. 粘性及热传导对于爆轰波的影响 [J]. 应用力学学报, 2012, 29(6): 630–635. DOI: 10.11776/cjam.29.06.D002.WU D, WANG J P. Influences of viscosity and thermal conductivity on detonation waves [J]. Chinese Journal of Applied Mechanics, 2012, 29(6): 630–635. DOI: 10.11776/cjam.29.06.D002. [16] CHANG S C. The method of space-time conservation element and solution element: a new approach for solving the Navier-Stokes and Euler equations [J]. Journal of Computational Physics, 1995, 119(2): 295–324. DOI: 10.1006/jcph.1995.1137. [17] CHASE JR M W. NIST-JANAF thermochemical tables [M]. 4th ed. New York: American Chemical Society, 1998. [18] EIDELMAN S, BURCAT A. Numerical solution of a nonsteady blast wave propagation in two-phase (separated flow) reactive medium [J]. Journal of Computational Physics, 1981, 39(2): 456–472. DOI: 10.1016/0021-9991(81)90164-9. [19] WANG G, ZHU H Y, SUN Q H, et al. An improved CE/SE scheme and its application to dilute gas-particle flows [J]. Computer Physics Communications, 2011, 182(8): 1589–1601. DOI: 10.1016/j.cpc.2011.04.004. [20] EIDELMAN S, BURCAT A. Evolution of a detonation wave in a cloud of fuel droplets. Ⅰ: influence of igniting explosion [J]. AIAA Journal, 1980, 18(9): 1103–1109. DOI: 10.2514/3.7711. [21] BURCAT A, EIDELMAN S. Evolution of a detonation wave in a cloud of fuel droplets. Ⅱ: influence of fuel droplets [J]. AIAA Journal, 1980, 18(10): 1233–1236. DOI: 10.2514/3.7717. [22] 洪滔, 秦承森. 气体-燃料液滴两相系统爆轰的数值模拟 [J]. 爆炸与冲击, 1999, 19(4): 335–342.HONG T, QING C S. Numerical modeling of detonation in gas fuel droplets system [J]. Explosion and Shock Waves, 1999, 19(4): 335–342. [23] 严传俊, 范玮. 燃烧学 [M]. 西安: 西北工业大学出版社, 2005: 427−428. [24] 翁春生, 王浩. 计算内弹道学 [M]. 北京: 国防工业出版社, 2006: 290−325. [25] 白桥栋, 翁春生. 二维粘性CE/SE方法在两相流内弹道计算中的应用 [J]. 火炮发射与控制学报, 2009(1): 13–17. DOI: 10.3969/j.issn.1673-6524.2009.01.004.BAI Q D, WENG C S. Application of two dimension viscous CE/SE method in two-phase flow interior ballistic computation [J]. Journal of Gun Launch & Control, 2009(1): 13–17. DOI: 10.3969/j.issn.1673-6524.2009.01.004. [26] GAMEZO V N, DESBORDES D, ORAN E S. Two-dimensional reactive flow dynamics in cellular detonation waves [J]. Shock Waves, 1999, 9(1): 11–17. DOI: 10.1007/s001930050134. [27] HISHIDA M, FUJIWARA T, WOLANSKI P. Fundamentals of rotating detonations [J]. Shock Waves, 2009, 19(1): 1–10. DOI: 10.1007/s00193-008-0178-2. [28] LI Q, LIU P X, ZHANG H X. Further investigations on the interface instability between fresh injections and burnt products in 2-D rotating detonation [J]. Computers & Fluids, 2018, 170: 261–272. DOI: 10.1016/j.compfluid.2018.05.005. [29] HAYASHI A K, KIMURA Y, YAMADA T, et al. Sensitivity analysis of rotating detonation engine with a detailed reaction model [C]//47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando: AIAA, 2009. DOI: 10.2514/6.2009-633. -






 下载:
下载: