Study on shock compression phase transition of single crystal siliconbased on molecular dynamics simulation
-
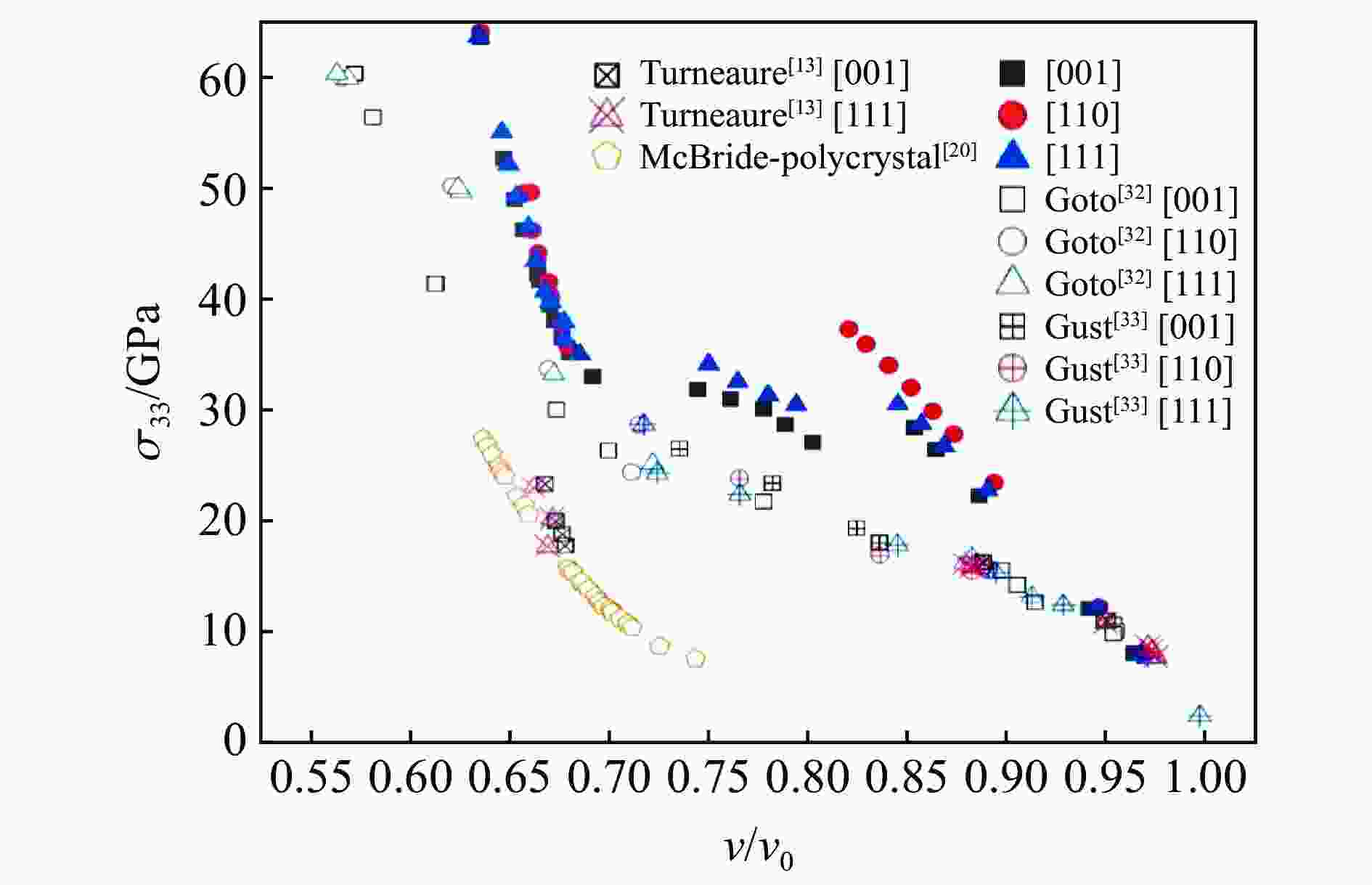
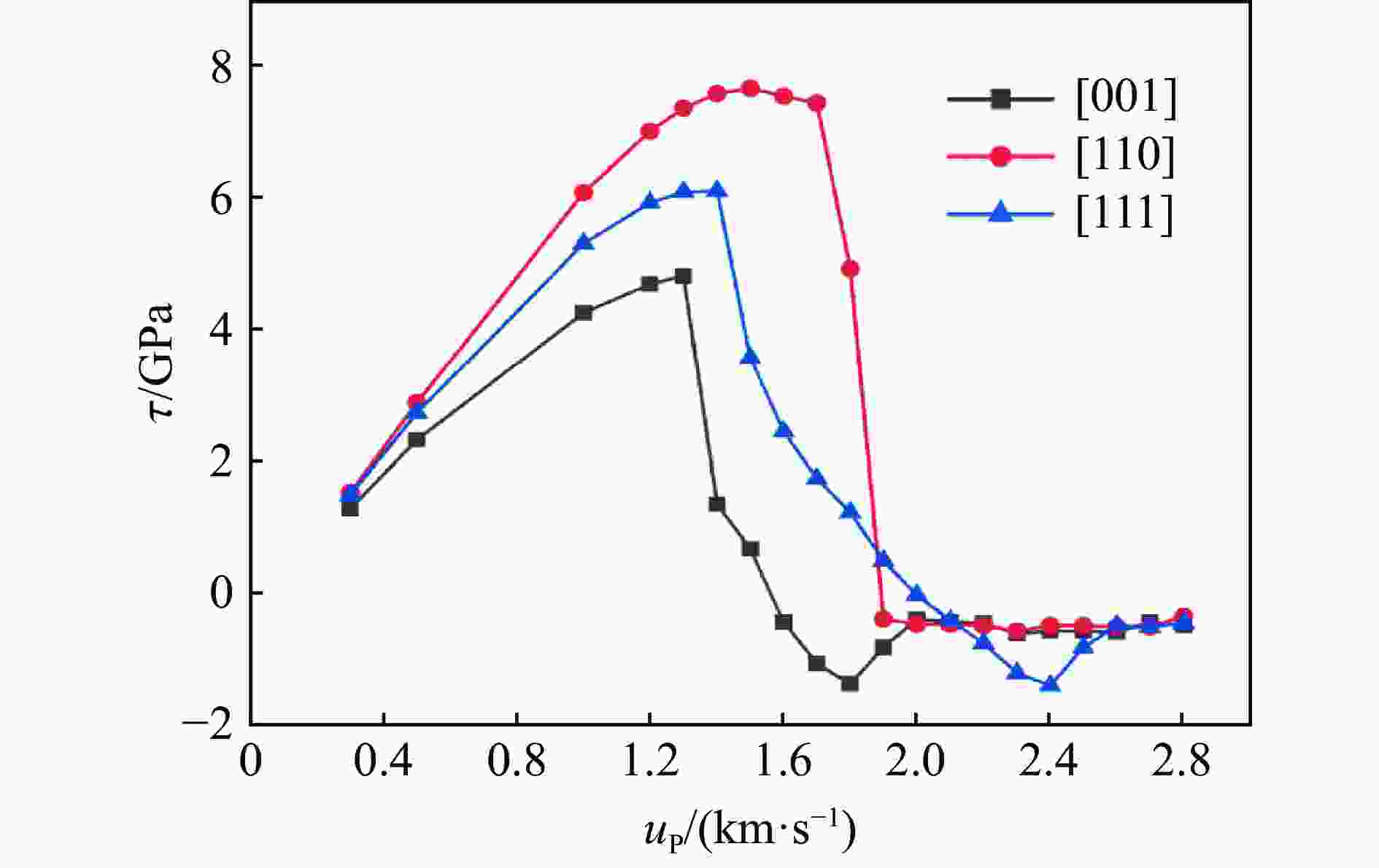
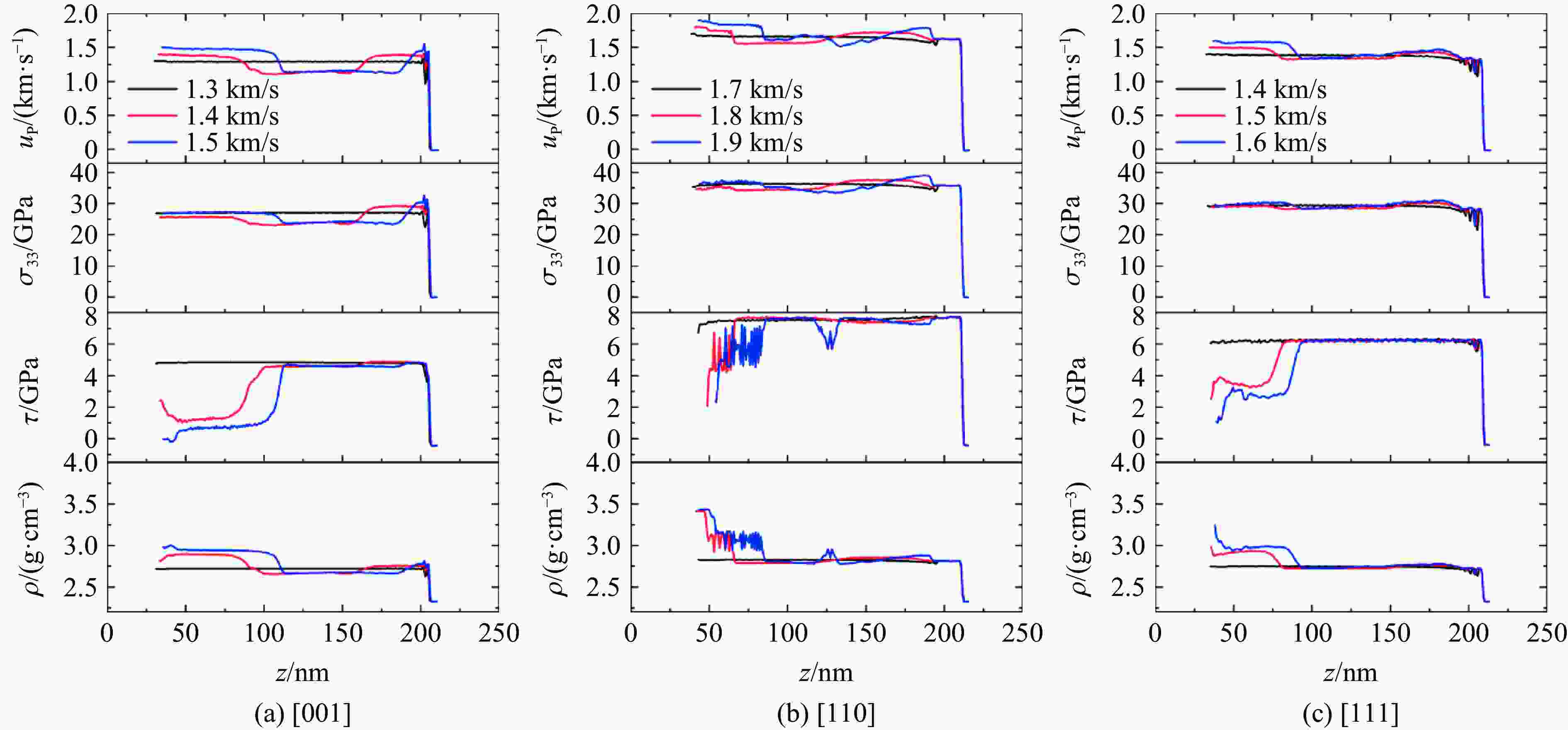
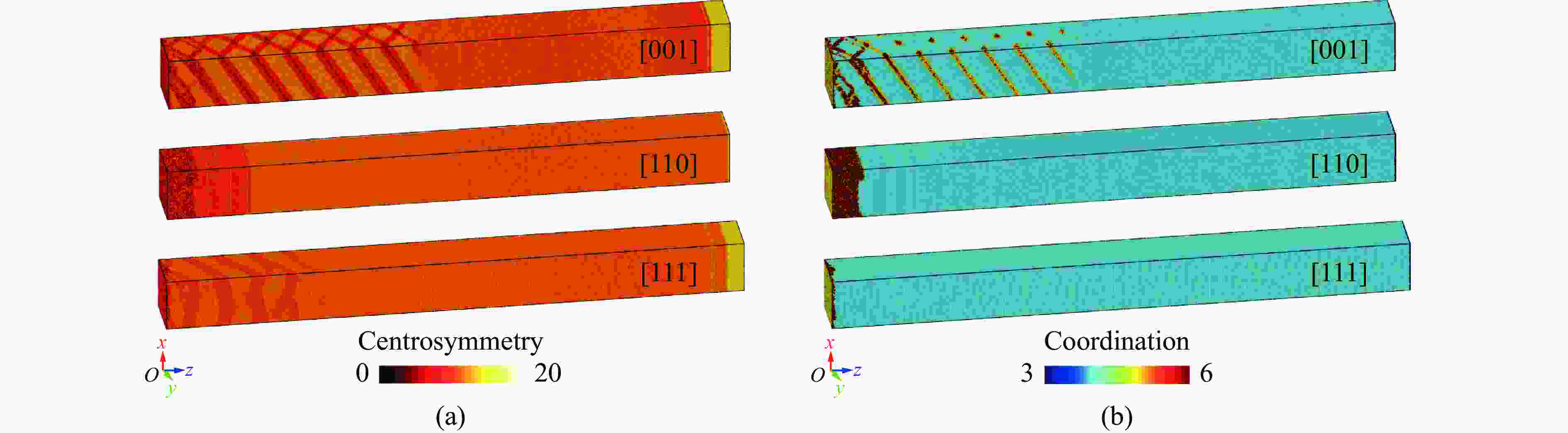
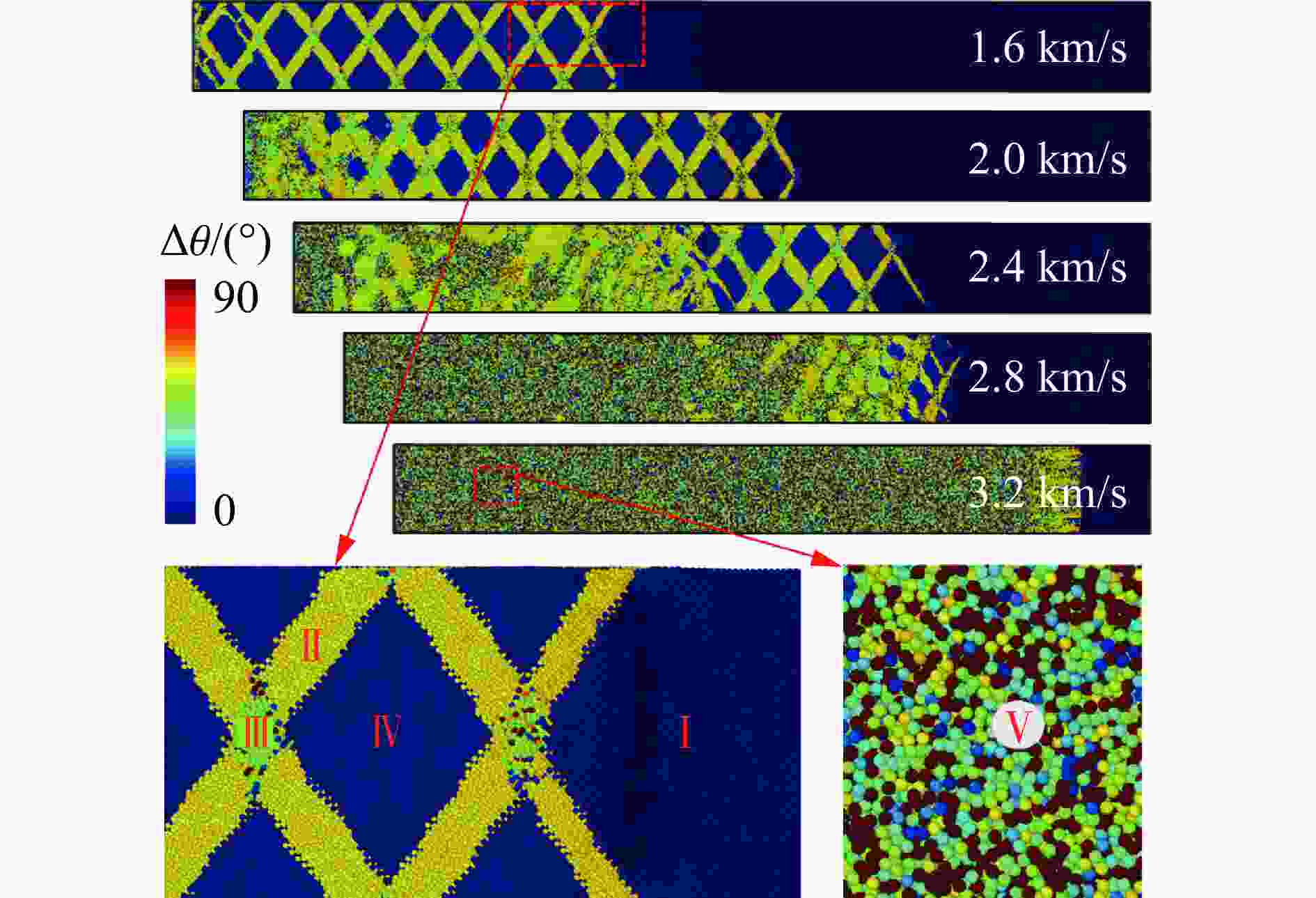
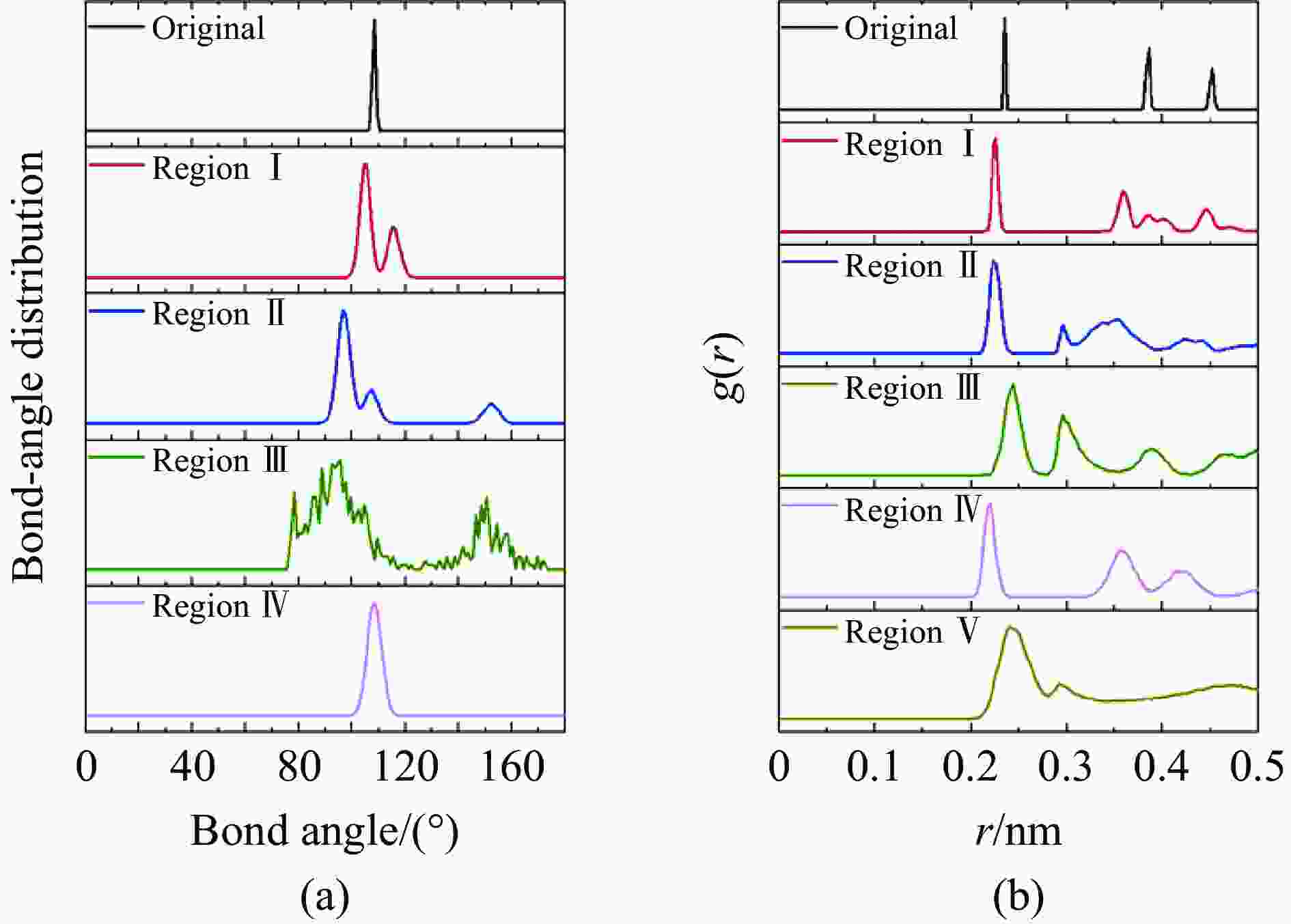
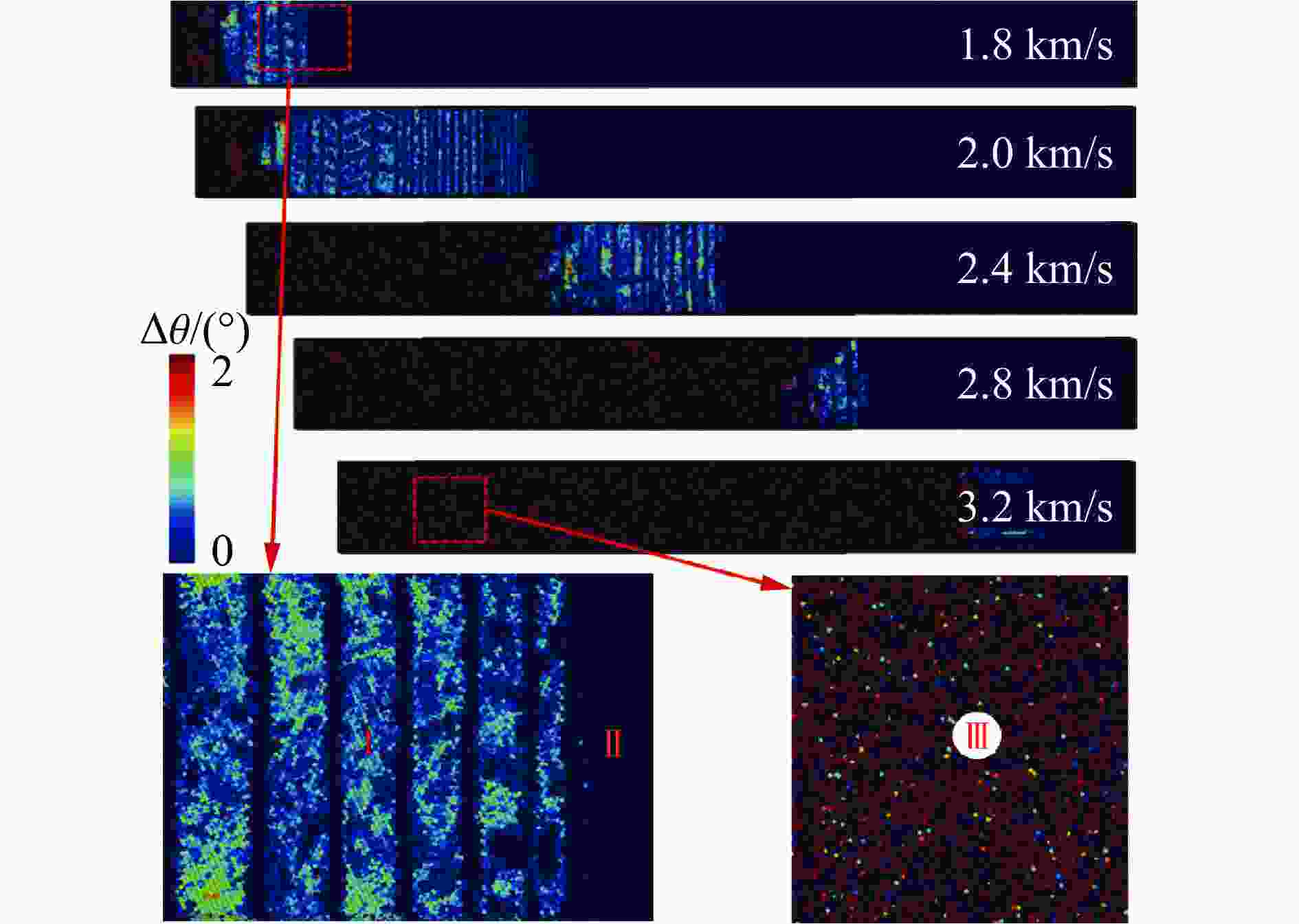
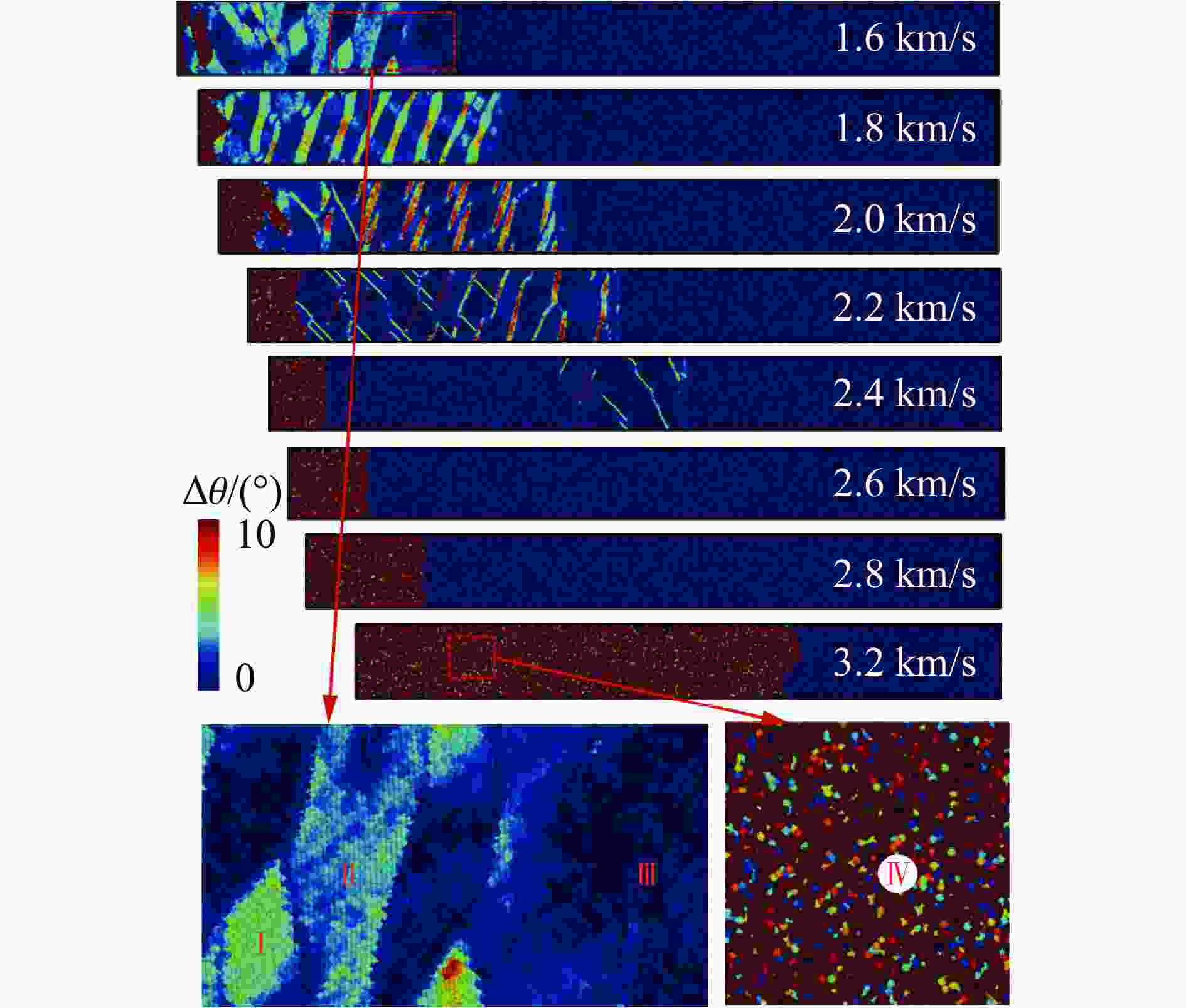
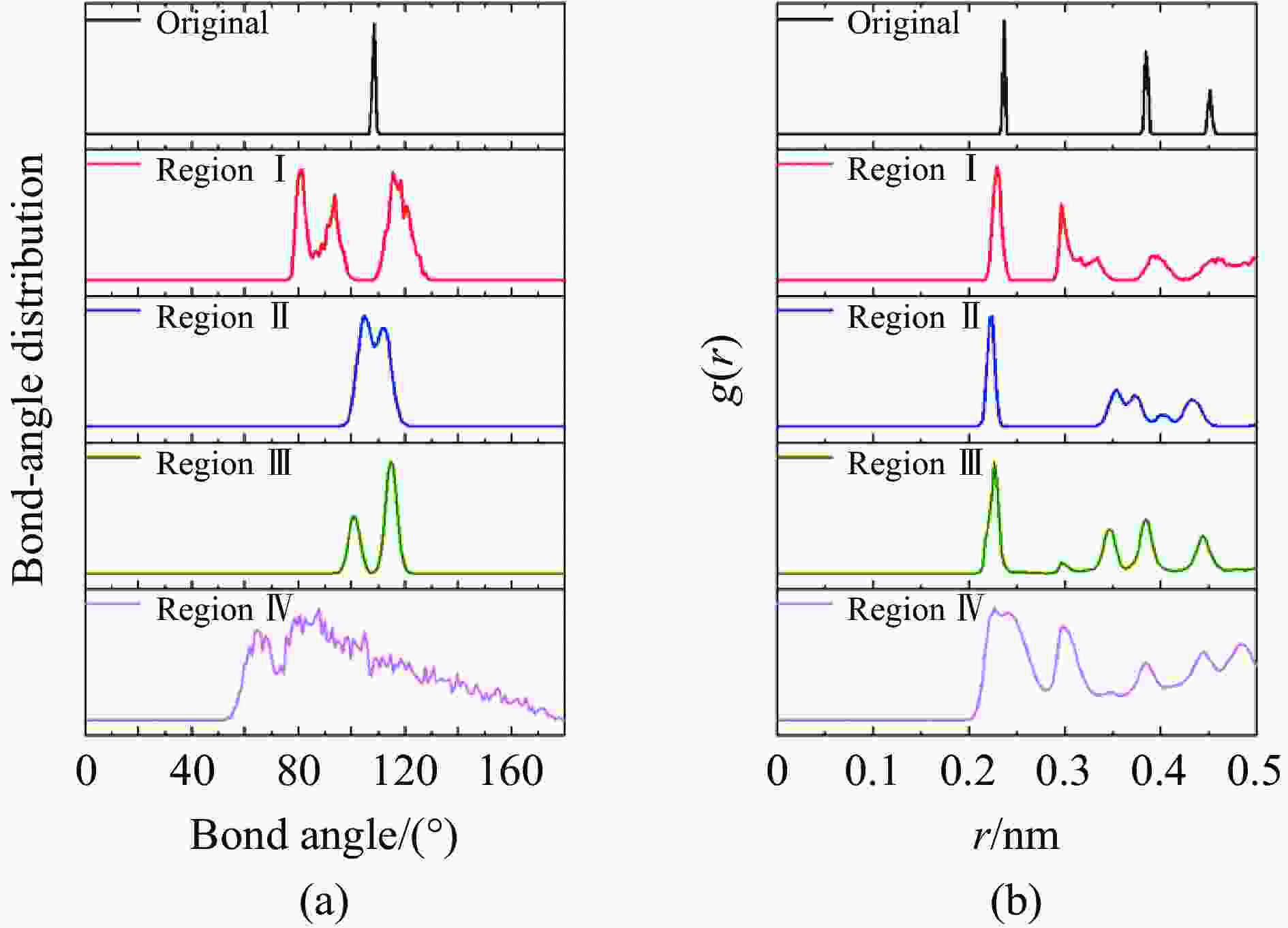
摘要: 晶体硅具有复杂的相变机制，在相图研究中受到广泛关注，其在动载荷下的变形机制是当前研究热点。为揭示晶体硅在强动加载下的变形和相变行为特征，基于分子动力学方法，采用平板冲击加载方式，模拟研究了单晶硅在初始环境温度为300 K时分别沿[001]、[110]和[111]晶向的不同强度下的冲击压缩行为，冲击粒子速度为0.3～3.2 km/s。研究发现，随着冲击粒子速度的增加，单晶硅剪切应力在逐渐增加后由于结构相变发生急剧下降，相变阈值和相变机制均呈现各向异性。其中，沿[001]晶向冲击压缩下观察到多种固-固相变以及固-液相变，并观察到与最新文献的实验高度一致的固-液共存现象。研究结果可为动加载下晶体硅的相变研究提供纳米尺度的结果支撑。Abstract: Crystalline silicon has a complicated phase transition mechanism, which has received extensive attention in the research field of phase diagram, and the deformation mechanism of silicon crystals under dynamic loading is the current research hotspot. In order to reveal its deformation and phase transition behaviors under intensive dynamic loading, molecular dynamics method was used to simulate the shock compression behavior of single crystal silicon along the crystal directions [001], [110] and [111] at an initial ambient temperature of 300 K, respectively. All simulations were carried out basing on the classical open-source codes LAMMPS and a Tersoff interatomic potential was adopted to describe the material responses of silicon under dynamic compression. Before shock loading, periodic boundary conditions were applied along the three independent directions, and an NPT ensemble was used to equilibrate the systems; then shock compression was applied by using the piston method, where a virtual piston wall impinges the sample such that the particle velocity in the sample is the same as the piston speed after the shock reaches a steady state. The shock particle velocities varied from 0.3 km/s to 3.2 km/s, and a timestep of 0.001 ps was adopted. During the stress wave formation and propagation, the simulation system was in the NVE ensemble with the absence of temperature control. The loading method and effect are similar to typical plane impact experiments. The results show that with the increase of shock particle velocity, the shear stress of single crystal silicon increases gradually and then decreases sharply due to the structural phase change. Both the phase transition threshold and the phase transition mechanism are anisotropic. Among them, a variety of solid-solid phase transitions and solid-liquid phase transitions are observed under shock compression along the [001] crystal direction. The phenomenon of solid-liquid coexistence is highly consistent with the recent international experiments. The research results provides new nano-scale results to support the study of phase transition of crystalline silicon under dynamic loading.
-
图 1 分子动力学模拟中单晶硅的冲击压缩示意图
Figure 1. Schematic of shock compression of single crystal Si in molecular dynamic simulations
图 3 冲击Hugoniot状态的剪切应力(τ)与粒子速度(up) 曲线
Figure 3. Shock Hugoniot shear stress as a function of particle velocity
图 4 单晶硅中分别沿[001]、[110]和[111]晶向的冲击波剖面
Figure 4. Shock profiles in single crystal Si along [001], [110] and [111] crystal orientation
图 5 单晶硅沿[001]、[110]、[111]晶向分别在1.4、1.8、1.5 km/s冲击压缩下的可视化
Figure 5. Visualizations of single crystal Si in [001], [110] and [111] crystal orientations with shock particle velocities of 1.4, 1.8, 1.5 km/s
图 6 不同冲击粒子速度下[001]单晶硅的结构演化
Figure 6. Structural evolutions of single crystal Si in [001] orientation at various shock particle velocities
图 7 对代表性局部区域的键角分析和径向分布函数分析
Figure 7. Bond-angle and radial distribution functions analysis for representative local regions
图 8 不同冲击粒子速度下[110]单晶硅的结构演化
Figure 8. Structural evolutions of single crystal Si in [110] orientation at various shock particle velocities
图 9 对图8代表性局部区域的键角分析和径向分布函数分析
Figure 9. Bond-angle and radial distribution functions analysis for representative local regions
图 10 不同冲击粒子速度下[111]单晶硅的结构演化
Figure 10. Structural evolutions of single crystal Si in [111] orientation at various shock particle velocities
图 11 对代表性局部区域的键角分析和径向分布函数分析
Figure 11. Bond-angle and radial distribution functions analysis for representative local regions
表 1 单晶硅计算模型详细参数
Table 1. Parameters of single crystal Si sample for MD simulation
加载晶向 x轴 y轴 z轴 模型原子数 晶向 模型尺寸/nm 晶向 模型尺寸/nm 晶向 模型尺寸/nm [001] [100] 16.3 [010] 16.2 [001] 217.0 ～2.84×106 [110] [$\bar{1}10 $] 16.3 [001] 16.2 [110] 217.0 ～2.84×106 [111] [$\bar{1}\bar{1}2 $] 16.0 [$1\bar{1} 0$] 16.2 [111] 214.8 ～2.76×106 
下载: 导出CSV
-
[1] EL-KAREH B, HUTTER L N. Review of single-crystal silicon properties [M] // EL-KAREH B, HUTTER L N. Silicon Analog Components. Cham: Springer, 2020: 25–63. DOI: 10.1007/978-3-030-15085-3_2. [2] JAMIESON J C. Crystal structures at high pressures of metallic modifications of silicon and germanium [J]. Science, 1963, 139(3556): 762–764. DOI: 10.1126/science.139.3556.762. [3] MCMAHON M I, NELMES R J. New high-pressure phase of Si [J]. Physical Review B, 1993, 47(13): 8337–8340. DOI: 10.1103/PhysRevB.47.8337. [4] MCMAHON M I, NELMES R J, WRIGHT N G, et al. Pressure dependence of the Imma phase of silicon [J]. Physical Review B, 1994, 50(2): 739–743. DOI: 10.1103/PhysRevB.50.739. [5] OLIJNYK H, SIKKA S K, HOLZAPFEL W B. Structural phase transitions in Si and Ge under pressures up to 50 GPa [J]. Physics Letters A, 1984, 103(3): 137–140. DOI: 10.1016/0375-9601(84)90219-6. [6] DUCLOS S J, VOHRA Y K, RUOFF A L. Hcp to fcc transition in silicon at 78 GPa and studies to 100 GPa [J]. Physical Review Letters, 1987, 58(8): 775–777. DOI: 10.1103/PhysRevLett.58.775. [7] HANFLAND M, SCHWARZ U, SYASSEN K, et al. Crystal structure of the high-pressure phase silicon Ⅵ [J]. Physical Review Letters, 1999, 82(6): 1197–1200. DOI: 10.1103/PhysRevLett.82.1197. [8] WENTORF R H JR, KASPER J S. Two new forms of silicon [J]. Science, 1963, 139(3552): 338–339. DOI: 10.1126/science.139.3552.338-a. [9] PILTZ R O, MACLEAN J R, CLARK S J, et al. Structure and properties of silicon Ⅻ: a complex tetrahedrally bonded phase [J]. Physical Review B, 1995, 52(6): 4072–4085. DOI: 10.1103/PhysRevB.52.4072. [10] MUJICA A, RUBIO A, MUÑOZ A, et al. High-pressure phases of group-Ⅳ, Ⅲ-Ⅴ, and Ⅱ-Ⅵ compounds [J]. Reviews of Modern Physics, 2003, 75(3): 863–912. DOI: 10.1103/RevModPhys.75.863. [11] GILEV S D, TRUBACHEV A M. Metallization of monocrystalline silicon under shock compression [J]. Physica Status Solidi (B), 1999, 211(1): 379–383. DOI: 10.1002/(SICI)1521-3951(199901)211:1<379::AID-PSSB379>3.0.CO;2-4. [12] LOVERIDGE-SMITH A, ALLEN A, BELAK J, et al. Anomalous elastic response of silicon to uniaxial shock compression on nanosecond time scales [J]. Physical Review Letters, 2001, 86(11): 2349–2352. DOI: 10.1103/PhysRevLett.86.2349. [13] TURNEAURE S J, GUPTA Y M. Inelastic deformation and phase transformation of shock compressed silicon single crystals [J]. Applied Physics Letters, 2007, 91(20): 201913. DOI: 10.1063/1.2814067. [14] ZHAO S, HAHN E N, KAD B, et al. Amorphization and nanocrystallization of silicon under shock compression [J]. Acta Materialia, 2016, 103: 519–533. DOI: 10.1016/j.actamat.2015.09.022. [15] SMITH R F, BOLME C A, ERSKINE D J, et al. Heterogeneous flow and brittle failure in shock-compressed silicon [J]. Journal of Applied Physics, 2013, 114(13): 133504. DOI: 10.1063/1.4820927. [16] LIU Y X, WU X Q, WANG X, et al. Deformation behavior of single crystal silicon induced by laser shock peening [C]// Proceedings of SPIE 8796, 2nd International Symposium on Laser Interaction with Matter (LIMIS 2012). Xi’an, 2013: 87962M. DOI: 10.1117/12.2011314. [17] KISHIMURA H, MATSUMOTO H. Effect of phase transition in shock-recovered silicon [J]. Journal of Applied Physics, 2008, 103(2): 023505. DOI: 10.1063/1.2830805. [18] TURNEAURE S J, SHARMA S M, GUPTA Y M. Nanosecond melting and recrystallization in shock-compressed silicon [J]. Physical Review Letters, 2018, 121(13): 135701. DOI: 10.1103/PhysRevLett.121.135701. [19] RENGANATHAN P, TURNEAURE S J, SHARMA S M, et al. Structural transformations including melting and recrystallization during shock compression and release of germanium up to 45 GPa [J]. Physical Review B, 2019, 99(13): 134101. DOI: 10.1103/PhysRevB.99.134101. [20] MCBRIDE E E, KRYGIER A, EHNES A, et al. Phase transition lowering in dynamically compressed silicon [J]. Nature Physics, 2019, 15(1): 89–94. DOI: 10.1038/s41567-018-0290-x. [21] PAUL R, HU S X, KARASIEV V V. Anharmonic and anomalous trends in the high-pressure phase diagram of silicon [J]. Physical Review Letters, 2019, 122(12): 125701. DOI: 10.1103/PhysRevLett.122.125701. [22] DOMNICH V V. Phase transformations in silicon induced by contact loading [D]. Chicago: University of Illinois at Chicago, 2002. [23] SWIFT D C, ACKLAND G J, HAUER A, et al. First-principles equations of state for simulations of shock waves in silicon [J]. Physical Review B, 2001, 64(21): 214107. DOI: 10.1103/PhysRevB.64.214107. [24] DEMKOWICZ M J, ARGON A S. Liquidlike atomic environments act as plasticity carriers in amorphous silicon [J]. Physical Review B, 2005, 72(24): 245205. DOI: 10.1103/PhysRevB.72.245205. [25] KUMAGAI T, IZUMI S, HARA S, et al. Development of bond-order potentials that can reproduce the elastic constants and melting point of silicon for classical molecular dynamics simulation [J]. Computational Materials Science, 2007, 39(2): 457–464. DOI: 10.1016/j.commatsci.2006.07.013. [26] HIGGINBOTHAM A, STUBLEY P G, COMLEY A J, et al. Inelastic response of silicon to shock compression [J]. Scientific Reports, 2016, 6: 24211. DOI: 10.1038/srep24211. [27] MOGNI G, HIGGINBOTHAM A, GAÁL-NAGY K, et al. Molecular dynamics simulations of shock-compressed single-crystal silicon [J]. Physical Review B, 2014, 89(6): 064104. DOI: 10.1103/PhysRevB.89.064104. [28] PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics [J]. Journal of Computational Physics, 1995, 117(1): 1–19. DOI: 10.1006/jcph.1995.1039. [29] ERHART P, ALBE K. Analytical potential for atomistic simulations of silicon, carbon, and silicon carbide [J]. Physical Review B, 2005, 71(3): 035211. DOI: 10.1103/PhysRevB.71.035211. [30] THOMPSON A P, PLIMPTON S J, MATTSON W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions [J]. The Journal of Chemical Physics, 2009, 131(15): 154107. DOI: 10.1063/1.3245303. [31] STUKOWSKI A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool [J]. Modelling and Simulation in Materials Science and Engineering, 2009, 18(1): 015012. DOI: 10.1088/0965-0393/18/1/015012. [32] GOTO T, SATO T, SYONO Y. Reduction of shear strength and phase-transition in shock-loaded silicon [J]. Japanese Journal of Applied Physics, 1982, 21(6A): L369–L371. DOI: 10.1143/jjap.21.l369. [33] GUST W H, ROYCE E B. Axial yield strengths and two successive phase transition stresses for crystalline silicon [J]. Journal of Applied Physics, 1971, 42(5): 1897–1905. DOI: 10.1063/1.1660465. [34] LI W H, HAHN E N, YAO X H, et al. Shock induced damage and fracture in SiC at elevated temperature and high strain rate [J]. Acta Materialia, 2019, 167: 51–70. DOI: 10.1016/j.actamat.2018.12.035. [35] LI W H, HAHN E N, BRANICIO P S, et al. Rate dependence and anisotropy of SiC response to ramp and wave-free quasi-isentropic compression [J]. International Journal of Plasticity, 2021, 138: 102923. DOI: 10.1016/j.ijplas.2020.102923. [36] KADAU K, GERMANN T C, LOMDAHL P S, et al. Atomistic simulations of shock-induced phase transitions [J]. AIP Conference Proceedings, 2004, 706(1): 229–234. DOI: 10.1063/1.1780223. [37] LANG JR J M, GUPTA Y M. Strength and elastic deformation of natural and synthetic diamond crystals shock compressed along [100] [J]. Journal of Applied Physics, 2010, 107(11): 113538. DOI: 10.1063/1.3448027. [38] OLEYNIK I I, ZYBIN S V, ELERT M L, et al. Nanoscale molecular dynamics simulaton of shock compression of silicon [J]. AIP Conference Proceedings, 2006, 845(1): 413–416. DOI: 10.1063/1.2263349. [39] STUBLEY P G, HIGGINBOTHAM A, WARK J S. Simulations of the inelastic response of silicon to shock compression [J]. Computational Materials Science, 2017, 128: 121–126. DOI: 10.1016/j.commatsci.2016.11.006. -
计量
- 文章访问数: 531
- HTML全文浏览量: 262
- PDF下载量: 109
- 被引次数: 0