Study on the formation mechanism of uranium aerosol under explosion load
-
摘要: 针对铀材料在爆炸载荷作用下形成放射性气溶胶的过程，采用光滑粒子流体动力学方法开展了数值模拟和实验研究。通过将颗粒动力学和SPH方法结合，建立了炸药爆轰作用于铀金属壳的数值模拟模型，以铀材料比内能为气溶胶转化判据，获得了铀材料转化为气溶胶的物理过程，得到了在相同爆炸当量下，不同质量铀材料的气溶胶转化效率，并与实验结果进行了对比分析。结果显示，铀材料在爆炸载荷作用下，当其比内能达到1.9 MJ/kg时，即可认为完全转变为气溶胶，对于本文中的爆炸装置结构形式，当炸药质量为铀材料质量的6倍时，转化率超过90%。实验验证了数值模拟结果，表明该方法能够对铀材料的气溶胶转化过程进行准确描述。
-
关键词:
- 铀 /
- 气溶胶 /
- 爆炸载荷 /
- 光滑粒子流体动力学方法
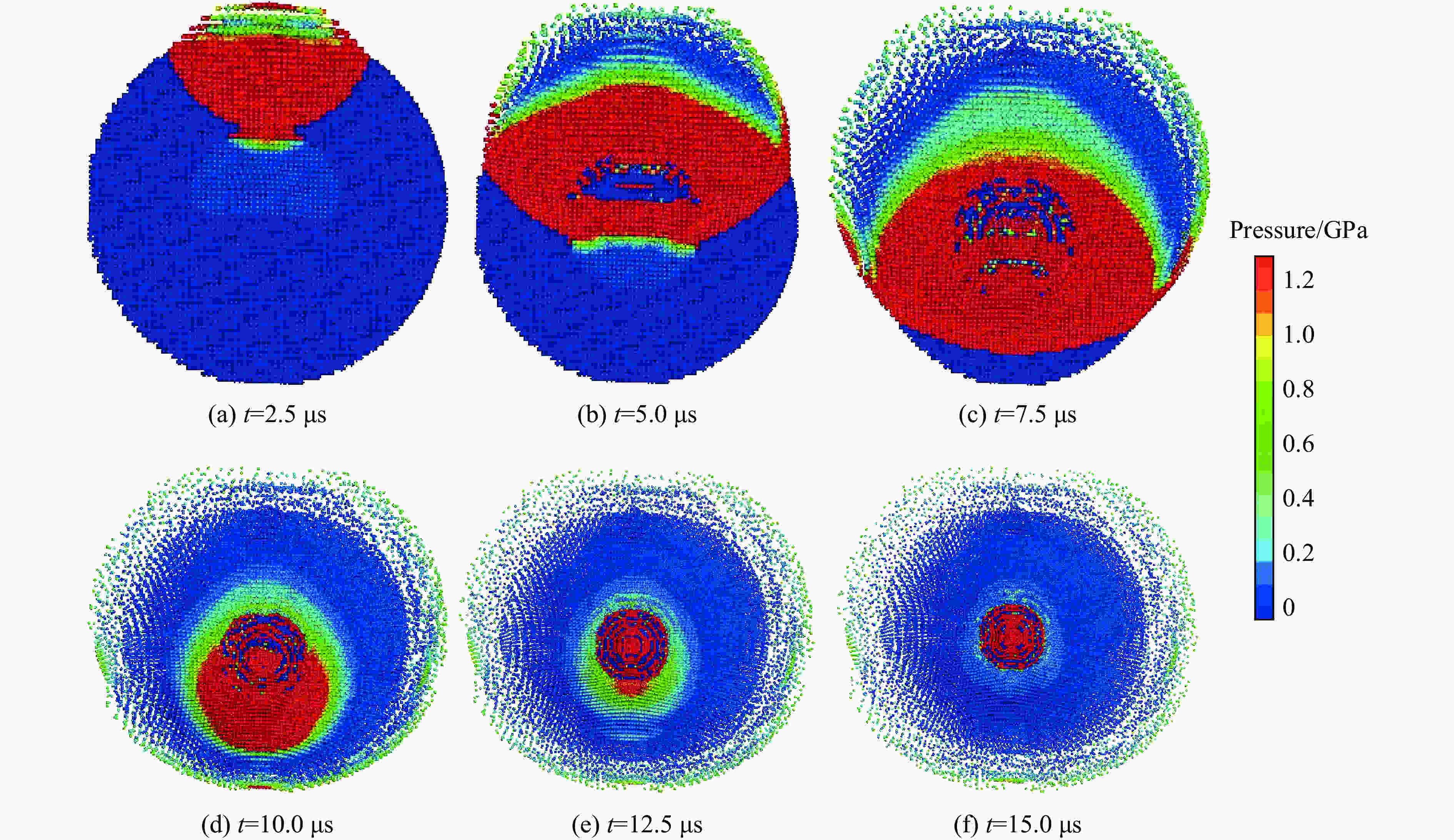
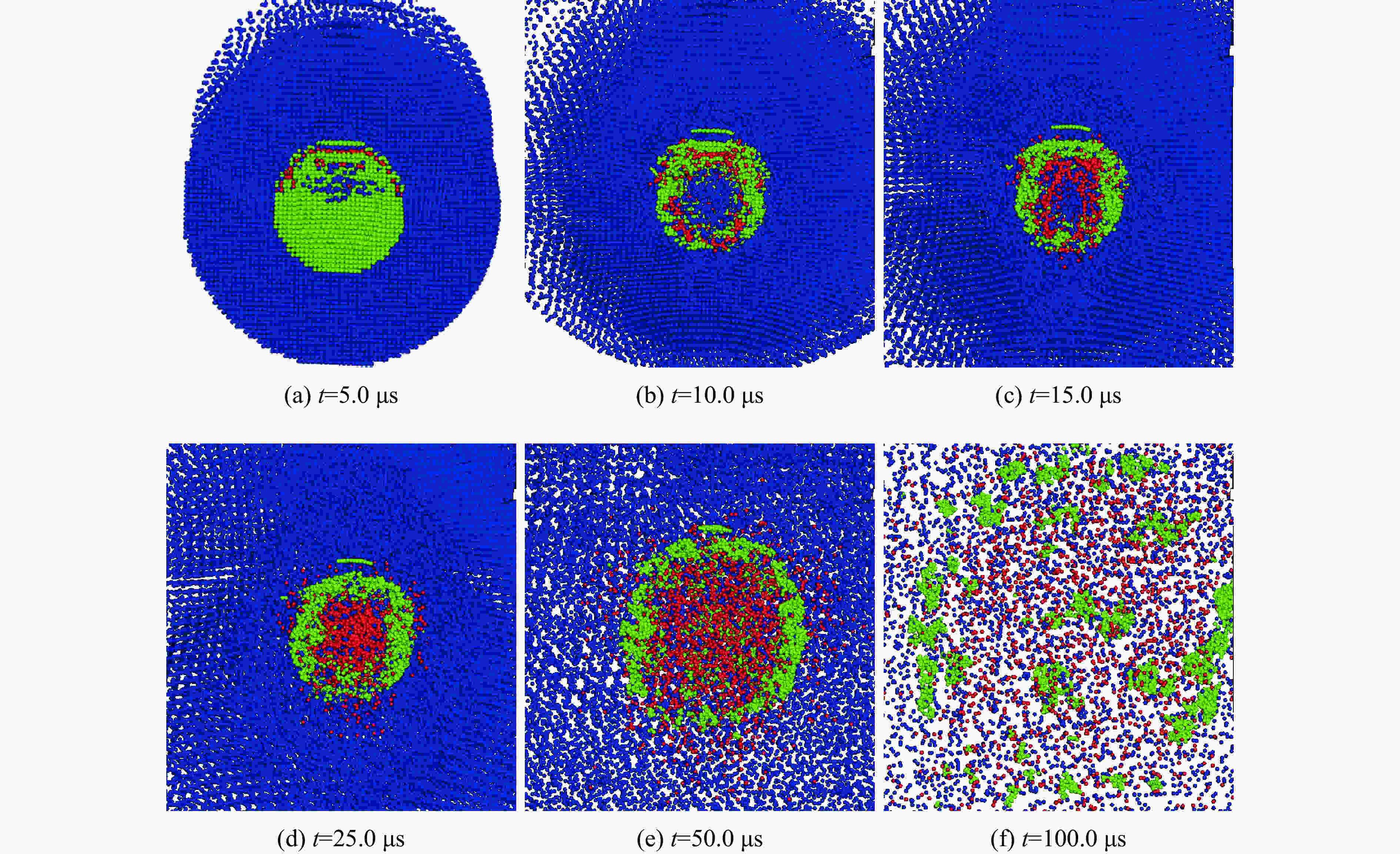
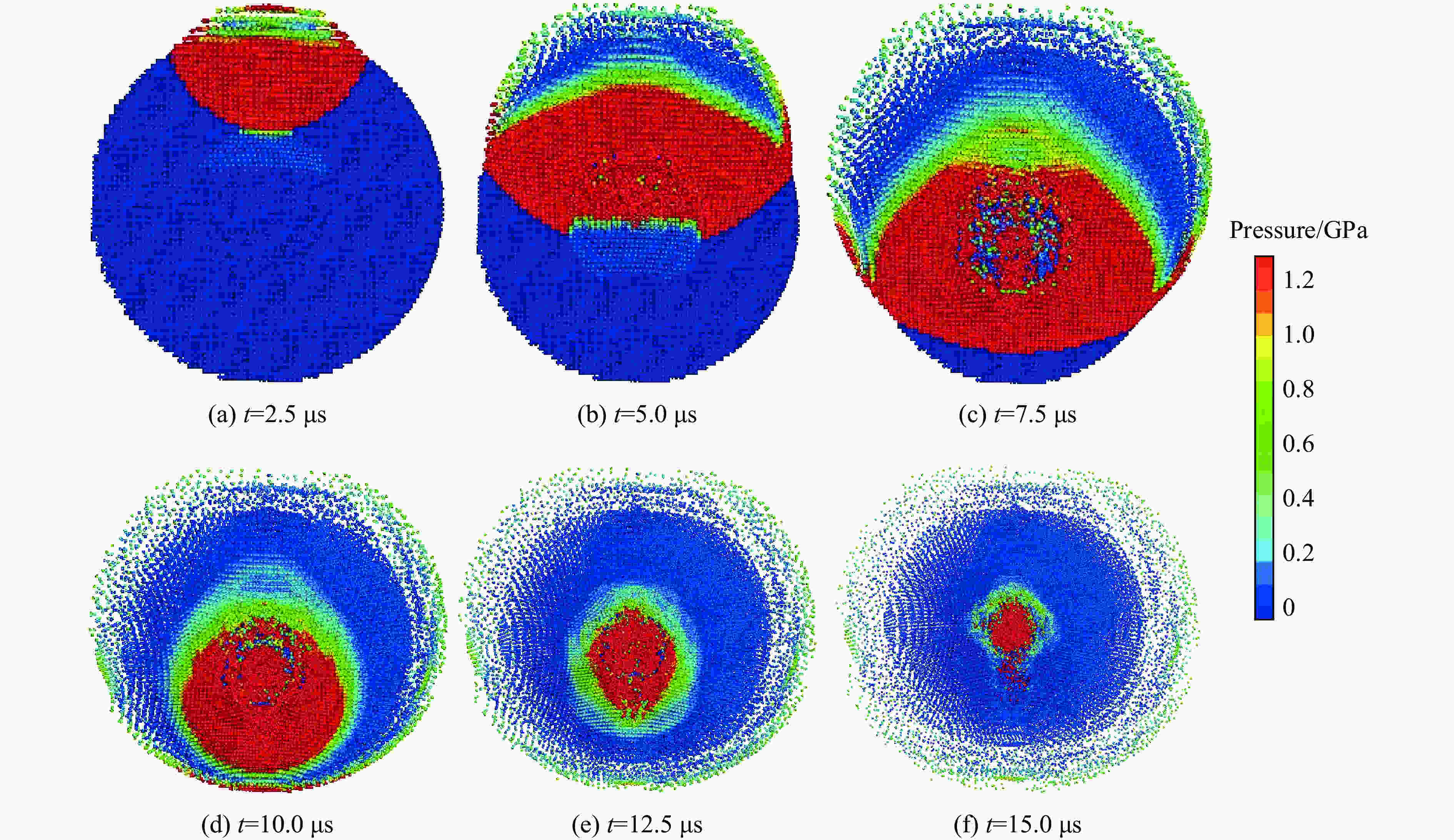
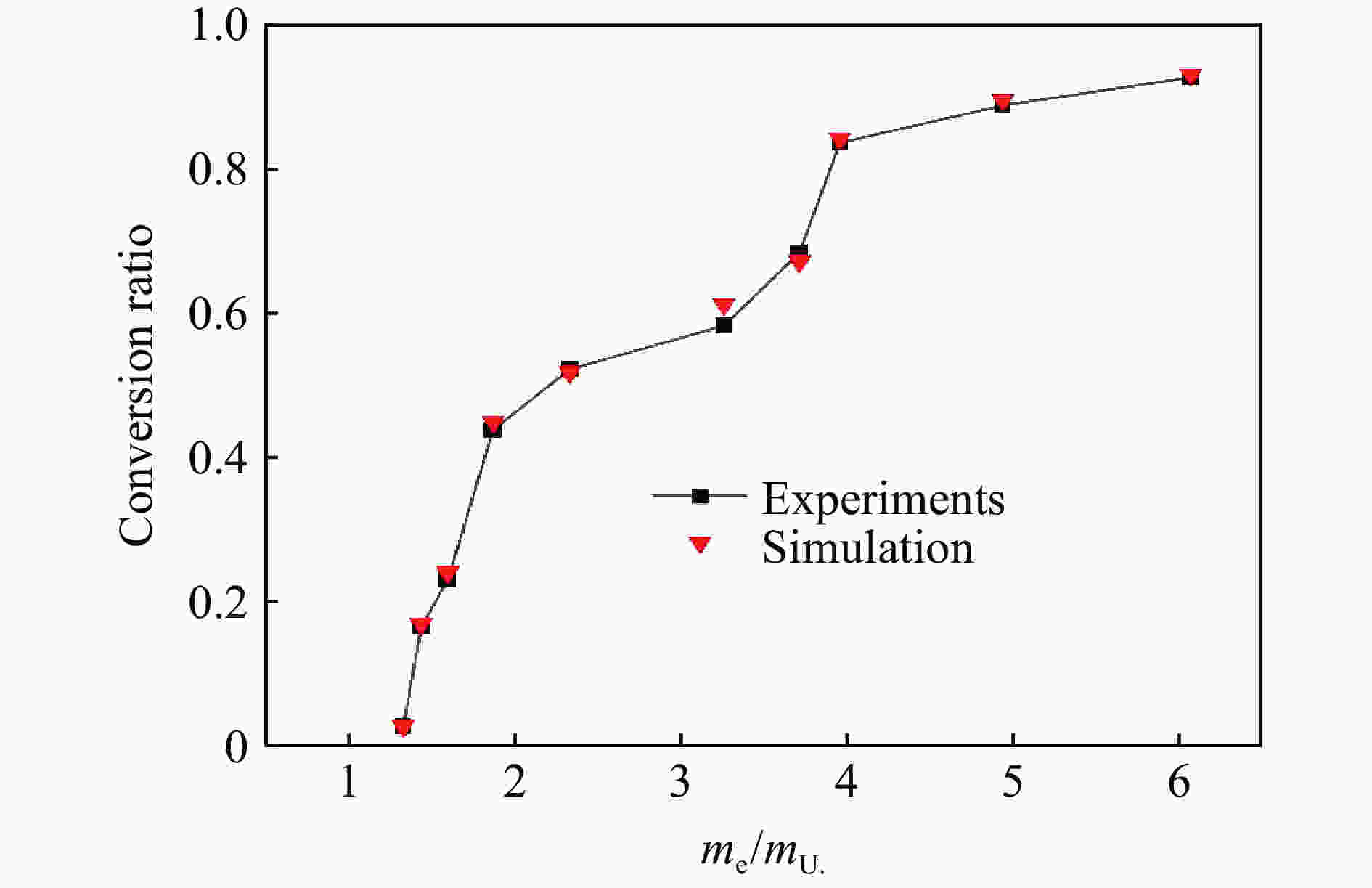
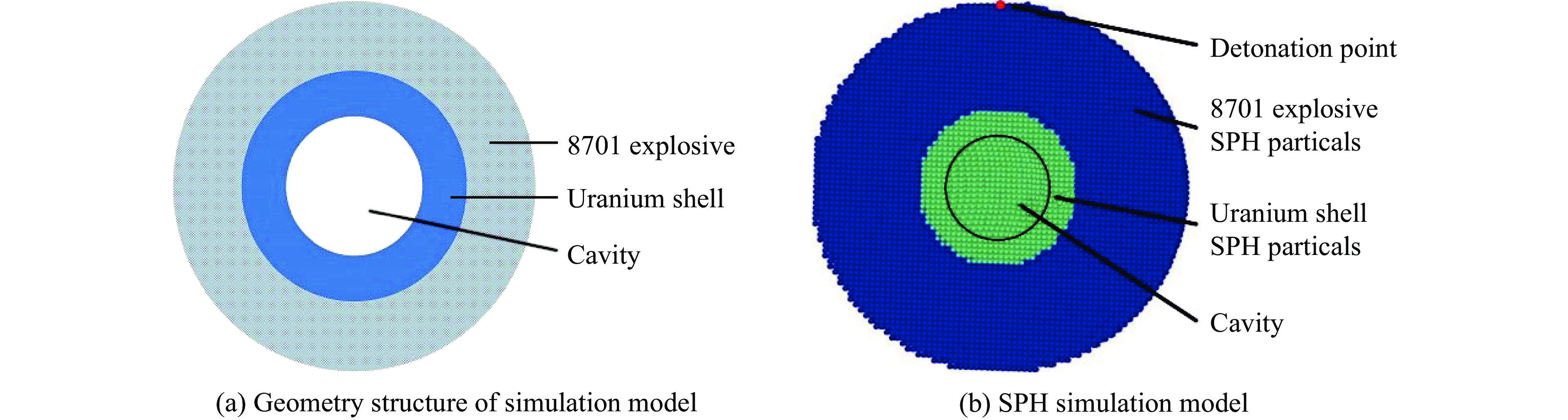
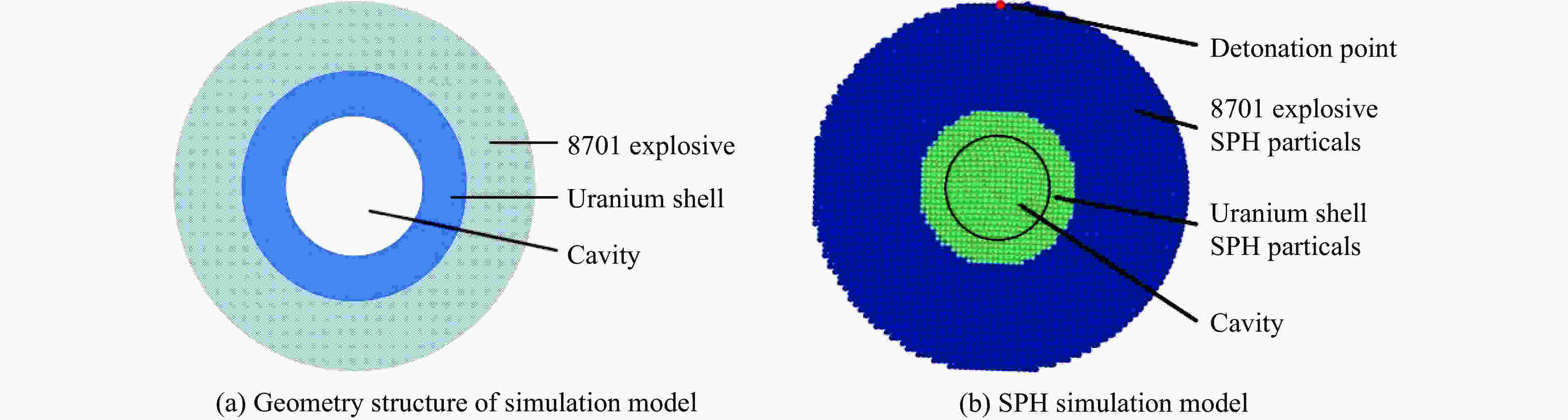
Abstract: Aiming at the process of uranium material forming radioactive aerosol under the action of explosion load, numerical simulation and experimental research were carried out based on the smoothed particle hydrodynamic method (SPH method). Through the combination of particle dynamics and SPH method, a numerical simulation model of explosive detonation acting on a uranium metal shell was established, which would be used to describe the formation process of uranium aerosol. The specific internal energy of uranium material was used as the aerosol conversion criterion, and the physical process of uranium material conversion into aerosol was obtained. We found two types of damage mode of the uranium under explosive load, one was overall damage when the uranium shell mass was close to the explosive mass, and the other one was crushing damage when the uranium shell mass was much less than the explosive mass. Under the same explosive equivalent, the aerosol conversion efficiencies of uranium materials with different mass were compared with the experimental results. The results show that uranium material can be considered to be completely converted into aerosol when its specific internal energy reaches 1.9 MJ/kg under explosive load. According to the explosive device structure in this paper, when the explosive mass is six times than the mass of uranium, the conversion ratio exceeds 90%. The experimental results have a good agreement with the numerical simulations, which shows that the method used in this paper can accurately describe the aerosol conversion process of uranium materials.-
Key words:
- uranium /
- aerosol /
- explosion load /
- smoothed particle hydrodynamics method
-
锆是一种具有极强耐腐蚀性能的稀有金属, 其耐蚀性能优于不锈钢、钛和镍合金, 可用于硝酸、盐酸、过氧化氢以及氯化乙烯等化工产品的生产和存储装置。由于锆的价格昂贵, 所以通常将锆与钢复合后使用, 目前主要通过爆炸焊接技术来制备大面积的锆/钢复合板[1-2]。爆炸焊接是一种高能率固相焊接方法, 它是利用炸药爆轰驱动复板与基板高速撞击来实现焊接的。焊接后, 在复板与基板的结合面处会产生准正弦波形状的波纹, 称为界面波[3]。界面波是判断爆炸焊接结合强度的一个标准, 细小而规则的界面波表示基复板结合强度高, 无界面波或界面波过大, 则表示结合强度较差[4-5]。
锆与钢直接复合时, 容易形成脆硬的金属间化合物, 降低复合板的结合强度。因此复合时, 需要在锆与钢之间添加过渡层[6]。钛、锆为同族元素, 材料冶金性能相近, 两者爆炸复合不会产生金属间化合物, 而钛与钢的爆炸复合工艺成熟, 可充分保证结合质量, 所以本文选用钛作为锆/钢复合板的过渡层。
本文中, 拟对锆/钢和锆/钛/钢进行小倾角法爆炸焊接实验, 测量各结合界面的波形参数和剪切强度, 分析过渡层及退火处理对剪切强度的影响。另外, 采用光滑粒子流体动力学(smoothed particle hydrodynamics, SPH)法模拟锆/钛/钢三层爆炸焊接, 计算碰撞速度和碰撞角, 获得锆/钛/钢最佳结合质量对应的最优爆炸焊接动态参数。
1. 小倾角爆炸焊接实验
小倾角法爆炸焊接实验是将复板和基板预置一定的角度, 一般为2°~6°, 使复板与基板的间距连续变化, 从而在不同加速距离下获得连续变化的碰撞速度和碰撞角[7], 实验装置如图 1所示。小倾角法可在一次实验中实现多组不同碰撞速度和碰撞角下的爆炸焊接, 适合进行爆炸焊接动态参数的优化。实验中采用的复板为Zr-3锆板, 基板为Q345钢板, 过渡层为TA1钛板。复板尺寸为400 mm×160 mm×3 mm, 基板尺寸为360 mm×160 mm×10 mm, 过渡层尺寸为360 mm×160 mm×2 mm。采用的炸药为改性铵油炸药, 装药密度0.84 g/cm3, 爆速2.6 km/s。
图 1 三层小倾角法爆炸焊接装置示意图Figure 1. The equipment of three-layer explosive welding at small angle锆/钢双层实验预置倾角为3°, 最大间距为19 mm, 装药厚度35 mm。锆/钛/钢三层实验的复板与过渡层间的预置倾角为3°, 最大间距为19 mm。过渡层与基板平行放置, 架高为8 mm。装药厚度为40 mm。各板间结合面均经抛光处理, 复板与炸药接触表面涂抹黄油防止烧蚀。
爆炸焊接后得到的锆/钢及锆/钛/钢复合板无空鼓和开裂, 表面无烧蚀, 经超声波检测其结合率为100%。在每块复合板上沿长度方向切割出360 mm×20 mm的长条, 再截断成40 mm长的小试样, 用于金相及剪切强度检测。
2. 结果与分析
2.1 波形参数
金属板爆炸焊接时会在结合界面形成界面波, 界面波的大小与爆炸复合板的结合强度有关。一般界面波细小时, 结合强度高, 无界面波或界面波粗大时, 结合强度低。界面波的大小可由波形参数来表示, 波形参数包括波长s、波高h和比波长s/h。
锆/钢复合板9个试样的界面波如图 2所示。可以看出, 试样1的结合界面平直无波纹, 试样2的左半部无波纹, 右半部开始出现细小波纹, 其他7个试样的结合界面都有波纹产生, 而且沿爆轰波传播方向界面波越来越明显。试样9的右半部没有界面波, 这是受爆炸焊接末端稀疏效应的影响所致。
为了测量各试样的波形参数, 在每个试样的中间位置, 对结合界面进行金相显微观察, 如图 3所示。可以看出, 试样1基本无界面波, 其余8个试样的界面波形状相似, 波长逐渐增大。在图 3中测量出界面波的波长和波高, 具体波形参数见表 1。图中的位置表示界面波波峰至起爆点的距离, 在距离起爆点60 mm处界面波的波长、波高和比波长均发生了突变, 说明开始产生界面波。此后随着远离起爆点, 波长和波高逐渐增加, 比波长先减小后增加。
表 1 复合板的波形参数Table 1. The interfacial wave parameters of the clad plates试样编号 s/mm h/mm s/h s/mm h/mm s/h s/mm h/mm s/h 锆/钢界面 锆/钛界面 钛/钢界面 1 0.189 0.011 17.18 0 0 0 0.500 0.111 4.50 2 0.511 0.133 3.84 0.120 0.110 1.09 0.889 0.200 4.45 3 1.056 0.278 3.80 0.222 0.167 1.33 0.833 0.189 4.41 4 1.444 0.411 3.51 0.389 0.278 1.40 1.111 0.222 5.00 5 1.944 0.711 2.73 0.445 0.333 1.34 1.278 0.278 4.60 6 2.111 0.833 2.53 0.556 0.389 1.43 1.444 0.333 4.34 7 2.333 0.722 2.23 0.611 0.444 1.38 1.611 0.333 4.84 8 2.444 0.822 2.97 0.667 0.500 1.33 1.667 0.333 5.00 9 2.833 0.777 3.64 0.844 0.510 1.65 1.889 0.333 5.67 采用同样方法测量锆/钛/钢试样的界面波波形参数。锆/钛/钢复合板包含2个界面, 锆/钛界面和钛/钢界面, 所以分别对2个界面进行金相显微观察, 然后将同一位置2个界面的图像合成在一起, 如图 4所示。由于篇幅所限, 只列举了1、6和9号试样。锆/钛界面在20 mm处无界面波, 在60 mm开始出现微小界面波, 此后波长和波高逐渐增加, 比波长为1.4左右。钛/钢界面在20 mm处就形成了界面波, 此后波长逐渐增加, 波高增加到0.333 mm后, 就不再变化, 其比波长值为5.0左右。锆/钛/钢复合板的波形参数见表 2。
表 2 复合板结合界面的剪切强度Table 2. The interfacial shear strength of clad plate试样编号 σs/MPa 锆/钛界面 钛/钢界面 锆/钢界面 爆炸态 退火态 爆炸态 退火态 爆炸态 退火态 1 57 41 63 185 47 160 2 77 68 124 180 110 160 3 103 94 150 193 138 166 4 115 101 163 163 147 132 5 142 121 155 191 144 157 6 155 131 164 217 148 179 7 124 110 158 183 143 165 8 84 78 166 156 146 131 9 51 46 133 131 115 112 2.2 剪切强度
爆炸复合板的结合强度是评价复合板质量的重要参数, 通常用剪切强度σs来表示。复合板的剪切强度一般根据GB/T 6396-2008[8]进行检测。按照该标准对锆/钢和锆/钛/钢试样进行加工, 复合板剪切强度检测装置及剪切后的试样如图 5所示。
各试样结合界面的剪切强度见表 2, 其中退火态是指经过退火处理消除了加工应力的试样, 退火温度为580 ℃, 保温1小时。爆炸态为没有经过退火处理的试样。从表 2可以看出, 退火后复合板结合界面的剪切强度降低约20%。
根据锆/钢复合板行业标准YST 777-2011[9]得知, 退火态锆/钢复合板结合界面的剪切强度应高于140 MPa。由表 2可以看出:在没有过渡层的情况下, 锆/钢复合板不同试样的退火态剪切强度均低于140 MPa; 而增加了过渡层后, 锆/钛/钢复合板的5、6和7号试样的锆/钛界面和钛/钢界面的剪切强度均高于140 MPa, 其中锆/钛/钢试样6在2个界面上的剪切强度均为最大值, 锆/钛界面的剪切强度为148 MPa, 钛/钢界面的剪切强度为179 MPa。这表明钛作为过渡层可提高锆/钢复合板的剪切强度, 使之达到行业标准要求。另外, 对比表 1可知:当锆/钛界面波波长约为0.5 mm, 钛/钢界面波波长约为1.5 mm时, 结合界面的剪切强度较高。
3. 数值模拟
为了获得小倾角实验的碰撞速度和碰撞角, 采用SPH法对锆/钛/钢三层爆炸焊接进行数值模拟。SPH法是一种拉格朗日无网格方法, 采用带有各种物理量的粒子构成离散计算域。任意粒子i的物理量fi可以通过其周围粒子插值得到。SPH法不用定义接触, 各材料的粒子就可实现相互作用。材料的变形不依赖网格, 能够避免有限元法的网格畸变, 因此被广泛应用于爆轰、侵彻等各种大变形问题的计算[10-11]。李晓杰等[12]和Wang Xiao等[13]将该方法用于爆炸焊接研究, 经与实验结果比较, 证明计算精度较高。
采用SPH法对锆/钛/钢小倾角法爆炸焊接进行数值模拟, 质点模型由5部分组成(见图 6):炸药、锆板、钛板、钢板和刚性壁, 其中刚性壁模拟爆炸焊接时钢板下方的垫板。爆炸焊接时架高的阻力可忽略不计, 所以模型中省略了架高。起爆点位于炸药左上角。由于是对整个爆炸焊接过程进行宏观模拟, 质点间距较大, 所以没有模拟出界面波。按照表 1中各试样的中点位置, 在锆板和钛板下表面依次各取9个点, 间隔均为40 mm, 计算得到各点的碰撞速度v和碰撞角β, 见表 3。
图 6 锆/钛/钢爆炸焊接的SPH模型Figure 6. The SPH model of explosive welding for Zr/Ti/steel clad plate表 3 锆/钛/钢界面的碰撞参数Table 3. Impact parameters for Zr/Ti/steel interface试样 v/(m·s-1) β/(°) v/(m·s-1) β/(°) 锆/钛界面 钛/钢界面 1 325 5.2 485 3.3 2 501 10.1 554 8.5 3 602 13.5 684 14.2 4 680 17.0 755 16.8 5 734 19.8 803 19.5 6 774 20.4 871 20.2 7 805 20.8 904 20.5 8 823 21.2 923 20.9 9 850 21.5 939 21.3 通过模拟, 得出了锆/钛/钢5、6和7号试样的碰撞速度和碰撞角。由此得到一组合理的锆/钛/钢碰撞参数, 即锆/钛界面的v为734~805 m/s, β为19.8°~20.8°; 钛/钢界面的碰撞速度为803~904 m/s, 碰撞角为19.5°~20.5°。
4. 结论
通过对锆/钛/钢进行了小倾角法爆炸焊接实验及数值模拟, 得出如下结论:(1)钛板作为过渡层, 可显著提高锆/钢复合板的剪切强度。(2)小倾角实验可获得波长连续变化的界面波, 当锆/钛界面波波长约为0.5 mm, 钛/钢界面波波长约为1.5 mm时, 结合界面的剪切强度较高。(3)当锆/钛界面的碰撞速度为734~805 m/s, 碰撞角为19.8°~20.8°, 钛/钢界面的碰撞速度为803~904 m/s, 碰撞角为19.5°~20.5°时, 锆/钛/钢三层复合板的锆/钛和钛/钢界面的剪切强度都能高于140 MPa。
-
图 2 不同比内能截断值时气溶胶转化率计算结果
Figure 2. Calculation results of aerosol conversion ratio at different specific internal energy cut-off values
图 3 铀壳体受冲击挤压气化转变过程
Figure 3. Gasification transformation process of uranium shell under impact extrusion
图 5 铀壳体气化转变及碎片运动过程
Figure 5. Uranium shell gasification transformation and fragment movement process
图 9 药壳质量比与转化率的关系
Figure 9. The relationship between explosive uranium mass ratio and conversion ratio
表 1 Project Roller Coaster实验状态
Table 1. The status of Project Roller Coaster
试验代号 炸药质量/kg 环境 爆炸烟云高度/m DT 53.5 钢板上 220 CS1 481.7 混凝土上 710 CS2 1016.9 掩体内 440 CS3 1016.9 掩体内 520 
下载: 导出CSV
表 2 铀金属的材料参数
Table 2. Material parameters of uranium metal
弹性模量/GPa 泊松比 密度/（kg·m−3） A/MPa B/MPa n C DC εd D1 D2 D3 D4 D5 132.6 0.3 19 050 800 684 0.083 0.012 0.3 0 0.0705 1.732 −0.54 −0.0123 0
下载: 导出CSV
表 3 转化率的实验与模拟结果对比(%)
Table 3. Comparison of experimental and simulational results of conversion ratio (%)
实验编号 实验结果 计算结果 绝对误差 实验编号 试验结果 计算结果 绝对误差 1 2.75 2.80 −0.05 6 58.38 61.30 −2.92 2 16.68 16.92 −0.24 7 68.48 67.26 1.22 3 23.03 24.12 −1.09 8 83.75 84.33 −0.58 4 43.87 45.03 −1.16 9 88.91 89.64 −0.73 5 52.29 51.91 0.38 10 92.80 92.85 −0.05
下载: 导出CSV
表 4 不同实验工况下铀气溶胶的质量和转化率
Table 4. Mass and conversion ratio of uranium aerosol among different experiments
试验编号 铀气溶胶质量/g 铀壳质量/g 转化率/% 1 6.2 225.7 2.75 2 34.8 208.6 16.68 3 43.3 187.9 23.03 4 86.3 160.2 43.87 5 67.2 128.5 52.29 6 53.6 91.8 58.38 7 55.2 80.6 68.48 8 48.2 75.6 83.75 9 53.8 60.6 88.91 10 45.7 49.3 92.80
下载: 导出CSV
-
[1] BARKER R B. DoD 5100.52-M nuclear weapon accident response procedures (NARP) [S]. Washington: Assistant to the Secretary of Defense, 1990. [2] CONDIT R H. Plutonium dispersal in fires: summary of what is known [R]. Livermore: Lawrence Livermore National Laboratory, 1993. [3] 周建辉, 孙新利, 聂虎, 等. 基于修正光滑粒子流体动力学的爆轰波对金属球壳的压强数值模拟 [J]. 弹箭与制导学报, 2009, 29(4): 116–118. DOI: 10.3969/j.issn.1673-9728.2009.04.033.ZHOU J H, SUN X L, NIE H, et al. Numerical simulation of metallic sphere-shell’s pressure caused by detonation wave based on modified SPH [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(4): 116–118. DOI: 10.3969/j.issn.1673-9728.2009.04.033. [4] 王凯民, 于宪峰, 蔡瑞娇, 等. 传爆序列飞片起爆理论研究及应用 [J]. 探测与控制学报, 2007, 29(4): 57–60, 64. DOI: 10.3969/j.issn.1008-1194.2007.04.015.WANG K M, YU X F, CAI R J, et al. Shock-initiation theory and computations of flyer plate impact [J]. Journal of Detection & Control, 2007, 29(4): 57–60, 64. DOI: 10.3969/j.issn.1008-1194.2007.04.015. [5] STEELE C M, WALD T L, CHANIN D I. Plutonium explosive dispersal modeling using the MACCS2 computer code [R]. Lawrence: Lawrence Livermore National Laboratory, 1998. [6] TITUS R W. Operation roller coaster: project officers report-project, 2.4 POR-2504 [R]. Las Vegas: United States Weather Bureau Research Station, 1965. [7] HASCHKE J M. Evaluation of source-term data for plutonium aerosolization [R]. Los Alamos: Los Alamos National Laboratory, 1992. [8] HASCHKE J M, MARTZ J C. Oxidation kinetics of plutonium in air from 500 to 3 500 °C: application to source terms for dispersal [J]. Journal of Alloys and Compounds, 1998, 266(1−2): 81–89. DOI: 10.1016/S0925-8388(97)00499-4. [9] MARTZ J C, HASCHKE J M. A mechanism for combustive heating and explosive dispersal of plutonium [J]. Journal of Alloys and Compounds, 1998, 266(1−2): 90–103. DOI: 10.1016/S0925-8388(97)00498-2. [10] 郝樊华, 刘晓亚, 肖成建, 等. 爆轰条件下的气溶胶粒径分布及Ag质量分数与粒径的关系 [J]. 核技术, 2009, 32(5): 343–346. DOI: 10.3321/j.issn: 0253-3219.2009.05.005.HAO F H, LIU X Y, XIAO C J, et al. Size distributing of explosion-generated particles in a sealed container [J]. Nuclear Techniques, 2009, 32(5): 343–346. DOI: 10.3321/j.issn: 0253-3219.2009.05.005. [11] 刘文杰, 胡八一, 李庆忠. 核事故条件下钚气溶胶源项研究综述 [J]. 安全与环境学报, 2011, 11(5): 259–263. DOI: 10.3969/j.issn.1009-6094.2011.05.058.LIU W J, HU B Y, LI Q Z. Review of plutonium aerosol source-term in nuclear accident [J]. Journal of Safety and Environment, 2011, 11(5): 259–263. DOI: 10.3969/j.issn.1009-6094.2011.05.058. [12] 唐秀欢, 杨宁, 包利红, 等. 核武器运输炸药爆炸事故气溶胶扩散数值模拟 [J]. 安全与环境学报, 2014, 14(1): 142–148. DOI: 10.13637/j.issn.1009-6094.2014.01.034.TANG X H, YANG N, BAO L H, et al. Numerical simulation of aerosol dispersion with the explosive’s detonation in the process of nuclear weapon transportation [J]. Journal of Safety and Environment, 2014, 14(1): 142–148. DOI: 10.13637/j.issn.1009-6094.2014.01.034. [13] SEO S, MIN O, LEE J. Application of an improved contact algorithm for penetration analysis in SPH [J]. International Journal of Impact Engineering, 2008, 35(6): 578–588. DOI: 10.1016/j.ijimpeng.2007.04.009. [14] 董晃晃. SPH的粒子生成方法及其在弹体侵彻金属靶中的应用[D]. 南昌: 华东交通大学, 2017: 24−38. [15] FAN H F, BERGEL G L, LI S F. A hybrid peridynamics-SPH simulation of soil fragmentation by blast loads of buried explosive [J]. International Journal of Impact Engineering, 2016, 87: 14–27. DOI: 10.1016/j.ijimpeng.2015.08.006. [16] 王志远, 王凤英, 刘天生, 等. 基于FEM/SPH算法弹丸侵彻多孔陶瓷板的数值模拟 [J]. 高压物理学报, 2017, 31(1): 35–41. DOI: 10.11858/gywlxb.2017.01.006.WANG Z Y, WANG F Y, LIU T S, et al. Numerical simulation of projectile penetration into porous ceramic plates based on FEM/SPH algorithm [J]. Chinese Journal of High Pressure Physics, 2017, 31(1): 35–41. DOI: 10.11858/gywlxb.2017.01.006. [17] 赵德, 谈乐斌, 林志宸, 等. 基于SPH的弹丸侵彻土壤回收箱的数值模拟 [J]. 兵器装备工程学报, 2020, 41(4): 10–14. DOI: 10.11809/bqzbgcxb2020.04.003.ZHAO D, TAN L B, LIN Z C, et al. Numerical simulation of projectile penetrating soil receiving tank based on SPH method [J]. Journal of Ordnance Equipment Engineering, 2020, 41(4): 10–14. DOI: 10.11809/bqzbgcxb2020.04.003. [18] LIU M B, ZHANG Z L, FENG D L. A density-adaptive SPH method with kernel gradient correction for modeling explosive welding [J]. Computational Mechanics, 2017, 60(3): 513–529. DOI: 10.1007/s00466-017-1420-5. [19] 强洪夫, 张国星, 王广, 等. SPH方法在宽速域岩石侵彻问题中的应用 [J]. 高压物理学报, 2019, 33(5): 055105. DOI: 10.11858/gywlxb.20180621.QIANG H F, ZHANG G X, WANG G, et al. Application of SPH method for problem of rock penetration within the wide-ranged velocity [J]. Chinese Journal of High Pressure Physics, 2019, 33(5): 055105. DOI: 10.11858/gywlxb.20180621. [20] 强洪夫, 孙新亚, 王广, 等. 基于SPH的分层钢板抗半球头弹侵彻的数值模拟 [J]. 高压物理学报, 2018, 32(5): 055102. DOI: 10.11858/gywlxb.20170664.QIANG H F, SUN X Y, WANG G, et al. Numerical simulation of anti-penetration of laminated steel plate by hemispherical-nosed projectile using SPH [J]. Chinese Journal of High Pressure Physics, 2018, 32(5): 055102. DOI: 10.11858/gywlxb.20170664. [21] FAN H F, LI S F. A Peridynamics-SPH modeling and simulation of blast fragmentation of soil under buried explosive loads [J]. Computer Methods in Applied Mechanics and Engineering, 2017, 318: 349–381. DOI: 10.1016/j.cma.2017.01.026. [22] 高本兵, 尹建平, 陈杰, 等. 基于SPH方法的不同材质射流毁伤性能研究 [J]. 北京理工大学学报, 2018, 38(4): 353–358. DOI: 10.15918/j.tbit 1001-0645.2018.04.004.GAO B B, YIN J P, CHEN J, et al. Study on damage characteristics of different jets based on SPH method [J]. Transactions of Beijing Institute of Technology, 2018, 38(4): 353–358. DOI: 10.15918/j.tbit 1001-0645.2018.04.004. [23] 顾鑫, 章青. 爆炸荷载作用下大坝破坏分析的数值模拟研究进展 [J]. 河海大学学报 (自然科学版), 2017, 45(1): 45–55. DOI: 10.3876/j.issn.1000-1980.2017.01.007.GU X, ZHANG Q. Progress in numerical simulation of dam failure under blast loading [J]. Journal of Hehai University (Natural Sciences), 2017, 45(1): 45–55. DOI: 10.3876/j.issn.1000-1980.2017.01.007. [24] 强洪夫, 范树佳, 陈福振, 等. 基于SPH方法的聚能射流侵彻混凝土靶板数值模拟 [J]. 爆炸与冲击, 2016, 36(4): 516–524. DOI: 10.11883/1001-1455(2016)04-0516-09.QIANG H F, FAN S J, CHEN F Z, et al. Numerical simulation on penetration of concrete target by shaped charge jet with SPH method [J]. Explosion and Shock Waves, 2016, 36(4): 516–524. DOI: 10.11883/1001-1455(2016)04-0516-09. [25] Los Alamos National Laboratory. Selected hugoniots [R]. Los Alamos: Los Alamos National Laboratory, 1969. [26] AMINI Y, EMDAD H, FARID M. A new model to solve fluid-hypo-elastic solid interaction using the smoothed particle hydrodynamics (SPH) method [J]. European Journal of Mechanics-B/Fluids, 2011, 30(2): 184–194. DOI: 10.1016/j.euromechflu.2010.09.010. [27] 李运禄, 尹建平, 王志军, 等. 基于SPH算法对混凝土裂纹扩展研究 [J]. 兵器材料科学与工程, 2015, 38(5): 19–22. DOI: 10.14024/j.cnki.1004-244x.20150831.003.LI Y L, YIN J P, WANG Z J, et al. Crack propagation of concrete based on SPH algorithm [J]. Ordnance Material Science and Engineering, 2015, 38(5): 19–22. DOI: 10.14024/j.cnki.1004-244x.20150831.003. [28] 胡德安, 孙占华, 朱婷. 三维自适应FE-SPH耦合算法在多层间隔金属靶侵彻问题中的应用 [J]. 爆炸与冲击, 2015, 35(3): 416–422. DOI: 10.11883/1001-1455-(2015)03-0416-07.HU D A, SUN Z H, ZHU T. Application of 3D FE-SPH adaptive coupling algorithm to penetration analysis of spaced multi-layered metallic targets [J]. Explosion and Shock Waves, 2015, 35(3): 416–422. DOI: 10.11883/1001-1455-(2015)03-0416-07. [29] 杨刚, 傅奕轲, 郑建民, 等. 基于SPH方法对不同药型罩线性聚能射流形成及后效侵彻过程的模拟 [J]. 振动与冲击, 2016, 35(4): 56–61. DOI: 10.13465/j.cnki.jvs.2016.04.009.YANG G, FU Y K, ZHENG J M, et al. Simulation of formation and subsequent penetration process of linear shaped charge jets with different liners based on SPH method [J]. Journal of Vibration and Shock, 2016, 35(4): 56–61. DOI: 10.13465/j.cnki.jvs.2016.04.009. [30] 高艳. 基于SPH方法的弹丸侵彻问题的数值模拟[D]. 西安: 长安大学, 2014: 34−41. [31] 尹冠生, 高艳, 赵庭. 基于SPH算法的刚性弹丸侵彻的数值模拟 [J]. 长安大学学报 (自然科学版), 2014, 34(3): 74–79. DOI: 10.19721/j.cnki.1671-8879.2014.03.012.YIN G S, GAO Y, ZHAO T. Numerical simulation for penetration of rigid projectile based on SPH method [J]. Journal of Chang’an University (Natural Science Edition), 2014, 34(3): 74–79. DOI: 10.19721/j.cnki.1671-8879.2014.03.012. -
下载:
计量
- 文章访问数: 483
- HTML全文浏览量: 300
- PDF下载量: 124
- 被引次数: 0