基于高速3D-DIC技术的砂岩动力特性粒径效应研究

邢灏喆; 王明洋; 范鹏贤; 王德荣

doi:10.11883/bzycj-2021-0088

基于高速3D-DIC技术的砂岩动力特性粒径效应研究

doi: 10.11883/bzycj-2021-0088

陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏南京 210007

基金项目: 国家自然科学基金（52009138，11772355，51979280）；江苏省自然科学青年基金（BK20200583）；陆军工程大学前沿创新基金

详细信息

作者简介:
邢灏喆（1989－　），男，博士，讲师，haozhexing@hotmail.com

通讯作者:
范鹏贤（1983－　），男，博士，副教授，fan-px@139.com

中图分类号: O347.3
计量
- 文章访问数: 571
- HTML全文浏览量: 323
- PDF下载量: 120
- 被引次数: 0
出版历程
- 收稿日期: 2021-03-15
- 修回日期: 2021-08-24
- 网络出版日期: 2021-09-29
- 刊出日期: 2021-11-23

Grain-size effect on dynamic behavior of sandstone based on high-speed 3D-DIC technique

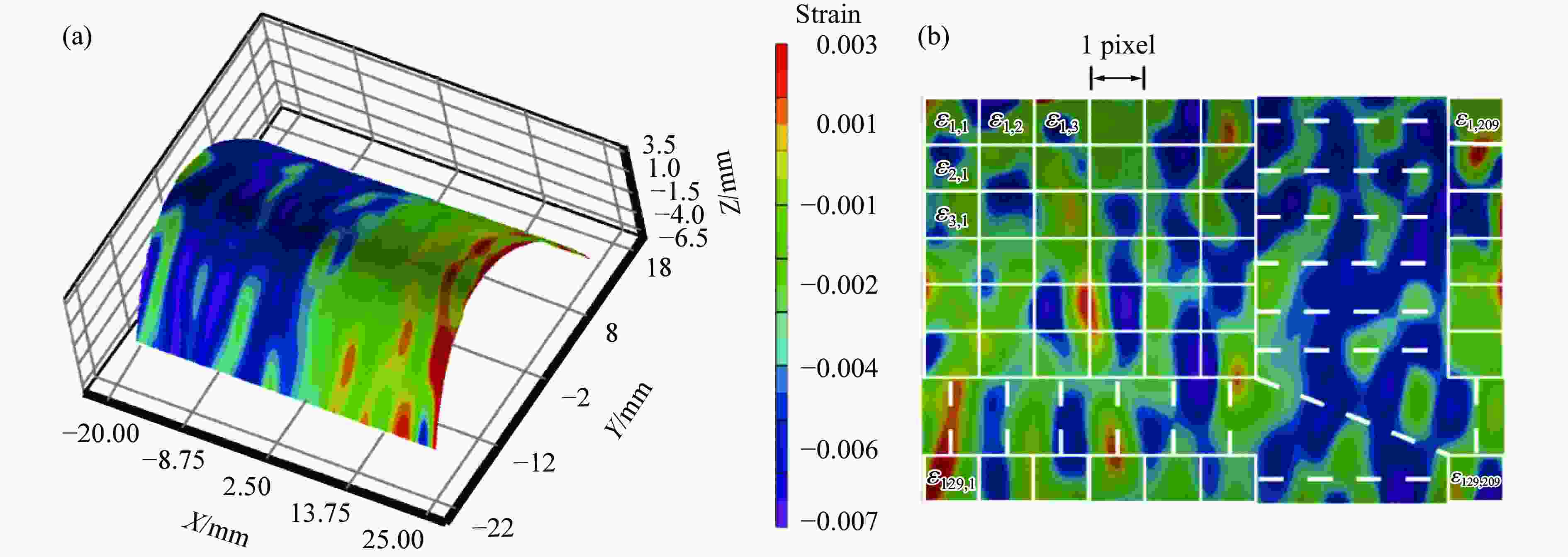
State Key Laboratory of Disaster Prevention and Mitigation of Explosion and Impact, Army Engineering University of PLA, Nanjing 210007, Jiangsu, China

摘要

摘要: 利用分离式霍普金森压杆（SHPB），对粗砂岩、中等粒径砂岩和细砂岩进行了应变率为69～83 s^–1的动态单轴抗压实验，研究了粒径尺寸效应对砂岩动力特性的影响。通过三维数字图像相关（3D-DIC）技术分析高速摄像图像，获得了砂岩的实时应变场，据此分析了动态荷载下3种粒径砂岩的动力变形特性和裂纹开展行为。结果表明，砂岩弹性应变储能可逆释放的临界应变率随着粒径的减小而升高，动态压缩强度随着粒径减小而增大，动态强度应变率敏感度则与强度规律相反。相较于静态条件下，中等粒径砂岩和细砂岩的动态弹性模量增长了2～3倍，粗砂岩的动态弹性模量增长达5倍以上。细砂岩的动态泊松比相较于静态提高了约25%，中等粒径砂岩的动态泊松比约为静态时的70%。动态裂纹首先出现于试件内部，然后传播至表面，呈现出应变局部化，动态荷载下岩石裂纹的孕育和扩展相比静态条件下均有所提前，其中细砂岩在动态荷载条件下的归一化裂纹起裂阈值仅为峰值强度的10%。微观分析表明，矿物粒径大小和黏土矿物含量分别在砂岩的动力力学性质和裂纹开展行为方面发挥主要作用。
- 砂岩 /
- 动态起裂 /
- 粒径效应 /
- 高速3D-DIC /
- 分离式霍普金森压杆
Abstract: The grain size effect on the dynamic behavior of sandstone was investigated through the compression tests on coarse-grained (CG), medium-grained (MG) and fine-grained (FG) sandstones by split Hopkinson pressure bar (SHPB) tests under the strain rates of 69–83 s^–1 based on the thin section and electron scanning microscopic (SEM) images analysis, the CG, MG and FG sandstone were mainly composed by quartz with the average grain size of 200–500, 90–500 and 55–120 µm, respectively. With the increasing grain size, the percentage of clay mineral was decreased correspondingly from 8% to 1%. During the dynamic compression, two high-speed cameras were applied to capture the deformation of sandstone at frame rate of 2×10⁵ s^–1 and resolution of 256×256. The real-time strain fields of rock were obtained by high-speed three-dimensional digital image correlation (3D-DIC) technique, the dynamic deformative properties, particularly the lateral strain of the specimen, were extracted by averaging the lateral strain field by pixels. The fracturing behavior of three sandstones was analyzed through the strain localization evolution within the strain fields. Results show that the critical strain rate for reversible release of elastic strain energy increases with the decreasing grain size. The dynamic strength ascends along with the reduction of grain size, while the strain rate sensitivity to the dynamic strength has an opposite trend. Compared to the quasi-static case, the dynamic elastic modulus increases by 2–3 times for MG and FG sandstone, particularly 5 times for CG sandstone. The Poisson’s ratio under dynamic loading in FG sandstone is grown by 25%, but drops at 70% of the static one in MG sandstone. The crack primarily generates inside the specimen and propagates to the surface of the specimen afterwards. The crack development is advanced under dynamic loadings, where the normalized stress threshold for crack initiation in FG sandstone is only 10%. Based on the microscopic analysis, mineral structure and clay percentage dominate the dynamic property and fracturing behavior of sandstone, respectively.
- sandstone /
- dynamic fracturing /
- grain-size effect /
- high-speed 3D-DIC /
- split Hopkinson pressure bar

HTML全文

图 1 细砂岩（FG）、中等粒径砂岩（MG）、粗砂岩（CG）试件

Figure 1. FG, MG and CG sandstone specimens

下载: 全尺寸图片幻灯片

图 2 三种粒径砂岩矿物组成的薄片显微照片

Figure 2. Section micrograph of mineral composition of three grain-sized sandstones

下载: 全尺寸图片幻灯片

图 3 分离式霍普金森压杆与双高速相机布置示意图

Figure 3. Setup of SHPB system integrated with two high-speed cameras

下载: 全尺寸图片幻灯片

图 4 中等粒径砂岩实验中应力平衡情况

Figure 4. Stress equilibrium status in MG experiment

下载: 全尺寸图片幻灯片

图 5 MG01和MG04实验的应力、应变、应变率时程曲线及动态应力应变曲线

Figure 5. Stress, strain, strain rate histories and stress strain curve in MG01 and MG04 experiments

下载: 全尺寸图片幻灯片

图 6 三种粒径砂岩动态应力应变曲线

Figure 6. Dynamic stress strain curves of three grain-sized sandstones

下载: 全尺寸图片幻灯片

图 7 三维重构试件应变场和应变场像素分布

Figure 7. Reconstructed 3D strain field of a sandstone specimen and pixel distribution in the strain field

下载: 全尺寸图片幻灯片

图 8 动态荷载下三种砂岩名义动态泊松比演化曲线

Figure 8. Nominal dynamic Poisson’s ratio curves for three types of sandstones under high strain rates

下载: 全尺寸图片幻灯片

图 9 MG01实验峰前应力应变曲线及裂纹开展各阶段应力阈值及应变场

Figure 9. Pre-peak stress strain curves and stress threshold for crack development with corresponding strain field in MG01

下载: 全尺寸图片幻灯片

图 10 三种砂岩试件在75 s⁻¹应变率时垂直方向应变局部化演化过程

Figure 10. Evolutions of vertical strain localization for three types of sandstones under the strain rate of 75 s⁻¹

下载: 全尺寸图片幻灯片

图 11 破坏前后三种砂岩微观颗粒形貌扫描电镜照片

Figure 11. SEM images of grain topography in three types of sandstones before and after failure

下载: 全尺寸图片幻灯片

表 1 三种粒径砂岩的基本物理力学参数

Table 1. Physical and mechanical parameters of three grain-sized sandstones

砂岩	ω（石英）/%	ω（黏土矿物）/%	密度/（kg·m⁻³）	准静态单轴抗压强度/MPa	弹性模量/GPa	波速/（m·s⁻¹）	泊松比
FG	95	<1	2 165	13	1.9	3 116	0.27
MG	92	4	2 214	41	6.9	2 110	0.21
CG	90	8	2 331	47	7.2	4 128	0.20

下载: 导出CSV

表 2 动态荷载下3种砂岩的动态力学特性

Table 2. Dynamic mechanical properties of three types of sandstones

试件	应变率/s⁻¹	动态单轴抗压强度（峰值应力*）/MPa	动态单轴抗压强度（峰值应力*）应变率敏感度/（MPa·s）
CG01	76	23	1.4
CG02	80	28	1.4
CG03	83	33	1.4
MG01	69	52*	1.0
MG02	75	57*	1.0
MG03	81	60*	1.0
MG04	83	67	1.0
FG01	68	59*	0.5
FG02	70	61*	0.5
FG03	78	64*	0.5
注：“*”代表峰值应力。

下载: 导出CSV

表 3 不同应变率下3种砂岩动态弹性模量与泊松比

Table 3. Dynamic Young’s modulus and Poisson’s ratio of three types of sandstones under different strain rates

试件	应变率/s^-1	动态弹性模量/GPa	动态泊松比
CG01	76	10.0	0.17
CG02	80	6.6
CG03	83	9.3
MG01	69	12.0	0.15
MG02	75	11.5	0.15
MG03	81	12.4	0.15
MG04	83	13.7	0.15
FG01	68	17.8	0.25
FG02	70	21.3	0.25
FG03	78	16.4	0.25

下载: 导出CSV

表 4 不同应变率下三种砂岩裂纹发展应力阈值

Table 4. Stress thresholds of sandstones at various strain rates

试件	应变率/s⁻¹	σ_ci/MPa	σ_cd/MPa	σ_dyn/MPa	σ_ci/σ_dyn	σ_cd/σ_dyn
CG01	76	5.5	12.6	23	0.24	0.54
CG02	80		8.3	28		0.30
CG03	83		6.7	33		0.20
MG01	69	16.1	31.5	52	0.31	0.61
MG02	75	13.4	29.9	57	0.24	0.53
MG03	81	11.6	24.4	60	0.19	0.41
MG04	83	8.6	19.0	67	0.13	0.29
FG01	68	9.1	21.8	59	0.15	0.38
FG02	70	8.1	16.1	61	0.13	0.26
FG03	78	6.1	13.8	64	0.10	0.22

下载: 导出CSV

参考文献(24)

[1]	THOMAS D C, BENSON S M. Carbon dioxide capture for storage in deep geologic formations-results from the CO₂ capture project: vol 2-geologic storage of carbon dioxide with monitoring and verification [M]. USA: Elsevier, 2015.
[2]	YUSOF N Q A M, ZABIDI H. Correlation of mineralogical and textural characteristics with engineering properties of granitic rock from Hulu Langat, Selangor [J]. Procedia Chemistry, 2016, 19: 975–980. DOI: 10.1016/j.proche.2016.03.144.
[3]	RÄISÄNEN M. Relationships between texture and mechanical properties of hybrid rocks from the Jaala-Iitti complex, southeastern Finland [J]. Engineering Geology, 2004, 74(3): 197–211. DOI: 10.1016/j.enggeo.2004.03.009.
[4]	HARELAND G, POLSTON C, WHITE W. Normalized rock failure envelope as a function of rock grain size [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1993, 33(5): 479–485. DOI: 10.1016/0148-9062(93)90012-3.
[5]	李柯萱, 李铁. 不同加载速率下砂岩弯曲破坏的细观机理 [J]. 爆炸与冲击, 2019, 39(4): 043101. DOI: 10.11883/bzycj-2018-0178. LI K X, LI T. Micro-mechanism of bending failure of sandstone under different loading rates [J]. Explosion and Shock Waves, 2019, 39(4): 043101. DOI: 10.11883/bzycj-2018-0178.
[6]	WASANTHA P, RANJITH P G, ZHAO J, et al. Strain rate effect on the mechanical behaviour of sandstones with different grain sizes [J]. Rock Mechanics and Rock Engineering, 2015, 48(5): 1883–1895. DOI: 10.1007/s00603-014-0688-4.
[7]	YU M, WEI C, NIU L. The coupled effect of loading rate and grain size on tensile strength of sandstones under dynamic disturbance [J]. Shock and Vibration, 2017: 6989043. DOI: 10.1155/2017/6989043.
[8]	XING H Z, ZHANG Q B, RUAN D, et al. Full-field measurement and fracture characterisations of rocks under dynamic loads using high-speed three-dimensional digital image correlation [J]. International Journal of Impact Engineering, 2018, 113: 61–72. DOI: 10.1016/j.ijimpeng.2017.11.011.
[9]	LIU X, YANG J, XU Z, et al. Experimental investigations on crack propagation characteristics of granite rectangle plate with a crack (GRPC) under different blast loading rates [J]. Shock and Vibration, 2020: 8885582. DOI: 10.1155/2020/8885582.
[10]	徐振洋, 杨军, 郭连军. 爆炸聚能作用下混凝土试件劈裂的高速3D DIC实验 [J]. 爆炸与冲击, 2016, 36(3): 400–406. DOI: 10.11883/1001-1455(2016)03-0400-07. XU Z Y, YANG J, GUO L J. Study of the splitting crack propagation morphology using high-speed 3D DIC [J]. Explosion and Shock Waves, 2016, 36(3): 400–406. DOI: 10.11883/1001-1455(2016)03-0400-07.
[11]	XING H Z, ZHAO J, WU G, et al. Perforation model of thin rock slab subjected to rigid projectile impact at an intermediate velocity [J]. International Journal of Impact Engineering, 2020, 139: 103536. DOI: 10.1016/j.ijimpeng.2020.103536.
[12]	SUTTON M A, ORTEU J J, SCHREIER H. Image correlation for shape, motion and deformation measurements: basic concepts, theory and applications [M]. USA: Springer Science and Business Media, 2009.
[13]	DAI F, HUANG S, XIA K, et al. Some fundamental issues in dynamic compression and tension tests of rocks using split Hopkinson pressure bar [J]. Rock Mechanics and Rock Engineering, 2010, 43(6): 657–666. DOI: 10.1007/s00603-010-0091-8.
[14]	ABEN F, DOAN M L, GRATIER J P, et al. High strain rate deformation of porous sandstone and the asymmetry of earthquake damage in shallow fault zones [J]. Earth and Planetary Science Letters, 2017, 463: 81–91. DOI: 10.1016/j.jpgl.2017.01.016.
[15]	LIU K, ZHAO J, WU G, et al. Dynamic strength and failure modes of sandstone under biaxial compression [J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 128: 104260. DOI: 10.1016/j.ijrmms.2020.104260.
[16]	王学滨. 加载速度对岩样全部变形特征的影响 [J]. 岩土力学, 2008, 29(2): 353–358. DOI: 10.3969/j.issn.1000-7598.2008.02.012. WANG X B. Effect of loading rate on entire deformational characteristics of rock specimen [J]. Rock and Soil Mechanics, 2008, 29(2): 353–358. DOI: 10.3969/j.issn.1000-7598.2008.02.012.
[17]	王学滨. 软化模量对岩样全部变形特征的影响 [J]. 岩土工程学报, 2006, 28(5): 600–605. DOI: 10.3321/j.issn:1000-4548.2006.05.010. WANG X B. Effect of softening modulus on entire deformational characteristics of rock specimen [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(5): 600–605. DOI: 10.3321/j.issn:1000-4548.2006.05.010.
[18]	王让甲, 樊冀安, 高学之. 岩石负泊松比的探讨 [J]. 探矿工程, 1996, 4: 17–19. WANG R J, FAN J A, GAO X Z. Note on rock with negative Poisson’s ratio [J]. Mine Exploring Engineering, 1996, 4: 17–19.
[19]	朱建明, 徐秉业, 岑章志. 岩石类材料峰后滑移剪膨变形特征研究 [J]. 力学与实践, 2001, 23(5): 19–22. DOI: 10.3969/j.issn.1000-0879.2001.05.004. ZHU J M, XU B Y, CEN Z Z. Study on the deformation mechanics of sliding dilation of post-failure rocks [J]. Mechanics in Engineering, 2001, 23(5): 19–22. DOI: 10.3969/j.issn.1000-0879.2001.05.004.
[20]	BURSHTEIN L S. Determination of Poisson's ratio for rocks by static and dynamic methods [J]. Soviet Mining, 1968, 4(3): 235–238. DOI: 10.1007/BF02501543.
[21]	GERCEK H. Poisson’s ratio values for rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(1): 1–3. DOI: 10.1016/j.ijrmms.2006.04.011.
[22]	XING H Z, ZHANG Q B, ZHAO J. Stress thresholds of crack development and Poisson’s ratio of rock material at high strain rate [J]. Rock Mechanics and Rock Engineering, 2018, 51: 945–951. DOI: 10.1007/s00603-017-1377-x.
[23]	BRACE W, PAULDING B, SCHOLZ C. Dilatancy in the fracture of crystalline rocks [J]. Journal of Geophysical Research, 1966, 71(16): 3939–3953. DOI: 10.1029/JZ071i016p03939.
[24]	MARTIN C, CHANDLER N. The progressive fracture of Lac du Bonnet granite [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1994, 31(6): 643–659. DOI: 10.1016/0148-9062(94)90005-1.