An investigating on explosive expanding fracture of 45 steel cylinders by SPH method
-
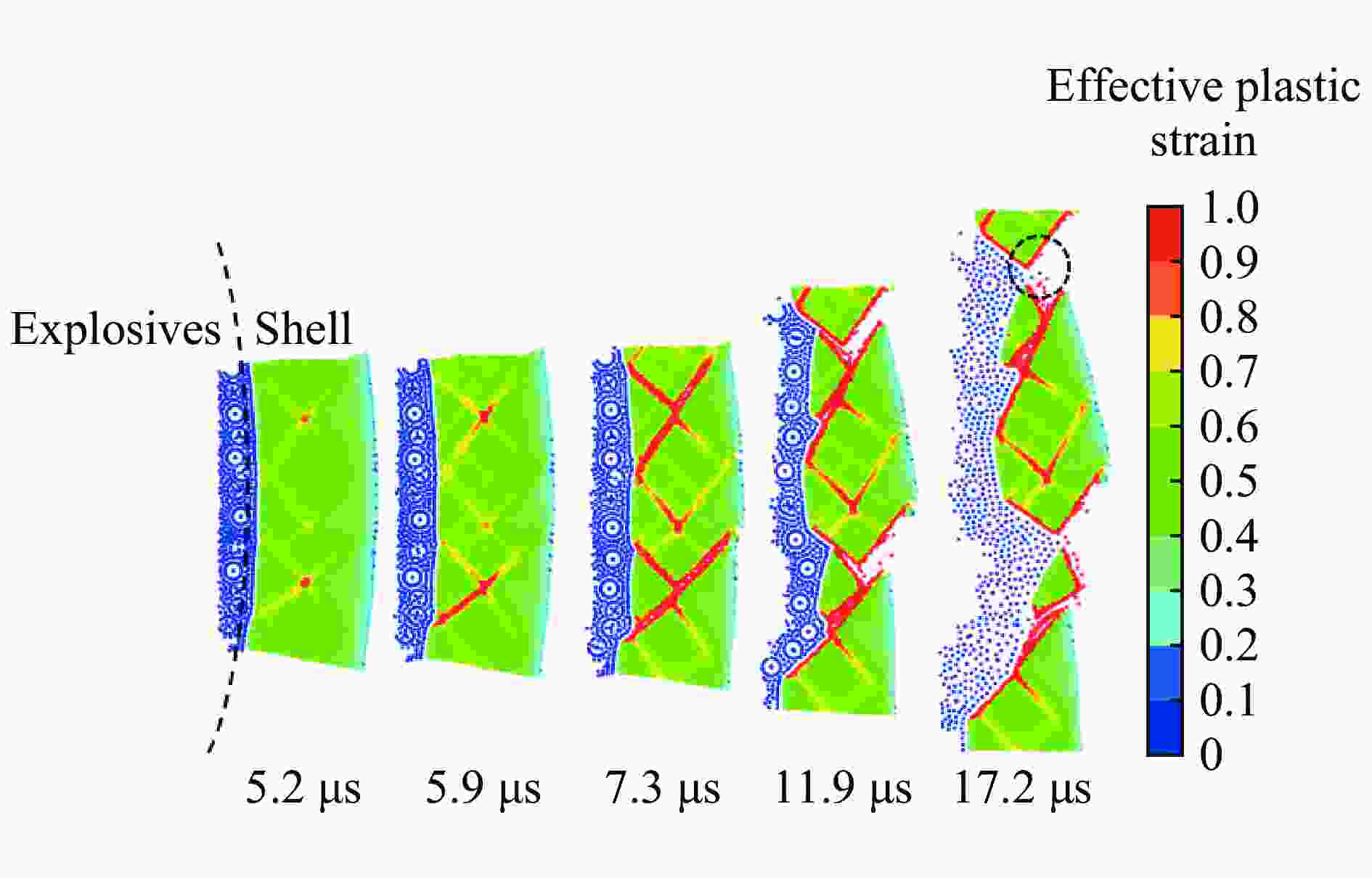
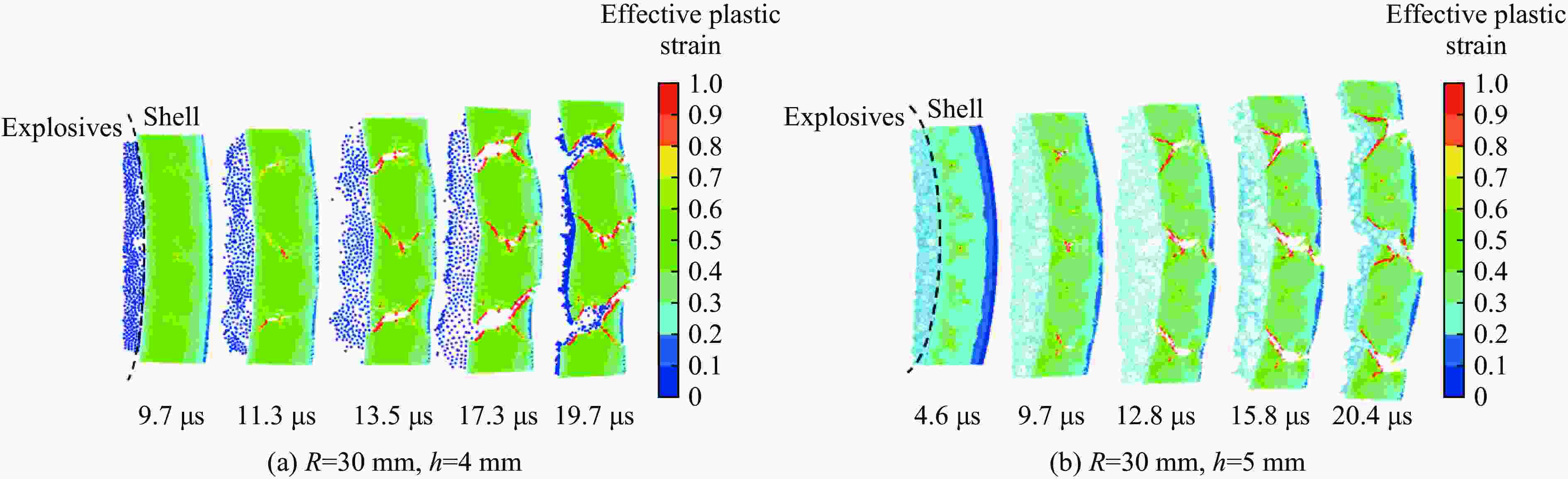
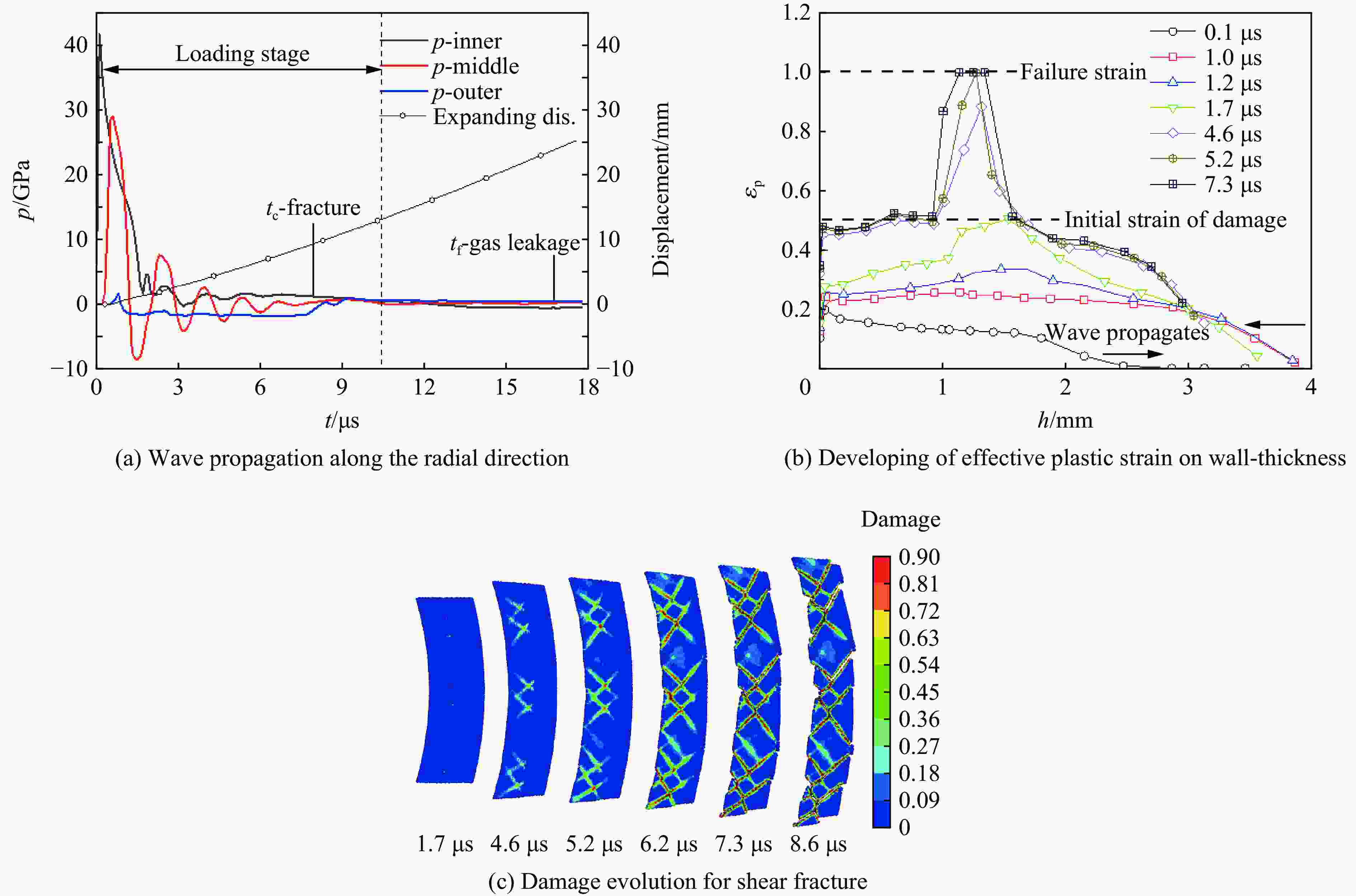
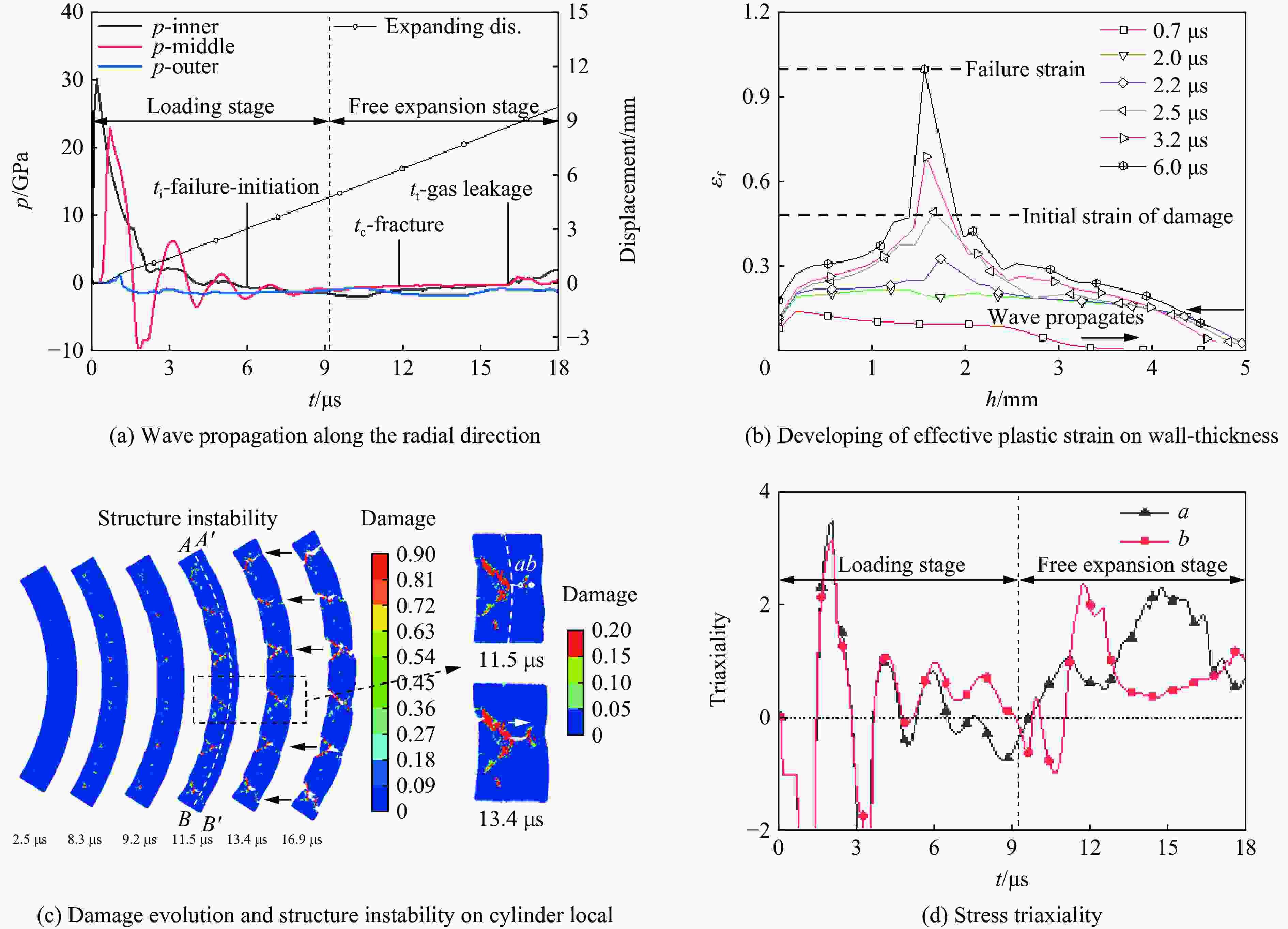
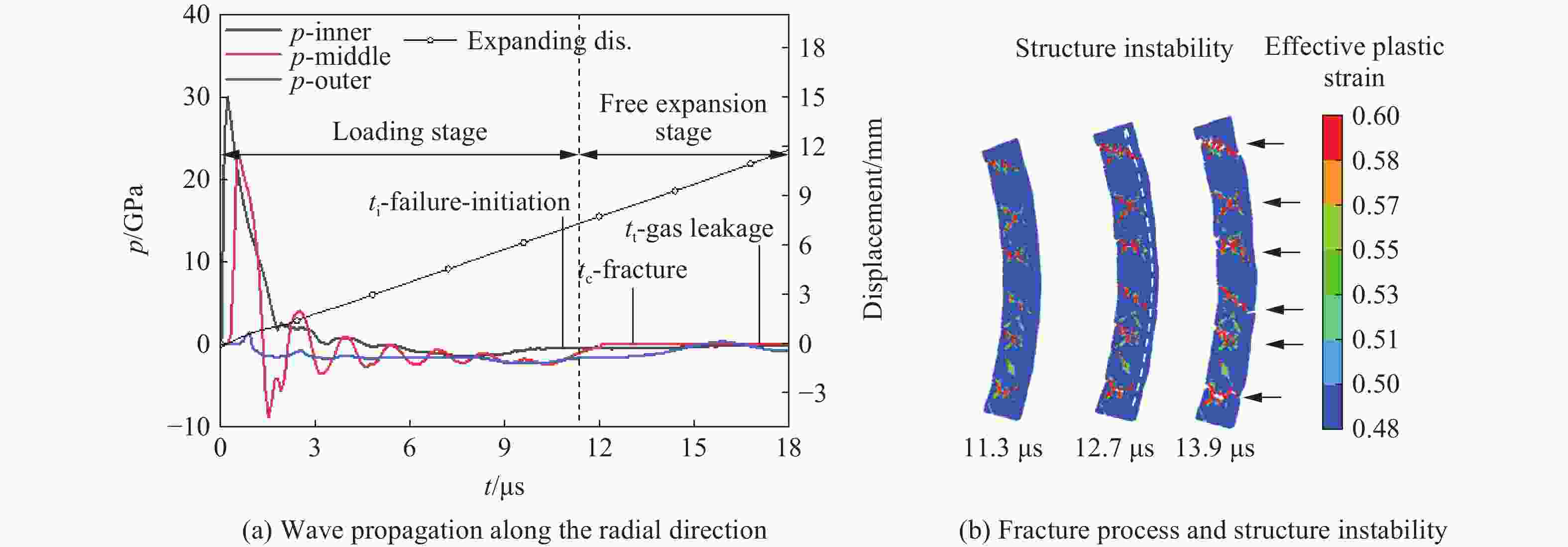
摘要: 金属柱壳爆炸膨胀断裂存在拉伸、剪切及拉剪混合等多种断裂模式，目前其物理机制及影响因素还不清晰。本文中采用光滑粒子流体动力学方法（smoothed particle hydrodynamics， SPH）对45钢柱壳在JOB-9003及RHT-901不同装药条件下的外爆实验进行了数值模拟，探讨柱壳在不同装药条件下发生的剪切断裂、拉剪混合断裂模式及其演化过程，模拟结果与实验结果一致。SPH数值模拟结果表明：在爆炸加载阶段，随着冲击波在柱壳内、外壁间来回反射形成二次塑性区，沿柱壳壁厚等效塑性应变演化呈凸形分布，壁厚中部区域等效塑性应变较内、外壁大；在较高爆炸压力（JOB-9003）作用下，柱壳断裂发生在爆轰波加载阶段，损伤裂纹从塑性应变积累较大的壁厚中部开始沿剪切方向向内、外壁扩展，形成剪切型断裂模式；而在RHT-901空心炸药加载下，虽然裂纹仍从壁厚中部开始沿剪切方向扩展，但随后柱壳进入自由膨胀阶段，未断区域处于拉伸应力状态，柱壳局部发生结构失稳，形成类似“颈缩”现象，裂纹从剪切方向转向沿颈缩区向外扩展，呈现拉剪混合断裂模式。拉伸裂纹占截面的比例与柱壳结构失稳时刻相关。可见，柱壳断裂演化是一个爆炸冲击波与柱壳结构相互作用的过程，不能简单将其作为一系列膨胀拉伸环处理。
-
关键词:
- 柱壳 /
- 爆炸膨胀加载 /
- 断裂模式 /
- 光滑粒子流体动力学方法 /
- 45钢
Abstract: The expanding fracture of ductile alloy cylinder subject to the explosion includes multiple fracture modes, such as tensile, shear, and mixed tensile-shear fracture. The mechanism and the factors influencing the fracture processes are still enigmatic and far from understood. In this paper, the smoothed particle hydrodynamics (SPH) method is used to simulate the explosion experiment of 45 steel cylinders shell with different charges of JOB-9003 and RHT-901. The shear fracture, tension-shear mixed fracture modes and the evolution process of cylindrical shell with different charges are discussed. The simulation results are consistent with the experimental trend. The SPH results show that due to the propagation and reflection of shock wave between the inner and outer surfaces of cylinder during the loading stage of detonation wave, the distribution of equivalent plastic strain on wall-thickness of the cylinder is a convex shape, i.e. the strain in the middle of wall-thickness is larger than that of in the inner and outer walls; when loading by a higher explosive pressure (JOB-9003), the fracture cracks initiate from the middle of wall-thickness, and then develop to the inner and outer walls along the direction of maximum shear in loading stage, showingthe shear fracture mode. However, under the loading caused by charge RHT-901 with relatively low pressure, although the crack still starts from the middle of wall-thickness and propagates along the shear direction, the shear crack could not grow through the section of the wall completely in the loading stage; then the cylinder experiences the stage of free expansion, the stress state of unbroken zone changes into triaxial tensile stress state and the structural instability, similar to “necking” occurs in the unbroken zone. Consequently, the cracks turn from the shear direction to the necking zone along the radial direction, showing the mixed tensile-shear fracture mode. The proportion of tension and shear cracks is related to the occurrence time of structural instability. The results show that the explosion expanding-fracture process of a metal cylinders involves the interaction between shock wave and cylinder structure, and cannot be treated as that of a series of expansion rings.-
Key words:
- cylinder /
- explosive-expanding /
- fracture modes /
- smoothed particle hydrodynamics /
- 45 steel
-
预防煤质变化情况下的炉膛爆燃是火力发电站锅炉安全运行的必要环节。电站锅炉的冷灰斗区域中有着复杂的粉尘环境，且附着在受热面上的焦块落入冷灰斗底部的水封后可能由气化反应生成一氧化碳(CO)、氢气(H2)等可燃性气体，进而导致局部爆燃[1]，进而影响机组的安全经济运行。
王育德等[2]、曲志明等[3]和毕明树等[4]通过对甲烷-煤粉混合爆燃实验研究，发现当煤粉加入量较少时，混合物爆压、爆速很低，处于爆燃状态，而当煤尘质量浓度升高至368 g/m3时，煤尘出现稳定爆轰；在一定粒径范围内，爆压和火焰传播速度随着煤尘粒度的减小而增大；在最优配比条件下，与单一甲烷空气或煤尘空气混合物相比，甲烷煤尘空气混合物的爆压和爆速明显增加。刘义等[5]和张引合等[6]分别研究了甲烷-煤尘混合系爆燃下限的变化规律，结果表明增大甲烷在整个混合系中配比或者煤尘中挥发分的含量，煤尘的爆燃下限明显会降低；而煤尘粒径对爆燃下限则影响较小。Y.F.Khalil[7]研究混合有活性炭的灰在氢气/空气的混合物中爆燃参数的影响，结果显示：所有灰与氢气浓度配比下的混合物所产生的爆燃压力和最大压力上升速率均大于单纯的氢气/空气混合物爆燃参数。D.Castellanos等[8]研究了不同粒度分散性对铝粉尘爆燃强度的影响，发现在一定范围内，粒度分散性越高，爆燃超压越高。
由以上可见，针对甲烷-煤粉这一杂混合物的爆燃特性已经有了较为细致的研究成果，然而针对冷灰斗区域环境中CO/H2气体和煤粉、焦炭粉、粉煤灰等粉尘杂混合物的爆燃特性尚缺乏细致的实验数据。因此本文中将对不同粉尘种类、粒径、质量浓度对CO/H2爆燃特性的影响进行实验研究。
1. 实验
1.1 实验装置
实验系统为立式爆燃试验台，包含配气系统、给粉系统、点火系统、爆燃管腔和测量系统5个部分，如图 1所示。为了与实际炉膛中的环境尽可能相似，本实验采用半开放的实验管腔，其上段尺寸为Ø42 mm×1 000 mm，壁厚3 mm，下段管腔尺寸为Ø60 mm×1 000 mm，壁厚为3.5 mm，两段无重合部分。管腔下半段均匀布置3个DYTRAN-1 300 V压电式压力传感器，从上到下编号依次为A、B、C，传感器采样频率为500 kHz，灵敏度为1.45 μV/Pa(±5%)。数据采集系统为DEWE-1201便携式数据采集系统，最高采样率为100 kHz。
1.2 实验准备
通过调节各气体组分的体积流量对管内混合气的当量比例进行控制，混合气总流量为1 L/s。为使混合气浓度均匀，在实验管道前安装一段混合格栅，实验前对混合格栅后的气体质量浓度进行标定以确保混合均匀。管道内送气1 min后开启微量螺旋给粉机送粉，并持续送粉至实验结束。通过观察，送粉1 min后，管内粉尘可以达到均匀分布。此时点火并记录实验数据。
实验中采用“弱点火”，在该点火条件下可以实现杂混合物中气相组分的直接爆燃，又不会产生爆轰或者固相组分的直接着火，这与本研究背景下的实际着火情况更为接近。
1.3 实验工况
考虑到锅炉炉膛环境中的实际情况，杂混合物中加入体积分数为10%的CO2作为稀释气体，CO/H2与空气中的O2按照化学当量比混合。
1.3.1 粉尘种类对爆燃特性的影响
为了研究粉尘种类对气体-粉尘杂混合物爆燃特性的影响规律，本实验选取3种煤粉、1种粉煤灰和1种焦炭粉作为实验样品。5种粉尘的工业分析如表 1所示，焦炭粉是利用银北煤为原料，在N2环境和1 300 ℃条件下通过沉降炉制备得到。
表 1 实验用煤粉的工业分析Table 1. Industrial analysis of the coal sample成分 质量分数/% 质量放热/(MJ·kg-1) 水分 灰分 挥发分 固定碳 全硫 蒙西(MX)煤样 16.77 10.38 38.92 45.56 1.16 16.70 宁东(ND)煤样 9.32 23.69 34.12 45.59 0.20 20.20 银北(YB)煤样 0.56 35.56 26.53 47.08 1.01 19.05 银北(YB)焦样 2.42 46.28 5.68 49.44 0.72 17.78 粉煤灰 0.07 95.51 1.04* 3.45 / / *：灰分含量为把粉尘样品中外部水分去除后的干燥基含量 1.3.2 粉尘粒径对爆燃特性的影响
对电站锅炉冷灰斗区域进行粉尘取样并对其进行粒径分析，实验中根据分析结果选取50~80、80~160和160~200 μm三种粒径范围作为实验工况。
1.3.3 粉尘质量浓度对爆燃特性的影响
冷灰斗区域的粉尘质量浓度在10~20 g/m3左右，故本实验中设定粉尘质量浓度范围为3~35 g/m3。
2. 结果与分析
杂混合物典型爆燃特性曲线如图 2所示，由图可见杂混合物在点火后会直接形成迅速上升的爆燃波，通过分析波峰可得到相应的爆燃超压，最大压力上升速度和爆燃波传播速度等。
2.1 粉尘种类对爆燃强度的影响
图 3所示为粉尘种类对杂混合物爆燃超压和最大压力上升速率的影响规律。图 3(a)中的5种粉尘颗粒粒径均为50~80 μm，挥发分含量从左到右依次降低。对于含粉煤灰的杂混合物，其爆燃超压与纯气体工况相似，可维持较高的爆燃强度水平，而挥发分含量较低的焦炭粉会使杂混合物的爆燃强度降低。对比3种煤粉，随着挥发分含量逐渐升高，混合物的爆燃超压也逐渐增强。此外不论何种粉尘，A、B、C三个测点(如图 1所示)的爆燃超压均先升高后降低，这表明爆燃压力在管腔内先聚集后释放的过程。
图 3 不同粉尘作用下杂混合物爆燃强度Figure 3. Deflagration severity on different dust-CO/H2 hybrid mixtures对后三种粉尘最大压力上升速率进行分析如图 3(b)所示，其变化规律与爆燃超压相似，粉煤灰作用下的气体爆燃最大压力上升速度最高，约为180 MPa/s，焦炭粉次之，而煤粉最低，约65 MPa/s。不同于爆燃超压，三个测点的最大压力上升速率依次升高。
不同粉尘种类对CO/H2杂混合物爆燃强度的影响主要由粉尘挥发分含量的不同所引起。当挥发分含量很低时，如粉煤灰，其在爆燃过程中几乎没有挥发分的析出，用于挥发分析出的热量也很少，从而可使杂混合物的爆燃强度维持在较高的水平；对于含有一定挥发分但含量又不高的粉尘，如本试验中的焦炭粉和银北粉煤，爆燃过程中挥发分的析出会吸收大量的热量，但是析出的挥发分重新参与反应又不足以弥补热量损失，从而导致杂混合物爆燃强度降低；随着挥发分含量继续升高，相比吸热作用，大量析出的挥发分重新参与反应开始占据优势地位，混合物的爆燃超压又逐渐升高。
2.2 粉尘粒径对爆燃强度的影响
图 4所示为不同煤粉粒径对混合物爆燃超压和最大压力上升速率的影响。由图 4可见，对于银北煤，在本试验研究的粒径范围内，混合物的爆燃超压和最大压力上升速率均随着粉尘粒径的减小而降低。银北煤挥发分含量适中，其组成的杂混合物在爆燃过程中挥发分析出吸热占优势地位。此时颗粒粒径越小，其比表面积越大，在极短的爆燃反应过程中，挥发分越容易快速的析出，吸收的热量也越多，从而对杂混合物爆燃强度的影响也越明显。
胡双启等[9]在研究超细煤粉在密闭管道内的爆燃特性时发现，随着粒径的减小，爆燃产生的压力及压力上升速率都将增大。这是因为一方面本研究所用的粉尘粒径相比超细粉尘要大得多，这时杂混合物在弱点火条件下的爆燃主要是由混合物中气相可燃物的点燃所引爆的，粉尘颗粒处于被点燃的状态，这与粉尘直接起爆的机理并不相同。另一方面，由于半开放的试验管腔，粉尘受热析出的部分挥发分并没有来得及参与爆燃反应就已经被冲击波压出管腔之外，导致了能量的损失。这是与炉膛内实际情况相似的，也是本试验爆燃超压较低的原因之一。
2.3 粉尘质量浓度对爆强度性的影响
各种类粉尘-CO/H2杂混合物的爆燃最大压力上升速率随粉尘质量浓度变化关系如图 5所示。对于粒径为50~80 μm的煤粉颗粒，随着管腔内粉尘质量浓度从4 g/m3升高到34.1 g/m3，混合物爆燃超压先降低后升高。当粉尘质量浓度为15 g/m3时，爆燃最大压力上升速率达到最小值，约3.2 MPa/s；而对于粒径范围为80~160 μm的煤粉颗粒，随着粉尘质量浓度的增加，混合物的爆燃超压同样呈先下降后上升的U型曲线趋势，在11.5 g/m3左右时达到最小值约4.1 MPa/s。图 5(c)为在粒径为50~80 μm的焦炭粉作用下爆燃超压随粉尘质量浓度的变化情况，可见随着粉尘质量浓度的增加，最大压力上升速率存在波动但并没有明显的变化趋势。
图 5 粉尘质量浓度对最大压力上升速率影响Figure 5. Influence of dust concentration on the maximum pressure increasing rate最大压力上升速率这种先下降后上升的变化规律是因为在粉尘质量浓度较低时，爆燃过程中析出挥发分所需的热量较少，气体燃烧释放的热量可使爆燃强度维持在较高的水平；而当粉尘质量浓度增大到一定程度后，尽管粉尘颗粒在析出挥发分的过程中吸收一定的热量，但挥发分本身参与爆燃反应又在一定程度上维持了总体混合物的爆燃强度。这两种作用相互竞争，使得压力峰值随粉尘质量浓度的增加呈U型曲线变化。50~80 μm煤粉作用曲线的极小值点相比80~160 μm煤粉作用曲线的极小值点出现在更高的粉尘质量浓度处，这说明在挥发分析出和挥发分自身参与爆燃的竞争关系中，挥发分析出的吸热作用占优势。而焦炭粉作用曲线不明显的变化规律是由于焦炭粉中挥发分含量很低，上诉两种竞争关系均很弱所致。
2.4 粉尘对气体爆燃下限的影响
图 6为在CO2体积分数为10%条件下，50~80 μm的粉尘种类对H2爆燃下限的影响规律。由图 6可见，相比纯气体条件，煤粉的加入使得混合气体的爆燃下限略有上升，灰分的加入对爆燃下限的影响几乎没有，而焦炭粉的加入使得混合物的爆燃下限有较为明显的降低。这说明，相比煤粉和粉煤灰，焦炭粉的加入使得混合物更容易进入爆燃区域。这是因为在火花塞点火起爆的过程中，随着煤粉的加入，挥发分析出的吸热降低了火花塞电极间的热量积累，从而升高了爆燃下限。而焦炭粉多孔的结构可以促进电极间的热量累积，从而在一定程度上降低爆燃下限。粉煤灰挥发分很低且不存在多孔的形态结构，因而对爆燃下限的影响很小。
图 7所示为煤粉粒径对爆燃下限的影响规律。由图可见，相比单纯的可燃性气体，不同粒径煤粉作用下的杂混合物的爆燃下限均略有升高。对比三种粒径，160~200 μm的银北煤粉对混合物爆燃下限的影响最小，这是因为在这种较大的煤粉粒径下，粉尘几乎来不及参与反应。粒径较小的50~80 μm银北煤样，在点火过程中，拥有很低点火能的挥发分的快速析出，这些挥发分明显的降低了混合物的最低点火能，增加了其爆燃的可能性，因而虽然有不少热量被吸收，但混合物的爆燃下限几乎保持不变。而80~160 μm的煤粉粒径介于上述两者之间，少量挥发分的析出吸收了热量但又不足以降低混合物的最低点火能，因而其爆燃下限最高。
图 7 煤粉粒径对爆燃下限的影响Figure 7. Influence of coal particle size on lower deflagration limit3. 结论
在半开放弱点火条件下，粉尘颗粒对气体爆燃特性的影响如下：
(1) 粉尘对杂混合物爆燃特性的影响主要是由于粉尘中挥发分析出吸热和重新参与爆燃反应两种作用相互竞争的结果。对高挥发分煤粉，挥发分析出参与反应占主导，增大爆燃强度；而对低挥发分煤粉，颗粒的吸热作用占主导，降低爆燃强度；
(2) 对于银北煤，随着粒径减小到50 μm，混合物的爆燃强度逐渐减弱，随着粉尘浓度从3 g/m3增加到35 g/m3，混合物的爆燃强度先降低后升高；而大于160 μm的煤粉颗粒对混合物的爆燃强度几乎没有影响；对于无挥发分的焦炭粉、飞灰颗粒，其爆燃强度随粉尘浓度的变化不明显；
(3) 在相同粒径条件下，对于易挥发分细煤粉，混合物的爆燃强度会随着挥发分含量的升高而升高，但低挥发分含量的焦炭颗粒会降低其爆燃强度；
(4) 在相同粒径条件下，细煤粉使混合物爆燃下限略有升高，焦炭粉可降低爆燃下限，而粉煤灰爆燃下限其影响不大，这分别是由于煤粉挥发分析出吸热和焦炭多孔结构减小了电极间散热所导致。
-
图 2 JOB9003炸药加载下柱壳膨胀断裂过程
Figure 2. Expanding fracture process of the explosively-driven cylindrical shell by JOB9003 charge
图 3 柱壳外表面径向膨胀速度
Figure 3. The radial expanding velocity of the outer surface of cylindrical shell
图 4 RHT-901空心炸药作用下不同R/h的柱壳膨胀断裂过程模拟结果
Figure 4. Simulation results on fracture process of the cylindrical shell with different R/h under RHT-901 charge
图 5 JOB-9003炸药加载下45钢柱壳的爆炸压力、膨胀及断裂演化过程
Figure 5. The explosive pressure, expanding deformation and fracture for 45# steel cylindrical shellwith JOB-9003 charge
图 6 RHT-901加载下5 mm壁厚柱壳的爆炸压力、膨胀及断裂过程
Figure 6. Explosive pressure, expanding deformation and fracture for 45 steel cylindrical shell (h = 5 mm) with RHT-901 charge
图 7 RHT-901加载下4 mm壁厚柱壳的爆炸压力及断裂演化过程
Figure 7. Explosive pressure, fracture process for 45 steel cylindrical shell (h= 4mm) with RHT-901
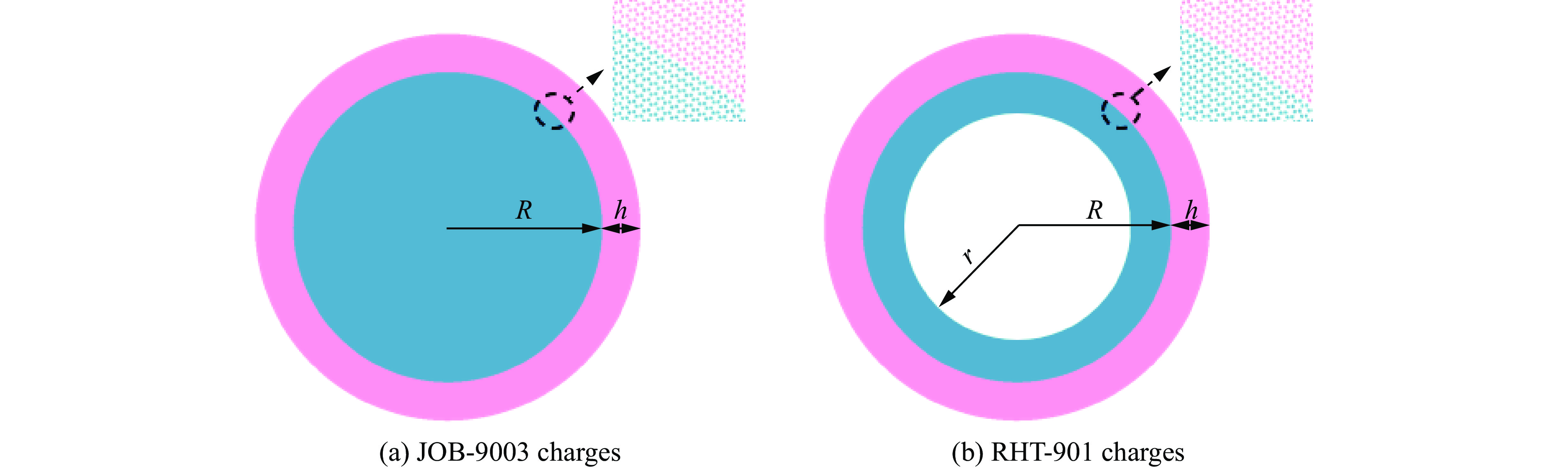
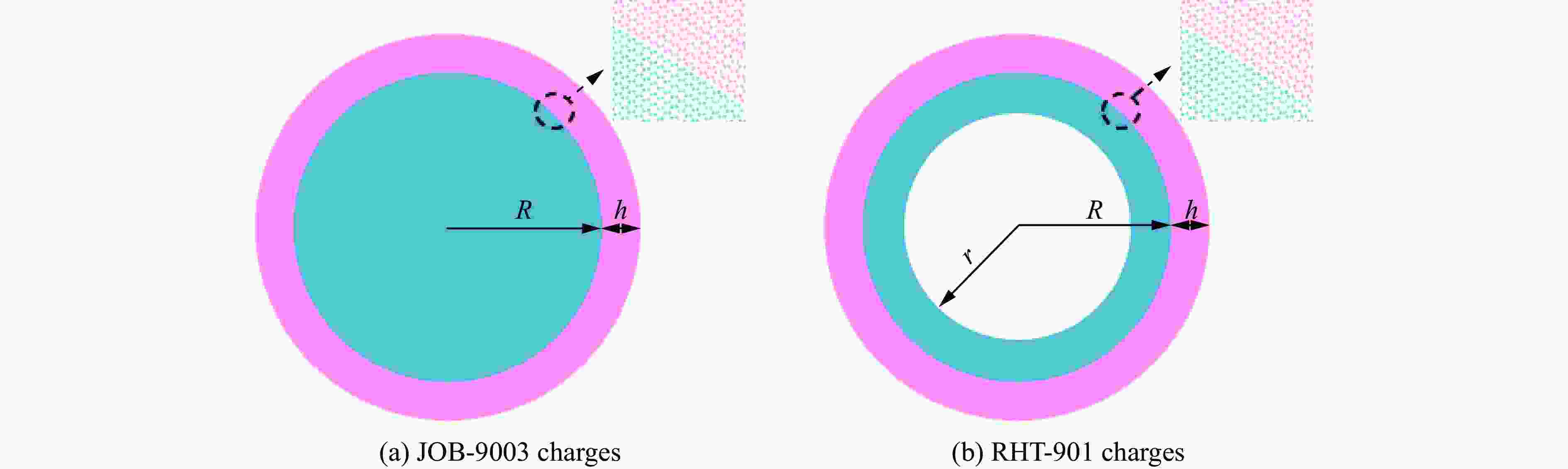
表 1 实验柱壳、加载条件及爆炸膨胀断裂实验结果[8]
Table 1. 1The fracturecharacteristics and failure modes of 45 steel cylindersunder different explosive conditions and geological parameters[8]
炸药 药柱尺寸 试样尺寸 爆炸膨胀断裂实验结果 外径R/mm 内径r/mm 内径R/mm 壁厚h/mm εc tc/µs εf tf/µs ˙ε/s−1 断裂模式 JOB-9003（实心） 20 0 20 4 0.40 7.5 1.31 19.5 7.1×104 纯剪切 RHT-901(空心) 30 20 30 4 0.24 8.8 0.43 15.4 2.9×104 拉剪混合 5 0.18 7.8 0.37 15.8 2.5×104 拉剪混合 
下载: 导出CSV
Johnson-Cook模型 Gr¨uneison状态方程 A/MPa B/MPa n m C ˙ε0/s−1 c/(m·s−1) s γ0 350 600 0.307 0.804 0.07 2×10-4 4600 1.49 2.17
下载: 导出CSV
炸药 A/GPa B/GPa ω R1 R2 E0/（GJ·m−3） pcj/GPa ρ/（kg·m−3） D/（m·s−1） JOB-9003 842.0 21.81 0.28 4.6 1.35 1.0 35 1884 8740 RHT-901 503.0 9.065 0.35 4.3 1.10 7.6 27 1658 7800
下载: 导出CSV
表 4 SPH数值模拟与实验结果比较
Table 4. Comparison betwwen SPH simulation and experimental results
炸药 内径R/mm 壁厚h/mm 方法 εc tc/µs εr tr/µs εf tf/µs ˙ε/s−1 断裂模式 JOB-9003 20 4 实验 0.40 7.5 1.31 19.5 7.1×104 双向剪切 模拟 0.37 7.3 0.37 7.3 1.07 17.2 7.1×104 双向剪切 RHT-901 30 4 实验 0.24 8.8 0.43 15.4 2.9×104 拉剪混合 模拟 0.30 13.1 0.31 13.5 0.41 17.3 2.7×104 拉剪混合 5 实验 0.18 7.8 0.37 15.8 2.5×104 拉剪混合 模拟 0.21 11.9 0.23 12.8 0.30 16.1 2.1×104 拉剪混合
下载: 导出CSV
-
[1] TAYLOR G I. The fragmentation of tubular bombs [M]. Cambridge: Cambridge University Press, 1963. [2] MEYERS M A. Dynamic behavior of materials [M]. New York: Wiley, 1994. [3] TAYLOR G I. Analysis of the explosion of a long cylindrical bomb detonated at one end [J]. Mechanics of Fluids, Scientific Papers of GI Taylor, 1941, 2: 277–286. [4] HOGGATT C R, RECHT R F. Fracture behavior of tubular bombs [J]. Journal of Applied Physics, 1968, 39(3): 1856–1862. DOI: 10.1063/1.1656442. [5] SINGH M, SUNEJA H R, BOLA M S, et al. Dynamic tensile deformation and fracture of metal cylinders at high strain rates [J]. International Journal of Impact Engineering, 2002, 27(9): 939–954. DOI: 10.1016/S0734-743X(02)00002-7. [6] 胡海波, 汤铁钢, 胡八一, 等. 金属柱壳在爆炸加载断裂中的单旋现象 [J]. 爆炸与冲击, 2004, 24(2): 97–107.HU H B, TANG T G, HU B Y, et al. An study of uniform shear bands orientation selection tendency on explosively loaded cylindrical shells [J]. Explosion and Shock Waves, 2004, 24(2): 97–107. [7] 汤铁钢, 谷岩, 李庆忠, 等. 爆轰加载下金属柱壳膨胀破裂过程研究 [J]. 爆炸与冲击, 2003, 23(6): 529–533.TANG T G, GU Y, LI Q Z, et al. Expanding fracture of steel cylinder shell by detonation driving [J]. Explosion and Shock Waves, 2003, 23(6): 529–533. [8] 汤铁钢, 李庆忠, 孙学林, 等. 45钢柱壳膨胀断裂的应变率效应 [J]. 爆炸与冲击, 2006, 26(2): 129–133. DOI: 10.11883/1001-1455(2006)02-0129-05.TANG T G, LI Q Z, SUN X L, et al. Strain-rate effects of expanding fracture of 45 steel cylinder shells driven by detonation [J]. Explosion and Shock Waves, 2006, 26(2): 129–133. DOI: 10.11883/1001-1455(2006)02-0129-05. [9] 胡八一, 董庆东, 韩长生, 等. 爆炸金属管的绝热剪切断裂宏观研究 [J]. 爆炸与冲击, 1992, 12(4): 319–325.HU B Y, DONG Q D, HAN C S, et al. The macroscopic study of adiabatic shear fracture of metal tubes under explosive loading [J]. Explosion and Shock Waves, 1992, 12(4): 319–325. [10] 胡八一, 董庆东, 韩长生, 等. 内部爆轰加载下的钢管膨胀断裂研究 [J]. 爆炸与冲击, 1993, 13(1): 49–54.HU B Y, DONG Q D, HAN C S, et al. Studies of expansion and fracture of explosive-filled steel cylinders [J]. Explosion and Shock Waves, 1993, 13(1): 49–54. [11] ZHANG Z B, HUANG F L, CAO Y, et al. A fragments mass distribution scaling relations for fragmenting shells with variable thickness subjected to internal explosive loading [J]. International Journal of Impact Engineering, 2018, 120: 79–94. DOI: 10.1016/j.ijimpeng.2018.05.013. [12] 罗渝松, 李伟兵, 陈志闯, 等. 内爆加载下金属柱壳的冻结回收方法 [J]. 爆炸与冲击, 2020, 40(10): 104101. DOI: 10.11883/bzycj-2020-0041.LUO Y S, LI W B, CHEN Z C, et al. A freezing recovery method for metallic cylinder shells under internal explosive loading [J]. Explosion and Shock Waves, 2020, 40(10): 104101. DOI: 10.11883/bzycj-2020-0041. [13] GOTO D M, BECKER R, ORZECHOWSKI T J, et al. Investigation of the fracture and fragmentation of explosively driven rings and cylinders [J]. International Journal of Impact Engineering, 2008, 35(12): 1547–1556. DOI: 10.1016/j.ijimpeng.2008.07.081. [14] 潘顺吉, 俞鑫炉, 董新龙. 不同载荷下TA2钛合金柱壳爆炸碎裂的实验研究 [J]. 高压物理学报, 2017, 31(4): 382–388. DOI: 10.11858/gywlxb.2017.04.005.PAN S J, YU X L, DONG X L. Experimental study of fragmentation behavior of exploded TA2 alloy cylinderswith varied charge [J]. Chinese Journal of High Pressure Physics, 2017, 31(4): 382–388. DOI: 10.11858/gywlxb.2017.04.005. [15] 张世文, 金山, 刘仓理. 含缺陷厚壁圆管爆轰膨胀断裂的数值模拟 [J]. 应用力学学报, 2010, 27(3): 622–625.ZHANG S W, JIN S, LIU C L. Simulation of the dynamic expanding process of thick-walled cylinder with defects [J]. Chinese Journal of Applied Mechanics, 2010, 27(3): 622–625. [16] 金山, 张世文, 龙建华. 缺陷对圆管膨胀断裂影响的实验研究 [J]. 高压物理学报, 2011, 25(2): 188–192. DOI: 10.11858/gywlxb.2011.02.017.JIN S, ZHANG S W, LONG J H. Experimental study on the influences of defects on expanding fracture of a metal cylinder [J]. Chinese Journal of High Pressure Physics, 2011, 25(2): 188–192. DOI: 10.11858/gywlxb.2011.02.017. [17] 俞鑫炉, 董新龙, 潘顺吉. 不同爆炸载荷下TA2钛合金圆管膨胀破坏过程 [J]. 爆炸与冲击, 2018, 38(1): 148–154. DOI: 10.11883/bzycj-2017-0014.YU X L, DONG X L, PAN S J. Fracture behaviors of explosively driven TA2 alloy cylinders under different loadings [J]. Explosion and Shock Waves, 2018, 38(1): 148–154. DOI: 10.11883/bzycj-2017-0014. [18] LIU M T, REN G W, FAN C, et al. Experimental and numerical studies on the expanding fracture behavior ofan explosively driven 1045 steel cylinder [J]. International Journal of Impact Engineering, 2017, 109: 240–252. DOI: 10.1016/j.ijimpeng.2017.07.008. [19] LIU G R, LIU M B, LI S. Smoothed particle hydrodynamics -a meshfree method [M]. NM (United States): World Scientific, 2004. [20] REMINGTON T P, OWEN J M, NAKAMURA A M, et al. Numerical simulations of laboratory-scale, hypervelocity-impact experiments for asteroid-deflection code validation [J]. Earth and Space Science, 2020, 7(4): e2018EA000474. DOI: 10.1029/2018EA000474. [21] JANKOWIAK T, ŁODYGOWSKI T. Smoothed particle hydrodynamics versus finite element method for blast impact [J]. Bulletin of the Polish Academy of Sciences Technical Sciences, 2013, 61(1): 111–121. DOI: 10.2478/bpasts-2013-0009. [22] KONG X S, WU W G, LI J, et al. A numerical investigation on explosive fragmentation of metal casing using smoothed particle hydrodynamic method [J]. Materials & Design, 2013, 51: 729–741. DOI: 10.1016/j.matdes.2013.04.041. [23] 任国武, 郭昭亮, 张世文, 等. 金属柱壳膨胀断裂的实验与数值模拟 [J]. 爆炸与冲击, 2015, 35(6): 895–900. DOI: 10.11883/1001-1455(2015)06-0895-06.REN G W, GUO Z L, ZHANG S W, et al. Experiment and numerical simulation on expansion deformation and fracture of cylindrical shell [J]. Explosion and Shock Waves, 2015, 35(6): 895–900. DOI: 10.11883/1001-1455(2015)06-0895-06. [24] 王礼立. 应力波基础 [M]. 2版. 北京: 国防工业出版社, 2005. [25] 胡昌明, 贺红亮, 胡时胜. 45号钢的动态力学性能研究 [J]. 爆炸与冲击, 2003, 23(2): 188–192.HU C M, HE H L, HU S S. A study on dynamic mechancial behaviors of 45 steel [J]. Explosion and Shock Waves, 2003, 23(2): 188–192. [26] 孙承纬, 卫玉章, 周之奎. 应用爆轰物理 [M]. 北京: 国防工业出版社, 2000. [27] 郑柯, 董新龙. 20钢柱壳外爆拉-剪切型断裂研究 [J]. 兵器材料科学与工程, 2018, 41(3): 61–64. DOI: 10.14024/j.cnki.1004-244x.20180428.005.ZHENG K, DONG X L. Tensile-shear failure of 20 steel cylindrical shells subjected to explosive loading [J]. Ordnance Material Science and Engineering, 2018, 41(3): 61–64. DOI: 10.14024/j.cnki.1004-244x.20180428.005. -
下载:
计量
- 文章访问数: 572
- HTML全文浏览量: 541
- PDF下载量: 233
- 被引次数: 0